本文用于计算的船舶由于其方形系数较小,一般采用将船体等效为船体梁的方法进行估算。但对于实船而言,其质量沿船长方向非均匀分布,剖面系数也不断变化,因此很难对其进行精确的理论求解。在现有计算方法中,普遍采用能量法、转移矩阵解析式法及有限元法等。
现有文献大多介绍了计算固有频率的各种方法,并没有对固有频率的影响因素做系统总结。本文以经验公式[1-3]对比有限元法[4-5]研究固有频率的计算精度,建立全船有限元模型,考虑附连水质量和大型设备重量,在评估工况下计算全船整体低频结构的模态,重点分析调整重心对固有频率的影响规律。
1 理论与数值计算 1.1 经验公式估算船体总振动的固有频率是用来处理船舶振动问题的重要参数之一。通过主机、螺旋桨等频率与固有频率进行比较,可以对共振现象进行有效的预防。固有频率的计算一般采用经验公式法、有限元法等。经验公式法是通过100多艘不同类型的船舶资料归纳总结出的,适用于船长不高于230 m的各类船舶,误差一般小于7%[6]。根据船级社关于振动的计算要求,应用经验公式法对全船固有频率进行的估算。
基于均匀等直梁的固有频率公式可得:
| $ {N_{V2}} = C\sqrt {{I_V}/{\Delta _V}{L^3}} \times 0.0167。$ | (1) |
式中:
求得垂向1阶固有频率为:
| $\begin{aligned}[b] {N_{V2}} =& 3409920 \sqrt {9.7825/6422\times{{112.7}^3}} \times 0.0167 = \\ & 1.8577\;{\rm{Hz}}。\end{aligned}$ | (2) |
推算公式
| $ {N_{V3}} = {(3 - 1)^{1.02}}{N_{V2}} = 3.7673\; {\rm{Hz}}。$ | (3) |
当中剖面惯性矩已知时,船体梁水平弯曲振动的第一阶固有频率为:
| $ {f_{ih}} = {a_{ih}}{K_{ih}}{E_{ih}}\sqrt {{I_{oh}}/{\Delta _h}{L^3}} + {b_{ih}}(i=2),$ | (4) |
| $\begin{split} {f_{2h}} = &0.473 \times {10^5} \times 0.943 \times 1 \times \sqrt {31.8111/6422 \times {{112.7}^3}} +\\ & 0.362 = 2.9859\;{\rm{Hz}},\\[-10pt] \end{split}$ | (5) |
| $ {f}_{3h}=(3-1{)}^{1.02}\times 2.9859=6.0552 \;{\rm{Hz}}。$ | (6) |
船舶在水上航行时,其周围的水也处于运动状态,因此船体也会受其影响产生较大振动,本文重点研究其惯性带来的影响。船舶航行时,惯性会促使一部分舷外水与船体共同运动,将这部分舷外水称为附连水[7-8]。
当半径为b的无限长圆柱体,在静止的无限液体中,以速度v运动时,其动能为:
| $ T = \frac{1}{2}\rho \text{π} {b^2}{v^2}。$ | (7) |
式中,
令
| $ T = \frac{1}{2}M{v^2} 。$ | (8) |
对于其他形状的剖面需将式(8)乘以剖面系数
| $ M = \text{π} c\rho {b^2} 。$ | (9) |
基于上述公式,并考虑水域对附加质量带来的影响因素,最终总结出船体垂向振动时的附连水质量公式为:
| $ {M_\alpha }V = \frac{1}{2}\text{π} {\alpha _V}{C_V}{K_i}\rho {B^2} 。$ | (10) |
式中:

|
图 1 前3阶附连水质量 Fig. 1 The first three attached water masses |
声固耦合法的核心思路是把流体用一种声学介质描述,通常采用总波公式及散射波公式,本文采用散射波公式。由于流体是线性的,可以忽略静压影响。在Abaqus中进行模态分析时,流体是声学介质,采用压力作为流体声学单元的自由度可以在精度不变的前提下使计算时间大大缩短。
2 有限元计算分析 2.1 有限元算例验证为验证本文计算的准确性,新建一段长为8 m、半径为0.5 m的圆柱,通过调整上下两段密度改变重心高度,得到与固有频率随重心变化的大致趋势,并与本模型计算趋势进行对比。圆柱模型如图2所示,以重心高度为x轴,固有频率为y轴,通过增加和减少下半段的密度值,来改变重心高度,得到频率随重心高度的变化趋势为随着重心高度增大而减小。

|
图 2 圆柱算例有限元模型 Fig. 2 Finite element model of cylindrical example |
实心圆柱前2阶固有频率随重心高度的变化曲线如图3所示。

|
图 3 实心圆柱前2阶固有频率随重心高度的变化曲线 Fig. 3 The natural frequencies of the first two orders of the solid cylinder vary with the height of the center of gravity |
通过Ansys软件建立有限元模型,全局采用笛卡尔坐标系,取0号肋位为原点,船首方向为正。本船总长128.6 m,宽16m。如图4所示,频率采用无量纲进行表示,其无量纲表达式为

|
图 4 船舶有限元模型 Fig. 4 Finite element model of ship |
表1为通过有限元法中的附加质量法与声固耦合法以及经验公式法计算得出的全船固有频率。可知,理论方法与有限元方法的计算结果非常吻合,而误差可能是由于简化模型和网格不够精密引起的,3种方案的计算结果对比误差均小于4%,可以认为选取的计算方法较为精确。全船的水平和垂向前2阶振型图如图5和图6所示。
|
|
表 1 不同计算方法计算全船固有频率结果对比 Tab.1 Comparison of results of natural frequency of whole ship calculated by different calculation methods |

|
图 5 垂向振型图 Fig. 5 Vertical mode diagram |

|
图 6 水平振型图 Fig. 6 Horizontal mode diagram |
可知,以上3种方法均能测出较为准确的计算固有频率,经验公式法较为粗糙,但计算简单方便,附加质量法较为精确且易于修改,声固耦合的结果较经验公式相对精确,较附连水耦合法更为简单,但无法精确验证重心高度对固有频率的实际影响。
在对全船进行建模时,其重量一般均匀分布于各层甲板上,讨论重心对无量纲固有频率的影响时,通过调整各层甲板的整体重量来调节全船重心,共设计7组重心位置(船体总重量不变),以全部甲板均匀分摊重量为标准工况,通过减去各层甲板上的附加重量来调节重心,各工况调整后固有频率计算结果如表2所示。全船垂向和水平振动固有频率值随重心位置的变化曲线如图7和图8所示。
|
|
表 2 全船不同重心位置的固有频率值 Tab.2 Natural frequency values of different barycenter positions of the whole ship |
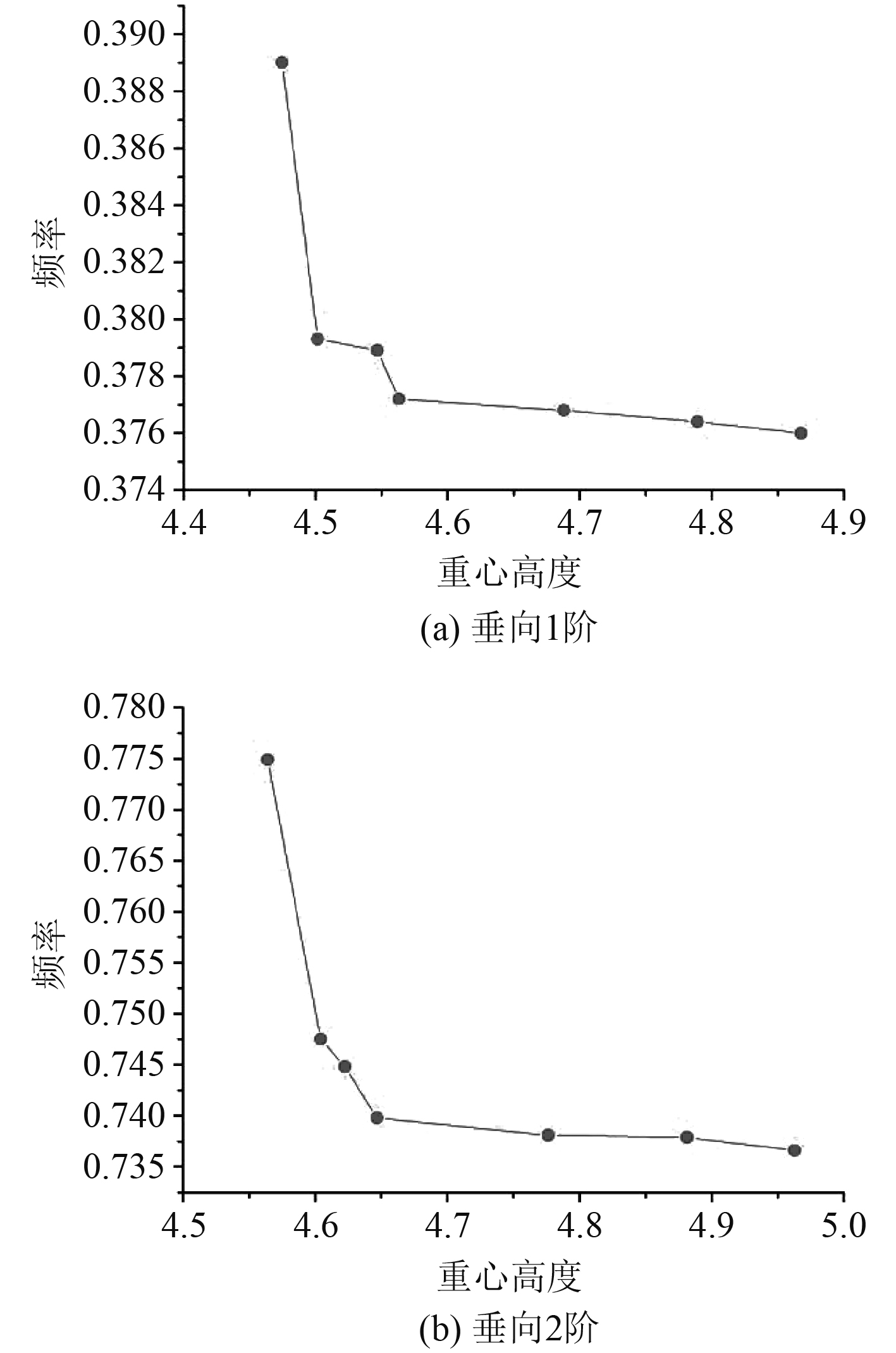
|
图 7 全船垂向固有频率值随重心位置变化曲线 Fig. 7 Vertical natural frequency of the whole ship with the position of the center of gravity |
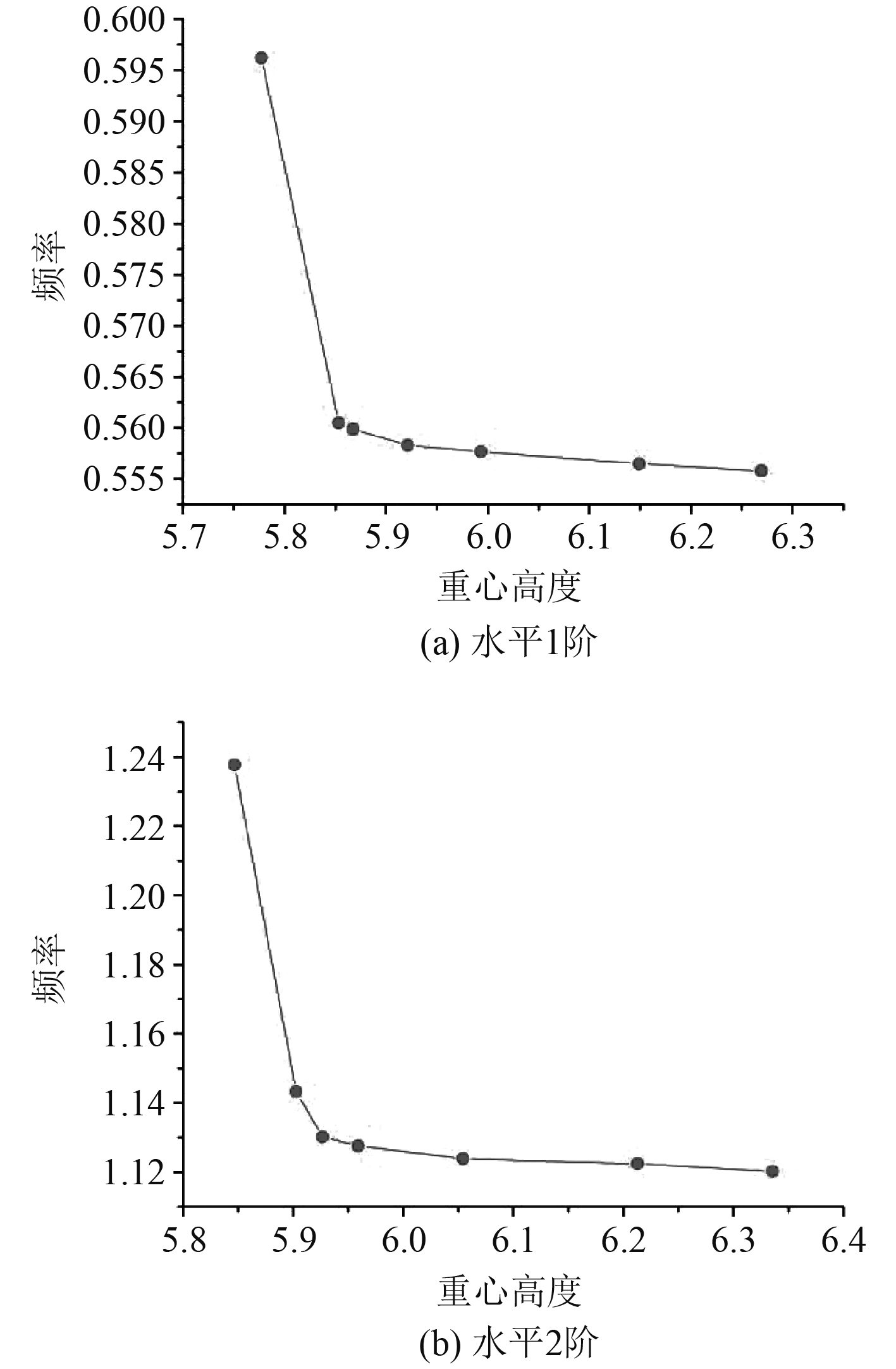
|
图 8 全船水平固有频率值随重心位置变化曲线 Fig. 8 The horizontal natural frequency of the whole ship varies with the position of the center of gravity |
可知,垂向1阶的无量纲固有频率在重心高度处于4.55~4.6 m之间变化幅度较大,4.6 m之后则趋于平缓;垂向2阶情况下,重心高度在4.55~4.65 m之间变化幅度较大,4.65 m之后趋于平缓,水平1阶在重心高度处于5.75~5.9 m之间变化较大,水平2阶在重心高度5.85~5.95 m之间变化较大,之后的变化较小可忽略不计。分析可得,固有频率会随着重心高度的增大而减小,变化趋势较上文圆柱案例基本一致,且随着重心高度的不断增大,固有频率减小的幅度则会相应减小,大致处于同一数量级。
4 结 语基于经验公式法、附加质量有限元法和声固耦合有限元法对全船振动固有频率进行研究,得出如下结论:
1)本文所采用的3种方法均能较为准确计算全船的固有频率,经验公式法较为简便但计算结果仅限前几阶模态且精度不高,一般用于估算结果进行对比验证;附加质量法较为精确,并易于修改,但计算附连水较为繁琐;声固耦合的结果较经验公式相对精确,较附连水的方法更为简单,但受计算水域的大小和水域网格大小较为敏感,需要一定的理论知识和经验才能得到精确的振动频率值。
2)计算全船固有频率时,提高重心高度会降低固有频率的大小,反之减小重心高度则会增大固有频率的大小,且随着重心高度的不断增大,变化趋势会趋于平缓,相对而言,固有频率对较小的重心高度变化更为敏感。
| [1] |
中国船级社. 船上振动控制指南[S]. 北京: 人民交通出版社, 2000: 174–189, 225–227
|
| [2] |
王鹏, 李天匀, 朱翔, 等. 浅水域中圆柱壳固有振动特性分析[J]. 中国造船, 2016, 57(3): 72-82. DOI:10.3969/j.issn.1000-4882.2016.03.009 |
| [3] |
姚熊亮. 船体振动[M]. 哈尔滨: 哈尔滨工程大学出版社, 2004.
|
| [4] |
姚熊亮, 张阿漫, 许维军. 声固耦合方法在舰船水下爆炸中的应用[J]. 哈尔滨工程大学学报, 2005, 26(6): 707-712. DOI:10.3969/j.issn.1006-7043.2005.06.003 |
| [5] |
史丰荣. 船体结构总体振动特性预测技术研究[J]. 中国造船, 2013, 54(2): 118-123. DOI:10.3969/j.issn.1000-4882.2013.02.015 |
| [6] |
金咸定, 夏利娟. 船体振动学[M]. 上海: 上海交通大学出版社, 2010
|
| [7] |
LEWIS F M. Vibration and engine balance in diesel ship[J]. S. N. A. M. E. , 1927.
|
| [8] |
LEWIS F M. The intertia of the water surrouding a vibration ship[J]. S. N. A. M. E. , 1929.
|
| [9] |
何欢. 船舶总体振动的附加水质量算法研究[D]. 大连: 大连理工大学, 2014.
|
| [10] |
刘强. 小水线面双体船附连水质量及振动特性研究[D]. 大连: 大连理工大学, 2015.
|
| [11] |
YE R, ZHAO N, YANG D, et al. Bending and free vibration analysis of sandwich plates with functionally graded soft core, using the new refined higher-order analysis model[J]. Journal of Sandwich Structures and Materials, 2020, 23(2): 680−710.
|
 2023, Vol. 45
2023, Vol. 45

