船舶在冰区航行期间,由于受到复杂的冰区条件影响,船冰之间作用会变得复杂。冰区的海冰类型,冰层的厚度,以及碎冰区域的密集度,都会影响到冰阻力的大小。船冰相互作用已经有很多系统研究,包括船首处碎冰堆积以及碎冰的重叠等问题的研究[1]。研究船舶和海冰在局部相互作用力的关键是能够有效地数值模拟这个航行过程[2]。
船冰之间的相互作用相当复杂,国内外研究方法包括实体的船舶试验、等比例船舶模型试验、经验公式以及数值模拟仿真[3-4]。数值仿真因成本低,得到结果快,数据方便采集等优点成为重要的研究手段。
船体在冰区航行的整个过程在数值模拟时,完整的冰层连续体会被破坏为许多单个的离散碎冰,并且在数值计算区域,尤其在碎冰区域,不同大小的碎冰相互堆积重叠,离散的特点十分突出,所以可以采用离散元的计算方法[5-6]。本文将使用离散元的方法模拟计算船舶在冰区航行的整个过程以及冰阻力,为船冰相互作用提供一种新的方法。
1 离散元海冰模型及计算域的建立 1.1 碎冰的离散元模型建立Strack和Cundall[7]构建了早期的离散元模型。由于高负载流体颗粒相互作用不容忽视,所以考虑到颗粒与颗粒之间运动的同时,拉格朗日公式被运用到颗粒运动方程中去。圆柱型离散元模型为论文计算使用,选择离散元模型以及拉格朗日多相作为物理模型。碎冰的主要形状选择为理想化的圆盘形,如图1所示。

|
图 1 离散元海冰模型 Fig. 1 DEM ice model |
海冰参数是参照G.W. Timco以及SANG-GAB LEE[8]的研究材料,如表1所示。
|
|
表 1 海冰材料属性 Tab.1 Ice material parameters |
本文研究对象为16万吨级油船。船首模型如图2所示。

|
图 2 船首模型 Fig. 2 Bow model |
船首数值模型设置为刚体的属性。同样需要设置船首的材料参数,如表2所示。
|
|
表 2 船体材料属性 Tab.2 Ship material parameters of |
大小为300 m×150 m×250 m计算域的物理特性利用欧拉多项流中的流体域体积(VOF)定义,水线面处于垂向方向Z=8 m处,Z>8 m为空气计算域,Z<8 m为水计算域;波浪状态选用欧拉多项流中的流体域体积波中的静水。
为减少计算时间,计算区域的网格在远离计算区域的位置大小为2 m×2 m×2 m,接近就算区域的位置进行网格细分,以得到更加精确的结果,大小为1 m×1 m×1 m,在2种大小的网格过渡区选用柱棱柱层网格过渡;在主要的船首位置到平行中体段对网格进行细化,尺寸为0.5 m×0.5 m。为了节省计算时间和计算资源,对没有参与计算部分船体进行适当的网格放大,从1 m×1 m的尺寸逐渐放大到24 m×24 m的网格。没有参与的计算水域以及计算空气域也进行适当的网格放大,但为了计算的精确性,对水线(Z=8)上下1 m附近的计算域进行网格细化尺寸为1 m×1 m×0.5 m。最终的模型网格如图3所示。
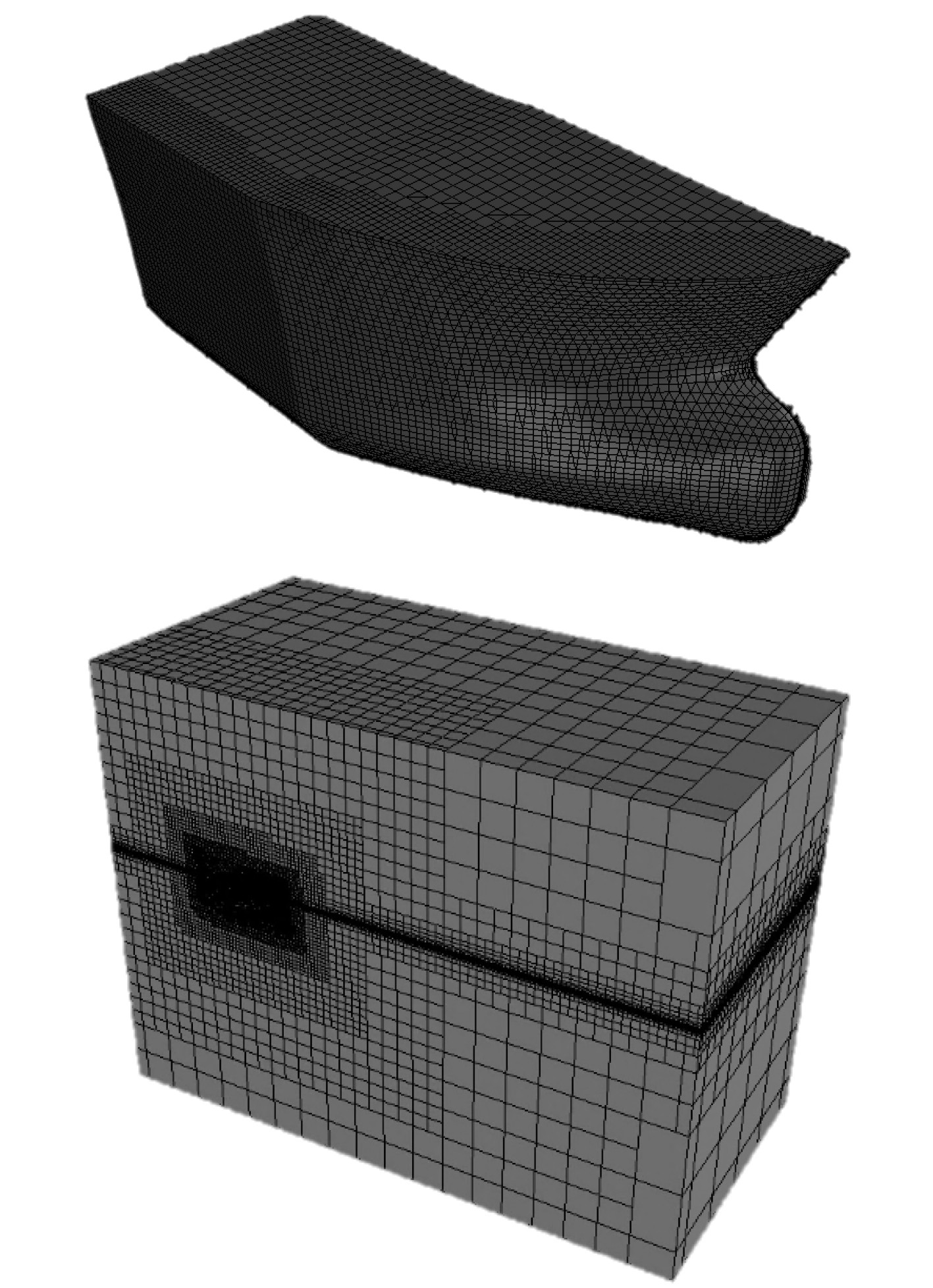
|
图 3 网格划分示意图(半宽) Fig. 3 Schematic diagram of meshing(half wide) |
为保证能在船冰的相互作用中测得更加具有参考价值的冰载荷,计算区域需要离散元模型设置多相互作用。设置的参数如表3所示。
|
|
表 3 计算主要参数 Tab.3 The main parameters of the calculation |
创建可以用于发射离散元碎冰模型喷射器,以设定的性质和状态将离散元碎冰模型发射到计算域中。船宽方向(Y方向)200 m范围均匀发射到计算区域,使其保持向前的运动状态。为了得到不同密集度的碎冰区域,调节喷射器点位的分布和数量,如图4所示。

|
图 4 离散元喷射器 Fig. 4 Discrete element method injector |
设置海冰单元直径为5 m,通过喷射器以固定的X方向速度(5 m/s)喷射到计算域中,冰单元的厚度为1 m。为了模拟整个航行的过程,碎冰单元被喷射器沿X方向以匀速从右到左喷射,保持船体静止,使其产生相对运动,时间步长设置为0.01 s,最终得到0~30 s的整个航行模拟过程。得到的结果显示,在船艏处碎冰有堆积现象,整个航行的过程中,船体和冰,冰和冰相互不停的接触碰撞。离散元模拟的整个航行过程如图5所示。
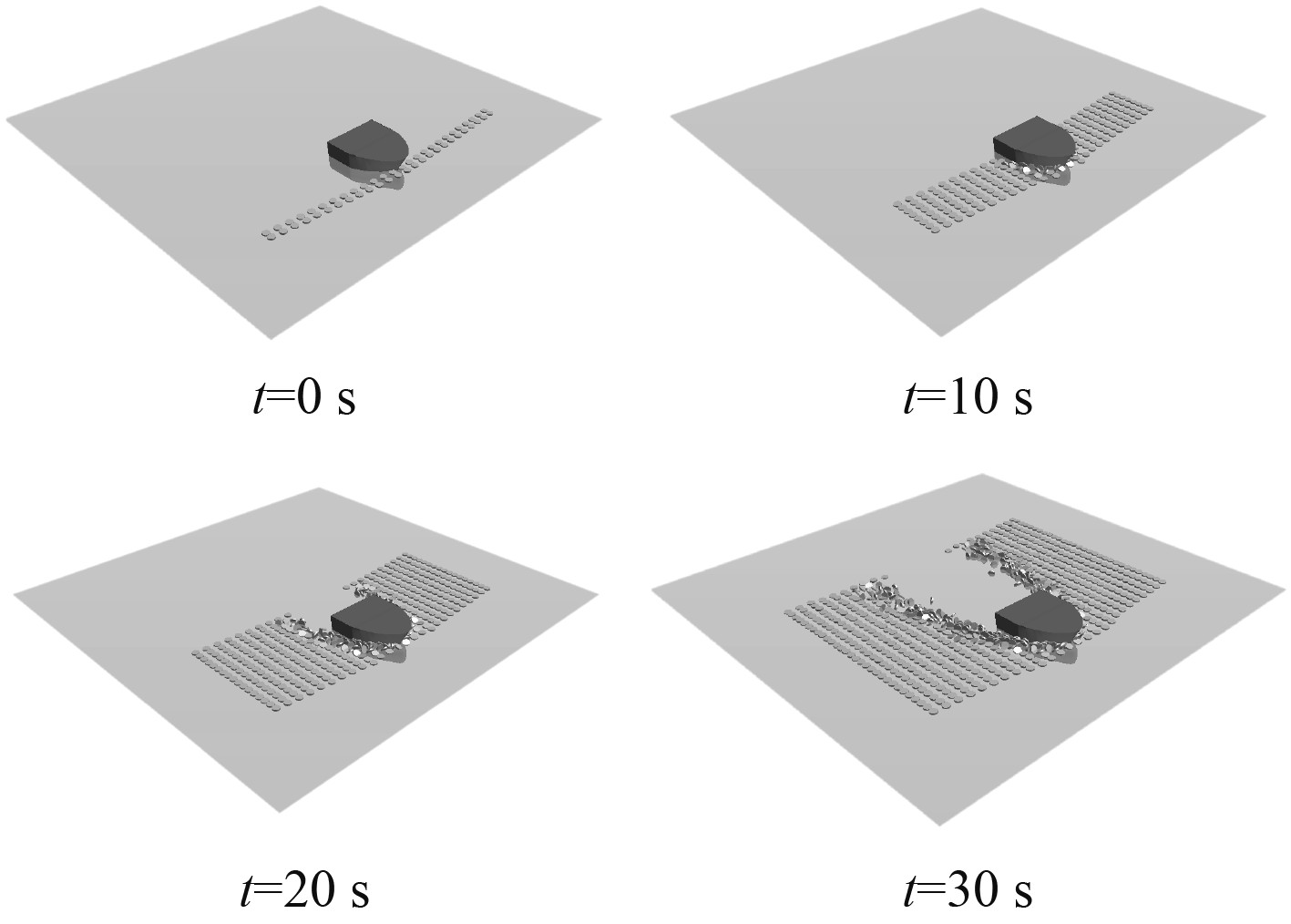
|
图 5 船体0~30 s航行过程 Fig. 5 0~30 s sailing process of hull |
航行的整个过程中,船和冰的相互作用十分复杂,通过离散元方法计算得到船体冰阻力的时程曲线图,如图6所示。
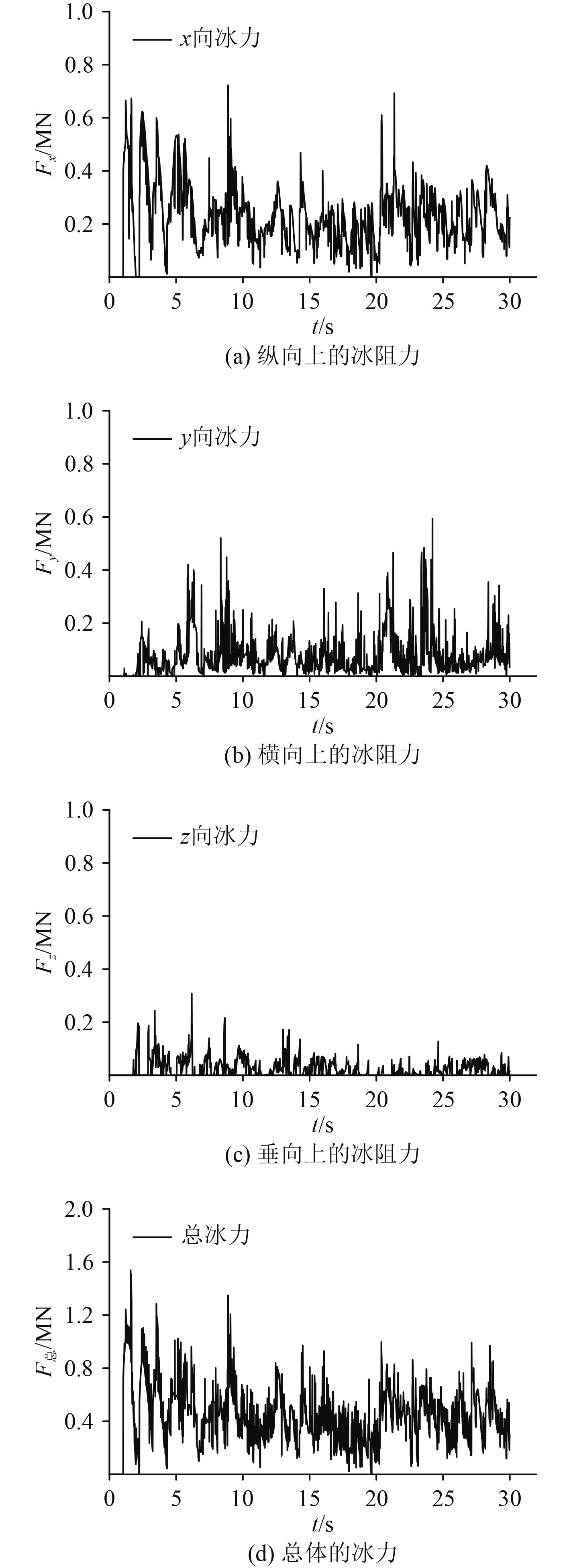
|
图 6 冰阻力时程曲线 Fig. 6 Ice resistance time-history curve |
船舶在碎冰区条件下航行时受到的冰阻力主要来自于船-冰间的碰撞、挤压和堆积作用[9]。整个航行过程冰阻力呈现出随机波动的现象,船舶航行的X方向上冰力相对较大,而且出现了多次的冰力峰值现象。Y,Z方向的冰阻力明显小于X方向,峰值出现的次数也较少。
X方向最大冰阻力0.71 MN,Y方向最大冰阻力0.58 MN,Z方向最大冰阻力0.32 MN,每个方向上的平均阻力X,Y,Z分别为0.23,0.07,0.03 MN。2组数据都能体现出,船体运行方向为冰阻力的主要集中方向。而总冰阻力同样体显出,强烈的随机性,其最大值为1.54 MN,均值为0.44 MN。
2.2 航速对于冰阻力的影响船体的航行速度同样对冰阻力产生影响,为研究航速对冰阻力影响,计算航速Vs分别为2 m/s,3 m/s,4 m/s,5 m/s和6 m/s时的冰阻力大小。随着航速的增加冰阻力最大值和平均值也呈现增长的趋势,而且增长幅度较大,说明航速对冰阻力影响较大。不同航速下冰阻力峰值为标注的Max,平均值为Mean,如图7所示。
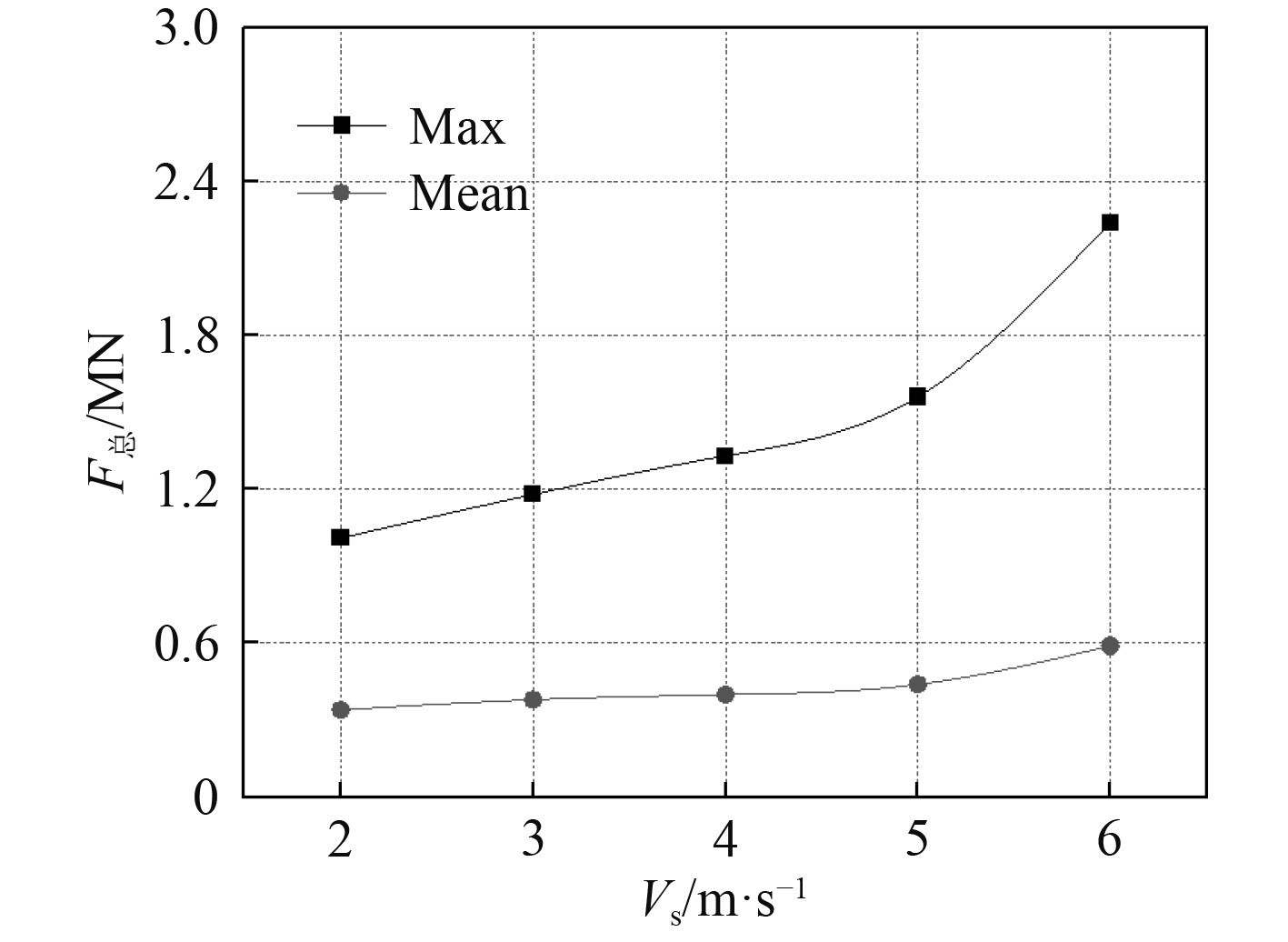
|
图 7 不同航速下冰阻力的大小 Fig. 7 The size of ice resistance under different speeds |
航速虽然提高了航行效率,但同时也影响着船体和冰体相互作用的冰阻力大小,对船体破坏也会随着增加。所以在极地航行的船舶,在满足经济效益的前提下,选择合适的航速能使整个航行的过程变得更加安全有效,本文通过离散元计算结果提供一定的参考。
2.3 海冰参数对冰阻力的影响海冰参数对冰阻力的大小产生影响[10]。海冰的各种参数包括冰厚、海冰直径和海冰密集度等,本文探讨上述参数对船体航行的影响。
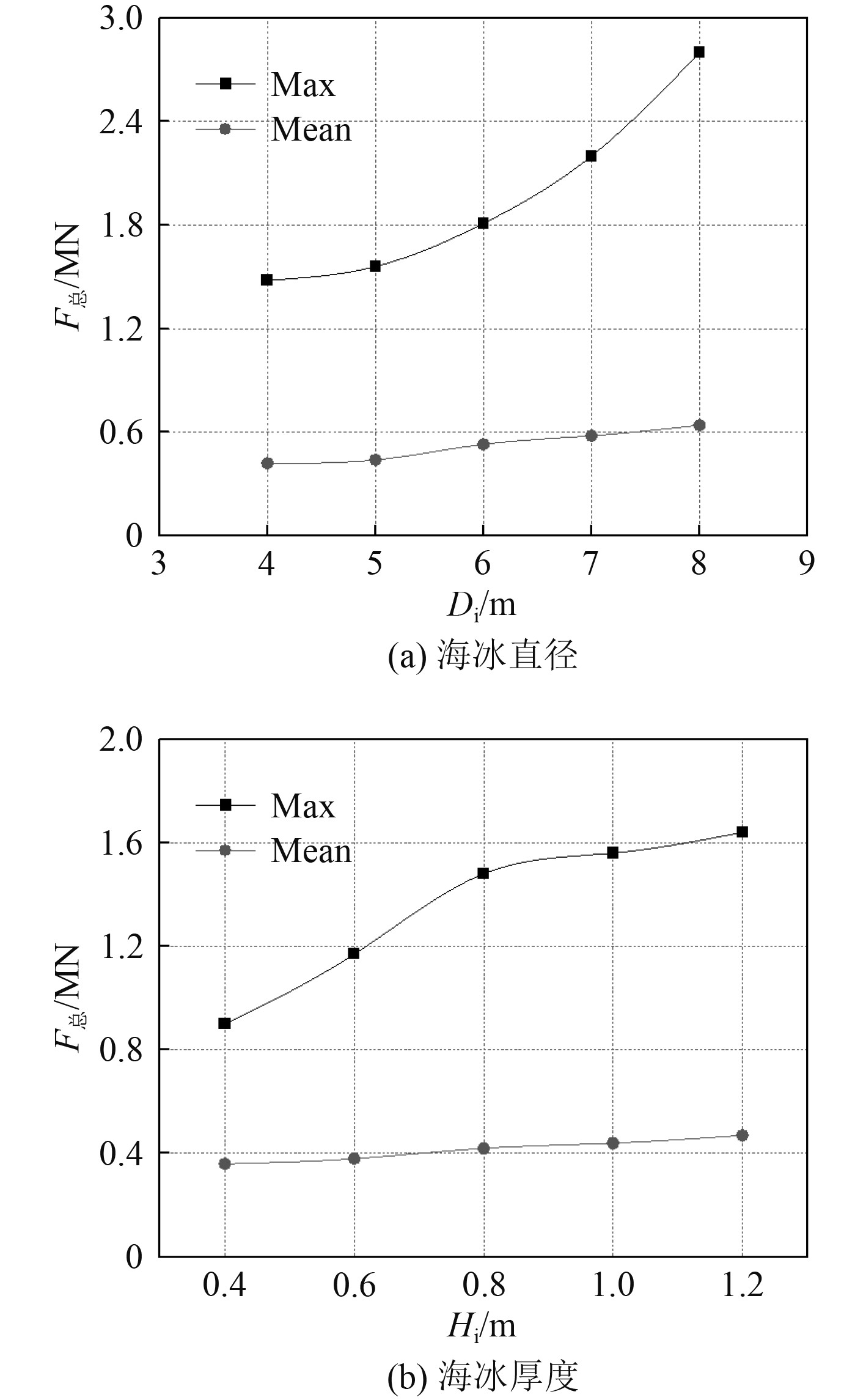
海冰直径和厚度为冰体单元最基本的参数。为研究2项参数对船冰相互作用的影响,设置海冰厚度为1 m,直径为4 m,5 m,6 m,7 m和8 m的不同冰体单元,用于研究海冰直径的影响情况。设置海冰直径为5 m,冰厚为0.4 m,0.6 m,0.8 m,1 m和1.2 m的不同单元,用于研究海冰厚度的影响情况。2种参数的研究都设置5 m/s的航速,计算结果如图8所示。
|
图 8 不同海冰条件下船体冰阻力 Fig. 8 Ice resistance under different ice conditions |
2种参数得到的冰阻力最大值和均值分别由标注的Max和Mean表示。由于固定了其他参数,而改变研究的参数,不难看出,冰体直径和冰体厚度的增加使得冰阻力增加,而且影响的幅度也较大。海冰的直径和厚度直接影响了冰体的质量,而间接地影响了冰体对船体的冲击动量,导致了冰阻力的增大。所以预知冰区海冰的直径和厚度至关重要。
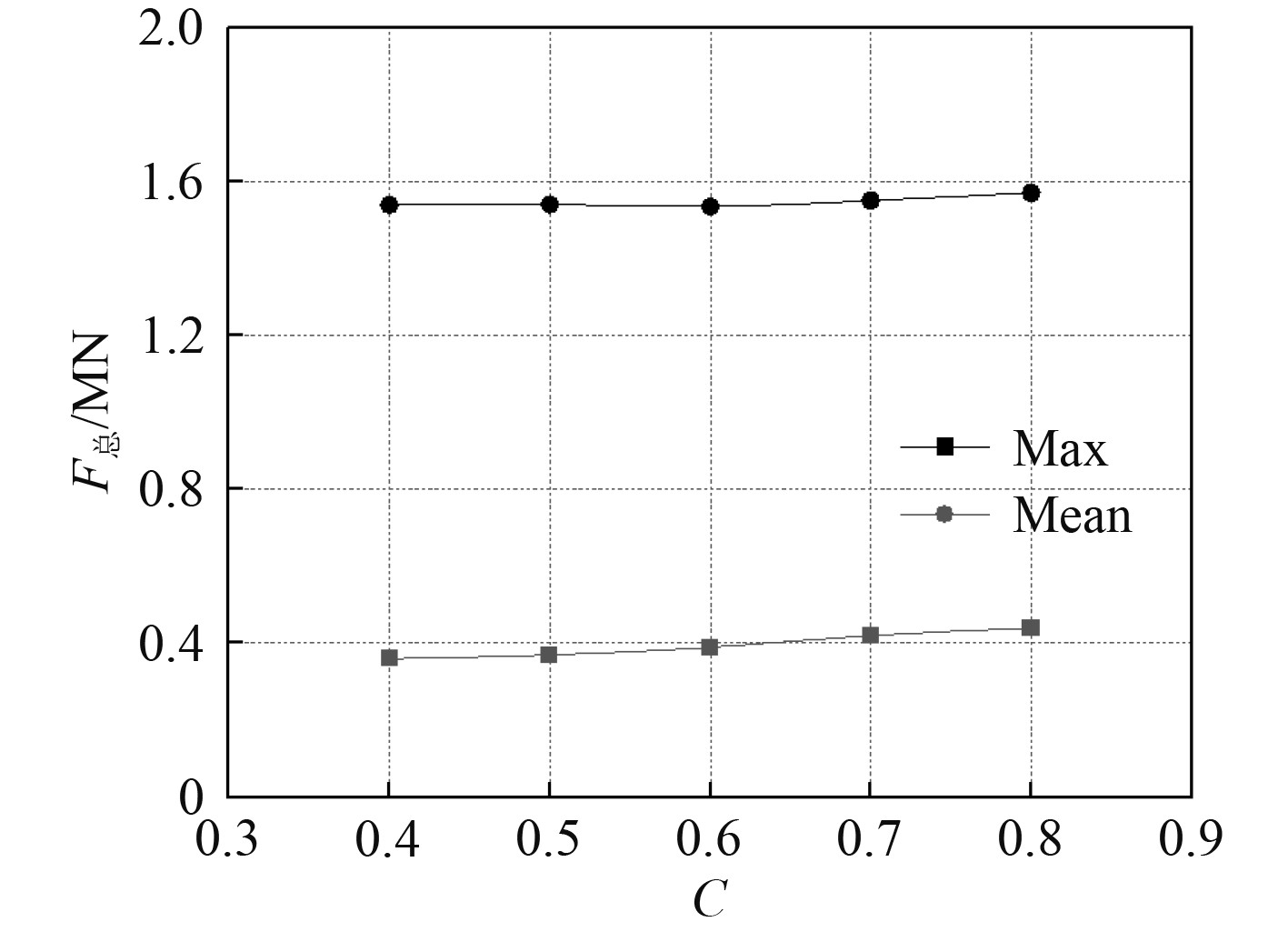
海冰的密集度反映了航行冰区的冰块数量,这决定了船与冰有效碰撞面积,从而间接的影响到冰阻力的大小。为研究海冰密集度对冰阻力的影响,设置冰厚为1 m,海冰直径为5 m,但海冰密集度为40%,50%,60%,70%和80%进行计算,得到的不同密集度下最大冰阻力和平均冰阻力的曲线如图9所示。
|
图 9 不同海冰密集度下的冰阻力 Fig. 9 Ice resistance under different intensity |
相比于海冰的厚度和海冰直径2个参数,海冰密集度对冰阻力的影响较为平缓,随密集度增加,冰阻力的变化不大。但明显看出平均冰阻力随着密集度增加而有缓慢的增加。海冰密集度直接影响了海冰数量,间接导致冰体与船体的相互作用次数,也使碎冰单元在船首堆积效果增加,所以冰阻力平均值有所增加。冰体单元的主要参数,海冰厚度和海冰直径,都没改变对船体的冲击力也就不会产生较大的改变,所以最大冰阻力变化不大。
3 离散元方法与有限元方法计算船-冰阻力的结果对比分析当前对冰阻力计算较为成熟的方法是有限元计算方法[11] ,本文将使用非线性有限元法计算模拟。为了验证离散元法的合理性,将离散元计算结果和有限元计算结果相互比较。
3.1 破冰场景的建立为了能够得到有效的比较,在有限元数值计算中也同样选取16万吨级的油船进行建模计算。为了简化计算,在Ansys中对船体进行简化建模,如图10所示。

|
图 10 油船船首模型 Fig. 10 Ship′s bow model |
利用非线性有限元软件Ls-dyna进行计算,单元网格的尺寸1 m×1 m。为保证船体沿着X方向航行,需要约束所有节点剩下的5个所有自由度。采用附加质量法对船舶破冰进行仿真计算,取0.05作为附连水质量系数。使用Ls-dyna中MAT_3的塑性随动材料模型构建船体的材料模型[12],材料参数如表4所示。
|
|
表 4 有限元计算所用船体材料参数 Tab.4 Hull material parameters used in finite element calculation |
碎冰模型的建立采用体单元,其网格尺寸为1 m×1 m×0.25 m,需要在112 m×60 m碎冰区域建立,除X,Y方向,其余4个自由度全部约束。选Ls-dyna中MAT_124的线弹塑性冰材料[13-14],具体参数如表5所示。
|
|
表 5 海冰材料参数 Tab.5 Ice material parameters |
为了和离散元计算数据比较,选取离散元计算的工况作为有限元计算工况,采用侵蚀接触算法[15],定义相关的速度−时间曲线,并让船体以匀速保持前进。设置航速为5 m/s,海冰的直径设置为5 m,海冰的厚度设置为1 m。总的计算时长为6 s,将时间步长设置为0.01 s。相比于离散元计算的结果,同样在有限元计算下可以看见海冰在船首的堆积现象,如图11所示。

|
图 11 船冰相互作用状态 Fig. 11 Ship-ice interaction state |
2种算法由于计算模型设置的不同,船和冰接触时间不同,选取离散元2.25~8.25 s这6 s内和有限元0~6 s内计算结果相互比较。其中标注为DEM的为离散元计算结果,标注为FEM的为有限元计算结果。在上述工况下,各个方向上的冰阻力以及总冰阻力的对比如图12所示。

|
图 12 不同计算方法下冰阻力对比曲线 Fig. 12 Ice resistance curve under different calculation methods |
2种计算结果所得到的时程曲线,都保持无规律的上下波动,频率很高,显示了船冰相互作用过程中船体与海冰,海冰和海冰之间的多次碰撞。有限元的计算结果中有很多处卸载的情况,而离散元出现的却很少,说明在离散元的计算中海冰与船体的接触频率相比于有限元计算会更高。有限元的计算结果得到的冰阻力峰值大多大于离散元所得到的结果,是由于有限元计算方法采用了附加质量法,没有了水的作用力,使船冰相互作用力增加,同时采用了侵蚀接触,冰体单元在接触时会被侵蚀消失,减少了船体与海冰,海冰与海冰的接触机会。离散元计算的过程中,冰体单元被设置为刚体,是不可破碎的,所以能增加海冰与海冰,船体与海冰的接触机会。具体数据直观显示出2种计算方法差值的大小。个别峰值的差值较大,均值的差距并不大。2种计算方法都有较高的可信度和可靠性,证明离散元方法在计算船冰相互作用具有可行性。2种计算方法得到的具体数值如表6所示。
|
|
表 6 两种计算方法下冰阻力数值对比 Tab.6 Numerical comparison of ice resistance under two calculation methods |
本文釆用离散元计算方法完整地模拟船体穿越冰区的整个过程,得到了整个航行过程的冰阻力大小,同时探讨了不同海冰参数对冰阻力大小的影响。最后将离散元计算得到的结果和相同工况下有限元计算方法得到的结果相比较,得到以下结论:
1)在X,Y,Z方向上的冰阻力均出现高频,无规律的振动特性,船体受到的载荷主要集中于X方向上,X方向上的冰阻力基本决定了总阻力的大小。
2)海冰的厚度和海冰的直径对冰阻力的影响较大,冰阻力随着海冰厚度和直径的增大而较为快的增大,而海冰的密集度对冰阻力影响较为缓和,但由于增加船冰之间的碰撞次数,同样产生正相关的影响。
3)同一工况下离散元计算方法和有限元计算方法计算结果都能呈现出高频的特性,但有限元在部分峰值较大,而离散元不会出现卸载情况。从冰阻力大小来看,两者除部分峰值相差较大,在均值上的相差较小,说明离散元计算方法具有较高的可信性。
| [1] |
狄少丞, 王庆, 薛彦卓, 等. 破冰船冰区操纵性能离散元分析[J]. 工程力学, 2018, 35(11): 249-256. DOI:10.6052/j.issn.1000-4750.2017.09.0698 |
| [2] |
蔡柯, 季顺迎. 平整冰与船舶结构相互作用的离散元分析[J]. 船舶与海洋工程, 2016, 32(5): 5-14. DOI:10.14056/j.cnki.naoe.2016.05.002 |
| [3] |
KUJALA P. Semi- empirical evaluation of long term ice loads on a ship hull[J]. Marine Structures, 1996(9): 849-871. DOI:10.1016/0951-8339(95)00047-X |
| [4] |
LIU Lu, JI Shunying. Ice load on floating structure simulated with dilated polyhedraldiscrete element method in broken ice field[J]. Applied Ocean Research, 2018(75): 53-65. DOI:10.1016/j.apor.2018.02.022 |
| [5] |
王超, 封振, 李兴, 等. 航行于碎冰区船舶冰阻力与冰响应探析[J]. 中国舰船研究, 2018, 13(1): 73-78. DOI:10.3969/j.issn.1673-3185.2018.01.011 |
| [6] |
JUKKA T, ARTTU P. A review of discrete element simulation of ice–structure interaction[J]. Philosophical Transactions of The Royal Society A Mathematical Physical and Engineering Sciences, 2018, 376(2129): 20170335. DOI:10.1098/rsta.2017.0335 |
| [7] |
CUNDALL, P. A., STRACK, O. D. L.. 1979. A discrete numerical model for granular assemblies[J]. Wave Motion, 2014, 47-65. DOI:10.1680/geot.1979.29.1.47 |
| [8] |
TIMCO G W, WEEKS W F. A review of the engineering properties of sea ice[J]. Cold Regions Science and Technology, 2010(60): 107-129. DOI:10.1016/j.coldregions.2009.10.003 |
| [9] |
金强, 张佳宁, 葛媛, 等. 基于离散元方法的极地浮碎冰区船舶冰阻力[J]. 船舶工程, 2020, 42(1): 35-41. JIN Qiang, ZHANG Jianing, GE yuan, et al. Ship ice resistance in polar floating ice breaking area based on discrete element method[J]. Shipbuilding Engineering, 2020, 42(1): 35-41. DOI:10.13788/j.cnki.cbgc.2020.01.07 |
| [10] |
GONG Hanyang, POLOJÄRVI A, TUHKURI J. Discrete element simulation of the resistance of a ship in unconsolidated ridges[J]. Cold Regions Science and Technology, 2019, 167(11): 55. DOI:10.1016/j.coldregions.2019.102855 |
| [11] |
丁仕风, 周利, 钟晨康, 等. 冰载荷作用下船体结构强度有限元分析方法[J]. 江苏科技大学学报(自然科学版), 2020, 34(1): 8-12+33. DOI:CNKI:SUN:HDCB.0.2020-01-002 |
| [12] |
杨金超, 朱发新, 吴文锋, 等. 基于Ansys/LS-DYNA的船冰碰撞数值分析[J]. 造船技术, 2017(3): 30-33+38. DOI:10.3969/j.issn.1000-3878.2017.03.007 |
| [13] |
ZHANG Jian, GAIDAI O, WANG Kaimin, et al. A stochastic method for the prediction of icebreaker bow extreme stresses[J]. Applied Ocean Research, 2019(87): 95-102. DOI:10.1016/j.apor.2019.03.019 |
| [14] |
GAO Y, HU Z, RINGSBERG J W, et al. An elastic–plastic ice material model for ship-iceberg collision simulations[J]. Ocean Engineering, 2015, 102(jul.1): 27-39. DOI:10.1016/j.oceaneng.2015.04.047 |
| [15] |
ZHANG Jian, HE Wen-xin, YUAN Zhi-ming, et al. Study on the structural strengthening design under the ship-ice collision load[J]. Journal of Ship Mechanics, 2016, 20(6): 722-735. DOI:10.3969/j.issn.1007-7294.2016.06.008 |
 2023, Vol. 45
2023, Vol. 45
