0 引　言

船舶动力系统的柴油发动机、主轴、齿轮箱、电力系统的发电机等均离不开旋转机械设备。随着现代工业的发展，旋转机械设备的精密程度越来越高，结构也越来越复杂，旋转机械内部的齿轮、轴承等部件相互耦合，子系统之间也存在复杂的交互关系，一旦其中某个部件出现故障，都会造成一系列的连锁反应，导致船舶出现大的事故。

船舶中的旋转机械部件往往工作环境更加恶劣，面临重载、高温等工作环境下，长时间的连续运行，不可避免地会发生一些故障。旋转机械的故障不仅会造成经济损失，甚至还会引起严重的人员伤亡事故。因此，研究旋转机械的故障诊断和状态预测具有重要意义。

本文针对船舶齿轮件、轴承的故障诊断进行研究，采用一种AR模型技术，实现旋转部件的状态预测。

1 船舶旋转机械部件齿轮的故障特性

在旋转机械中，滚动轴承、齿轮是最为广泛使用，也是最易损坏的几个部件。大量统计数据表明，船舶旋转机械设备的失效中，轴承引起的故障占比为70%左右，齿轮引起的船舶机械设备失效占比为19%左右，而船舶齿轮箱的失效中，齿轮导致的失效占比更是高达60%左右。

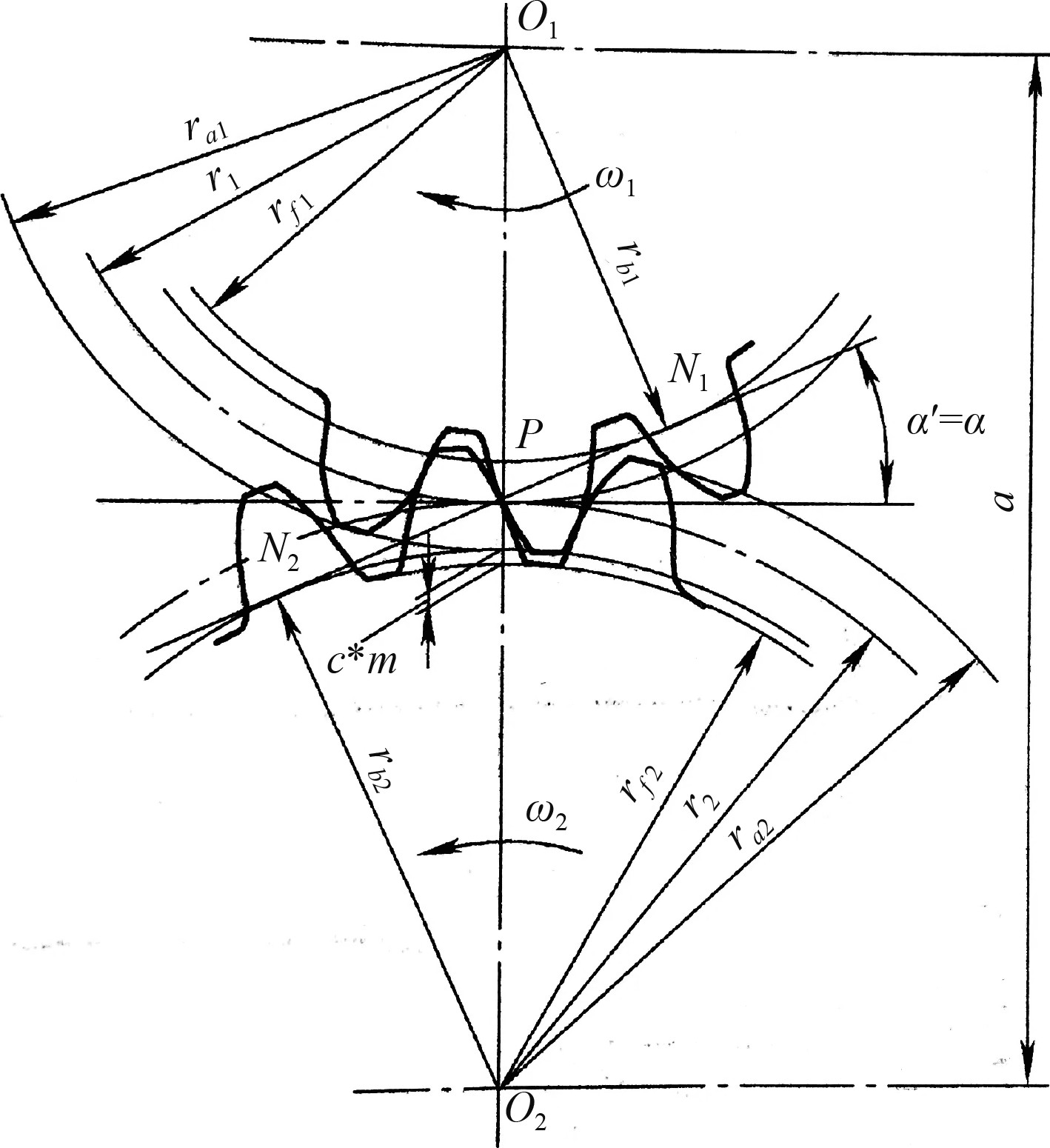
齿轮的失效与其啮合过程密切相关，图1为渐开线齿轮啮合的示意图。

图中， ${r_{a1}}$ 为齿轮的齿顶圆， ${r_1}$ 为齿轮箱的分度圆， ${r_{f1}}$ 为齿轮箱的齿根圆， ${w_1}$ 为齿轮的角速度， ${r_{b1}}$ 为齿轮箱的节圆， ${N_1}$ 为齿轮的齿数， $P$ 为相互啮合的中心距， $\alpha$ 为齿轮的压力角。

齿轮相互啮合过程中产生的振动信号能够反映齿轮的工作状态，当齿轮发生故障时，由于啮合过程受到故障位置的影响，齿轮的振动信号峰值会瞬间增加，通常齿轮故障时会产生明显的冲击振动，导致整个系统的噪声和振动增加。

齿轮故障类型主要包括断齿、齿面磨损、齿面点蚀、齿面胶合等，根据齿轮啮合原理，可以建立齿轮副的动力学方程为：

$M\ddot x + C\dot x + k\left( t \right)x = F\left( t \right)。$

式中： $F\left( t \right)$ 为啮合副受到的外力； $k\left( t \right)$ 为齿轮的啮合刚度；C为齿轮副的等效阻尼；M为齿轮的等效质量，按下式计算：

$M = \frac{{{m_1}\cdot {m_2}}}{{{m_1} + {m_2}}} \text{，}$

齿轮的啮合频率为：

${f_z} = \frac{N}{{60}}Z \text{，}$

式中：N为齿轮转速；Z为齿轮的齿数。

假设齿轮的故障频率为：

${f_0} = \frac{N}{{60}}Z \text{，}$

则故障频率的调制信号可表示为：

${X_c}(t) = \sum\limits_{m = 0}^M {{A_m}} \cos \left( {2{\text{π}} m{f_z} + {\varphi _m}} \right) \text{，}$

式中： ${A_m}$ 为调制信号的幅值； ${\varphi _m}$ 为调制信号的相位。

齿轮故障频率信号的建立有助于后续对齿轮故障进行监测和诊断。

2 船舶旋转机械部件轴承的故障特性

在旋转机械部件中，轴承是必不可少的部件，本文聚焦的轴承类型为船舶发动机上使用的双列调心滚子轴承，在滚动轴承生产和制造中，轴承的材料缺陷、装配误差、轴电流、白腐蚀等都是需要重点针对的故障类型。

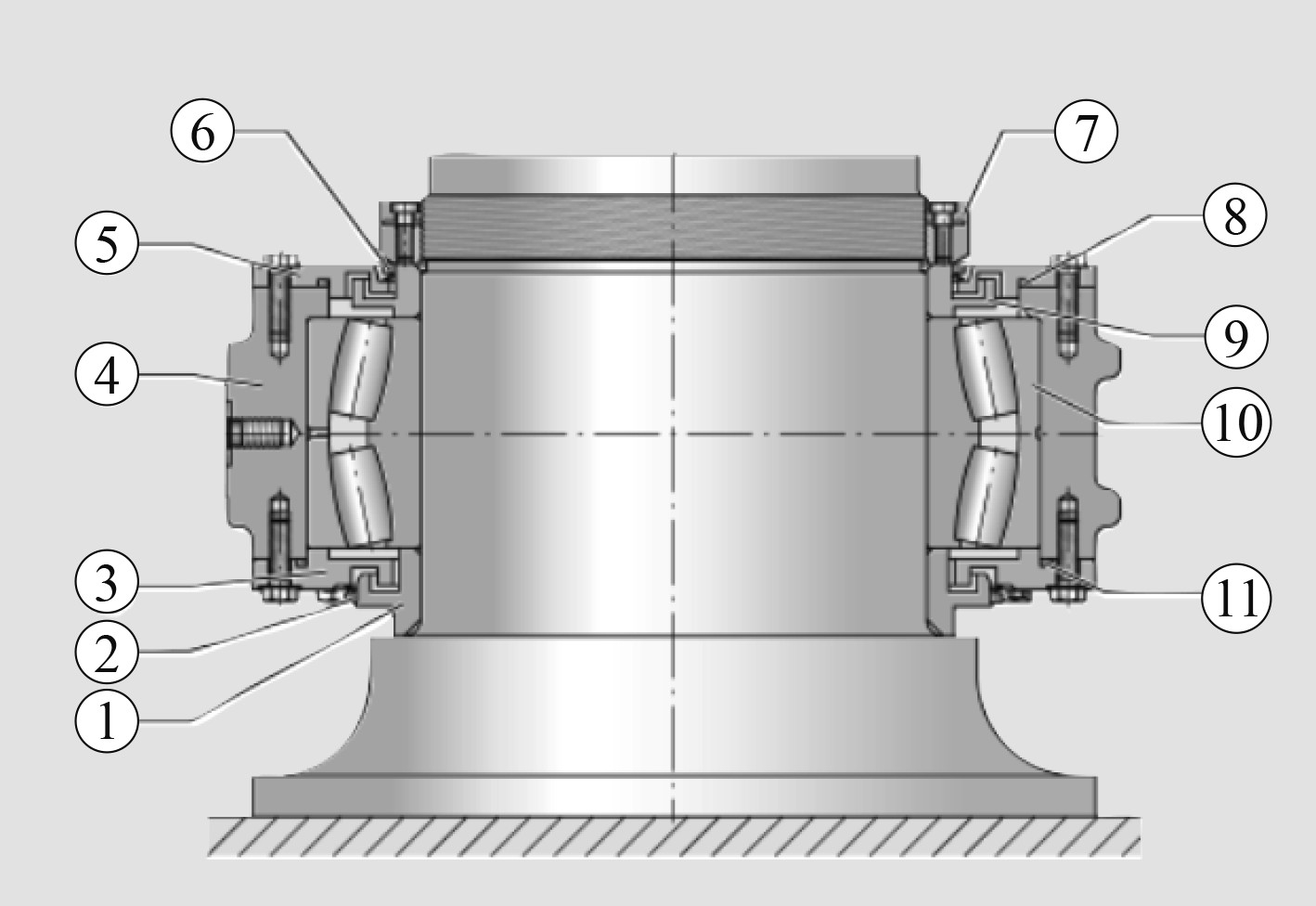
图2为船舶发动机滚动轴承的结构示意图。

轴承工作过程中必须要保证预紧力和润滑。图2中，①为发电机输出端一侧的迷宫式密封圈，②为发电机输出侧的V形圈，③为发电机输出端的轴承端盖，④为轴承座，⑤为发电机输入端的轴承端盖，⑥为发电机输入端的V形圈，⑦为锁紧螺母，⑧～⑩为密封O形圈。

船舶旋转部件轴承常出现的故障类型^[1]包括：

1）胶合失效

常发生在船舶的齿轮箱中，受到高速、重载的工作环境影响，一旦船舶轴承润滑不良，轴承滚子与内外圈之间的接触面就会产生大量的热量，造成滚子和接触面的烧伤，严重时产生黏连，出现轴承的胶合失效形式。

2）腐蚀失效

腐蚀失效是指轴承的工作环境中侵入异物，这些异物与轴承滚子、保持架、内外圈产生复杂的电化学或氧化还原反应，造成轴承表面成分的腐蚀失效，对轴承产生大量损伤。

3）疲劳剥落

疲劳剥落是指轴承在长时间连续运行后，表面产生疲劳破坏，滚动体与内外圈之间反复摩擦，造成金属的表面剥落，剥落的金属产生细小的磨粒，进一步对轴承造成损伤。

4）塑性变形

当轴承运行过程中受到较大的冲击应力时，滚子与滚道之间产生应力集中，造成塑性变形。塑性变形可能发展到表面剥落，会造成轴承的噪声、振动异常信号。

图3分别为船舶轴承的电腐蚀、表面剥落、塑性变形等故障图。

船舶轴承滚动体的故障频率^[2]为：

${f_{{n_{}}}} = 0.212\frac{{Eg}}{{R\gamma }}。$

式中： $E$ 为弹性模量； $R$ 为轴承半径； $\gamma$ 为轴承的材料密度。

轴承内外圈的故障频率按下式计算：

${f_n} = \frac{{n\left( {{n^2} - 1} \right)}}{{2{\text{π}} {{(D/2)}^2}\sqrt {{n^2} + 1} }}\sqrt {\frac{{EIg}}{{\gamma A}}}。$

式中，n为轴承振动的阶数。

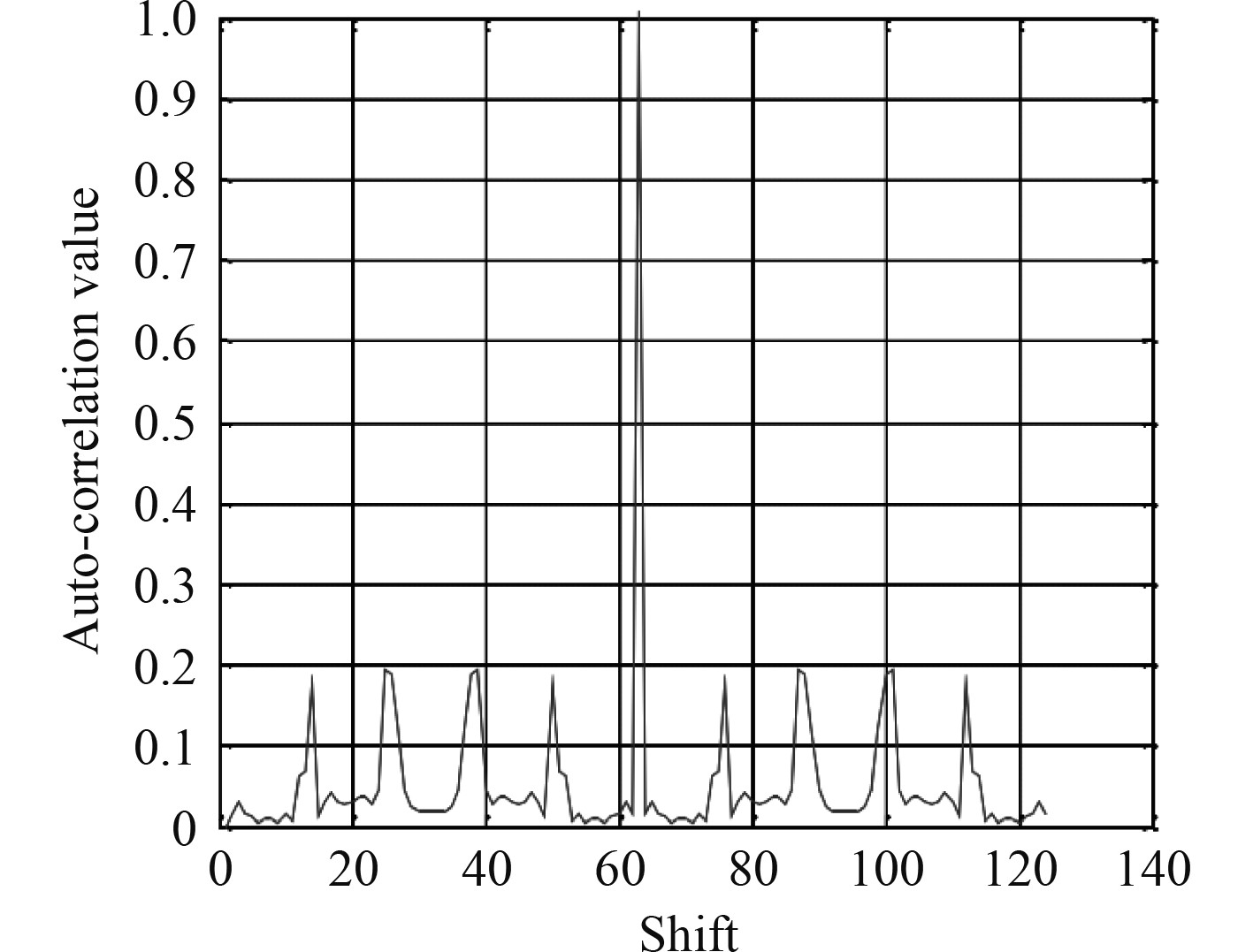
典型船舶轴承故障振动频率信号示意图如图4所示。

3 基于AR模型的船舶旋转机械故障诊断和状态预测 3.1 时间序列AR模型原理

在机械设备故障诊断中，时间序列AR模型的应用原理是利用时间序列的数据分析，从随机过程中发现背后的规律。

本文在建立船舶旋转机械故障诊断和状态预测系统时，采用平稳时间序列 $\left( {{x_k}} \right),k = 1,2,\cdots ,N$ ，其标准差 $E\left( {{x_k}} \right) = 0$ 。

建立AR时间序列模型为：

${x_k} = \sum\limits_{k = 1}^m {{\phi _i}} {x_{k - 1}} + {a_k} \text{，}$

式中， ${\phi _i}$ 为自回归系数 $i=1,2,\cdots ,N$ 。

基于AR时间序列模型的状态估计，根据已知的观测数据 $\left( {{x_k}} \right),k = 1,2,\cdots ,N$ ，估计出一定时间阶段的状态量为：

${a_k} = {\phi _1}{x_{k - 1}} - {\phi _2}{x_{k - 2}} = \cdots \cdot {\phi _m}{x_{k - m}} \text{，}$

状态量 ${a_k}$ 的均方差为：

$\delta _a^2 = E\left( {a_k^2} \right) = \frac{1}{N}\sum\limits_{k = 1}^N E \left( {{x_k} - {\phi _1}{x_{k - 1}} \cdots \cdots - {\phi _m}{x_{k - 1}}} \right.) 。$

3.2 基于AR模型的旋转机械故障诊断和状态预测

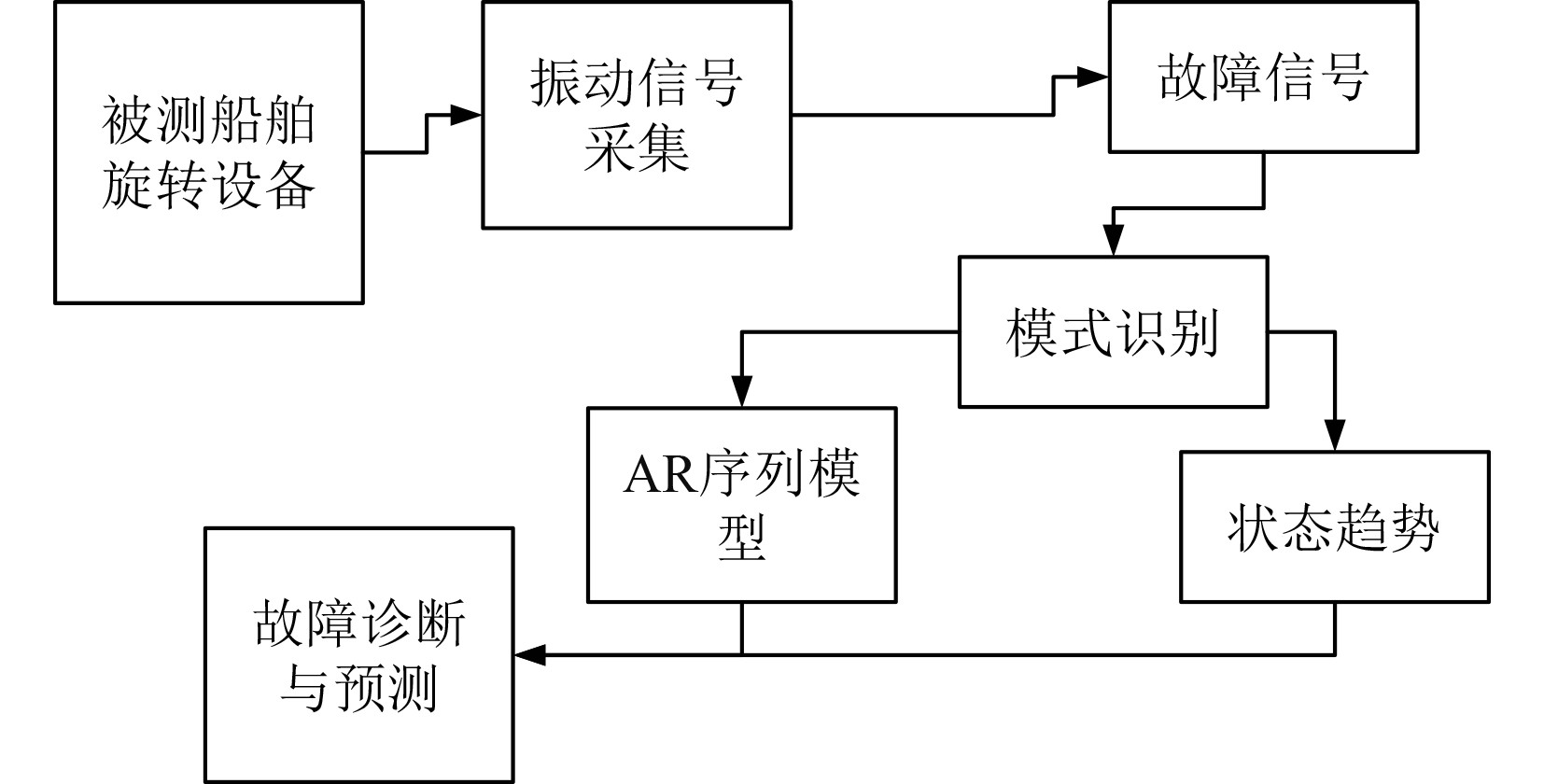
结合旋转机械故障信号和AR时间序列模型，建立船舶旋转机械故障诊断与预测系统，原理图如图5所示。

船舶动力系统轴承的转速为1890 r/min，在船舶动力系统轴承外圈上安装加速度传感器^[3]，采集的加速度数据如表1所示，单位为g。

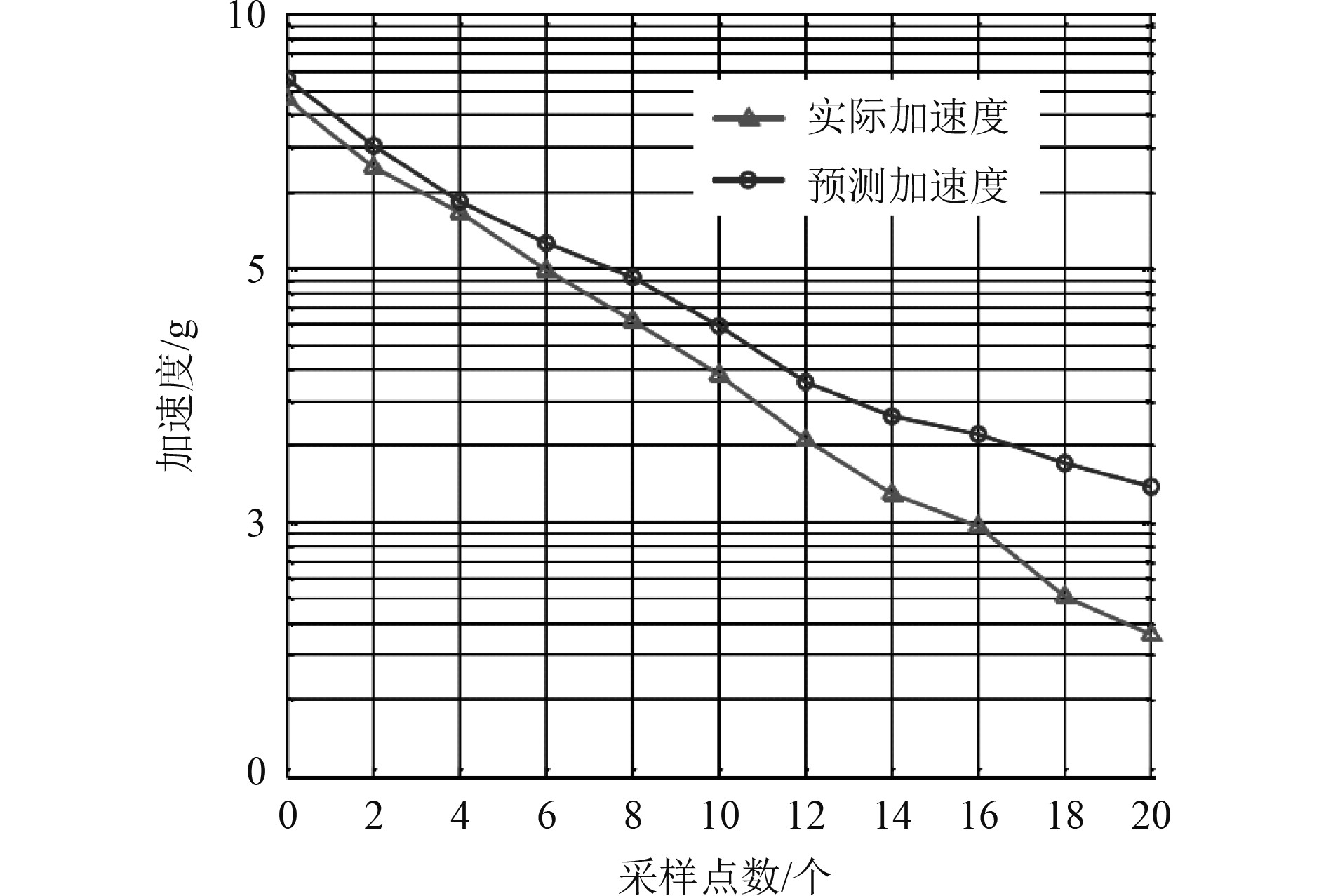
整理得到船舶轴承实际振动加速度与AR预测加速度的对比曲线如图6所示。

4 结　语

船舶机械设备的运行稳定性意义重大，本文以船舶旋转机械设备中使用量最大，同时也是故障率最高的齿轮和轴承为研究对象，介绍齿轮和轴承的故障特性，基于AR时间序列模型建立了故障诊断和预测系统。