0 引　言

遥感技术是通过各类型传感仪器完成不同地面目标辐射电磁波的采集，并通过处理获得遥感图像信息的先进探测技术^[1]。早期，遥感技术只应用于军事作战中，侦察敌方舰船类型、位置等信息等。数据通信、图像处理等技术的高速发展，对遥感技术的广泛应用起到了极大的促进作用，使其不断向民用领域扩展，为其带来极其广阔的发展空间^[2-3]。另外，无人机技术的成熟与应用，为遥感技术带来了新的发展机遇。无人机遥感监测平台在对舰船遥感图像进行采集时，会因光学镜头的固有缺陷以及传感器姿态的不规则性而产生非线性畸变，使得舰船遥感图像发生扭曲、失真等问题^[4-5]，不仅严重影响图像的视觉效果，也会对后期的图像目标识别等带来诸多不利。因此，舰船遥感图像的非线性畸变校正对提升遥感图像视觉效果以及舰船目标识别具有极其重大的现实意义^[6]。

王士伟等^[7]针对航天遥感相机成像存在的光响应非均匀度过高等非线性畸变问题，提出基于自适应移动窗口的畸变校正方法。陈一超等为解决红外遥感图像的畸变问题，根据红外遥感相机模型的投影变换原理构建等距投影校正模型，以确定待校正像点与原始像点间的映射关系，通过三次卷积差值法获取全成像信息，利用畸变校正模型确定插值后红外遥感图像的像点坐标，并将最近邻像点像素值赋予给该像点，实现红外遥感图像的畸变校正。该方法所用校正模型具有计算简便、参数量少的特点，但对切向畸变未能起到较好的校正效果。因此，本文研究舰船遥感图像非线性畸变自适应校正，以期获得更高的畸变校正精度，提高舰船遥感图像质量。

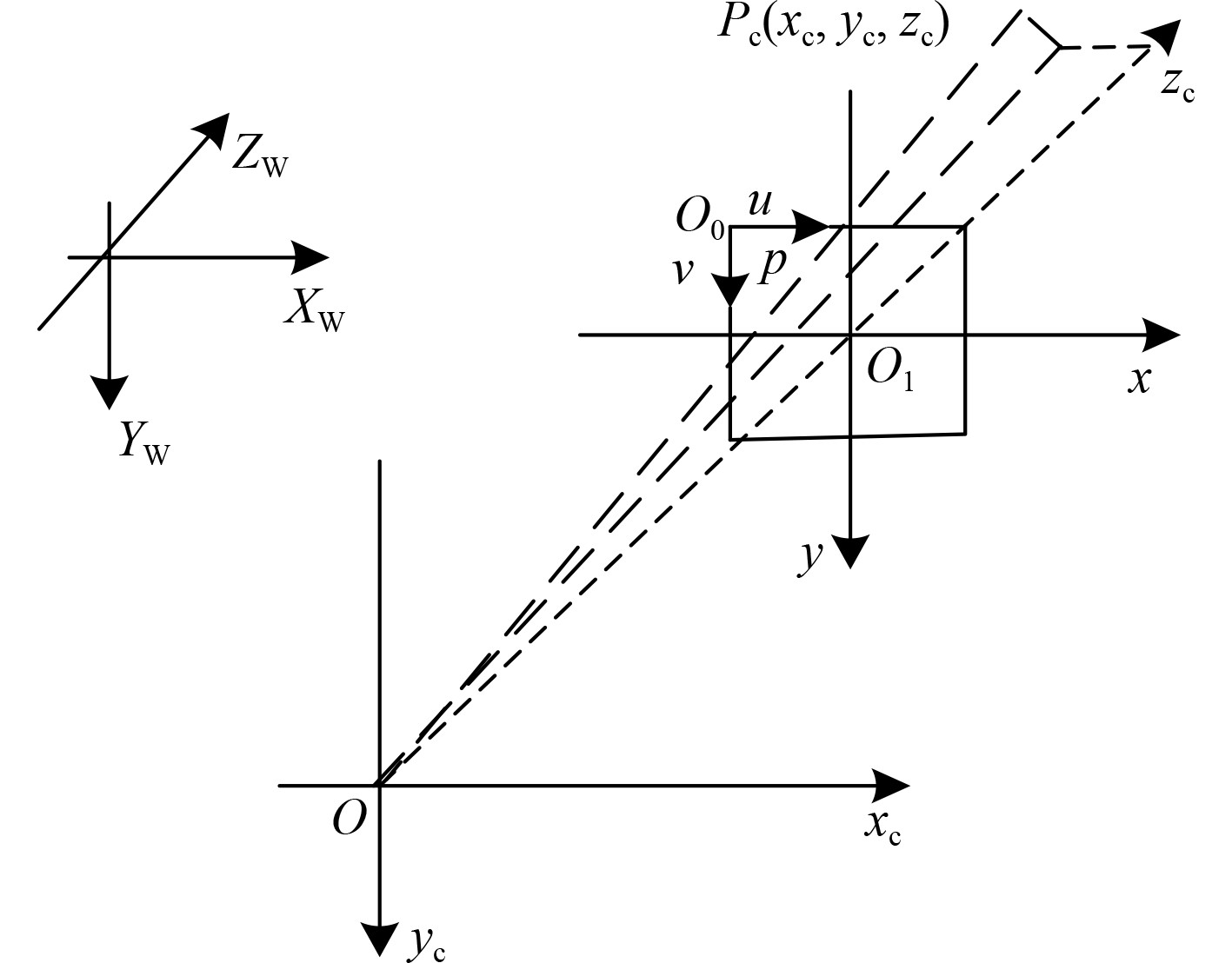
1 舰船遥感图像非线性畸变自适应校正 1.1 遥感摄像机成像模型

舰船遥感摄像机成像模型中共含有4个坐标系，分别为图像物理、像素坐标系、世界坐标系以及摄像机坐标系。 $ {P_c}\left( {{x_c},{y_c},{z_c}} \right) $ 用于表示摄像机坐标系中的任意一点，对应于图像物理坐标系下的成像点为 $ p $ ，光学中心为 $ o $ ， $ o{z_c} $ 与图像垂直，交点即为成像平面中心点为 $ {o_1} $ ， $ f $ 表示摄像机的焦距，即为 $ o{o_1} $ 线的长度。遥感摄像机成像过程如图1所示。

摄像机坐标系中的每个点都位于空间之内，可通过世界坐标系对其进行表示，对于点 $ {P_c}\left( {{x_c},{y_c},{z_c}} \right) $ ，可将其转换到世界坐标系下，转换后与之对应的世界坐标系下的点表示为 $ \left( {{X_w},{Y_w},{Z_w}} \right) $ 。转换公式描述为：

$ \left[ \begin{array}{c} {x_c} \\ {y_c} \\ {z_c} \\ 1 \end{array} \right] = \left[ \begin{array}{cc} Q & t \\ {0^{\rm{T}}} & 1 \end{array} \right]\left[ \begin{array}{c} {X_w} \\ {Y_w} \\ {Z_w} \\ 1 \end{array} \right] 。$

(1)

式中： $ Q $ 为正交单位矩阵，其阶数为 $ 3 \times 3 $ ； $ t $ 为三维平移向量， $ {0^{\rm{T}}} = {\left( {0,0,0} \right)^{\rm{T}}} $ 。点 $ {P_c}\left( {{x_c},{y_c},{z_c}} \right) $ 在图像物理坐标系下的成像点为 $ p $ ，其坐标用 $ \left( {x,y} \right) $ 表示，在图像像素坐标系下，点 $ p $ 的坐标表示为 $ \left( {u,v} \right) $ ，点 $ {o_1} $ 的坐标为 $ \left( {{u_0},{v_0}} \right) $ 。 $ x $ 轴、 $ y $ 轴下各像素点的物理大小通过 $ {\rm{d}}x $ 和 $ {\rm{d}}y $ 描述，对于舰船遥感图像中的随机像素点，其在图像物理坐标系、像素坐标系下的坐标可通过下式进行转换：

$ \left[ \begin{array}{c} u \\ v \\ 1 \end{array} \right] = \left[ \begin{array}{ccc} \dfrac{1}{{{\rm{d}}x}} & 0 & {u_0} \\ 0 & \dfrac{1}{{{\rm{d}}y}} & {v_0} \\ 0 & 0 & 1 \end{array} \right]\left[ \begin{array}{c} x \\ y \\ 1 \end{array} \right] 。$

(2)

由相似三角形关系，可完成图像物理坐标系下点 $ p $ 坐标的计算，公式描述为：

$ \left\{ \begin{gathered} x = \frac{{f{x_c}}}{{{z_c}}}，\\ y = \frac{{f{y_c}}}{{{z_c}}}。\\ \end{gathered} \right. $

(3)

将其转换为矩阵形式可有：

$ s\left[ \begin{array}{c} x \\ y \\ 1 \end{array} \right] = \left[ \begin{array}{*{20}{c}} f & 0 & 0 & 0 \\ f & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right]\left[ \begin{array}{c} {x_c} \\ {y_c} \\ {z_c} \\ 1 \end{array} \right]。$

(4)

式中： $ s $ 为比例系数。通过上述公式即可确定摄像机成像模型。

1.2 非线性畸变模型的构建

遥感摄像机成像模型描述世界坐标系下每个点与其理想成像点的映射关系。遥感摄像平台在采集舰船遥感图像时，其镜头根本无法达到理想线性透视成像技术要求，因此会产生非线性畸变误差，致使舰船遥感图像失真。对于点 $ {P_c}\left( {{x_c},{y_c},{z_c}} \right) $ ，其理想成像点坐标为 $ \left( {x,y} \right) $ ，因摄像机成像过程中的非线性畸变误差，实际成像点会与理想坐标点发生偏离，用 $ \left( {{x_d},{y_d}} \right) $ 表示， $ {\delta _x} $ 和 $ {\delta _y} $ 为其中径向畸变； $ {\alpha _x} $ 和 $ {\alpha _y} $ 表示离心畸变； $ {\eta _x} $ 和 $ {\eta _y} $ 为薄棱镜畸变。理想成像点坐标可描述为：

$ \left\{ \begin{gathered} x = {x_d} + {\delta _x}\left( {{x_d},{y_d}} \right) + {\alpha _x}\left( {{x_d},{y_d}} \right) + {\eta _x}\left( {{x_d},{y_d}} \right) \\ y = {y_d} + {\delta _y}\left( {{x_d},{y_d}} \right) + {\alpha _y}\left( {{x_d},{y_d}} \right) + {\eta _y}\left( {{x_d},{y_d}} \right) \\ \end{gathered} \right. $

(5)

Tsai畸变模型与Brown畸变模型是摄像机非线性畸变校正中常应用的模型。前者通过下式进行畸变模型的描述：

$ \left\{ \begin{gathered} x = {x_d}\left( {{k_1}{r^2} + {k_2}{r^4} + 1} \right) \\ y = {y_d}\left( {{k_1}{r^2} + {k_2}{r^4} + 1} \right) \\ \end{gathered} \right. $

(6)

其中： $ r $ ， $ {r^2} = {x_d}^2 + {y_d}^2 $ 为成像点与主点间距， $ {k_1} $ 和 $ {k_2} $ 为畸变系数。

Tsai具有模型简化、计算难度低的特点，但因其只能对径向畸变进行校正，故难以取得突出校正效果。后者的畸变模型通过下式进行描述：

$ \left\{ \begin{gathered} x - {x_d} = {a_1}{x_d} + {a_2}{y_d} + {a_5}{y_d}^2 + {a_6}x_d^2{y_d} + {a_7}{x_d}{y_d}^2 + \\ \qquad \quad\;\; {x_d}\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right) + {p_1}\left( {{r^2} + 2x_d^2} \right)+ \\ \qquad \quad\;\; 2{p_2}{x_d}{y_d} + {\delta _{x0}} \\ y - {y_d} = {b_1}{x_d} + {b_2}{y_d} + {b_5}{y_d}^2 + {b_6}x_d^2{y_d} + {b_7}{x_d}{y_d}^2 + \\ \qquad \quad\;\; {y_d}\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right) + {p_2}\left( {{r^2} + 2y_d^2} \right)+ \\ \qquad \quad\;\; 2{p_1}{x_d}{y_d} + {\delta _{y0}} \\ \end{gathered} \right. $

(7)

其中： $ {a_i} $ 和 $ {b_i} $ 为底片变形系数； $ {\delta _{x0}} $ 和 $ {\delta _{y0}} $ 为内、外方位元素变量； $ {k_i} $ 和 $ {p_i} $ 分别为径、切向畸变参数。该模型虽能够对更复杂的非线性畸变进行描述，但所用参数量大，计算难度较高。因此，本文建立的畸变模型不仅要考虑畸变参数与阶数的适应度，还要能够有效提高实际畸变校正效果。

对于理想成像点 $ \left( {x,y} \right) $ ，其与实际成像点 $ \left( {{x_d},{y_d}} \right) $ 间的关系可通过下式描述：

$ \left[ \begin{array}{c} x \\ y \\ 1 \end{array} \right] = \left[ \begin{array}{ccc} {f_v} & {r_0} & {v_0}\\ f & {f_u} & {u_0} \\ 0 & 0 & 1 \end{array} \right]\left[ \begin{array}{c} {x_d} \\ {y_d} \\ 1 \end{array} \right]。$

(8)

其中： $ \left[ \begin{array}{ccc} {f_v} & {r_0} & {v_0} \\ f & {f_u} & {u_0} \\ 0 & 0 & 1 \end{array} \right] $ 表示摄像机内部参数矩阵，在成像平面下， $ {f_u} $ 和 $ {f_v} $ 分别为横向、纵向等效焦距， $ \left( {{u_0},{v_0}} \right) $ 为主点坐标， $ {r_0} $ 为该平面坐标轴的扭转系数。离心畸变模型可描述为：

$ \left\{ \begin{gathered} {\alpha _x} = 3\left( {{p_1}{r^2} + {p_2}{r^4}} \right)\sin \left( {\varphi - {\varphi _0}} \right) ，\\ {\alpha _y} = 3\left( {{p_1}{r^2} + {p_2}{r^4}} \right)\cos \left( {\varphi - {\varphi _0}} \right)。\\ \end{gathered} \right. $

(9)

其中： $ \varphi $ 为切向轴与正方向相交角度， $ {\varphi _0} $ 为最大角度。传感器 $ x $ 、 $ y $ 轴间存在倾角，其余弦值表示为 $ a $ ，该值与 $ {r_0} $ 大小直接相关，即 $ {r_0} = a{f_u} $ 。畸变参数过多不仅对标定效果的提升无益，而且会使标定结果产生波动，因此不考虑公式(5)中的薄棱镜畸变，其原因是根据工业相机的应用特点，无需对其底片变形进行衡量。与 $ {k_3} $ 对应的非线性畸变波动性更强，也更为敏锐，当无法达到校正精度目标时，舰船遥感图像将更加扭曲，因此，不宜将 $ {k_3} $ 计入校正模型。改进后的Brown畸变模型可描述为：

$ \left\{ \begin{gathered} x - {x_d} = {x_d}\left( {1 + {k_1}{r^2} + {k_2}{r^4}} \right) + {p_1}\left( {{r^2} + 2x_d^2} \right) + \\ \qquad\quad\;\; 2{p_2}{x_d}{y_d} + {\delta _{x0}}，\\ y - {y_d} = {y_d}\left( {1 + {k_1}{r^2} + {k_2}{r^4}} \right) + {p_2}\left( {{r^2} + 2y_d^2} \right) + \\ \qquad\quad\;\; 2{p_1}{x_d}{y_d} + {\delta _{y0}} 。\\ \end{gathered} \right. $

(10)

1.3 光学畸变校正算法

为提高舰船遥感图像的非线性畸变校正效果，本文通过实验场校验法实现遥感摄像机光学畸变系数、内外方位元素变量的校正处理。实验场检校方法的原理是根据舰船遥感图像所在实验场内各给定控制点坐标以及与其对应的成像点实际坐标，根据式(4)、式(10)实现传感器内外方位元素变量与畸变系数的解算，由此获取误差方程的矩阵表示为：

$ v = A \cdot {x_e} + B \cdot {x_i} + C{x_c} - L 。$

(11)

式中： $ v = {[ {{v_x},{v_y}} ]^{\rm{T}}} $ 为成像点坐标的修正结果，舰船遥感图像采集时，传感器内、外方位元素变量修正结果分别为 $ {x_i} = {\left[ {{\rm{d}}f,{\rm{d}}{x_0},{\rm{d}}{y_0}} \right]^{\rm{T}}} $ ， $ {x_e} = \left[ {\rm{d}}{X_c},{\rm{d}}{Y_c},{\rm{d}}{Z_c},{\rm{d}}\varphi , {\rm{d}}w,{\rm{d}}k \right]^{\rm{T}}$ ，二者系数分别为 $ B $ 、 $ A $ ，其中： $ f $ ， $ {x_0},{y_0} $ 为内方位元素； $ \varphi $ ， $ w $ ， $ k $ 为外方位元素；常数项用 $ L $ 描述，畸变差系数修正值为 $ {x_c} $ ，畸变差系数矩阵用 $ C $ 表示，可通过计算畸变系数 $ {\left[ {{k_1},{k_2},{p_1},{p_2}} \right]^{\rm{T}}} $ 的一阶导数获得。

给定 $ n $ 个控制点的实际成像坐标为 $ \left( {{x_d},{y_d}} \right) $ ，与之对应的地面坐标为 $ {P_c}\left( {{x_c},{y_c},{z_c}} \right) $ ，可通过最小二乘平差法确定未知数修正结果，计算公式为：

$ x = {\left[ {{x_e},{x_i},{x_c}} \right]^T} = \frac{{\displaystyle\sum\limits_{i = 1}^n {\left( {\left[ {A,B,C} \right]_i^{\rm{T}} \cdot L} \right)} }}{{\left[ {\displaystyle\sum\limits_{i = 1}^n {\left( {\left[ {A,B,C} \right]_i^{\rm{T}} \cdot \left[ {A,B,C} \right]_i^{}} \right)} } \right]}}。$

(12)

由于未知数 $ x $ 的初始取值较为粗略，故需进行迭代循环运算，内、外方位元素初值可通过直接线性变换法获得，开始迭代操作时，可令光学畸变差的初始取值为0，一旦未知数修正值低于给定阈值0.01 pixel时，则停止迭代。

1.4 舰船遥感图像重采样

完成成像点坐标校验后，采用双线性内插值法对原始舰船遥感图像作重采样处理，获取某像素2 pixel×2 pixel领域采样点均值，以其周围4个像素灰度值分别沿横、纵方向作差值处理，获得校正后的舰船遥感图像。

2 实验结果与分析

以某无人机摄影平台采集的舰船遥感图像为研究对象，构建数据集，数据集中共有50张舰船遥感图像，设定无人机飞行航高为1000 m左右，地面分辨率为4 m，采集的舰船遥感图像尺寸为800 pixel×800 pixel。

随机选取的一张原始舰船遥感图像，因传感器姿态的无规则性改变，获取的舰船遥感图像存在非线性畸变，使得舰船遥感图像效果失真严重。采用本文方法对采集的舰船遥感图像进行非线性畸变校正，并与基于Tsai畸变模型与基于Brown畸变模型的校正结果进行对比，3种方法的校正效果如图2所示。通过畸变误差均值E_mean指标、畸变百分比（各像素至光轴间距与误差均值之比）指标对各方法的非畸变校正效果进行评价，分析各指标的变化验证本文方法的畸变校正效果，实验结果如表1所示。结合图2和表1结果可知，采用3种方法对原始舰船遥感图像的非线性畸变进行校正处理，均取得一定的校正效果，本文方法处理后的舰船遥感图像，基本不存在图像扭曲、失真问题，舰船遥感图像视觉效果突出，同时本文方法校正后舰船遥感图像的误差均值及畸变百分比指标为三者中最低。采用Tsai畸变模型的校正方法对舰船遥感图像进行非线性畸变校正的视觉效果最差，畸变情况并未得到有效处理，且畸变误差均值、畸变百分比最大；基于Brown畸变模型的校正方法的校正效果高于Tsai模型方法，但低于本文方法。原因是：基于Tsai畸变模型的校正方法只对原始舰船遥感图像中的径向畸变进行了校正处理，而未衡量切向畸变对其校正效果的影响；基于Brown畸变模型的校正方法对底片弯曲、内外方位元素变量以及切向、径向畸变等进行综合考量，需计算的未知参数量过大，计算难度大幅增加，降低了非线性畸变校正精度；本文方法通过对Tsai模型、Brown畸变模型进行改进处理，使得构建的非线性畸变模型维持了畸变参数与阶数间的平衡，更有利于舰船遥感图像畸变校正效果的提升。因此，本文方法的畸变校正效果突出。

3 结　语

将本文方法应用于舰船遥感图像的非线性畸变校正中，并与基于Tsai畸变模型与基于Brown畸变模型的校正方法进行对比，通过分析不同方法的舰船遥感图像畸变校正结果验证本文方法的畸变校正性能。实验结果表明：本文方法校正后的舰船遥感图像，基本无扭曲、失真问题，畸变校正效果突出。