2. 广西职业师范学院,广西 南宁 530007
2. Guangxi Vocational Normal University, Nanning 530007, China
随着当代科学技术的飞速发展,全球科研人员不断地对自然环境中的不确定现象进行研究。弱信号是一种比混沌背景噪声小的信号,其主要特点在于幅值和信噪比相对而言比较小。时域平均法以及自适应噪声法是2种常见的微弱信号提取方法。时域平均法通过多次采样取平均值的方法消除噪声,实现信号的提取。自适应噪声法是通过滤波器对信号进行提取。噪声对信号检测会产生不利的影响,但是在混沌海杂波背景下,传统方法很难对微弱信号进行提取,混沌背景下的弱信号可以看作是非线性系统建模问题。本文基于神经网络对混沌海杂波背景下的信号检测技术进行研究,这有助于我国船舶信号检测技术的快速发展。
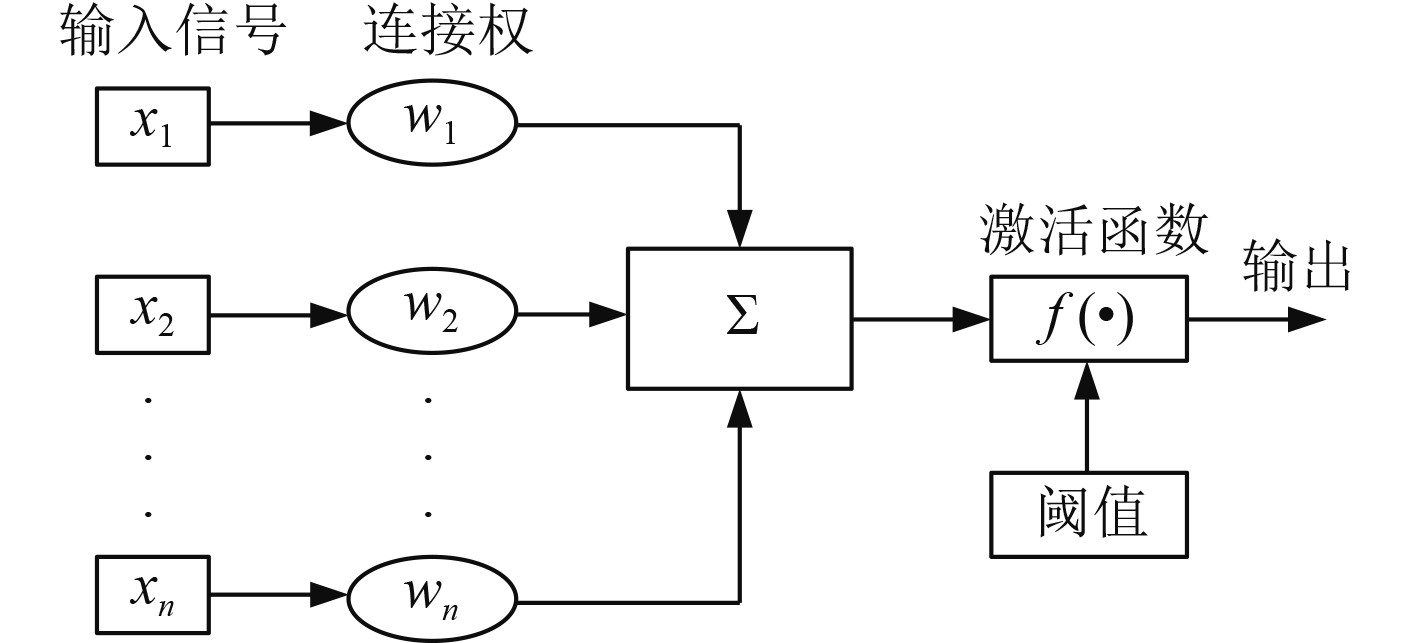
1 神经网络技术 1.1 神经元模型人工神经网络是通过构建很多的内部运算节点,同时对这些节点进行实时调整,最终使得计算结果可以逼近任何一种函数曲线,从而实现对数据信息进行加工处理的技术。随着神经网络内部节点的实时调节能力不断提升,神经网络技术发挥的作用不断增大。作为神经网络最基本的结构,神经元的结构如图1所示。
|
图 1 神经元模型 Fig. 1 Neuron model |
图1中的神经元模型是由激活函数、连接权、输入信号等共同构成的,并且输入信号和连接权相乘之后的结果通过加法器进行运算,同时将计算结果传递给激活函数,激活函数则对整体输入进行描述,并对输出进行限制。
可以在神经元模型中添加外部偏置bk。外部偏置对神经元的影响取决于该偏置的数据是正数还是负数,如果偏置bk>0,则神经元模型中的激活函数的输入会增加;反之,神经元模型中的激活函数的输入则会降低。神经元模型的数学描述为:
| $ {u_k} = \sum\limits_{i = 1}^m {{w_{ik}}{x_i}} \text{,} $ | (1) |
| $ {y_k} = f\left( {{u_k} + {b_k}} \right)\text{。} $ | (2) |
式中:xi为输入信号;wik为权重值;bk为外部偏置。激活函数的数学公式如式(3)所示;阈值函数的数学公式如式(4)所示;分段转移函数的数学公式如式(5)所示;非线性转移函数的数学公式如式(6)所示。
| $ v = {u_k} + {b_k}\text{。} $ | (3) |
| $ f\left( v \right) = \left\{ {\begin{array}{*{20}{c}} {1,v \geqslant 0},\\ {0,v \lt 0} 。\end{array}} \right. $ | (4) |
| $ {\text{g}}\left( v \right) = \left\{ {\begin{array}{*{20}{l}} {1,v \geqslant 1},\\ {v, - 1 \lt v \lt 1},\\ { - 1,v \leqslant - 1} 。\end{array}} \right. $ | (5) |
| $ h\left( v \right) = \frac{1}{{1 + {e^{ - v}}}}\text{。} $ | (6) |
式(6)中的非线性转移函数是[0,1]之间的非连接函数,非线性转移函数的解算优点在于函数本身及其导数是连续的,同时可以显示出神经元的饱和度,因此非线性转移函数被广泛地应用到神经元模型中。
1.2 神经网络模型及学习方法径向基函数神经网络的设计思想是将输入的信息映射至神经网络的隐藏层中,径向基函数神经网络的隐藏层空间是利用隐单元来创建的。确定径向基函数神经网络的中心点之后,神经网络的输入量和隐藏空间之间的对应关系也就确定了。径向基函数神经网络通过隐藏层得到的输入信号的线性加权之和即为神经网络的输出数据。径向基函数神经网络的神经元的传递数学模型多种多样,其中最常用的是高斯函数,其数学模型为:
| $ radbas\left( {\left\| {dist} \right\|} \right) = {e^{ - {{\left\| {dist} \right\|}^2}}}\text{。} $ | (7) |
式中,||dist||为输入向量和权重向量之间的距离。径向基函数神经网络是一种非线性函数,当||dist||的数据减小的时候,高斯函数输出的结果就会不断增大,当||dist||的值接近0的时候,高斯函数的输出值则会接近最大值1,此时径向基函数神经网络系统产生的响应比较小,当||dist||的值比较小的时候,径向基函数神经网络产生的响应比较大。径向基函数神经网络的结构以及输入的参数对该神经网络的性能有很大的影响。网络中隐含层节点是神经网络的主要结构,其主要参数有基函数的中心以及宽度。神经网络在训练过程中,可以先设置节点数为0,如果输出的结果和期望值之间的误差比较大,则可以逐渐增加节点数,直到输出结果满足期望值。径向基函数神经网络通常采用K-meas方法进行非监督学习,首先解算出基函数的宽度以及中心,然后使用最小二乘法对权重值进行解算,最后进行神经训练。径向基函数神经网络的数据处理数学模型为:
| $ y = \sum\limits_{i = 1}^n {{\omega _n}\phi \left( {\left\| {X - {C_i}} \right\|} \right)} \text{。} $ | (8) |
式中:X为神经网络的输入信号;ϕ为神经网络的径向基函数;ωn为权重值。当使用高斯径向基函数的时候,则可以得到:
| $ \phi \left( {\left\| {X - {C_i}} \right\|} \right) = \exp \left( { - \frac{{{{\left\| {X - {C_i}} \right\|}^2}}}{{2\delta _i^2}}} \right)\text{。} $ | (9) |
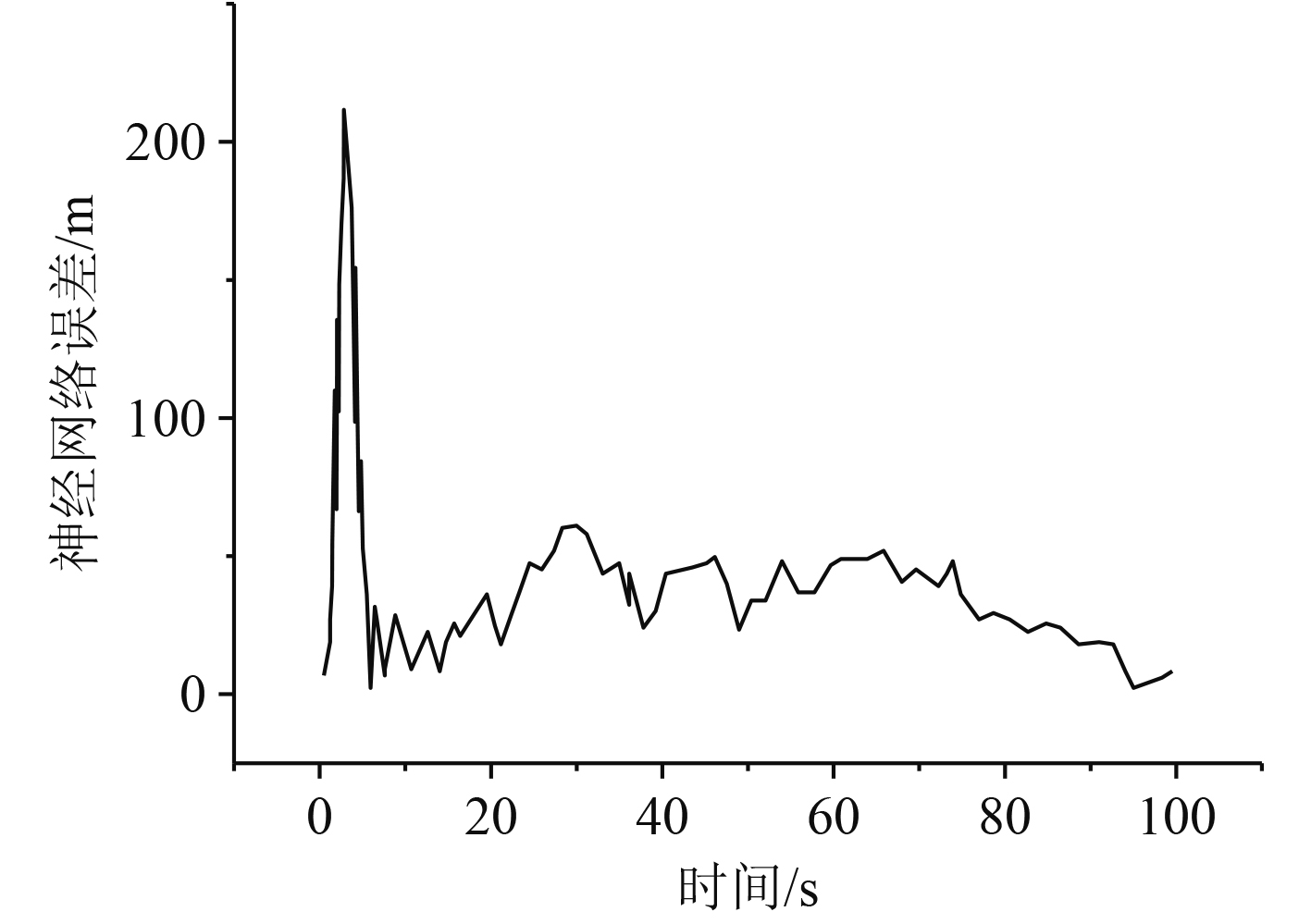
式中:δ为基函数的宽度。结合式(8)和式(9),则可以得到式(10)。基函数的宽度δ的计算方法如式(11)所示;式(10)中权重值ω的计算方法如式(12)所示,基函数的中心Ci的计算方法如式(13)所示。径向基函数神经网络的训练误差随时间变化如图2所示。
|
图 2 神经网络误差随时间变化 Fig. 2 The error of neural network changes with time |
| $ y = \sum\limits_{i = 1}^n {{\omega _i}\exp \left( { - \frac{{\left\| {{X_t} - {C_i}} \right\|}}{{2{\sigma ^2}}}} \right)} \text{,} $ | (10) |
| $ {\delta _i} = \frac{{{C_{\max }}}}{{\sqrt {2M} }}\text{,} $ | (11) |
| $ {\omega _i} = \exp \left( { - \frac{M}{{C_{\max }^2}}\left\| {{X_t} - {C_i}} \right\|} \right)\text{,} $ | (12) |
| $ {C_i}\left( {n + 1} \right) = \left\{ {\begin{array}{*{20}{l}} {C_i}\left( n \right) + \eta \left[ {{X_k}\left( n \right) - {C_i}\left( n \right)} \right],&i = i\left( {{X_k}} \right)\text{,} \\ {C_i}\left( n \right),& 0 < \eta < 1 \text{。} \end{array}} \right. $ | (13) |
混沌系统属于一种非线性的动力系统,并且混沌系统的状态方程是确定的。混沌是指在激励的作用之下,非线性系统对初始状态产生了一种十分敏感的运动,因此混沌系统既具备确定性的运动状态,同时也具备随机运动的运动状态。通常情况下,在一个确定的系统中,如果输入的信号是确定信号,那么其输出的信号也是确定的,但是在实际情况下,即使在确定的系统中输入确定的输入信息,其输出的结果也会出现类似于随机的无规则现象,这种现象即为混沌现象。混沌系统从运动过程上来看属于无规则的非线性系统的运动状态,但是混沌系统内部结构有序排列,因此混沌系统是一种新型的非线性系统。
根据Li-York理论,混沌系统中函数f的周期集P(f)=N,并且有S0:X-Per(f)满足
| $ \left\{ {\begin{array}{*{20}{l}} {\mathop {\lim }\limits_{n \to \infty } \sup d\left( {{f^n}\left( x \right),{f^n}\left( y \right)} \right) \gt 0,\forall x,y \in {S_0},x \ne y},\\ {\mathop {\lim }\limits_{n \to \infty } \inf d\left( {{f^n}\left( x \right),{f^n}\left( y \right)} \right) = 0,\forall x,y \in {S_0}} ,\\ {\mathop {\lim }\limits_{n \to \infty } \sup d\left( {{f^n}\left( x \right),{f^n}\left( p \right)} \right) \gt 0,\forall x \in {S_0},\forall p \in per\left( f \right)} 。\end{array}} \right. $ | (14) |
式中:f为Li-York理论下的混沌;S0为混沌集;per(f)为混沌f的周期点集。混沌现象是一种存在于确定的非线性系统中的复杂运动,和其他复杂的运动现象相比较,混沌运动具有5个独特的特征:1)是对混沌系统初始状态的高度敏感性;2)是运动状态的随机性;3)是在有限的时间内遍历所有的状态点;4)是运动轨迹的分维性;5)是不随运动方程的变化而变化的普适性。
2.2 海杂波混沌识别在实际解算过程中通常使用定量分析的方法对海杂波混沌进行识别,并且利用实时解算得到的关联维数、Lyapunov指数这2个特征参数对混沌系统的动态特征进行描述。在时间序列混沌的系统中,需要满足有限的关联维数以及正的Lyapunov指数这2个要求,根据这2个条件则可以验证海杂波的混沌动态特征。混沌系统中的动态空间的分布情况是通过关联维数来实现的,并且关联维数是最常见的统计特征,因此关联维数对描述非线性动态系统的几何构造以及需要的嵌入维数有着重要的作用。关联维数又被称作关联维数法,一般是通过G-P算法进行求解获得的。关联维数的求解方法为:
| $ D = \mathop {\lim }\limits_{r \to 0} \frac{{\log {C_n}\left( r \right)}}{{\log r}}\text{,} $ | (15) |
式中,Cn(r)为关联积分,其解算方法为:
| $ {C_{\text{n}}}\left( r \right) = \frac{1}{{N\left( {N - 1} \right)}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {H\left( {r - \left\| {{X_i} - {X_j}} \right\|} \right)} } \text{。} $ | (16) |
空间中轨道相互接近的平均指数速率用Lyapunov指数来表示,因此Lyapunov指数可以对海杂波时间序列混沌特性进行判断。Lyapunov指数不但可以分析混沌系统对初始状态的敏感性,还可以测量相邻轨道之间的平均发散率。Lyapunov指数的求解方法为:
| $ y\left( i \right) = \frac{1}{{\Delta t}}\left( {In{d_j}\left( i \right)} \right)\text{。} $ | (17) |
式中,dj(i)为平均发散率的估计值,其解算方法为:
| $ {d_j}\left( i \right) = {C_j}{e^{{\lambda _i}\left( {i\Delta t} \right)}}\text{。} $ | (18) |
系统运动状态可以通过Kolmogorov熵来表述,Kolmogorov熵是一种混沌不变量,可以通过该量来判断该系统是否是混沌系统。Kolmogorov熵的求解方法为:
| $ K = \sum\limits_{{\lambda _i} \gt 0} {{\lambda _i}} \text{。} $ | (19) |
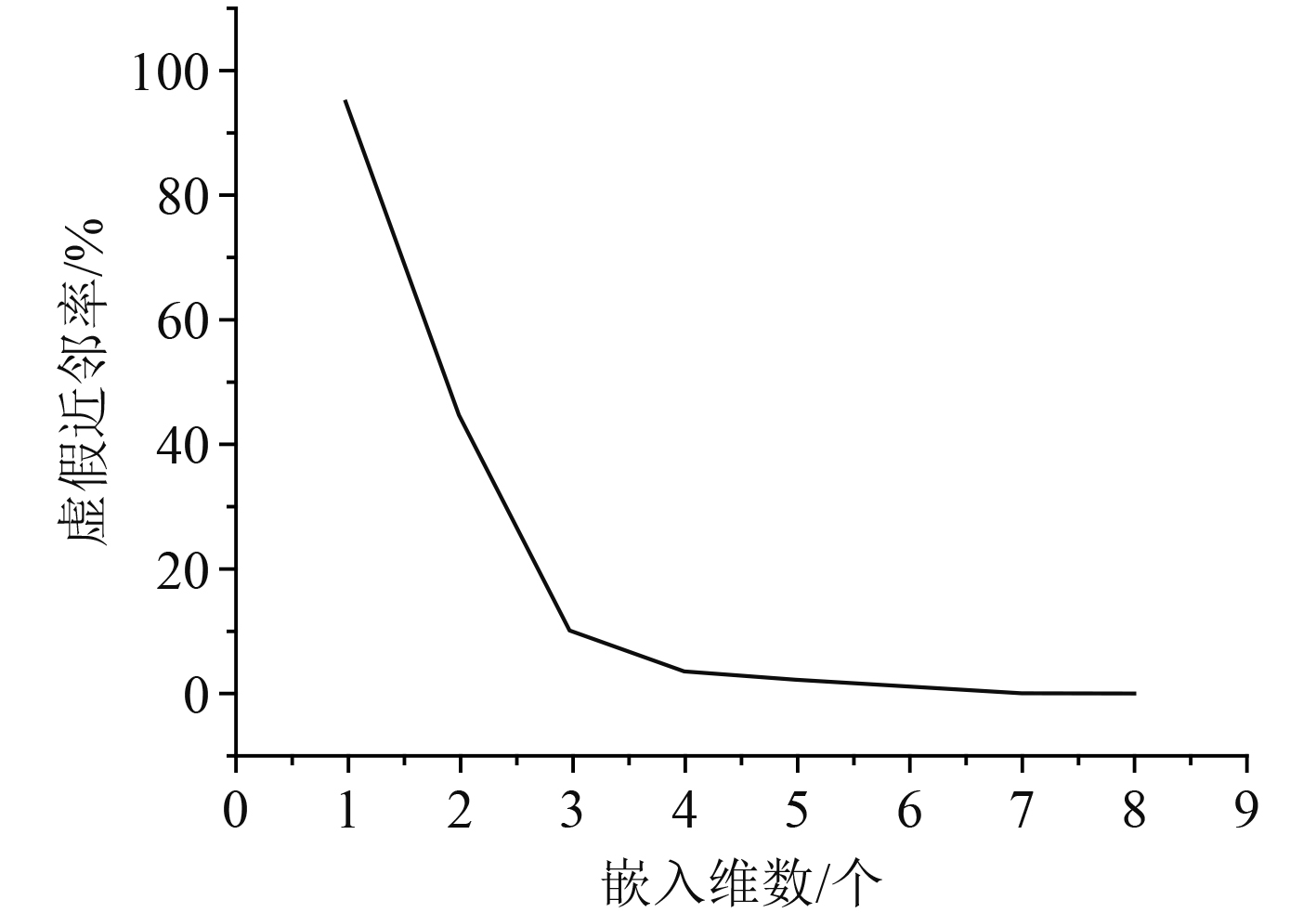
|
图 3 虚假近邻率随嵌入维数的变化曲线 Fig. 3 Curve of false nearest neighbor rate changing with embedding dimension |
以径向基函数为基础对混沌海杂波下的信号进行检测,首先需要构建出混沌海杂波的预测模型,接着以混沌海杂波预测模型为基础对周围海杂波数据进行判断,最终完成目标信号的检测。由于海面周围的各种自然环境对海杂波的分布有着很大的影响,因此通常把海杂波看成是高维非线性系统并进行分析。由于船舶上的雷达接收机收到的信号是一维的时间序列,因此需要通过径向基函数神经网络模型进行相空间重构,并得到海杂波混沌检测模型,最后利用预测误差检测方法识别出海杂波背景下的弱信号。预测误差计算方法如式(20)所示,总误差的均方值的计算方法如式(21)所示,均方根的误差可以通过式(22)计算。
| $ \varepsilon \left( n \right) = x\left( n \right) - \hat x\left( n \right)\text{,} $ | (20) |
| $ {R_\varepsilon } = \frac{1}{N}\sum\limits_{n = 1}^N {{\varepsilon ^2}\left( n \right)} \text{,} $ | (21) |
| $ RMSE = \sqrt {\frac{1}{N}\sum\limits_{n = 1}^N {{{\left( {x\left( n \right) - \hat x\left( n \right)} \right)}^2}} } \text{。} $ | (22) |
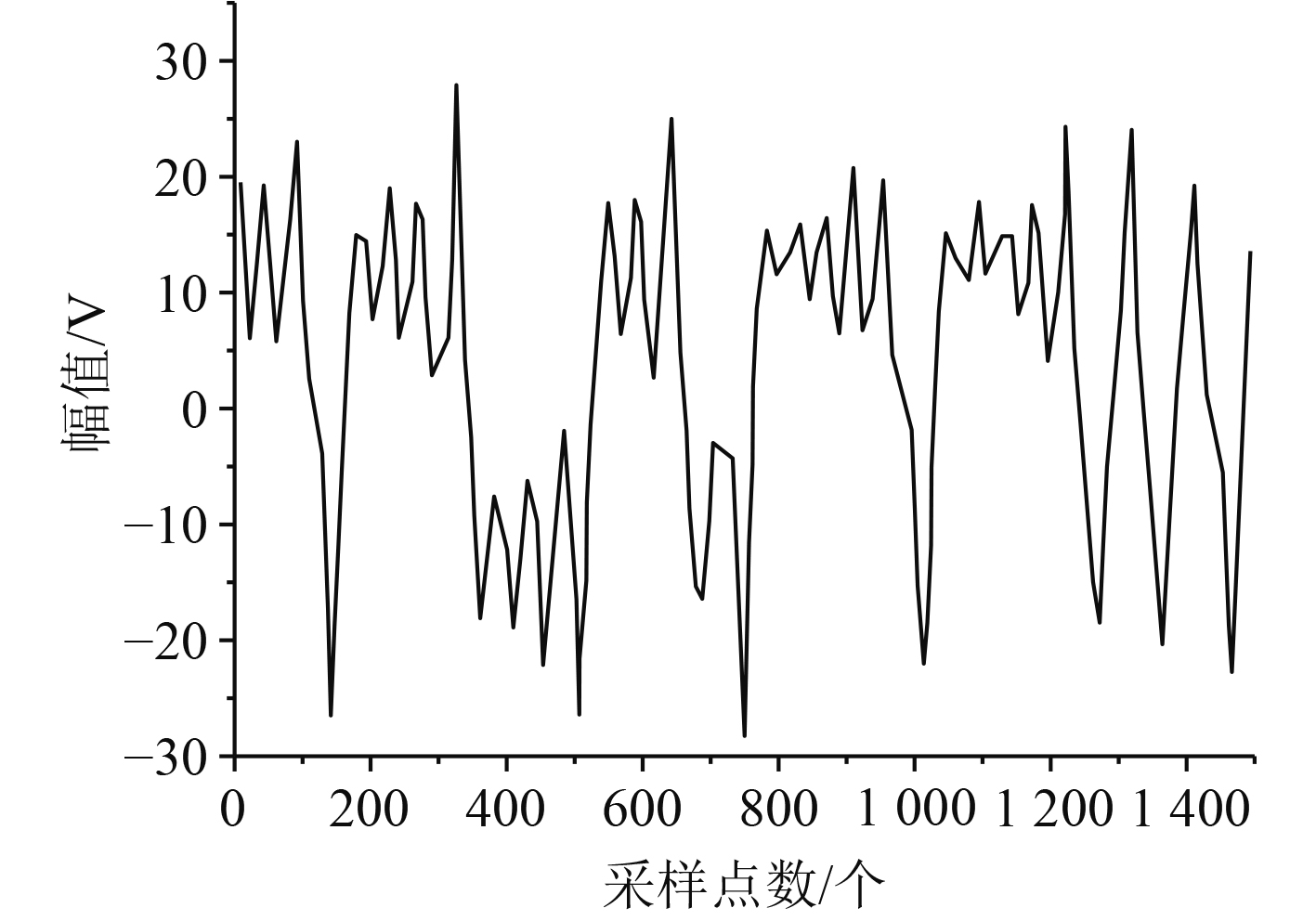
通过均方根的误差可以对神经网络检测误差的大小进行判断,混沌背景下存在海杂波的目标信号可以通过式(23)来描述。图4给出了混沌时间序列曲线。
|
图 4 混沌时间序列曲线 Fig. 4 Chaotic time series curve |
| $ \left\{ {\begin{array}{*{20}{l}} {{H_0}:x\left( n \right) = c\left( n \right)}\text{,} \\ {{H_1}:x\left( n \right) = s\left( n \right) + c\left( n \right)} \text{。} \end{array}} \right.$ | (23) |
随着非线性科学的快速提升,非线性科学极大地提升了人类认识、分析以及解决问题的能力。由于海杂波具备混沌的特点,因此早期对海杂波的各类建模研究均存在精度低、适应性差、模型构建过程复杂等特点,这些海杂波的模型只是使用了海杂波的随机性质,没有充分地研究海杂波的物理本质。海杂波混沌的性质可以通过确定海杂波的混沌参数进行分析,由于混沌参数会受到噪声的影响,因此可以结合神经网络技术对海杂波进行分析。使用海杂波的特点对船舶周围海面上的目标进行探测,这对提升国家海洋的监控安全有着积极地意义。
| [1] |
石嘉, 夏德平. 海杂波背景下的PSO-RBF弱目标检测[J]. 电子测量技术, 2019(42): 35-39. DOI:10.19651/j.cnki.emt.1802251 |
| [2] |
温晓君. 海杂波背景下基于神经网络的目标检测[J]. 系统仿真学报, 2007(19): 1639-1641. DOI:10.3969/j.issn.1004-731X.2007.07.058 |
| [3] |
许述文, 白晓惠, 郭子薰, 等. 海杂波背景下雷达目标特征检测方法的现状与发展[J]. 雷达学报, 2020(9): 684-714. |
| [4] |
杜鹏飞, 王永良, 孙文峰. 混沌海杂波背景下的弱信号检测[J]. 系统工程和电子技术, 2022(24): 65-67+98. |
| [5] |
孙江, 行鸿彦, 吴佳佳. 基于IA-SVM模型的混沌小信号检测方法[J]. 探测与控制学报, 2020(42): 119-125. |
| [6] |
朱丽莉, 张永顺, 李兴成. 基于RBF神经网络的混沌背景下瞬态弱信号检测[J]. 空军工程大学学报, 2006(7): 61-63. |
| [7] |
王海峰, 行鸿彦, 陈梦, 等. 基于SSA-SVM的海杂波背景下小信号检测方法[J]. 电子测量与仪器学报, 2022(36): 24-31. DOI:10.13382/j.jemi.B2105061 |
| [8] |
谢红梅, 俞卞章. 基于神经网络预测器的混沌海杂波弱信号检测[J]. 现代雷达, 2022(36): 24-31. |
| [9] |
商庆健, 张金敏, 王厅长. 基于有效K均值-有效极限学习机的混沌海杂波背景中微弱信号检测[J]. 计算机应用, 2015(35): 896-900. |
| [10] |
张先芝, 尚尚, 戴圆强, 等. 强海杂波背景下目标检测方法综述[J]. 遥测遥控, 2022(43): 13-20. |
 2022, Vol. 44
2022, Vol. 44
