舰载相控阵雷达是舰船防御作战系统的重要组成部分,担负对空对海搜索、目标指示、多目标跟踪等任务,其测量精度影响舰船作战效能和生存能力[1,2]。对于新装配雷达设备,按GJB 403A-1998《舰载雷达通用规范》测量误差指标要求进行调试和试验验证。测量误差主要包括由天线幅相误差、零深误差、目标起伏因素等引起的系统误差和由系统热噪声误差、多路径误差引起的随机误差[3-4],以及平台修正、参数装订引入误差等。其中,平台参数引入误差是雷达生产试验中需特别关注的一项重要内容。吕向阳等[5,6]研究了机械转台下的舰载雷达天线电子稳定方程,将平台剩余误差引入方程进行二次修正,应用于转台伺服系统。雷杰等[7-8]研究了平台罗经状态参数对雷达天线指向和雷达测角的影响;陶军等[9]分析了阵面装订参数误差对雷达测角的影响;李洪梅[10]分析了不同平台传感器探测偏差影响因素。上述文献均涉及到了舰载雷达平台坐标转换的基本原理,仅对某个转换节点进行单一分析,未结合实际应用做具体研究。基于此,本文结合舰载某大型数字相控阵雷达生产试验中标校任务,综合考虑舰姿态参数(横摇、纵摇、航向)、阵面姿态参数(阵面倾角、不水平度、法向角)等引入误差,研究在不同雷达扫描角下的误差传递情况,为标校数据的有效性和平台参数的正确性分析提供依据。
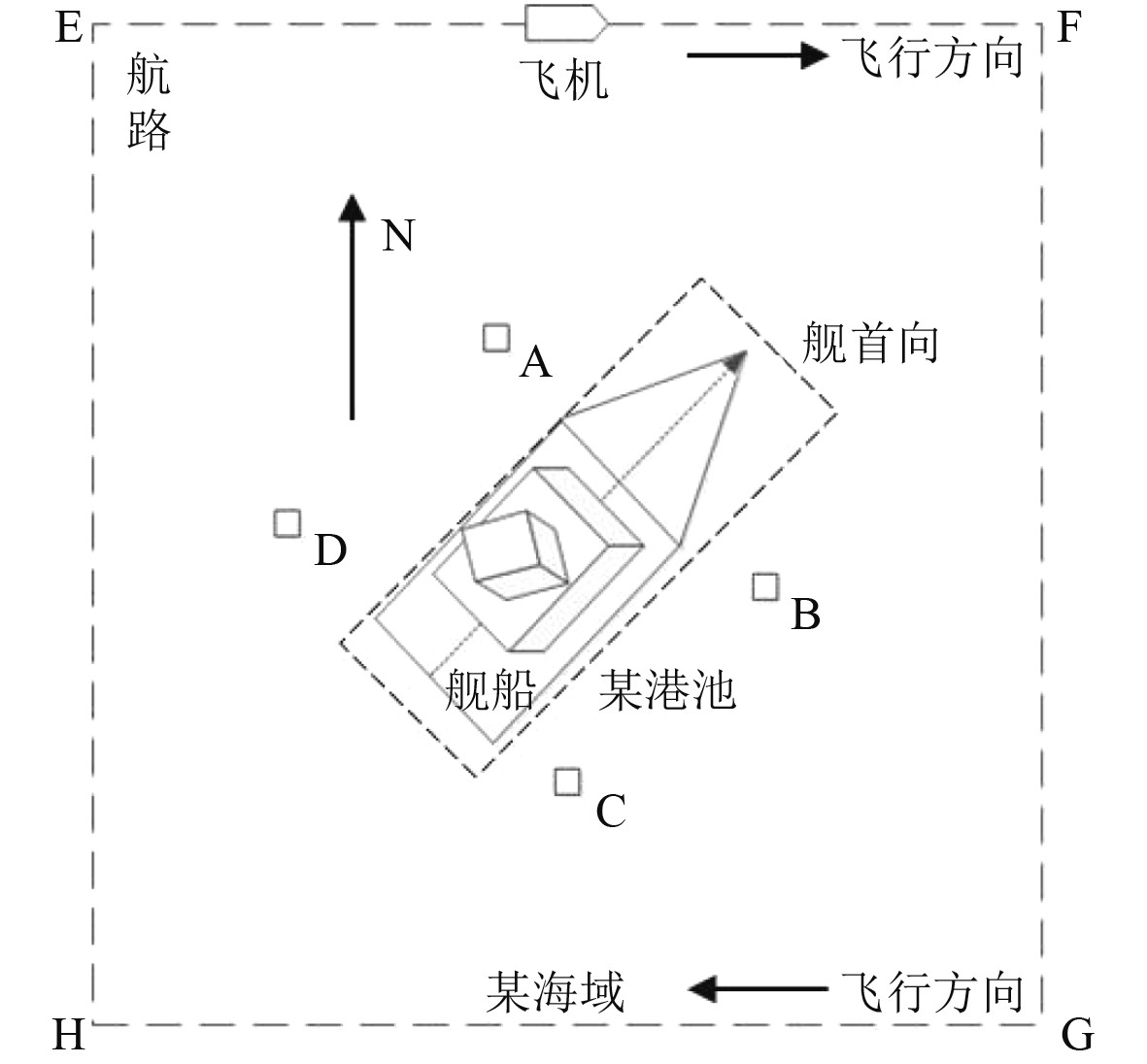
1 标校方法介绍标校方案如图1所示。静态标校:场地一般选为某港池,舰船处于半蹲状态;A,B,C,D点为标校塔位置,塔顶架设信号源,辐射与雷达工作频点一致的电磁波信号;雷达处于接收状态,根据波瓣测量得出辐射源位置信息,作为测量值;通过激光陀螺仪标定出源相对于阵面中心的位置信息,作为真值;计算测量值与真值的一次差以及均方根值,完成系统零位一致性对准的初步评估。动态标校:场地一般选为某海域,舰船处于低速航行状态;配试飞机配备差分全球定位系统(GPS),沿航路E-F-G-H飞行;舰上架设GPS测量基站和数据记录设备,差分得出相对位置信息,作为标校真值;雷达开机加激励,捕获目标飞机,实时记录目标数据,作为测量值;测量值与真值作一次差,完成系统大角度误差等总体性能评估。工程实现流程如图2所示。
|
图 1 标校方案简示图 Fig. 1 Schematic diagram of calibration scheme |
|
图 2 标校工程实现简要流程 Fig. 2 Chart of calibration implementation |
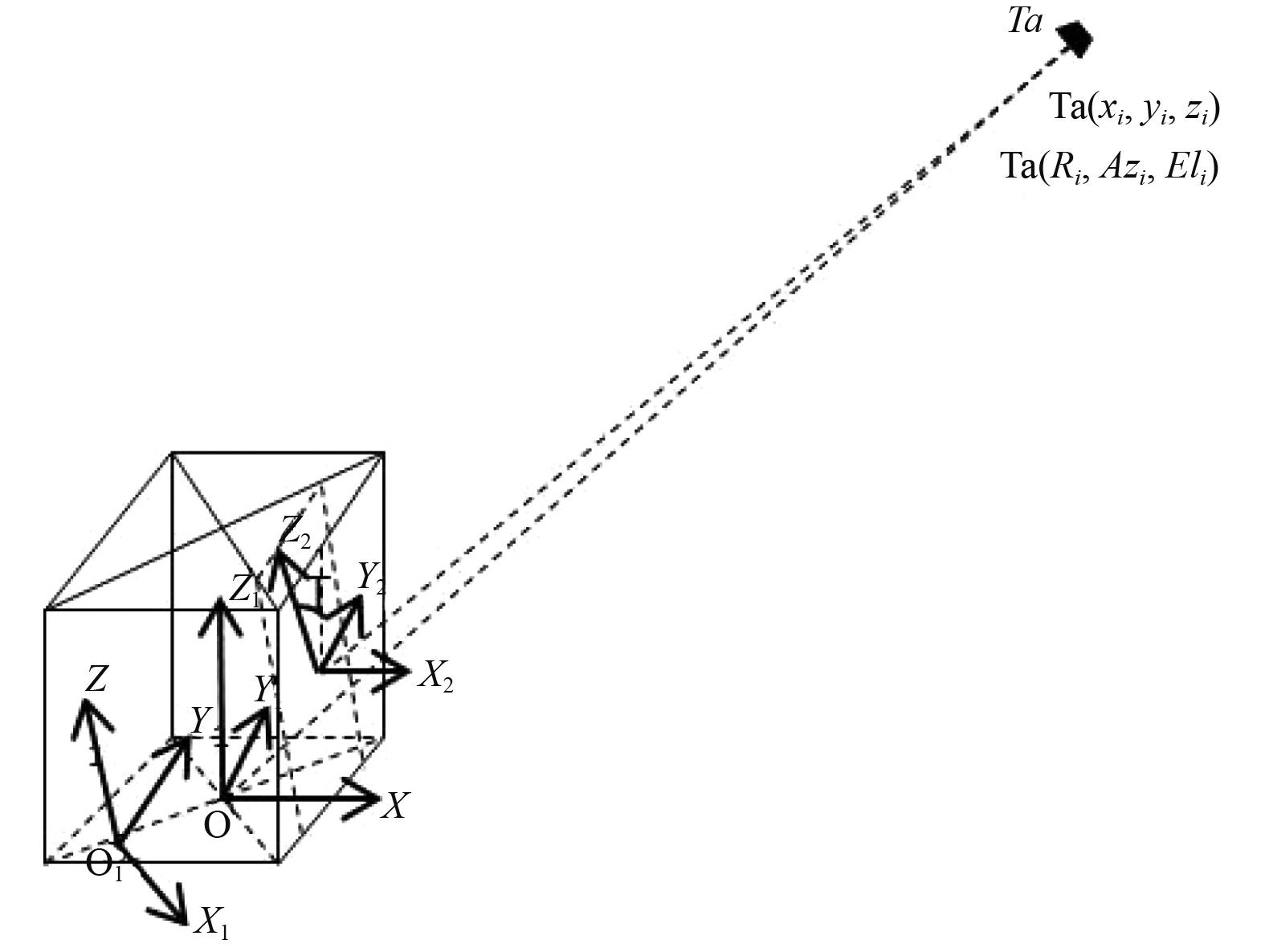
数字相控阵雷达根据波控系统提供的波控码控制信号,改变每个天线单元的相移,实现波束扫描[11]。根据回波信息,雷达测角模块首先给出阵面坐标系的目标信息。而舰载雷达人工交互界面给出的目标信息为天线阵面坐标系→甲板坐标系→站心坐标系变换的结果,转换过程中引入阵面姿态和舰姿态参数,以此建立如图3所示的转换模型。O-XYZ为站心坐标系:O点为坐标原点(雷达回转中心);X轴指向地理东,Y轴指向地理北,Z轴指向天空;3个坐标轴满足右手定则。O1-X1Y1Z1为甲板坐标系:O1点为坐标原点(平台罗经中心);Y1轴为舰船首尾线,指向舰首;Z1轴垂直于舰船基面,向上为正;3个坐标轴满足右手定则。O2-X2Y2Z2为阵面坐标系:O2为坐标原点(阵面中心);X2轴为阵面法向,向上为正;Z2轴垂直于阵面与舰船基面的交线,向上为正;3个坐标轴满足右手定则。Ta点为目标位置,
|
图 3 平台修正简易模型 Fig. 3 Model of platform modification |
规定角度顺时针为正,目标的方向向量为:
| $\begin{aligned}[b] {\vec C_i}(A{z_i},E{l_i}) = &(\cos (E{l_i})\cos (A{z_i}), -\\ & \cos (E{l_i})\sin (A{z_i}),\sin (E{l_i}))^ \wedge {\rm{T}} 。\end{aligned} $ | (1) |
式中:
| $ {{\vec C}_0}(A{z_0}',E{l_0}) = {M_1}{{\vec C}_1}(A{z_1},E{l_1}),$ | (2) |
| $ {{\vec C}_1}(A{z_1}',E{l_1}) = {M_2}{{\vec C}_2}(A{z_2},E{l_2})。$ | (3) |
其中:
| $ A{z_0} = A{z_0}' + \alpha 。$ | (4) |
其中:
| $ A{z_1} = A{z_1}' + (\beta + \Delta \beta )。$ | (5) |
| $ {{\boldsymbol{M}}_1} = \left[ \begin{gathered} \cos (R){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \sin (R) \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \\ \sin (R){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cos (R) \\ \end{gathered} \right] \cdot \left[ \begin{gathered} 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cos (P){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sin (P) \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \sin (P){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cos (P) \\ \end{gathered} \right] ,$ |
| $\begin{split} {{\boldsymbol{M}}_2} =& \left[ {\begin{array}{*{20}{c}} {\cos (T + \Delta T)} & 0 & { - \sin (T + \Delta T)}\\ 0 & 1 & 0\\ {\sin (T + \Delta T)} & 0 & {\cos (T + \Delta T)} \end{array}} \right] \times \\ &\left[ {\begin{array}{*{20}{c}} 1 & 0 & 0\\ 0 & {\cos (\sigma + \Delta \sigma )} & {\sin (\sigma + \Delta \sigma )}\\ 0 & { - \sin (\sigma + \Delta \sigma )} & {\cos (\sigma + \Delta \sigma )} \end{array}} \right]。\end{split}$ |
式中:
以雷达回转中心为坐标原点作归心修正,便可实现目标在阵面坐标系到站心坐标系的转换。归心修正表达式为:
| $ \begin{split} & Az = {\tan ^{ - 1}}\left(\frac{{y' - \Delta y}}{{x' - \Delta x}}\right),\\ & El = {\tan ^{ - 1}}\left(\frac{{z' + \Delta z}}{{\sqrt {{{(x' - \Delta x)}^2} + {{(y' - \Delta y)}^2}} }}\right)。\end{split} $ | (6) |
式中:
从上述电子修正方法可得,站心坐标系下目标角误差主要来源于阵面测角误差、舰姿态参数误差和阵面姿态参数误差。阵面测角误差来源于设计因素,不在本文讨论范围。舰姿态参数由平台罗经系统为舰载雷达提供,存在随机误差和系统误差,通过多传感器信息融合和卡尔曼滤波等滤波技术进行平滑,但仍存在输出信息误差放大的现象[8]。阵面姿态参数为通过陀螺仪或激光测距仪测量得出的数据,测量精度较高[12]。但在计算测量值时,存在左或右偏离理想值的正负判断失误的情况,得出误差偏大的数据;阵面姿态参数为需装订的系统参数,其误差为固定误差。本文分析舰姿态单次测量误差和阵面姿态固定误差对不同扫描角目标的雷达测量精度影响情况。
1)舰姿态误差传递
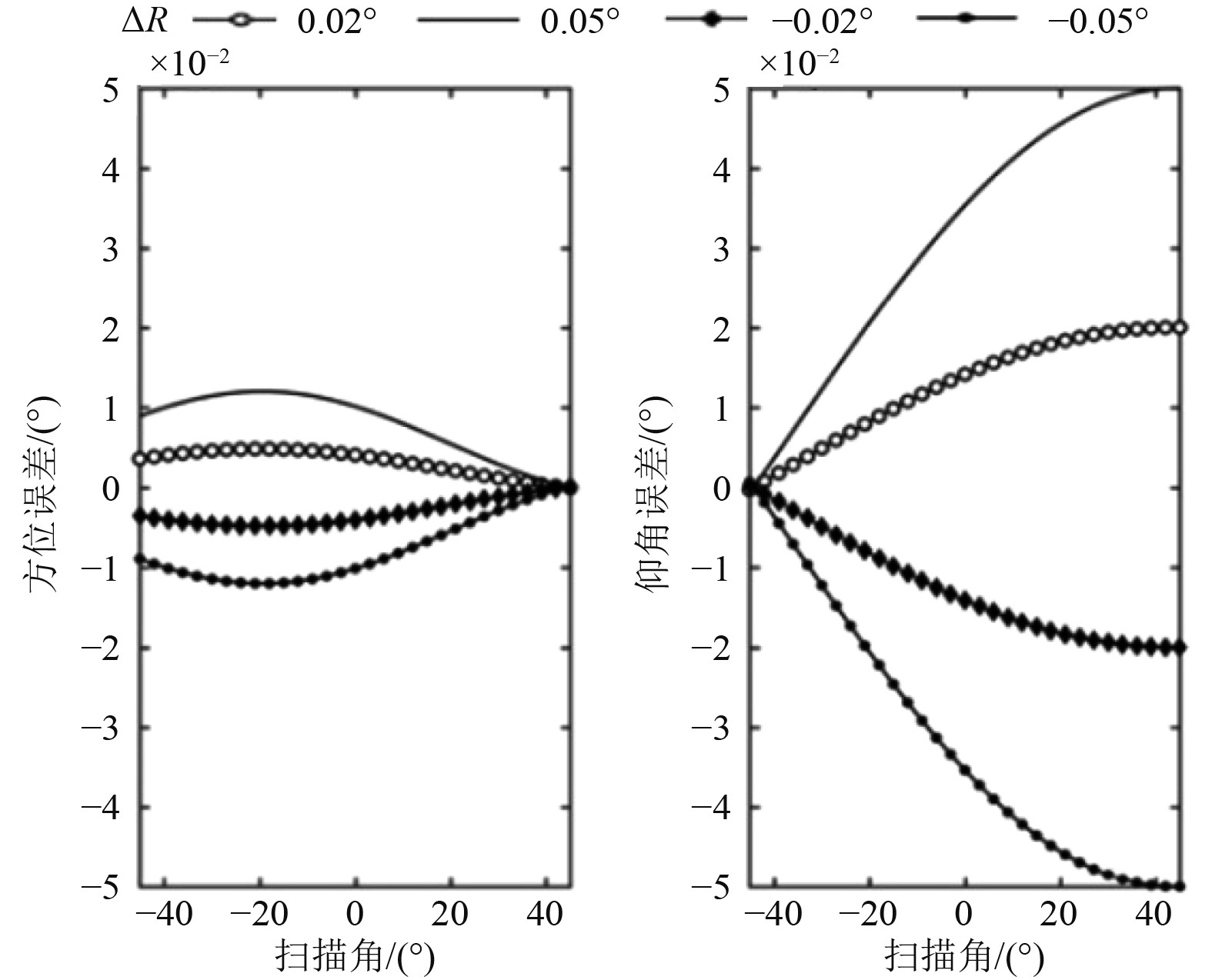
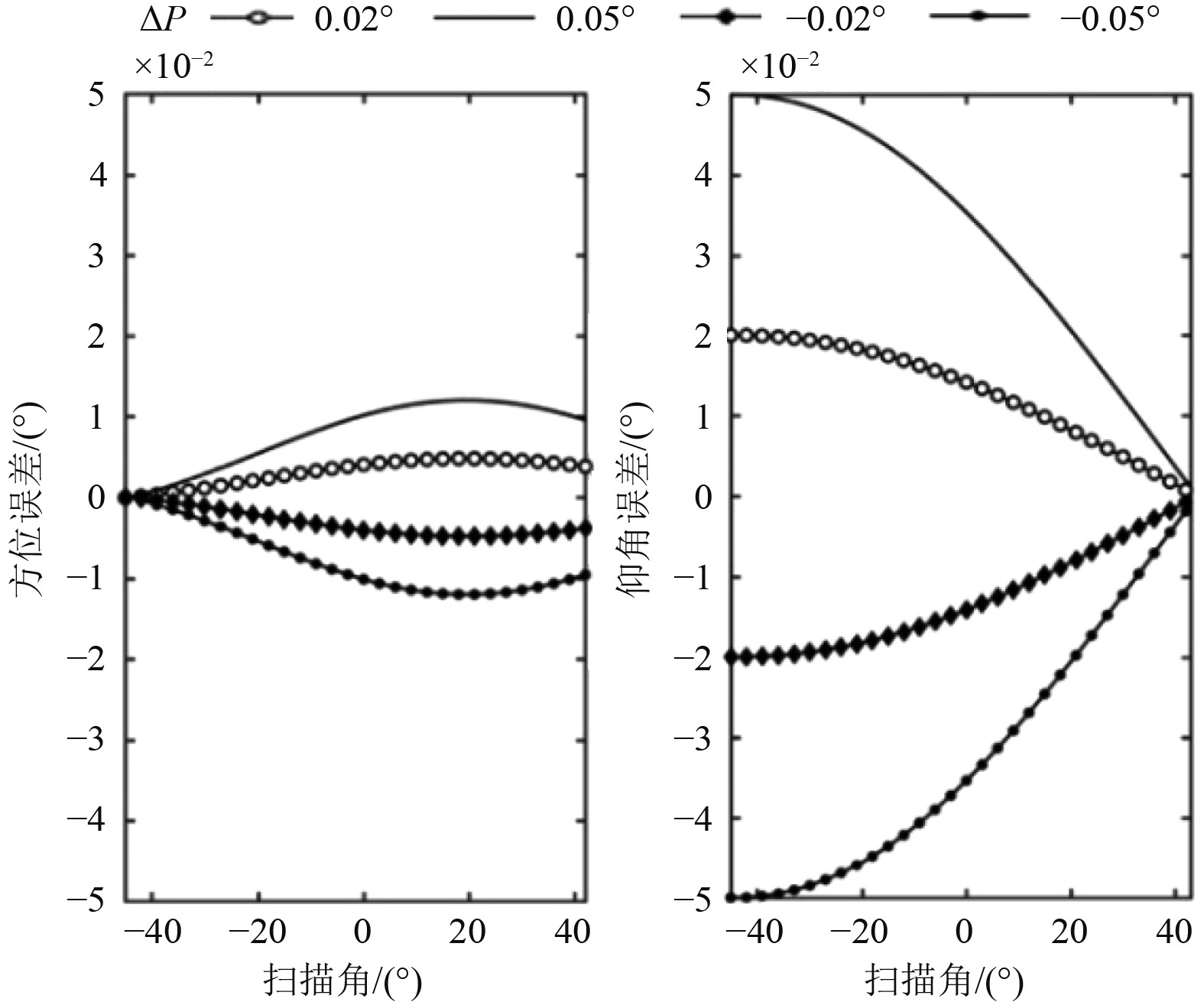
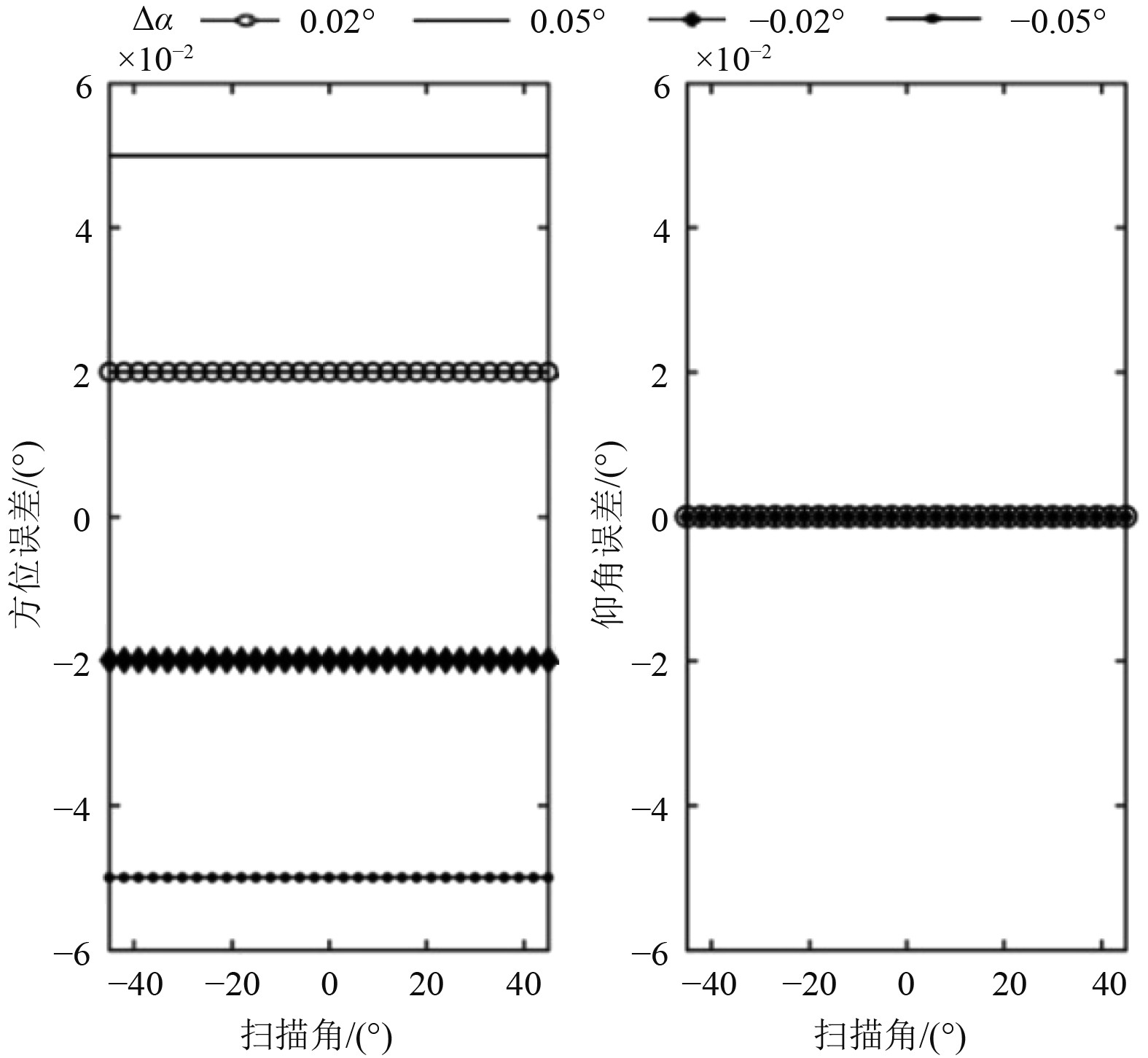
图4~图6分别为舰船横摇、纵摇和航向角误差对雷达测角在不同扫描角(0°为阵面法向)下的传递情况。可以看出:雷达测角误差随舰姿态参数误差增大而变大;纵横摇误差对雷达方位测量的影响较小,随扫描角差异小;纵横摇对雷达仰角测量的影响灵敏度相对高,不同扫描角下影响差异明显;横摇影响下误差绝对值随扫描角(–45°~45°)增大,纵摇影响下误差绝对值随扫描角(–45°~45°)减小;航向角误差对雷达方位测量误差为线性传递关系,不受扫描角调制;航向角误差不影响雷达测量仰角的精度。
|
图 4
横摇误差
|
2)阵面姿态误差传递
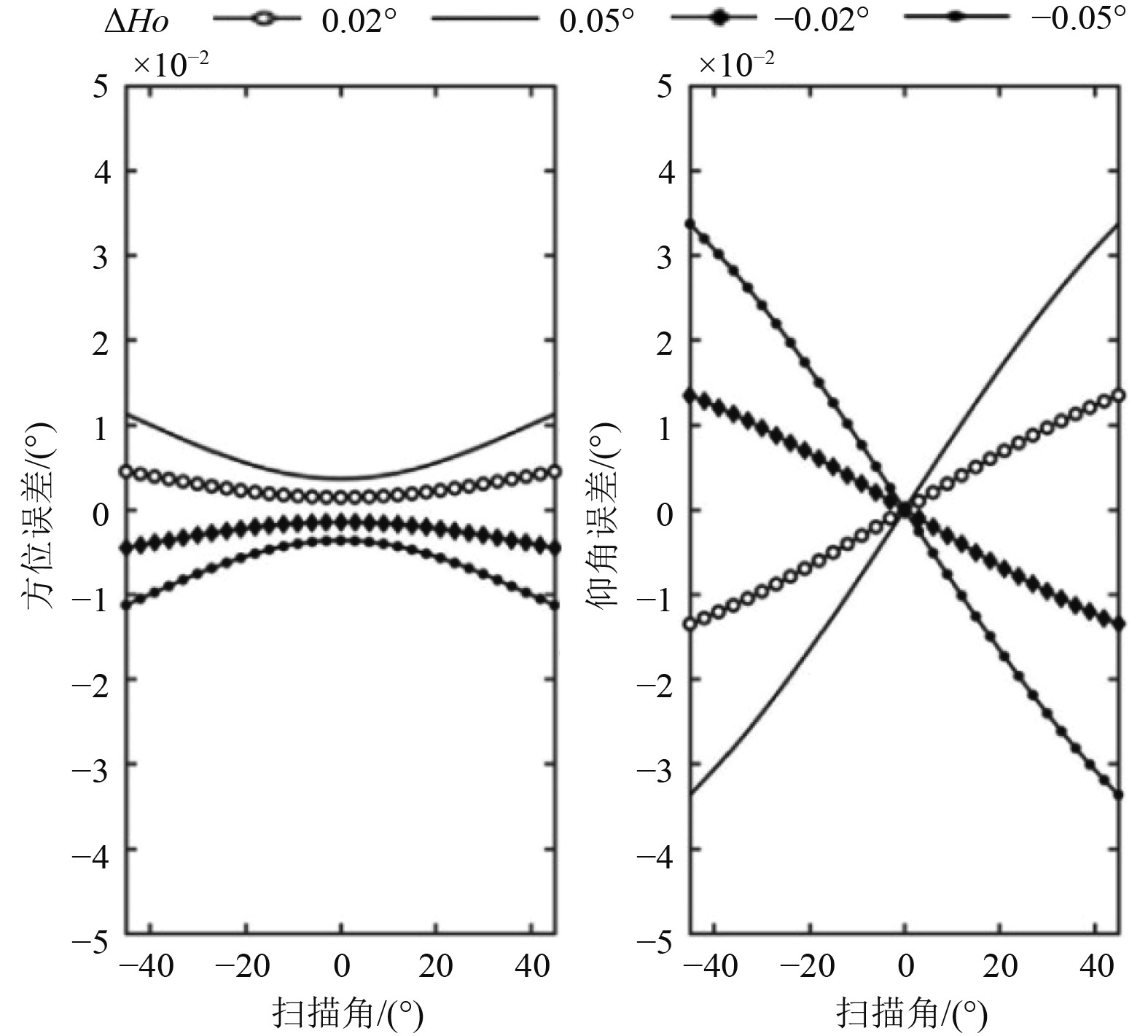
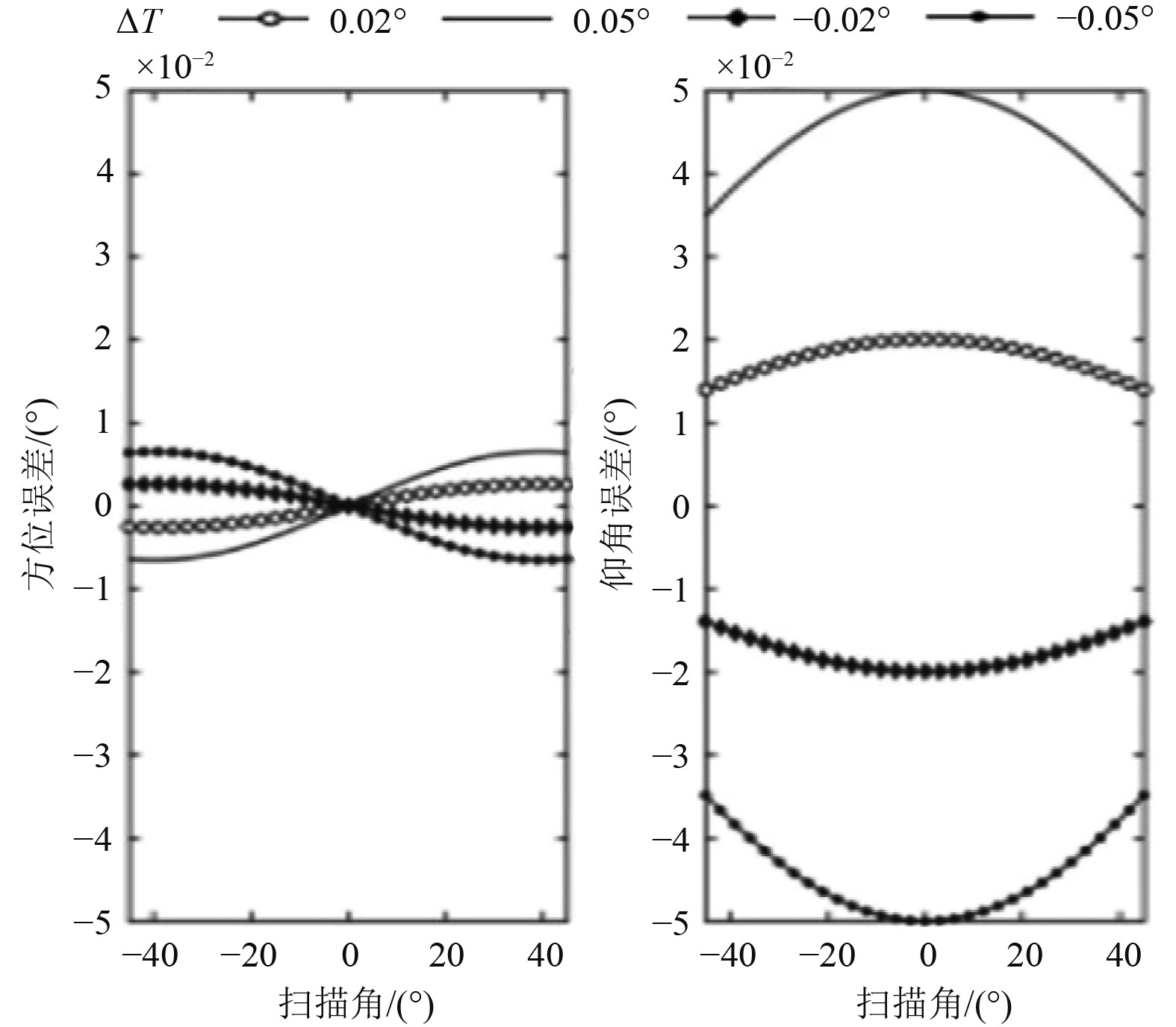
图7~图9分别为阵面不水平度、倾角和法向角误差对雷达测角在不同扫描角(0°为阵面法向)下的传递情况。可以看出:雷达测角误差随阵面姿态参数误差增大而变大;不水平度误差和倾角误差对雷达方位测量的影响较小,随扫描角差异小;不水平度误差和倾角误差对雷达仰角测量的影响灵敏度高,随扫描角变化较为明显(误差绝对值在阵面法向两边趋向于对称;在不水平度误差影响下,仰角误差绝对值随扫描角变大(不水平度误差为正时,仰角误差整体趋势向右倾斜;不水平度误差为负时,仰角误差整体趋势向左倾斜);在倾角误差影响下,仰角误差在法向反而大,绝对值随扫描角减小);法向角误差对雷达方位测量误差为线性传递关系,不受扫描角调制;法向角误差不影响雷达仰角测量精度。
|
图 5
纵摇误差
|
|
图 6
航向角误差
|
|
图 7
不水平度误差
|
|
图 8
倾角误差
|

|
图 9 法向角误差对测角的影响 Fig. 9 Influence of on angle measurement |
根据所述方案开展某舰校飞试验,对所记录的动态标校数据进行分析(因某些限制,不给出具体误差精度,仅评估整体趋势状态;且仅给出存在异常以及修正后验证的数据)。图10为2个阵面的仰角一次差(仰角测量值-仰角真值)分析图。图10(a)为首次校飞数据,2阵面各扫描角下的误差在指标要求范围内,但1阵面存在测量误差随大角度增大的现象;结合姿态参数数据对测角误差的影响情况,重新装订阵面不水平度后重演数据,符合指标要求。图10(b)为复核试验校飞数据,符合指标要求。
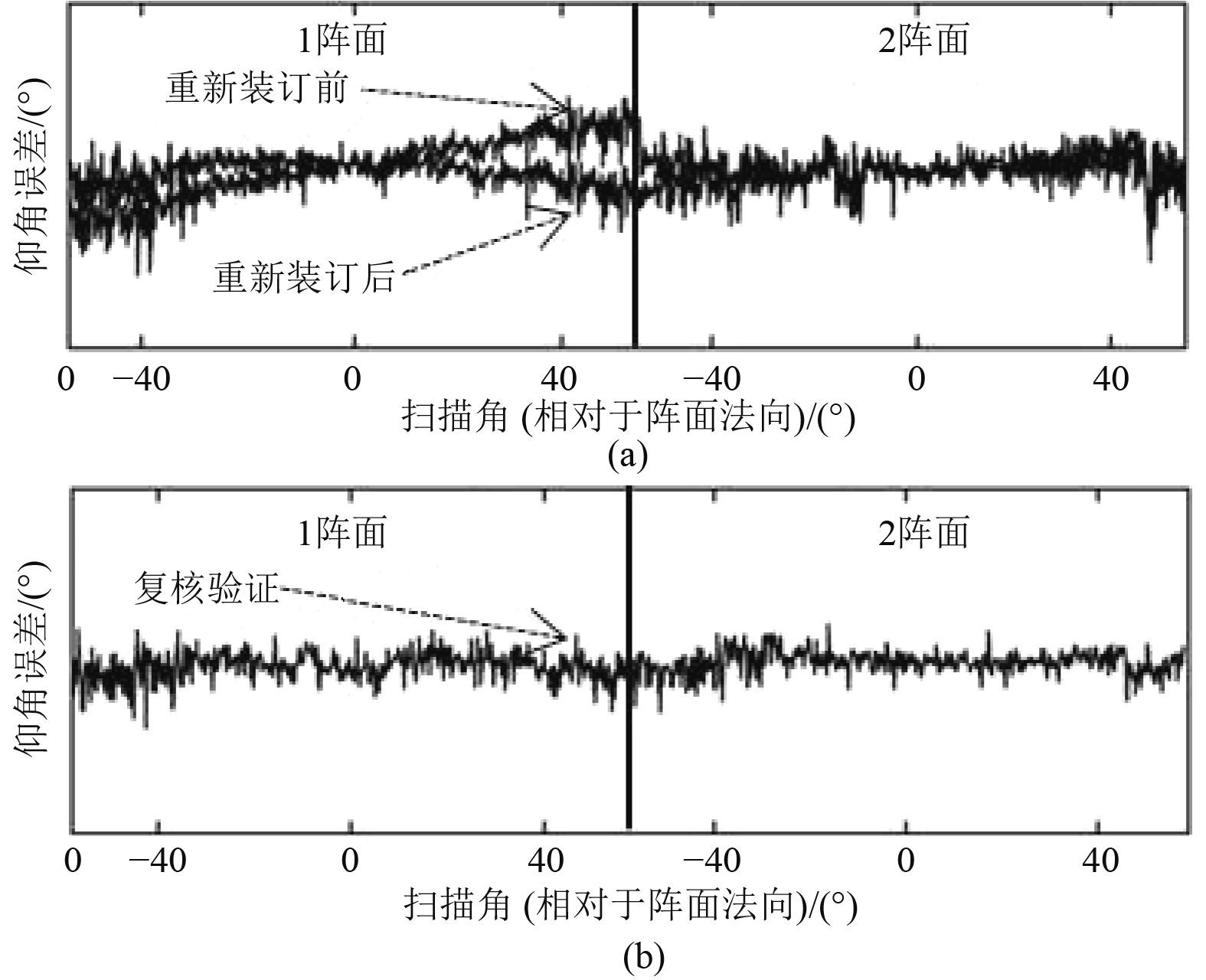
|
图 10 试验数据处理 Fig. 10 Processing of test data |
本文结合雷达生产过程中的一致性校准试验,建立基于目标方向向量的平台修正模型,分析舰船姿态和阵面姿态对雷达测角的影响,得出以下结论:
1)平台参数误差传递在静态单点标校下表征不明显,而在动态标校大角度对比下表征明显;
2)舰船航向角误差和阵面法向角误差仅影响雷达方位角测量精度,不影响雷达仰角测量精度;方位角测量误差不受扫描角调制,随航向角误差和阵面法向角误差趋于线性增加;
3)舰船横摇、纵摇误差和阵面不水平度、倾角误差对雷达仰角测量精度的影响度更强,大角度误差差异大;对雷达方位测量精度的影响度小,大角度误差差异小;
4)舰船横摇、纵摇误差影响下,雷达仰角测量误差单调变化;阵面不水平度、倾角误差影响下,雷达仰角测量误差在阵面法向两边趋于对称。
结合舰船雷达测量技术指标要求,对舰载某相控阵雷达标校数据进行分析,为数据有效性和平台装订参数正确性提供评判依据,对舰船雷达列装试验有指导性意义。
| [1] |
段静玄, 郑剑飞, 赵复政, 等. 基于全球定位系统的舰载三坐标雷达动态标校方法[J]. 中国舰船研究, 2012, 39(4): 100-104. DUAN J X, ZHENG J F, ZHAO F Z, et al. A GPS based dynamic calibration method for shipborne three-dimensional radar[J]. Chinese Journal of Ship Research, 2012, 39(4): 100-104. DOI:10.3969/j.issn.1673-3185.2012.04.017 |
| [2] |
季勤超, 姚申茂, 杨利斌, 等. 基于无人机和差分GPS的舰载雷达动态标校方法[J]. 计算机与数字工程, 2018, 348(10): 1984-1988. JI Q C, YAO S M, YANG L B, et al. Dynamic calibration method of shipboard radar based on unmanned aerial vehicle and differential GPS[J]. Computer& Digital Engineering, 2018, 348(10): 1984-1988. DOI:10.3969/j.issn.1672-9722.2018.10.010 |
| [3] |
方棉佳, 吕涛. 单脉冲和差波束测角的精度研究[J]. 雷达科学与技术, 2013, 11(6): 645-649. DOI:10.3969/j.issn.1672-2337.2013.06.015 |
| [4] |
王晓楠. 基于相控阵雷达波束扫描的目标测角误差分析[J]. 舰船电子对抗, 2018, 279(3): 74-78. |
| [5] |
吕向阳. 舰载雷达天线电子稳定方程在三轴稳定转台雷达上的应用分析[J]. 雷达与对抗, 2017, 193(4): 54-57. LV X Y. Application of electronic stabilization equation of ship-borne radar antenna in radars with three-axis stabilizing rotary platform[J]. Radar& ECM, 2017, 193(4): 54-57. |
| [6] |
雷杰, 严康, 郭锐. 舰载雷达三轴转台稳定方程推导[J]. 现代雷达, 2017, 320(7): 66-69. |
| [7] |
曹正才. 舰载雷达常用稳定方式坐标变换[J]. 雷达与对抗, 2010, 162(1): 47-52. |
| [8] |
陈欣. 平台罗经误差对舰载雷达测角精度的影响分析[J]. 江苏科技信息, 2017, 521(8): 52-54. DOI:10.3969/j.issn.1004-7530.2017.08.021 |
| [9] |
陶军, 唐晓雷, 黄晓辉. 阵面安装误差对相控阵雷达测角精度的影响[J]. 数据采集与处理, 2017, 146(6): 1179-1186. TAO J, TANG X L, HUANG X H. Angle measurement accuracy of phased array radar with array installation errors[J]. Journal of Data Acquisition and Processing, 2017, 146(6): 1179-1186. |
| [10] |
李洪梅, 潘江怀, 何佳洲, 罗双喜. 舰载雷达探测误差传递与灵敏度分析[J]. 数据采集与处理, 2012, 114(4): 474-479. LI H M, PAN J H, HE J Z, et al. Error transfer and sensitivity analysis of ship-borne radar detecting[J]. Journal of Data Acquisition and Processing, 2012, 114(4): 474-479. DOI:10.3969/j.issn.1004-9037.2012.04.013 |
| [11] |
金东勇, 陈俊霞, 李艳华. 平面相控阵天线波束控制技术[J]. 太赫兹科学与电子信息学报, 2021, 19(1): 75-79. JIN D Y, CHEN J X, LI Y H. Beam-steering of planar phased array antenna[J]. Journal of Teraherta Science and Electronic Information Technology, 2021, 19(1): 75-79. DOI:10.11805/TKYDA2019433 |
| [12] |
梅启元, 沈文军. 一种大型相控阵雷达阵面的安装调整方法[J]. 电子机械工程, 2014, 172(6): 36-39. MEI Q Y, SHEN W J. An installing and adjusting method for antenna array of large phased array radar[J]. Electro-Mechanical Engineering, 2014, 172(6): 36-39. DOI:10.3969/j.issn.1008-5300.2014.06.011 |
 2022, Vol. 44
2022, Vol. 44
