2. 哈尔滨工程大学 水下机器人技术重点实验室, 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001
2. Science and Technology on Underwater Vehicle Laboratory, Harbin Engineering University, Harbin 150001, China;
3. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
无人水下航行器(unmanned underwater vehicle, UUV)因具备独立自主的作业能力,在深海资源勘探、海底地形测绘、广域环境侦察和远程战场投送等民用和军事领域有着广阔的应用前景。在军事应用方面,广域环境侦察和远程战场投送等任务需求的增加,对UUV的长期、隐蔽和精确导航提出了更高的要求。传统的水下导航方法包括惯性导航和水声导航等。惯性导航会存在不可避免的误差积累,不利于长时间、长航程的导航;声学定位系统不存在时间积累误差,但需要预设水下声学基阵或母船携带基阵辅助,导航范围受限严重。因此,传统的水下导航方式无法满足UUV的长期隐蔽精确作战需求。海底地形匹配导航(terrain aided navigation, TAN)方法以现有水下地形图作为先验地图,利用自身搭载的多波束测深声呐等设备得到UUV当前海域实际地形,通过在先验地图中寻找与当前实测地图相似区域,得到UUV当前在先验地形图中的位置估计,无需卫星或水声定位等精确定位手段辅助,可解决UUV在任务执行过程中的长期、隐蔽、精确潜航问题,是UUV执行长时序、远距离作战任务的重要导航手段。
海底地形匹配导航系统通过UUV当前位置与先验海图的匹配获取自身位置估计,这就导致其定位结果的有效性严重依赖于UUV所在位置海底地形起伏程度。由于海底地形整体趋于平坦,倘若UUV当前位置缺乏足够特征,先验地图中将有大量区域与当前实测地形相似,TAN系统将很难在先验地图中获取UUV位置的唯一估计。因此,需要对海底地形的起伏程度做量化分析,以选择地形起伏程度即地形适配性高的区域执行误差约束,将地形适配性作为路径规划算法的重要指标,规划一条地形匹配效果好的路径以确保UUV在任务执行过程中实现实时、准确位置估计。
在UUV的路径规划方面,相关研究较为成熟。沈鹏[1]提出一种在水下地形适配区域进行扇形搜索的路径规划方法,并通过仿真验证了在合适的扇形区域半开角及限制角设定下,该方法具有可行性。Wei等[2]提出了一种基于蚁群算法的全局路径规划方法,并利用粒子滤波导航算法对给定路径进行了仿真验证,其结果表明该路径规划方法可用于海底地形匹配导航。Shen等[3]提出基于粒子群优化的海底地形匹配导航最优路径规划方法,其方法将地形信息和路径长度作为优化目标。Li等[4]提出海底地形匹配导航的A*算法,并将地形信息添加到代价函数中。Ma等[5]提出一种用于海底地形匹配导航的水下定位和路径规划算法,其算法考虑了地形复杂度并采用粒子滤波器对水下无人航行器进行定位和路径规划,仿真结果证明了其算法的可靠性。
海底地形匹配导航系统易在地形平坦区域出现匹配误差过大甚至匹配失效问题,严重影响了海底地形匹配导航的准确性和稳定性。因此在路径规划前对海底地形做量化分析以获取适配性高的地形区域至关重要。在相关方法研究方面,沈鹏[1]针对地形高程熵值进行仿真试验,并给出了地形适配区域判别的地形高程熵临界值。结果表明,高程熵值低于临界值的地形区域为适配区域。徐晓苏等[6]考虑了地形标准差、粗糙度、地形高度熵及相关系数等地形信息量,提出了一种基于熵值法赋权灰色关联决策的地形辅助导航适配区选择方法。饶喆等[7]选取地形特征信息统计参量中地形高程标准差、地形粗糙度、地形相关系数和地形信息熵进行耦合,并利用灰色模糊综合决策理论对耦合值进行分析,提出一种地形适配性的多指标评价方法。通过仿真试验,验证了该方法的可行性。王立辉等[8]在Fuzzy模糊决策应用的基础上,提出基于Vague集模糊推理的地形适配性综合评价方法。Shen等[9]利用多指标灰色决策理论,耦合多个地形信息统计指标,提出了一种海底地形适配性的综合判别方法,并通过水下地形匹配仿真试验验证了方法的正确性。以上方法均用统计学方法做地形的适配性分析,然而单一的统计学变量无法可靠表征海底地形的适配性;而用多个统计学变量的判断方法,其变量间的耦合关系较为复杂且具有一定的不确定性。综上,用统计学变量分析海底地形适配性的鲁棒性较差。
本文基于PointNetKL网络模型,提出一种面向海底地形匹配导航系统的地形适配性在线判断方法。基于历史海测子地图,用蒙特卡罗迭代生成PointNetKL网络的训练集,通过迭代学习实现子地图适配性的准确、高效判断。最后,结合模板匹配算法对判断结果进行评估,并给出子地图适配性的判断标准。
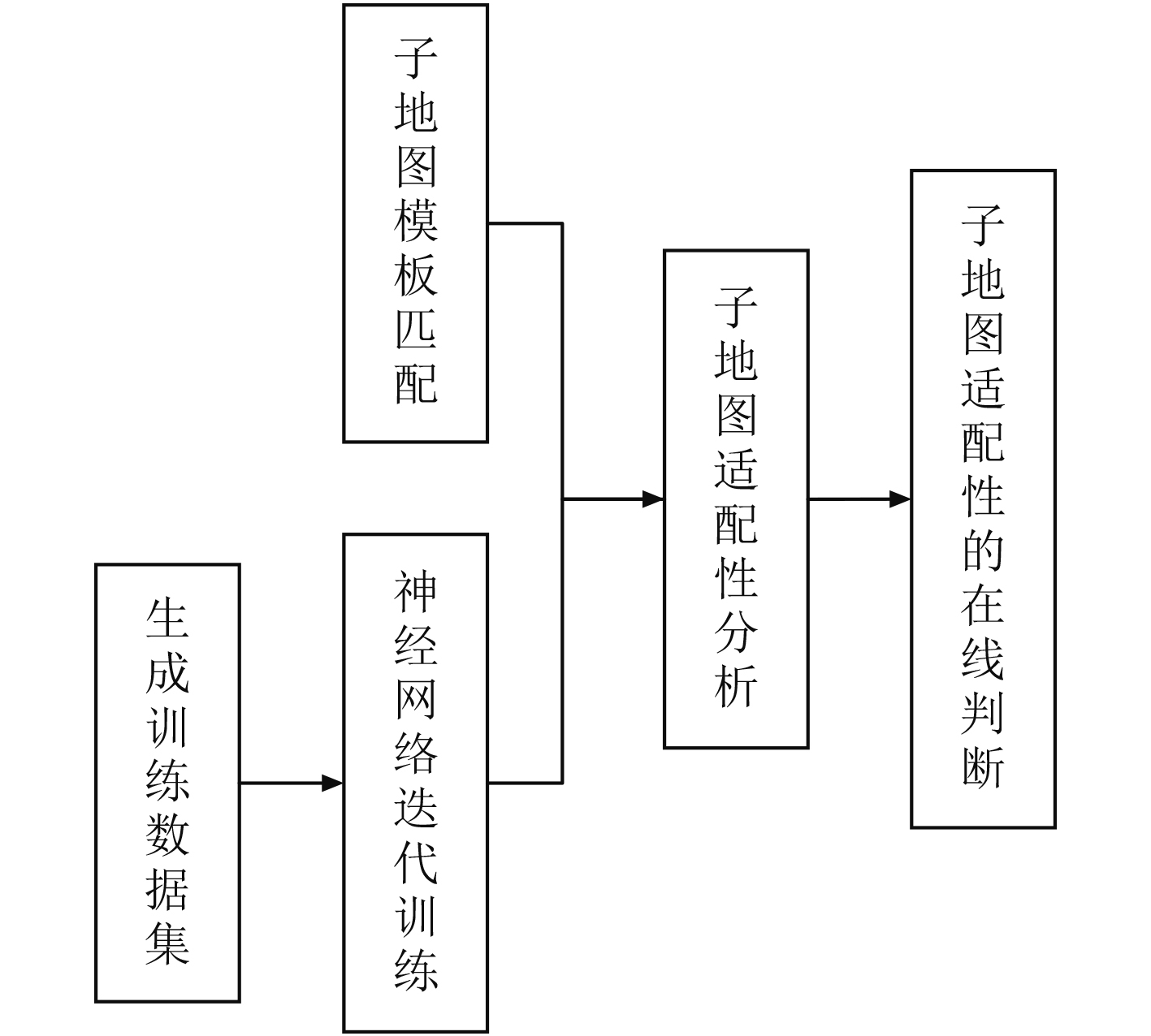
1 海底地形适配性在线判断方法框架海底地形适配性在线判断方法通过PointNetKL神经网络预测子地图的全局协方差矩阵,实现子地图的适配性在线判别。图1为本文提出的海底地形适配性在线判断方法框架,该框架主要分为5个部分。
|
图 1 基于PointNetKL的海底地形适配性在线判断方法框架 Fig. 1 The framework of online judgment of the suitablilty for submap registration |
该方法的主要步骤包括:
1)基于蒙特卡罗迭代生成PointNetKL训练集;
2)用PointNetKL网络训练蒙特卡罗数据;
3)子地图的模板匹配蒙特卡罗模拟;
4)基于蒙特卡罗数据、PointNetKL数据和子地图模板匹配蒙特卡罗模拟结果进行子地图的适配性分析;
5)实现子地图适配性的在线判断。
2 海底地形点云配准不确定性预测 2.1 PointNetKL训练集的蒙特卡罗迭代生成方法通过将点云的局部或整体的不确定性建模为高斯分布概率模型,可以表示点云配准的不确定性,它考虑了点云的局部或整体空间特征。影响点云配准不确定性的因素有很多,其中,点云配准错误收敛的影响无法避免。除此外,本文主要考虑传感器噪声的影响。
目前,有多种方法可以实现点云配准不确定性的建模,而最准确的方法被认为是通过蒙特卡罗迭代。Brujic等[10]在理论层面上研究分析了自由曲面配准不确定性的蒙特卡罗模拟。Iversen等[11]利用蒙特卡罗方法估计了合成深度图像上的ICP位姿不确定性。由于蒙特卡罗迭代计算的准确度高且方法实现较为容易,故采用蒙特卡罗迭代的结果作为PointNetKL神经网络的训练数据。
2.1.1 子地图采样在进行蒙特卡罗迭代前,要先对海试的实测地图进行性划分。首先对原始测量数据进行网格化处理,得到网格分辨率为1 m的891 m×922 m网格化点云地图,如图2所示。

|
图 2 891 m×922 m的网格化地图 Fig. 2 891 m×922 m girdded map |
在上述网格地图中子地图进行采样,采样得到350个50 m50 m子地图,分别命名为submap1,submap2,......,submap350,并记录各个子地图的实际位置(用子地图左上方角点的坐标表示)。
2.1.2 迭代计算完成采样后,先对点云进行x和y方向的去中心化处理,然后通过蒙特卡罗迭代计算各个子地图的配准不确定性。给定一个三维点云
| $ e_l =\log ({\exp}(Tj') Tj) ,$ | (1) |
用该误差计算点云的不确定性分布,用子地图的全局协方差矩阵Qi 来表示。
| $ {\boldsymbol{Q}}_i=\frac{2}{(L-1)}\sum^l_{l=1}e_l {e_l}^{\rm{T}}。$ | (2) |
其中:L为每个点云的蒙特卡罗迭代次数,在实际的迭代过程中L设置为3000次。
2.1.3 模板匹配完成各个子地图的蒙特卡罗迭代后,以350个子地图作为模板在采样地图中进行模板匹配,分别计算子地图的实际位置与模板匹配判断位置的欧氏距离Li,若Li小于5,则认为一次模板匹配的结果正确;若Li大于5,则认为一次模板匹配的结果错误。试验中,分别对每个子地图进行20次模板匹配蒙特卡罗模拟,而获取16次及以上正确的匹配结果的子地图,其状态为“1”;正确匹配的次数小于16次,则子地图的状态为“0”,表1列出了模板匹配的相关参数,其中,实测噪声添加在子地图的高程上。
|
|
表 1 子地图的模板匹配相关参数 Tab.1 Relevant parameter template matching for submaps |
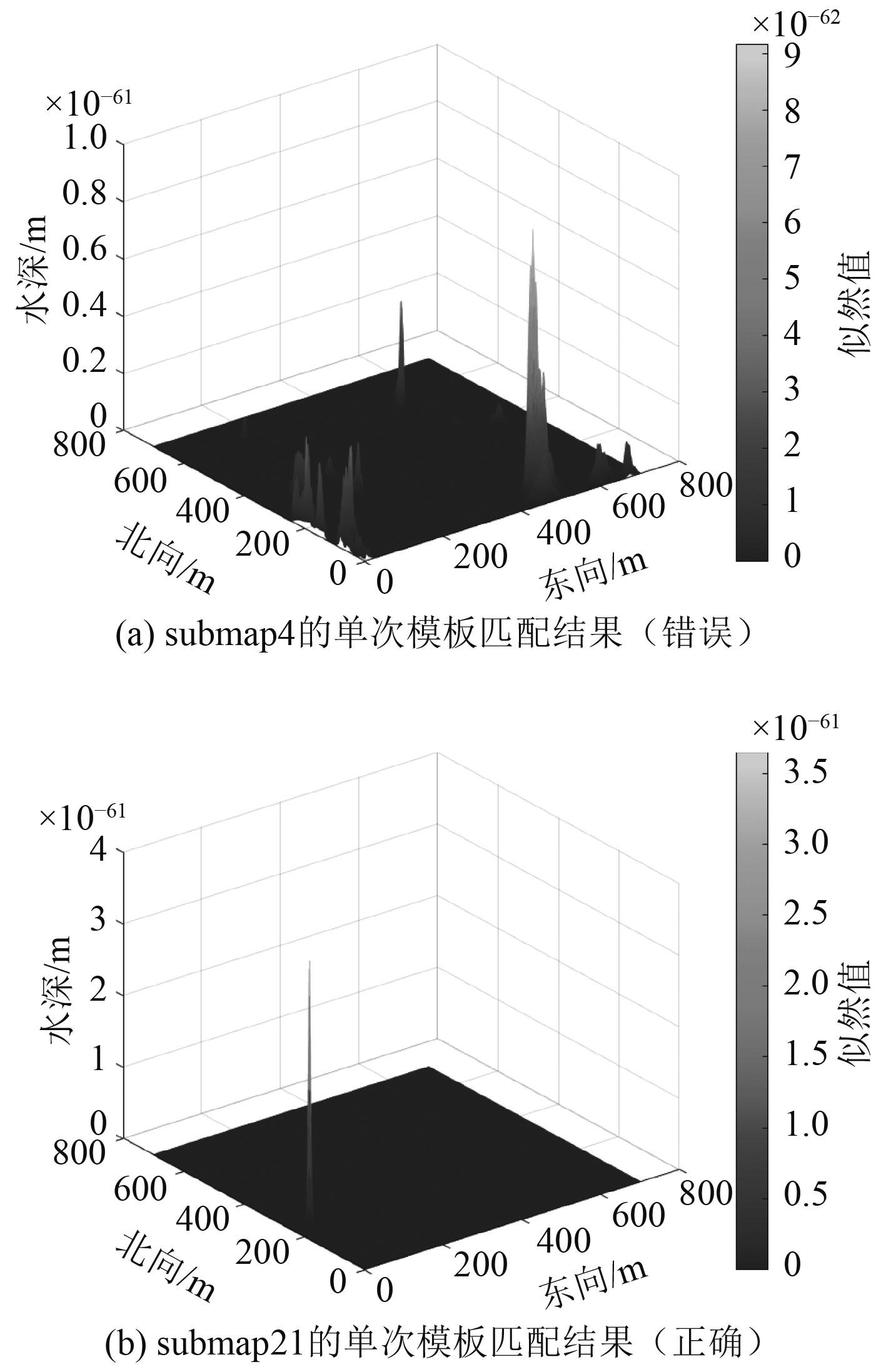
对子地图的高程添加适当倍数的测量噪声后进行模板匹配蒙特卡罗模拟,得到各个子地图的模板匹配结果,图3分别给出了某2个子地图单次模板匹配的结果示意图。
|
图 3 模板匹配示意图 Fig. 3 The sketch map of template matching |
统计350个子地图20次模板匹配的结果,能够得到各个子地图的状态(“0”或“1”),2种状态对应的子地图个数由表2给出。
|
|
表 2 模板匹配结果 Tab.2 The result of The sketch map of template matching |
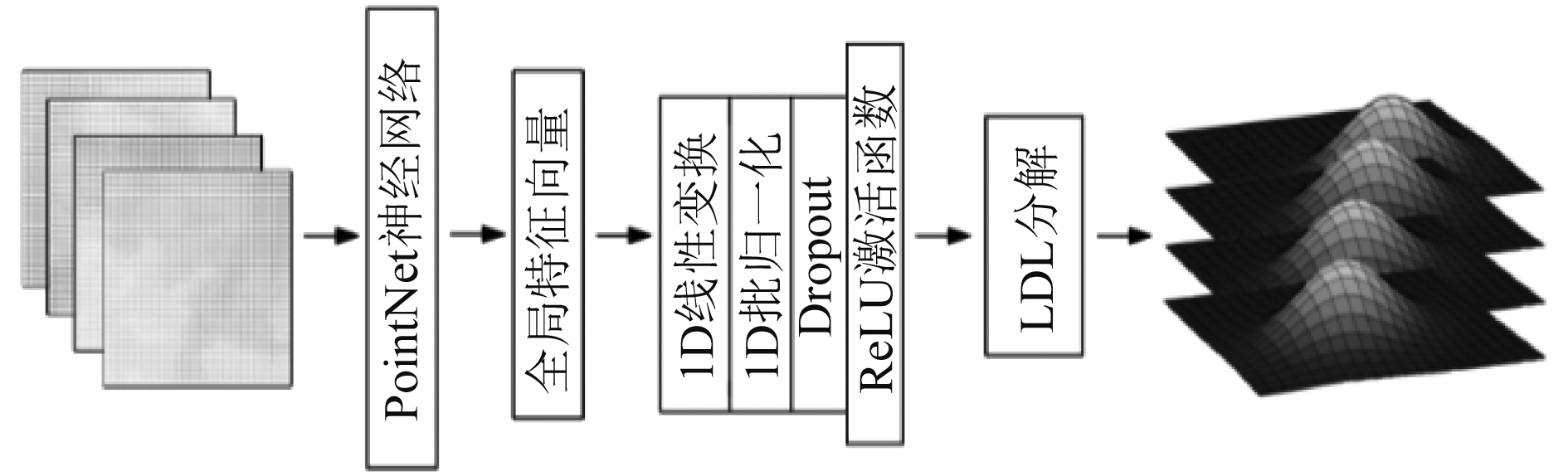
图4为PointNetKL的网络架构模型。
|
图 4 PointNetKL的网络架构 Fig. 4 The network architecture of PointNetKL |
PointNetKL神经网络能够将点云数据映射为多元高斯概率分布[13]。首先利用PointNet网络的全局特征提取结构将等深线点云数据映射为一个多维的向量描述符,用来描述等深线点云数据的特征
| $ \varphi \left( {Si} \right):{R^{U \times V}} \to {R^Z} 。$ | (3) |
其中:
进一步将特征向量映射到多元高斯概率分布
| $ \psi \left( {Si} \right):{R^{U \times V}} \to {R^{M \times M}}。$ | (4) |
其中,从Z维特征向量到多元高斯概率分布的映射通过LDL分解实现。通过多层感知机后,网络生成
| $ \Sigma_{i}=L(l_i) D(d_i) L(l_i)^{{\rm{T}}}: l_i \in R^{\left(M^{2}-M\right) / 2}, d_i \in R^{M}。$ | (5) |
其中:
| $ \Sigma_{i}=L(l_i) D\left({\rm e}^{d_i}\right) L\left(l_i\right)^{{\rm{T}}}: l_i {\in} R^{(M^2-M)/2}, d_{i} \in R^{M} 。$ | (6) |
回放试验中使用的海底地形数据来源于青岛中沙礁附近海域进行的船载数据获取海上试验。在海试中,搭建了鲁棒BSLAM海上试验系统。
其中,多波束声呐为CMBS200高精度多波束声呐,该声呐的水平波束宽度优于1°,垂直波束开角优于2°,水平视场角≥140°,测距离≥300 m,距离分辨率优于2 cm;参考导航系统为StarNeto XW-GI5651导航系统,该系统可以提供试验船的首向角、横倾角、纵倾角和东北天三轴的GPS位置,系统给出的首向角测量误差约为0.1°,横倾角、纵倾角测量误差约为0.01°。
3.2 建立数据集和训练超参数设置根据PointNetKL网络的训练数据集格式,建立2个网格化点云子地图的数据集submap1_2和submap2_2,两数据集中分别包含225和125个经零均值化和归一化网格子地图,以及用蒙特卡罗方法估算得到的子地图协方差矩阵。
神经网络的训练参数设置如表3所示。
|
|
表 3 超参数设置 Tab.3 Setting HyperParameters |
PointNetKL神经网络完成50000次迭代训练后得到的在训练集和验证集上的最佳的收敛结果如表4所示。
|
|
表 4 在训练集和验证集上的损失函数均值 Tab.4 The loss function value of training set and validation set |
根据训练集和验证集上的收敛结果可知,该神经网络具有较好的收敛性和泛化性。
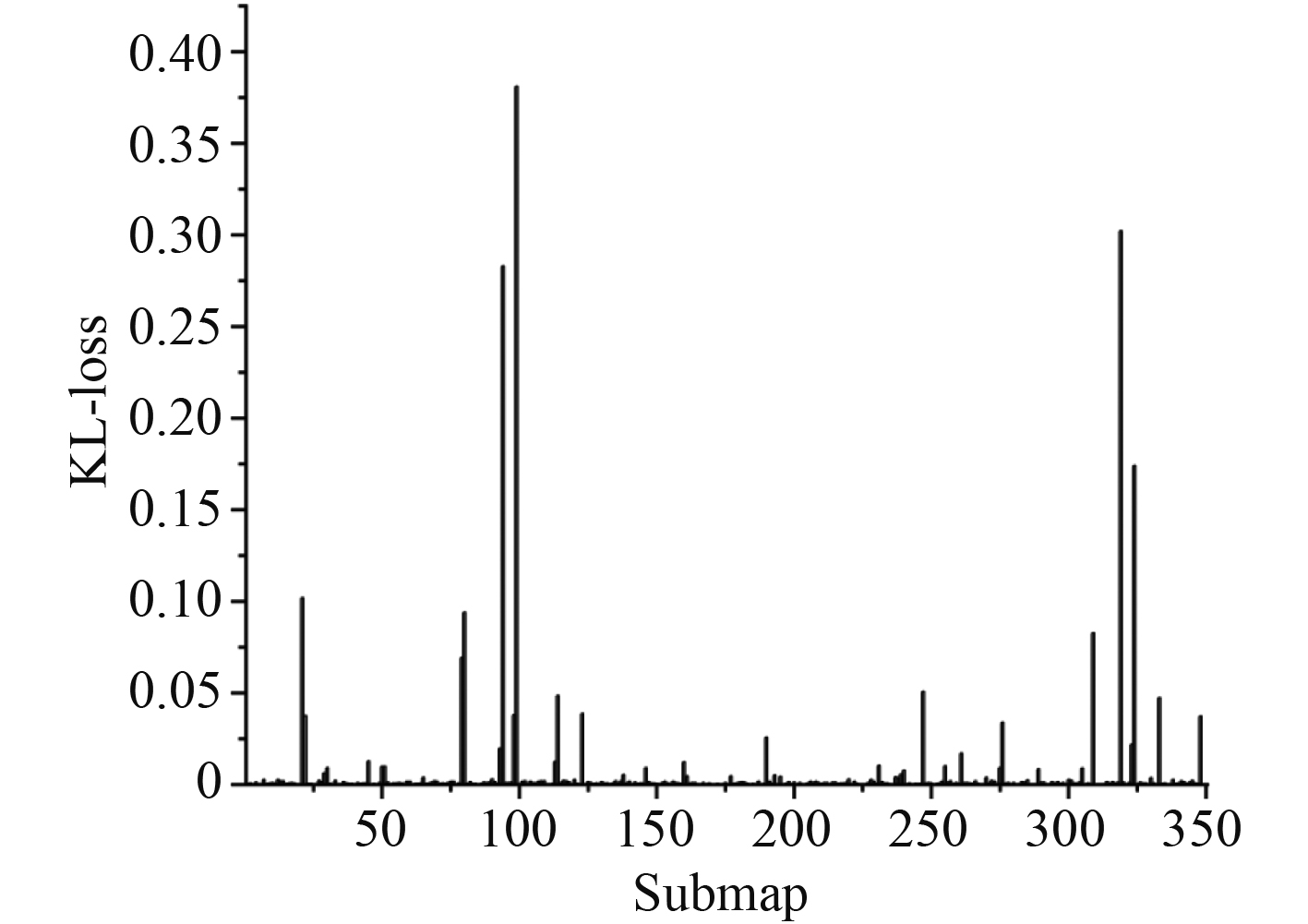
子地图的损失函数值如图5所示。可以看出有几个子地图的损失函数值相对较高,故在进行适配性分析时,将这几个子地图剔除掉。
|
图 5 各个子地图的损失函数值 Fig. 5 The loss function value of each submap |
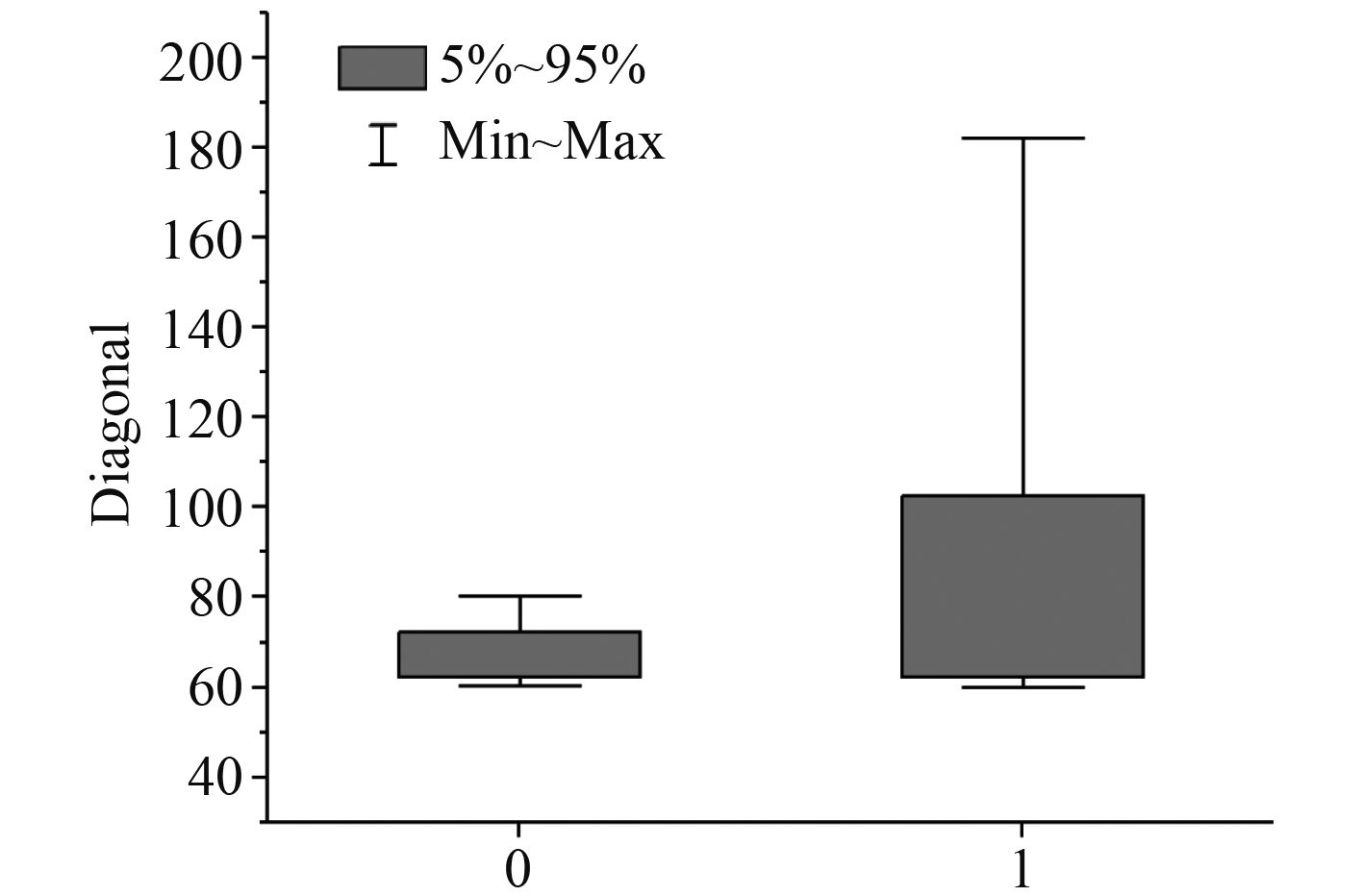
根据子地图的模板匹配蒙特卡罗模拟结果分别绘制子地图的蒙特卡罗迭代算得的协方差矩阵和PointNetKL预测的协方差矩阵分布箱型图。其中,y轴的参考值为协方差矩阵的对角线元素的乘积。
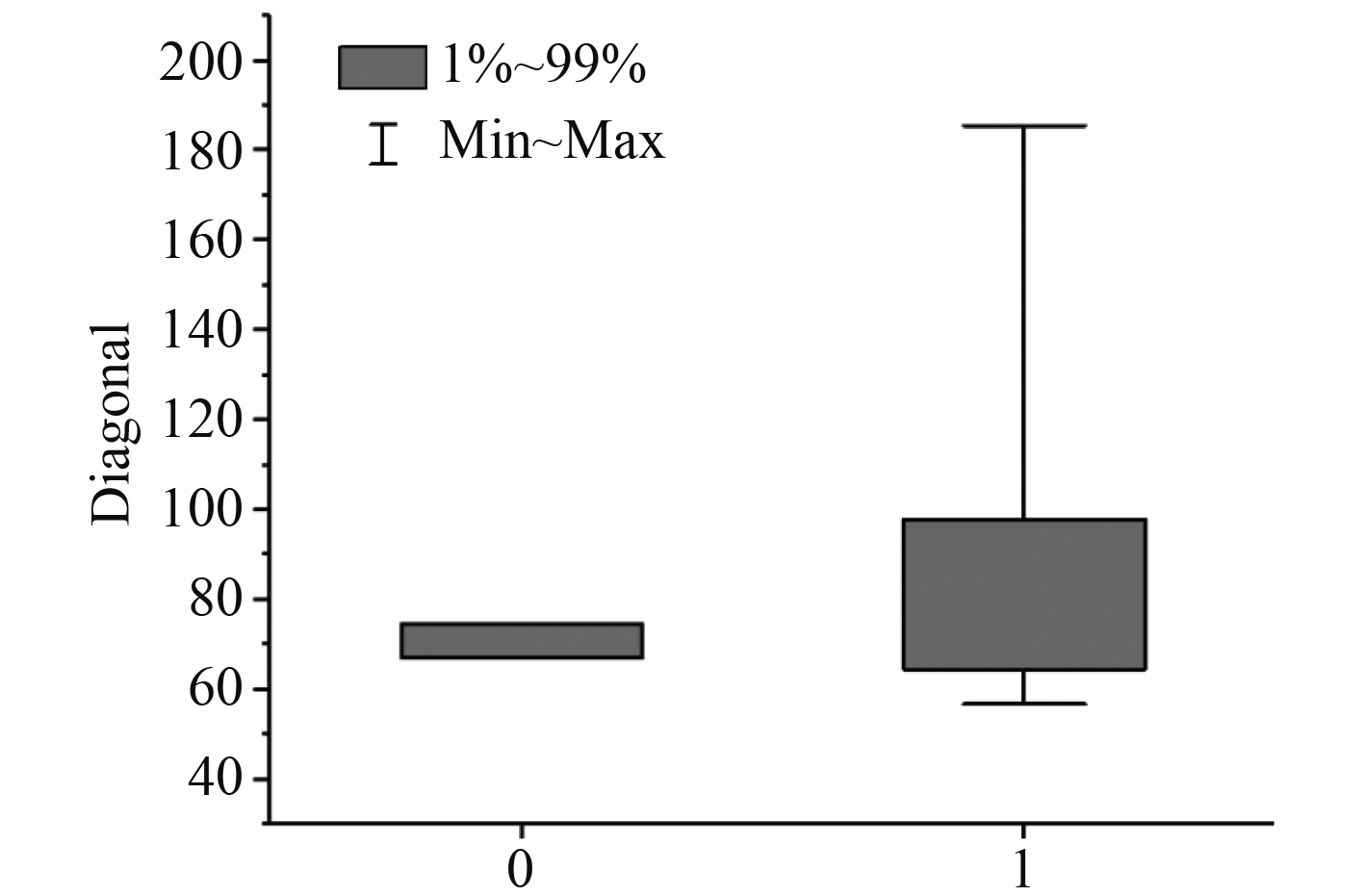
根据箱型图的统计结果可以给出蒙特卡罗迭代和PointNetKL的子地图状态对应的协方差矩阵对角线元素乘积的取值范围,如表5所示。可知,2种方法算得的子地图不同状态的diagonal取值范围基本一致,故可以给出用PointNetKL神经网络判断子地图状态的阈值。
|
|
表 5 diagonal取值范围 Tab.5 The value range of diagonal |
|
图 6 蒙特卡罗结果箱型图 Fig. 6 The box figure of Monte-Carlo result |
|
图 7 PointNetKL结果箱型图 Fig. 7 The box figure of PointNetKL result |
最后,在15.9GB RAM的英特尔11代酷睿i7-11700处理器上对比了MC迭代和PointNetKL神经网络的平均运行时间,如表6所示。可知,PointNetKL的计算时间明显小于蒙特卡罗迭代。
|
|
表 6 蒙特卡罗迭代和PointNetKL计算协方差矩阵的平均运行时间 Tab.6 The average execution time of the covariance matrix calculated by Monte-Carlo iteration and PointNetKL |
本文针对海底地形SLAM在特征贫乏海域的算法失效问题,提出一种海底地形起伏程度的在线判断方法。不同于以往的用地形粗糙度、地形熵和地形高程标准差等地形信息表示地形起伏程度方法,本文借助新型人工神经网络PointNetKL,计算子地图的不确定性协方差矩阵,并利用协方差矩阵的对角线乘积量化子地图的地形起伏程度。对试验数据的分析结果表明,用PointNetKL神经网络能够实现海底地形适配性的在线判断。
| [1] |
沈鹏. AUV水下地形匹配导航的路径规划方法[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [2] |
WEI Feng, ZHE Rao, ZHONg Wang. Research on the Application of Ant Colony Algorithm in Underwater Path Planning[C]. Guangzhou, China, 2016.
|
| [3] |
SHEN J , HENG L I , ZHANG J Y . Optimal Path Planning Method for Underwater Terrain-aided Navigation[J]. Torpedo Technology, 2012.
|
| [4] |
LI YE, MA TENG, CHEN PENGYUN, et al. Autonomous underwater vehicle optimal path planning method for seabed terrain matching navigation[J]. Ocean engineering, 2017, 133(Mar.15): 107-115. DOI:10.1016/j.oceaneng.2017.01.026 |
| [5] |
MA Teng, LI Ye, ZHAO Yuxin, et al. An AUV localization and path planning algorithm for terrain-aided navigation[J]. ISA Transactions. 2020, 103: 215-227.
|
| [6] |
徐晓苏, 汤郡郡, 张涛, 岳增阳. 基于熵值法赋权灰色关联决策的地形辅助导航适配区选择[J]. 中国惯性技术学报, 2015, 23(2): 201-206. DOI:10.13695/j.cnki.12-1222/o3.2015.02.012 |
| [7] |
饶喆, 张静远, 冯炜. 一种地形匹配导航区域的可导航性评价方法[J]. 河南大学学报(自然科学版), 2016, 46(1): 89-95. DOI:10.15991/j.cnki.411100.2016.01.011 |
| [8] |
王立辉, 乔楠, 余乐. 水下地形导航匹配区选取的模糊推理方法[J]. 西安电子科技大学学报, 2017, 44(1): 140-145. |
| [9] |
SHEN J , XIONG L , XIA Q . Research on Multi-index Comprehensive Evaluation Method for Terrain Navigability of Underwater Autonomous Vehicle. 2019.
|
| [10] |
BRUJIC D, RISTIC M. Monte Carlo simulation and analysis of free-form surface registration[J]. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture, 1997, 211(8): 605-617. DOI:10.1243/0954405981516544 |
| [11] |
IVERSEN T M , BUCH A G , KRAFT D . Prediction of ICP pose uncertainties using Monte Carlo simulation with synthetic depth images[C]// 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2017.
|
| [12] |
BARFOOT T D, FURGALE P T. Associating Uncertainty With Three-Dimensional Poses for Use in Estimation Problems[J]. IEEE Transactions on Robotics, 2017, 30(3): 679-693. |
| [13] |
TORROBA I, SPRAGUE C I, BORE N, et al. PointNetKL: Deep Inference for GICP Covariance Estimation in Bathymetric SLAM[J]. IEEE Robotics and Automation Letters, 2020, PP(99): 1-1. |
 2022, Vol. 44
2022, Vol. 44
