0 引　言

海洋资源是未来人类生存发展所需资源的重要来源，但海洋资源勘测和开发难度大，需要依靠高科技手段^[1]。自主式潜航器（autonomous underwater vehicle, AUV）是目前备受青睐的工具之一，其核心关键技术包括运动控制、路径规划、水下探测识别等。随着AUV技术不断进步，应用范围不断扩展延伸，不再局限于观测型任务，逐渐转向具有一定的作业能力，如海底捕捞、管道对接等^[2-3]。相比于观测型，作业型AUV自身重力、水动力参数不确定性更大，需要在三维空间中机动，运动控制伴随着海水暗流等强扰动。为高效完成预定任务，对作业型AUV运动控制精度、响应时间、可靠性和鲁棒性提出更为苛刻的要求。因此，实现对不确定参数及强扰动下的AUV三维空间运动控制具有重要的学术价值。

非线性H_∞控制方法成为近年来研究热点，文献[4]通过求解HJI不等式获得用于AUV目标跟踪的非线性H_∞导引律。但当控制对象为非线性系统时，直接求解HJI不等式非常困难。文献[5]提出一种基于区域函数的非线性H_∞控制方法，对参数不确定性、外部干扰具有强鲁棒性，区域跟踪误差一致最终有界。文献[6]设计AUV首向非线性H_∞控制器，采用非线性矩阵不等式（NLMI）描述HJI不等式，然后将NLMI转化为线性矩阵不等式（LMI）限制下的凸优化问题，能够有效跟踪样条曲线和圆形曲线。但存在随着状态向量维数增加，输出保守的问题。文献[7]通过泰勒级数展开法求解HJI不等式，获得用于AUV垂直面路径跟踪的非线性H_∞控制策略，具有显著的扰动抑制能力。文献[8]提出一种无需任何AUV动力学模型信息的控制方法，通过在线强化学习方法获得HJI方程的最优解，提高了系统鲁棒性能。文献[9]基于自适应动态规划和策略迭代算法，借助评价神经网络近似求解HJI方程，进而获得机器人轨迹跟踪最优控制策略。

考虑存在AUV内部参数可变、机械手工作以及外部环境干扰，并且干扰上界无法获取的情况，为提高运动控制精度、稳定性以及鲁棒性能，本文提出一种基于递归神经网络和HJI理论的作业型AUV三维空间运动控制方法，实现非线性运动轨迹跟踪。利用对角递归神经网络对系统中存在不确定性和控制输入受限进行估计并补偿到控制律；构造存储函数，以HJI不等式为基础设计控制律，保证AUV闭环系统具有稳定性。

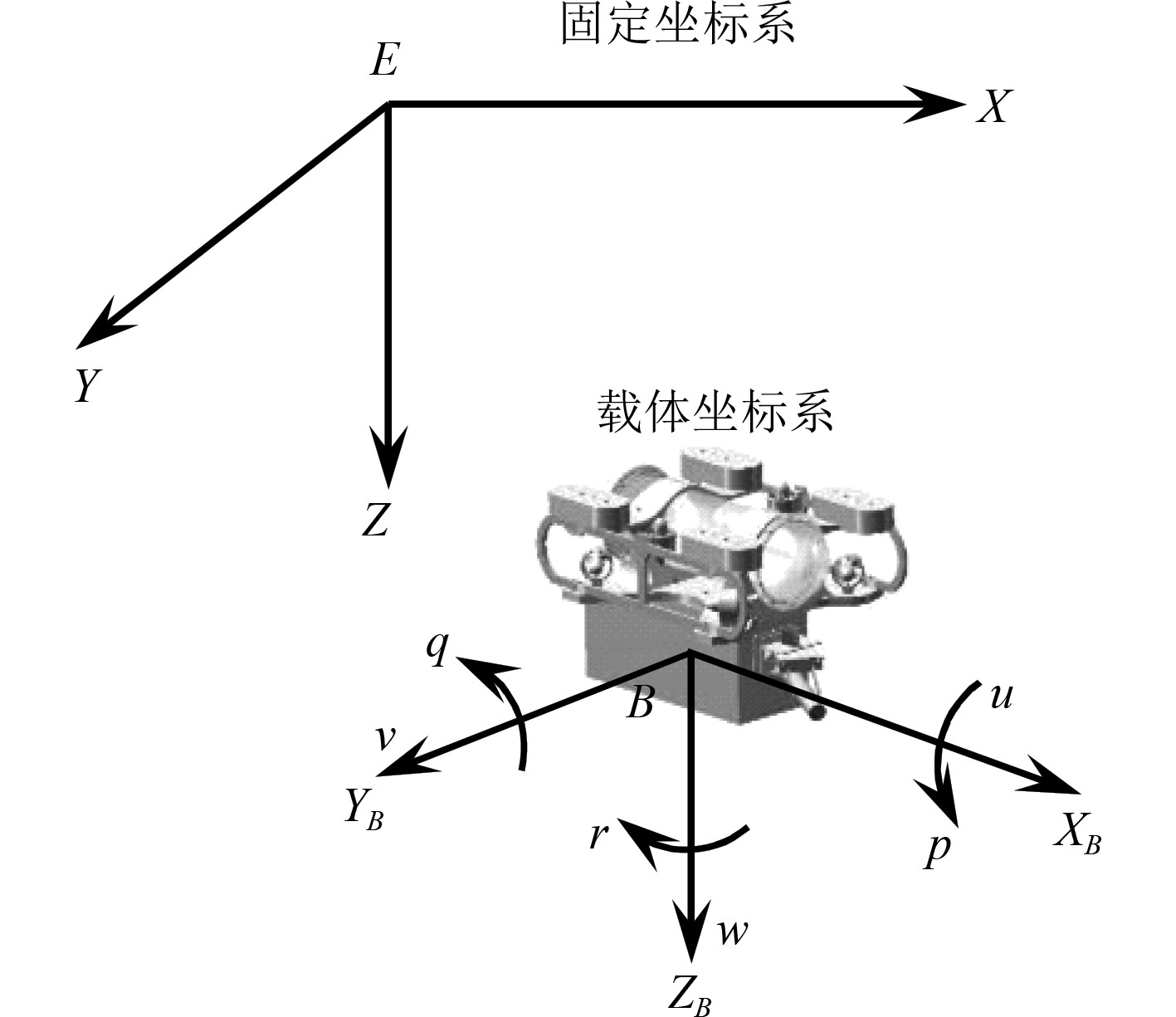
1 AUV数学模型建立 1.1 运动学模型

本文以一类模块化作业型AUV为控制对象，该类AUV采用全驱动形式，为便于推导运动学模型，定义作业型AUV固定坐标系E-XYZ 和载体坐标系B- X_BY_BZ_B，如图1所示。

固定坐标系中AUV的位姿矢量表示为η = [x, y, z, ϕ, θ, ψ]^T，载体坐标系中AUV速度矢量表示为v = [u, v, w, p, q, r]^T，使用绕X, Y, Z三个轴旋转的欧拉角 ϕ, θ, ψ描述位姿矢量和速度矢量之间的转换关系表示为：

$ \dot \eta = J(\eta )v = \left[ {\begin{array}{*{20}{c}} {{J_1}(\eta )}&{{{\text{0}}_{3 \times 3}}} \\ {{{\text{0}}_{3 \times 3}}}&{{J_2}(\eta ){\text{ }}} \end{array}} \right]v。$

(1)

式中： $0 \in {R^{3 \times 3}}$ 代表零矩阵；转换矩阵 ${J_1}(\eta )$ 和 ${J_2}(\eta )$ 定义如下：

$ {J_1}(\eta )= \left[ {\begin{array}{*{20}{c}} {{\rm{c}}\psi {\rm{c}}\theta }&{{\rm{c}}\psi {\rm{s}}\theta {\rm{s}}\phi - {\rm{s}}\psi {\rm{c}}\phi }&{{\rm{c}}\psi {\rm{s}}\theta {\rm{c}}\phi + {\rm{s}}\psi {\rm{s}}\phi } \\ {{\rm{s}}\psi {\rm{c}}\theta }&{{\rm{s}}\psi {\rm{s}}\theta {\rm{s}}\phi + {\rm{c}}\psi {\rm{c}}\phi }&{{\rm{s}}\psi {\rm{s}}\theta {\rm{c}}\phi - {\rm{c}}\psi {\rm{s}}\phi } \\ { - {\rm{s}}\theta }&{{\rm{c}}\theta {\rm{s}}\phi }&{{\rm{c}}\theta {\rm{c}}\phi } \end{array}} \right]，$

(2)

$ {J_2}(\eta )=\left[ {\begin{array}{*{20}{c}} 1&{{\rm{s}}\phi {\rm{t}}\theta }&{{\rm{c}}\phi {\rm{t}}\theta } \\ 0&{{\rm{c}}\phi }&{ - {\rm{s}}\phi } \\ 0&{{\rm{s}}\phi /{\rm{c}}\theta }&{{\rm{c}}\phi /{\rm{c}}\theta } \end{array}} \right]。$

(3)

其中：sin(·)，cos(·)，tan(·)简写为s(·)，c(·)，t(·)。由式（3）可知，当纵倾角θ = ± π/2时无意义。本文研究的作业型AUV，在实际应用中受到稳心的恢复力及恢复力矩作用，纵倾角不会接近奇异点π/2。

1.2 动力学模型

针对存在重力、水动力参数不确定性，且具有机械手工作、海流等外部干扰的作业型AUV动力学模型结构如图2所示。

图中 $M \in {R^{6 \times 6}}$ 为由惯性质量和附加质量组成的惯性矩阵； $C(v) \in {R^{6 \times 6}}$ 为包含有非线性力和力矩的科式力以及向心力矩阵； $D(v) \in {R^{6 \times 6}}$ 为由势流阻尼和粘性效应耦合构成的阻尼矩阵； $g(\eta ) \in {R^6}$ 为包含重力和浮力的恢复力向量； $ {M}_{0}，{C}_{0}(v)，{D}_{0}(v)，{g}_{0}(\eta ) $ 为系统的名义值； $ \Delta M，\Delta C(v)，\Delta D(v)，\Delta g(\eta ) $ 为系统中存在的未知不确定项； $ {\tau _d} \in {R^6} $ 为海洋环境中时变的外部扰动； $ \tau \in {R^6} $ 为轨迹跟踪所需控制力和力矩向量。

为便于控制器设计，定义未知不确定项和外部扰动组成系统的总干扰项，动力学模型可描述为下式：

$ \begin{gathered} {M_0}\dot v + {C_0}(v)v + {D_0}(v)v + {g_0}(\eta ) + {\tau _s} = \tau ，\\ {\tau _s} = \Delta M\dot v + (\Delta C(v) + \Delta D(v))v + \Delta g(\eta ) + {\tau _d}。\\ \end{gathered} $

(4)

将运动学模型式（1）代入式（4），整理得到固定坐标系下AUV动力学模型描述如下式：

$ {M_\eta }(\eta )\ddot \eta + {C_\eta }(v,\eta )\dot \eta + {D_\eta }(v,\eta )\dot \eta + {G_\eta }(\eta ) + {\tau _{\eta s}} = {\tau _T} 。$

(5)

式中：

$\begin{aligned}[b] & {M_\eta }(\eta ) = {J^{ - {\rm{T}}}}{M_0}{J^{ - 1}} ，\\ & {C_\eta }(v,\eta ) = {J^{ - {\rm{T}}}}({C_0}(v) - {M_0}{J^{ - 1}}\dot J){J^{ - 1}}，\\ & {D_\eta }(v,\eta ) = {J^{ - {\rm{T}}}}({D_0}(v)){J^{ - 1}} ，\\ &{G_\eta }(\eta ) = {J^{ - {\rm{T}}}}{g_0}(\eta )，\\ & {\tau _{\eta s}} = {J^{ - {\rm{T}}}}{\tau _s} ，\\ & {\tau _T} = {J^{ - {\rm{T}}}}\tau 。\end{aligned}$

(6)

2 HJI理论及神经网络设计 2.1 HJI理论

基于存在内部不确定和外部扰动的作业型AUV系统非精确模型，建立描述轨迹跟踪闭环控制误差模型如下：

$ \left\{ \begin{gathered} \dot x = \alpha (x) + \beta (x)\delta (t)，\\ \Lambda = h(x) 。\\ \end{gathered} \right. $

(7)

式中： $ \delta (t) $ 是误差系统中存在的外界干扰； $\Lambda $ 为系统的评价信号。为衡量干扰信号 $ \delta (t) $ 的能量大小，定义其L₂范数为：

$ {\left\| {\delta (t)} \right\|_2} = {\left\{ {\int_0^\infty {{\delta ^{\rm{T}}}(t)\delta (t){\rm{d}}t} } \right\}^{{\text{1/2}}}}。$

(8)

为量化AUV系统整体的鲁棒性能，定义作业型AUV系统的L₂增益指标为：

$ J=\mathop {{\text{sup}}}\limits_{\left\| \delta \right\| \ne 0} \frac{{{{\left\| \Lambda \right\|}_{\text{2}}}}}{{{{\left\| {\delta (t)} \right\|}_{\text{2}}}}}。$

(9)

式中：J为AUV系统鲁棒性，其数值越小，系统鲁棒性越好。由此可知，通过调整J值大小，改变外界干扰对跟踪误差的作用，进而达到控制要求。

定理1（HJI不等式）^[10]：对任意给定一个正数γ，如果存在连续可微的半正定函数V(x)，满足HJI不等式如下：

$ \frac{{\partial V}}{{\partial x}}\alpha (x) + \frac{1}{{2{\gamma ^2}}}\frac{{\partial V}}{{\partial x}}\beta (x){\beta ^{{\rm{T}}}}(x){\left( {\frac{{\partial V}}{{\partial x}}} \right)^{\rm{T}}}{\text{ + }}\frac{1}{2}{h^{\rm{T}}}(x)h(x) \leqslant 0 ，$

(10)

或

$ \begin{aligned}[b] \dot V =& \frac{{\partial V}}{{\partial x}}\dot x = \frac{{\partial V}}{{\partial x}}\alpha (x) + \frac{{\partial V}}{{\partial x}}\beta (x)\delta (t)\leqslant \\ & \frac{1}{2}\left\{ {{\gamma ^2}\left\| \delta \right\|_{}^2 - \left\| \Lambda \right\|_{}^2} \right\}{\text{ (}}\forall \delta {\text{)}}。\end{aligned}$

(11)

则J ≤ γ，说明作业型AUV控制系统既满足渐近稳定，也满足有界输入—有界输出稳定。

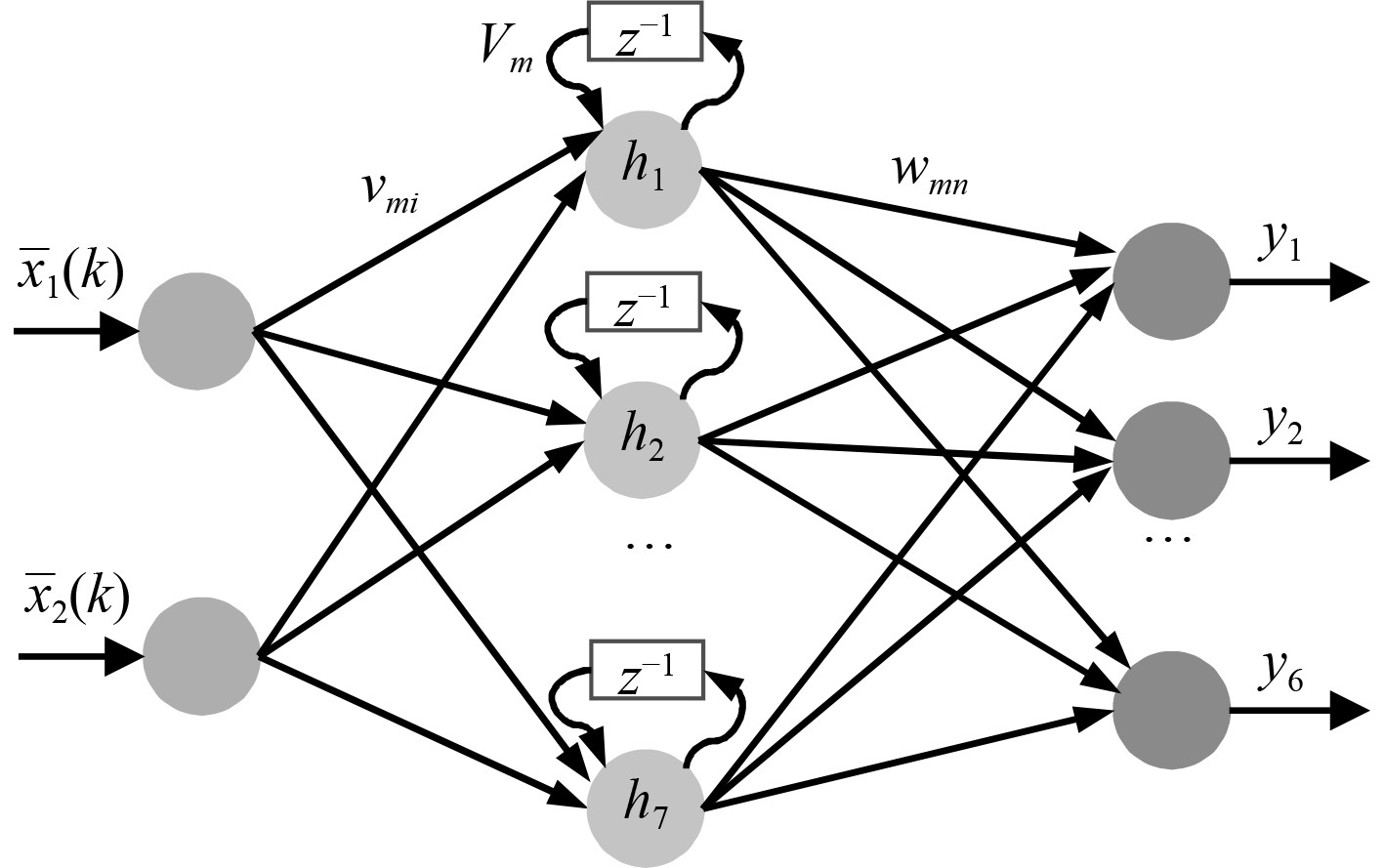
2.2 对角递归神经网络设计

对角递归神经网络是一种结构简化的动态神经网络，网络各层之间连接权值调整允许采用在线学习替代离线学习。与前馈神经网络相比，最大区别是隐含层神经元的输入由输入层神经元参数和隐含层神经元自反馈参数两部分组成，该特点决定了网络能够捕捉非线性对象动态行为，具有更好的逼近能力^[11]。引入对角递归神经网络逼近动力学建模中的非线性总干扰项并补偿到控制律中，设计的神经网络具有3层，各层节点数目分别为2，7，6，如图3所示。位姿误差和位姿误差变化率 $\bar x(k) = {[e,{\text{ }}\dot e]^{\rm{T}}}$ 作为神经网络的输入，隐含层输入为：

$ {S_m}(k) = V_m^{}{h_m}(k - 1) + \sum\limits_{i = 1}^2 {v_{mi}^{}{{\bar x}_i}(k)}，$

(12)

选取Sigmoid函数作为隐含层激活函数，其输出为：

$ {h_m}(k) = g({S_m}(k)) ，$

(13)

输出层神经元的输出可描述为如下加权函数：

$ {y_n} = \sum\limits_{m = 1}^7 {w_{nm}^{} \cdot {h_m}} ,{\text{ }}n = 1,2, \cdots ,6 ，$

(14)

令

$ \begin{gathered} V = \left[ {\begin{array}{*{20}{c}} {{v_{11}}}&{{v_{11}}}& \cdots &{{v_{1m}}} \\ {{v_{21}}}&{{v_{22}}}& \cdots &{{v_{2m}}} \end{array}} \right]，\\ {\text{ }}W = \left[ {\begin{array}{*{20}{c}} {{w_{11}}}&{{w_{12}}}& \cdots &{{w_{1n}}} \\ {{w_{21}}}&{{w_{22}}}& \cdots &{{w_{2n}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{w_{m1}}}&{{w_{m2}}}& \cdots &{{w_{mn}}} \end{array}} \right], m = 7,n = 6 ，\\ \end{gathered} $

(15)

$ h({V^T}x) = \left[ {\begin{array}{*{20}{c}} {{h_1}} \\ {{h_2}} \\ \vdots \\ {{h_7}} \end{array}} \right],{\tau _{\eta s}} = \left[ {\begin{array}{*{20}{c}} {{\text{ }}{y_1}} \\ {{\text{ }}{y_2}} \\ \vdots \\ {{\text{ }}{y_6}} \end{array}} \right] 。$

(16)

则递归神经网络的输出表示为：

$ {\tau _{\eta s}} = {W^{\rm{T}}}h({V^{\rm{T}}}\bar x) + \varepsilon 。$

(17)

式中： $\varepsilon $ 代表网络的近似误差；W和V分别为理论上输入层与隐含层、隐含层与输出层之间的最优权值；V的第一列也作为隐含层神经元自反馈的权值。借助神经网络对AUV动力学建模中总干扰项在线逼近的输出描述如下：

$ {\hat \tau _{\eta s}} = {\hat W^T}h({\hat V^{\rm{T}}}\bar x)。$

(18)

其中， $ \widehat{W}和\widehat{V} $ 为理想权值W和V的估计值。

3 运动控制设计及稳定性分析 3.1 运动控制设计

作业型AUV系统存在自身重力、水动力参数时变形成的系统内部不确定性，同时存在海洋环境中的复杂多变的外部干扰。考虑上述因素很难获得该类AUV的精确动力学模型，简化上述因素则会导致轨迹跟踪精度下降。为有效解决上述存在的问题，提升系统控制性能，将对角递归神经网络和HJI理论相结合，设计合适的控制律满足式（11）。

设定AUV的期望跟踪轨迹为 ${\eta _d}$ ，实际轨迹为 $\eta $ ，则可定义跟踪误差 $e = \eta - {\eta _d}$ ，误差变化率 $\dot e = \dot \eta - {\dot \eta _d}$ ，评价信号选择由位置误差和误差变化率组成的滑模函数，表示为：

$ \Lambda = \dot e + {\boldsymbol{c}}e ，$

(19)

式中，c为正定矩阵。

根据节AUV系统的动力学方程式（5），结合递归神经网络在线逼近总干扰项式（17）。得到下式：

$ {M_\eta }\dot \Lambda = {\tau _{\rm{T}}} - {W^{\rm{T}}}h({V^T}\bar x) - \varepsilon - {C_x}\Lambda + \omega - {M_\eta }{\ddot \eta _d} 。$

(20)

式中：

$ {C_x} = {C_\eta }(v,\eta ) + {D_\eta }(v,\eta )，$

(21)

$ \omega = {C_x}ce - {C_x}{\dot \eta _d} - {G_\eta }(\eta ) + {M_\eta }c\dot e 。$

(22)

为获得 $ \widehat{W}和\widehat{V} $ 的自适应律，将函数 $ h({V^{\rm{T}}}\bar x) $ 在 $ {\hat V^{\rm{T}}}\bar x $ 点Taylor级数展开如下：

$ h({V^{\rm{T}}}\bar x) = h({\hat V^{\rm{T}}}\bar x) + h'({\hat V^{\rm{T}}}\bar x){\tilde V^{\rm{T}}}\bar x + O{({\tilde V^{\rm{T}}}\bar x)^2} ，$

(23)

则

$\begin{aligned}[b] & {W^{\rm{T}}}h({V^{\rm{T}}}\bar x) + \varepsilon = {{\hat W}^{\rm{T}}}h({{\hat V}^{\rm{T}}}\bar x) + {{\tilde W}^{\rm{T}}}h({{\hat V}^{\rm{T}}}\bar x) + \\ & {{\hat W}^{\rm{T}}}h'({{\hat V}^{\rm{T}}}\bar x){{\tilde V}^{\rm{T}}}\bar x + \varsigma ，\end{aligned}$

(24)

$ \varsigma = \tilde W^{\rm{T}} h'({\hat V^{\rm{T}}}\bar x){\tilde V^{\rm{T}}}\bar x + {W^{\rm{T}}}O{({\tilde V^{\rm{T}}}\bar x)^2} + \varepsilon 。$

(25)

式中： $ \tilde{W}=W-\widehat{W}；\tilde{V}=V-\widehat{V} $ 。

为使用HJI理论，定义状态变量 $ {x_1} = e $ ， $ {x_2} = \Lambda $ ，将式（19）和式（20）改写为下式：

$ \left\{ \begin{gathered} \dot x = \left[ \begin{gathered} {x_2} - c{x_1} \\ M_\eta ^{ - 1}({\tau _T} - {{\hat W}^{\rm{T}}}h'({{\hat V}^{\rm{T}}}\bar x){{\tilde V}^{\rm{T}}}\bar x + \\ {{\tilde W}^{\rm{T}}}h({{\hat V}^{\rm{T}}}\bar x) + {{\hat W}^{\rm{T}}}h({{\hat V}^{\rm{T}}}\bar x) + \\ \omega - {C_x}{x_2} - {M_\eta }{{\ddot \eta }_d}) \\ \end{gathered} \right] + \left[ \begin{gathered} 0 \\ - M_\eta ^{ - 1} \\ \end{gathered} \right] \varsigma ，\\ z = {x_2} 。\\ \end{gathered} \right. $

(26)

设计的作业型AUV运动控制系统结构如图4所示，系统的反馈控制律、神经网络权值在线更新自适应律设计为：

$ {\tau _T} = - \omega + \hat W^{\rm{T}} h({\hat V^{\rm{T}}}\bar x) + {C_x}{x_2} + {M_\eta }\left({\ddot \eta _d} - \frac{1}{{2{\gamma ^2}}}\Lambda - \frac{1}{2}\Lambda \right) ，$

(27)

$ \dot {\hat W} = - {\Gamma _1}M_\eta ^{ - 1}h({\hat V^{\rm{T}}}\bar x){\Lambda ^{\rm{T}}} ，$

(28)

$ \dot {\hat V} = - {\Gamma _2}\bar x{\Lambda ^{\rm{T}}}M_\eta ^{ - 1}{\hat W^{\rm{T}}}h'({\hat V^{{\rm{T}}}}\bar x)。$

(29)

3.2 稳定性分析

基于李雅普诺夫第二法，证明设计的控制律、权值更新自适应律满足闭环系统稳定性要求。构造如下Lyapunov函数：

$ L = \frac{1}{2}{\Lambda ^{\rm{T}}}\Lambda + \frac{1}{2}tr({\tilde W^{\rm{T}}}\Gamma _1^{ - 1}\tilde W) + \frac{1}{2}tr({\tilde V^{\rm{T}}}\Gamma _2^{ - 1}\tilde V)，$

(30)

求导得：

$ \dot L = {\Lambda ^{\rm{T}}}\dot \Lambda + tr({\tilde W^{\rm{T}}}\Gamma _1^{ - 1}\dot {\tilde W}) + tr({\tilde V^{\rm{T}}}\Gamma _2^{ - 1}\dot {\tilde V}) ，$

(31)

将式（20）、控制律式（27）、自适应律（28）和（29）代入，整理得：

$\begin{aligned}[b] \dot L = & {\Lambda ^{\rm{T}}}\Bigg( - \frac{1}{{2{\gamma ^2}}}\Lambda - \frac{1}{2}\Lambda - \varsigma \Bigg) + \\ & tr({{\tilde W}^{\rm{T}}}(\Gamma _1^{ - 1}\dot {\tilde W} - M_\eta ^{ - 1}h({{\hat V}^{\rm{T}}}\bar x){\Lambda ^{\rm{T}}})) + \\ & tr({{\tilde V}^{\rm{T}}}(\Gamma _2^{ - 1}\dot {\tilde V} - \bar x{\Lambda ^{\rm{T}}}M_\eta ^{ - 1}{{\hat W}^{\rm{T}}}h'({{\hat V}^{\rm{T}}}\bar x)))= \\ & {\Lambda ^{\rm{T}}}\Bigg( - \frac{1}{{2{\gamma ^2}}}\Lambda - \frac{1}{2}\Lambda - \varsigma \Bigg) 。\end{aligned} $

(32)

定义：

$ H = \dot L - \frac{1}{2}{\gamma ^2}\left\| \varsigma \right\|_{}^2 + \frac{1}{2}\left\| \Lambda \right\|_{}^2，$

(33)

将式（32）代入式（33）得：

$ H = {\Lambda ^{\rm{T}}}\left( - \frac{1}{{2{\gamma ^2}}}\Lambda - \frac{1}{2}\Lambda - \varsigma \right) - \frac{1}{2}{\gamma ^2}\left\| \varsigma \right\|_{}^2 + \frac{1}{2}\left\| \Lambda \right\|_{}^2 ，$

(34)

将式(34)展开得到如下：

$ \left\{ \begin{gathered} {\Lambda ^{\rm{T}}}\Bigg( - \frac{1}{{2{\gamma ^2}}}\Lambda - \varsigma \Bigg) - \frac{1}{2}{\gamma ^2}\left\| \varsigma \right\|_{}^2 = - \frac{1}{2}\left\| {\frac{1}{\gamma }\Lambda + \gamma \varsigma } \right\|_{}^2 \leqslant 0 ，\\ - \frac{1}{2}{\Lambda ^{\rm{T}}}\Lambda + \frac{1}{2}\left\| \Lambda \right\|_{}^2 = 0。\\ \end{gathered} \right. $

(35)

推导出H ≤ 0，进一步得：

$ \dot L \leqslant \frac{1}{2}{\gamma ^2}\left\| \varsigma \right\|_{}^2 - \frac{1}{2}\left\| \Lambda \right\|_{}^2 。$

(36)

由HJI理论可知J ≤ γ，证明完毕。

4 系统数值仿真结果

在Matlab/Simulink软件下设计AUV轨迹跟踪仿真实验，验证融合递归神经网络和HJI理论（HJIRNN）的控制方法有效性和鲁棒性。选择基于传统滑模控制方法（SMC）、反步法（BS）设计的控制器作为对照。其中，使用饱和函数改善传统滑模控制存在的抖振问题，更具有工程实现意义。

表1列出仿真中使用的AUV模型参数，利用MSS工具箱计算科氏力矩阵C(v)。控制器关键参数 $ c=3{I}_{6}，\gamma =0.05，{\varGamma }_{1}=5{I}_{6}，{\varGamma }_{2}=5{I}_{7}，$ 仿真总时间为70 s，固定步长设置为0.01s，选取三维期望轨迹为如下：

$ \left\{ \begin{gathered} {x_d}(t) = \sin (0.2t)\;{\rm{m}} ，\\ {y_d}(t) = \cos (0.2t)\;{\rm{m}}，\\ {z_d}(t) = 0.2t\;{\rm{m}} ，\\ {\phi _d}(t) = 0\;{\rm{rad}}，\\ {\theta _d}(t) = 0\;{\rm{rad}}，\\ {\psi _d}(t) = 0.2t\;{\rm{ rad}} 。\\ \end{gathered} \right. $

(37)

仿真中采用时变函数作为模拟的总干扰项，表示为：

$ \left\{ \begin{gathered} {\tau _{\eta s1}} = - 5\sin (0.6t){\text{ N}} ，\\ {\tau _{\eta s2}} = - 10\sin (0.5t){\text{ N}}，\\ {\tau _{\eta s3}} = - 10\sin (0.4t) - 5\cos (0.2t){\text{ N}}，\\ {\tau _{\eta s4}} = - 4\cos (0.2t){\text{ N}} \cdot {\text{m}}，\\ {\tau _{\eta s5}} = - 2\cos (0.2t) - 3\cos (0.3t){\text{ N}} \cdot {\text{m}}，\\ {\tau _{\eta s6}} = - 6\cos (0.1t){\text{ N}} \cdot {\text{m}}。\\ \end{gathered} \right. $

(38)

AUV初始位置和初始速度为[x, y, z, ϕ, θ, ψ]^T=[0.5, 0.5, –0.5, 0, 0, 0]^T，[u, v, w, p, q, r]^T= [0, 0, 0, 0, 0, 0]^T。

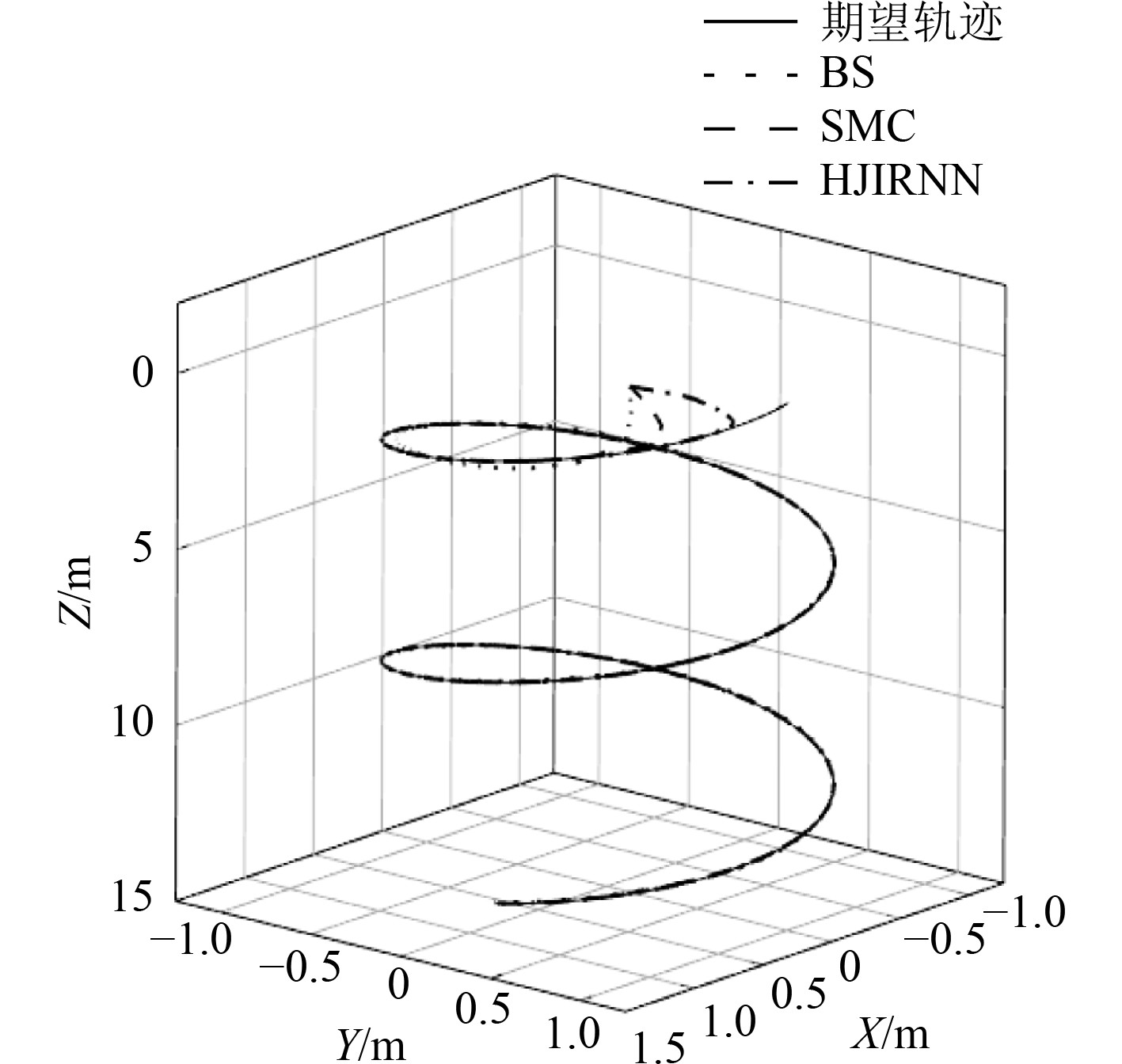
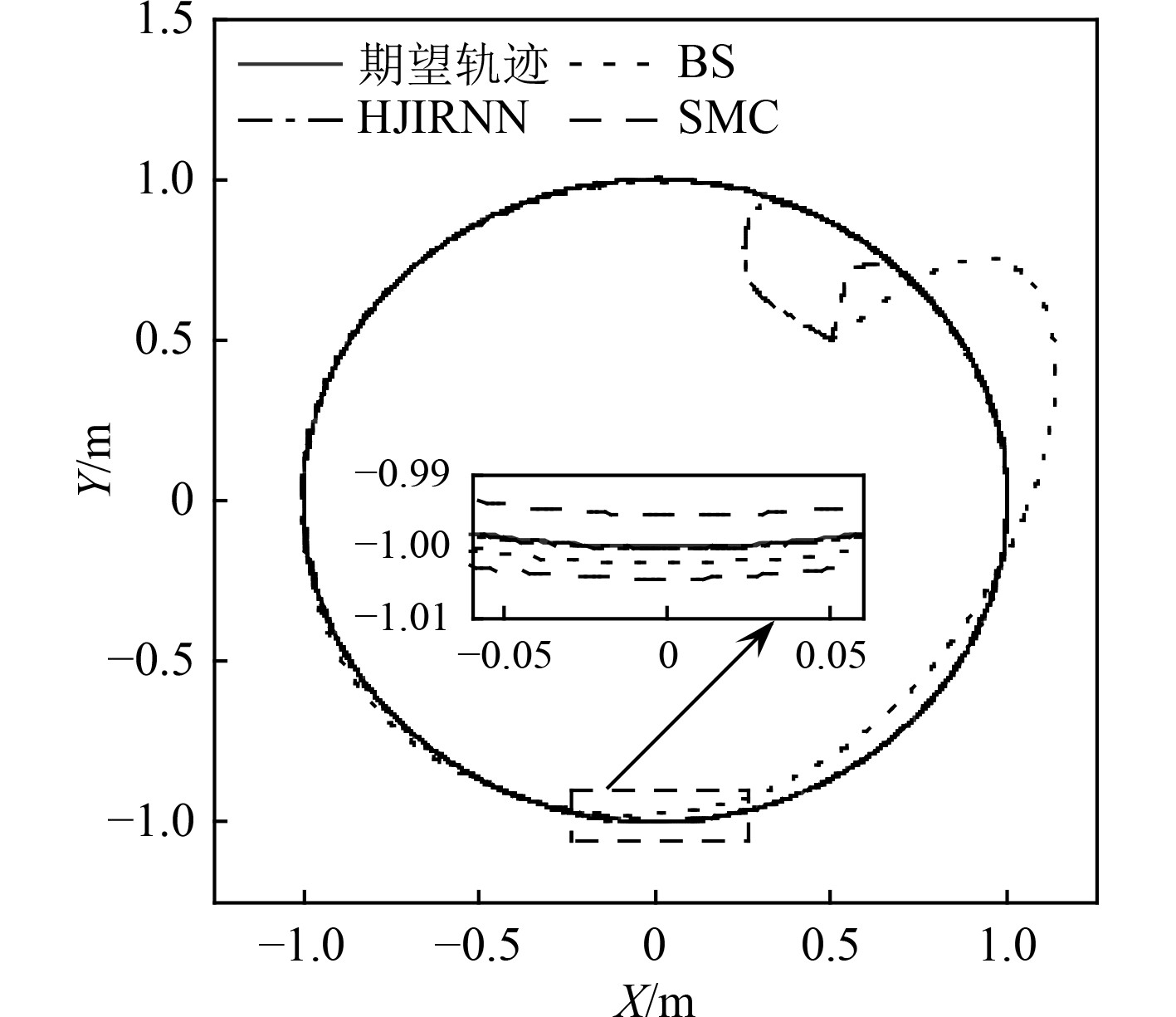
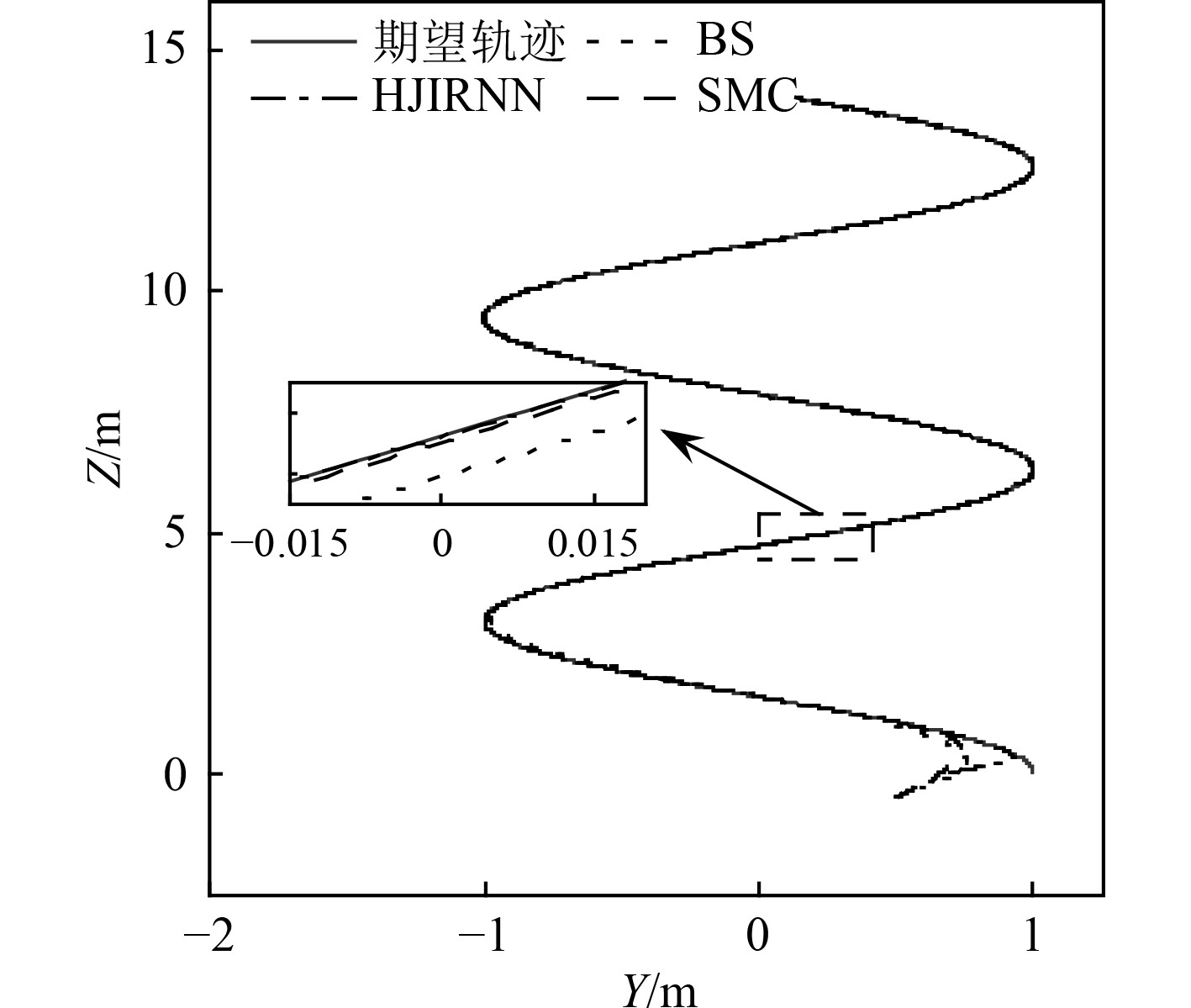
存在多种不确定性扰动时，三维轨迹跟踪仿真结果如图5所示，3种方法均能有效跟踪期望轨迹。轨迹跟踪曲线在X-Y，X-Z和Y-Z平面的投影如图6～图8所示。在仿真初始条件相同时，融合递归神经网络和HJI理论设计的控制器在收敛时间、超调量指标均优于对比方法，稳态时跟踪误差更小。

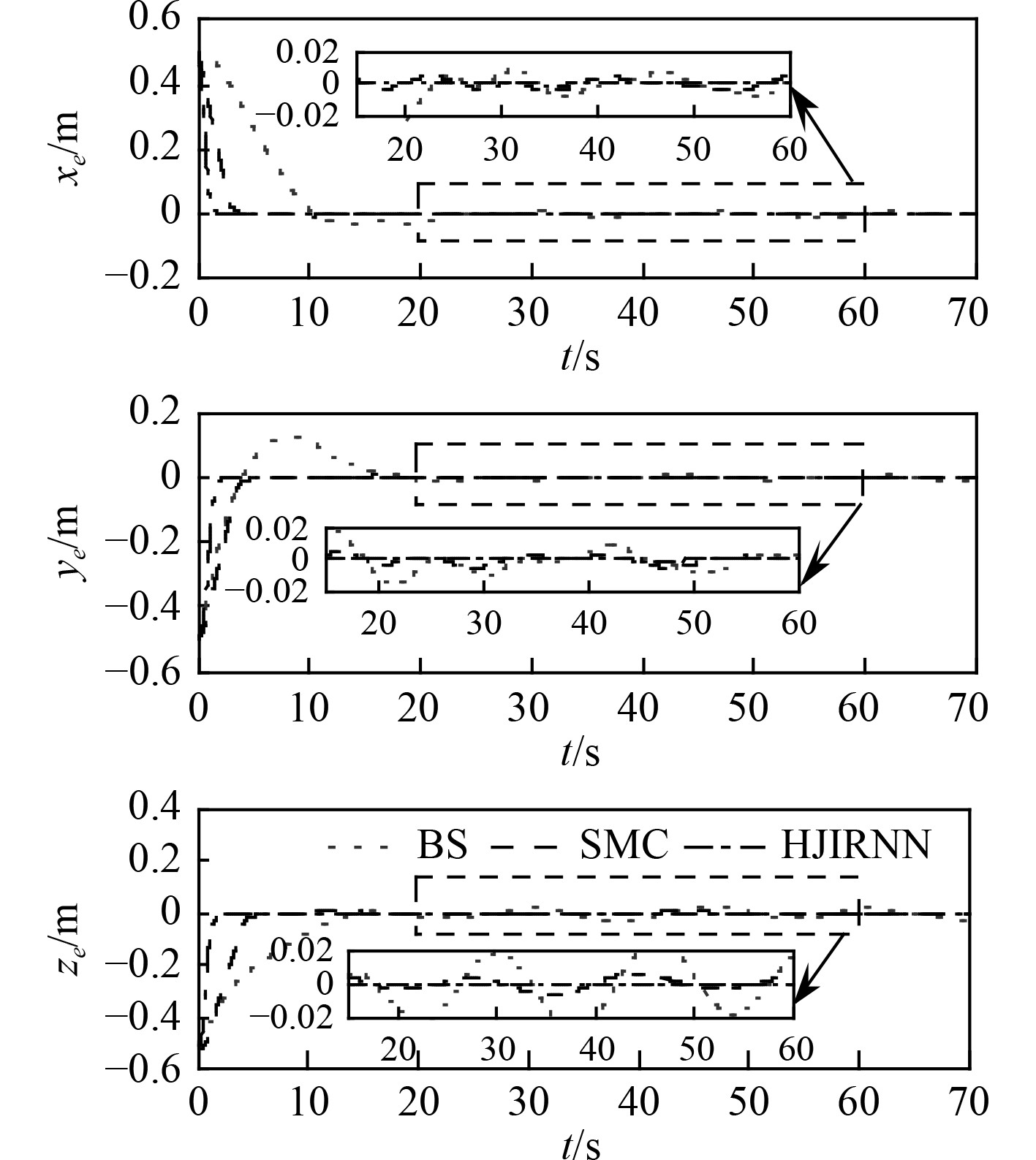
跟踪轨迹在X，Y和Z轴方向位置误差对比如图9所示，表2列出X，Y，Z轴方向误差和三维空间中位置误差平均值。由上述数据可知，采用反步法的控制器稳态误差范围和平均值最大，鲁棒性能最差。融合递归神经网络和HJI理论设计的控制器跟踪误差最小，收敛至0的任意小邻域内，鲁棒性能较好。滑模控制方法的鲁棒性能介于二者之间，其稳态误差的大小与饱和函数边界层范围确定存在一定关系，为抑制抖振，牺牲一定的控制精度，但相比于不采用抖振抑制方法的滑模控制更具有实际应用意义。

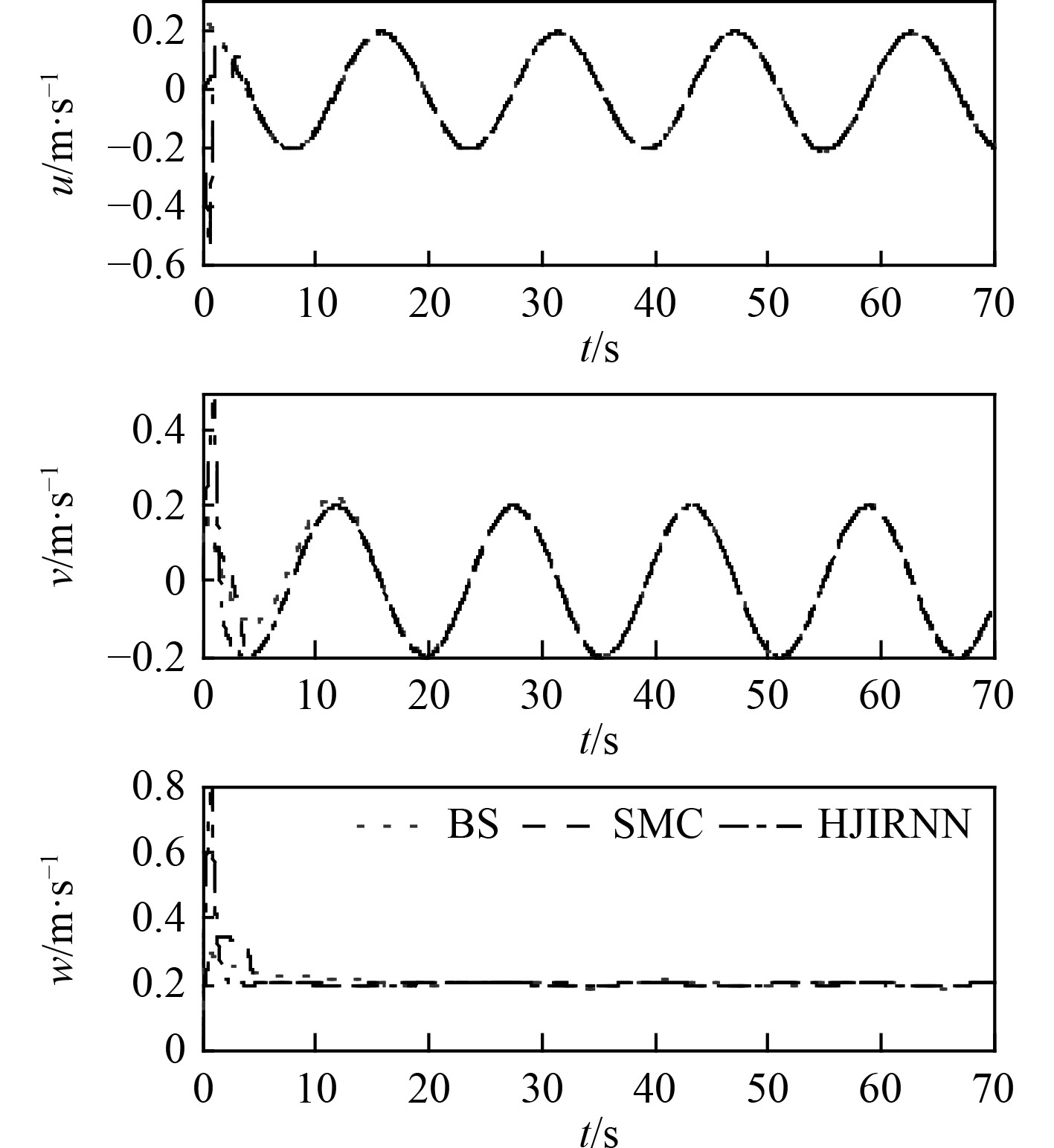
AUV轨迹跟踪时线速度变化曲线如图10所示，满足时间约束要求。融合递归神经网络和HJI理论设计的控制器为迅速收敛至期望轨迹，从初始位置趋近于期望轨迹期间的速度大于对比方法。

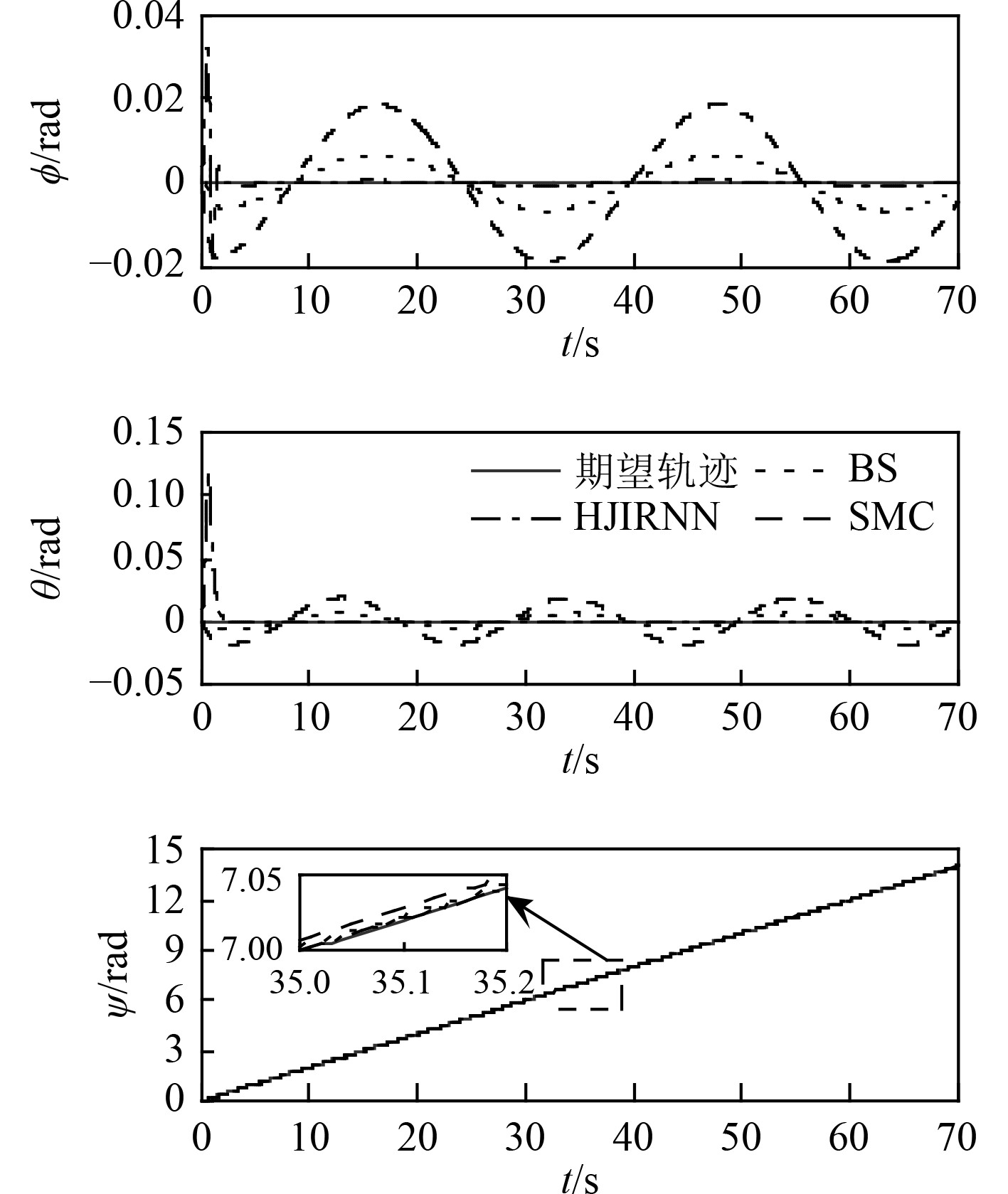
在姿态控制方面，如图11所示，设计的方法控制性能更为优越，对比控制方法则存在0.02 rad范围内的微小误差波动。AUV下潜深度的变化通过保持纵倾角θ恒等于0°，使用垂向推进器实现。

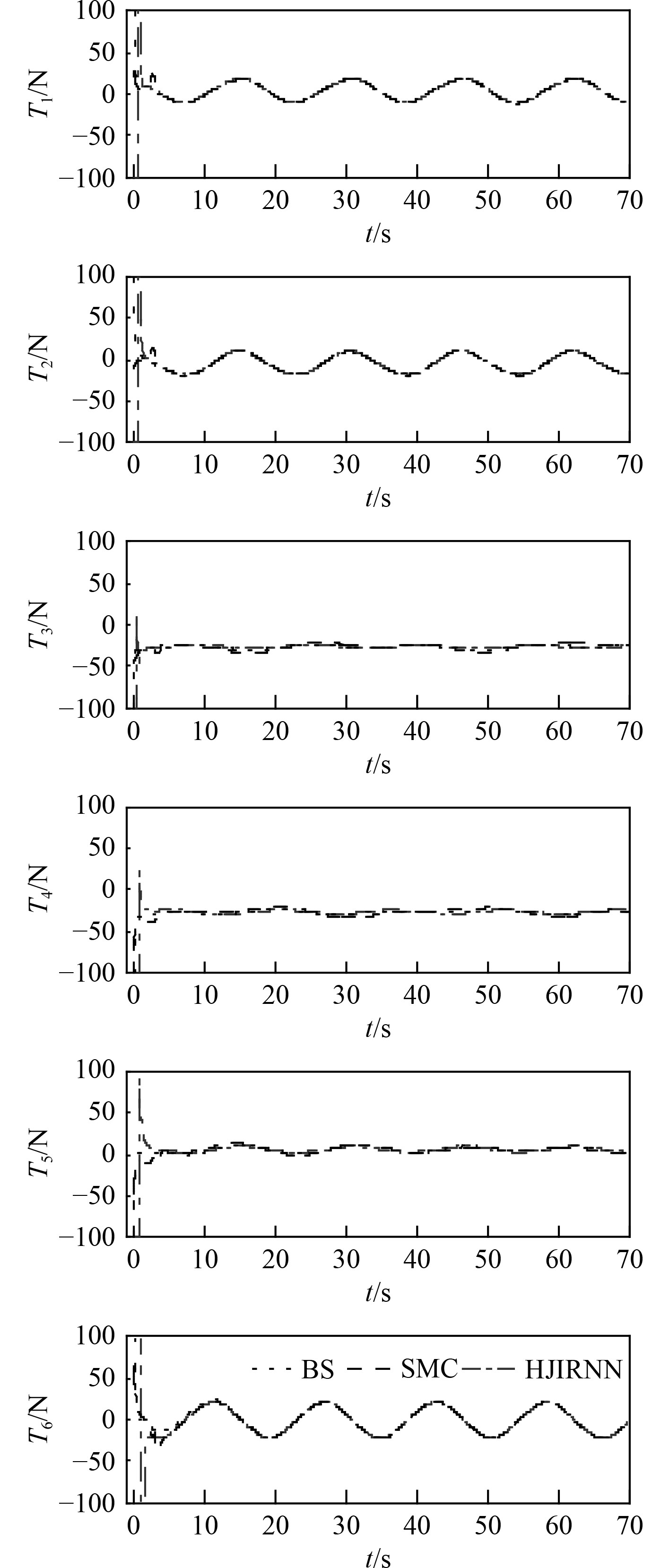
从图12可以看出，3种方法控制输出保证在执行器输入饱和范围内，符合工程应用要求，并且滑模控制在该仿真条件下的控制输出抖振得到有效抑制。

5 结　语

针对作业型AUV自身特点的三维轨迹跟踪控制需求以及现有运动控制方法中存在的不足，提出一种利用HJI理论并基于递归神经网络的复合运动控制策略。引入对角递归神经网络补偿作业过程中模型内部参数变化以及外部扰动；构造满足HJI不等式鲁棒条件的控制律，借助李雅普诺夫第二法证明闭环系统的稳定性。通过理论分析和仿真结果可知，与基于反步法、传统滑模控制方法相比，该方法具有更优秀的控制品质，有效的减少调整时间，对于时变扰动，具有良好的鲁棒性，实现了对非线性轨迹的稳定跟踪控制。将该方法在开发的作业型AUV样机上进行实验，进一步优化控制效果是未来研究的内容。