0 引　言

随着无人平台智能化水平不断提升，未来战争形势正在由信息化转向智能化。在追求作战人员零伤亡的背景下，无人集群自主协同作战是未来战场的新型主流作战样式^[1]。水下作战作为海战场全域联合作战的重要组成部分，水下无人潜航器（UUV）、水面无人艇（USV）、无人机（UAV）等机动无人平台和浮标、潜标、预置平台等固定无人平台正在成为海战场重要作战力量。水下无人集群能够突破人体极限，到达高威胁水域，长时间、高强度执行情报侦察、目标探测与跟踪、环境测量、反水雷、水声对抗、火力打击等多种任务^[2-3]，已成为各国海军的重要发展方向之一。

水下无人集群不同于水面舰艇、潜艇等有人平台，需要在弱通信条件下完全自主完成目标检测跟踪、情报收集和行动控制，面临着海洋环境复杂多变、无人值守等困难。水下无人集群主要通过平台搭载的主被动声呐载荷探测感知水下目标，但水声信道是时变空变的，且对声波呈现梳状滤波特性^[4-6]，导致不同的声呐工作模式和工作参数对探测效能影响较大。加之集群中单个节点的探测范围十分有限，如果集群成员阵位分布不合理，就会在任务区域内出现探测盲区。尤其在执行远海作战任务时，潜艇、水面舰等投放平台携带的无人兵力数量有限，无法通过投放冗余节点弥补探测盲区。因此，优化部署问题的研究是水下无人集群作战效能发挥的关键^[7-9]。本文旨在组合使用和声-粒子群算法解决水下无人集群的协同探测阵位优化问题，考虑任务要求、气象海洋环境、平台工作参数等因素影响，建立多准则约束下的综合评分方法，作为和声记忆库的适应度值计算函数，基于多任务约束条件自动生成水下无人集群的优化阵位，对水下无人集群的智能任务规划进行初步探索。

1 问题描述 1.1 应用场景

随着现代潜艇辐射噪声级的不断下降和艇载反舰武器射程的大幅提高，海上编队面临的水下威胁日益严峻，对潜防御作战是其重要任务之一。海上编队可利用核潜艇、水面舰等有人平台携带多部UUV，在编队与敌潜艇有信号接触后，有人平台撤出至敌鱼雷武器射程之外，释放UUV集群进入敌潜艇可能存在区域，接替有人兵力执行对潜搜索任务。UUV集群也可以作为前出兵力，辅助有人兵力在编队水下重要威胁方向或我方潜艇难以下潜的深水区遂行水下目标探测任务，进一步扩大编队对潜警戒范围。

无人集群利用水声通信载荷实现水下自组网，按照任务分工、作战编成与部署，利用探测声呐、侦察设备、环境测量等传感器载荷，进行对潜态势的协同感知。结合任务区域的海洋环境和目标威胁情况，集群自适应完成编队队形、声呐工作方式及工作频段等参数的优化调整，完成复杂海洋条件下对敌潜艇目标的检测定位和水文、地理环境的探测感知，通过中继通信节点将情报回传编队指挥中心，为反潜作战提供情报信息。

1.2 约束条件

水下无人集群在遂行区域搜潜任务时，协同任务规划和调整受到多种因素影响，本文在计算集群探测效能时主要考虑协同探测任务要求、气象海洋环境和无人平台工作参数3个约束条件。

1）协同探测任务要求

随着战场态势变化，对于集群的任务要求也会发生变化。当编队中有兵力与敌方目标信号接触，但无法定位目标位置信息时，无人集群的任务要求是搜索一段时间内敌潜艇可能逃逸的整个区域。集群中的各节点需合理规划并占据适当位置，实现对任务区域的有效探测全覆盖，或能够覆盖尽可能大的区域；当编队中有兵力与敌方目标信号接触，并报出目标的首点位置时，无人集群的任务要求是在有效覆盖关注位置点的基础上，实现对任务区域的有效探测覆盖最大化，而尽量使重点关注位置点周围的目标探测能力最大；在没有敌情时，无人集群的任务要求是在编队重点威胁方向一定距离上建立连续的对潜检测区带，形成对编队的水下防护“栅栏”，能够作为警戒线分隔外界与编队作战活动区域，防止水下威胁目标侵入编队内层防御圈。

2）气象海洋环境

海洋环境是影响声呐探测效能的重要因素。水下声信道具有时变空变特性，对声信号具有频率选择性衰落、多径传播等效应。海水温度、盐度、密度、声速梯度、海底底质等水文参数会影响声信号的传播损失、传播轨迹，从而影响会聚区和声影区的分布。海况、降雨等气象参数会影响无人平台目标检测时的背景噪声。气象海洋环境通过影响水下无人平台的探测性能，从而影响无人集群的任务规划。

3）无人平台工作参数

无人平台自身和搭载声呐设备的工作参数会对声呐作战距离、探测概率、相互之间辐射噪声干扰等产生影响，从而影响集群协同探测时的部署阵位。平台参数包括自身尺寸、航行速度、搭载声呐类型等。声呐工作参数包括工作模式、发射声源级、指向性指数、脉冲宽度、工作频段、检测阈阵元数等。

1.3 评估准则

在评价无人集群部署效能时，需要建立多约束条件下的综合评估准则。本文建立区域有效探测覆盖率和区域综合覆盖率2个指标，对集群优化部署效能进行综合评估。

将海区范围内执行探测任务的m个发射节点和n个接收节点组合配对，得到m×n个双节点组合，对任务海区进行网格划分，根据声呐方程计算每个双节点组合在任一网格处的目标检测概率 $ {P}_{{i}} $ ，得到多节点检测概率矩阵为 $\left[{{P}_{1},{P}_{2,\cdots ,}P}_{i,\cdots ,}{P}_{m\cdot n}\right]$ ，则整个海区无人集群对某一网格处的目标检测概率为：

$ {P_d} = 1 - \prod\limits_{i = 1}^{m \cdot n} {(1 - {p_i})} 。$

(1)

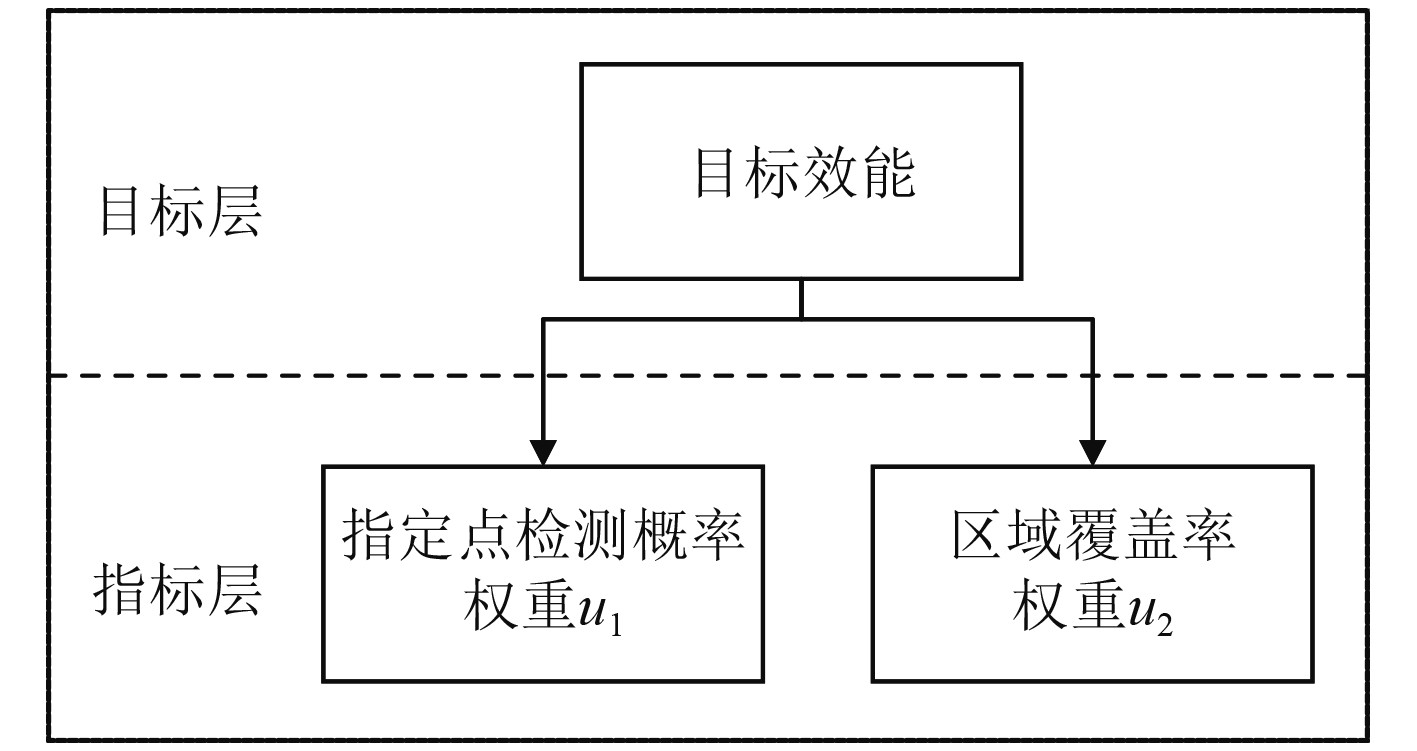
规定检测概率大于70%的网格区域为有效覆盖区，覆盖率即有效覆盖区域面积占总待评估区域面积的百分比。利用层次分析法的思想^[10]，将该问题分解为“指标层”和“目标层”2个层次。指标层为具体评价指标项，可根据实际任务中约束条件而定，本文采用关注点检测概率和区域覆盖率2个指标项，其权重向量为 $ {u}=[{{u}}_{1},{{u}}_{2}] $ 。目标层为整体效能评价，通过将各指标项加权求和得到。根据实际任务需要和工程经验，建立检测概率与评价分数之间的映射关系，采用的映射关系见表1。

若对关注点的检测概率评分为a，对区域覆盖率评分为b，则对优化部署方案的综合评分可表示为：

$ S=a\cdot {u}_{1}+{b\cdot u}_{2}。$

(2)

2 算法设计

和声搜索算法（harmony search, HS）是Geem等^[11-13]提出的一种群智能优化算法。受启发于乐队演奏音乐的过程，将每个音符看作是评价函数的自变量，乐师通过反复调整乐队里各乐器音调以达到最优美动听的和声状态，相当于不断搜索最合适的自变量使得评价函数不断优化达到最小值的过程。和声算法因其搜索随机性较大，具有很好的全局优化搜索性能，已经得到工程应用，但存在算法收敛速度慢导致搜索用时较长的问题。而粒子群优化算法（Particle Swarm Optimization，PSO）^[14-16]中各粒子运动方向始终受到历史最优和全局最优解的吸引，搜索目的性强，搜索初期收敛速度快，已广泛应用于多个领域，但存在搜索后期容易陷于局部最小而不能获得全局最优的缺点。考虑水下无人集群的适用性，搜索算法需要简单、稳定、快速，本文采用和声-粒子群优化算法（HS-PSO），将和声算法良好的跳出局部最优解的能力和粒子群算法在优化初期的快速收敛能力结合使用^[17-18]，以平衡2种算法的性能，满足水下无人集群的应用需求。

1）建立和声记忆库

在解空间内随机生成 HMS个和声向量，同时记录粒子群算法中粒子历史最优记录，构建如下形式的和声记忆库：

$ {\boldsymbol{HM}} = \left[ {\begin{array}{*{20}{c}} {{x_1}}&{f({x_1})}&\vline & {x_1^p}&{f(x_1^p)} \\ {{x_2}}&{f({x_2})}&\vline & {x_2^p}&{f(x_2^p)} \\ \vdots & \vdots &\vline & \vdots & \vdots \\ {{x_{HMS}}}&{f({x_{HMS}})}&\vline & {x_{HMS}^p}&{f(x_{HMS}^p)} \end{array}} \right]。$

(3)

式中： $ {x_i} $ 为第i个和声向量，对集群阵位进行优化时由场景内所有水下无人平台的位置坐标组成，初始值随机生成； $ f({x_i}) $ 是该和声向量的适应度值，本文为水下无人集群区域有效探测覆盖的综合评分，通过式（1）和式（2）计算得到； $ x_i^p $ 为第i个和声的历史最优解， $ i = 1,2,\cdots ,HMS $ ，每次更新时选择区域有效探测覆盖综合评分最高的和声向量作为最优解。HM中左半部分的和声参与寻优，右半部分为左侧和声的历史最优记录。建立一个空向量 $[ {{x_g}}\quad{f({x_g})} ]$ 来记录和声记忆库中的历史最优和声作为全局最优解。

2）产生新的和声向量

定义和声记忆库取值概率 $HMCR$ ，生成随机数 $rand$ ，若 $rand < HMCR$ ，在 $HM$ 中搜索生成新和声，反之则随机生成新和声。具体实现表达式为：

$\begin{split} &{x'_i} = \left\{ {\begin{array}{*{20}{l}} {{{x'}_i} \in \{ x_1^{},x_2^{}, \cdots ,x_{HMS}^{}\} }，&{rand < HMCR}, \\ {{{x'}_i} \in {X_i}}，&{{\rm{else}}} , \end{array}}\right.\\ &i = 1,2, \cdots ,HMS。\end{split} $

(4)

式中： $ rand $ 为[0，1]区间内均匀分布的随机数， $ {X_i} $ 为变量的定义域。

若新的变量取自 $HM$ ，为增加解的多样性以扩大搜索范围，以概率值 $ PAR $ 进行扰动微调。具体实现表达式为：

$\begin{split}& {x'_i} = \left\{ {\begin{array}{*{20}{l}} {{{x'}_i} + (2 \cdot rand'' - 1) \cdot BW}，&{rand' < PAR}，\\ {{{x'}_i}}，&{{\rm{else}}} ，\end{array}} \right.\\ &i = 1,2, \cdots ,HMS。\end{split} $

(5)

式中：BW为微调宽度，一般取值[0.01，0.1]，单位为km， $ rand' $ 与 $ rand'' $ 均为[0，1]区间内均匀分布的随机数。微调时需要监测变量微调后是否仍在定义域内，若微调量过大使得变量跳出定义域则重新进行微调步骤。

3）更新和声记忆库

比较新和声与 $HM$ 中已存在和声的适应度值，若新和声的适应度优于 $HM$ 中最差的和声，则用新和声将其替换；若新和声的适应度劣于 $HM$ 中最差和声，则保持 $HM$ 不变。

4）利用粒子群算法对和声进行优化

对 $HM$ 中的和声向量进行粒子群优化，将 $HM$ 中的每个和声当作一个粒子，依据式（6）和式（8）对各粒子的运动速度及位置更新，并给出各粒子的适应度值。

粒子的运动速度更新实现表达式为：

$ \begin{split} {v_i}(t) =& \omega \cdot {v_i}(t - 1) + {c_1} \cdot rand\left( {} \right) \cdot \left( {{p_i} - {x_i}(t - 1)} \right) + \\ &{c_2} \cdot rand\left( {} \right) \cdot \left( {g - {x_i}(t - 1)} \right)。\end{split} $

(6)

式中： $ {v_i}(t) $ 为t时刻粒子的运动速度； $ {c_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{c_2} $ 为学习因子，分别为粒子的历史最优与全局最优解对下一时刻粒子运动速度的影响； $ {p_i} $ 为粒子i的历史最优解；g为集群的全局最优解；为确保更新过程的稳定，应对 $ {v_i} $ 的取值范围进行限制。 $\omega $ 为惯性权重，控制粒子上一时刻速度对当前时刻速度的影响。为了使优化初期能有较好的全局搜索能力，且后期能有较好的局部搜索能力，通常会应用线性递减权值策略，该策略会使 $\omega $ 随着迭代的进行而线性减小：

$ \omega {\text{ = }}\left( {{\omega _{start}} - {\omega _{end}}} \right)\left( {\frac{{{t_{\max }} - t}}{{{t_{\max }}}}} \right) + {\omega _{end}}。$

(7)

式中： ${\omega _{start}}$ 和 ${\omega _{end}}$ 分别为迭代开始时与结束时的惯性权重； ${t_{\max }}$ 为最大迭代次数；t为当前迭代次数。

粒子i在第t时刻的位置更新实现表达式为：

$ {x_i}(t) = {x_i}(t - 1) + {v_i}(t)。$

(8)

5）更新历史最优值

对于 $ HM $ 中的第i个和声，若 $ f({x_i}) $ 优于 $ f(x_i^p) $ ，则用 $ {x_i} $ 替换 $x_i^p$ 并更新 $ f(x_i^p) $ ，反之则保持不变；对每个记录历史最优的和声，若其 $ f(x_i^p) $ 优于全局最优和声的适应度值 $ f({x_g}) $ ，则用 $x_i^p$ 替换 $ {x_g} $ 并更新 $ f({x_g}) $ 。

6）判断粒子群算法部分是否满足停止条件

首先判断粒子群迭代次数是否达到粒子群最大迭代次数 $MI$ ，是则进行步骤7，否则转到步骤4。

7）判断和声搜索部分是否满足停止条件

判断进行和声更新的次数是否达到最大迭代次数NI，是则结束迭代，输出全局最优解 $ {x_g} $ 及 $ f({x_g}) $ ，否则跳转到步骤2。

随着迭代过程的不断深入，记忆库中最差的和声逐渐被取代，新和声在微调优化，整体和声向着适应度最优的方向发展，同时以一定概率随机加入新和声，提高算法跳出局部最优的能力。迭代次数MI，NI可根据无人平台的计算能力和算法稳定度等实际情况决定。

3 仿真试验分析 3.1 单准则约束下集群阵位优化分析

对水下无人集群的各节点阵位进行优化搜索，生成最优规划方案，并利用区域有效覆盖率作为使用度值进行评估。对标准和声算法、粒子群算法、和声-粒子群混合算法搜索寻优后的有效覆盖率和用时进行统计分析。

主要仿真试验参数：任务海区范围40 km×40 km，区域步长0.1 km，场景内共4个平台，其中2个为发射平台，2个为接收平台。

和声算法参数： $ HMS = 5 $ ， $ HMCR = 0.9 $ ， $ PAR = 0.3 $ ， $ BW = 0.01 $ ， $ NI = 500 $ 。

粒子群算法参数： ${\omega _{start}} = 0.9$ ， ${\omega _{end}} = 0.3$ ， ${c_1} = 2$ ， ${c_2} = 2$ ， ${v_{\max }} = 2$ ， ${t_{\max }} = 500$ 。

和声-粒子群算法参数：外层和声搜索部分 $HMS = 5$ ， $HMCR = 0.9$ ， $NI = 100$ ；内层粒子群部分 ${\omega _{start}} = 0.9$ ， ${\omega _{end}} = 0.3$ ， ${c_1} = 2$ ， ${c_2} = 2$ ， ${v_{\max }} = 2$ ， $MI = 5$ 。

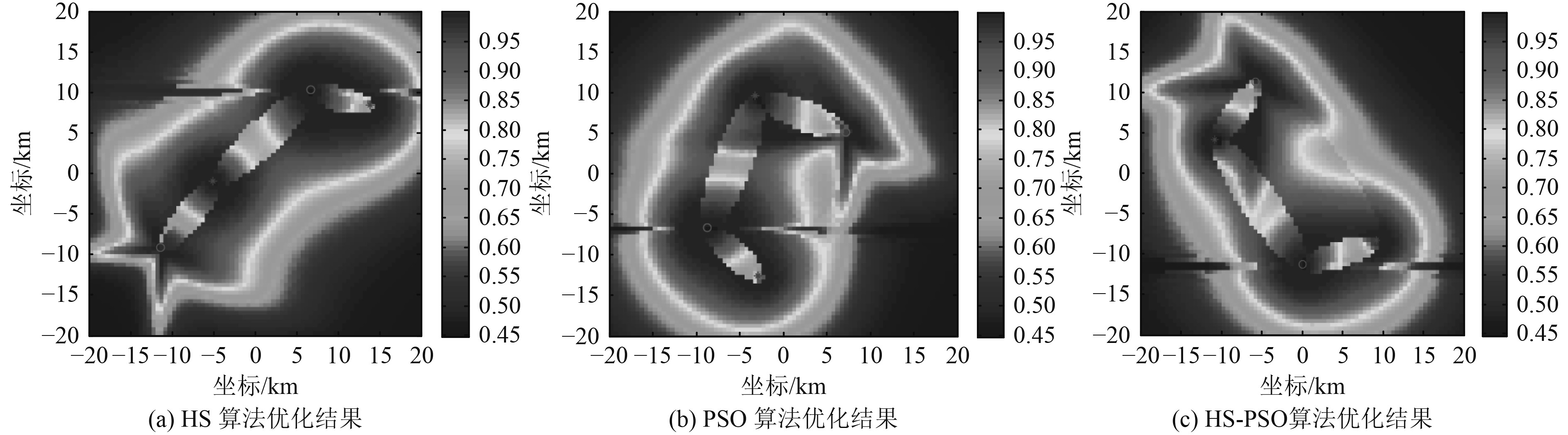
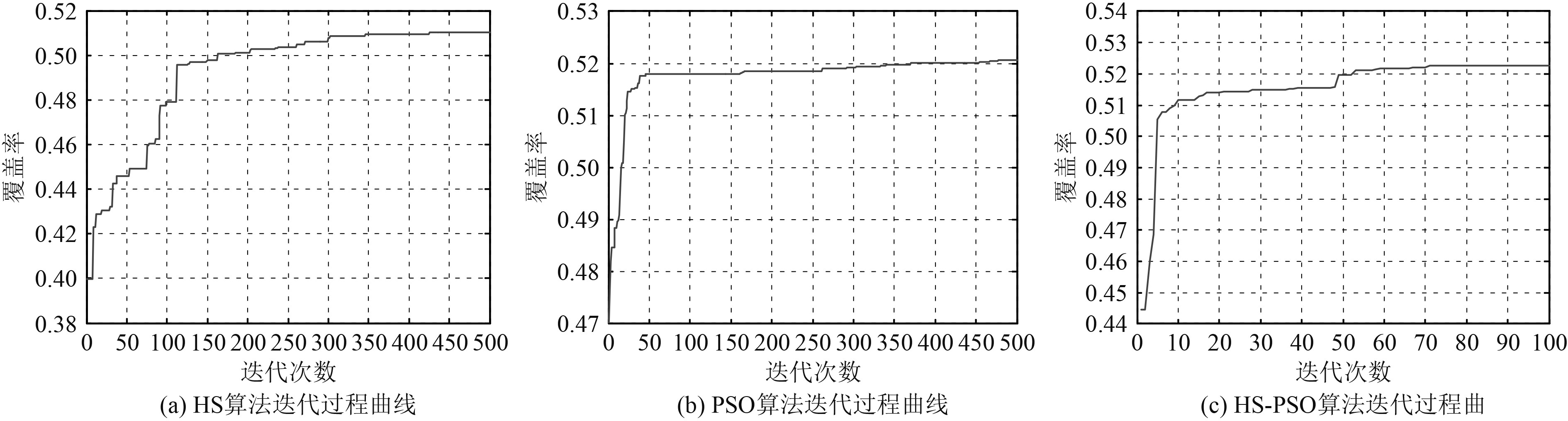
对标准和声算法和粒子群算法分别进行500次迭代寻优处理，对和声-粒子群混合算法进行外层100次和内层5次迭代处理，共进行100次仿真试验。随机选择其中第15次仿真结果进行分析，图3为3种算法优化处理结果，图4为3种算法迭代过程曲线，表2为第15次仿真时3种算法优化处理结果以及100次仿真试验的有效覆盖率平均结果。

分析图4可知，HS算法在迭代350次后基本趋于收敛。PSO算法在迭代50次后曲线接近平缓，而且有效覆盖率仍在缓慢上升，说明该算法收敛迅速，且拥有较好的局部精细搜索能力。而HS-PSO算法在迭代60次时基本趋于收敛，在第48次迭代时的跃变说明该算法具备一定跳出局部最优解的能力。该算法的迭代过程曲线与PSO算法的曲线更为近似，相比于HS搜索算法，HS-PSO算法的收敛速度更快，进化更为平稳。

对比图5和表2的可知，3种算法单次优化处理结果相近，但100次统计结果显示HS-PSO算法的有效覆盖率高于HS算法和PSO算法。检查100次优化结果发现，PSO算法多次出现优化结果远低于其他各组寻优结果的情况。这是由于该算法当前优化陷入局部最优而无法找到全局最优解，从而导致平均覆盖率降低，而HS-PSO算法的具有相对稳定的全局寻优能力。

3.2 多准则约束下集群阵位优化分析

对多重约束条件的情况进行仿真，要求在任务海区对坐标为（0，0）的位置点附近进行重点检测，同时实现对整个海区的探测最大化覆盖，约束准则的权重向量u=[0.7, 0.3]。为了进一步验证HS-PSO算法对无人集群阵位的优化处理效果，将算法寻优结果与根据人的经验布放的结果进行对比。

主要仿真参数为：场景内平台数量4，任务海区范围40 km×40 km，区域步长0.1 km， ${\omega _{start}} = 0.9$ ， ${\omega _{end}} = 0.3$ ， ${c_1} = 2$ ， ${c_2} = 2$ ， $MI = 5$ ；主体优化中 $HMS = 5$ ， $HMCR = 0.9$ ， $PAR = 0.3$ ， $BW = 0.01$ ， $NI = 500$ 。

优化前的初始状态，是将4个无人节点对称布放在关注点（0,0）周围，对区域的有效覆盖情况如图5（a）所示，经和声-粒子群算法优化后的结果如图5（b）所示，100次的迭代过程曲线如图5（c）所示，优化前后的区域有效覆盖对比情况见表3。

优化前无人集群对任务海区的关注点检测概率为84.37%，综合评分为7.4。经过HS-PSO算法优化调整，点检测概率提升为99.96%，综合评分提升为9.6。分析图5（a）和5（b）可知，优化前由于直达波干扰，无人集群的整体探测包络内存在多处检测概率明显低于70%的弱视区甚至检测盲区，会造成对目标的漏检，经优化后不仅提高了对关注位置点的检测概率，更是大幅减小了集群整体探测范围内的盲区。与单纯依靠人的经验进行阵位部署相比，优化效果明显。

4 结　语

针对水下无人集群在执行协同探测任务时的阵位优化部署问题，本文采用和声-粒子群优化算法，实现集群内多节点的阵位自动寻优。建立区域覆盖率、点检测概率等评估指标，在多准则约束下对优化部署方案进行评价。仿真试验结果表明，HS-PSO算法可用于水下无人集群的阵位优化处理，与人工部署相比，经该算法优化后有效探测区域覆盖率明显提升，与标准和声算法、粒子群算法相比，HS-PSO算法的收敛迅速，具有相对稳定的全局寻优能力。本文研究了水下无人集群阵位优化问题，但实际应用时还有更多维度的变量需要优化，后续将进一步改进算法模型，研究声呐工作参数、平台机动时间等更多维度变量的联合优化问题。