0 引　言

随着我国对海洋开发的不断深入，大型无人潜航器（以下简称为潜航器）越来越多的被应用资源勘探、海底地形勘察、海洋环境监测等。另外，其也可适用于目标搜索、敌情侦察、对敌打击等军事用途^[1-2]。在水面/水下状态转换、内部载荷变化以及外部环境等因素的影响下，潜航器会产生纵倾，大纵倾会严重影响潜航器的操纵性和安全性，纵倾平衡系统作为潜航器姿态调节的重要实现部分，可保证潜航器达到零纵倾或规定的纵倾，因此有必要针对大型无人潜航器，开展纵倾平衡系统的应用研究。

纵倾平衡系统可在不改变潜航器排水体积的前提下，依靠内部纵向载荷的调整，消除作用在潜航器上的纵向不平衡力矩达到均衡的目的。目前常用的方法有：1）通过调水实现，需在潜航器内部设置首尾纵倾平衡水舱，使用水泵或压缩空气移动首尾纵倾平衡水舱的水调节纵倾；2）通过垂推实现，在潜航器靠首部或尾部安装垂向推进器，依靠垂向推进器正反转产生作用于潜航器的垂向力来调节纵倾；3）通过质量块移动实现，依靠潜航器内部设置的质量块纵向移动改变潜航器重心，以此达到调节潜航器纵倾的目的。纵倾平衡水舱内的水会产生自由液面，削弱潜航器的稳心高，且潜航器内部空间有限，不便布置内部水舱以及搭建水管路；通过垂推调节纵倾，需要安装垂向推进器，且调节过程中潜航器潜深不易恒定；通过质量块移动来调节纵倾，噪声小，潜航器隐身性能较好，且作用效率高，可以作为下一步的研究方向。

周克秋等^[3]为作业型水下机器人研究了一套姿态调节装置，该装置利用滚组丝杠、铁块等组成滑台，并建立了装置控制模型；苏浩等^[4]充分利用潜航器内部空间，将电池包作为质量块进行位置调节，进而达到改变潜航器重心的目的。孙伟成等^[5]设计了一种姿态调节装置，可以同时实现水下滑翔机纵倾和回转运动的控制。

针对潜航器纵倾平衡系统研究现状，并结合具体应用场景，本文提出一种机械式纵倾平衡系统，其采用伺服电机驱动滚珠丝杠带动质量块纵向滑动实现潜航器的纵倾平衡，并且将质量块与耐压壳做了共形设计，使该系统具有占用空间小、操作简便、运行精度高等优点。同时结合潜航器操纵性，分析不同应用场景下纵倾平衡系统的工作方式。

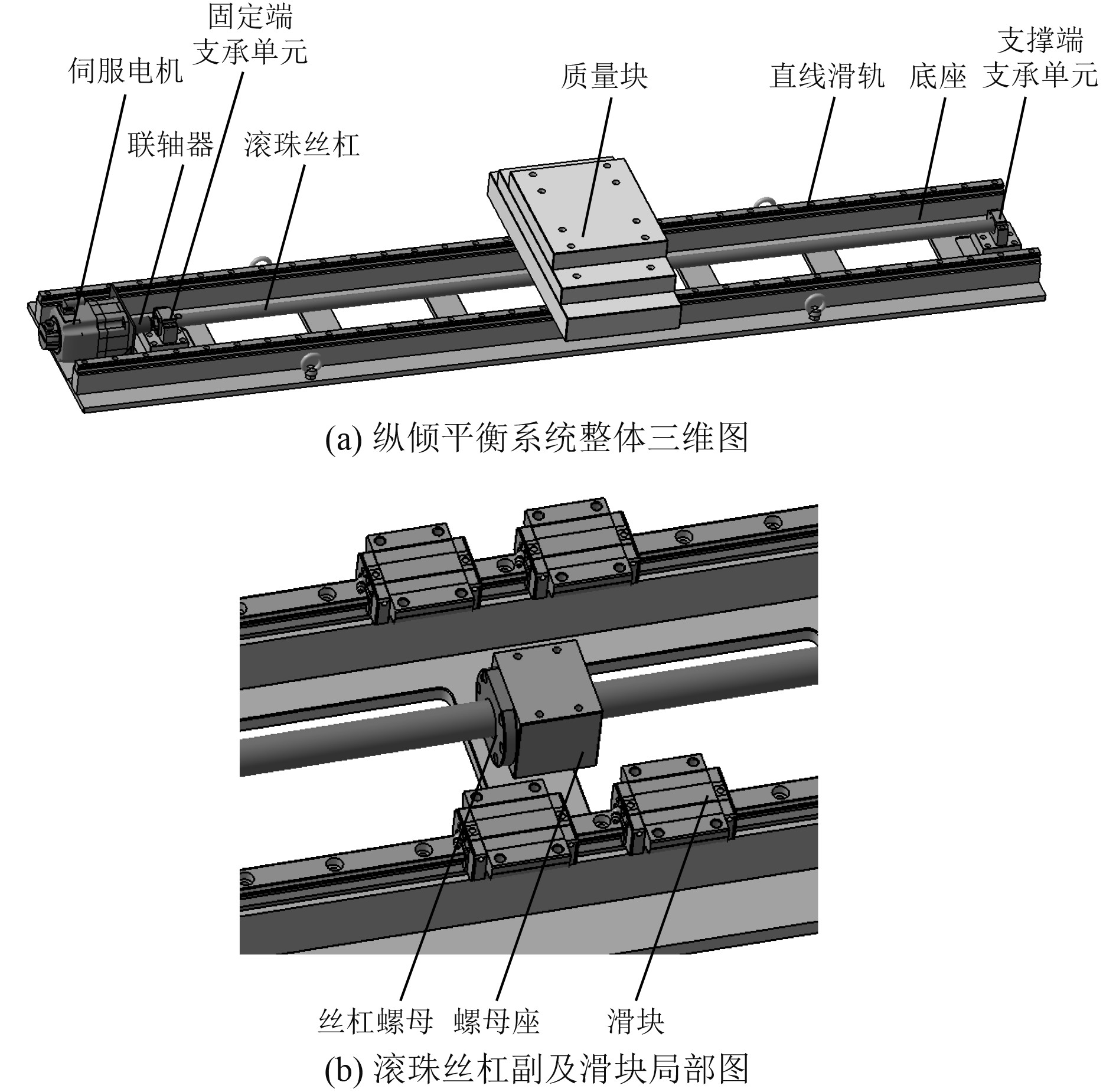
1 系统组成

本文设计的纵倾平衡系统结构形式如图1所示，主要由伺服电机、联轴器、丝杠、质量块、直线滑轨、底座等组成。为减少安装程序，纵倾平衡系统在潜航器中采用模块化安装的方式，伺服电机通过螺钉固定在底座上，滚珠丝杠通过固定端支承单元和支撑端支承单元固定在底座上，伺服电机输出端通过联轴器与滚珠丝杠相连接，底座上表面加工有2条平行的凸起，在凸起顶面通过螺钉安装有直线滑轨，在每条直线滑轨上配合安装2个滑块，丝杠螺母与滚珠丝杠组成运动副，将旋转运动转变为直线运动，螺母座与丝杠螺母通过螺钉相连接，质量块与4个滑块以及螺母座通过螺钉连接，质量块自下而上分3部分组成，各部分之间通过沉头螺钉连接。

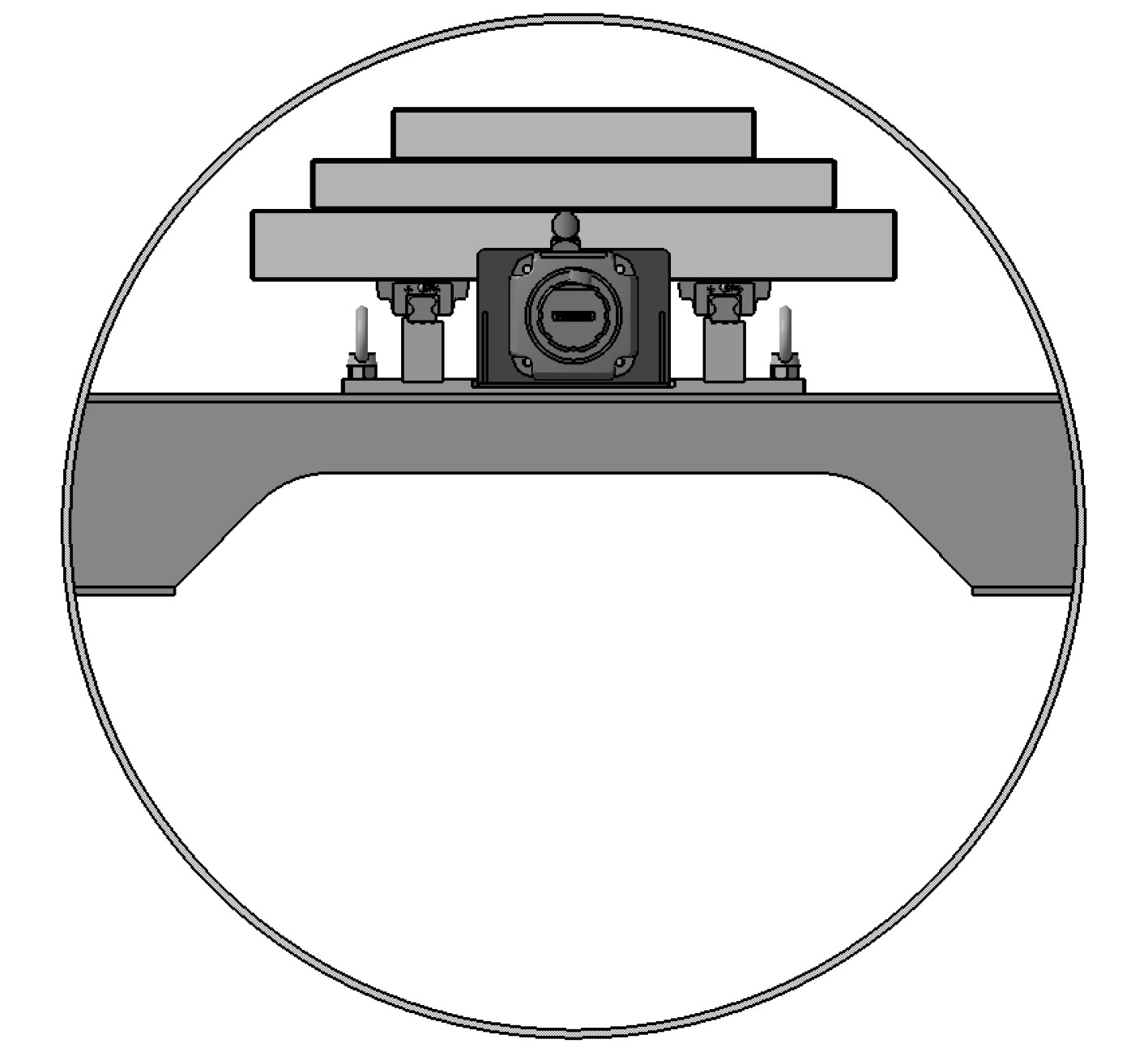
纵倾平衡系统安装位置主要考虑潜航器总布置、滑块活动空间以及对潜航器稳性的影响，为节省潜航器耐压壳内的下部空间，通过安装支架固定在耐压壳的上层，并且将质量块由下而上分3块设计，3个质量块宽度相同，长度由下而上逐渐减小，各质量块之间通过螺钉连接，安装完成后与耐压壳共形，充分利用了潜航器的内部空间。在实际操作中，若设计的纵倾平衡系统纵倾调节能力不足，可改换密度更大的金属质量块，若纵倾调节能力过剩，可将最上层质量块取出，增加了现场操作的灵活性。

2 工作原理

本文纵倾平衡系统依靠质量块沿潜航器纵向滑动改变潜航器重心从而达到调节纵倾的目的，在需要调节纵倾时，伺服电机通过联轴器带动滚珠丝杠旋转，丝杠螺母将旋转运动转变为直线运动，带动螺母座及质量块滑动。在潜航器无纵倾时，质量块在丝杠的中间位置，将此位置定义为质量块运动的零点，向首为正，向尾为负，当潜航器发生首倾时，质量块向负方向移动，当潜航器发生尾倾时，质量块向正方向移动。移动距离和移动速度可根据潜航器实际情况而定，调节过程需结合纵倾角、航速、浮力调整系统等参数，由航控计算机通过程序精准实现^[6]。

在程序控制过程中，可选择开环控制或闭环控制。开环控制即是由航控计算机根据潜航器状态计算出质量块移动距离，在质量块移动结束后指令即结束；闭环控制将质量块移动后的潜航器纵倾姿态信息反馈回航控计算机，由航控计算机决定是否需要进一步调节。

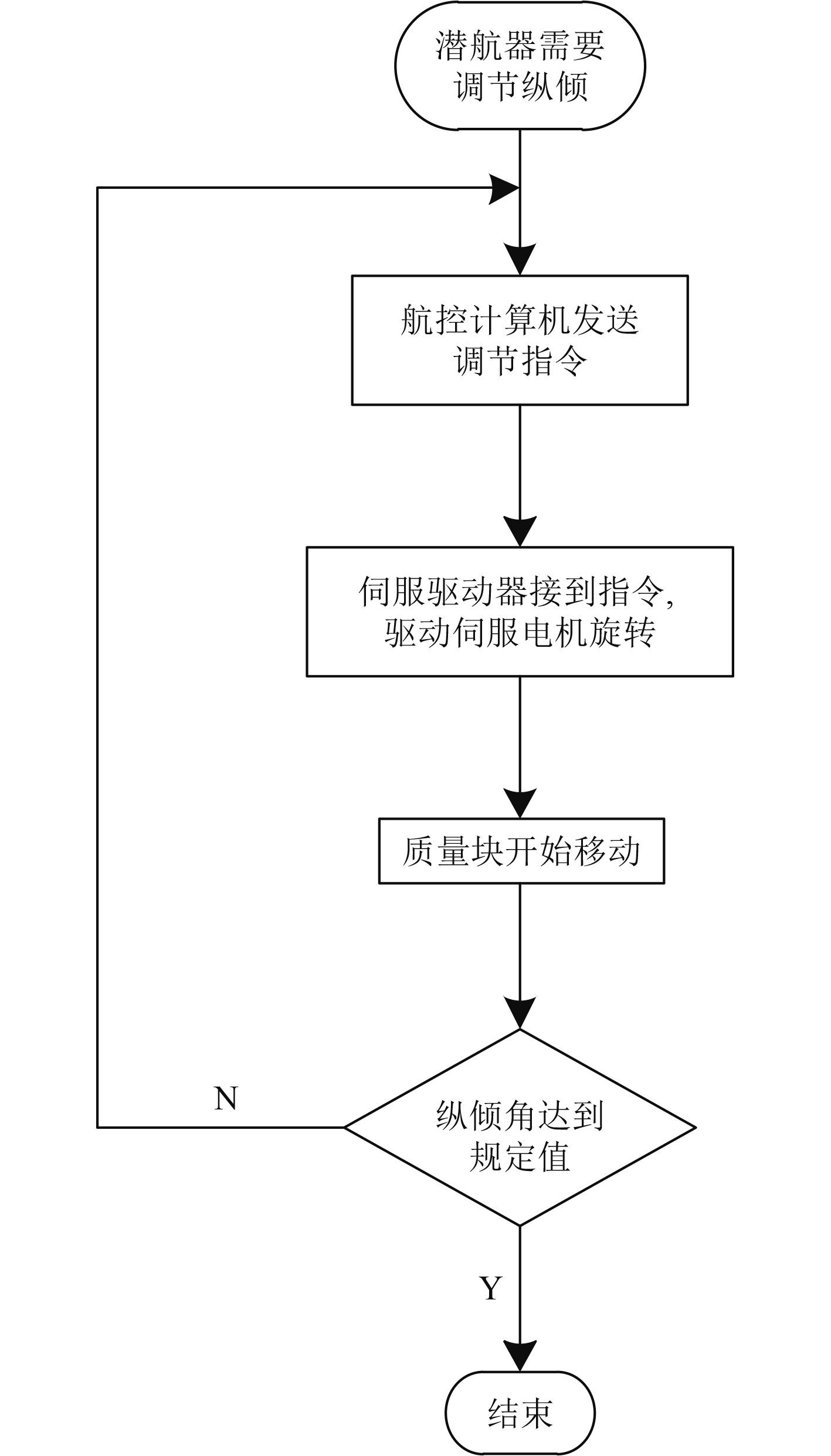
闭环控制操作流程图如图3所示。

本装置优点如下：1）采用模块化设计，简化安装程序；2）采用质量块与耐压壳共形设计，节省潜航器的内部空间；3）采用伺服电机驱动，操作性强，定位精度高；4）噪声源少，振动噪声传递小，隐身性能优越。

3 系统工作方式研究

潜航器在不同的应用环境下，对纵倾平衡系统的需求不同，相对应的系统工作方式也会变化，本文对潜航器常见状态下的机械式纵倾平衡系统工作方式进行研究。

3.1 水面状态

潜航器在水面状态发生纵倾时，可以求得复原力矩为：

$ {M_{RL}} = \Delta \uparrow g \cdot \overline {G{M_L}} \cdot \sin \theta。$

(1)

式中： $\Delta \uparrow $ 为水上排水量； $\overline {G{M_L}} $ 为纵稳心高； $\theta $ 为纵倾角。

$ \overline {G{M_L}}=\overline {KB}+\overline {B{M_L}}-\overline {KG} 。$

(2)

式中： $\overline {KB} $ 为浮心高度或浮心垂向坐标； $\overline {B{M_L}} $ 为纵稳心半径； $\overline {KG} $ 为重心高度或重心垂向坐标。

依靠机械式纵倾平衡系统调节潜航器纵倾，则质量块需要移动的距离为：

$ l = \frac{{{M_{RL}}}}{m} = \frac{{\Delta \uparrow \overline {G{M_L}} \cdot \sin \theta }}{m}。$

(3)

式中，m为质量块的质量（含滑块、丝杠螺母等移动部件的质量）。

由式（3）可看出，质量块的大小和滑移距离的设计受潜航器纵稳心高 $\overline {G{M_L}} $ 的影响，一般情况下，水面状态 $\overline {G{M_L}} $ 与潜航器总长度是一个量级，水下状态纵稳心高 $\overline {G{M_L}} \downarrow $ 为浮心和重心之间的距离，相比 $\overline {G{M_L}} $ 为一小量值，若依靠水面状态设计纵倾平衡系统相关参数，则质量块质量m以及滑移距离l均是较大值，造成水下纵倾平衡能力过剩，因此水面状态的纵倾调节主要以调整潜航器内部载荷位置为主，纵倾平衡系统不起作用。

3.2 水下悬浮静止状态

当潜航器通过压载水舱注水，完成水面状态向水下状态转变后，首先处于水下悬浮静止状态，因潜航器首尾形状不完全对称，在水压作用下潜航器会有纵倾角 $\theta $ ，此时复原力矩^[7]为：

$ {M_{RL}} \downarrow = \Delta \downarrow g({z_B} \downarrow - {z_G} \downarrow )\sin \theta 。$

(4)

式中： $\Delta \downarrow ({z_B} \downarrow - {z_G} \downarrow ) = \Delta \uparrow ({z_B}_0 - {z_G} \uparrow )$ ； ${M_{RL}} \downarrow $ 为水下状态纵倾复原力矩； $\nabla \downarrow $ 为水下排水量； ${z_B} \downarrow $ ， ${z_G} \downarrow $ 为增加重力法得到的浮心、重心垂向坐标； ${z_{B0}}$ 为固定浮容积的几何形心坐标； ${z_G} \uparrow $ 为损失浮力法得到的重心垂向坐标。

此状态下，式（3）变为如下形式：

$ l = \frac{{{M_{RL}} \downarrow }}{m} = \frac{{\Delta \uparrow ({z_B}_0 - {z_G} \uparrow )\sin\theta }}{m} = \frac{{\Delta \uparrow a \sin\theta }}{m}。$

(5)

式中，a为损失浮力法得到的水下稳心高。

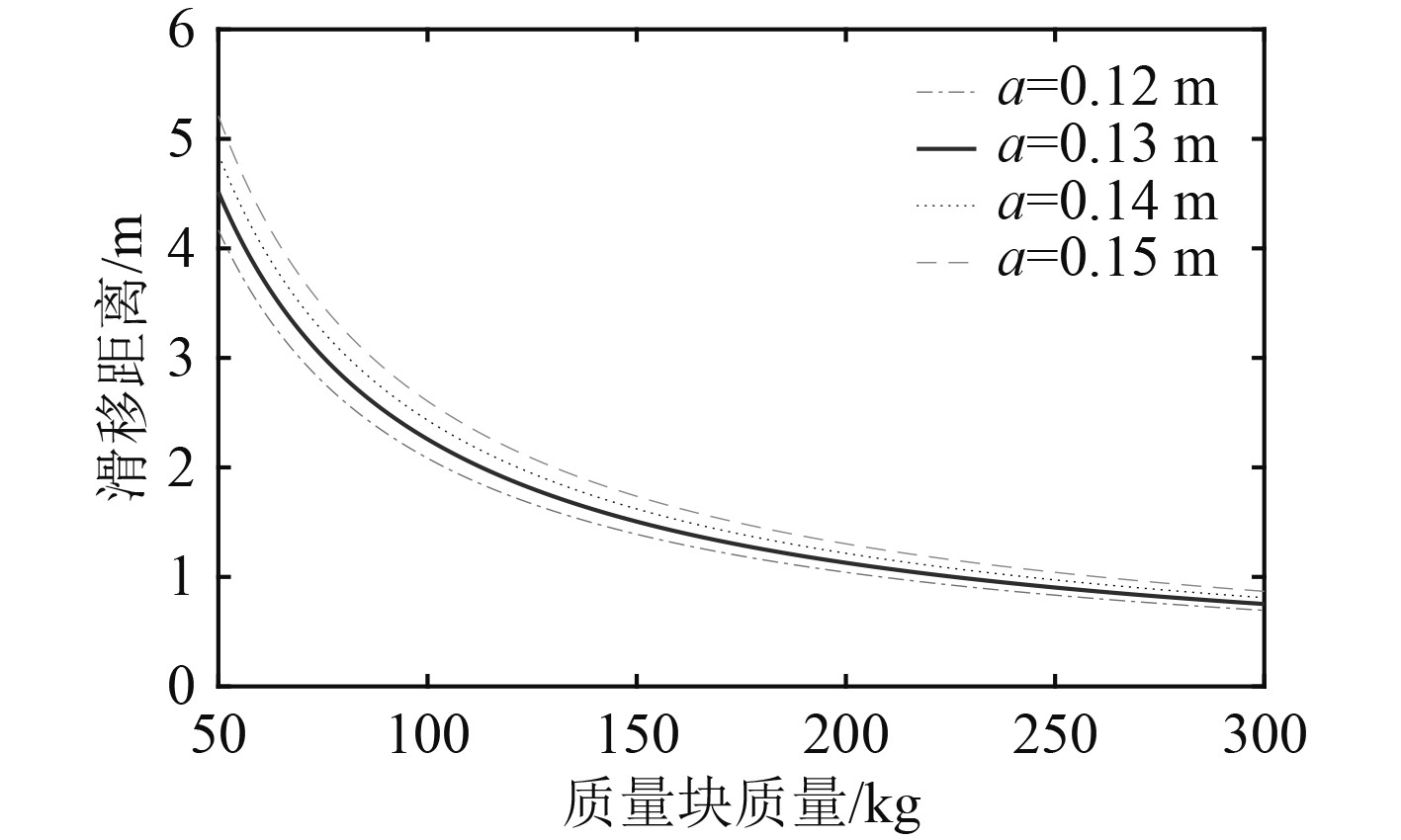
式（5）可作为纵倾平衡系统质量块滑移距离l和质量m的设计公式。可以看出，系统设计主要与排水量 $\Delta \uparrow $ 、水下稳心高a和纵倾调节角度 $\theta $ 有关，在潜航器基本参数和最大调节纵倾角度确定的情况下，l与m成反比，质量块质量越大，调节纵倾所移动的距离越小。设计输入参数如下： $\Delta \uparrow = 10\;{\text{t}}$ ，a=0.13 m，需调节的最大纵倾角±10°，此时最大复原力矩可计算到0.226 t·m，l与m之间的关系如图4所示。根据式（5）和图4，若通过改变潜航器内的设备位置配置来改变稳心高，对装置的设计亦有影响，水下稳心高越大，所设计的机械式纵倾平衡系统质量块质量越大，或调节相同纵倾角度所需滑移的距离越长。

设定质量块在零点位置沿潜航器纵向位置首和尾2个方向最大滑移距离均为1.2 m，由式（3）可求得质量块质量为188 kg，选择Q235材料，密度为7850 kg/m³，根据系统安装高度和共形设计原则可确定出每个质量块形状尺寸。

3.3 无纵倾等速直线定深运动状态

潜航器在水下的运动可划分为垂直面内运动、水平面内运动以及复杂空间运动等，纵倾平衡系统的应用主要与垂直面内运动相关，垂直面内运动以无纵倾等速直线定深运动为典型，分析此典型运动下机械式纵倾平衡系统的工作方式，亦可作为其他场合下系统工作方式的参考。

潜航器在水下多数时间是以无纵倾等速直线定深运动航行，此时潜航器纵倾角为0，纵轴与航速方向一致，运动平衡方程^[8]如下：

$ \left\{ \begin{gathered} Z_0' + Z_{{\delta _s}}'{\delta _s} + Z_{{\delta _b}}'{\delta _b} + P' = 0 ，\\ M_0' + M_{{\delta _s}}'{\delta _s} + M_{{\delta _b}}'{\delta _b} + M_P' + {a_T}z_T' = 0，\\ \end{gathered} \right. $

(6)

$ \left\{ \begin{gathered} M_P' = - {P'}x_P' ，\\ {P'} = \frac{P}{{\frac{1}{2}\rho {L^2}{U^2}}},{a_T} = \frac{{{X_T}}}{{\frac{1}{2}\rho {L^2}{U^2}}},z_T' = \frac{{{z_T}}}{L} 。\\ \end{gathered} \right. $

(7)

式中： $Z_0'$ 为零升力 ${Z_0}$ 的无因次化； ${\delta _b}$ 为首升降舵舵角； ${\delta _s}$ 为尾升降舵舵角； $Z_{{\delta _b}}',Z_{{\delta _s}}'$ 为舵力导数的无因此化； $M_{{\delta _b}}',M_{{\delta _s}}'$ 为舵力矩导数的无因此化；P为作用在潜航器上的静载，作用点坐标为 ${x_p}$ ，静载力矩为 ${M_P}$ ， $P'$ 为P的无因次化， $M_P'$ 为 ${M_P}$ 的无因次化； ${\alpha _T}$ 为螺旋桨推力； ${z_T}$ 为螺旋桨轴线的垂向坐标， $z_T'$ 为 ${z_T}$ 的无因次化； $M_0'$ 为零升力矩 ${M_0}$ 的无因次化； $\rho $ 为潜航器航行水域密度；L为潜航器长度； $U$ 为潜航器航速。

在已经过均衡重力与浮力相等的情况下，当潜航器首尾升降舵均保持零舵角向前航行时，因外形的不对称，作用在潜航器Z方向的力有零升力Z₀，其绕Y轴的力矩为零升力矩M₀，因螺旋桨轴线设计的偏心性，其绕Y轴的力矩为螺旋桨推力矩M_T，这两对力和力矩不会自动平衡，因此潜航器会发生潜深和姿态变化，可采用调节均衡系统、操升降舵或二者共用的方法来控制平衡。

当采用调节均衡系统的方法保持潜航器在首尾零升降舵角情况下无纵倾等速直线航行时，即使用浮力调整水舱注排水平衡垂向力，使用机械式纵倾平衡系统来平衡纵倾力矩，潜航器平衡方程（6）简化为：

$ \left\{ \begin{gathered} Z_0' + {P'} = 0 ，\\ M_0' + M_P' + {\alpha _T}z_T' = 0 。\\ \end{gathered} \right. $

(8)

由式（8）可得出：

$ \left\{ \begin{gathered} P = - \frac{1}{2}\rho {L^2}{U^2}Z_0' ，\\ {M_P} = - \frac{1}{2}\rho {L^3}{U^2}(M_0' + {\alpha _T}z_T')。\\ \end{gathered} \right. $

(9)

对于已定型号的潜航器， $Z_0'$ 与（ $M_0' + \alpha Tz_T'$ ）为确定值，可由式（9）得出浮力调整水舱注排水体积和机械式纵倾平衡系统质量块移动的距离。浮力调整水舱注排水量为：

$ \Delta {P_1} = P，$

(10)

当 $\Delta {P_1} > 0$ 时，向浮力调整水舱注水，当 $\Delta {P_1} < 0$ 时，由浮力调整水舱向舷外排水。

纵倾平衡系统质量块移动的距离为：

$ l = \frac{{{M_p} + \Delta {P_1} \cdot {x_v}}}{m} 。$

(11)

式中， ${x_v}$ 为所使用的浮力调整水舱容积重心至潜航器重心之间的距离。

若l>0，则质量块向潜航器尾部移动，若l<0，则质量块向潜航器首部移动。

单纯依靠均衡系统去保证潜航器在零舵角时的无纵倾等速直线运动，当潜航器航速变化或航行水域条件变化，均衡系统须一直动作，机动性不强。在实际运用中，经常是调节均衡系统与操舵共用，此时的潜航器平衡方程即为式（6）。给定潜航器浮力调整水舱的注排水量 $\Delta {P_2}$ 以及质量块移动的距离l，则可求得 ${\delta _s}$ 和 ${\delta _b}$ 为：

$ \left\{ \begin{gathered} {\delta _s} = \frac{{ - (M_0' + {\alpha _T}z_T' + M_P')Z_{{\delta _b}}' + (Z_0' + {P'})M_{{\delta _b}}'}}{{M_{{\delta _s}}'Z_{{\delta _b}}' - M_{{\delta _b}}'Z_{{\delta _s}}'}} ，\\ {\delta _b} = \frac{{ - (Z_0' + {P'})M_{{\delta _b}}' + (M_0' + {\alpha _T}z_T' + M_P')Z_{{\delta _b}}'}}{{M_{{\delta _s}}'Z_{{\delta _b}}' - M_{{\delta _b}}'Z_{{\delta _s}}'}}。\\ \end{gathered} \right. $

(12)

式中：

$ \left\{ \begin{gathered} {P'} = \dfrac{{\Delta {P_2}}}{{\dfrac{1}{2}\rho {L^2}{U^2}}}，\\ M_P' = \dfrac{{l \cdot m + \Delta {P_2} \cdot {x_v}}}{{\dfrac{1}{2}\rho {L^3}{U^2}}}。\\ \end{gathered} \right. $

(13)

3.4 行进间均衡

潜航器经长时间的航行，由于内部载荷的消耗以及所处的海水温度、密度等内外因素，会存在浮力差和力矩差，此时应进行潜航器行进间均衡，在均衡深度按照均衡航速，操纵首尾升降舵使潜航器作有纵倾等速直线定深运动^[9]，此时可求得潜航器的浮力差P和力矩差 ${M_P}$ 为：

$ \left\{ \begin{gathered} P = - \frac{1}{2}\rho {L^2}{U^2}(Z_0' + Z_{{\delta _b}}'{\delta _b} + Z_{{\delta _s}}'{\delta _s} + Z_w'\theta )，\\ {M_P} = - \frac{1}{2}\rho {L^2}{U^3}[\Delta P_1' \cdot x_v' + M_0' + M_{{\delta _b}}'{\delta _b} + \\ \qquad\;\;\; M_{{\delta _s}}'{\delta _s} + (M_w' + M_\theta')\theta ]。\\ \end{gathered} \right. $

(14)

式中： ${M_\theta }$ 为潜航器水下扶正力矩；h为对应水下全排水量的初稳心高， ${M_\theta } = - mgh\sin \theta $ ； $Z_w'$ 为位置导数的无因次化； ${w'}$ 为垂向速度的无因次化。首升降舵舵角 ${\delta _b}$ 、尾升降舵舵角 ${\delta _s}$ 以及纵倾角 $\theta $ 可由潜航器的传感器反馈得来，其余系数对一定潜航器在一定的均衡航速时是个常数。

则潜航器浮力调整水舱的注排水量为：

$ \Delta P = P = - \frac{1}{2}\rho {L^2}{V^2}(Z_0' + Z_{{\delta _b}}'{\delta _b} + Z_{{\delta _s}}'{\delta _s} + Z_w'\theta )，$

(15)

当 $\Delta P > 0$ 时，向浮力调整水舱注水，当 $\Delta P < 0$ 时，由浮力调整水舱向舷外排水。

机械式纵倾平衡系统质量块移动的距离为：

$\begin{split} l = &\frac{{{M_P}}}{m} = - \frac{1}{{2m}}\rho {L^2}{V^2}[\Delta P_1 \cdot x_v' + M_0' + M_{{\delta _b}}'{\delta _b} +\\ &M_{{\delta _s}}'{\delta _s} + (M_w' + M_\theta')\theta ] 。\end{split} $

(16)

若l>0，质量块向尾部移动，若l<0，质量块向首部移动。

4 试验验证

所设计的机械式纵倾平衡系统加工完成后，在安装伺服电机之前，推动质量块可以平稳地在导轨上滑动，安装伺服电机后，进行出厂前调试，使用上位机控制均衡控制箱内的PLC，PLC向伺服驱动器发送指令，伺服驱动器控制伺服电机旋转带动质量块移动。同时进行模拟潜航器纵倾试验，使用行车使纵倾平衡系统倾斜约30°，在此情况下伺服电机可正常驱动质量块移动，并且伺服电机使能状态及抱闸状态，质量块均不会向下滑落。

将该机械式纵倾平衡系统安装在某型号的潜航器上，经过陆上联调及系泊试验后正式投入使用。经试验验证，其可以满足最大纵倾角±10°的要求，且在操作过程中可随时通过改变伺服电机转速改变质量块移动的速度，满足了潜航器的应用需求，验证了设计的正确性。

5 结　语

针对目前大型无人潜航器纵倾平衡系统的不足，设计一种由伺服电机驱动的机械式纵倾平衡系统，并完成了试验验证，主要结论如下：

1）机械式纵倾平衡系统采用伺服电机驱动滚珠丝杠带动质量块沿潜航器纵向滑动，通过改变潜航器重心来达到实现纵倾平衡的目的，并且质量块与耐压壳共形设计，使该系统具有占用空间小、操作简便以及运行精度高等优点。

2）潜航器在水面状态发生纵倾时，纵倾平衡系统不起作用；在水下悬浮静止状态发生纵倾时，可以在此状态下进行质量块滑移距离和质量块质量的设计。

3）在无纵倾等速直线定深运动过程中，可单独使用机械式纵倾平衡系统配合浮力调整系统，或与操舵并用的方法调节潜航器平衡，调节过程可定量计算得出。

4）在行进间均衡时，由首、尾升降舵舵角及纵倾角可计算出浮力调整水舱注排水量以及质量块移动的距离。