2. 九江职业技术学院船舶工程学院,江西 九江 332007
2. Jiujiang Vocational and Technical College, Ship Engineering College, Jiujiang 332007, China
主机与传动轴是整个船舶的关键部件,其工作性能直接关系到船舶的可靠性、机动性,乃至整个船舶的航行与运转[1-3]。这种以径向滑动轴承为主体的轴承,在船舶发电机的主轴、后轴承、主电机曲轴的主轴承、连杆轴承等重要零件中得到了广泛应用。船舶轴承的承载能力、工作效率、可靠性都将直接关系到传动轴和主机的寿命,主电动机的摩擦功率损失一直都是主要的动力损失源,在主电动机磨损中所占的比重超过20%,而在传动轴中,后2个支座的摩擦力损失较大。
考虑到油液的粘度随着压力和温度的变化、轴承的弹性变形、轴承表面摩擦等因素的影响,进行液压油润滑研究十分必要。本文基于这一思路对弹性流体润滑技术在船用滑动轴承的应用展开润滑特性分析,对于技术确定、技术优化和选择轴承带来一定指导。
1 船用滑动轴承润滑特性分析 1.1 经典二维Reynolds方程为方便分析说明,轴向坐标由x表示,y表示支撑方向的坐标,z表示润滑油液膜半径方向的厚度坐标。在导出具体公式的过程中,本文提出8个假定条件,分别为:1)未将体积力的作用考虑在内;2)非滑动极限;3)假设沿薄膜的厚度方向液体薄膜压力不变;4)因为轴承衬套的厚度比润滑介质液体薄膜的厚度要大得多,所以可以忽略润滑介质液体膜曲率对转速方向的影响;5)将润滑介质假定为牛顿流体;6)将润滑介质的移动视为分层流动;7)惯性力一般小于粘性力,因而可以忽略惯性力的作用;8)径向受力一般不会改变润滑介质的密度和粘度。
最后,根据以上假定,由NS和连续2个方程推导出经典的雷诺方程S的通用表达式:
| $ \begin{split}\frac{\partial }{{{\partial _{{x}}}}}\left( {\frac{{\rho {{{h}}^3}}}{\eta }\frac{{\partial {{p}}}}{{{\partial _{{x}}}}}} \right) + & \frac{\partial }{{{\partial _{{y}}}}}\left( {\frac{{\rho {{{h}}^3}}}{\eta }\frac{{\partial {{p}}}}{{\partial {{y}}}}} \right) = 6\left( {{U_1} - {U_2}} \right)\frac{{\partial \left( {\rho {{h}}} \right)}}{{\partial {{x}}}} +\\ & 6\rho {{h}}\frac{\partial }{{{\partial _{{x}}}}}\left( {{U_1} + {U_2}} \right) + 12\frac{{\partial \left( {\rho {{h}}} \right)}}{{\partial {{t}}}}。\end{split}$ |
式中:U1,U2分别为上、下固态表面的流速;x为润滑介质的密度;h为润滑介质的厚度;p为润滑剂内的压力[4-5]。
传统的Reynolds方程在船舶轴承的润滑计算中经常要作适当的简化。若不计密度及粘性的改变,则需要在不考虑其他影响因素的情况下对该方程进行优化,Reynolds方程可以简单地分解成等温二维雷诺方程,它仅存在于压力和剪切2种情况下。
| $ \frac{\partial }{{{\partial _{{x}}}}}\left( {\frac{{{{{h}}^3}}}{\eta }\frac{{\partial {{p}}}}{{{\partial _{{x}}}}}} \right) + \frac{\partial }{{{\partial _{{y}}}}}\left( {\frac{{{{{h}}^3}}}{\eta }\frac{{\partial {{p}}}}{{\partial {{y}}}}} \right) = 6U\frac{{\partial {{h}}}}{{\partial {{x}}}} 。$ |
式中:
Reynolds的量化公式具有结构紧凑、模型变量小的特点,一般用于复杂结构的轴承,重点分析其主要参数对其润滑特性的影响。根据经验,一般无量纲的Reynolds方程为:
| $ \frac{\partial }{{\partial \theta }}\left( {{H^3}\frac{{\partial P}}{{\partial \theta }}} \right) + {\left( {\frac{D}{L}} \right)^2}\frac{\partial }{{\partial \lambda }}\left( {{H^3}\frac{{\partial P}}{{\partial \lambda }}} \right) = \frac{{\partial H}}{{\partial \theta }} 。$ |
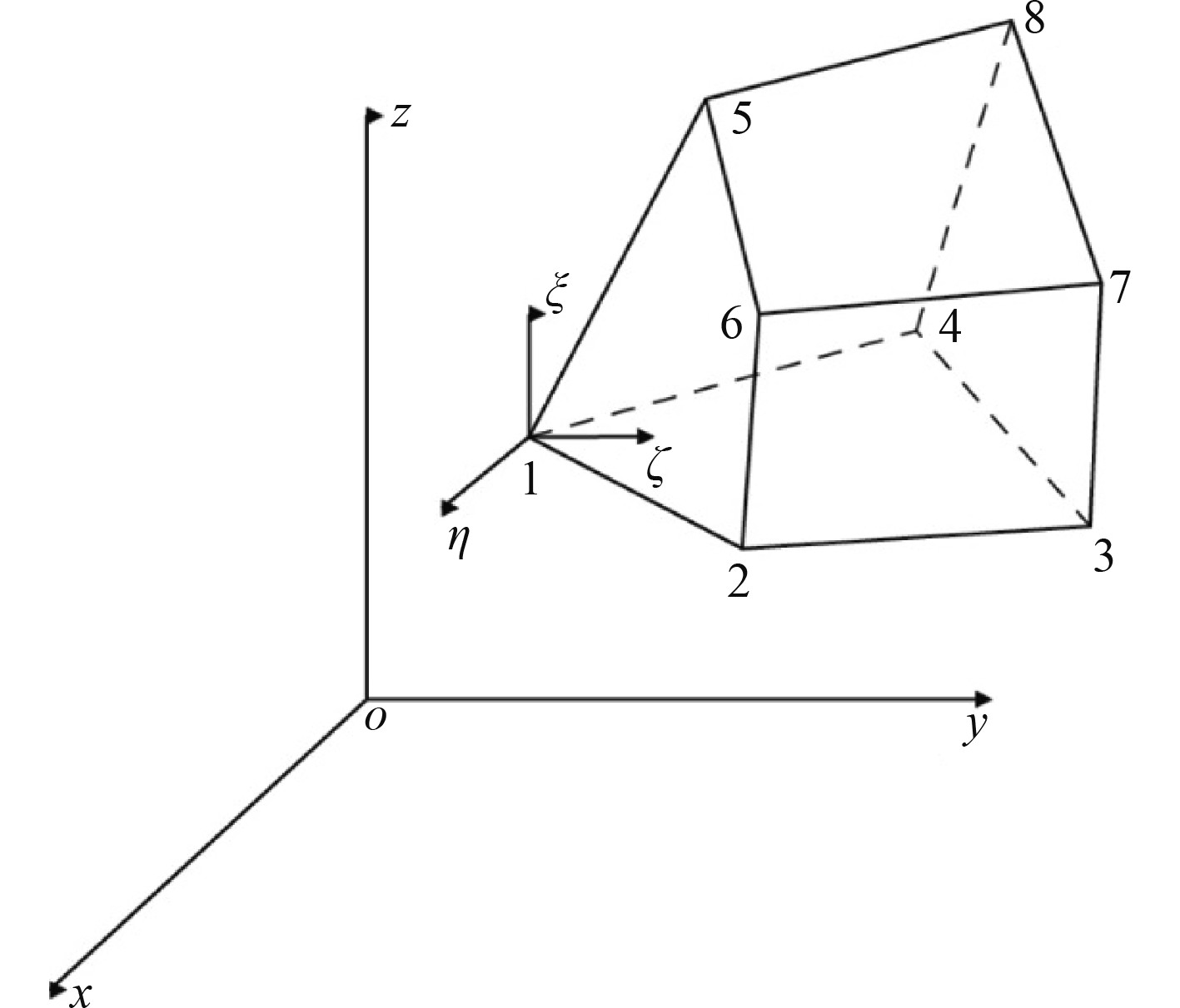
建立一维弹性变形方程模型,该模型由半无限平面(体)弹性变形模型和FEM方程模型组成。结果表明,上述2个假定与实际变形有很大差异,所以采用FDM有限元方法对雷诺方程进行优化,结合有限元-位移比,对其进行分析。对有限元的基本思路和方法进行阐述,六面体单元与坐标如图1所示。
|
图 1 六面体单元与坐标 Fig. 1 The hexahedral units and coordinates |
可知,六面体单元由8个结点组成。定义一个本地坐标系统(x,y,z),在各正方形的中心位置上建立一个原点。可以通过节点坐标内插获得其形状函数(3个线性函数):
| $ \begin{gathered} x = \sum\limits_{i = 1}^8 {{N_i}} \left( {\xi ,\eta ,\zeta } \right){x_i},\\ y = \sum\limits_{i = 1}^8 {{N_i}} \left( {\xi ,\eta ,\zeta } \right){y_i},\\ z = \sum\limits_{i = 1}^8 {{N_i}} \left( {\xi ,\eta ,\zeta } \right){z_i}。\\ \end{gathered} $ |
局部坐标系中的形状函数为:
| $ {N_i} = \frac{1}{8}\left( {1 + {\xi _i}} \right)\left( {1 + {\eta _i}} \right)\left( {1 + {\zeta _i}} \right) 。$ |
利用上述形函数求解弹性变形,然后进行下一次的迭代计算。结果表明,薄膜厚度与压力场之间存在着一定的相互作用。在此基础上,利用Matlab软件进行弹性流体力学耦合的数值模拟。该方法具有程序简单、直观的特点,但由于整体刚性矩阵是一种较大的稀疏矩阵,且具有较强的计算能力,因此计算时间较长。
2.2 轴承静特性分析当轴颈处于稳定状态,也就是垂向负荷与液膜的反作用力相等时,偏心角度
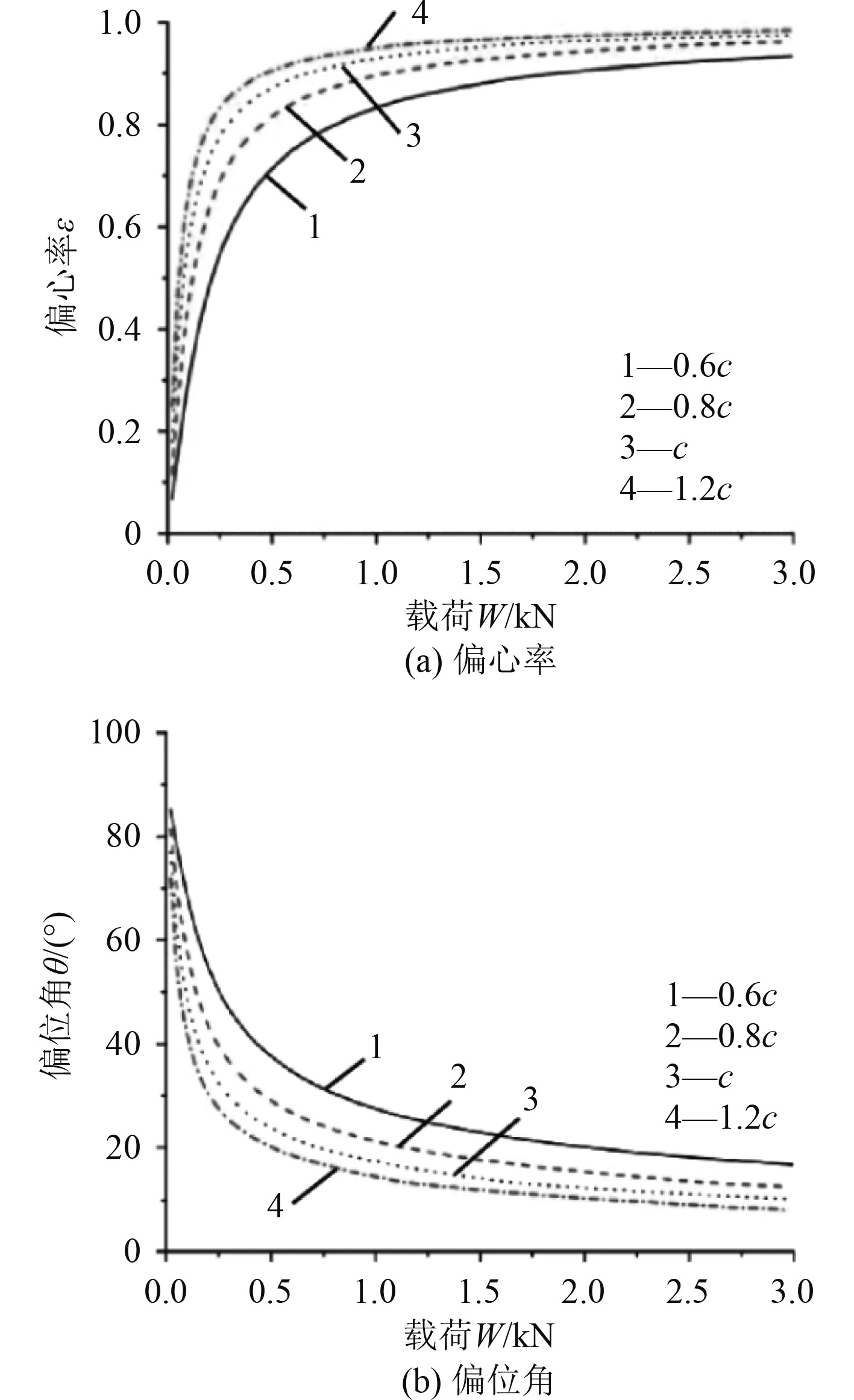
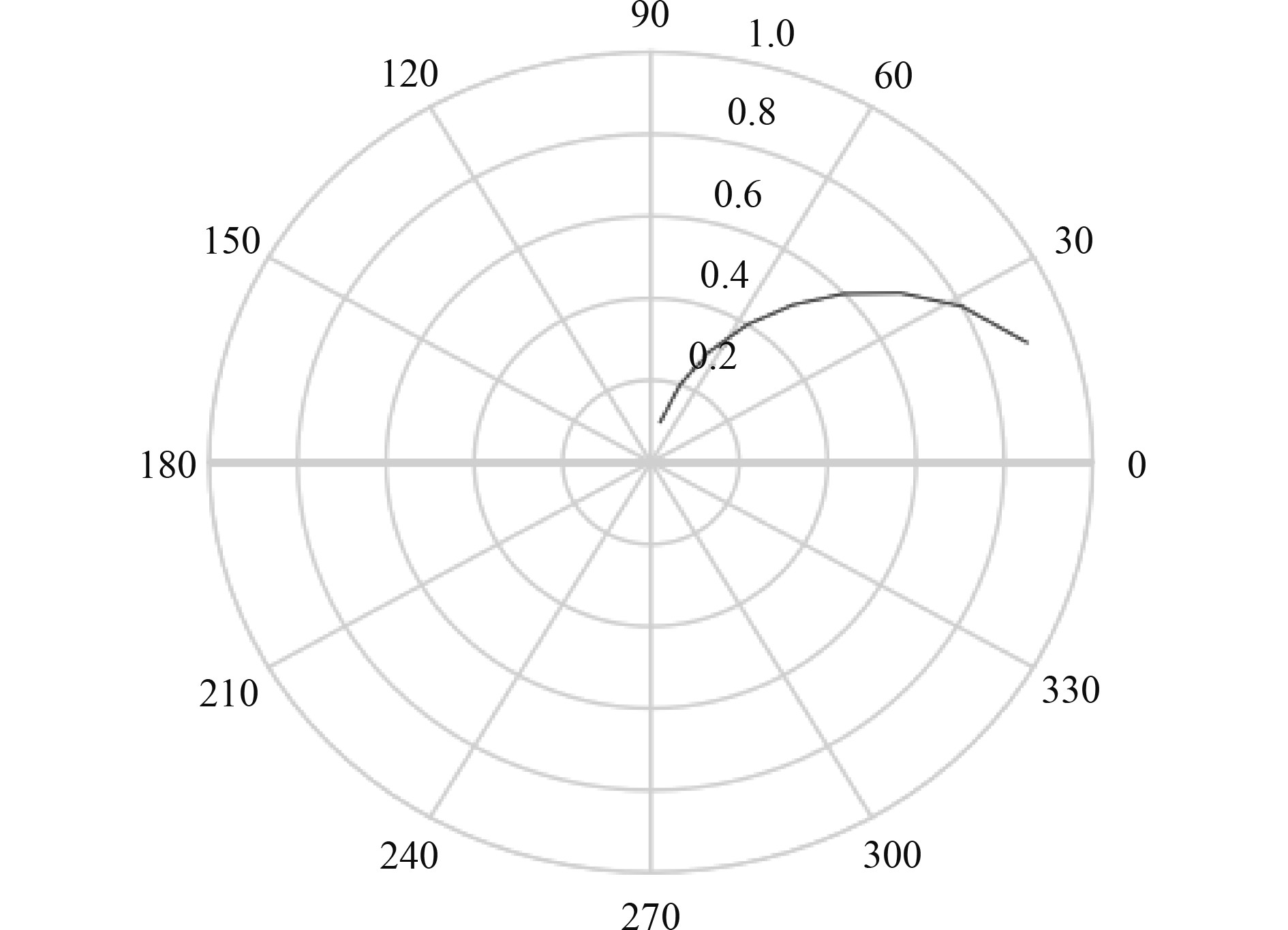
选取一个参数分析储存参数。根据不同的支撑宽度,对常用的大直径比轴承进行计算和分析。在纬度直径比率为2的情况下,选取在极坐标系统下面的平衡半圆,偏位角与偏心率如图2所示。平衡半圆图如图3所示。
|
图 2 偏位角与偏心率 Fig. 2 Deflection angle and eccentricity |
|
图 3 平衡半圆图 Fig. 3 Balance semicircle diagram |
在4种长宽比条件下,随着偏心率的增大,偏转角度逐渐降低,呈现出非线性下降趋势。偏心值小于0.5时,两者的偏差角差异非常小;大偏心距时,大直径比轴承具有更大的倾角。从极坐标天平的半圆图上可以看出,偏心越大,其偏转角度越大,越接近于圆,即支点的运动方向与载荷作用的方向无关,这是液体薄膜与普通的机械部件(如弹簧、阻尼器等)的特性。
3 弹性流体润滑技术应用分析近几年,随着船舶动力轴系统和主机的设计目标(高速度、大功率)不断提高,主要支撑构件如主轴承的工作环境日益恶化。所以,必须突破常规轴承理论中的“全膜润滑”和“等温光滑”的假定。通过对轴承在运转时的温度场进行分析,找出最大温度值和最大湿度值,从而为轴承的设计和计算提供依据。
本文主要针对全圆轴承进行分析。根据前面所提出的弹性流体润滑(EHD),将微凸接触模型与广义Reynolds方程和润滑膜能量方程进行结合。用迭代法对多个物理场进行耦合,并根据模型方程,对不同工作状态下的弹性流体润滑特性展开分析。
3.1 温度场控制方程与边界条件首先,推导出润滑介质的温度控制公式:
| $\begin{split}& c\rho \left( {u\frac{{\partial T}}{{\partial x}} + v\frac{{\partial T}}{{\partial y}} + w\frac{{\partial T}}{{\partial z}} + \frac{{\partial T}}{{\partial t}}} \right) = k\left( {\frac{{{\partial ^2}T}}{{\partial {x^2}}} + \frac{{{\partial ^2}T}}{{\partial {y^2}}} + \frac{{{\partial ^2}T}}{{\partial {z^2}}}} \right) - \\ &\qquad\qquad \frac{T}{\rho }\frac{{\partial \rho }}{{\partial T}}\left( {u\frac{{\partial p}}{{\partial x}} + v\frac{{\partial p}}{{\partial y}} + w\frac{{\partial p}}{{\partial z}} + \frac{{\partial p}}{{\partial t}}} \right) + \varPhi。\end{split}$ |
因为薄膜厚度比轴承尺寸小得多,因此沿着薄膜厚度(z方向)的热传导比另外2个方向都要大,而雷诺方程假定薄膜厚度方向上的压力恒定。在稳定状态下,可以将其简化为:
| $ {c_p}\rho \left( {u\frac{{\partial p}}{{\partial x}} + v\frac{{\partial p}}{{\partial y}} + w\frac{{\partial p}}{{\partial z}}} \right) = k\frac{{{\partial ^2}T}}{{\partial {z^2}}} - \frac{T}{\rho }\frac{{\partial \rho }}{{\partial T}}\left( {u\frac{{\partial p}}{{\partial x}} + v\frac{{\partial p}}{{\partial y}}} \right) + \varPhi 。$ |
式中:c,k,p为恒压比热、热传导和密度,Φ为薄膜的热耗。在接下来的研究中,本文基于薄膜表面粗糙度的参数继续采用前文公式,在牛顿流体的情况下,得出薄膜总热耗之和。
| $ \varPhi = \eta \left[ {{{\left( {\frac{{\partial u}}{{\partial z}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial z}}} \right)}^2}} \right] + \left( {{U_2} - {U_1}} \right)\frac{{{\mu _c}{p_c}{A_c}}}{{{h_T}A}} \text{,} $ |
式中,A为润滑表面干摩擦系数(一般小于0.3)。
在对轴承套的导热控制公式进行计算时,提出了如下假定:轴承材料具有各向同性,并且具有一定的物理性能。那么可以得到轴瓦的导热公式为:
| $ \frac{1}{{{r_b}^2}}\frac{{{\partial ^2}{T_b}}}{{\partial {\theta ^2}}} + \frac{1}{{{r_b}}}\frac{{\partial {T_b}}}{{\partial {r_b}}} + \frac{{{\partial ^2}{T_b}}}{{{\partial _{{r_b}}}^2}} + \frac{{{\partial ^2}{T_b}}}{{\partial {y^2}}} = 0 \text{,} $ |
由于全轴温度场在一般情况下难以测定,因此在采用由转子的热传导方程来计算其表面温度场,最终得出以下结果:
| $ \left\{ {\begin{array}{*{20}{l}} {{T_i} = {T_j}},\\ {\displaystyle\int_0^{2\text{π} } {\frac{{\partial {T_j}}}{{\partial z}}{\rm{d}}\theta = 0} } 。\end{array}} \right. $ |
在注油口的边界条件下,假设油膜区在径向上满足一次方程,其抛物线表达式如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{T_b}^{inled} = {a_b} \cdot {r_b} + {b_b}},\\ {{T_l}^{inled} = {a_l} \cdot {z^2} + {b_l} \cdot z + {c_l}} 。\end{array}} \right. $ |
轴瓦的线性多项式分布存在2个不确定因素,这2个因素可以用2个点来确定,也就是在油膜交界处的油温和回油点。润滑油部件存在3个不确定因素,油膜轴承壳体的界面符合周期边界条件,油膜轴颈界面符合循环边界条件,达到了节约能源的目的。
3.2 稳态弹流润滑求解为解决弹性流体动力润滑问题,必须对负荷均衡进行评价。所以,在进行温度场计算后,需对偏置角度加以收敛。采用迭代算法,利用稳态热弹性流体力学对其求解,具体思路如下:
首先,对轴承壳体油膜的厚度展开迭代计算,然后对其温度进行迭代计算,最后进行轴颈位置的调节。每一次迭代都要进行:将迭代过程记录下来,对初值进行调节,对代数公式进行运算,再进行误差的计算,以决定是否达到精确。
在此基础上,考虑到轴承的弹性流体润滑问题,需要一个较好的初值,从而使计算效率得到很大的提高。因此,在进行流动分析之前,首先对同一轴承的弹性流体进行常温、常压下的弹性流体润滑计算。对弹流润滑进行分析,得出偏心矩、偏角和弹流润滑的压力场,并对其进行数值模拟。如前所述,初始温度场通过轴承外表面的温度确定。
根据以上分析结果,TEHD的分析应该包括:输入轴承座和销座的结构参数;轴承及润滑油的性能指标如转速、负荷等操作状态参数,并对微凸体的接触模式进行研究。首先设定初始压力场与温度场,并求出弹性变形所需要的整体刚度。在不考虑弹性变形的前提下,考虑初始偏心力矩和偏转角度,求出初始层厚的分布,然后在目前的压力和温度下,计算其粘度。
整体而言,本文采用FDM与FEM耦合的弹-水力学耦合解,对其进行力学分析。在压力场收敛后,对压力和粘性进行迭代。得出当对压力进行调整收敛后,可以对油膜的温度、粘度、热耗等因子进行预处理。而计算求解的温度场,则以LU-ADI法求解径向代数方程最佳,然后在轴向方向上逐级求解,可以得到理想结果。但是如若前置角度不能收敛,则需再对计算压强和温度进行调整计算,从而达到最终理想的预期结果。
4 结 语针对含多种影响的船用轴承,本文采用有限元的分析方法,分别对稳定弹流体压力润滑(EHD)进行研究。通过研究可知,采用割线法对轴承的静平衡进行校正,采用有限元方法对轴瓦的弹性变形进行求解,可以得到较高的精度。在对热弹性流体压力润滑展开计算时,则需要综合考虑到温度、压力和密度的变化。唯有设计一个较为全面的技术模型,才能使弹性流体润滑技术在应用中拥有较好的润滑特性。
| [1] |
纪敬虎, 周莹超, 田朋霖, 等. 局部凹坑织构化径向滑动轴承流体动力润滑数值分析[J]. 表面技术, 2021(10): 050. |
| [2] |
宋新涛, 吴维, 苑士华. 考虑磨损和紊流的径向滑动轴承混合润滑分析[J]. 华南理工大学学报(自然科学版), 2022, 50(6): 121-128. |
| [3] |
阎心怡, 崔毅, 付艳, 等. 低速船用柴油机主轴承弹流润滑性能分析[J]. 柴油机, 2020, 42(4): 22-29. |
| [4] |
左名玉, 王优强, 菅光霄, 等. 换向工况下非对称聚合物齿轮瞬态弹流润滑分析[J]. 机械工程学报, 2022, 58(11): 241-248. |
| [5] |
王丽丽, 袁国腾, 耿欢, 等. 考虑润滑油黏温效应的动压滑动轴承性能分析[J]. 润滑与密封, 2020, 45(1): 5. DOI:10.3969/j.issn.0254-0150.2020.01.009 |
 2022, Vol. 44
2022, Vol. 44
