非均匀流体作用在桨叶表面,引起的脉动波动经桨叶调制后传递到轴系上,最后通过推力轴承作用在船体上,形成轴承力,它是螺旋桨激振力的主要成分[1]。在激振力的传递方面,通常可以采用实验法和数值计算法进行计算[2]。Pan Jie通过实验法,计算了伴流场中桨叶的纵向激振力及其在轴系上的传递特性。冯国平[3]通过功率流传递法,分析了纵向激振力在艇体尾部的传递规律。俞强[4]利用锤击法研究轴系3个方向上的传递特性,发现推力轴承处的纵向激励响应远大于水平和垂向方向。在振动控制方面,LI Liang-Wei[5]用过改变推力轴承的质量、刚度,对动力吸振器进行优化。张赣波[6]采用当量计算法求解某轴系的纵向振动固有频率,并研究了推力轴承的刚度对纵向激励的响应影响。
随着大侧斜螺旋桨和复合材料螺旋桨的推广,越来越多学者开始考虑螺旋桨的弹性效应对于水动力性能和结构振动的影响,尤其是激振力的传递特性[7]。倪臻[8]建立了螺旋桨的等效模型,通过传递矩阵法计算其固有频率,并分析了螺旋桨单位载荷在推力轴承处的力传递率。谢基榕[9]通过集质量法计算轴系子系统固有频率和螺旋桨激振力的传递特性,得出螺旋桨首阶模态对激振力有放大作用的结论。但是这些研究大多不考虑轴系与桨之间的耦合关系,而忽略激振力从桨叶到轴系的传递过程。
本文建立质量点桨-轴系统和弹性桨-轴系统2个模型,对比分析其传递路径的区别,研究了桨叶弹性效应对纵向激振力的传递调制作用,比较了不同材料桨-轴系统在推力轴承处的响应和力传递率,并对弹性桨-轴系统进行频率匹配设计,分析桨叶弹性效应对减震降噪的作用。
1 计算方法 1.1 振动方程螺旋桨-轴系的通用运动方程:
| $ [M]\{\ddot u\}+[C]\{\dot u\}+[K]\{u\}=\{F\}。$ | (1) |
式中:[K] ,[C] ,[M]分别代表结构的阻尼、质量和刚度;
谐响应是通过扫频法采用简谐载荷对结构在一定频率范围内的振动响应进行计算,其谐响应方程解的形式如下:
| $ \left\{ u \right\} = \left\{ {{u_{\max }}{e^{i\varphi }}} \right\}{e^{i\Omega t}}。$ | (2) |
式中:umax代表最大位移,m;i代表常数−1的平方根;φ代表位移的相位角弧度;Ω代表外加载荷圆频率,Hz;t代表时间,s。结构在不同的自由度上umax和φ的值不同,其复数形式的解如下:
| $ \left\{ u \right\} =\left\{ {{u_{\max }}\left( {\cos \varphi + i\sin \varphi } \right)} \right\}{e^{i\varOmega t}} = \left( {\left\{ {{u_1}} \right\} + i\left\{ {{u_2}} \right\}} \right){e^{i\varOmega t}}。$ | (3) |
式中:
| $ \begin{split} \left\{ F \right\} =& \left\{ {{F_{\max }}{e^{i\varphi }}} \right\}{e^{i\varphi \Omega }} = \\ &\left\{ {{F_{\max }}\left( {\cos \varphi + i\sin \varphi } \right)} \right\}{e^{i\varphi \Omega }} = \left( {\left\{ {{F_1} + i{F_2}} \right\}} \right){e^{i\varphi \Omega }} ,\\ \end{split} $ | (4) |
此时:
| $ \begin{gathered} \left( { - {\varOmega ^2}{{M + }}\varOmega {{C + K}}} \right)\left( {\left\{ {{x_1}} \right\} + i\left\{ {{x_2}} \right\}} \right) = \left( {\left\{ {{F_1}} \right\} + i\left\{ {{F_2}} \right\}} \right),\\ \end{gathered} $ | (5) |
用复数形式表示该方程的解,转换方式如下:
| $ {{{u}}_{\max }}{\text{ = }}\sqrt {{u_1}^2 + {u_2}^2},$ |
| $ \varphi {\text{ = }}\arctan \frac{{{u_1}}}{{{u_2}}} 。$ |
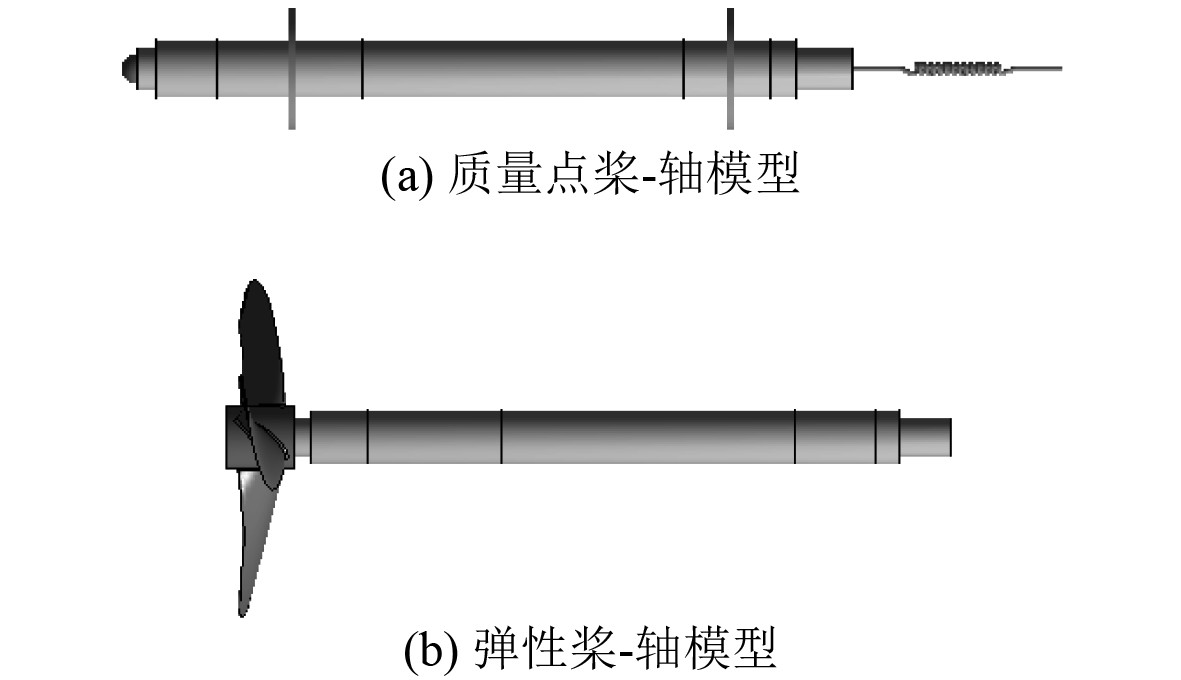
本文的研究对象为某船的螺旋桨-轴系统。为凸显桨叶的弹性效应,分别建立质量点桨-轴系统和弹性桨-轴系统2种模型。采用镍铝青铜材料和玻璃纤维材料分别作为“刚性桨”和 “弹性桨”的代表,其三维模型分别如图1所示。
|
|
表 1 螺旋桨的主要参数 Tab.1 Main parameters of propeller |
|
图 1 桨-轴系统模型 Fig. 1 Model of the propeller shaft system |
2种形式的桨-轴系统,其前后尾轴承采用弹簧单元进行模拟,刚度各向同性均为4.6E9 N/m,不计交叉刚度,轴系旋转速度240 r/min。推力轴承均采用其中Body-ground弹簧单元进行模拟,刚度7.2E7 N/m,为弹簧一端与轴系连接,另一端设置为ground。
2.3 扫频设置由于螺旋桨的高阶振动多体现在桨叶的叶梢及导边,为了凸显桨叶的弹性效应,选择桨叶的0.75R处作为载荷的施加点。桨叶的纵向激振力可以分解为各阶简谐激励的综合,因此采用单位正弦载荷,3个桨叶分别施加0.333 N,合计约1 N,如图2所示。为了兼顾计算精度和效率,谐响应的扫频范围设置为0~300 Hz,计算步数为600步,计算方法采用模态叠加法。

|
图 2 激振力施加位置及方向图 Fig. 2 Position and direction diagram of excitation force applied |
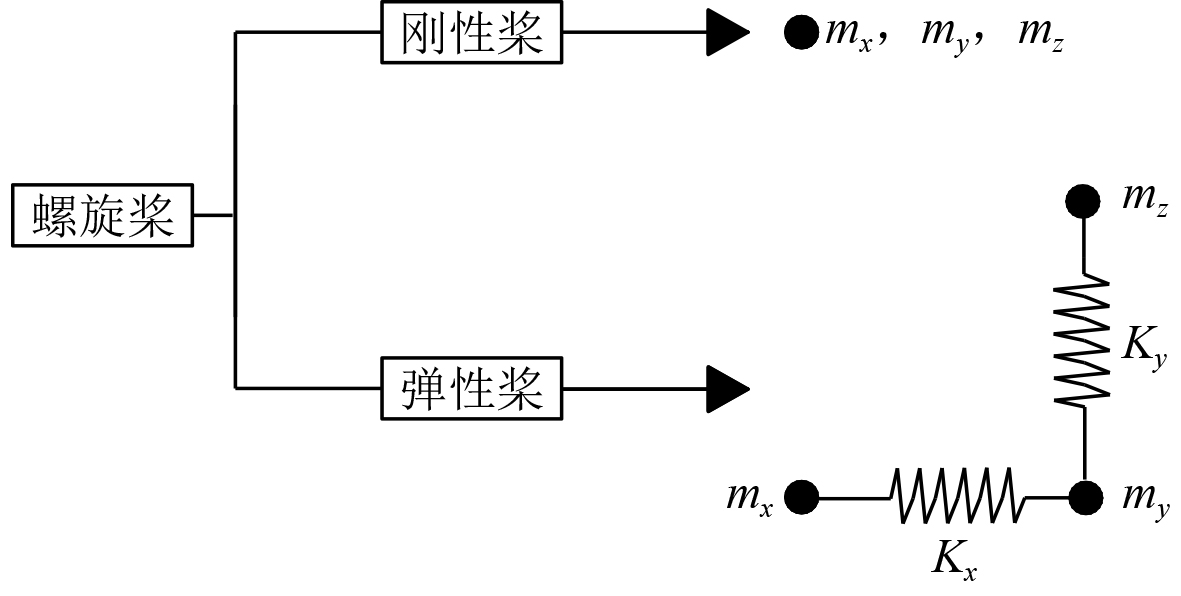
螺旋桨纵向激励主要是通过轴系传动系统传递到船体上的,其传递路径较为简单。当把螺旋桨分别视为“刚性桨”和“弹性桨”时,其桨叶到轴系之间的传递路径又有所区别:“刚性桨”只需要考虑其在3个方向上的质量,通过对桨叶上的载荷进行积分,可以得到桨毂处的合力;而“弹性桨”需要考虑3个方向上的质量,以及和轴向和径向上的刚度产生的调制作用,二者区别如图3所示。
|
图 3 刚性桨与弹性桨区别 Fig. 3 Difference between rigid paddle and elastic paddle |

|
图 4 质量点桨-轴系统纵向激振力的传递路径 Fig. 4 Transmission path of longitudinal excitation force of mass propeller shaft system |

|
图 5 弹性桨-轴系统纵向激振力的传递路径 Fig. 5 Transmission path of longitudinal excitation force of elastic propeller shaft system |
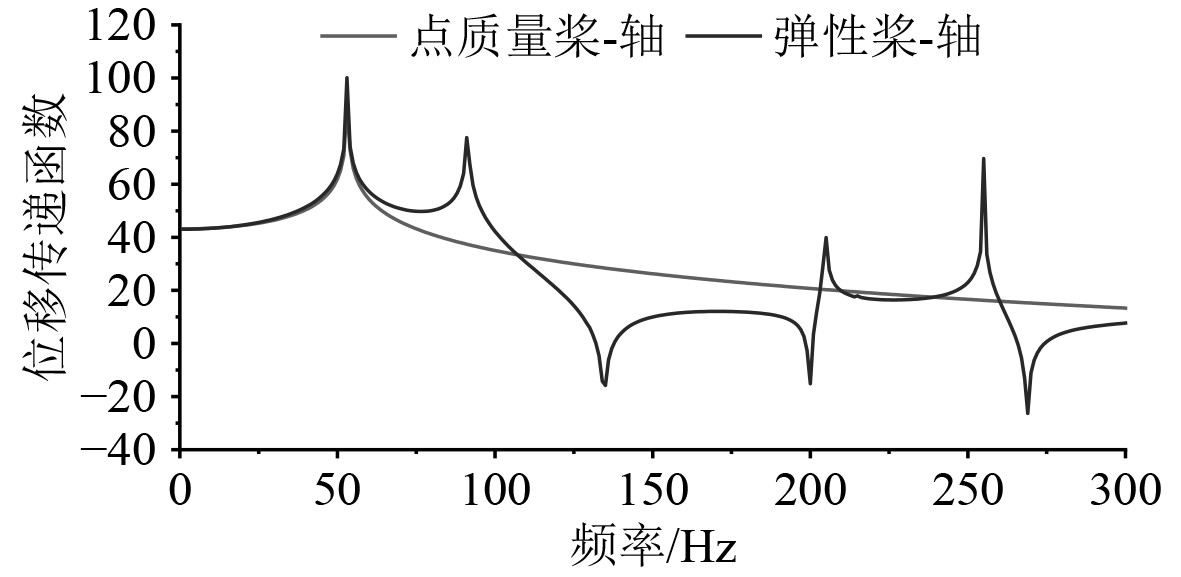
采用式(6)计算螺旋桨纵向激振力在推力轴承处的位移传递函数Hi,如图6所示。
|
图 6 玻璃纤维桨-轴的位移传递函数图 Fig. 6 Displacement transfer function diagram of glass fiber propeller shaft system |
| $ {H_i} = 20 \times {\rm{lg}}\left(\left( {\frac{{\left| {{u_i}} \right|}}{{{F_0}}}} \right)/Ref\right) ({\rm{dB}})。$ | (6) |
式中:ui代表第i轴向位移度;F0代表激振力;Ref代表Hi的参考值,取1
从图6可以看出,在0~300 Hz范围内,质量点桨-轴系统和弹性桨-轴系统的峰值点分别为1个和4个,其中质量点桨-轴系统峰值点对应其一阶纵向模态固有频率,弹性桨-轴系统的峰值点对应其低阶伞形模态固有频率。
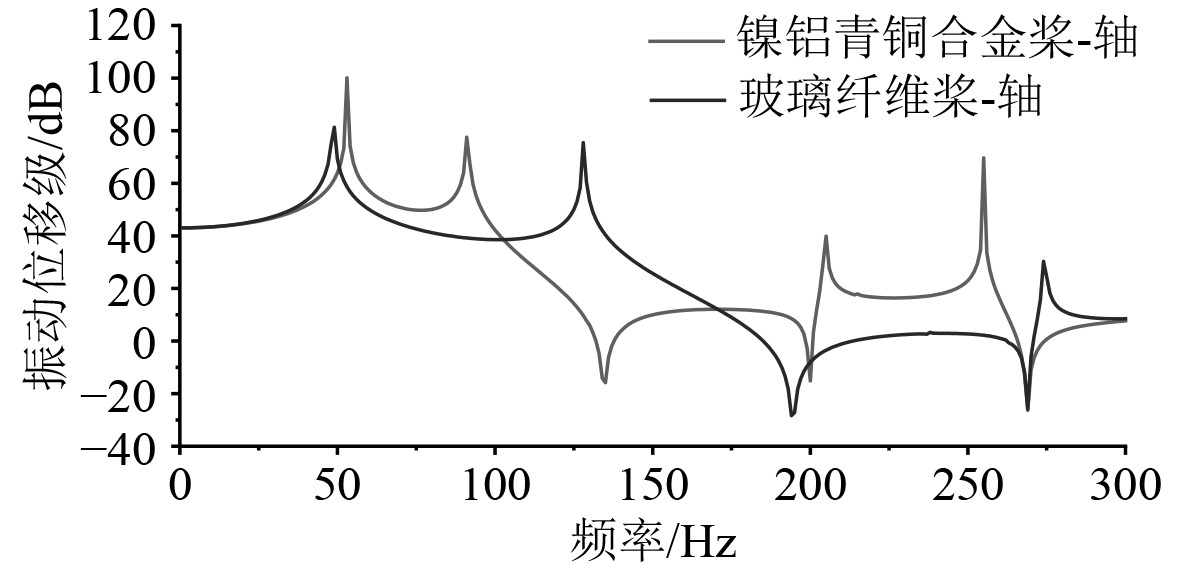
3.3 桨叶弹性效应对推力轴承处位移和加速度响应影响分别采用式(7)和式(8),计算2种材料桨-轴系统在推力轴承处位移响应(TDL)和加速度响应(TAL)。2种材料桨-轴振动位移响应和加速度响应曲线分别如图7和图8所示。
|
图 7 推力轴承位置的位移响应对比图 Fig. 7 Displacement response comparison diagram of thrust bearing position |
|
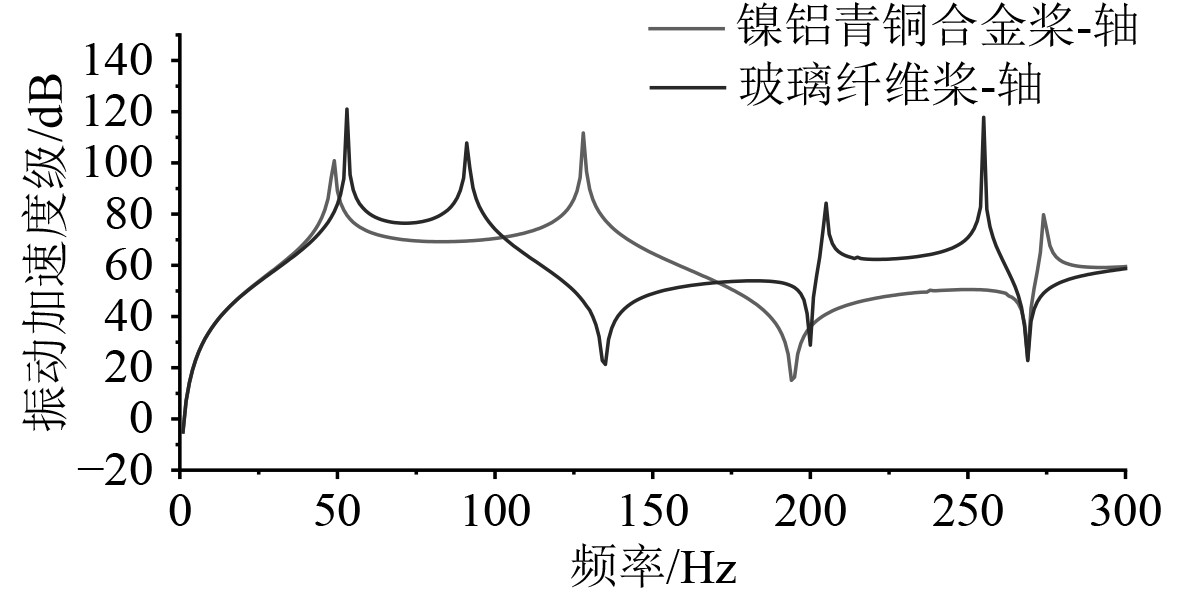
图 8 推力轴承位置的加速度响应对比图 Fig. 8 Acceleration response comparison diagram of thrust bearing position |
| $ TDL = 20\lg ({{{u_{\rm out}}} / {{u_0}}})({\rm{dB}}) ,$ | (7) |
| $ TAL = 20\lg ({{{a_{\rm out}}} / {{a_0}}})({\rm{dB}})。$ | (8) |
式中:
可以看出,加速度响应与位移响应曲线基本趋势相同,其峰值位置均出现在弹性桨-轴的固有频率处。对比2种材料桨-轴的振动响应曲线可以看出,受伞形模态影响,除一阶纵向固有频率外(主要受轴系及推力轴承影响,与螺旋桨关系不大),玻璃纤维桨-轴其余各阶峰值频率点均左移,这意味着其更容易掉入螺旋桨的宽频激励集中范围,引发轴系共振。
3.4 桨叶弹性效应对推力轴承处力传递率影响采用式(9)计算2种材料桨-轴的纵向激振力在推力轴承处的力传递率R,如图9所示。
|
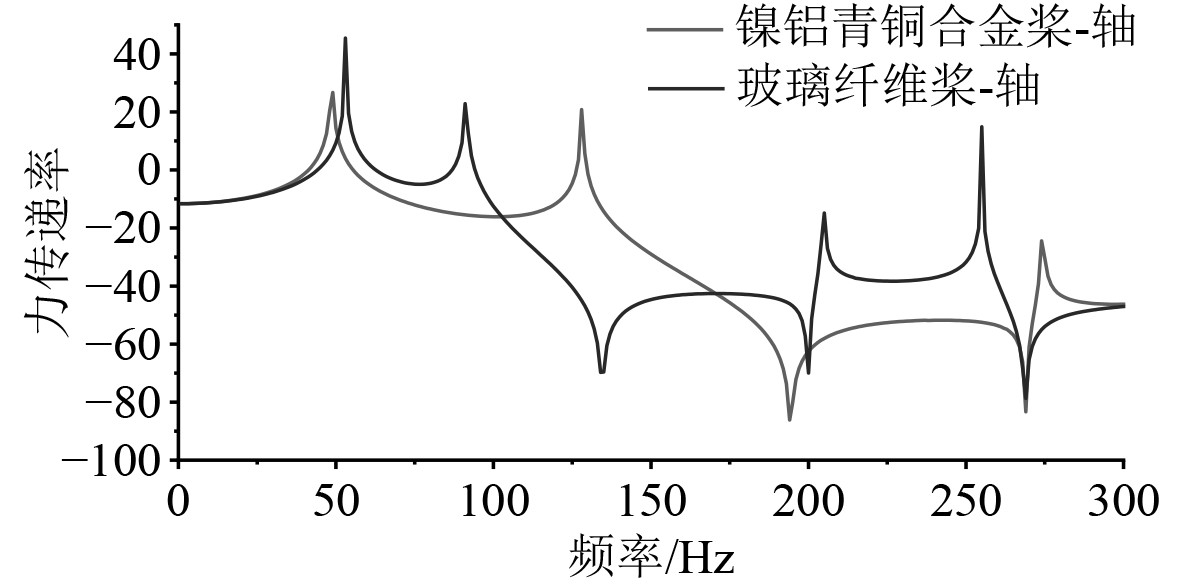
图 9 推力轴承位置的力传递率对比图 Fig. 9 Comparison diagram of force transfer rate at thrust bearing position |
| $ R = 20\lg ({{{F_{\rm out}}} \mathord{\left/ {\vphantom {{{F_{\rm out}}} {{F_{in}}}}} \right. } {{F_{in}}}})({\rm{dB}})。$ | (9) |
其中:R代表激振力传递率;Fin代表激振力;Fout代表传递到推力轴承上的力。
可以看出,在力传递率曲线中,2种材料的力传递率最大值均出现在其一阶纵向固有频率处,即影响力传递的主要因素是轴系和推力轴承。另外,在弹性桨前几阶伞形模态(波峰)处,力传递率被明显放大,此时噪声辐射较大。而在峰值之间的波谷处,力传递率被衰减降低,此时噪声辐射值较低。
4 弹性桨-轴动力学特性匹配设计推力轴承刚度为定值,分别取螺旋桨弹性模量5E9 Pa,6E9 Pa,7E9 Pa,8E9 Pa,9E9 Pa,对桨叶和轴系进行频率的参数化匹配设计。在0~150 Hz范围内,弹性桨-轴的一阶纵向固有频率为f1,一阶伞形模态固有频率为f2,2个模型的力传递率曲线如图10所示,弹性桨-轴系统在推力轴承位置的力传递率如图11所示。

|
图 10 推力轴承位置的力传递率对比 Fig. 10 Comparison of force transfer rate at thrust bearing position |

|
图 11 桨叶弹性效应对力传递率的影响图 Fig. 11 Influence of blade elastic effect on force transfer rate |
从图10和图11可以看出,f1对应质量点桨-轴的一阶纵向固有频率,其主要影响因素是推力轴承和轴系的纵向刚度,因此不受桨叶弹性的影响;f2的主要影响因素是桨叶的弹性,因此当桨叶弹性模量降低时,f2逐渐左移,当弹性模量为7E9Pa,f2逐渐靠近f1,此时峰值最高,力传递率最大;当两者错开时,峰值降低。
在船舶传动系统设计,除了传统的匹配设计和振动、强度校核外,可以尝试以推力轴承处的振动响应为优化目标,调整桨叶弹性参数,对弹性桨-轴动力学特性匹配设计,达到船舶推进系统的减震降噪的最优化设计。
5 结 语本文建立了质量点桨-轴系统和弹性桨-轴系统2个模型,对比分析其传递路径的区别,研究桨叶弹性效应对纵向激振力的传递调制作用,比较不同材料桨-轴系统在推力轴承处的响应和力传递率,并对弹性桨-轴系统进行频率匹配设计,分析桨叶弹性效应对减震降噪的作用,得出的主要结论如下:
桨叶的弹性效应对纵向激振力的传递有调制作用,尤其是螺旋桨的低阶伞形模态对应的频率波峰处,振动传递会被放大。而在伞形模态和反共振频率之间的波谷,振动传递被衰减。通过对桨叶进行弹性的参数化调整,匹配好伞形模态频率和轴系纵振频率,可以实现传动系统的减震降噪最优化设计。
| [1] |
MASSARO M, GRAHAM J M R. The effect of three-dimensionality on the aerodynamic admittance of thin sections in free stream turbulence[J]. Journal of Fluids & Structures, 2015, 57: 81-90. |
| [2] |
赵耀, 张赣波, 李良伟. 船舶推进轴系纵向振动及其控制技术研究进展[J]. 中国造船, 2011, 52(4): 259-269. DOI:10.3969/j.issn.1000-4882.2011.04.031 |
| [3] |
冯国平, 谌勇, 黄修长, 等. 舰艇艉部纵向激励传递特性分析[J]. 噪声与振动控制, 2009, 29(6): 132-135. |
| [4] |
俞强, 王磊, 刘伟. 舰船推进轴系的螺旋桨激励力传递特性[J]. 中国舰船研究, 2015, 10(6): 81-86. DOI:10.3969/j.issn.1673-3185.2015.06.012 |
| [5] |
LI L W, ZHAO Y, LI T Y, et al. Parameters optimization of the dynamic absorber to control the axial vibration of marine shafting system[J]. Journal of Ship Mechanics, 2012, 16(3): 307-319. |
| [6] |
张赣波. 船舶主推进轴系纵向振动主动控制方法研究[D]. 武汉: 华中科技大学, 2012.
|
| [7] |
NICOLE K. Structural and acoustic responses of a submarine hull due to propeller forces[J]. Journal of Sound & Vibration, 2009, 325(1): 266-286. |
| [8] |
倪臻, 黄修长, 华宏星. 基于等效模型的螺旋桨轴系纵向振动频率匹配设计[C]//第十二届全国振动理论及应用学术会议, 中国广西南宁, 2017.
|
| [9] |
谢基榕, 吴有生, 沈顺根. 船舶轴系子系统力传递特性研究[J]. 中国造船, 2011, 52(1): 80-89. DOI:10.3969/j.issn.1000-4882.2011.01.010 |
 2022, Vol. 44
2022, Vol. 44
