2. 海军装备部驻武汉地区第一军事代表室,湖北 武汉 430060
2. The First Military Representative Office of Naval Armament Department in Wuhan, Wuhan 430060, China
船舶中有很多复杂的管路系统以及对应的隔振设备,轴系海水系统是最典型的代表之一,其包含海水泵浮筏、空间复杂走向管路、减振元器件等。在管路安装过程中往往会引入偏差[1],使得管路中存在应力,而该应力可通过管路传递到隔振装置及设备,一般使得刚度较低的隔振元器件发生变形,从而引起隔振设备姿态及振动响应发生变化,进而影响隔振效果。
轴系海水系统工作状态下,除管路安装偏差引入的静载荷外,海水泵电机的周期性振动载荷也会引起系统的动力学响应,导致系统隔振效果发生变化。
动力响应可通过子结构综合法:将整个模型分为多个子结构,分别进行谐响应分析得到其传递函数,最后得到计算整体结构的变形随频率的变化规律。这其中包括对子结构如刚性管道、挠性管,隔振器建模,并用隔振落差对各子结构的振动传递进行评估,同时评价隔振器的重要参数如刚度对隔振姿态(效果)的影响。本文采用传递函数方法[2-6]进行在只有电机振动激励下,隔振系统的动力学响应分析。
1 频响函数计算方法基本原理相比其他用于分析的合成方法,频响函数合成法针对频域进行研究,具有表达式简单、易于编程,能够直接使用试验数据,能够组合使用试验或理论分析、数值模拟数据,只需要连接面数据就能进行合成等优点[6]。随着大量高精密测量仪器的应用,频响函数测试的精度在不断提升。基于频响函数的子结构合成方法在结构的动力学分析中的重要性日益突出,且频响函数的子结构综合方法避免了模态分析过程中可能引入的误差,同时也更便于进行不同连接件的验证分析,其便利性引人注目。
设一个系统由A和B两个子结构组成,i表示结构内坐标,c表示结构连接面坐标(以下类同),则A和B结构对应的频响函数矩阵如下:
| $ {{\boldsymbol{H}}_{\boldsymbol{A}}} = \left[ {\begin{array}{*{20}{c}} {H_{ii}^A}&{H_{ic}^A} \\ {H_{ci}^A}&{H_{cc}^A} \end{array}} \right] ,$ |
| $ {{\boldsymbol{H}}_{\boldsymbol{B}}} = \left[ {\begin{array}{*{20}{c}} {H_{ii}^B}&{H_{ic}^B} \\ {H_{ci}^B}&{H_{cc}^B} \end{array}} \right],$ |
对于子结构A:
| $ \left[ {\begin{array}{*{20}{c}} {X_i^A} \\ {X_c^A} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {H_{ii}^A}&{H_{ic}^A} \\ {H_{ci}^A}&{H_{cc}^A} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {f_i^A} \\ {f_c^A} \end{array}} \right] ,$ |
| $ \left[ {\begin{array}{*{20}{c}} {X_i^B} \\ {X_c^B} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {H_{ii}^B}&{H_{ic}^B} \\ {H_{ci}^B}&{H_{cc}^B} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {f_i^B} \\ {f_c^B} \end{array}} \right]。$ |
式中:x为位移,f为节点处受力,下标i代表内点,下标c代表连接点面节点。对于连接点处由受力和位移的相互关系可知,有约束条件:
| $ f_c^A + f_c^B = {F_c} ,$ |
| $ f_i^A = F_i^A ,$ |
| $ f_i^B = F_i^B ,$ |
| $ X_i^A = x_i^A ,$ |
| $ X_i^B = x_i^B ,$ |
| $ {X_C} = x_c^A = x_c^B 。$ |
式中:小写字母表示子结构各节点,大写字母为各子结构合并为整体后的对应节点。
整理可得:
| $ \begin{array}{*{20}{l}} & \left\{ {\begin{array}{*{20}{l}} {X_i^A} \\ {{X_c}} \\ {X_i^B} \end{array}} \right\} = \left( \left[ {\begin{array}{*{20}{c}} {H_{ii}^A}&{H_{ic}^A}&0 \\ {H_{ci}^A}&{H_{cc}^A}&0 \\ 0&0&{H_{ii}^B} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {H_{ic}^A} \\ {H_{cc}^A} \\ { - H_{ic}^B} \end{array}} \right]\times\right.\\ & \left.{{{\left( {H_{cc}^B + H_{cc}^A} \right)}^{ - 1}}{\left[ {\begin{array}{*{20}{c}} {H_{ic}^A} \\ {H_{cc}^A} \\ { - H_{ic}^B} \end{array}} \right]^{\rm{T}}}} \right)\left\{ {\begin{array}{*{20}{c}} {F_i^A} \\ {{F_C}} \\ {F_i^B} \end{array}} \right\}。\end{array}$ |
上式即为以子结构A的连接点处频响函数合成公式的表达式。同理,若以子结构B的连接点处频响函数表达式来表达的话,可以得到同样的结果。
2 载荷计算参数80 t及100 t海水泵转子质量m=90 kg,转速n=2900 r/min;25 t海水泵转子质量m=11 kg,转速n=2900 r/min。平衡精度等级G按普通泵的叶轮选取6.3。经计算,3台海水泵的转子许用不平衡度(偏心距)均为:
建模时将海水泵质量集中在重心位置的质量单元,计算输入载荷施加在质量单元所在节点上。
隔振器、挠性接管等计算参数采用试验室实际测得的机械阻抗参数(频率范围10~1000 Hz)。
3 边界条件海水泵通过隔振器与筏架连接,筏架通过隔振器与基座连接,基座焊接在舱壁上,所以在计算中,将基座与舱壁焊接部分进行位移约束。
管路由弹性支架连接基础,所以将弹性支架与基础连接部位进行位移约束[7]。
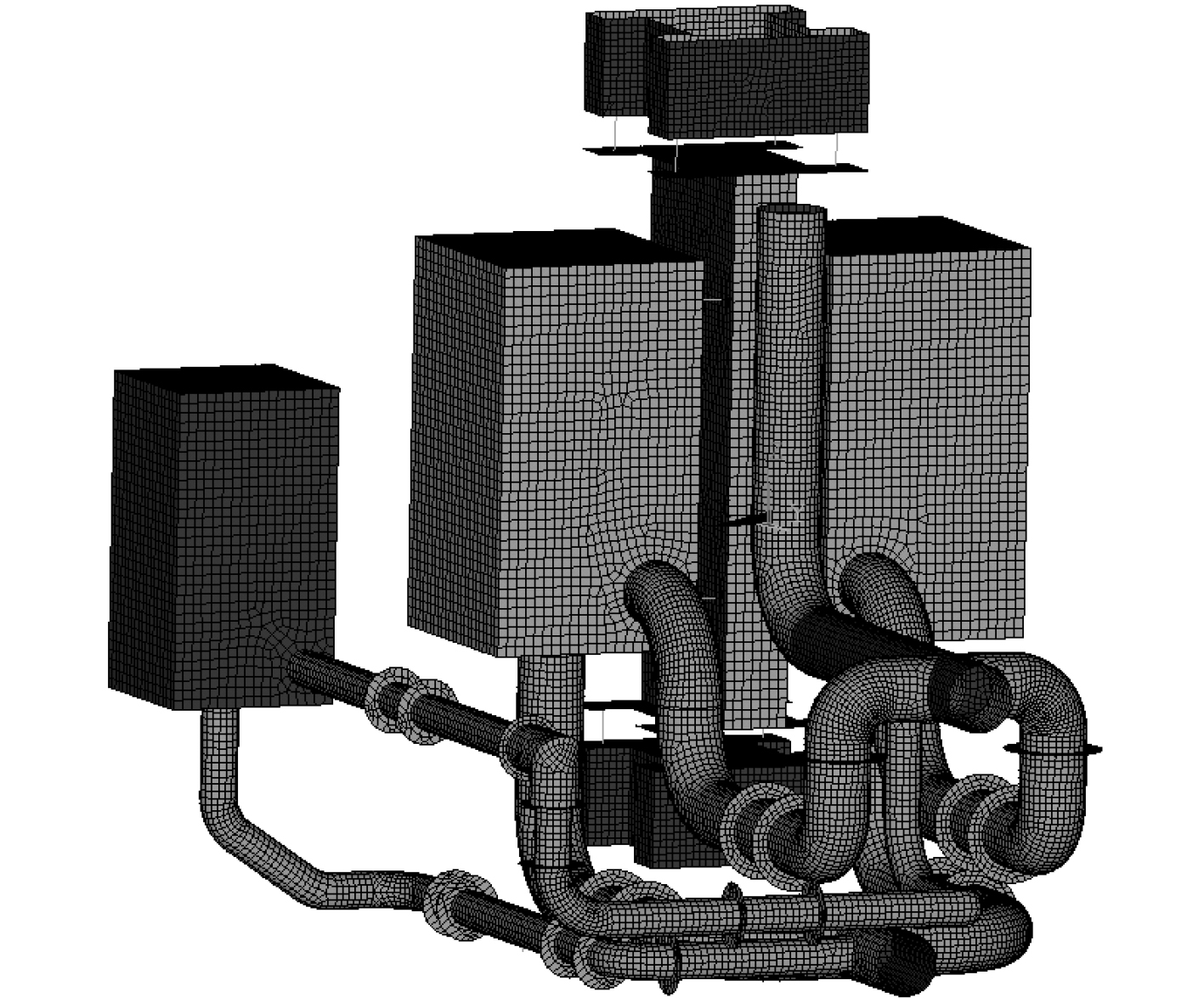
4 实体几何模型及子结构划分依据实验室台架图纸建立包含海水泵、浮筏、泵进出口管路及隔振器、挠性接管的隔振系统简化模型,如图1所示。
|
图 1 实体模型 Fig. 1 Solid model |
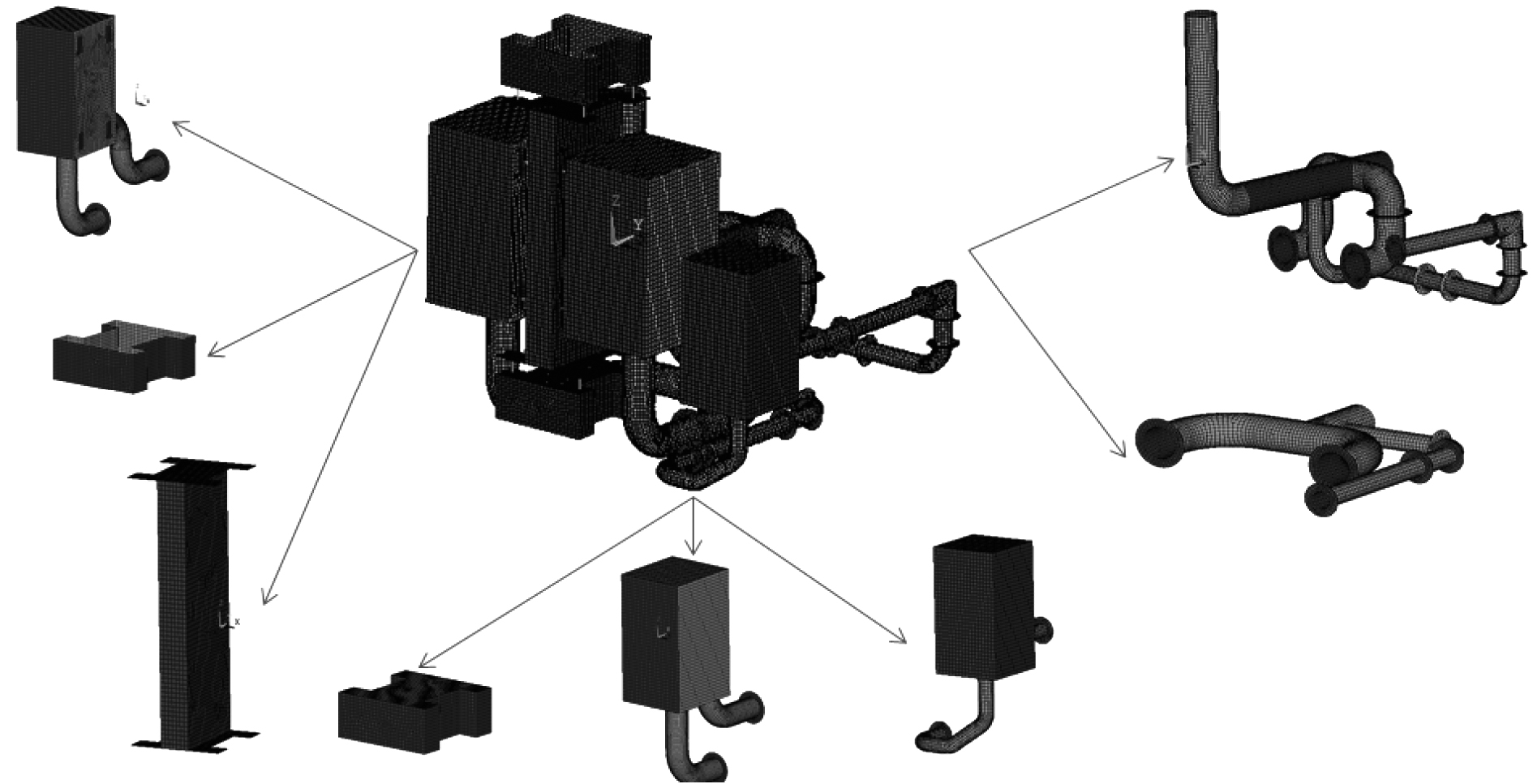
根据隔振元件位置(阻抗突变)对浮筏隔振系统进行子结构划分,如泵与筏架结构间由4个相同型号的隔振器连接,4个隔振器参数基本一致,将其简化为一个连接点,其他位置划分原则相同。根据隔振元件的位置对整个结构进行划分,整个系统被划分为8个子结构,如图2所示。
|
图 2 子结构划分图 Fig. 2 Substructure division diagram |
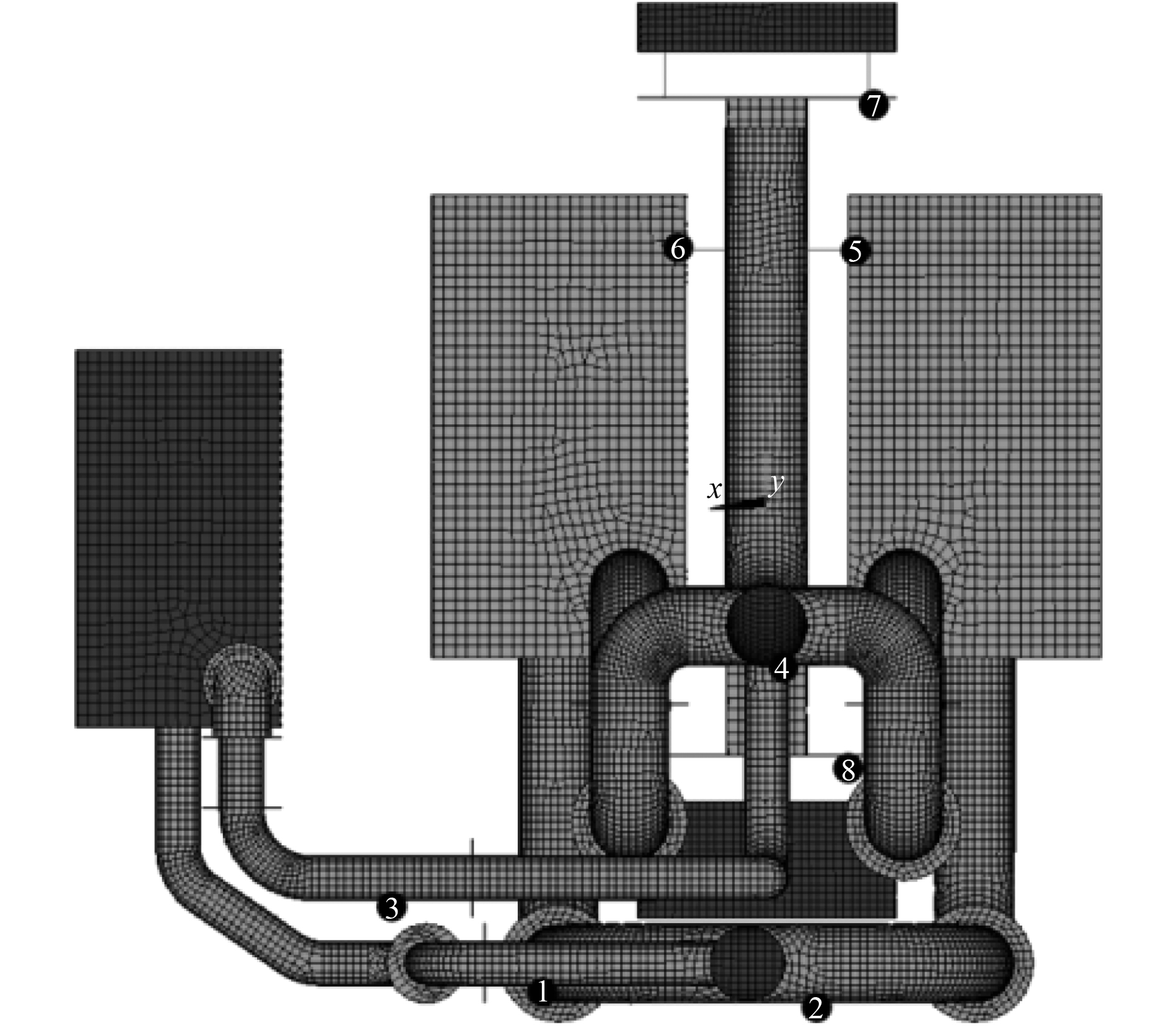
为了方便区分计算的节点,对节点进行编号如图3所示。其中编号1~4为管路上隔振元件的节点,编号5~8为隔振装置及设备上隔振元件的节点。
|
图 3 子结构动力学计算节点编号 Fig. 3 Dynamic calculated node numbers of substructure |
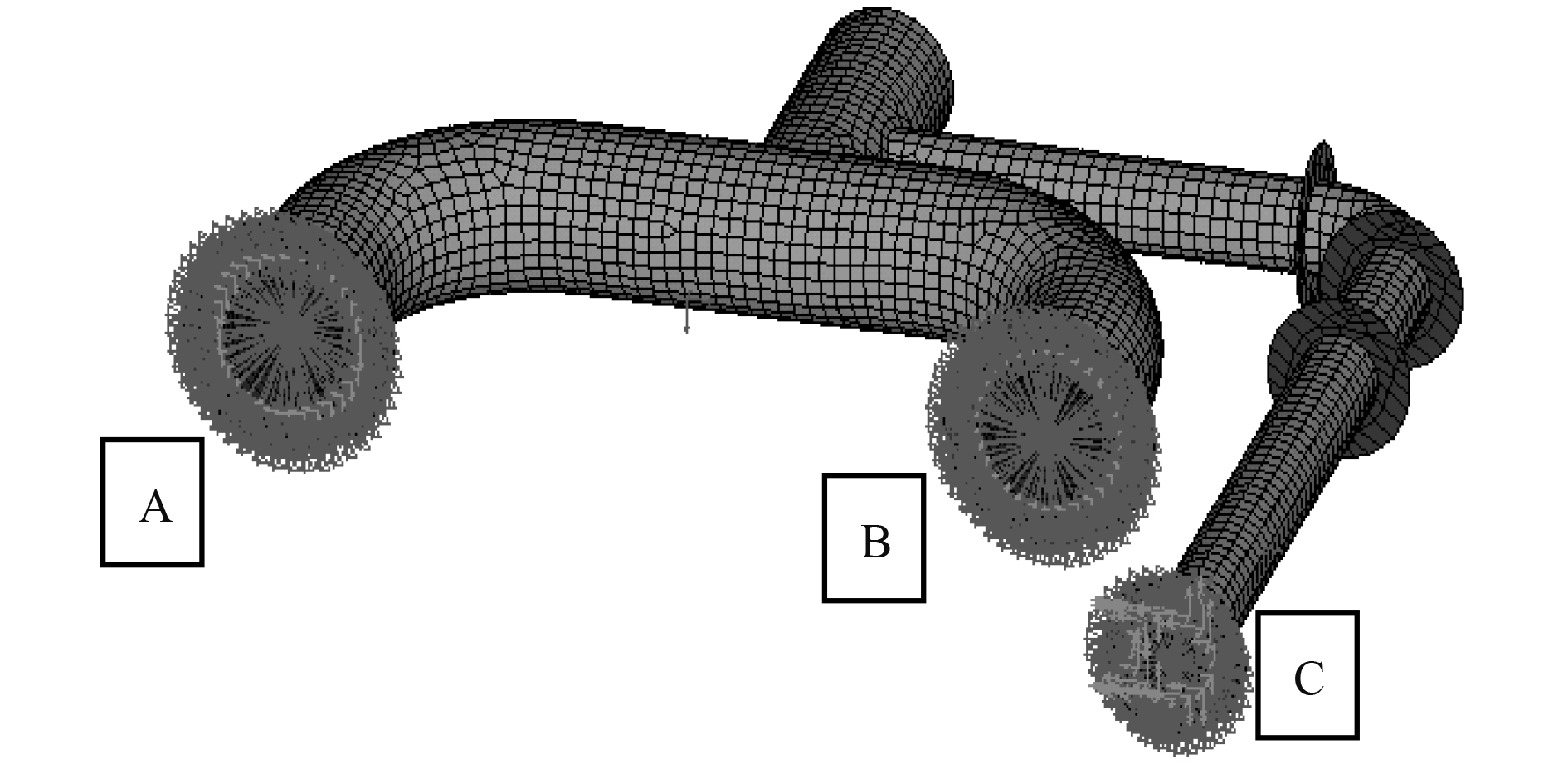
对于其中任意一个子结构(见图4),根据子结构与其他子结构的连接关系设置连接点。结构中有3个连接点A,B,C,首先分别在A点施加X,Y,Z三个方向的单位激励力,计算得到A,B,C三个方向的位移输出。经过整理可以得到A点的原点频响函数矩阵、B点关于A点的跨点频响函数矩阵、C点关于A点的跨点频响函数矩阵。
|
图 4 子结构计算连接点 Fig. 4 The calculated connection node of substructure |
重复上述步骤,可以得到子结构上每个连接点的原点频响函数矩阵以及相对于其他连接点的跨点频响函数矩阵。对8个子结构做同样的计算,将挠性接管、隔振器、弹性马脚等通过试验测量的数据整理并转换成频响函数矩阵,然后求解频响函数矩阵得出隔振元件节点的位移响应。
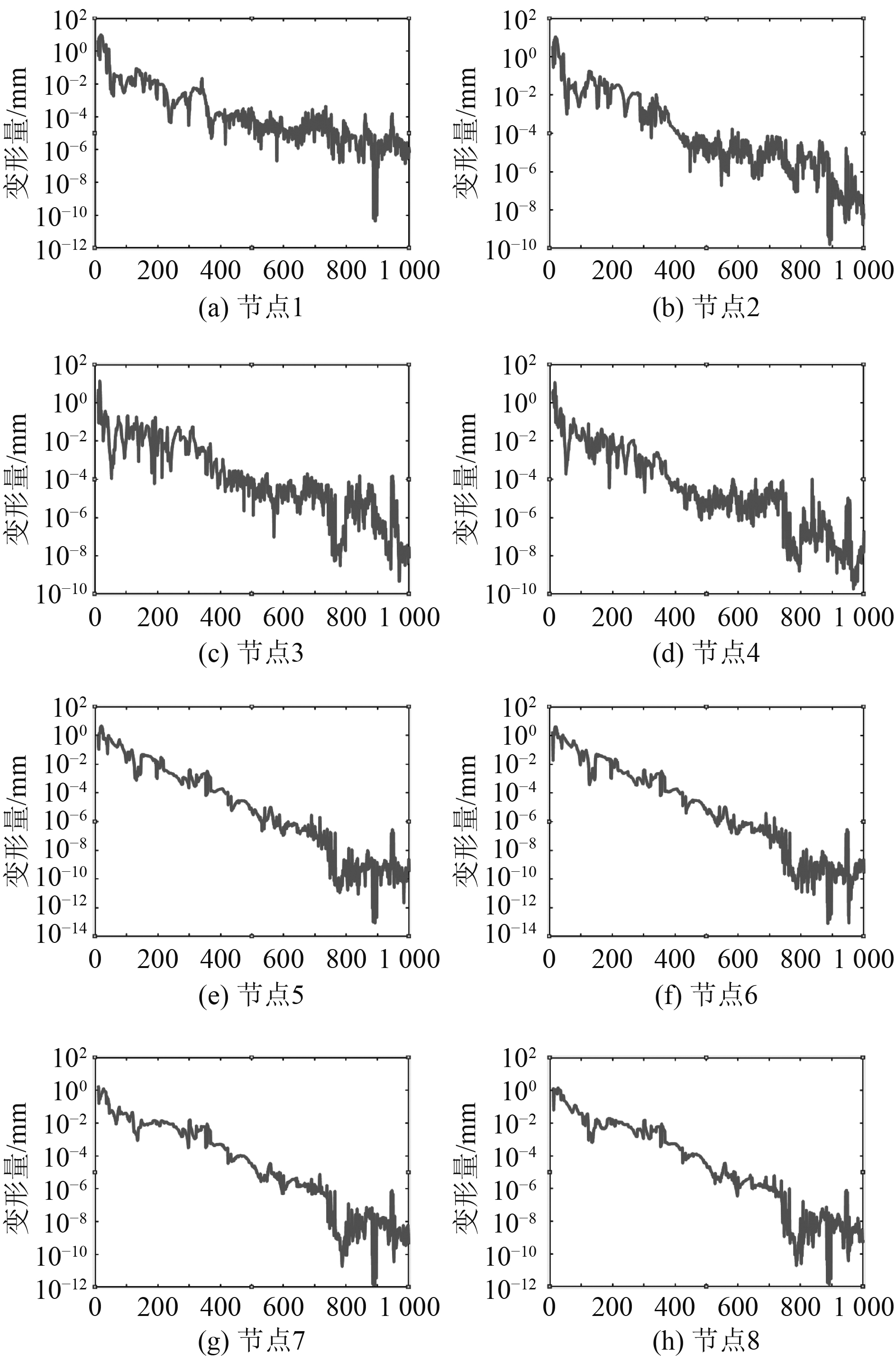
5 计算结果计算得到在海水泵运转的情况下各节点的位移响应如图5所示。
|
图 5 各节点的位移响应(10~1000 Hz) Fig. 5 Displacement response of nodes (10~1000 kHz) |
可知,在海水泵运转的情况下,各节点(隔振元件)位置均会产生一定位移的晃动,且随着频率的提高,各节点的变形呈减小的趋势,具体如下:
1)在10~100 Hz的频率范围内,各节点变形量均较大,100~1000 Hz的频率范围内,各节点变形量均较小,位移接近零变化。
2)浮筏隔振元件(7号、8号)的变形量最大不超过10 mm,随着频率增大,变形量呈减小趋势。
3)设备隔振元件(5号、6号)的变形量最大不超过6 mm,随着频率增大,变形量呈减小趋势。
4)进出口管路隔振元件(1号、2号、3号、4号)的变形量最大值达到15 mm,随着频率增大,变形量呈减小趋势。
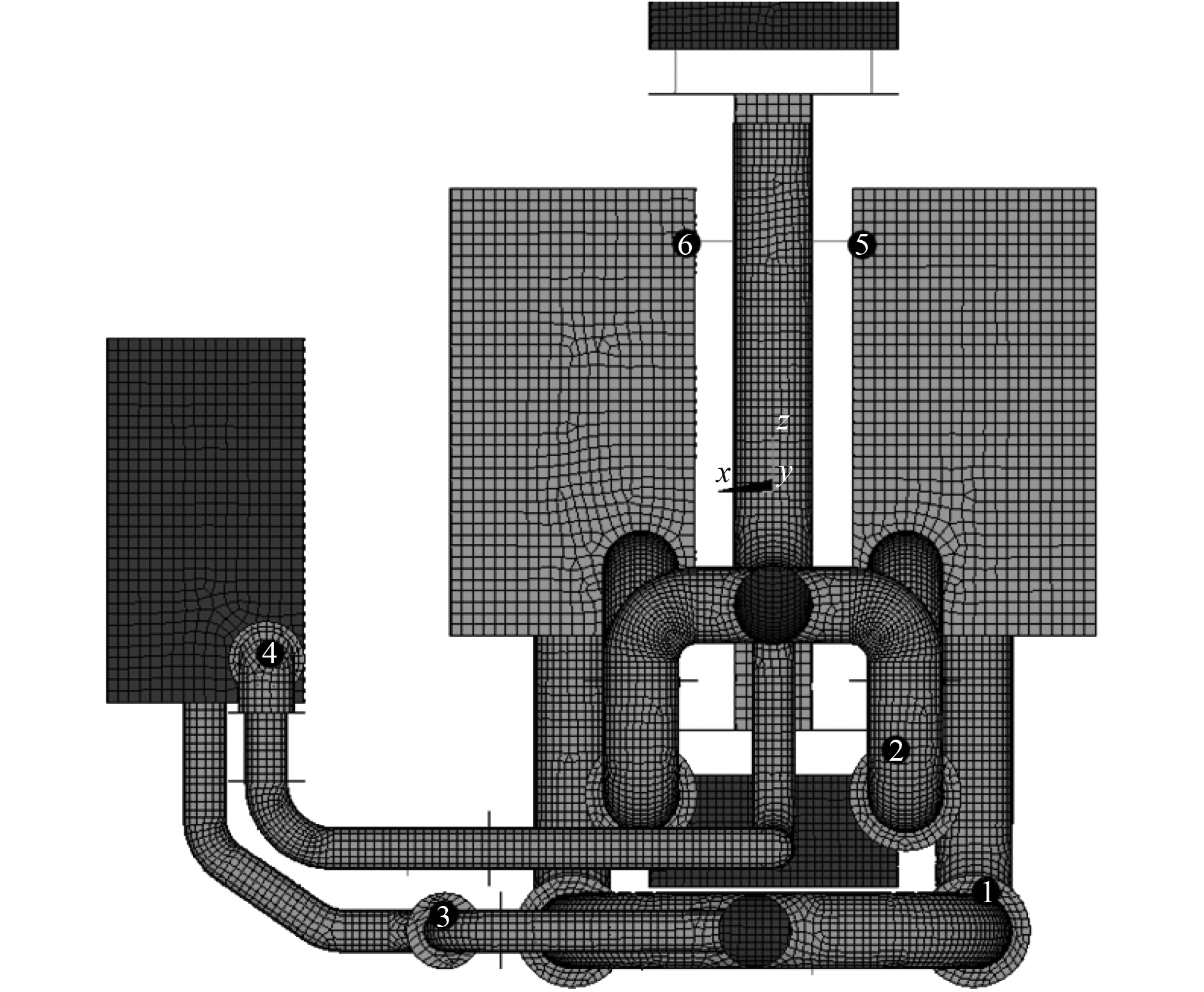
在海水泵运转的情况下对隔振系统中隔振元件进行振级落差声学计算,隔振元件编号如图6所示,计算结果如图7所示。
|
图 6 振级落差计算元件编号 Fig. 6 Calculated parts numbers of vibration level drop |
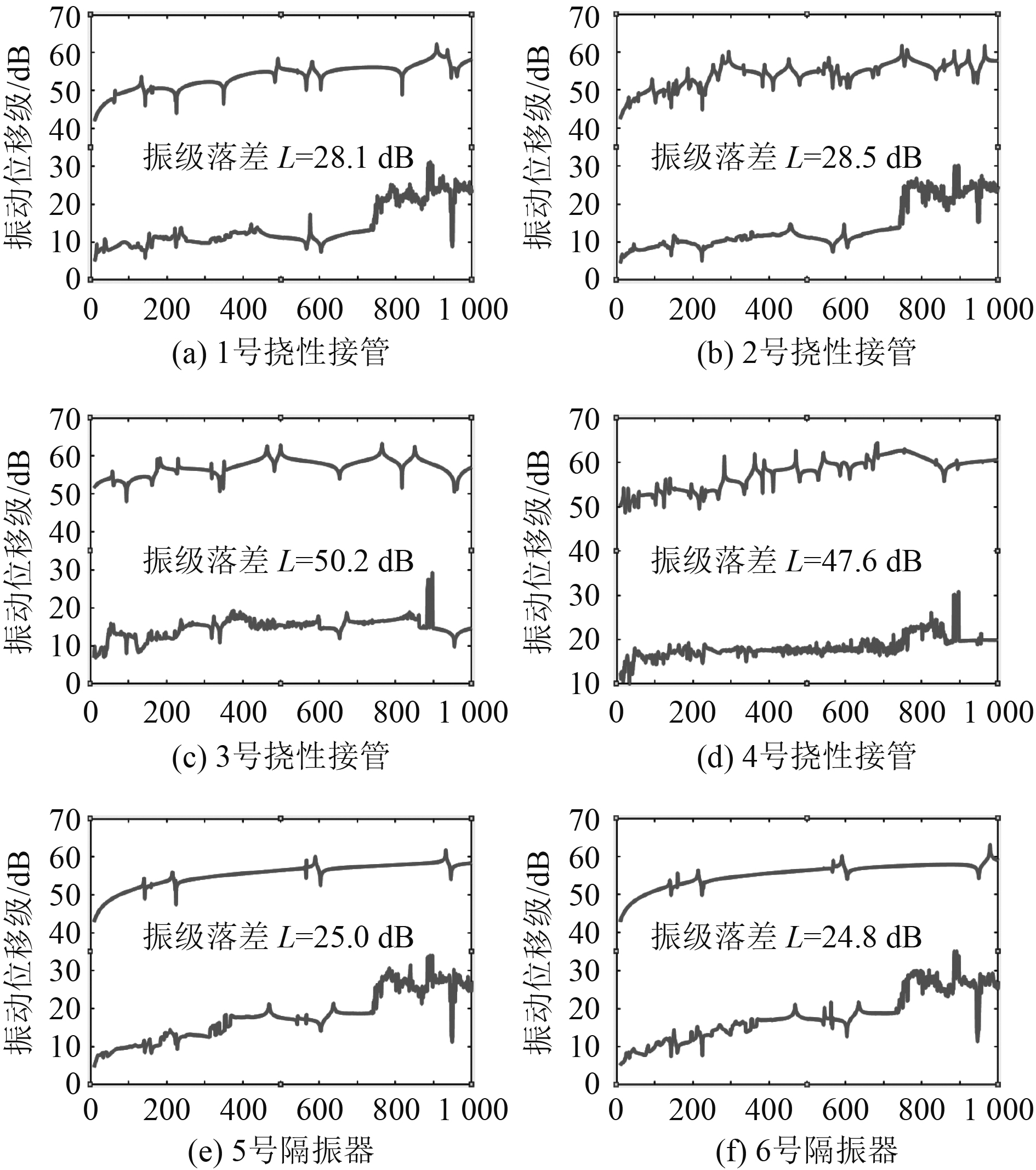
|
图 7 隔振元件振级落差计算结果(10~1000 Hz) Fig. 7 Calculation result of vibration level drop of vibration isolators (10~1000 kHz) |
可知,100 t海水泵的进出口挠性接管(1号、2号)在频率10~1000 Hz范围内振级落差分别达到28.1 dB和28.5 dB;25 t海水泵的进出口挠性接管(3号、4号)在频率10~1000 Hz范围内振级落差分别达到50.2 dB和47.6 dB;设备隔振器(5号、6号)的振级落差在频率10~1000 Hz范围内振级落差分别达到25 dB和24.8 dB。说明在忽略阻尼条件下,海水泵运转时各隔振元件的振级落差均优于设计效果,各隔振元件隔振效果较好。
6 结 语通过采用频响函数法计算,分析轴系海水系统海水泵运行对隔振系统影响,得出如下结论:
1)轴系海水系统在海水泵运行时会产生一定的位移变化,局部变化可能会超过15 mm,在系统安装、检验过程中,应严格按照技术要求规定设置隔振系统与周围结构、设备、管路等间距,以防系统工作时相碰。
2)虽然海水泵运行时会对隔振元件产生一定的位移变化,但各隔振元件的振级落差效果均较好,系统工作时位移变化不会影响隔振元件隔振效果的发挥。
| [1] |
贾晓丹, 张生乐, 潘国雄, 等. 通海管路系统隔振器变形测试分析[J]. 舰船科学技术, 2020, 42(6): 61-64. DOI:10.3404/j.issn.1672-7649.2020.06.012 |
| [2] |
JOHNSON D C. The mechanics of vibration[M]. University Press, 1960.
|
| [3] |
LIU W, EWINS D J. Substructure synthesis via elastic media[J]. Journal of Sound & Vibration, 2002, 257(2): 361-379. |
| [4] |
FERREIRA J V, EWINS D J. Nonlinear receptance coupling approach based on describing functions [J]. Proceedings of SPIE-The International Society for Optical Engineering, 1996.
|
| [5] |
REN Y, BEARDS C F. On substructure synthesis with FRF data [J]. Journal of Sound and Vibration, 1995, 185(5).
|
| [6] |
JETMUNDSEN B, BIELAWA R L, FLANNELLY W G. Generalized frequency domain substructure synthesis[J]. Journal of the American Helicopter Society, 1988, 33(1): 55. DOI:10.4050/JAHS.33.1.55 |
| [7] |
刘国庆. Ansys工程应用教程——机械篇[M]. 北京: 中国铁道出版社, 2003.
|
 2022, Vol. 44
2022, Vol. 44
