2. 广船国际有限公司,广东 广州 510000
2. Guangzhou Shipyard International Co., Ltd., Guangzhou 510000, China
船舶内部遍布各类液舱,对于非液货装载型船舶,液舱常布置在双层底、边舱内,具有范围广、质量大、靠近振动激励源等特点。舱内液体与结构之间存在流固耦合问题,影响船舶机械设备振动的传递和水下辐射噪声。因此对于大型船舶而言,准确、高效的液舱模拟方法对机械噪声数值计算具有重要意义。
机械噪声是船舶水下辐射噪声的主要成分,准确的机械噪声预报能为船舶水下辐射噪声控制提供良好的支撑[1]。杨德庆[2-3]采用有限元/边界元方法对某船的水下辐射特性进行分析,仿真结果与实测结果吻合良好,在工程中被广泛应用。庞福振[4]提出了船舶结构噪声截断模型预报的系统化方法,对载荷、结构以及外流域进行截断,规范了船舶结构噪声截断模型预报流程,降低了船舶机械噪声计算规模。刘晗[5]采用大质量法将加速度载荷转化的力载荷,为船舶机械噪声数值计算中的激励载荷施加方法提供参考。高晟耀[6]通过研究船舶中低频机械噪声统计能量法误差产生机理,建立了方案设计阶段船舶结构中低频噪声统计能量修正方法,为船舶中低频机械噪声预报提供新的数值计算思路。Ding Ding Lu[7]提出一种结合机械激振力估计和机声传递函数估计的船舶结构实时辐射噪声预测方法,通过激振力修正因子,进一步提高了船舶机械噪声计算的准确性。
综上,众多学者正逐步规范船舶机械噪声数值计算流程,但针对大型船舶机械噪声计算过程中的液舱模拟方法鲜有研究。常用的液舱模拟方法有质量点法[8]、源汇法[9]和声学单元法等,但对于大型船舶而言,液舱分布广,船体尺度大,单一的液舱模拟方法,难以兼顾计算效率和计算精度。为此,本文结合现有的液舱模拟方法和船体结构振动传递特点,提出液舱杂交模拟方法,即结合不同液舱模拟方法,因液舱位置制宜,兼顾计算效率和计算精度,开展液舱模拟方法对典型三舱段模型和船舶舱段模型水下辐射噪声的影响研究。最后,基于液舱杂交模拟方法,计算某大型船舶在主机激励下的机械噪声,为大型船舶机械噪声的精细化预报提供一定参考。
1 船舶机械噪声计算的液舱模拟方法 1.1 声固耦合计算原理船舶结构振动与流体之间存在声固耦合问题,一方面,声辐射由结构振动引起;另一方面,辐射声场反过来又会对结构振动产生反作用。不考虑流体的作用,结构经有限元离散后的运动方程可以写为:
| $ \left[ {{{\boldsymbol{M_s}}}} \right]\left[ {\ddot U} \right] + \left[ {{{\boldsymbol{C_s}}}} \right]\left\{ {\dot U} \right\} + \left[ {{{\boldsymbol{K_s}}}} \right]\left\{ U \right\} = \left\{ {{{\boldsymbol{F_s}}}} \right\}。$ | (1) |
式中:
当结构置于无限深水介质中时,必须考虑水介质的耦合作用。假设周围的流体介质是理想流体,则声波动方程为:
| $ {\nabla ^2}p = \frac{1}{{{c^2}}}\frac{{{\partial ^2}p}}{{{\partial ^2}t}} 。$ | (2) |
式中:
结构流体耦合作用方程可写为:
| $\begin{array}{*{20}{l}} & \left[ {\begin{array}{*{20}{l}} {\left[ {{M_s}} \right]}&{\left[ 0 \right]} \\ {{\rho _f}\left[ R \right]}&{\left[ {{M_f}} \right]} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {\left\{ {\ddot U} \right\}} \\ {\left\{ {\ddot P} \right\}} \end{array}} \right\} + \\ & \left[ {\begin{array}{*{20}{c}} {\left[ {{C_s}} \right]}&{\left[ 0 \right]} \\ {\left[ 0 \right]}&{\left[ {{C_f}} \right]} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {\left\{ {\dot U} \right\}} \\ {\left\{ {\dot P} \right\}} \end{array}} \right\} +\\ & \left[ {\begin{array}{*{20}{c}} {\left[ {{K_s}} \right]}&{ - {{\left[ R \right]}^T}} \\ {\left[ 0 \right]}&{\left[ {{K_f}} \right]} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {\left\{ U \right\}} \\ {\left\{ P \right\}} \end{array}} \right] = \left\{ {\begin{array}{*{20}{c}} {\left\{ {{F_s}} \right\}} \\ {\left\{ 0 \right\}} \end{array}} \right\}。\end{array}$ | (3) |
式中:
对于单频激励,波动方程式有如下形式的Helmholtz积分解:
| $\begin{aligned}[b] & p\left(\overrightarrow{{r}_{p}}\right)=\alpha \left(\stackrel{\rightharpoonup }{{r}_{p}}\right)\displaystyle \underset{S}{\iint }\\ & \left[p\left(\stackrel{\rightharpoonup }{{r}_{q}}\right)\frac{\partial G\left(\stackrel{\rightharpoonup }{{r}_{p}},\stackrel{\rightharpoonup }{{r}_{q}}\right)}{\partial n}-G\left(\stackrel{\rightharpoonup }{{r}_{p}},\stackrel{\rightharpoonup }{{r}_{q}}\right)\frac{\partial p\left(\stackrel{\rightharpoonup }{{r}_{p}}\right)}{\partial n}\right]{\rm{d}}S\left(\stackrel{\rightharpoonup }{{r}_{q}}\right) 。\end{aligned}$ | (4) |
式中:
对于单频激励,基于波动方程式的Helmholtz积分解和边界元技术,将声源表面离散可得到如下矩阵方程:
| $ {{P_f}} = A {{P_s}} + B {P_{s,n}'}\; C {P_s} = D {P_{s,n}'} 。$ | (5) |
根据式(5),在已知结构s处的声压和位移时,可得声场中任意一点的声压为:
| $ \left\{ {{P_f}} \right\} = \left( {\left[ A \right]{{\left[ C \right]}^{ - 1}}\left[ D \right] + \left[ B \right]} \right)\left\{ {P_{s,n}'} \right\}。$ | (6) |
在进行声固耦合数值计算时,考虑激励源附近液舱内液体对结构振动传递的影响,因此需对舱内液体采用合适的模拟方法,常见的液舱模拟方法主要有:
1)质量点法
将液体质量用质量单元模拟,均布在舱内强构件单元的节点上,或者通过调节液舱结构单元材料密度来模拟液体质量,并确保重心位置的准确;
2)源汇法
基于Nastran软件平台,使用边界元法在湿表面上分布一系列的源汇来求解拉普拉斯方程,通过匹配相应的边界条件求解线性方程组,进而得到面元上的压力;
3)声学单元法
采用声学单元对液舱进行模拟,建立结构与流体的耦合系统模型,通过结构有限元和流体有限元相结合的方式计算该耦合系统的动力特性。
1.2.1 船舶典型三舱段模型为进一步分析上述3种液舱模拟方法对船舶机械噪声数值结算结果的影响,建立典型的船舶三舱段简化模型,该模型示意图如图1所示。模型总长27 m,型宽6 m,吃水1 m,型深4 m,排水量162 t,材料为普通钢,其杨氏模量为2.06×1011 Pa,泊松比为0.3。

|
图 1 典型三舱段模型示意图 Fig. 1 Schematic diagram of a typical three-cabin model |
根据三舱段模型几何尺寸建立其结构有限元模型,基座及其附近区域进行局部网格细化[10],以匹配计算频率;在基座中心上方建立质量点,和弹簧单元通过MPC连接,模拟基座上方的设备和隔振器;为降低数值计算规模,仅在2#双层底位置建立液舱,1#和3#液舱为空舱。所建立的质量点法模型、源汇法模型和声学单元法模型如图2所示。
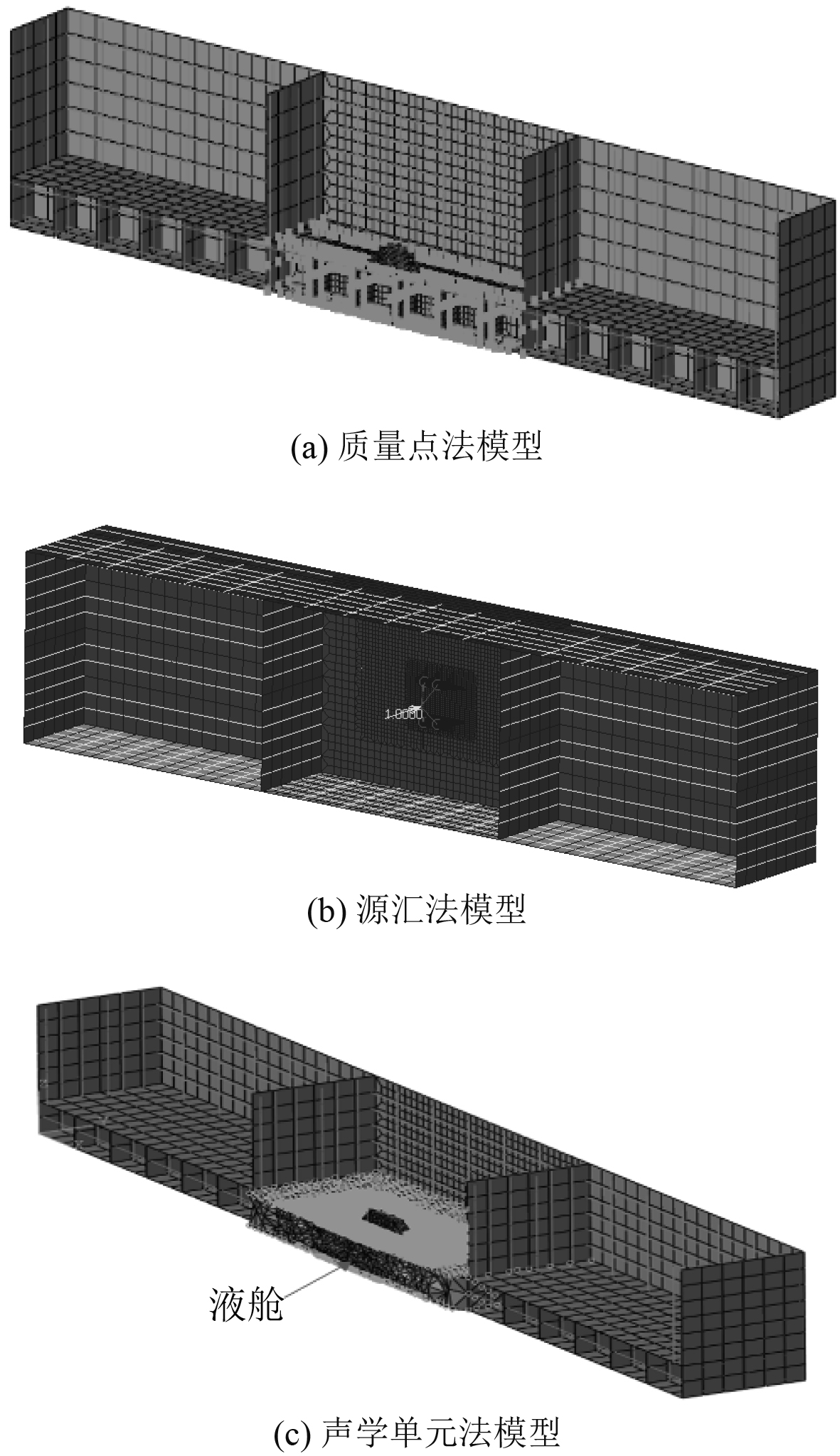
|
图 2 辐射噪声计算模型(半剖视图) Fig. 2 Radiated noise calculation model (half view) |
计算内容分为:1)对比分析不同液舱模拟方法对三舱段振动模态的影响;2)在基座上方质量点位置施加垂直单位力载荷,对比分析不同液舱模拟方法对三舱段机械噪声的影响。
1.2.3 计算结果及分析1)模态计算结果
模态结果如表1所示,质量点法、源汇法、声学单元法等3种液舱模拟方法对模型的模态影响较小。主要由于三舱段模型的固有频率较低,质量效应占主导地位,且3种方法均能准确模拟液舱内液体质量。
|
|
表 1 模态计算结果对比 Tab.1 Comparison of modal calculation results |
2)水下辐射噪声计算结果
将采用不同液舱模拟方法的三舱段模型机械噪声计算结果进行对比,如图3所示。

|
图 3 水下辐射噪声计算结果 Fig. 3 The calculation results of the underwater radiated noise |
可知,在80 Hz以下的低频范围,声功率计算结果趋势吻合良好,但在峰值位置处,采用源汇法及声学单元法模拟液舱的计算结果更小,较质量点法计算结果小5 dB左右,说明声学单元法与源汇法能保留液舱的阻尼作用。随频率增大,不同液舱模拟方法的声功率计算结果存在明显的错峰,说明不同液舱模拟方法对中高频计算结果存在一定影响。
综上,相比于质量点法,声学单元法和源汇法在准确模拟液舱附加质量的基础上,同时兼顾液体的阻尼效应,更符合工程实际。
3)计算效率
采用不同液舱模拟方法的舱段模型,其机械噪声计算时间如表2所示。可知,声学单元法计算精度高但求解规模较大,质量点则相反,源汇法的计算精度和计算效率均处于其余2种方法之间。
|
|
表 2 计算时间对比 Tab.2 Computation time comparison |
在开展大型船舶机械噪声数值计算工作时,考虑到大型船舶结构复杂,液舱分布广,源汇法在计算此类问题时,由于湿表面单元过多常常导致计算效率较低,而单一采用声学单元法或者质量点法对液舱进行模拟时,难以兼顾计算效率和计算精度。为此提出适用于大型船舶机械噪声计算的液舱模拟方法:在激励力所在舱段的底部液舱采用声学单元法模拟,舷侧液舱及其他舱段的液舱采用质量点法模拟。将上述液舱模拟方法称为液舱杂交模拟方法。
该方法优势在于:1)由于大部分液舱采用质量点法模拟,因此该方法相比于声学单元法具有更高的计算效率;2)船体结构低频振动传递距离远,全船大部分结构振动对低频水下辐射噪声具一定影响,而声学单元法与质量点法均具有较好的低频振动计算精度,水下辐射噪声的低频计算精度得以保障;3)船舶结构中高频振动衰减迅速,传递距离近,采用质量点法模拟的液舱与激励源较远,对计算结果精度影响较小,因此,机械噪声的中高频计算精度得以保障。
2 液舱杂交模拟方法有效性研究 2.1 船舶典型三舱段模型水下辐射噪声计算 2.1.1 船舶典型三舱段水下辐射噪声计算模型三舱段模型主尺度和激励载荷与上文保持一致,但1#、2#和3#均设置为液舱,液舱分别以质量点法、声学单元法和液舱杂交模拟方法进行模拟,建立的模型如图4所示。

|
图 4 典型三舱段有限元模型 Fig. 4 Typical finite element model of three cabins |
辐射声功率计算结果如图5所示。可知:1)80 Hz以下的低频范围内,3种液舱模拟方法的计算结果吻合良好;2)80~500 Hz频率范围内,声学单元法与液舱杂交模拟方法计算结果在趋势上吻合良好,辐射声功率总级上,质量点法为76.2 dB,液舱杂交模拟方法为65.5 dB,声学单元法为66.7 dB,液舱杂交模拟方法与声学单元法相差1.2 dB。
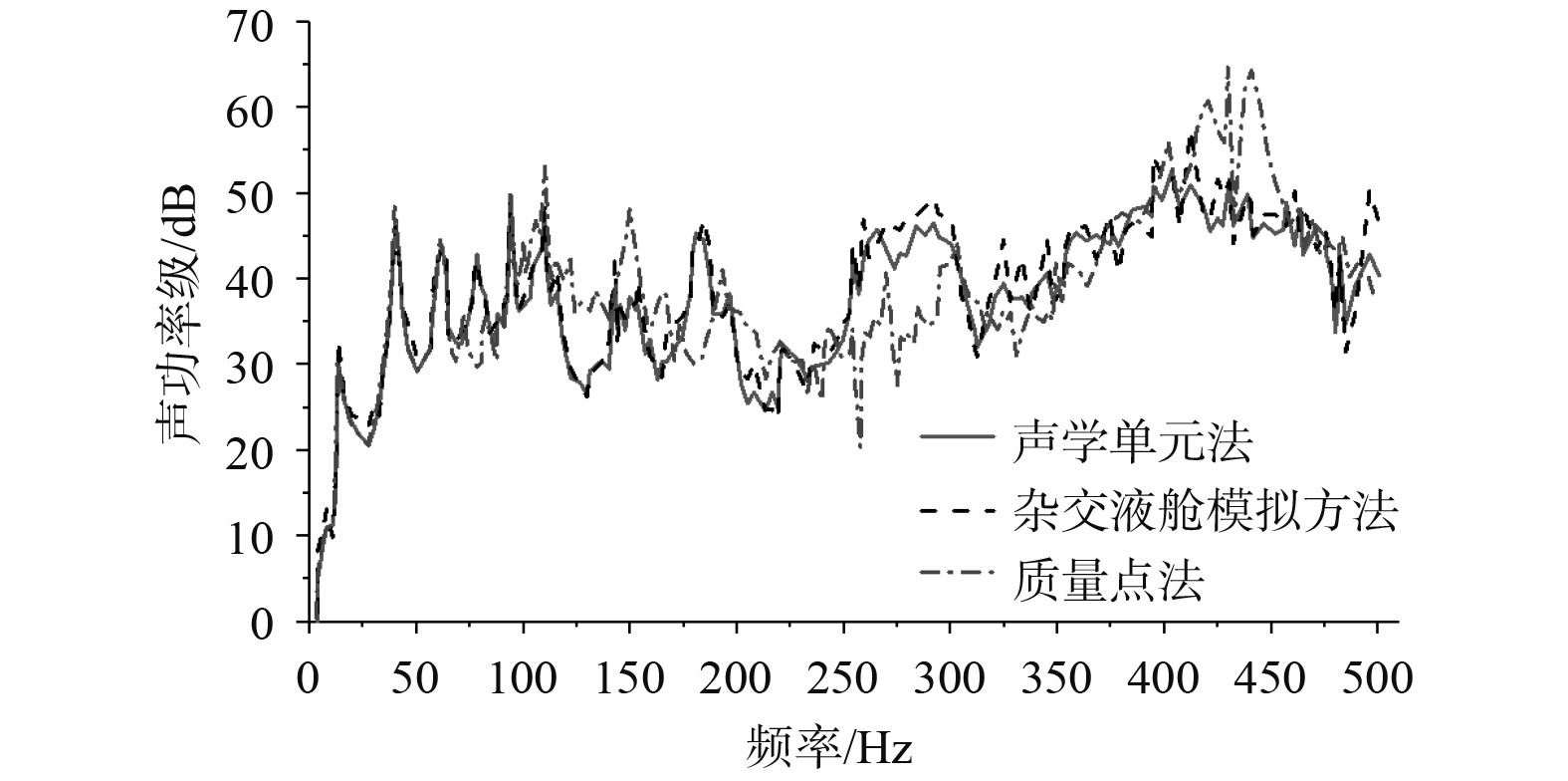
|
图 5 水下辐射噪声计算结果 Fig. 5 The calculation results of the underwater radiated noise |
在计算效率上,声学单元法共计40 min,质量点法共计17 min,液舱杂交模拟方法共计25 min,可见液舱杂交模拟方法较声学单元法在计算效率上有大幅提升。
综上,液舱杂交模拟方法在计算精度上与声学单元法相当,且计算效率更高。
2.2 某船舱段模型水下辐射噪声计算 2.2.1 某船舱段水下辐射噪声计算模型为进一步验证液舱杂交模拟方法的有效性,考虑计算规模,截取某船后主机舱附近舱段,同时截去对水下辐射噪声影响较小的上层建筑结构,开展后主机基座位置在单位力作用下的机械噪声计算。舱段有限元模型如图6所示。

|
图 6 某船舱段有限元模型 Fig. 6 Finite element model of a cabin section of a ship |
该舱段模型舷侧及双层底内均设有液舱,且液舱数量较多,全部采用声学单元法建模将导致计算成本较高。为此,在工况1中,将后主机基座下液舱设置为声学单元,其余舱室采用质量点法进行建模,即杂交液舱模拟法;在工况2中,采用质量点法对全部液舱进行建模;工况3作为对照组,将全部液舱设置为空舱。3种工况的有限元模型如图7所示。
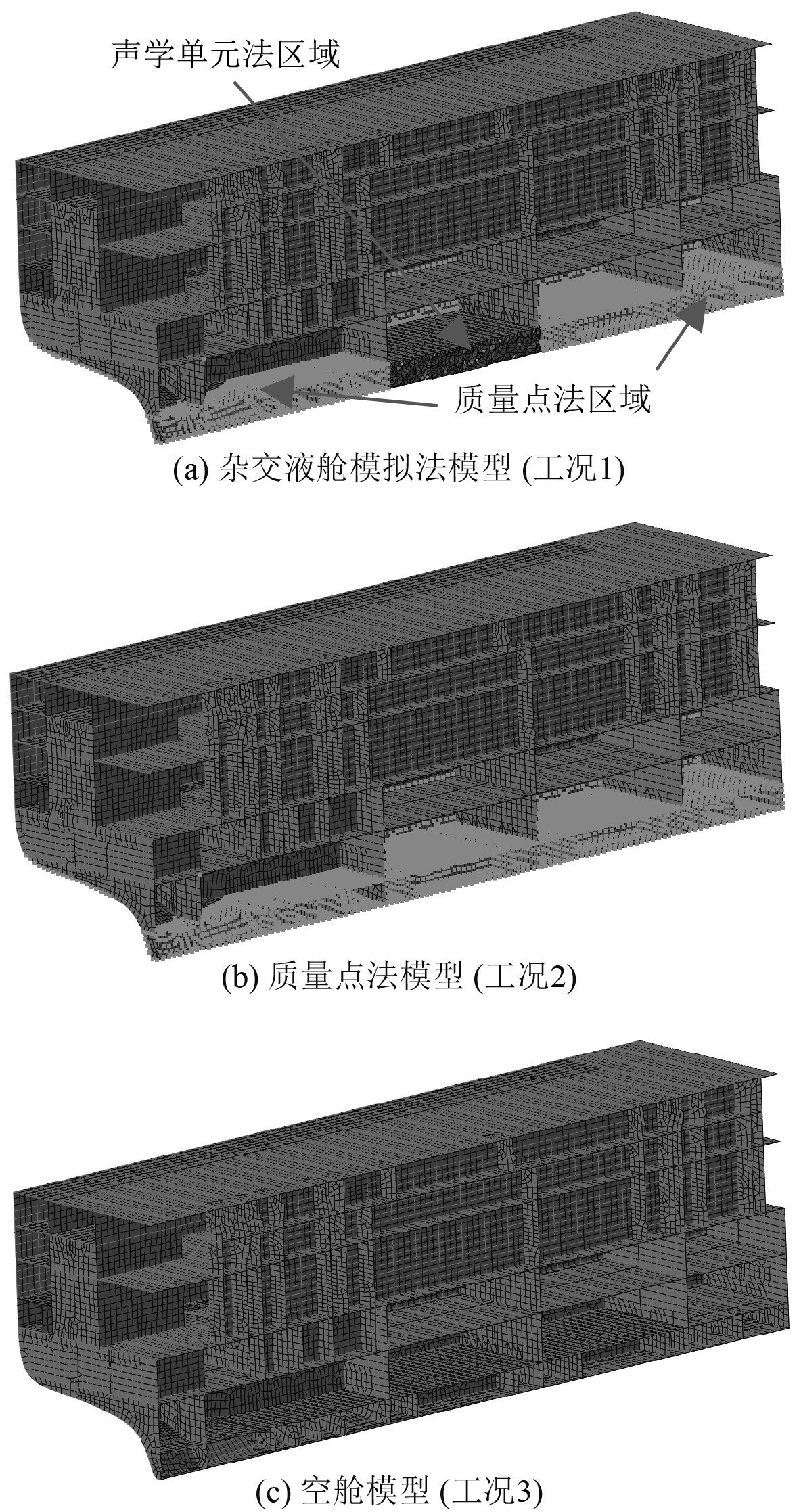
|
图 7 舱段有限元模型(半剖视图) Fig. 7 Finite element model of cabin (half view) |
在基座位置单位力作用下,得到的机械噪声声源级如图8所示。可以看出,3种工况的计算结果在趋势上基本保持一致,质量点法和杂交建模方法计算结果在低频范围内吻合良好;在总级上,空舱计算结果总级最大,液舱杂交模拟方法的水下辐射噪声计算结果最小,相较质量点法低1.3 dB。可以看出,杂交模型能更好反映液舱的阻尼特性,符合工程实际。
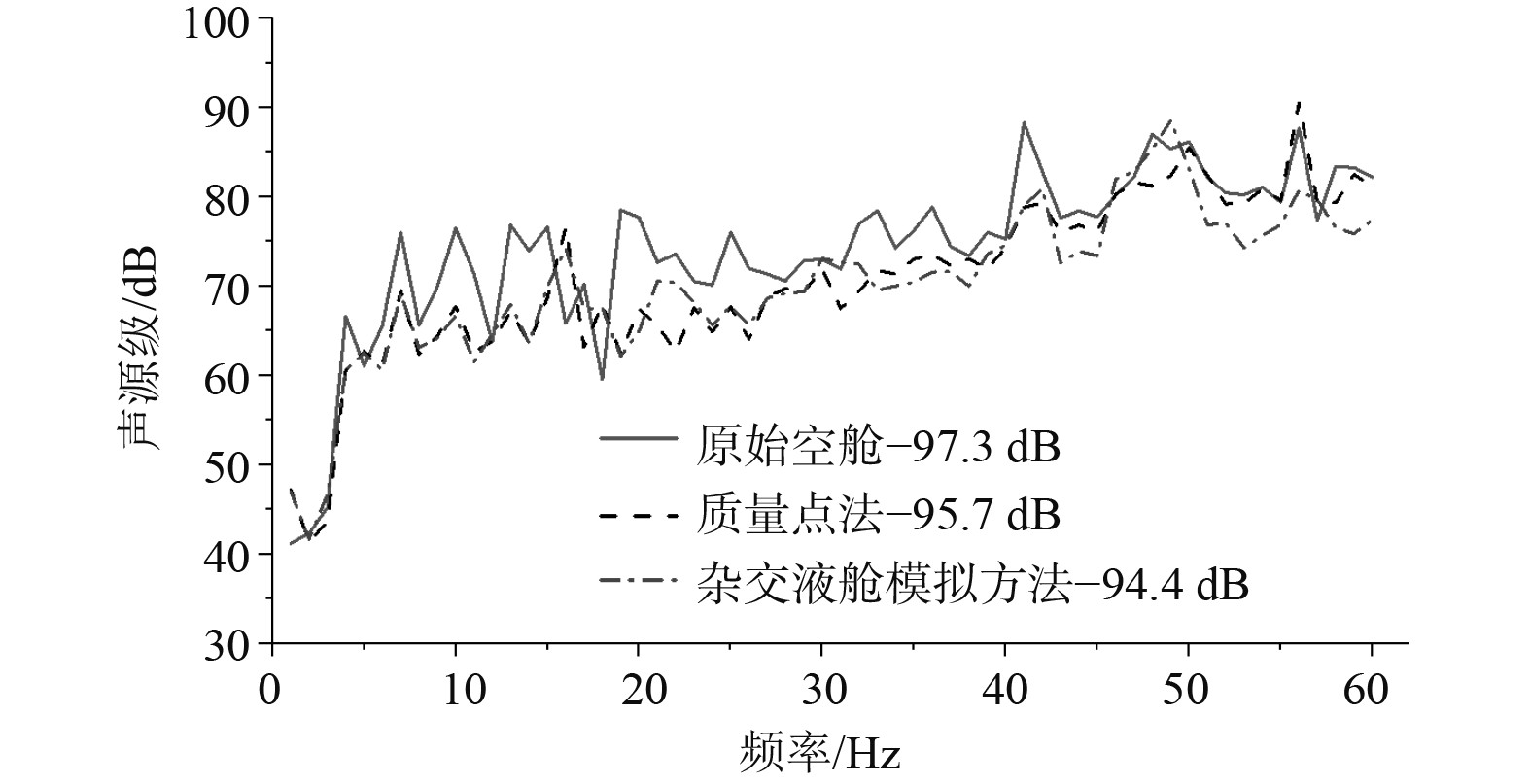
|
图 8 舱段水下辐射噪声计算 Fig. 8 Calculation of underwater radiated noise in the cabin |
基于某船总布置图、基本结构图、型线图等图纸资料,建立全船的有限元模型,如图9所示。其中,舱段壳体、甲板、舱壁等结构采用shell单元建立,纵骨等型材采用beam单元建立,忽略围栏、扶手等不参与船舶强度的小构件,外部流场采用声学单元建立。

|
图 9 某船机械噪声计算模型 Fig. 9 Calculation model of mechanical noise of a ship |
液舱采用液舱杂交模拟方法建立,即在主机下方的双层底液舱采用声学单元法建模,其余液舱采用质量点法建模。全船结构网格及流体网格共计1564357个。
3.2 激励载荷本船参考功率、类型相近主机的机脚振动加速度实测值,10~200 Hz下的频域激励加速度载荷如图10所示。

|
图 10 机脚振动加速度 Fig. 10 The vibration acceleration of the machine foot |
通过声固耦合有限元-边界元方法计算,液舱采用液舱杂交模拟方法建立,得到机械噪声声功率级,再根据球面波衰减规律,进一步将声功率级转换为声源级,得到该船主机激励下的机械噪声声源级线谱如图11所示。
|
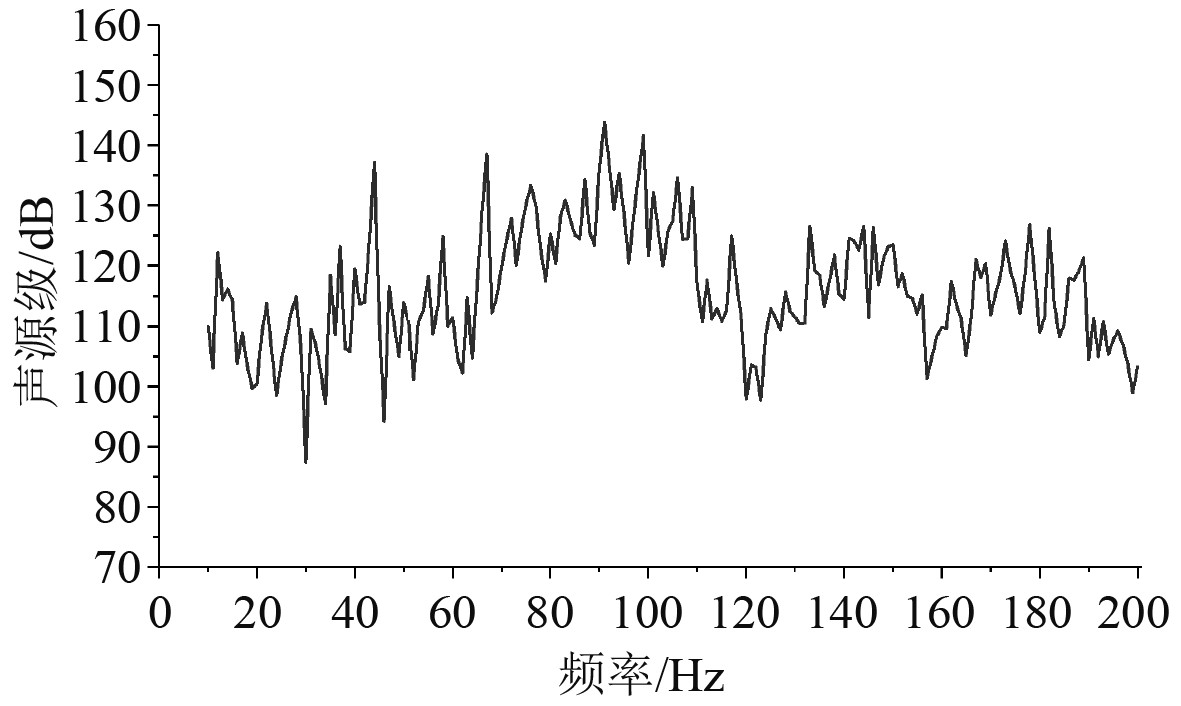
图 11 主机激励下的某船机械噪声计算结果 Fig. 11 Calculation results of mechanical noise of a ship under the excitation of the main engine |
可以看出,该船在主机激励载荷作用下的机械噪声10~200 Hz频率范围内总级为150.0 dB,在44 Hz,67 Hz,91 Hz以及99 Hz存在明显峰值,其中44Hz,67 Hz,91 Hz与激振载荷峰值频率吻合,部分频率下的声场分布如图12所示。

|
图 12 不同频率下的声场分布 Fig. 12 Sound field distribution at different frequencies |
本文对比分析了3种液舱模拟方法的计算效率及计算精度,提出适用于大型船舶机械噪声计算的液舱模拟方法,即液舱杂交模拟方法;以三舱段模型和某大型船舶舱段模型验证了液舱杂交模拟方法的有效性;最后计算了某船主机激励下的机械噪声。主要结论如下:
1)相比于声学单元法、质量点法和源汇法,液舱杂交模拟方法能够兼顾计算精度和计算效率,适用于大型船舶的机械噪声计算中的液舱模拟。
2)针对三舱段模型的辐射噪声计算,杂交建模方法与声学单元法的计算结果吻合良好,总级偏差1.2 dB,计算时间缩短37.5%。
3)针对某船舱段模型的辐射噪声计算,杂交建模方法低于质量点法的声功率总级约1.3 dB,能够反映液舱中液体的阻尼效应。
4)采用杂交液舱模拟法模拟液舱中液体,计算得到某船主机引起的水下辐射噪声为150.0 dB。
| [1] |
刘致豪. 舰船水下噪声预报与优化设计[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [2] |
杨德庆, 郑靖明, 王德禹, 等. 基于 SYSNOISE 软件的船舶振动声学数值计算[J]. 中国造船, 2002, 43(4): 32-38. YANG De-qing, ZHENG Jing-ming, WANG De-yu, et al. Numercial analysis of vibro-acoustic characters of ship withSysnoise software[J]. Ship Building of China, 2002, 43(4): 32-38. DOI:10.3969/j.issn.1000-4882.2002.04.006 |
| [3] |
杨德庆, 王德禹, 刘洪林, 等. 某型艇近场噪声和自噪声数值计算[J]. 声学学报, 2003(5): 421-424. YANG Deqing, WANG Deyu, LIU Honglin, et al. Numerical calculation of near-field noise and self-noise of a certain type of boat[J]. Acoustic Sinica, 2003(5): 421-424. DOI:10.15949/j.cnki.0371-0025.2003.05.007 |
| [4] |
庞福振. 船舶结构噪声截断模型数值预报方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [5] |
刘晗, 李天匀, 朱翔. 船舶机械噪声预报模型中激励载荷的施加方法分析[C]//第十七届船舶水下噪声学术讨论会论文集, 2019: 86−91.
|
| [6] |
高晟耀, 杜圆, 王雪仁, 等. 船舶中低频机械噪声统计能量修正方法研究[C]//2019中国西部声学学术交流会论文集. 2019: 245−248.
|
| [7] |
LU Ding Ding, HE Lin. Real-time calculation of noise radiated by ship structure via machinery exciting force estimation[J]. Applied Mechanics and Materials, 2012, 2031(226−228):
|
| [8] |
刘洋, 刘宝, 王蕾. 一种分析水中结构声振耦合特性的等效源方法[J]. 海军工程大学学报, 2021, 33(1): 34-40. LIU Yang, LIU Bao, WANG Lei. An equivalent source method for analyzing the acoustic-vibration coupling characteristics of underwater structures[J]. Journal of Naval Engineering University, 2021, 33(1): 34-40. DOI:10.7495/j.issn.1009-3486.2021.01.007 |
| [9] |
王国强, 杨建民. 用线性三角形元源汇法计算振动船体的附连水质量[J]. 上海交通大学学报, 1988(3): 99-103. WANG Guoqiang, YANG Jianmin. Calculation of attached water mass of vibrating hull by linear triangle element source-sink method[J]. Journal of Shanghai Jiaotong University, 1988(3): 99-103. |
| [10] |
刘西安, 杨德庆, 李清. 船舶基座阻抗计算的梯度网格模型方法[J]. 中国造船, 2020, 61(4): 20-31. LIU Xi'an, YANG Deqing, LI Qing. Gradient grid model method for impedance calculation of ship foundation[J]. China Shipbuilding, 2020, 61(4): 20-31. DOI:10.3969/j.issn.1000-4882.2020.04.003 |
 2022, Vol. 44
2022, Vol. 44
