近年来,功能梯度材料(functionally graded materials,FGM)的发展受到了越来越多的重视。FGM作为新型的复合材料,在高强度和高硬度等方面具有良好的卓越性能,并且与传统的复合材料相比,在降低界面应力、物理特性连续变化等方面更有优势。这使得FGMs在高性能航空飞行器、超音速飞行器、舰船、汽车部件等领域具有广泛的应用前景[1]。
船体的减震降噪一直是研究热点,而功能梯度材料可以通过自主设计来满足预期的功能。与外界阻抗相匹配,并且同时满足内部的声衰减要求,一般考虑使用功能梯度材料作为船体的外部消声层使用。由于功能梯度材料是人为设计的,所以可以设计出不同的梯度材料应用于不同情境中,如可以使用一些具有高强度高硬度的材料作为功能梯度材料的外部材料,内部选择吸声效果良好的材料作为填充,使其呈梯度分布,在满足船体外壳强度的前提下,更好地减少船体噪声。功能梯度材料在船体的减震降噪方面具有广阔的应用前景。
20世纪70年代,Bever M B等首先提出梯度结构这个构想。到了1984年日本学者新野正之等提出功能梯度材料概念,其目的是为了应用于未来超高音速飞行器壳体[2]。1997年,Suresh和Mortensen正式定义为功能梯度材料。
Loy等[3]采用Love壳理论中的应变-位移关系进行分析,采用Rayleigh-Ritz方法得到特征值控制方程,研究圆柱体的固有频率、组成体积分数的影响以及组成材料的结构对频率的影响。李学斌[4]基于Flügge经典薄壳理论和波动法,讨论了圆柱壳的频散特性,从频率、振型和波数等方面详细研究了波法的有效性和准确性。Loy等[5]根据Love一阶近似理论,给出了几种边界条件下固有频率的振型。杜长城等[6]研究了功能梯度材料制成的薄壁圆柱壳的自由振动,根据Donnell壳体理论推导出圆柱壳线性振动的简化控制方程。梁斌等[7]根据Love薄壳理论,确定功能梯度材料圆柱壳的内力、位移、应变和曲率的关系式。李世荣等[8]在半解析法的基础上分析了在扭转作用下的夹层圆柱壳的弹性稳定情况,其中上下表面为均匀复合材料,中间层为沿着厚度方向材料属性变化的功能梯度材料。
以上文献表明,大部分学者研究基于圆柱壳或者功能梯度薄壁圆柱壳的一般弹性边界条件,以及功能梯度材料圆柱夹层壳的理论模型研究。对于夹层壳圆柱体整体结构情况少有研究。事实上,圆柱体的结构、材料参数特性是影响结构振动特性的重要因素,对其研究十分必要。
1 力学模型假定功能梯度圆柱软芯夹层壳的力学模型如图1所示

|
图 1 FGM圆柱夹层壳模型 Fig. 1 Model of FGM cylindrical sandwich panel |
R表示功能梯度圆柱软芯夹层壳中曲面半径(平均半径),R0和R1分别为圆柱的内半径和外半径,L表示圆柱体长度,ht与hb表示内外夹层壳的厚度,hc为中间功能梯度软夹层的厚度,圆柱软芯夹层壳的厚度h=ht+hb+hc。在圆柱中面上建立正交坐标系(x,θ,z),其中x,θ,z分别表示圆柱的轴向、周向以及径向的坐标。在本文研究中设置为简支条件,可以假定为圆柱软芯夹层壳在轴向压力下的研究。
根据圆壳柱的经典理论可以得到以下位移公式:
| $ U = {{u}} - \frac{{{{z}}w'}}{{{R}}},V = \frac{{(R + Z)v}}{R} - \frac{{{{z}}{{{w}}^\cdot}}}{R},W = {{w}} 。$ | (1) |
式中:u(x,θ),v(x,θ),w(x,θ)分别为中曲面上一点沿着母线方向、周向以及厚度方向的位移;U,V,W分别为在剖面上任意一点在(x,θ,z)上的位移。用微分符号分别表示的无量纲坐标x/R和θ[9],分别为:
| $ R\dfrac{{\partial \left( {} \right)}}{{\partial x}} = {\left( {} \right)^\prime }, \dfrac{{\partial \left( {} \right)}}{{\partial \theta }} = {\left( {} \right)^\prime }。$ | (2) |
根据Flügge理论,可以得到应变分量:
| $ \mathop \varepsilon \nolimits_{{x}} = \frac{{U'}}{R'},\mathop \varepsilon \nolimits_\theta = \frac{{{v^\cdot} + w}}{{R + z'}},{\gamma _{x\theta }} = \frac{{V^u}}{R} + \frac{{{U^*}}}{{R + z}}。$ | (3) |
由于圆柱壳的材料是各向同性的,但是在厚度方向是非均匀的,其本构关系为:
| $ \begin{split} & {\sigma _{{x}}} = \frac{E}{{1 - {v^2}}}({\varepsilon _{{x}}} + v{\varepsilon _\theta }),{\sigma _\theta } = \frac{E}{{1 - {v^2}}}({\varepsilon _\theta } + v{\varepsilon _\theta }),\\ & {\tau _{x\theta }} = \frac{E}{{2(1 + v)}}{\gamma _{x\theta }}。\end{split} $ | (4) |
式中:E为弹性模量,v为泊松比。假定圆柱壳内外夹层为同一种均匀材料,中间软夹层为是由各个方向同性的功能梯度材料构成,在厚度方向上的弹性模量是连续分布的,其弹性模量是关于坐标z的连续函数。
功能梯度圆柱软芯夹层壳的杨氏模量和泊松比只在厚度方向上(z轴)连续变化,E=E(Z),μ=μ(Z),研究表明材料参数泊松比对于变形的影响远小于杨氏模量的影响[9]。因此假定夹层壳的泊松比为常数,夹层壳的材料性能随芯材厚度的变化成幂率变化分布。Delale与Erdogan研究得出了泊松比对功能梯度材料夹层壳弯曲性能的影响可以忽略,可给出
| $ {{{E}}_{{c}}}(z) = ({{{E}}_{{a}}} - {{{E}}_{{d}}}){(z/{{{h}}_{{c}}})^p} + {{{E}}_{{d}}},\;0 \leqslant z \leqslant {{{h}}_{{c}}}。$ | (5) |
式中:Ec表示内部功能梯度材料的弹性模量,Ea和Ed分别为内外夹层壳的弹性模量,p为材料沿厚度变化的指数。
2 数值计算与分析 2.1 正确性和有效性验证利用Ansys经典界面,通过具体案例与之进行分析对比,验证本文方法的正确性和准确性。表1给出与其他文献所得数据对比的结果,文献[9,11-12]分别采用波动法、数值逼近法以及Rayleigh-Ritz方法。壳体材料参数给出:E=2.1×1011 N/m,ρ= 7.85×103 kg/m3, nu=0.3,两端边界条件设置为简支。
|
|
表 1 两端简支下圆柱壳固有频率对比验证 Tab.1 Comparison and verification of natural frequencies of cylindrical shells simply supported at both ends |
功率指标p对功能梯度圆柱软芯夹层壳的固有频率影响如图2所示。可以发现,对于给定的几何性质,幂指数p越大,其固有频率值逐渐减小。如果p大于某一特定值,则自由振动频率值几乎相等(p=3)。

|
图 2 p值对固有频率的影响 Fig. 2 The effect of p value on the natural frequency |
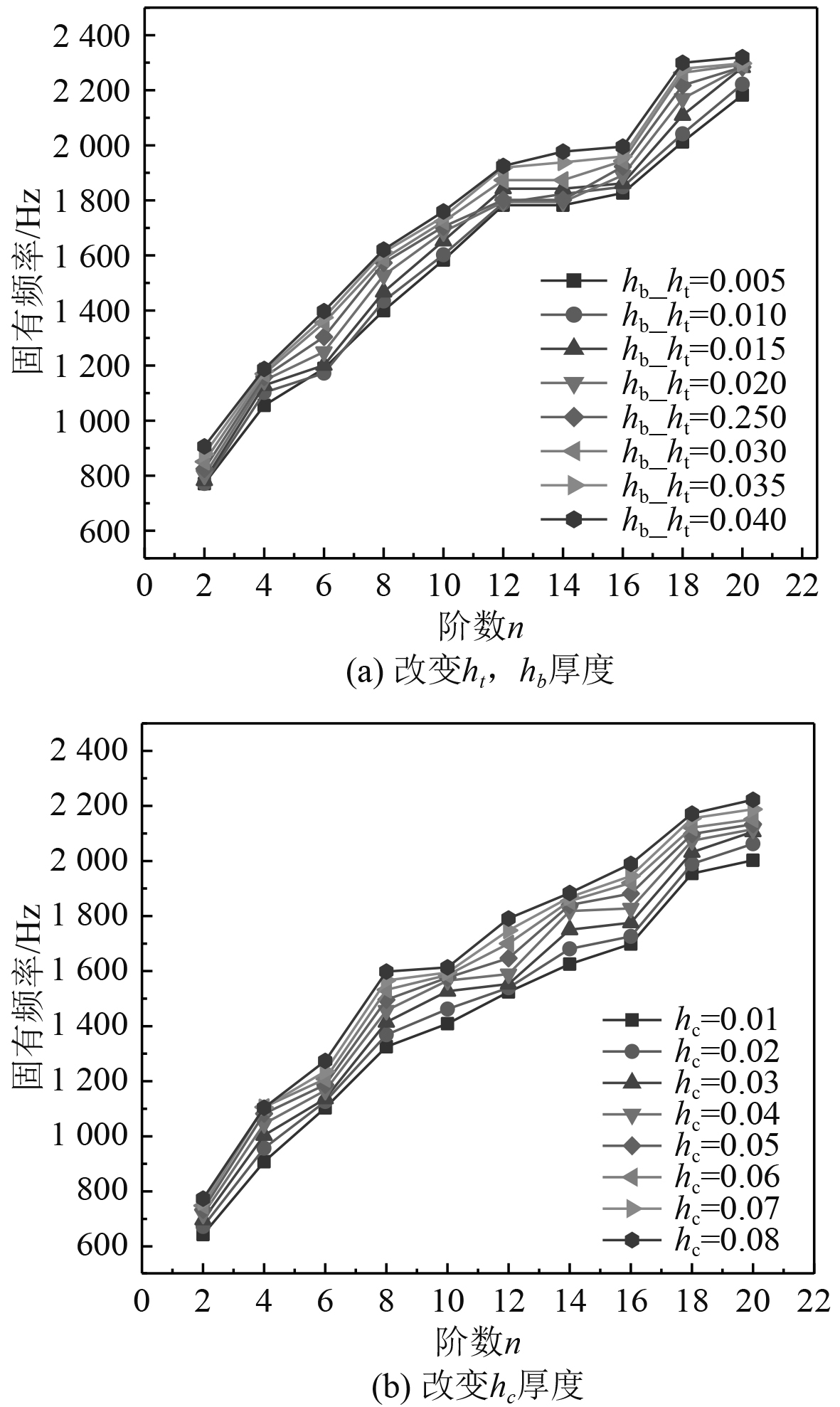
如图3(a)所示,当保持p值不变时,圆柱体的固有频率随着内外层夹层壳的厚度增大而增大。如图3(b)所示,当保持p值不变时,增大内层芯材的厚度,圆柱体的固有频率也随之增大。
|
图 3 内外夹壳与芯材厚度对固有频率的影响 Fig. 3 Influence of thickness of inner and outer splint and core material on natural frequency |
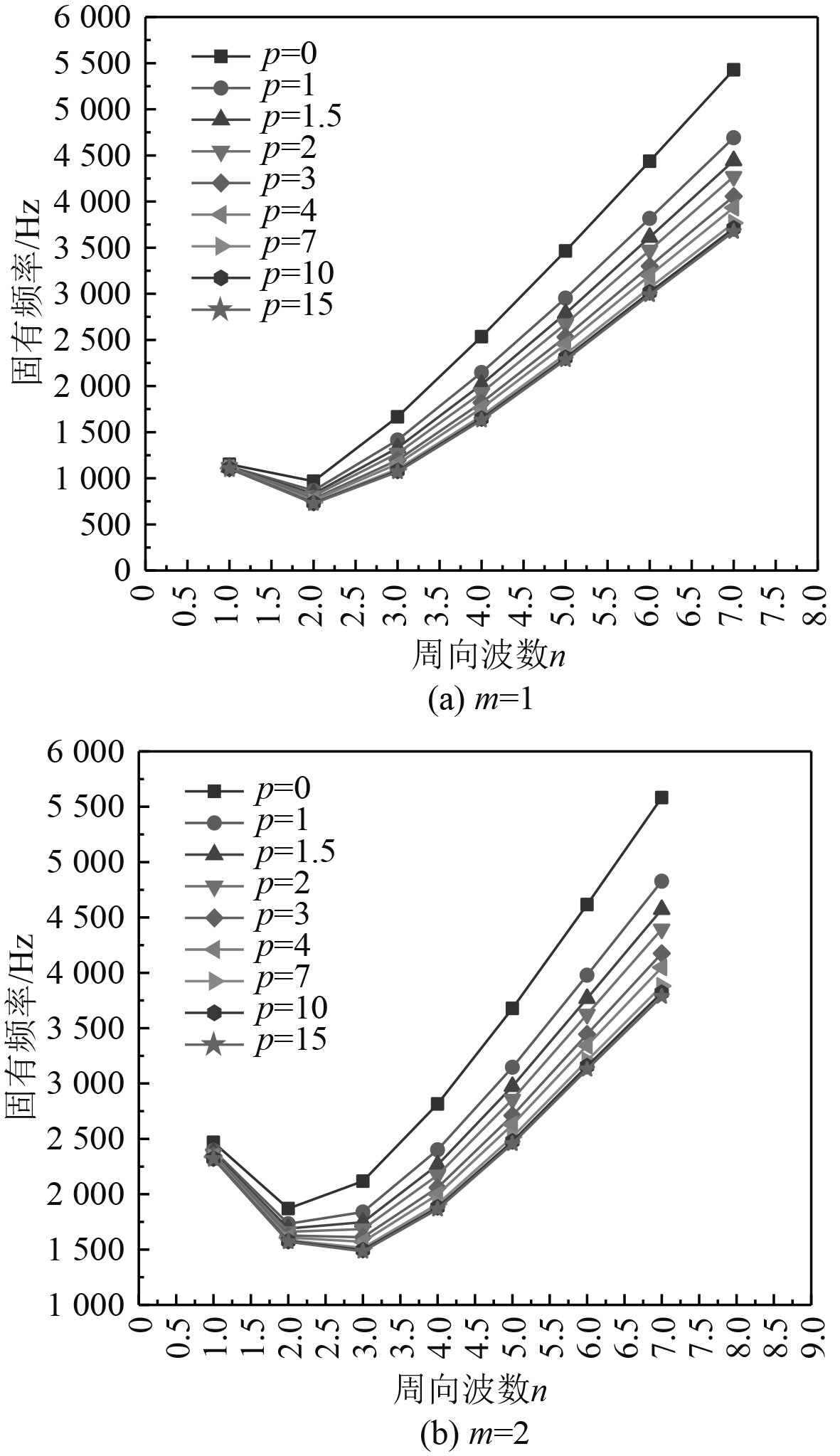
图4为轴向半波数m=1,2时固有频率变化规律,其中周向波数n取1~7,可以看出其云图固有频率随着p值的增大而逐渐减小,功率指数p值偏大,就会导致较小的自由振动值,在给定几何参数和模态数的情况下,幂律分布的幂指数p的增大会导致频率衰减率的减小。当p值达到一定程度时,几乎保持不变(p=10)
|
图 4 轴向半波数m=1,2云图固有频率变化曲线 Fig. 4 Natural frequency variation curves of nephograms with axial half wave number m=1, 2 |
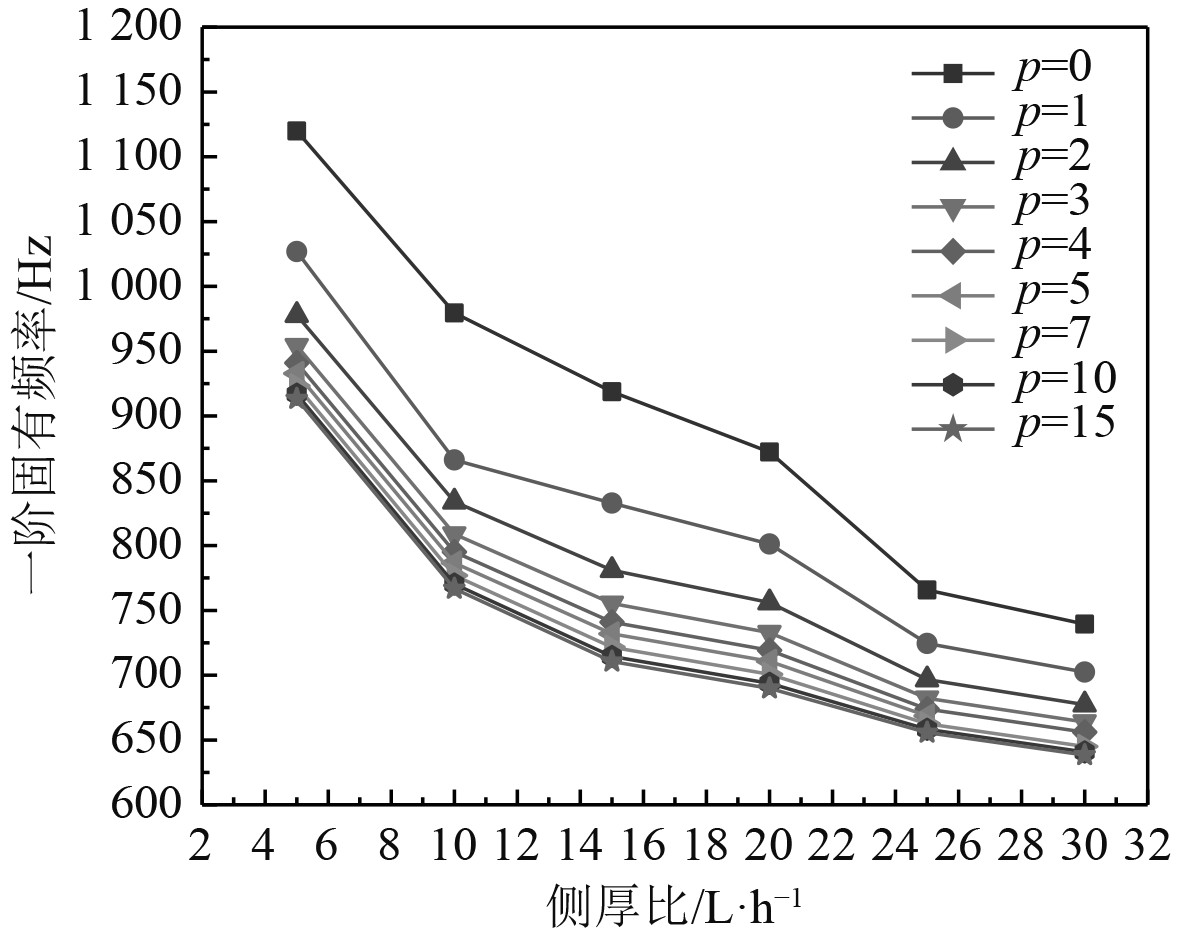
图5为在不同L/h值下圆柱夹层结构的一阶固有频率变化。可以看出,随着L/h的不断增大,其一阶固有频率不断减少,固有频率衰减率逐渐减小。比较不同功率指数p下一阶固有频率的变化,可以发现随着功率指数p值的不断增大,固有频率频率随之不断减小。当p值增大到一定程度时,夹层壳圆柱体的固有频率几乎保持一致(p=5)。
|
图 5 不同侧厚比对固有频率的影响 Fig. 5 Influence of different side thickness ratios on natural frequency |
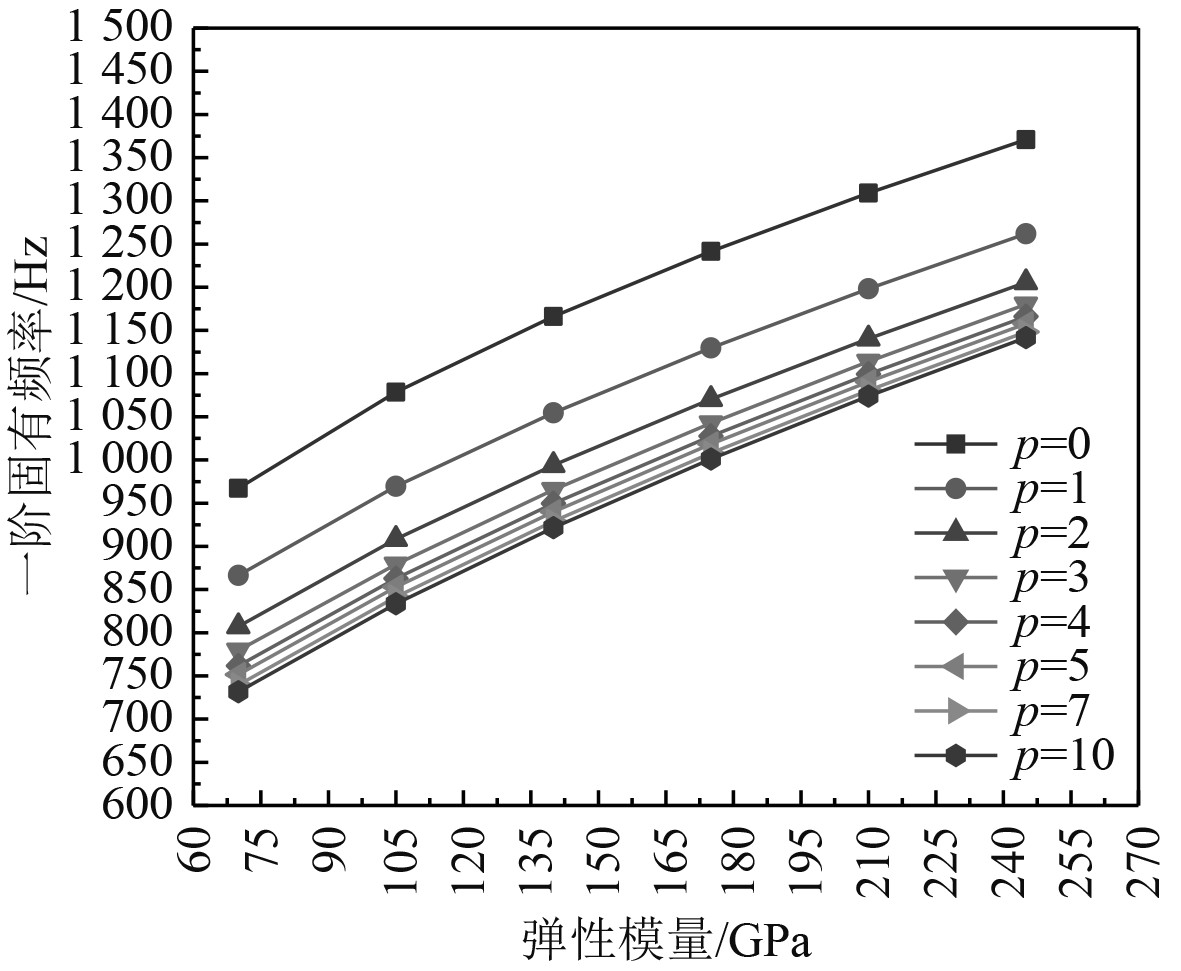
改变圆柱内外层夹层壳的弹性模量,在不同的弹性模量下,圆柱体的一阶固有频率的变化如图6所示。可以发现,随着弹性模量的不断增大,一阶固有频率几乎呈线性变化。通过比较不同功率指数p下的一阶固有频率,可以发现固有频率随着功率指数p的增大而减小,并且随着p值的不断增大,一阶固有频率逐渐趋于固定数值。
|
图 6 弹性模量对固有频率的影响 Fig. 6 Effect of elastic modulus on natural frequency |
改变不同的芯材密度,圆柱夹层壳的一阶固有频率的变化曲线如图7所示。可以得到当芯材密度不断增加时,一阶固有频率呈现线性变化,不断降低。通过比较不同的功率指数p值,当圆柱夹层壳密度不变时,其固有频率随着功率指数的增大而减少,并且当p值增大到一定程度时,固有频率几乎保持不变。

|
图 7 芯材密度对固有频率的影响 Fig. 7 Influence of core density on natural frequency |
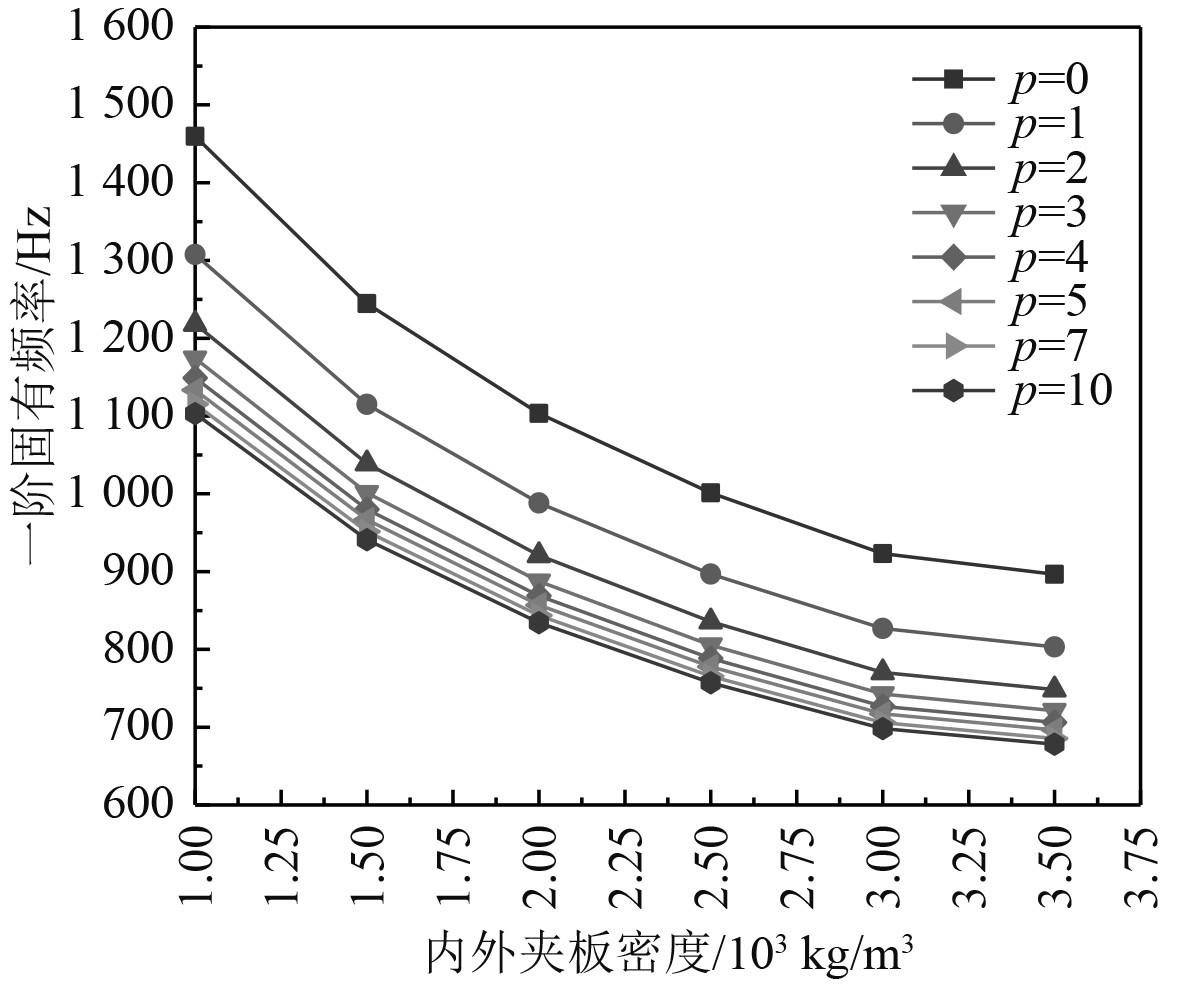
改变内外夹层壳的密度,圆柱夹层壳的一阶固有频率变化如图8所示。如同改变芯材密度一样,当不断增加内外夹层板的密度时,其固有频率不断减少,并且其衰减指数不断下降。当增大功率指数p时,固有频率也随之降低。与改变芯材密度相同,当p值增大到一定程度时,其固有频率几乎保持不变。
|
图 8 内外加层壳密度对固有频率的影响 Fig. 8 Influence of density of inner and outer laminates on natural frequency |
本文对功能梯度圆柱软芯夹层壳模型进行振动特性分析。对功能梯度圆柱软芯夹层壳结构进行仿真计算,得到其振动特性规律以及材料性能对结构整体的影响。研究具有各种材料和几何参数的FGM圆柱软芯夹层壳的自由振动,可以得出以下结论:
1)圆柱体的固有频率随着功率指数p的增大而减小;当功率指数p不变时,改变内外层夹层壳以及芯材厚度,圆柱体的固有频率随着厚度的增大而增大,并且当增大到一定程度时,固有频率趋于稳定。
2)其结构一阶二阶振型固有频率随着p值的增大而减小,并且逐步趋于稳定。
3)不断增大L/h的比值,其固有频率随着功率指数p值的增大而减小,并且当p值增大到一定程度时,固有频率值几乎不变。
4)增大内外软夹层壳的弹性模量,其固有频率值不断增加,但随着功率指数p的增大,固有频率逐渐减小。增大内外软夹层壳与芯材的密度,结构的固有频率呈指数下降,并且当p值增大时,固有频率也随之减小。
| [1] |
LAM K Y, LOY C T. Analysis of rotating laminated cylindrical shells by different thin shell theories[J]. Journal of Sound and Vibration, 1995, 186(1): 23-35. DOI:10.1006/jsvi.1995.0431 |
| [2] |
张宇民, 赫晓东, 韩杰才. 梯度功能材料[J]. 宇航材料工艺, 1998(5): 5-10+56. |
| [3] |
LOY C T, LAM K Y, REDDY J N. Vibration of functionally graded cylindrical shells[J]. International Journal of Mechanical Sciences, 1999, 41(3).
|
| [4] |
李学斌. 悬臂正交各向异性圆柱壳的自由振动分析[J]. 舰船科学技术, 2008, 30(1): 41-44. LI Xue-bin. Free vibration of cantilever orthotropic circular cylindrical shell[J]. Ship Science and Technology, 2008, 30(1): 41-44. |
| [5] |
陈金晓, 梁斌. 弹性边界条件下的功能梯度圆柱壳振动特性研究[J]. 船舶力学, 2017, 21(7): 880-887. CHEN Jin-xiao, LIANG Bin. Study on the vibration of functionally graded material cylindrical shells under elastic boundary conditions[J]. Journal of Ship Mechanics, 2017, 21(7): 880-887. |
| [6] |
杜长城, 李映辉. 功能梯度薄壁圆柱壳的自由振动[J]. 动力学与控制学报, 2010, 8(3): 219-223. DU Chang-cheng, LI Ying-hui. Free vibration of functionally graded cylindrical thin shells[J]. Journal of Dynamics and Control, 2010, 8(3): 219-223. |
| [7] |
梁斌, 李戎, 张伟, 等. 功能梯度材料圆柱壳的振动特性研究[J]. 船舶力学, 2011, 15(Z1): 109-117. LIANG Bin, LI Rong, ZHANG Wei, et al. Vibration characteristics of functionally graded materials cylindrical shells[J]. Journal of Ship Mechanics, 2011, 15(Z1): 109-117. |
| [8] |
李世荣, 王爽. 夹层FGM圆柱壳在扭转载荷作用下的弹性稳定性[J]. 力学学报, 2010, 42(6): 1172-1179. LI Shi-rong, WANG Shuang. Elastic stability of circular cylindrical shells with FGMs layers under end torsion force[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(6): 1172-1179. |
| [9] |
杨萌, 李戎, 梁斌. 基于Flügge理论的功能梯度圆柱壳自由振动响应均匀化转换计算方法[J]. 振动与冲击, 2020, 39(24): 63-68+90. YANG Meng, LI rong, LIANG Bin. A homogenization transformation method for free vibration response of functionally graded cylindrical shells based on the Flügge theory[J]. Journal of Viberation and Shock, 2020, 39(24): 63-68+90. |
| [10] |
RENCHUAN Y, et al. Bending and free vibration analysis of sandwich plates with functionally graded soft core, using the new refined higher-order analysis model[J]. Journal of Sandwich Structures and Materials, 2021.
|
 2022, Vol. 44
2022, Vol. 44
