2. 河南省水下智能装备重点实验室,河南 郑州 450015;
3. 海军装备部驻郑州地区军事代表室,河南 郑州 450015
2. Henan Key Laboratory of Underwater Intelligent Equipment, Zhengzhou 450015, China;
3. The Military Office of PLA Navy in Zhengzhou Area, Zhengzhou 450015, China
负载水下发射时,发射平台一般都具有一定的运行速度,以维持平台的稳定性。负载弹射出管过程中横向流使负载在发射管内发生偏移,布置于发射筒内筒壁的减振垫,为负载提供合适的约束力,发挥适配、支撑、导向等作用,使负载以良好的姿态出管,从而降低水下发射载荷,在此过程中,弹体所受到的横向力引起发射摩擦力对内弹道性能产生重要影响。
本文通过负载出管过程中的横向动力学计算模型,研究特定发射条件下,不同方法计算的摩擦力的一致性,并分析横向力作用对发射负载出管运动参数的影响,对横向力引起摩擦力的计算和发射系统的设计具有指导意义。
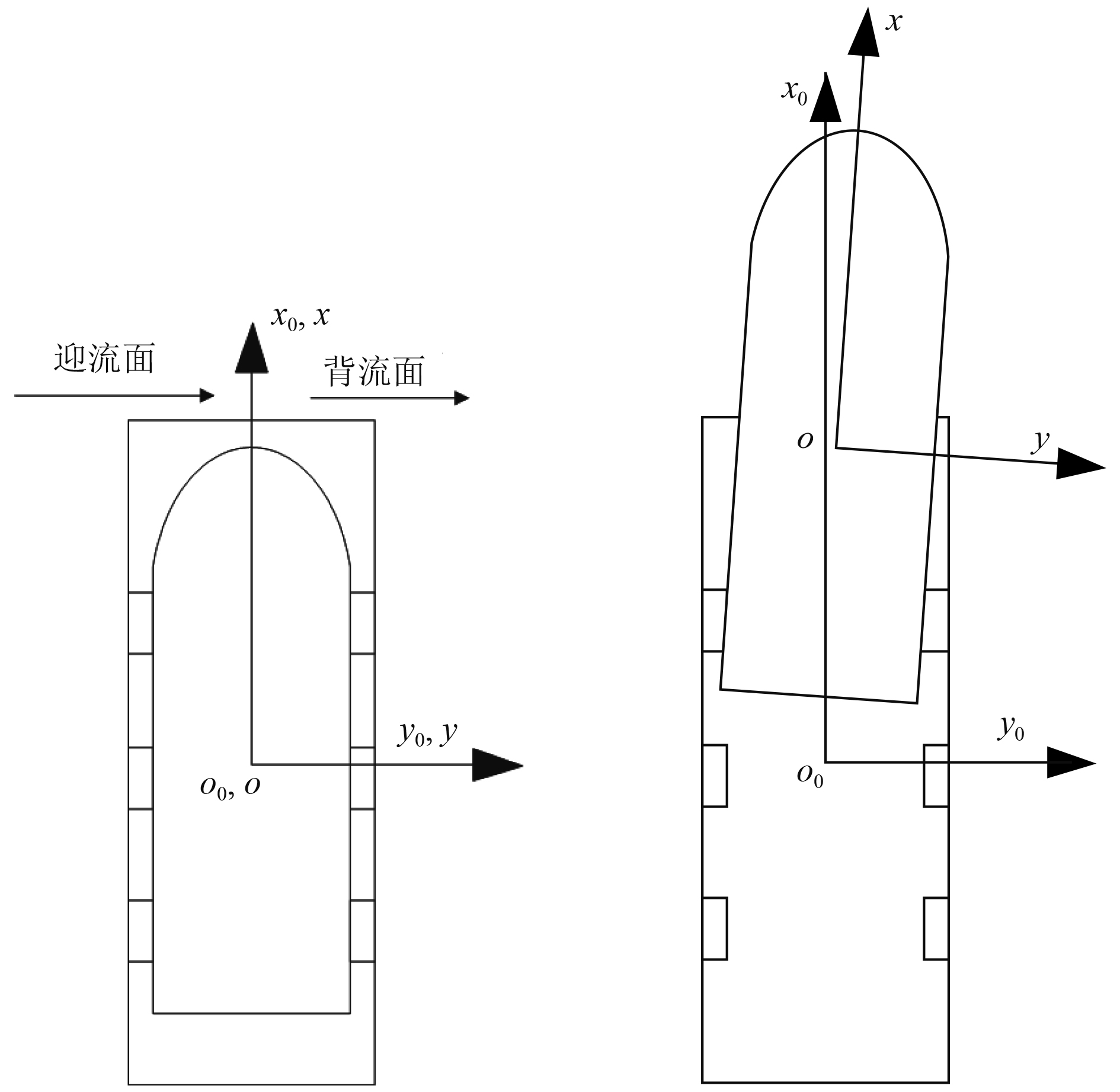
1 负载出筒过程中横向动力学计算 1.1 横向力作用下负载运动模型为了研究负载发射时横向流的影响,取负载质心为坐标系原点,假设负载与发射管的结构为径向对称,负载和发射管为刚体,建立负载三自由度平面运动模型如图1所示。
|
图 1 负载管内运动示意图 Fig. 1 The representation of the load movement in the pipe |
| $ {\rm{d}}Q = {\rm{d}}U + P{\rm{d}}V,$ | (1) |
| $ P = \sum {\frac{{{m_i} \cdot {R_i}{T_i}}}{{{V_i}}}} ,$ | (2) |
| $ M\frac{{{\rm{d}}{\upsilon _X}}}{{{\rm{d}}t}} = {F_T} - {F_Z},$ | (3) |
| $ (M + {\lambda _{22}})\frac{{{\rm{d}}{\upsilon _Y}}}{{{\rm{d}}t}} = {F_Y} - {F_Y}_S - {\omega _Z}M{\upsilon _X} - {\lambda _{26}}\frac{{{\rm{d}}{\omega _Z}}}{{{\rm{d}}t}},$ | (4) |
| $ ({J_Z} + {\lambda _{66}})\frac{{{\rm{d}}{\omega _Z}}}{{{\rm{d}}t}} = {M_Z} - {M_{PY}} - {\lambda _{26}}\frac{{{\rm{d}}{\upsilon _Y}}}{{{\rm{d}}t}},$ | (5) |
| ${{\rm{d}}\vartheta }/{{\rm{d}}t}$ | (6) |
| $ {\raise0.7ex\hbox{${{\rm{d}}{X_0}}$} \mathord{\left/ {\vphantom {{{\rm{d}}{X_0}} {{\rm{d}}t}}}\right.} \lower0.7ex\hbox{${{\rm{d}}t}$}} = {\upsilon _X}\cos \vartheta - {\upsilon _Y}\sin \vartheta ,$ | (7) |
| $ {\raise0.7ex\hbox{${{\rm{d}}{Y_0}}$} \mathord{\left/ {\vphantom {{{\rm{d}}{Y_0}} {{\rm{d}}t}}}\right.} \lower0.7ex\hbox{${{\rm{d}}t}$}} = {\upsilon _X}\sin \vartheta + {\upsilon _Y}\cos \vartheta 。$ | (8) |
式中:
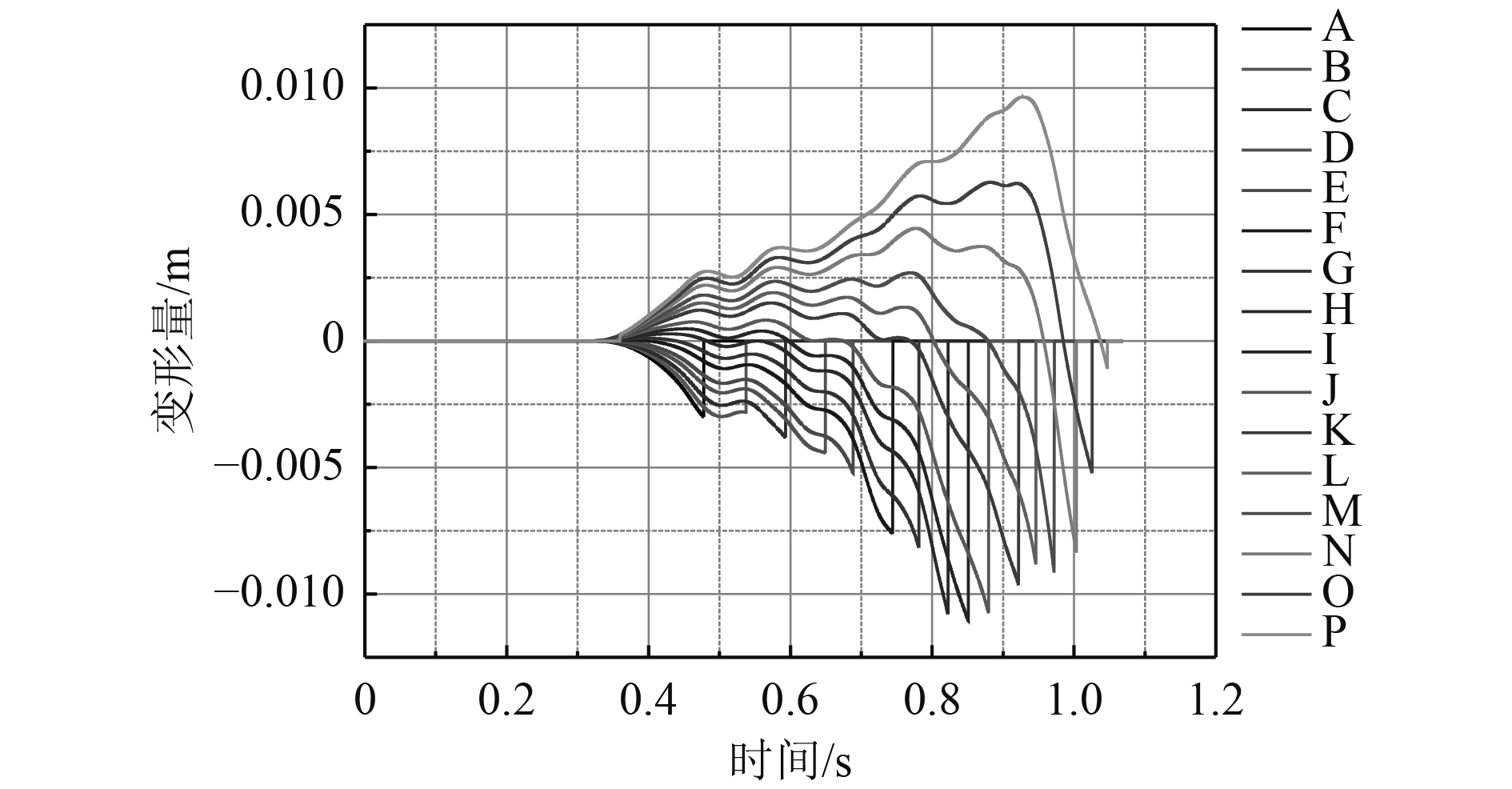
采用横向动力学计算模型,横向力影响下的负载运动参数进行计算,获得减震垫的变形量,在特定条件下各圈减震垫变形计算结果如图2所示。由于上述模型为平面模型,获取的减震垫变形量为迎流方向的减震垫变形。
|
图 2 各圈减震垫的变形 Fig. 2 The deformation of the damping pad |
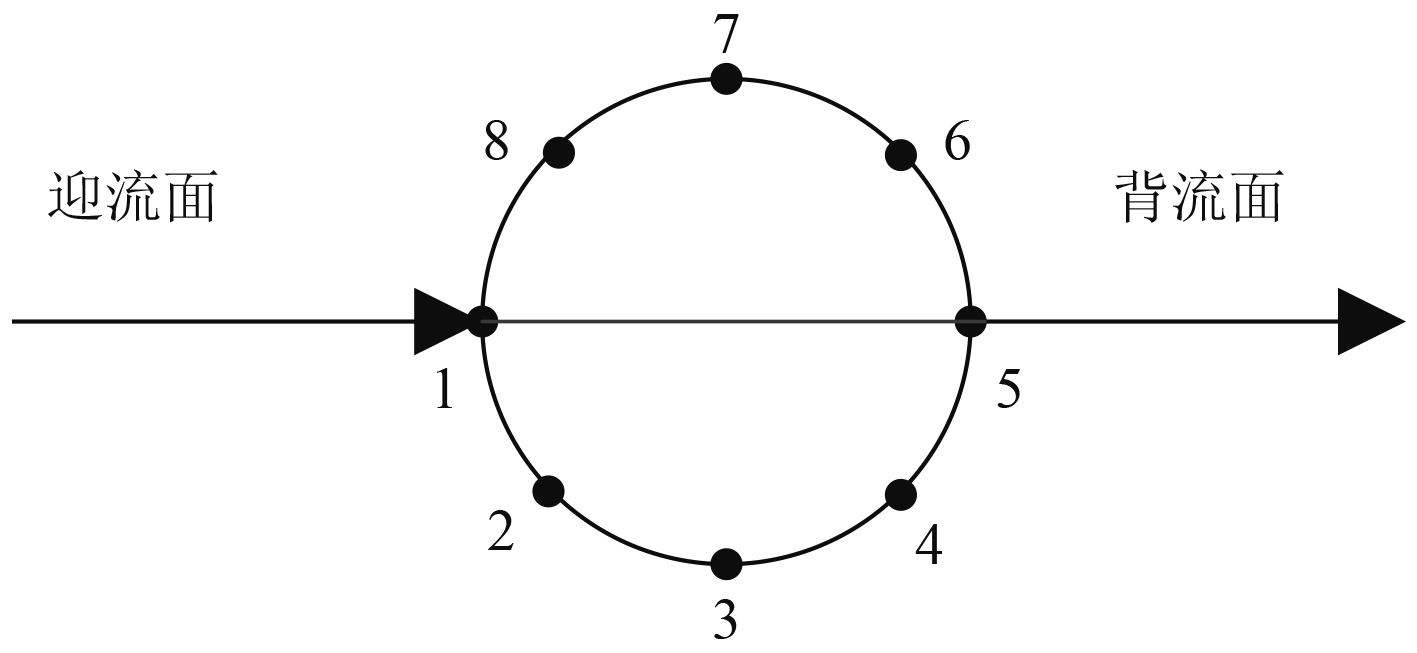
由于横向流计算模型为平面模型,仅获取了迎流方向减震垫的变形,而周向减震垫的变形亦会对模型运动产生摩擦阻力,假设横向流引起减震垫的压缩量沿圆周呈余弦分布规律,减震垫布置示意图如图3所示。
|
图 3 每圈减震垫的布局位置图 Fig. 3 The layout of the damping pad |
余弦假设分布规律的公式为:
| $ z = \frac{{{z_1} + {z_5}}}{2} + \frac{{{z_1} - {z_5}}}{2}\cos \theta 。$ | (9) |
其中:
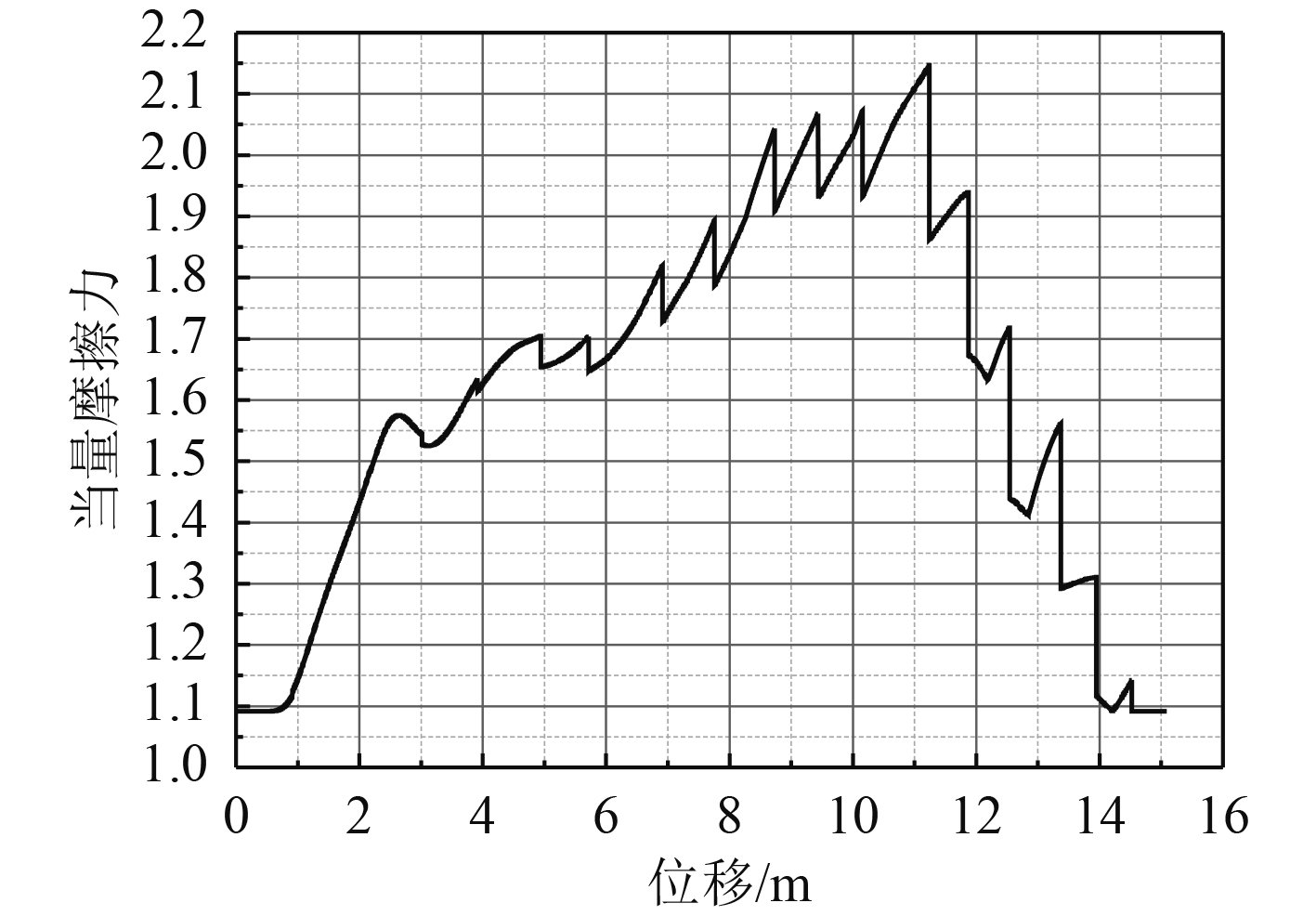
在平台移动5 kn的初始条件下,采用横向力平面模型计算减震垫1和减震垫5的压缩量,按照上述余弦分布规律,计算出圆周各减震垫的压缩量,根据减震垫刚度数据获得负载出管过程中的发射摩擦力,如图4所示。
|
图 4 减震垫发射过程中对负载产生的摩擦力 Fig. 4 The friction originated by the compression of damping pad |
依据平面横向流计算模型获取的迎流方向减震垫的变形数据,假设发射负载和发射筒为刚体,依照几何关系,计算各圈各块减振垫的压缩量;依据减振垫刚度特性,计算得出筒过程中每圈中每一块减振垫压缩产生摩擦力随时间变化历程,每块减震垫产生摩擦力的总和为负载出筒过程中所受摩擦力变化特征。
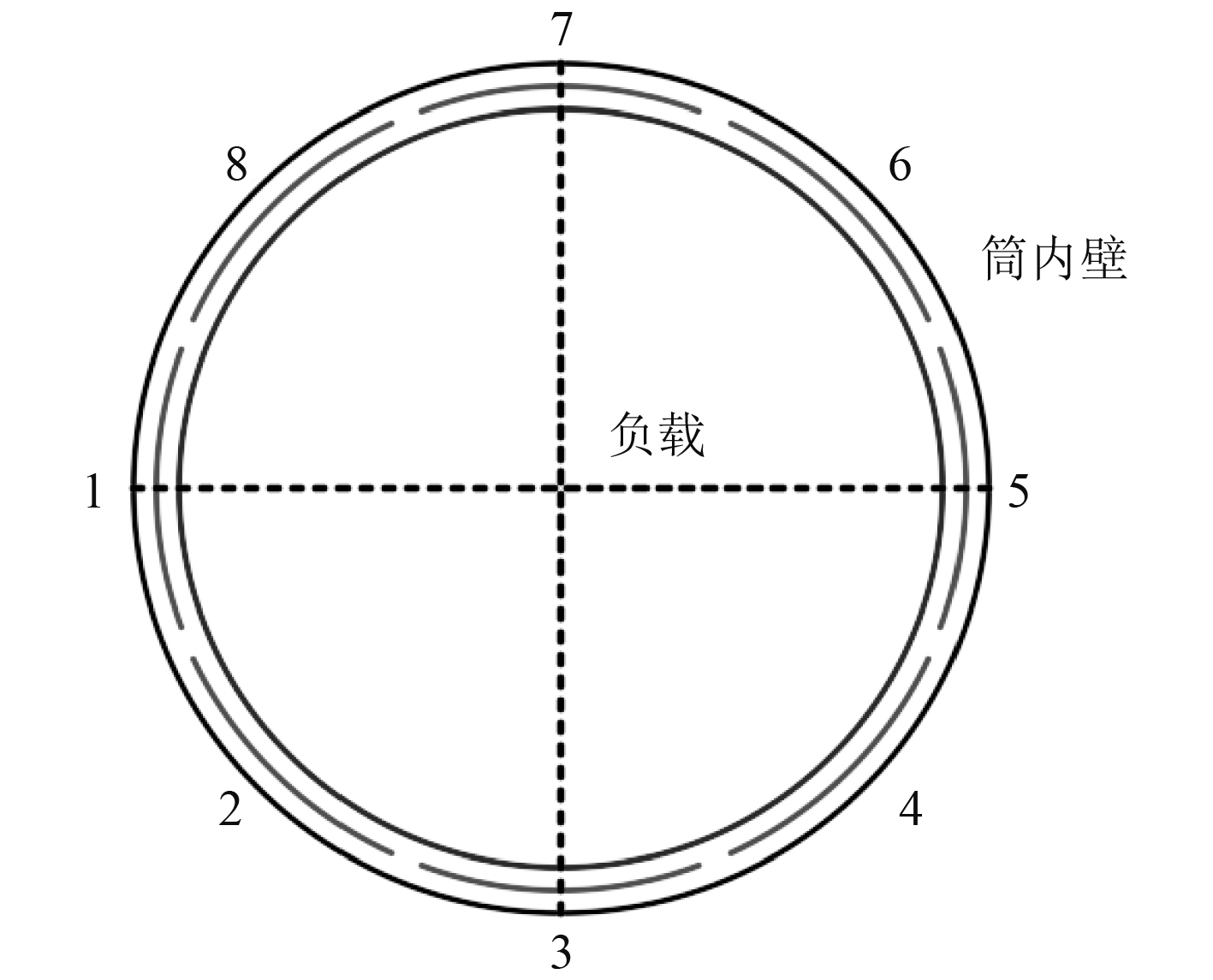
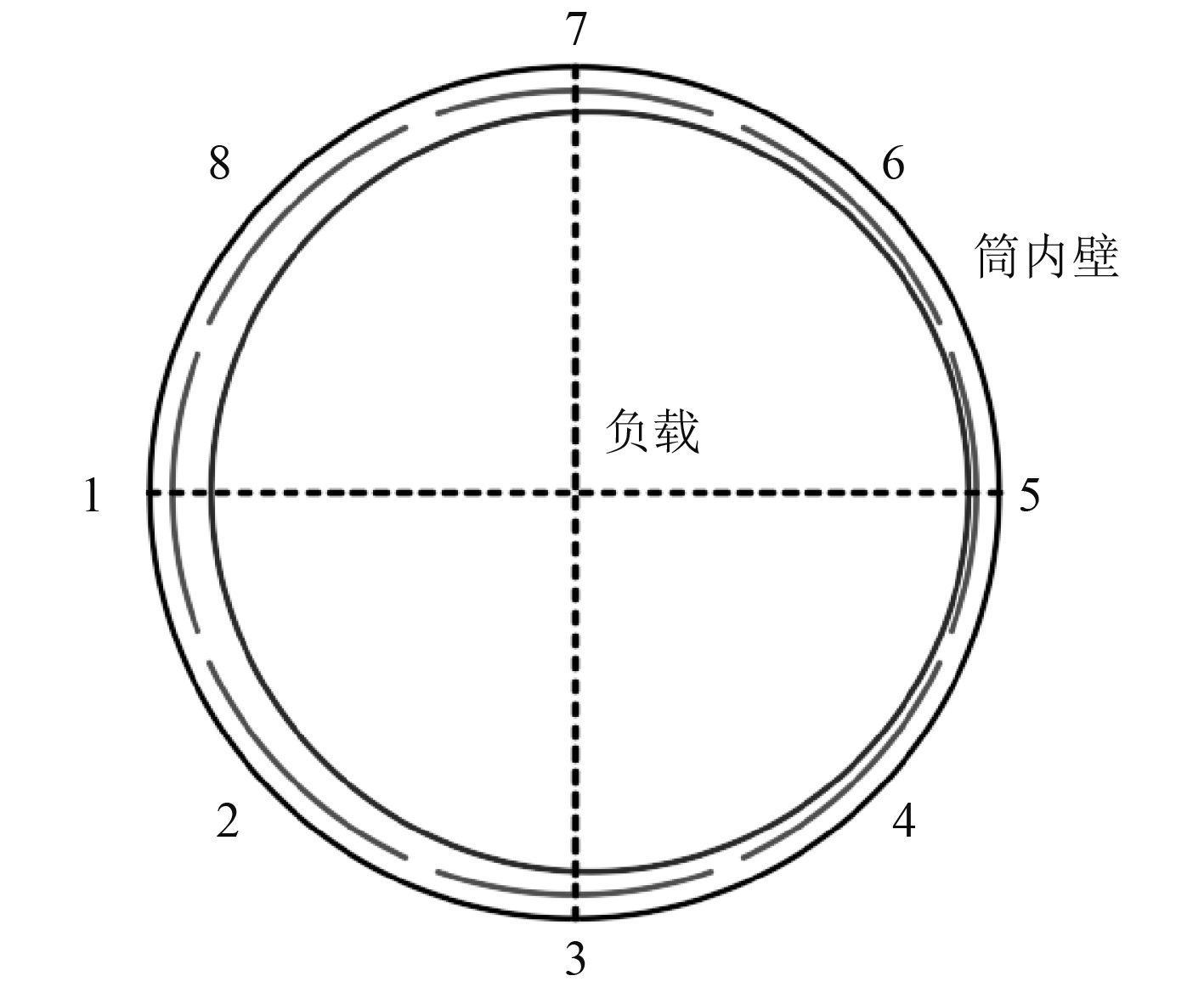
发射前负载与发射筒质心处截面如图5所示。图6给出了平台移动5 kn,负载运动5 m时,负载与发射筒质心处截面图。
|
图 5 发射前负载与发射筒质心处截面 Fig. 5 The transverse section of the load and the pipe before launch |
|
图 6 5 m行程时负载与发射筒质心处截面 Fig. 6 The transverse section of the load and the pipe when travel 5 m |
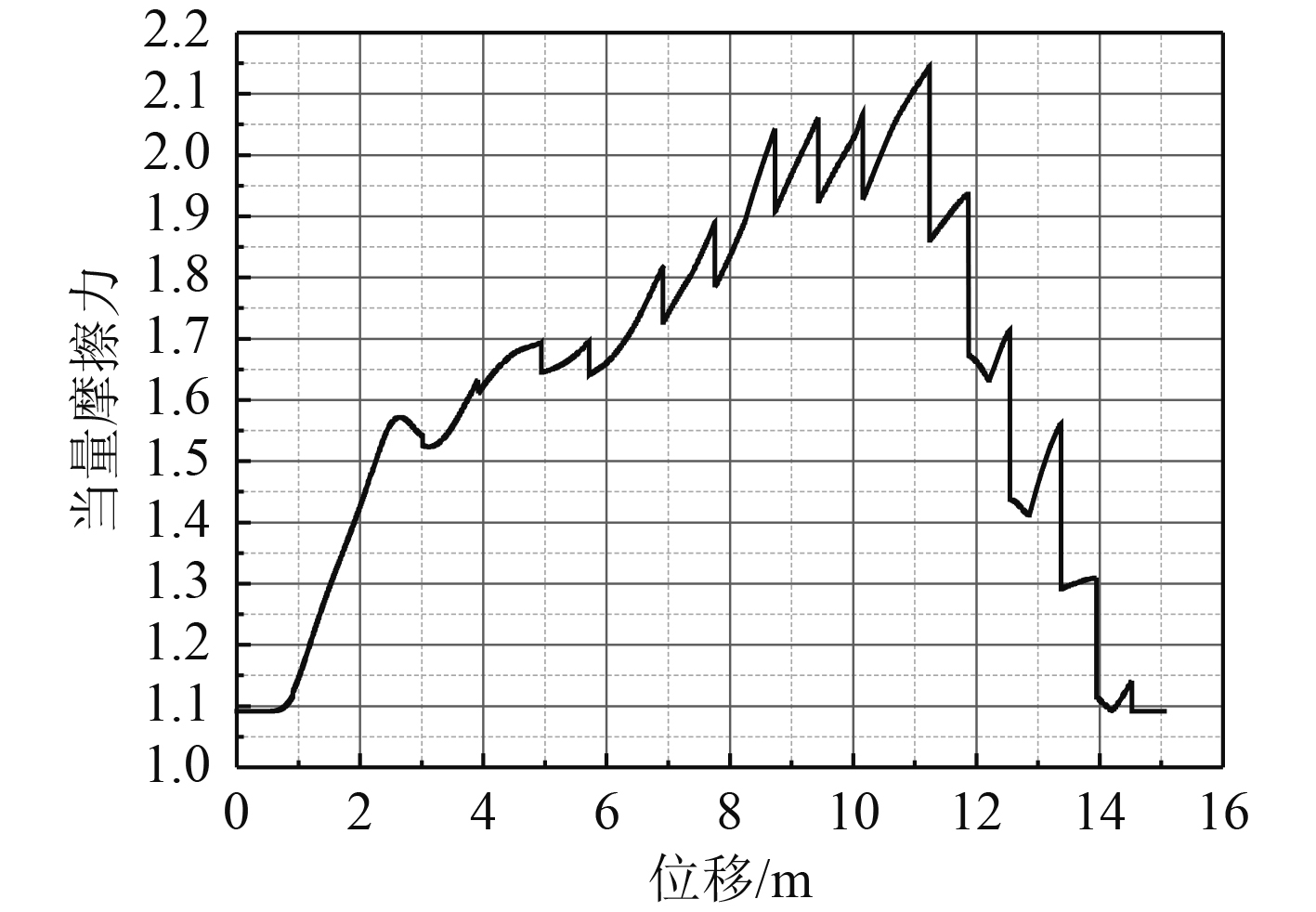
依据计算的各圈各块减振垫的压缩量和其刚度特性,计算得出筒过程中每圈中每一块减振垫压缩产生摩擦力随时间变化历程,每块减震垫产生摩擦力的总和为负载出筒过程中所受摩擦力,获得负载出筒过程中的发射摩擦力,如图7所示。
|
图 7 减震垫发射过程中对负载产生的摩擦力 Fig. 7 The friction originated by the compression of damping pad |
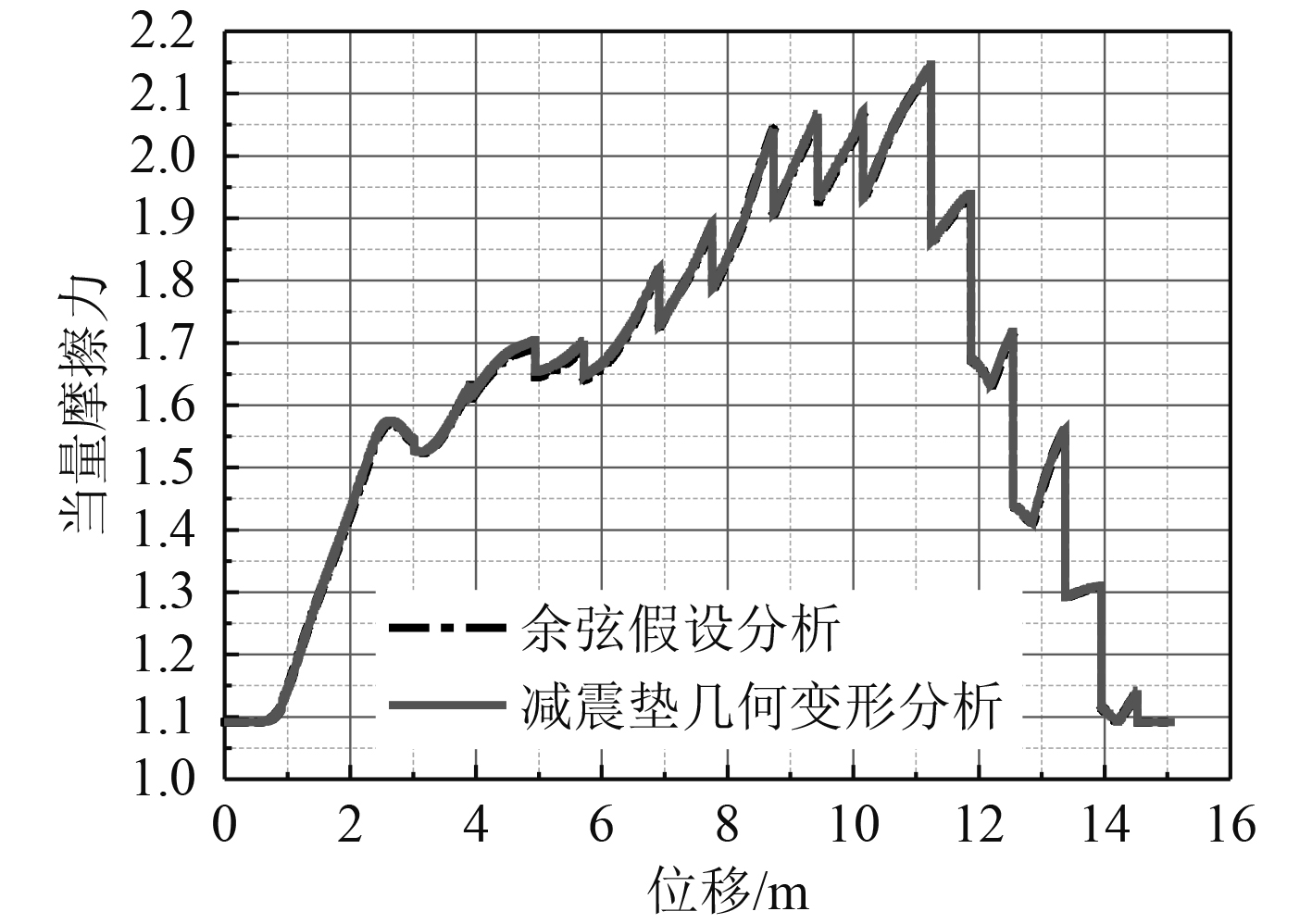
采用横向动力学平面计算模型,对横向力影响下的负载运动参数进行计算,获得迎流方向上减震垫的变形量;通过余弦假设和减震垫周向几何变形关系2种方法计算负载在筒内运动过程中横向力引起的摩擦力,2种计算方法计算结果曲线对比见图8。可以看出,2种方法计算摩擦力一致性较好,表明减震垫周向变形余弦假设合理可行。
|
图 8 不同方法计算的摩擦力对比曲线 Fig. 8 The correlation curve of the friction calculated by different methods |
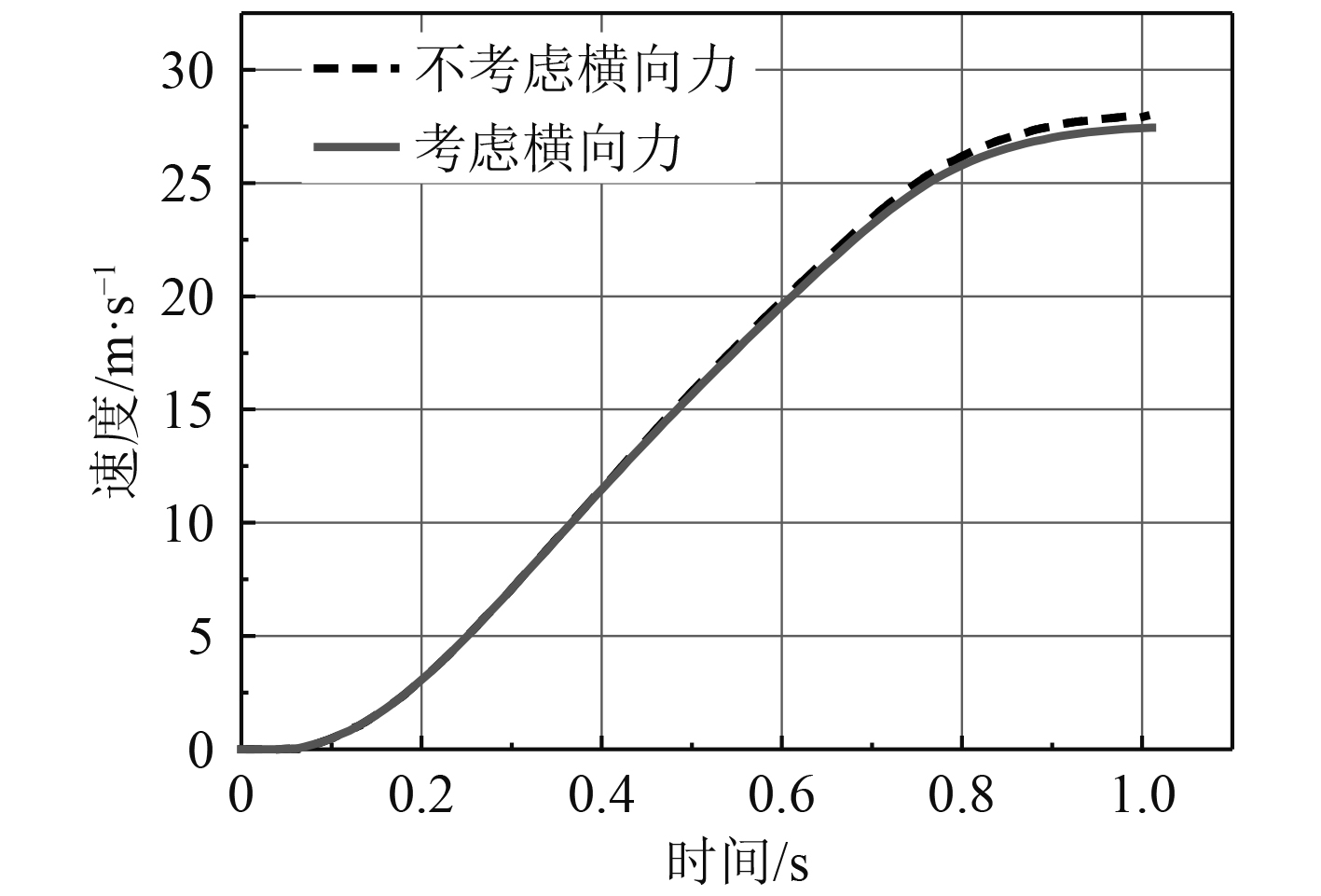
采用负载运动模型开展上述发射摩擦力对发射内弹道性能的影响研究,在某特定的工况下,将不考虑横向力和考虑横向力的内弹道计算结果进行对比,计算结果对比情况见表1,计算曲线对比见图9~图11。
|
|
表 1 内弹道计算结果对比表 Tab.1 The result of the interior ballistics calculation |
|
图 9 负载运动速度随时间变化曲线图 Fig. 9 The velocity-time curves |
|
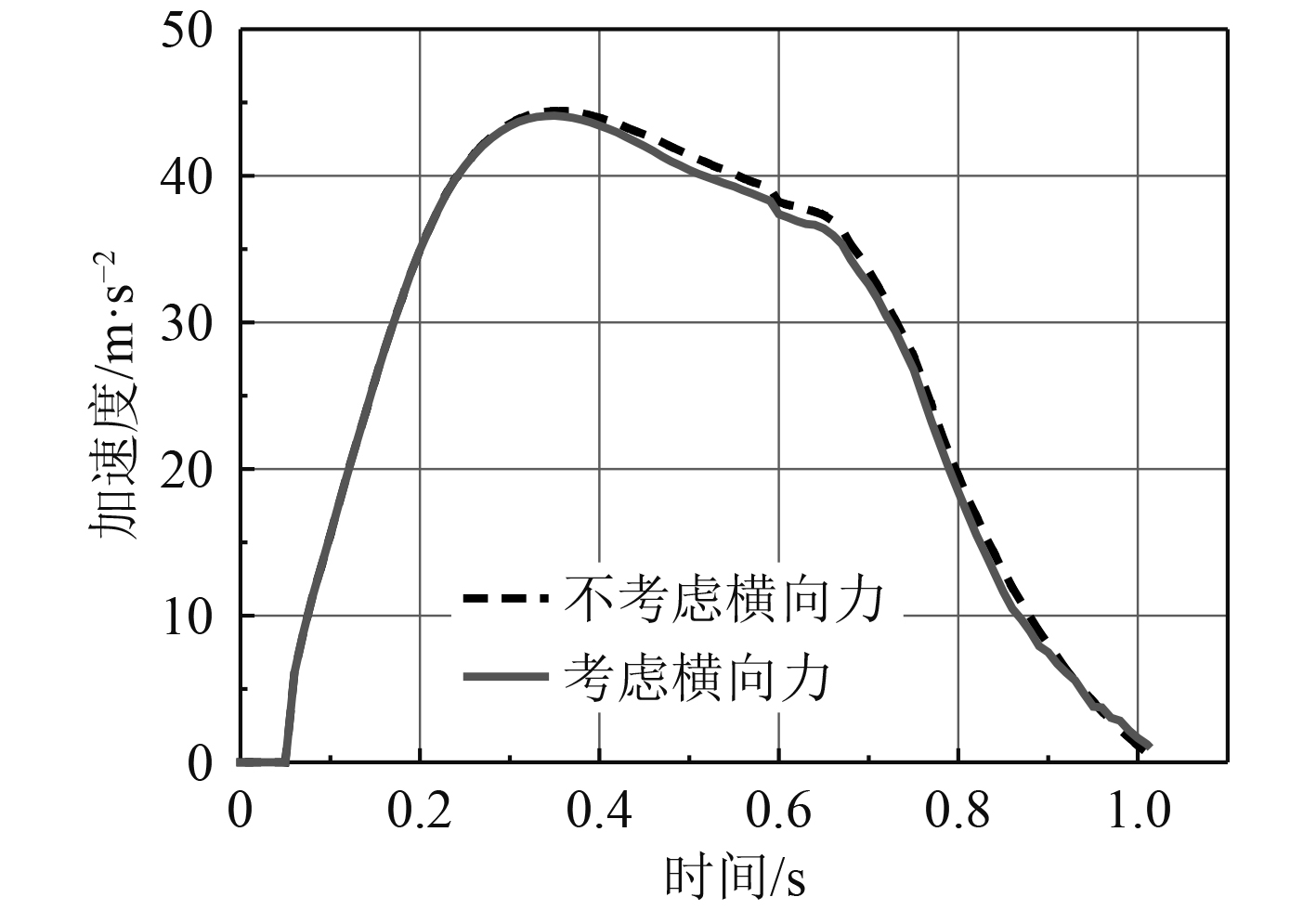
图 10 负载运动加速度随时间变化曲线图 Fig. 10 The acceleration-time curves |
|
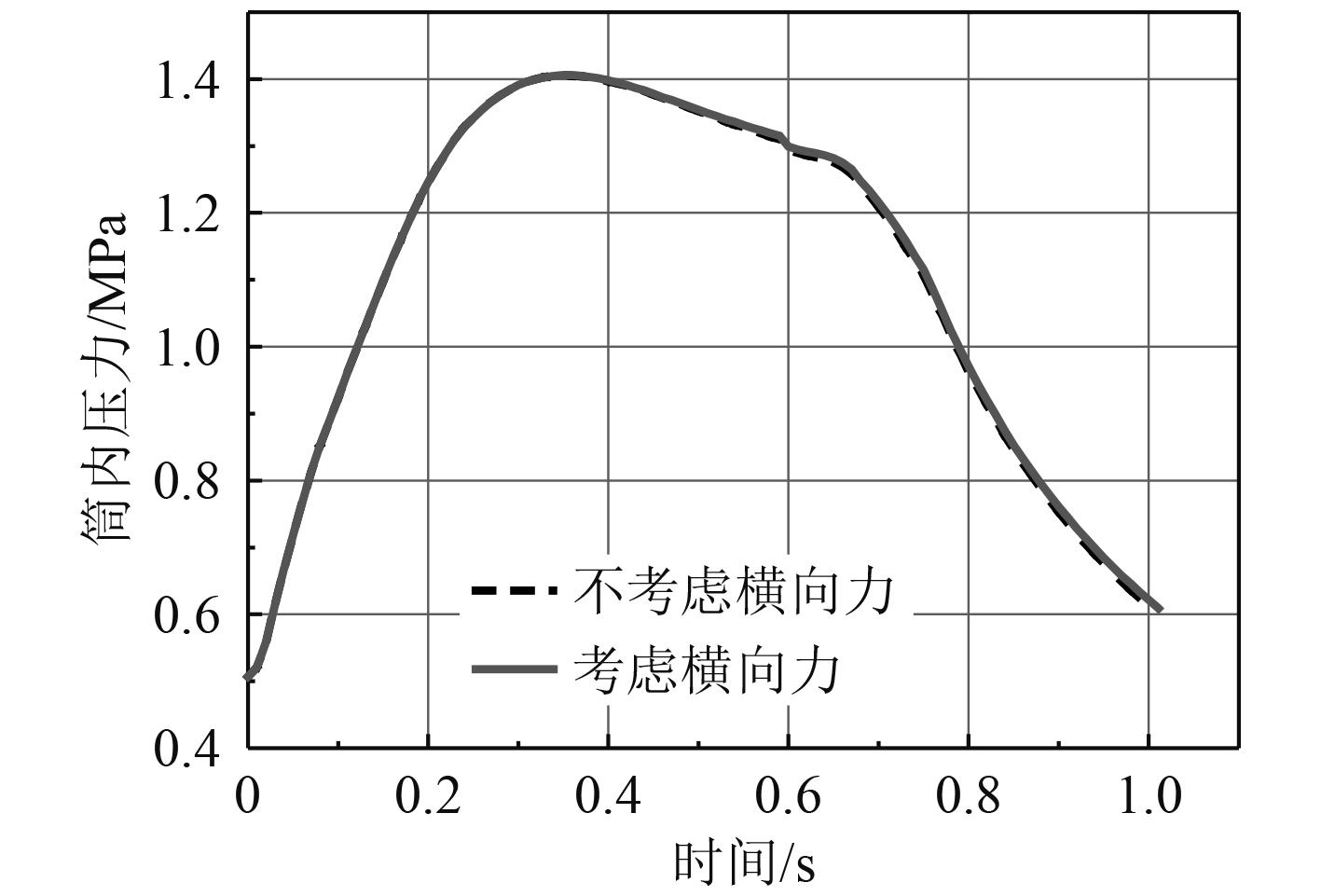
图 11 发射管内压力随时间变化曲线图 Fig. 11 The pressure-time curves |
计算结果表明,在某特定的工况下,负载管内运动弹道计算时考虑横向力影响和不考虑横向力影响对内弹道性能有一定的影响,其中负载出管速度影响约1.82%,负载运动最大加速度影响约0.66%,对发射管内最大压力基本没有影响。
4 结 语建立横向流影响下的负载水下发射出管弹道平面计算模型,采用余弦假设和周向减震垫几何变形2种方法对5 kn速度下负载出管过程中减震垫压缩量进行计算,通过对计算结果的对比分析验证了余弦假设的可行性。基于减震垫变形计算获取的负载发射摩擦力,在出管弹道计算时针对考虑横向力和不考虑横向力进行对比分析。结果表明,考虑横向力影响后对出管速度有一定的影响,对负载运动最大加速度和管内最大压力影响较小。
| [1] |
李咸海, 王俊杰. 潜地导弹发射动力系统[M]. 哈尔滨: 哈尔滨工程大学出版社, 2000.
|
| [2] |
赵险峰, 王俊杰. 潜地弹道导弹发射系统内弹道学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2000.
|
| [3] |
赵世平, 蔡体敏. 横向流对潜艇垂直发射导弹的影响, 船舶力学, 2006, (4): 33-37.
|
| [4] |
卢丙举, 朱珠. 潜空导弹垂直发射出筒适配器受载变形仿真研究[J]. 舰船科学技术, 2017, 39(9): 139-142.
|
| [5] |
朱珠, 卢丙举. 潜空导弹垂直发射出筒横向载荷特性, 应用力学学报, 2018, 35(3): 452-457+681.
|
| [6] |
尚书聪, 孙建中, 秦丽萍. 潜载导弹水下发射出筒横向动力学特性研究, 振动与冲击, 2012, 31(23): 82-86.
|
| [7] |
姚保太, 都军民. 一种航行体水弹道的数值仿真与试验研究, 舰船科学技术, 2015, 37(7): 104-107+127.
|
| [8] |
赵世平, 李江, 何国强, 等. 固体燃气发生器动力模拟水下发射试验研究[J] , 固体火箭技术, 2006(1): 5-8.
|
| [9] |
肖虎斌, 赵世平. 燃气蒸汽式发射动力装置复杂内流场数值模拟[J] , 固体火箭技术, 2009, 32(4): 392-395.
|
| [10] |
沈国. 蒸汽弹射系统内弹道数值模拟与参数设计[D]. 南京: 南京理工大学, 2011.
|
| [11] |
吕翔, 李江, 陈剑, 等. 变深度水下发射系统内弹道实验研究[J]. 固体火箭技术, 2012, 35(1): 24-28.
|
 2022, Vol. 44
2022, Vol. 44
