起锚机作为船舶主甲板上锚固和系泊的关键机械装置,主要由支架、离合器、液压泵站等构成。工作原理是通过电动机工作使传动齿轮减速,从而达到持续运转的目的。尤其是起锚机中的离合器更是船舶传动装置中传动、装卸机械的重要组成部分,也是调整船速的重要保障[4-5]。然而在平时对其进行运维的过程中,却常因齿轮等部件会出现磨损,或是离合器不能啮合、松开、不正常的干涉以及其他可能会造成设备负荷的故障,造成不良后果。因此,对船舶起锚机离合器的故障进行检测,就显得尤为重要。
随着人工智能技术的提升,大量的计算机辅助设备也逐渐应用到船舶的监控及诊断中。如BP神经网络技术,其在应用的过程中就可以有效地防止或减小事故,或是通过故障诊断,迅速发现船舶起锚机离合器的故障原因并进行检修,从而降低因排障延误或是检修不及时而给相关设备造成的连带损失,能够极大降低维修费用。不少学者也基于BP神经网络将其应用到各种机械设备中,并得出该技术应用效果良好,应当是一种在工业控制领域可以广泛应用的故障反馈智能算法。据此,本文以船舶起锚机离合器为例,从BP神经网络技术的理论研究及实际应用出发,探讨其在船舶起锚机离合器故障诊断技术上的相关应用效果。本文研究可以为船舶起锚机离合器的故障检测提供一定参考,从安全性和经济性对相关技术发展带来积极的推动作用。
1 BP神经网络技术在故障检测中的应用思路 1.1 BP神经网络技术基本概述BP神经网络是一种具有自主学习能力的记忆网络,其特点是可以实现线性和非线性函数之间的映射,并以此为基础对网络中存储的记忆进行训练,从而提高企业价值评估结果的精准度。由于该技术具备泛化性质,因此面对船舶起锚机离合器这种多故障诱因,在实际应用中也可以起到一个科学系统的运算作用,使其在随机样本的计算检测中,通过大数据运算得出理想的排障结果[4-5]。
1.2 BP神经网络技术的运算原理BP神经网络技术,主要是基于BP算法(反向误差传播算法)的一种人工神经网(ANN),并在近年的发展中成为了一种最广泛的监督学习算法。在具体的运算原理上,BP神经网络技术首先是根据输入各权值和阀值产生输出信号,若实际输出与期望输出不相符,则转入误差的反向传播过程。而其中的误差反向传播过程,指的则是当网络拟合的输出与实际的输出数据不符时,网络会依据误差对其各项权值和阀值加以调整。待神经网络经过上述反复训练后,最终就会将其中的误差排除,从而保证整体的拟合精度提升,构建出神经网络。
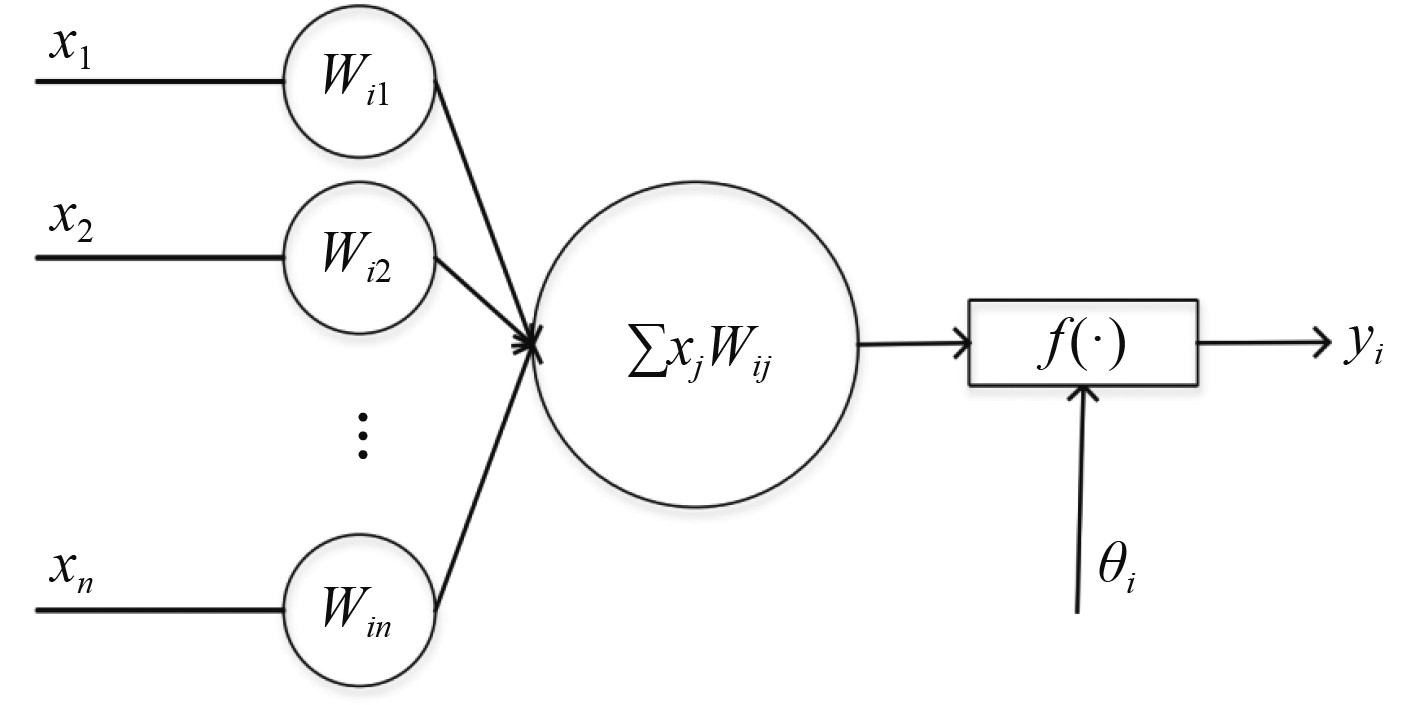
以本次的故障检测为例,为了可以将其与BP神经网络的工作原理进行紧密联系并加以应用,着重阐述人工神经网络的运行原理。BP神经网络技术这种仿生学技术,其在应用的过程中主要是模拟人脑神经元的功能,以此来构筑一种信息处理模型,人工神经网络模型如图1所示。
|
图 1 人工神经网络模型 Fig. 1 Artificial neural network model |
由图1表达结果可知,其神经元的连接权系数yi,表示是第i个神经元输出。其函数关系见下式:
| $ {y_i} = f \left(\sum\limits_{j = 1}^n {{w_{ij}}{x_j}} - {\theta _i}\right) \text{,} $ |
其中激活函数的净激活(net activation)用neti表示,得出下式:
| $ ne{t_i} = \sum\limits_{j = 1}^n {{w_{ij}}} {x_j} - {\theta _i} \text{。} $ |
其中的净激活值net可以是正的,也可以是负的。若net为正,说明神经元呈现出被激活的fire状态,若其结果为负,则说明被抑制。整体而言,BP神经网络技术在工作原理上可以基于相关参数进行预测,减少人为因素干预,让指标体系更科学化。
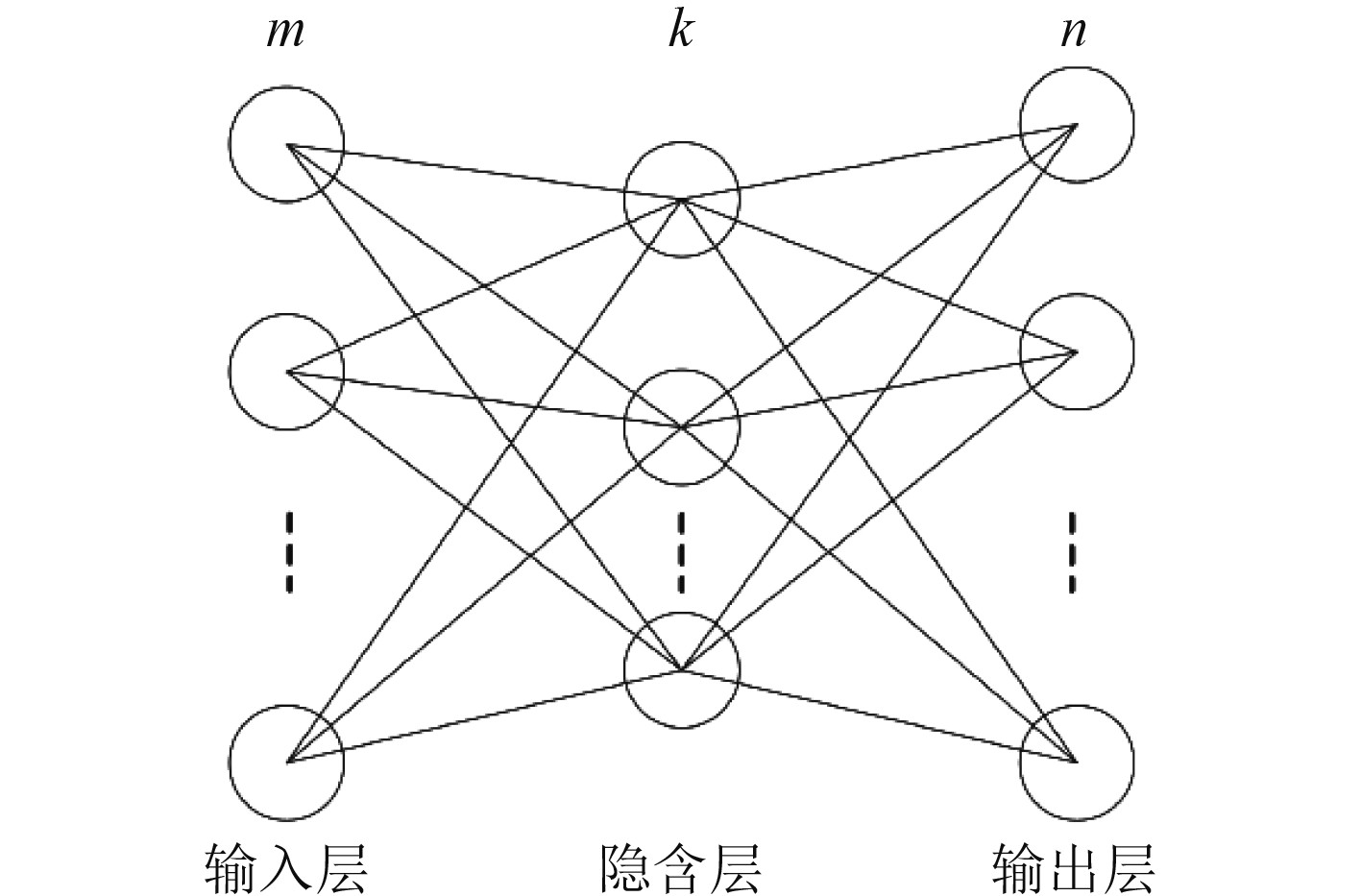
从船舶起锚机离合器中引入BP神经网络,共有输入层、隐含层、输出层3层(见图2),也是希望能基于这种较为成功的神经网络算法,对船舶起锚机离合器的既往数据加以整理,根据每次训练的结果和误差,最终得出与预期输出相一致的模型,从而提高船舶运维效率。
|
图 2 三层BP神经网络结构图 Fig. 2 Three layer BP neural network structure |
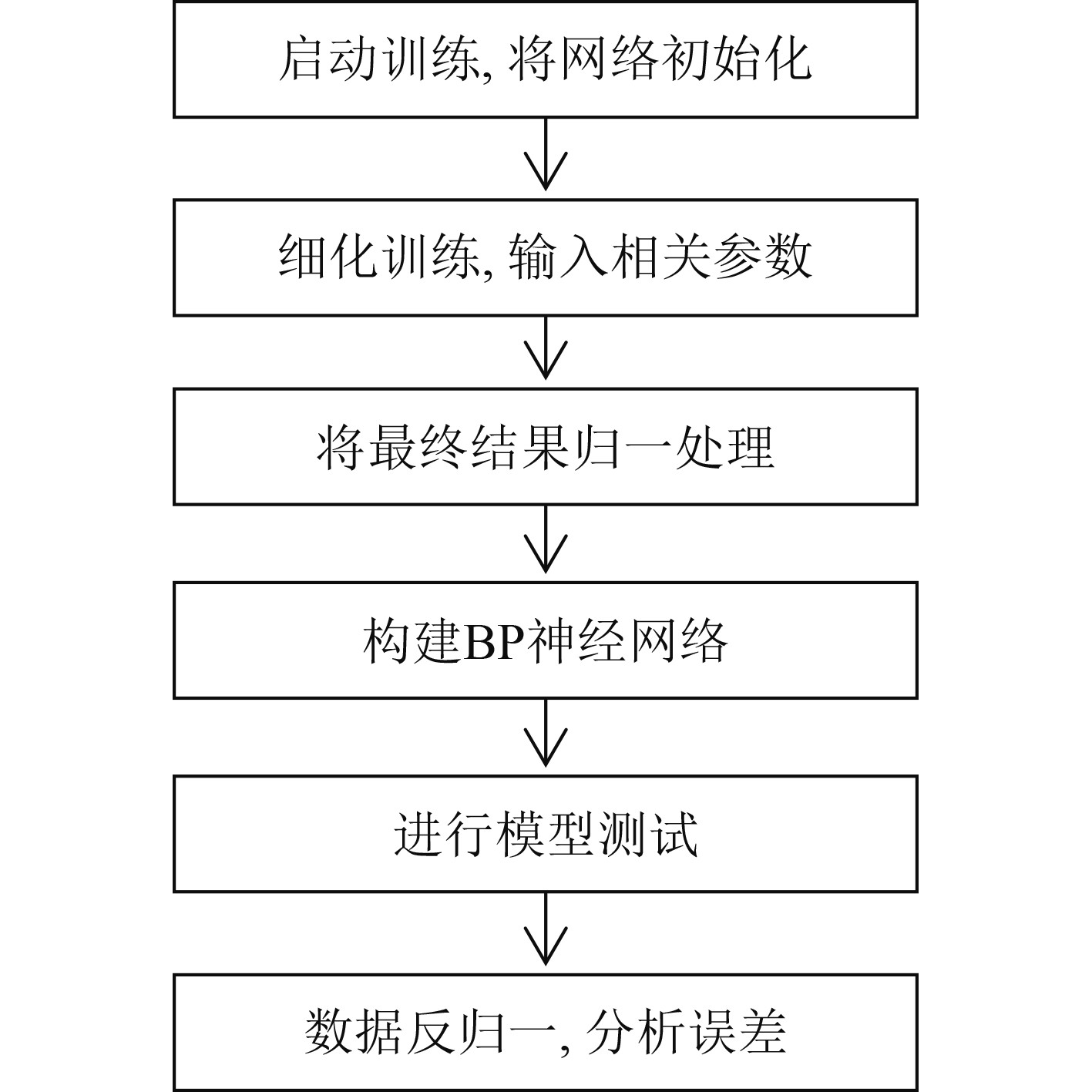
BP神经网络的拓扑结构与多层感知器的拓扑结构一样。因为BP神经网络也是一种感知器,结构越复杂的感知器,预测过程越复杂,最后得到的结果偏差越大。很多时候遇到的问题都是简单的非线性问题,这种问题3层感知器就可以解决,故而很多时候都用的是3层感知器。而本次研究将通过引入BP神经网络的原理,在Matlabr2014a软件上对船舶起锚机离合器的算法进行编码,在甄别算法的优缺点后进行细化实施,从而达到BP神经网络对相关设备故障检测的创建、训练和模拟。BP神经网络实现流程图如图3所示。
|
图 3 BP神经网络实现流程图 Fig. 3 BP Neural Network Implementation Flow Chart |
为将BP神经网络技术应用于船舶起锚机离合器的故障检测中,先对起锚机离合器的相关故障加以呈现,在指出其现状问题后,对造成故障的原因加以说明,具体见表1。
|
|
表 1 起锚机离合器故障类型 Tab.1 Fault types of windlass clutch |
将故障按照代码序号进行了简化,列出故障检测公式:
| $ {{\rm X}_\kappa } = \frac{{{{\rm X}_\kappa }{{ - }}{{\rm X}_{{\text{min}}}}}}{{{{\rm X}_{{\text{max}}}}{{ - }}{{\rm X}_{{\text{min}}}}}} \text{。} $ |
其中:Xk为BP神经网络归一化后,船舶离合器故障特征向量;Xmax与Xmin分别为船舶离合器故障最大与最小值。
2.2 离合器数据记录仪设置考虑到船舶起锚机离合器在工作过程中,主要依靠其转速差进行啮合与脱开,因此在BP神经网络的相关参数输入中,对其转速信号设定为:
| $ {{n}} = \frac{{{f}}}{{{z}}} \text{,} $ |
扭矩信号计算公式为:
| $ MP = \frac{{N\left( {f - {f_o}} \right)}}{{{f_p} - {f_o}}} \text{,} $ |
| $ M{\text{r}} = \frac{{N\left( {{f_o} - f} \right)}}{{{f_o}{\text{ - }}{f_{\text{r}}}}} \text{。} $ |
基于以上参数,对其展开训练。
2.3 起锚机离合器故障检测通过对本次船舶起锚机离合器故障特征进行学习,最终完成了对船舶起锚机离合器的故障检测。而在后续的检验过程中,继续对BP神经网络展开训练,其思路大致如下:
步骤1 初始化网络中的扭矩信号权值和偏置项,分别记为:w(0),b1(0),v(0),b2(0),然后再基于以上各层期望值,对其进行输出设置,得出损失函数:
| $ { E}\left( \theta \right) = \frac{1}{2}{\sum\limits_{{{i}} = 1}^2 {\left( {{{{y}}_{{i}}}{{ - }}{{{{\hat y}}}_{{i}}}} \right)} ^2} \text{。} $ |
其中:θ为参数集合;yi为真实值;最终得出本次船舶起锚机离合器的故障损失函数期望值:
| $ { E}\left( \theta \right) = \frac{1}{{{n}}}{\sum\limits_{{{i}} = 1}^2 {\left( {{{{y}}_{{i}}}{{ - }}{{{\rm{\hat y}}}_{{i}}}} \right)} ^2} \text{,} $ |
若真实值与输出值表示为yn×m,则起锚机离合器的故障可表示为:
| $ { E}\left( \theta \right) = \frac{1}{{{{mn}}}}{\left( {{{y - \hat y}}} \right)^{\rm T}}\left( {{{y - \hat y}}} \right) \text{。} $ |
步骤2 依据前文提及的3层BP神经网络结构,对船舶起锚机离合器设定神经元函数,并展开输出层输出计算。其中输入层链式法则:
| $ \nabla \left( \kappa \right)\upsilon = \frac{{\partial {E}}}{{\partial \nu }} = \frac{{\partial {{ne}}{{{t}}_2}}}{{\partial \nu }}\frac{{\partial {{\hat y}}}}{{\partial {{ne}}{{{t}}_2}}}\frac{{\partial {\rm E}}}{{\partial {{\hat y}}}} \text{,} $ |
| $ \nabla \left( \kappa \right){{\text{b}}_2} = \frac{{\partial { E}}}{{\partial {{{b}}_2}}} = \frac{{\partial {{ne}}{{{t}}_2}}}{{\partial {{{b}}_2}}}\frac{{\partial {{\hat y}}}}{{\partial {{ne}}{{{t}}_2}}}\frac{{\partial { E}}}{{\partial {{\hat y}}}} \text{。} $ |
隐含层链式法则:
| $ \nabla \left( \kappa \right)\omega = \frac{{\partial { E}}}{{\partial \omega }} = \frac{{\partial {{ne}}{{{t}}_1}}}{{\partial \omega }}\frac{{\partial {{h}}}}{{\partial {{ne}}{{{t}}_1}}}\frac{{\partial {{ne}}{{{t}}_2}}}{{\partial {{h}}}}\frac{{\partial {{\hat y}}}}{{\partial {{ne}}{{{t}}_2}}}\frac{{\partial {E}}}{{\partial {{\hat y}}}} \text{,} $ |
| $ \nabla \left( \kappa \right){{{b}}_1} = \frac{{\partial { E}}}{{\partial {{{b}}_{{1}}}}} = \frac{{\partial {{ne}}{{{t}}_1}}}{{\partial {{{b}}_{{1}}}}}\frac{{\partial {{h}}}}{{\partial {{ne}}{{{t}}_1}}}\frac{{\partial {{ne}}{{{t}}_2}}}{{\partial {{h}}}}\frac{{\partial {{\hat y}}}}{{\partial {{ne}}{{{t}}_2}}}\frac{{\partial { E}}}{{\partial {{\hat y}}}} \text{。} $ |
步骤3 在基于误差计算后,最终更新神经网络的权值、偏置项,并对输出单元参数更新:
| $ {\nu }^{\left(\kappa \right)}={\nu }^{\left(\kappa -1\right)}-\eta \nabla {\left(\kappa \right)}^{\upsilon }={\upsilon }^{\left(\kappa -1\right)}-\eta \frac{\partial { E}}{\partial \upsilon }\text{,}{{b}}_{2}{}^{\left(\kappa -1\right)}-\eta \frac{\partial { E}}{\partial {{b}}_{2}} \text{,} $ |
再对隐含单元参数更新:
| $ {\omega }^{\left(\kappa \right)}={\omega }^{\left(\kappa -1\right)}-\eta \nabla {\left(\kappa \right)}^{\omega }={\omega }^{\left(\kappa -1\right)}-\eta \frac{\partial { E}}{\partial \omega }\text{,}{{b}}_{1}{}^{\left(\kappa -1\right)}-\eta \frac{\partial { E}}{\partial {{b}}_{1}} \text{。} $ |
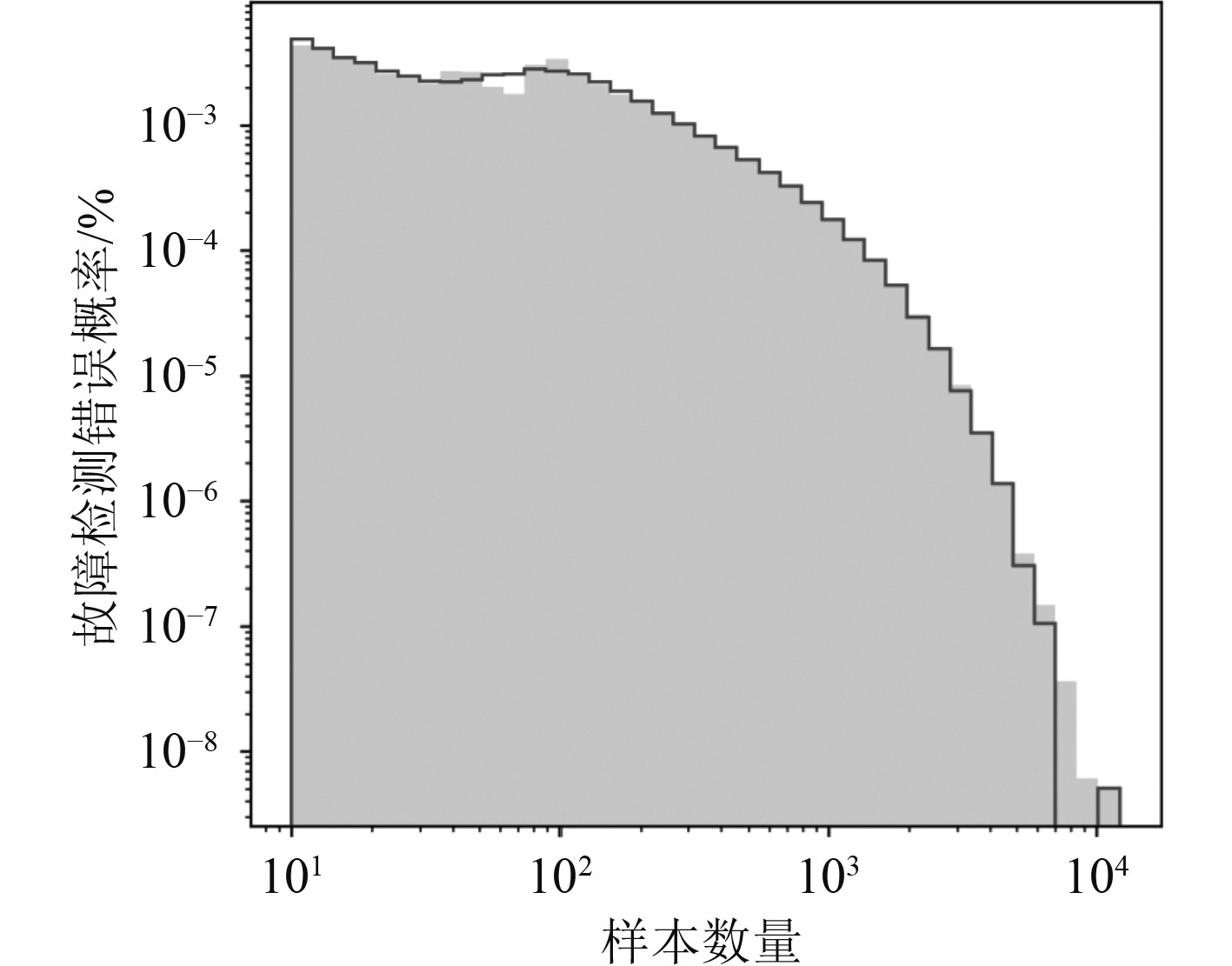
最终,构建出船舶起锚机离合器故障检测的BP神经网络,得到船舶起锚机离合器故障特征向量集合,基于BP神经网络技术诊断离合器故障,实现起锚机离合器故障的监测,并得出如图4所示的检测结果。归一化后的错误分布如图5所示。
|
图 4 起锚机离合器故障检测训练结果 Fig. 4 Windlass Clutch Fault Detection Training Results |

|
图 5 归一化后的错误分布图 Fig. 5 Normalized Error Distribution Plot |
通过上述步骤可见,采用BP神经网络技术对起锚机离合器进行了检测。从应用结果来看,整个应用程序规范,算法准确。
3 结 语本文采用BP神经网络模型对船舶起锚机离合器故障进行预测,并通过对其训练过程进行观察、测试及数据分析,论证了BP神经网络技术在船舶起锚机离合器故障检测中的可行性。
| [1] |
徐鹏, 杨海燕, 程宁, 等. 基于优化BP神经网络的船舶动力系统故障诊断[J]. 中国舰船研究, 2021, 16(1): 8. XU Peng, YANG Hai-yan, CHENG Ning, et al. Fault diagnosis of ship power system based on optimized BP neural network[J]. China Ship Research, 2021, 16(1): 8. DOI:10.19693/j.issn.1673-3185.02453 |
| [2] |
蒋佳炜, 胡以怀, 方云虎, 等. 船舶动力装置智能故障诊断技术的应用与展望[J]. 中国舰船研究, 2020, 15(1): 56-67. JIANG Jia-wei, HU Yi-huai, FANG Yun-hu, LI Fang-yu. Application and Prospect of Intelligent Fault Diagnosis Technology of Ship Power Plant[J]. Chinese Ship Research, 2020, 15(1): 56-67. DOI:10.19693/j.issn.1673-3185.01679 |
| [3] |
林驰, 陈军, 王波, 等. 浅析工程船舶动力机械状态监测与故障诊断现状及发展[J]. 中国设备工程, 2021(22): 175-177. LIN Chi, CHEN Jun, WANG Bo, ZHAO Xin, CHEN Hai-feng. Analysis on the Status and Development of Condition Monitoring and Fault Diagnosis of Engineering Ship Power Machinery[J]. China Equipment Engineering, 2021(22): 175-177. DOI:10.3969/j.issn.1671-0711.2021.22.093 |
| [4] |
杨奕飞, 冯静. 基于HMM-SVR的船舶动力设备故障模式识别与状态预测研究[J]. 船舶工程, 2018, 40(3): 68-72+97. YANG Yi-fei, FENG Jing. Research on Fault Mode Recognition and State Prediction of Ship Power Equipment Based on HMM-SVR[J]. Ship Engineering, 2018, 40(3): 68-72+97. DOI:10.13788/j.cnki.cbgc.2018.03.068 |
| [5] |
李乐, 舒越超, 吴健鹏, 等. 基于PSO-BP神经网络湿式摩擦元件损伤预测模型[J]. 北京理工大学学报自然版, 2022, 42: 1-10. LI Le, SHU Yue-chao, WU Jian-peng, et al. Damage prediction model of wet friction elements based on PSO-BP neural network[J]. Journal of Beijing Institute of Technology, 2022, 42: 1-10. |
 2022, Vol. 44
2022, Vol. 44
