主动声呐可以获得目标的精确位置等参数,但双程传播衰减使得探测距离较短,若要使单基地主动声呐获得更远的探测距离,就必须提高发射机的功率,这不仅要求发射基阵具有更大的尺寸,而且会带来声呐被敌方发现的严重后果。被动声呐隐蔽性好,但探测能力依赖于目标的辐射噪声且难以对目标精确定位。双基地声呐在一定程度上综合了主动声呐和被动声呐的优点,收发分置后,接收基地远离发射基地,避开了发射基地平台的强噪声干扰,具有隐蔽性好和定位精度高等优点。
双基地声呐在国外军事领域已得到了广泛应用,美军从20世纪60年代就装备了“朱莉”系统[1-2],被动声呐阵接收来自空投信号弹的爆炸声在潜艇上产生的回波进行远程定位。随着装备和技术不断改进,这种收发分置式的声呐系统的探测能力已得到了更大的提高。国内对双基地声呐的研究虽起步较晚但从未间断,1996年,阎宜生[3]基于声呐方程简单估计了双基地声呐作用距离;杨丽[4]根据能量关系推导了双基地声呐系统最大可探测范围,并进行声呐配置研究;张小凤[5]基于TOL(声波到达时间)算法,研究了时间测量误差对双基地声呐定位精度的影响,但以上文献均没有对双基地声呐的距离误差进行系统性研究。为了深入研究双基地声呐的定位性能,本文基于双基地声呐的定位原理,建立双基地声呐距离误差估计模型,分析影响双基地声呐探测精度的主要因素并给出仿真分析,为进一步研究双基地声呐探测能力提供理论依据。
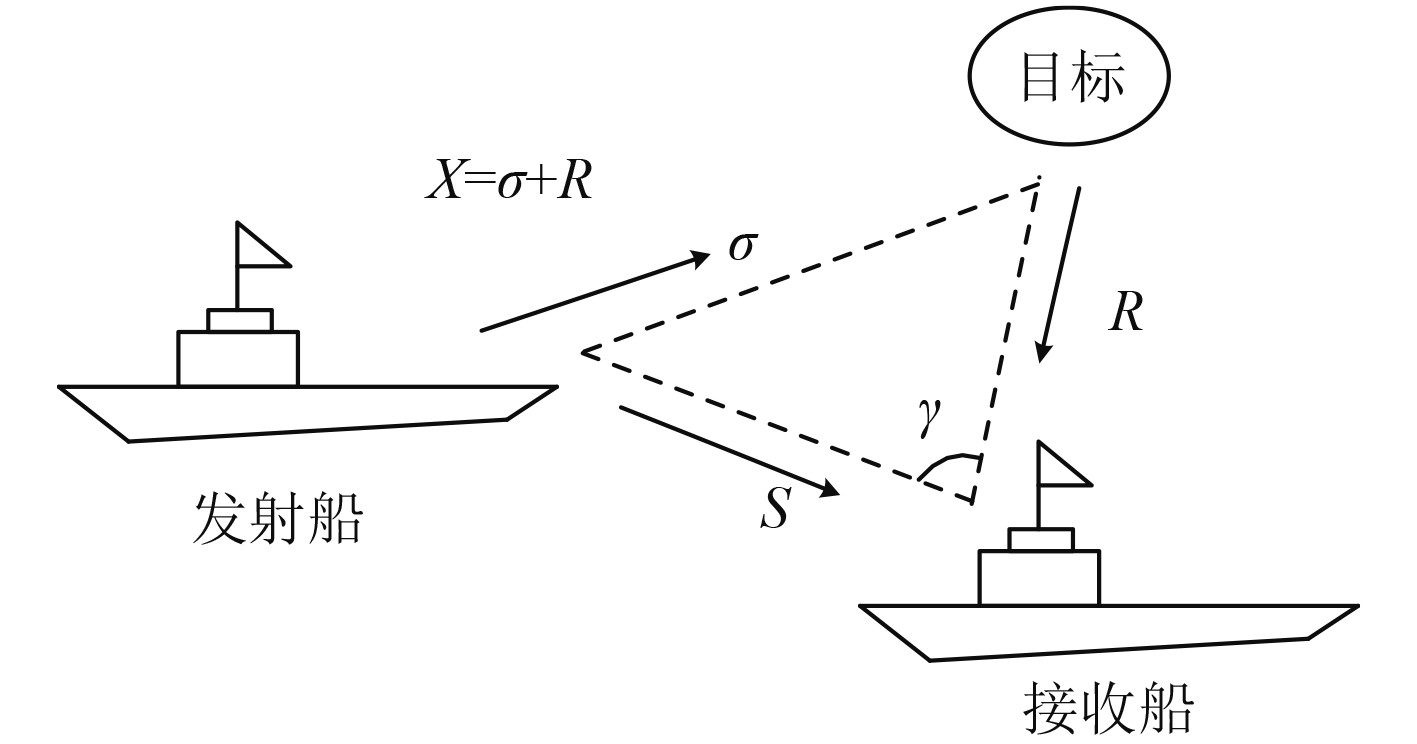
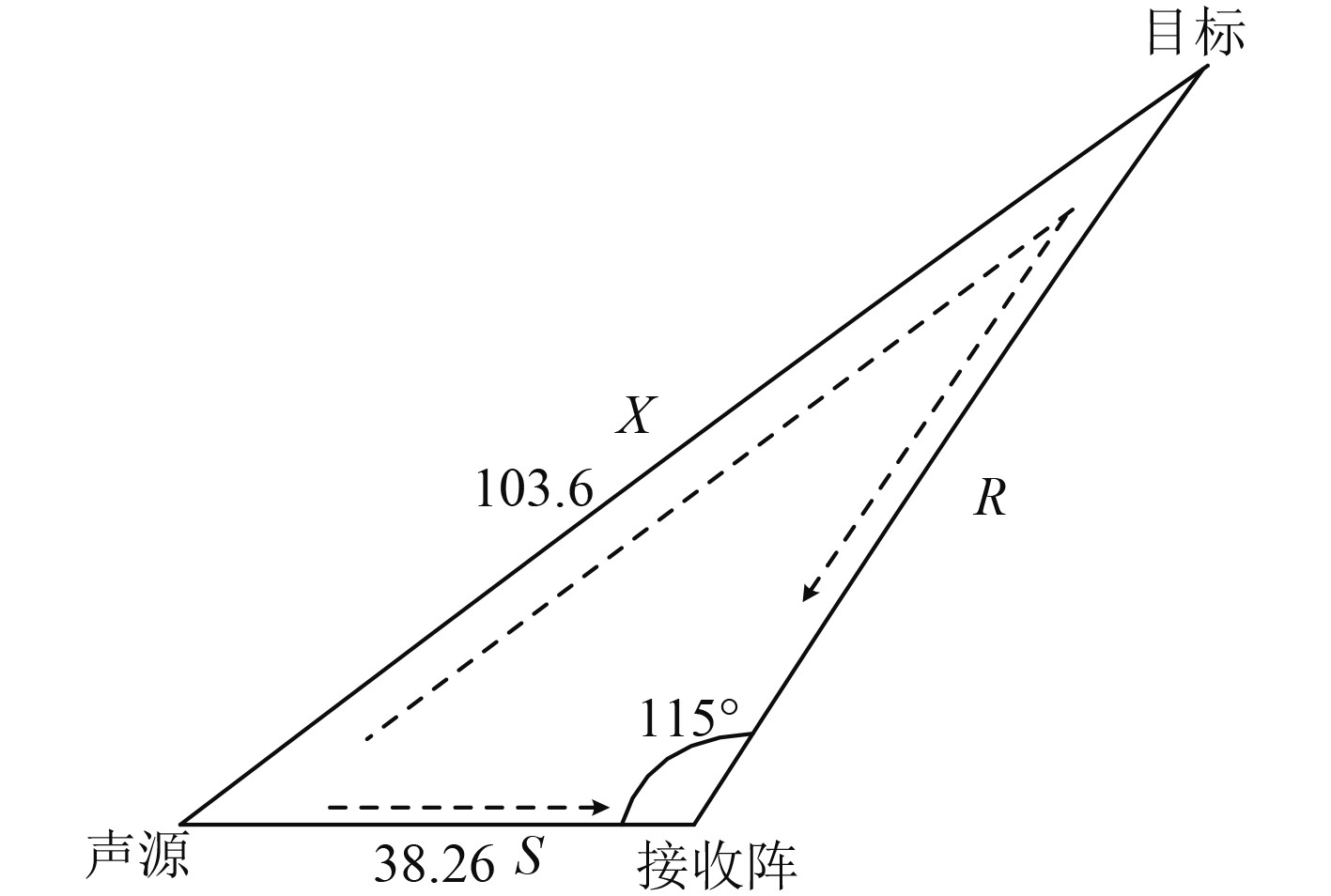
1 双基地声呐定位原理双基地声呐的几何关系如图1所示,发射船发射主动声呐信号,声波经目标反射后到达的接收基阵,声信号传播距离为
|
图 1 双基地声呐配置 Fig. 1 The deployment for bistatic soar |
由图1所示几何关系可得到:
| $ {(X - R)^2} = {R^2} + {S^2} - 2RS\cos \gamma,$ | (1) |
当目标位于双基地声呐的作用距离范围内时,如果已知收发距离
| $ R = \dfrac{{{X^2} - {S^2}}}{{2(X - S\cos \gamma )}}。$ | (2) |
为了充分利用双基地声呐低噪声干扰、良好隐蔽性的优点,接收船一般远离发射船和目标,收发距离
| $ {t_X}{\text{ = }}t + {t_S} ,$ | (3) |
所以,测得目标回波与直达波的时延差
| $ R = \dfrac{{V(t_X^2 - t_S^2)}}{{2({t_X} - {t_S}\cos \gamma )}}。$ | (4) |
由于海洋水声环境的复杂性,海洋声速存在不确定性,声速值受时空变化的影响较大,在声波沿不同路径传播时,声速值往往不同,所以由式(4)进行探测距离估算时,引入了由于声速变化带来的误差。设声波沿间接路径
| $ R = \dfrac{{{{(U{t_X})}^2} - {{(V{t_S})}^2}}}{{2(U{t_X} - V{t_S}\cos \gamma )}}。$ | (5) |
使用
| $ R = \dfrac{{V(\tau _X^2 - t_S^2)}}{{2({\tau _X} - {t_S}\cos \gamma )}}。$ | (6) |
实际上,如果已知式(6)中除
| $ e = \dfrac{S}{X} = \dfrac{{V{t_S}}}{{U{t_X}}} = \dfrac{{{t_S}}}{{{\tau _X}}},$ | (7) |
该椭圆也称为定位椭圆,在理想海水介质中(
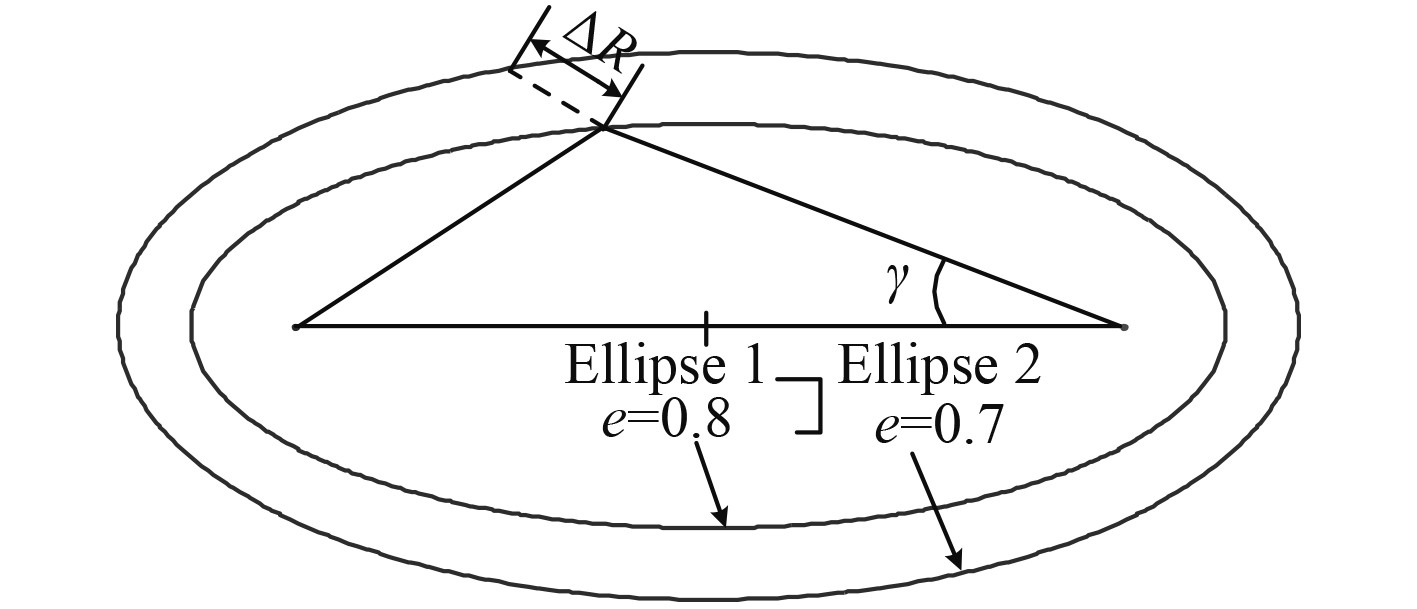
|
图 2 时间测量误差示意图 Fig. 2 Timing estimation error |
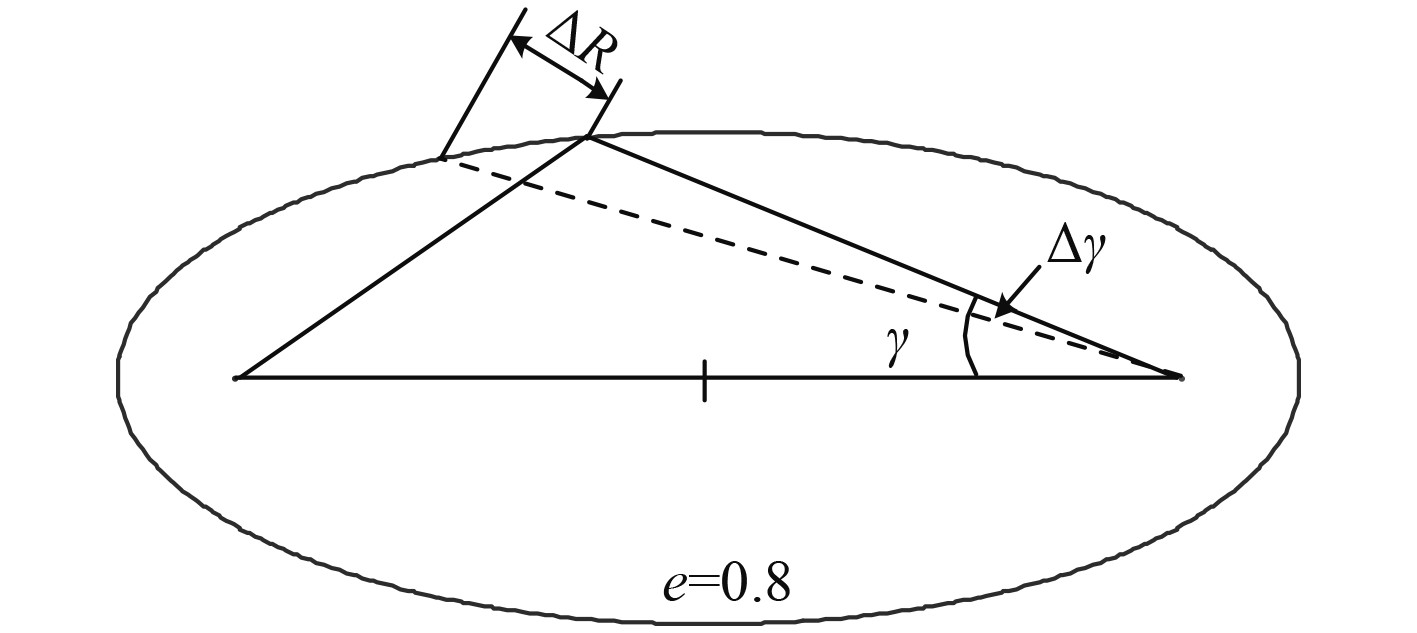
|
图 3 方位测量误差示意图 Fig. 3 Bearing estimation error |
| $ R = \dfrac{{V{t_S}(1 - {e^2})}}{{2e(1 - e\cos \gamma )}} = \dfrac{S}{{2e(1 - e\cos \gamma )}} ,$ | (8) |
式(8)表明,影响双基地声呐探测距离精度的主要因素为测量值
| $ \dfrac{{\Delta R}}{R} = \dfrac{1}{R}\dfrac{{\partial R}}{{\partial V}}\Delta V + \dfrac{1}{R}\dfrac{{\partial R}}{{\partial {\tau _X}}}\Delta {\tau _X} + \dfrac{1}{R}\dfrac{{\partial R}}{{\partial {t_S}}}\Delta {t_S} + \dfrac{1}{R}\dfrac{{\partial R}}{{\partial \gamma }}\Delta \gamma。$ | (9) |
根据式(8)得到误差表达式(9)中的各个系数:
| $ \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {\dfrac{1}{R}\dfrac{{\partial R}}{{\partial V}} = \dfrac{1}{V}} ,\\ {\dfrac{1}{R}\dfrac{{\partial R}}{{\partial {\tau _X}}} = \dfrac{{2{\tau _X}}}{{\tau _X^2 - t_S^2}} - \dfrac{1}{{{\tau _X} - {t_S}\cos \gamma }}} ,\\ {\dfrac{1}{R}\dfrac{{\partial R}}{{\partial {t_S}}} = \dfrac{{ - 2{\tau _X}}}{{\tau _X^2 - t_S^2}} + \dfrac{{\cos \gamma }}{{{\tau _X} - {t_S}\cos \gamma }}} ,\end{array}} \\ {\dfrac{1}{R}\dfrac{{\partial R}}{{\partial \gamma }}= -\dfrac{{{t_S}\sin \gamma }}{{{\tau _X} - {t_S}\cos \gamma }}} 。\end{array}} \right. $ | (10) |
将这些系数代入式(9)得到计算相对误差的表达式:
| $ \begin{aligned}[b] & \dfrac{{\Delta R}}{R} = \dfrac{{\Delta V}}{V} + \left( {\dfrac{{2{\tau _X}}}{{\tau _X^2 - \tau _S^2}} - \dfrac{1}{{{\tau _X} - {t_S}\cos \gamma }}} \right)\Delta {\tau _X} - \\ & \begin{array}{*{20}{l}} {}&{ \left( {\dfrac{{2{t_S}}}{{\tau _X^2 - \tau _S^2}} - \dfrac{{\cos \gamma }}{{{\tau _X} - {t_S}\cos \gamma }}} \right)} \end{array}\Delta {t_S} - \dfrac{{{t_S}\sin \gamma }}{{{\tau _X} - {t_S}\cos \gamma }}\Delta \gamma。\end{aligned} $ | (11) |
记:
| $ \begin{aligned}[b] & \dfrac{{\Delta R}}{R} = \dfrac{{\Delta V}}{V} + \left( {\dfrac{2}{{1 - {e^2}}} - \dfrac{1}{{1 - e\cos \gamma }}} \right)\dfrac{{\Delta {t_X}}}{{{t_X}}}+ \\ & \begin{array}{*{20}{c}} {}&{ \left( {\dfrac{{ - 2{e^2}}}{{1 - {e^2}}} - \dfrac{{e\cos \gamma }}{{1 - e\cos \gamma }}} \right)} \end{array}\dfrac{{\Delta {t_S}}}{{{t_S}}} - \dfrac{{e\sin \gamma }}{{1 - e\cos \gamma }}\Delta \gamma。\end{aligned} $ | (12) |
在工程测量中,常常使用均方根误差衡量观测值同真值之间的偏差。如果已知测量值
| $ \left\{ {\begin{array}{*{20}{l}} {{A_X} = \dfrac{2}{{1 - {e^2}}} - \dfrac{1}{{1 - e\cos \gamma }}} ,\\ {{A_S} = \dfrac{{ - 2{e^2}}}{{1 - {e^2}}} + \dfrac{{e\cos \gamma }}{{1 - e\cos \gamma }}} ,\\ {{A_G} = \dfrac{{ - e\sin \gamma }}{{1 - e\cos \gamma }}} 。\end{array}} \right. $ | (13) |
则目标距离的均方根误差模型可以简写为:
| $\begin{aligned}[b] & \dfrac{1}{R}(\Delta R)rms = \\ & \sqrt {{{\left( {\dfrac{{\Delta V}}{V}} \right)}^2} + A_X^2{{\left( {\dfrac{{\Delta {t_X}}}{{{t_X}}}} \right)}^2} + A_S^2{{\left( {\dfrac{{\Delta {t_S}}}{{{t_S}}}} \right)}^2} + A_G^2{{(\Delta \gamma )}^2}} \end{aligned} 。$ | (14) |
由式(12)可知,影响均方根误差大小的因素由各测量值相对误差和误差系数两部分组成,其中测量值相对误差包括固定误差和随机误差,固定误差即设备误差,决定于仪器加工制作的工艺水平,对于给定的测量设备,这部分误差不能消除。随机误差即人为操作误差,这部分误差可以通过不断提高测量人员对设备操作的熟练程度逐渐减小。一般情况下,测量值相对误差均在一个较小的范围内随机变化(0~1)[5],对式(12)均方根误差的影响不大,而误差系数
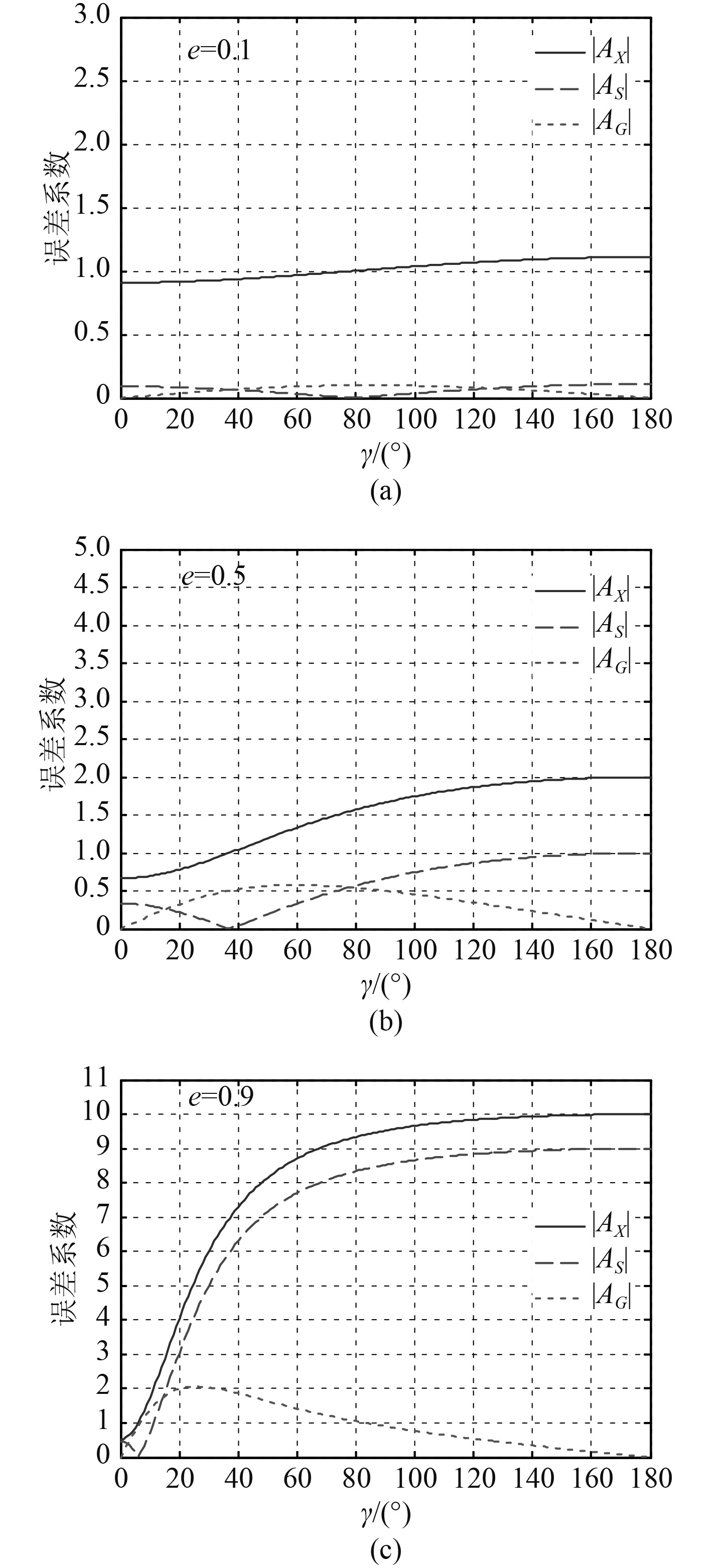
|
图 4 方位角和离心率对误差系数的影响 Fig. 4 The error coefficient affected by bearing and eccentricity |
由图4可知,误差系数
1)离心率越小,即椭圆越扁平,
2)离心率越大,即椭圆越圆满,
3)不论离心率取何值,在
基于图1所示的声呐配置,根据式(5)和式(12),分别计算目标距离值和距离估计的均方根误差。假设已知条件为:
|
|
表 1 计算结果 Tab.1 Results of calculation |
将以上已知值分别代入式(5)和式(12)得到目标真实距离值和均方根误差:
| $ \begin{aligned}[b] & \dfrac{1}{R}(\Delta R)rms = \\ & \sqrt {{{\left( {\dfrac{{\Delta V}}{V}} \right)}^2} + A_X^2{{\left( {\dfrac{{\Delta {t_X}}}{{{t_X}}}} \right)}^2} + A_S^2{{\left( {\dfrac{{\Delta {t_S}}}{{{t_S}}}} \right)}^2} + A_G^2{{(\Delta \gamma )}^2}}=0.005 \end{aligned}。$ | (15) |
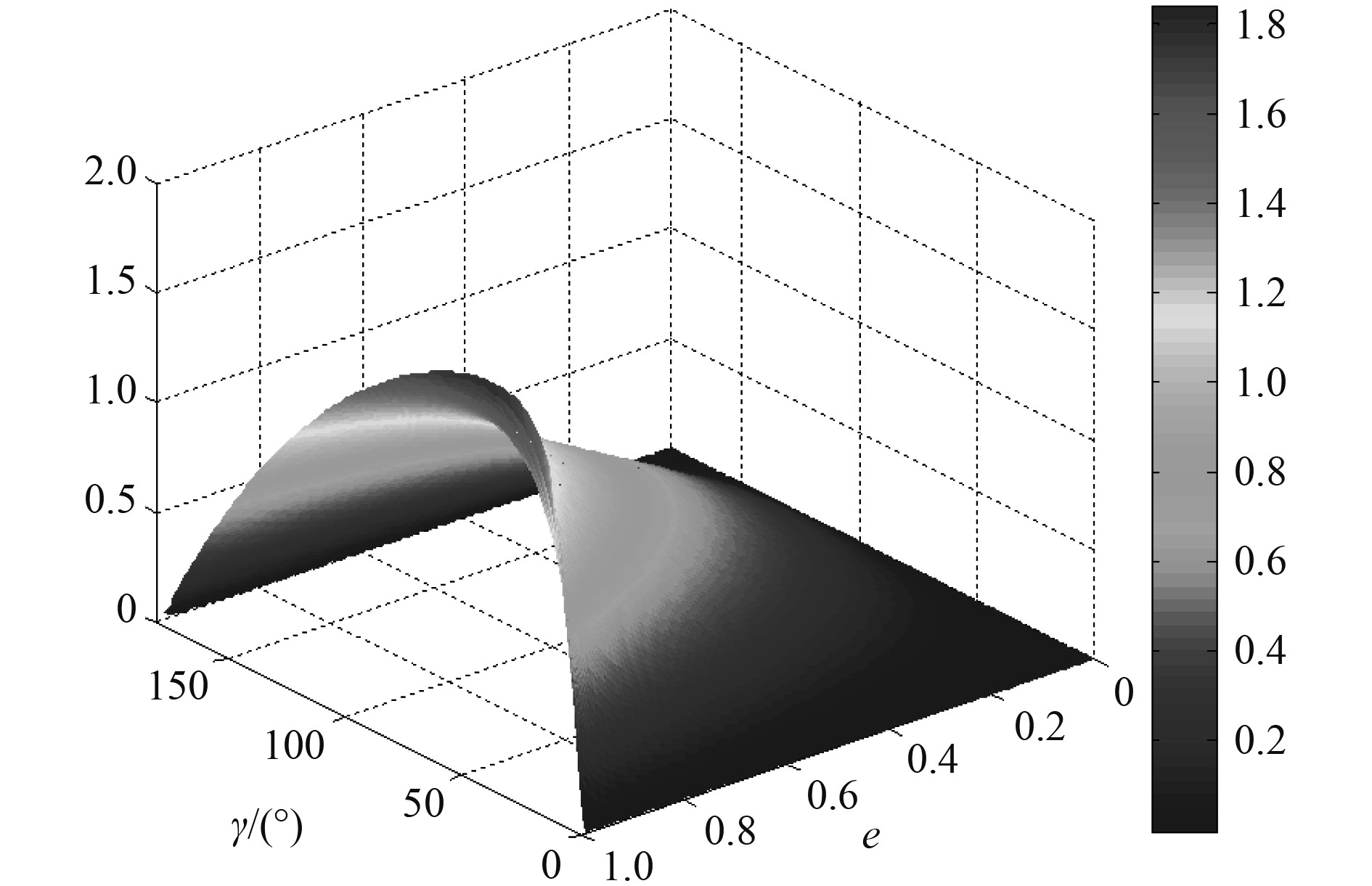
在测量误差不变的情况下,改变目标相对于收发点的相对距离和方位(见图5),可得到离心率和方位角变化对距离均方根误差的影响关系,如图6所示。均方根误差对离心率变化及其敏感,特别是离心率较大时,均方根误差急剧增大,呈指数增长的趋势。均方根误差随方位角度增大,先增大达到最大值然后减小,这种变化规律是由式(12)中误差系数
|
图 5 目标态势 Fig. 5 The state of target and receiver |
|
图 6 均方根误差随离心率和方位角的变化 Fig. 6 Mean square error vary with the eccentricity and bearing |
综上所述,利用双基地声呐进行目标定位时,目标所处方位和距收发点距离远近程度对距离估计影响最大,在收发距离一定时,目标越远离收发点(离心率小),方位角度对距离估计的影响也随之减小,均方根误差也维持在一个较低的范围。这也充分说明,双基地声呐实现远距离探测不仅有较好的隐蔽性,而且具有较高的定位精度。
4 结 语本文从双基地声呐的定位原理出发,推导双基地声呐距离计算式和误差估计公式,考虑了时间测量误差、测向误差和声速测量误差等因素对双基地声呐探测精度的影响,详细分析了定位椭圆离心率和方位角度大小对距离均方根误差的影响。通过理论分析指出,在利用双基地声呐进行目标定位时,目标所处方位和距收发点距离远近程度对距离估计影响最大,所以,在军事活动中实施对敌探测时,进行合理的声呐配置,不仅可以在隐蔽条件下实现远距离探测,而且还可以保持较高的定位精度。
| [1] |
WANG C, YAO Y, WANG Y M, etal. Bistatic soanrt data fusion based on extend kalman filter and its application[C]//Proc of the 2nd International Conference on Computer Engineering and Technology, 2010: 615–617.
|
| [2] |
LIU J B, LLIU W X, ZHOU Q D, et al. Optimal parametric design of bulkhead vibration control for underwater structure[J]. Chinese Journal of Ship Research, 2010, 5(6): 21-25. |
| [3] |
阎宜生, 丁玮等 双基地声呐作用距离估计[J]. 西北工业大学学报, 1996, (4): 545–560.
|
| [4] |
杨丽, 蔡志明 双基地声呐探测范围分析[J]. 兵工学报 2007, 28 (7): 839–843.
|
| [5] |
张小凤, 赵俊渭, 等 双基地声呐定位精度和算法研究[J]. 系统仿真学报, 2003, 315(10): 1471–1473.
|
 2022, Vol. 44
2022, Vol. 44
