0 引　言

随着海洋开发和海洋防卫的发展，水声通信技术在海洋领域得到极大重视。在高速水声通信中，由于信道混响和反射等因素影响，会产生严重的码间干扰，严重影响水下通信质量。因此，水声通信系统的接收端需要采用信道均衡技术对这些影响进行补偿。

传统的MIMO（multi-input multi-output，MIMO）信道自适应均衡技术有最小均方误差法（LMS）和递归最小二乘法（RLS）。RLS算法的收敛速度比LMS算法快，均方误差更小，均衡效果更好^[1]。由于实际的水声信道具有时变、空变、频变、多途、高环境噪声等复杂特征，因此通常采用决策反馈均衡（DFE）对其进行处理。传统的基于RLS算法的自适应MIMO决策反馈均衡器算法（RLS-DFE）简单，运算量低，且收敛和跟踪速度较快^[2]，但在信噪比较低时信道分配不合理导致误码率较高、性能较差；而深度学习网络在进行水声信道均衡方面具有优势，可有效解决通信的码间干扰问题，优化信道性能，提高通信的精度^[3]。

深度学习网络具有强大的学习能力和高度的兼容性，可利用网络模型来学习并减轻码间干扰，从而获得优良的水声信道均衡性能^[4]。本文针对传统信道均衡方法的不足，对比研究了3种基于深度学习网络的水声信道均衡技术，结果表明在低信噪比情况下，采取深度学习方式进行信道均衡误码率更低、传输信息更准确。

1 MIMO水声信道均衡技术

信道均衡技术能够有效补偿码间干扰对信道造成的影响，大大提高通信系统质量。常用的均衡器有线性均衡器和判决反馈均衡器，由于判决反馈均衡器的误码率更低、收敛速度更快，因此在水声信道均衡上得到广泛应用。传统均衡算法在DFE的基础上，利用RLS算法收敛快的特点，提出递归最小二乘-判决反馈均衡器（recursive least square-decision feedback equalization, RLS-DFE）方法。

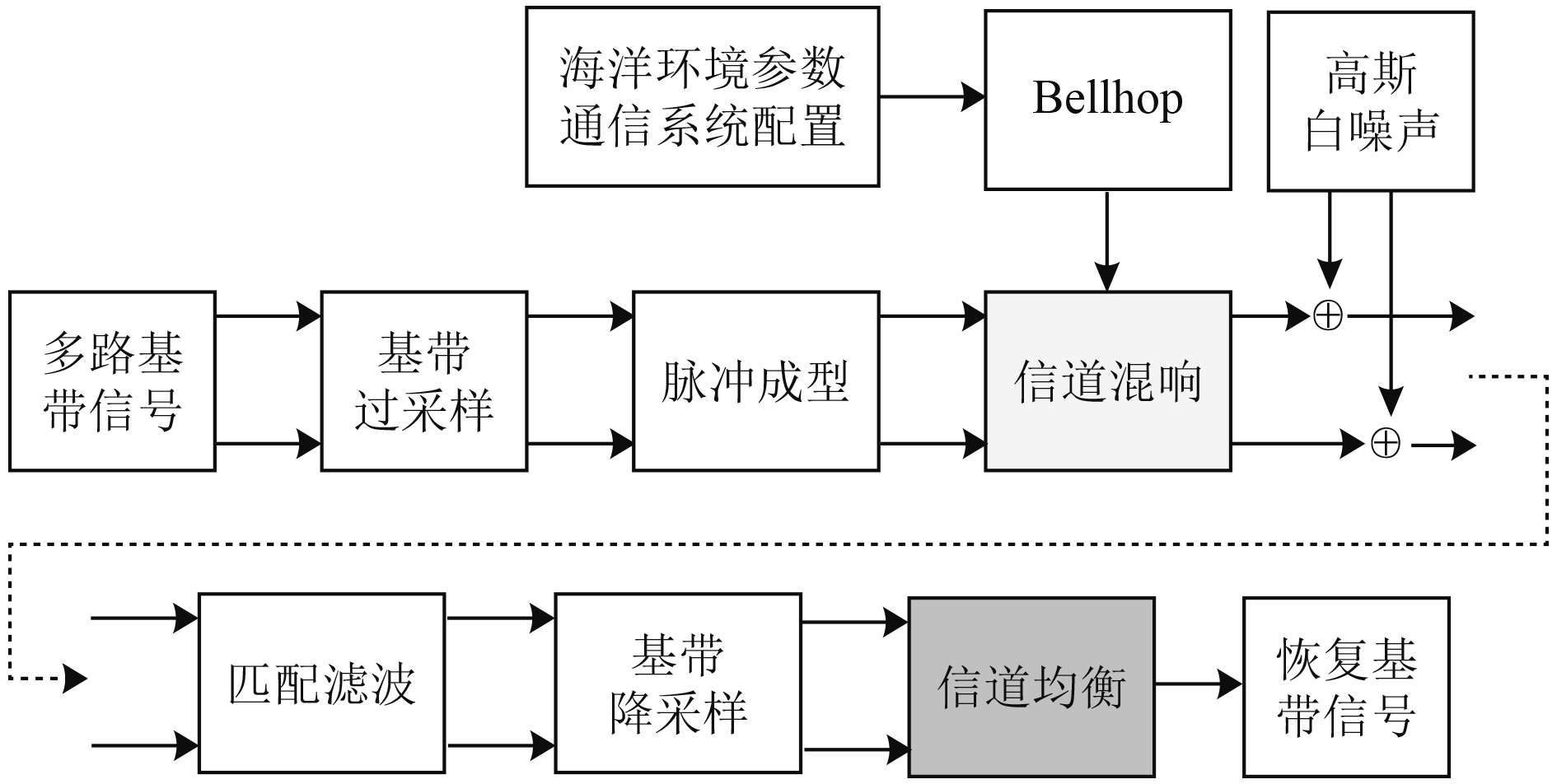
MIMO水声信道均衡算法仿真的关键在于信道均衡算法的设计和各子信道冲激响应的模拟^[5]，其主要流程如图1所示。利用Bellhop仿真软件对信道环境进行配置，对多路基带信号进行过采样、脉冲成型处理，通过信道卷积，叠加高斯白噪声至接收端进行匹配滤波和降采样处理，最后通过信道均衡降低码间干扰的影响^[6]，从而顺利恢复多路基带信号。

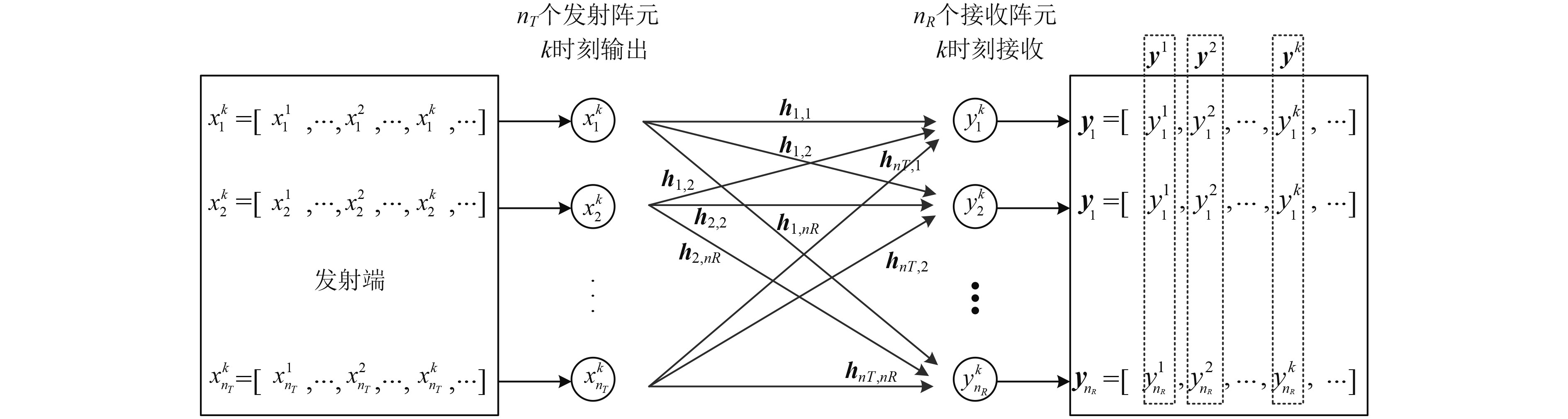
MIMO水声系统基带传输模型如图2所示，包含 ${n_T}$ 个发射阵元和 ${n_R}$ 个接收阵元。k时刻，第n个发射阵元的输出基带信号为 $ x_n^k $ ；k时刻，第m个接收阵元的输入信号为 $y_m^k$ 。

假设信道长度为L，则MIMO水声系统的基带传输可用下面模型进行表达：

$ {y}_{m}^{k}={\displaystyle \sum _{n=1}^{{n}_{T}}{\displaystyle \sum _{l=0}^{L}{x}_{n}\left(k-l\right)}}·{h}_{n,m}\left(k,l\right)+{v}_{m}^{k}。$

其中： $v_m^k$ 为第m个接收阵元k时刻的加性高斯白噪声；h_n,m为第m个接收阵元接收来自第n个发射阵元基带信号的信道冲激响应。

2 基于深度学习网络的MIMO水声信道均衡算法

在高速水声通信领域应用深度学习网络进行均衡具有巨大优势。神经网络具有非线性决策边界的复杂决策区，能够在输入和输出空间进行多重映射，这符合非线性均衡器结构的功能特点^[7]。基于神经网络的非线性特性，提出基于深度学习网络的均衡算法。

2.1 基于深度神经网络（MIMO-DNN）的均衡算法

深度神经网络（deep neural networks，DNN）包含输入层、隐含层和输出层3个部分，能够通过感知器增加多个隐含层，通过简单的非线性激励函数实现复杂的非线性逻辑问题，将利用深度神经网络进行MIMO水声信道均衡的算法记为MIMO-DNN。

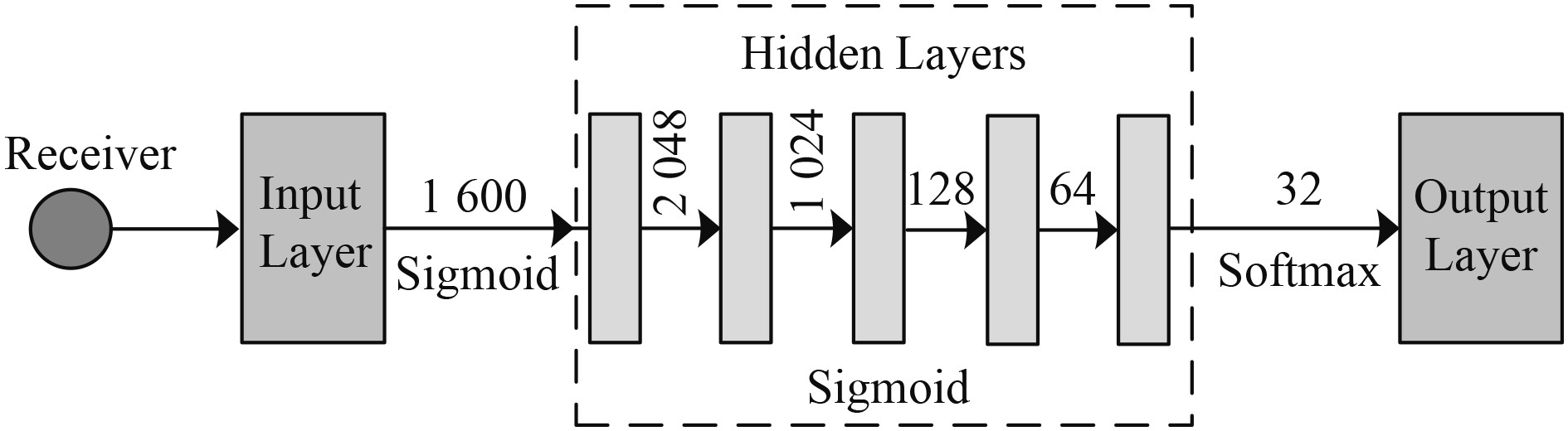
MIMO-DNN的网络结构如图3所示，包含1个输入层、5个隐含层和1个输出层。输入层每个神经元直接对应原始数据，是输入信息的直接来源，可以向隐含层传达信息；隐含层的每个节点对输入层有不同的接收权重，用于特征提取^[8]；输出层的激活函数具有非线性，决定了神经元是否被激活，从而决定信息是否丢弃，最后输出均衡结果。

DNN采用一位有效编码的方式，利用N位状态寄存器对N个状态进行编码，进行多目标分类，各目标之间相互独立，分类不为互斥关系，允许输出层各神经元输出概率之和大于1。MIMO-DNN将信道均衡问题转化为分类问题，通过调制将信号映射到星座图，星座图各点的位置集合视为不同的类别，进而将接收到的信号恢复到对应类别，最后恢复基带信号。

2.2 基于卷积神经网络的均衡算法

卷积神经网络（convolutional neural network，CNN）广泛应用于计算机视觉和图像处理领域，它能对较大维数的数据进行特征提取，加快神经网络的训练过程^[9]。CNN网络主要包含输入层、卷积层、池化层、全连接层和输出层。CNN通过在一般神经网络输入层与隐含层之间添加卷积层进行特征提取与降采样来降低待更新系数的个数。将利用卷积神经网络进行MIMO水声信道均衡的算法记为MIMO-CNN。

MIMO-CNN的网络结构如图4所示，包括1个输入层、3个卷积层（含池化层）、1个全连接层和1个输出层。DNN输出层同样采用一位有效编码方式进行分类，输入层数据格式为4×NL维矩阵，NL表示时域窗口长度占据的码元周期个数，4代表了4路接收信号，包含2个接收阵元的虚部与实部。假设当前时刻为k时刻，以k为中心分别截取每个接收端水听器NL个码元长度的数据，将所有水听器数据拼接后取实部与虚部，就组合成一个4×NL维矩阵的输出数据。

2.3 基于长短期记忆网络的均衡算法

递归神经网络（recursive neural network，RNN）广泛应用于时间序列处理领域。MIMO水声信道均衡中，均衡器输出与当前时刻及之前时刻的输入数据有密切关系，这与RNN提出的应用背景契合。

RNN只能处理短期依赖问题，时间跨度过长会导致梯度消失，进而导致训练失败。而长短期记忆网络（long short-term memory，LSTM）作为一种特殊的RNN，与传统RNN的区别在于其内部增加了3个门控制单元：忘记门、输入门、输出门，这使得它能够有效解决梯度消失与爆炸问题，从而高效处理长时序关系的时间序列问题。

考虑到水声信号属于复杂的时间序列，且单层LSTM中抽头数量较多会使数据无法有效传递到最后时刻，因此需要采用多层双向LSTM网络进行信道均衡处理。双向LSTM包含正反2个方向的LSTM网络，输入数据在时间顺序上相反，这可以有效提高序列分类的性能。将利用长短期记忆网络进行MIMO水声信道均衡的算法记为MIMO-LSTM。

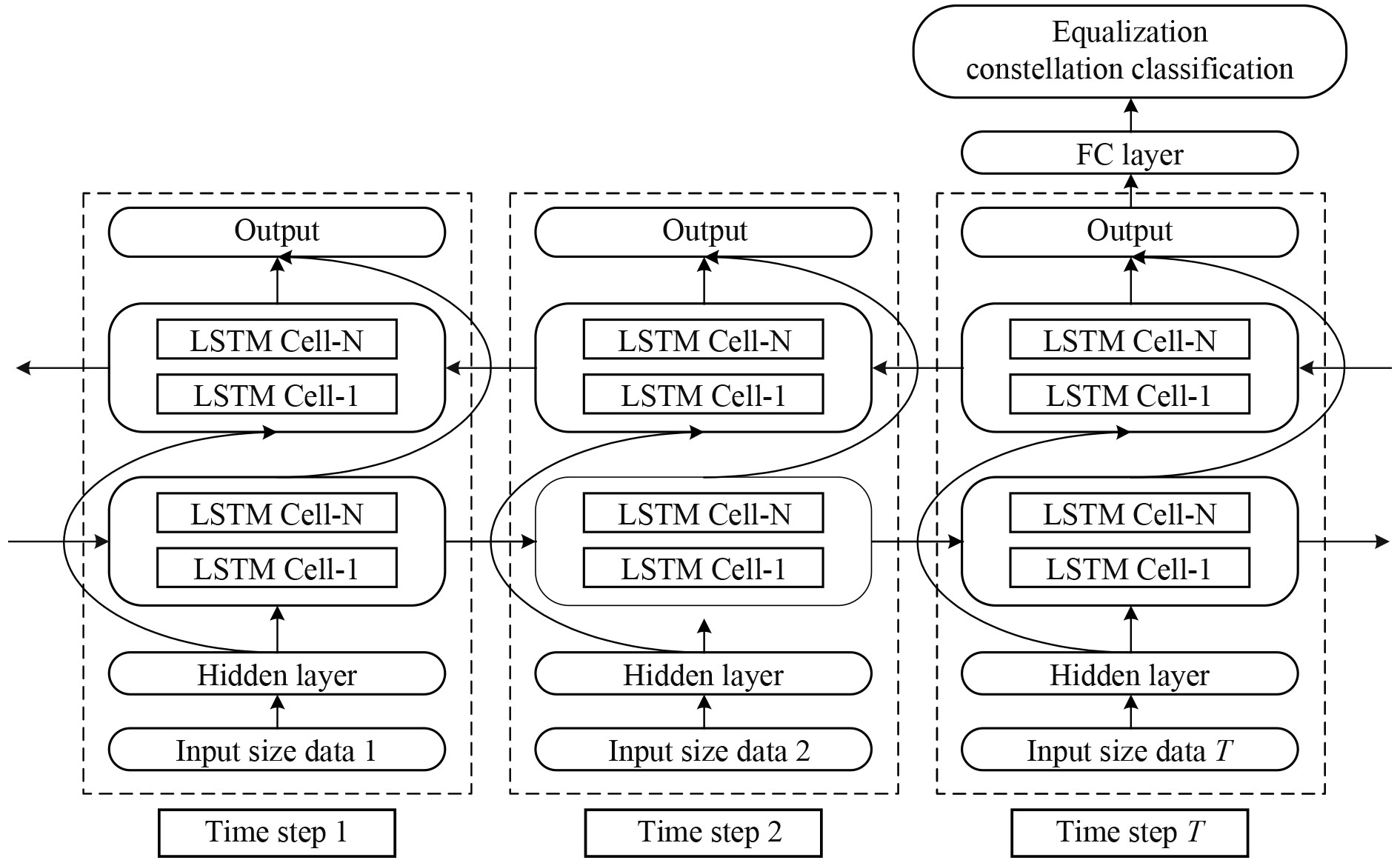
MIMO- LSTM的网络结构如图5所示。其中每个时刻输入一定长度的数据，通过隐含层输入到多层LSTM网络中，最终时刻输出结果通过全连接层进行星座图分类，从而实现信道均衡。

3 算法仿真 3.1 仿真环境与参数设置

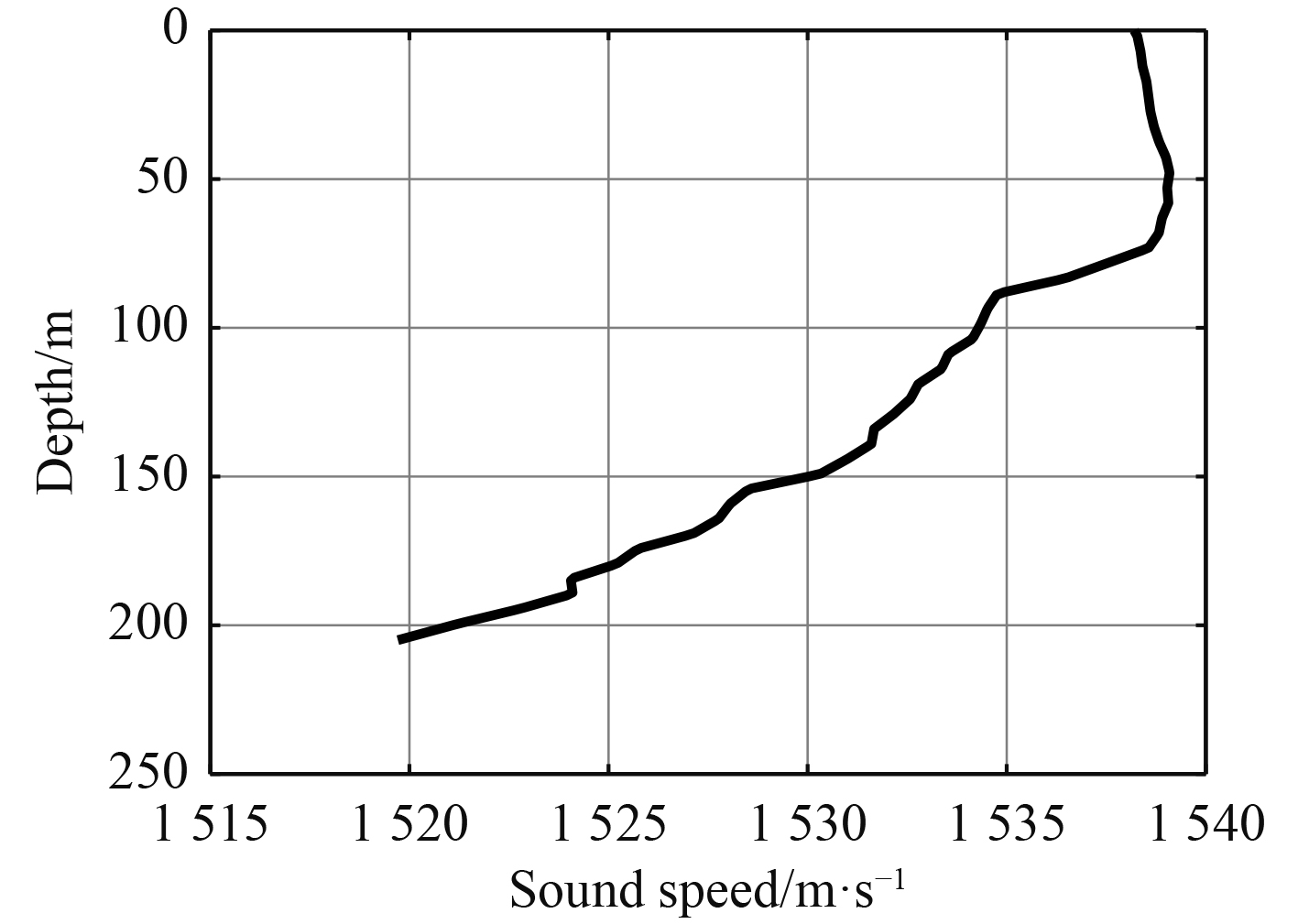
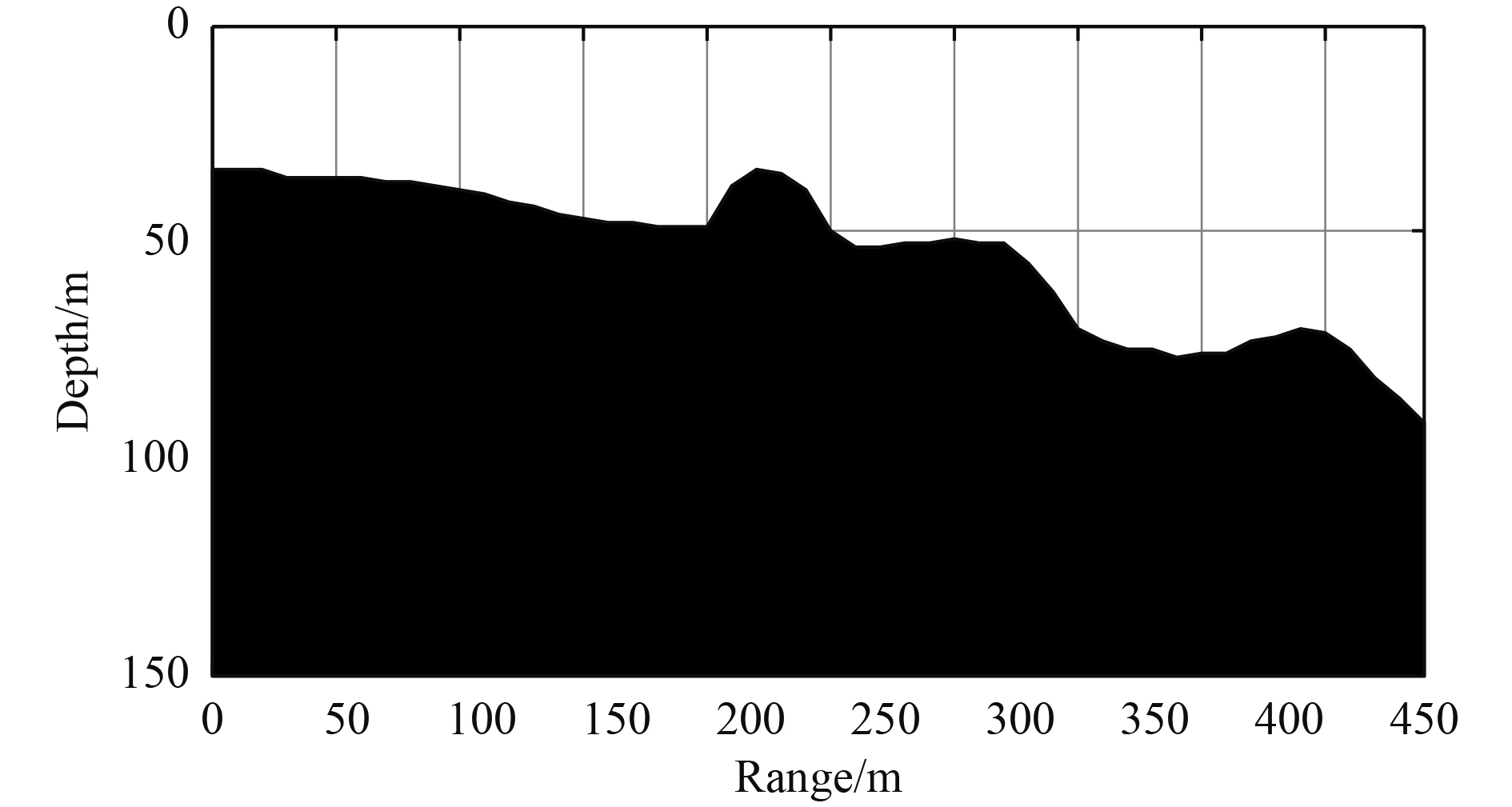
使用Bellhop软件模拟海洋通信环境，采用典型的海域声速剖面及海底地形测高数据构造海洋环境，其中海洋声速剖面曲线如图6所示，海洋测高图如图7所示。

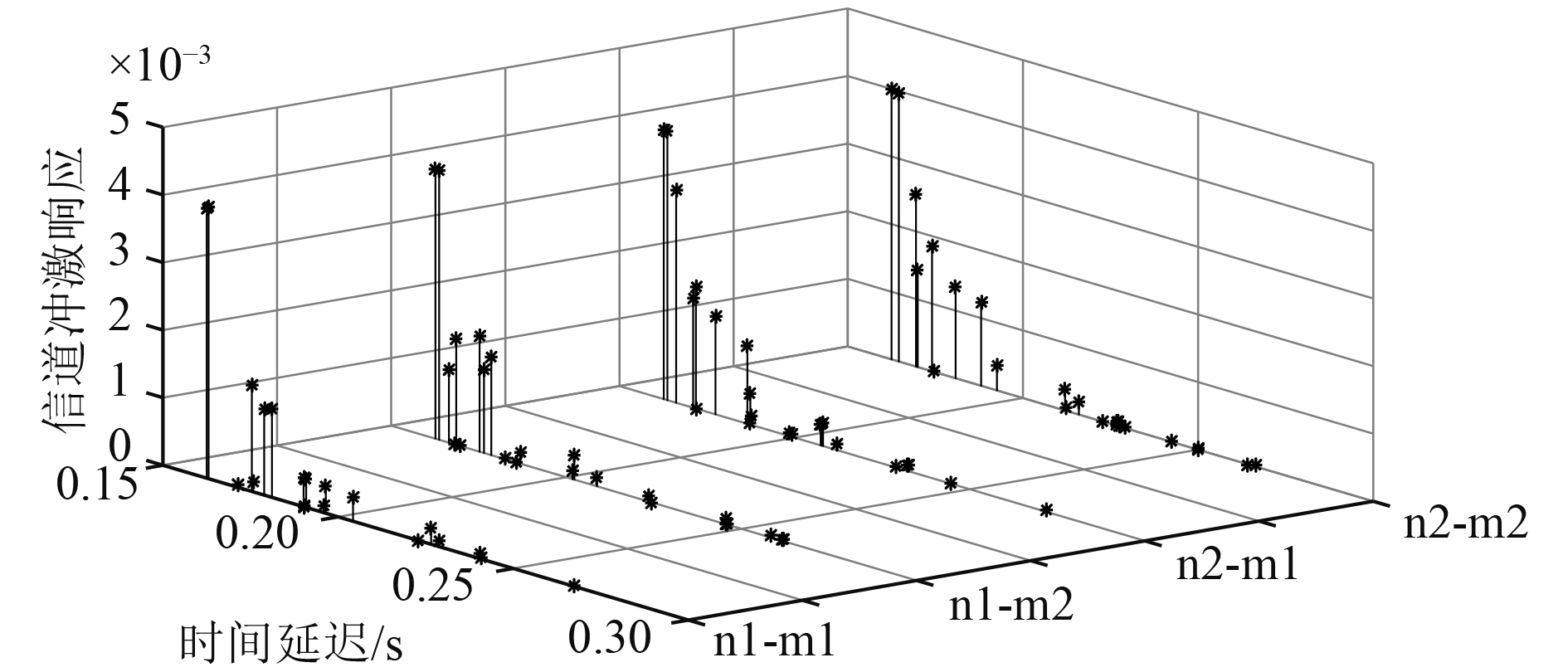
信道冲激响应仿真条件为：通信距离为250 m，水深小于200 m，载波频率 ${f_c} = 10\;{\rm{kHz}}$ ，发射阵元 ${n_T} = 2$ ，接收阵元均为 ${n_R} = 2$ ，发射阵元深度为[10 m, 20 m]。发射阵元的2个发射结点分别发射正交相移键控（quadrature phase shift keying，QPSK）信号，根据信道冲激响应，进行信道卷积，之后叠加高斯白噪声，通过多径传输在接收阵元叠加形成接收信号。本文2×2的MIMO水声信道冲激响应如图8所示，从中可以看出水声信道呈现明显的稀疏特性。

进行MIMO-DNN仿真时，训练数据40000组，测试数据10000组。DNN1网络包含1个输入层，2个隐含层，1个输出层，各层神经元个数： ${J^1} = 1\;600$ ， ${J^2} = 2\;048$ ， ${J^{\text{3}}} = {\text{32}}$ ， ${J^{\text{4}}} = {\text{4}}$ ；DNN2包含1个输入层，5个隐含层，1个输出层，各层神经元个数： ${J^1} = 1\;600$ ， ${J^2} = 2\;048$ ， ${J^{\text{3}}} = 1024$ ， ${J^{\text{4}}} = 128$ ， ${J^5} = {\text{32}}$ ， ${J^6} = 16$ ， ${J^7} = 4$ 。各隐含层激活函数均使用softmax，loss计算采用softmax交叉熵函数，迭代优化器选择Adam，学习速率10⁻³。

MIMO-CNN的卷积核大小均设定为1×N，激活函数使用tanh，池化层选择平均池化（avg_pooling），包含卷积核在内的所有参数均采用随机赋值方式进行初始化。卷积层与全连接层激活函数为tanh，激活函数选择softmax。

MIMO-LSTM的输入数据格式为( batch_size, time_steps, input_size )，其与滑动窗长度N的关系为： $time\_steps \times input\_size = 2NL \times {n_R}$ ，表明LSTM网络的时间跨度为NL个码元周期，设置( batch_size, time_steps, input_size )=（1000,4,400），LSTM Layer cell =[512, 256, 128]；双向LSTM中，fc1的cell=64, dropout=0.2, fc2的cell=32, dropout=0.2,，激活函数使用tanh。输出层的cell=16，激活函数选择softmax。

3.2 仿真结果与分析

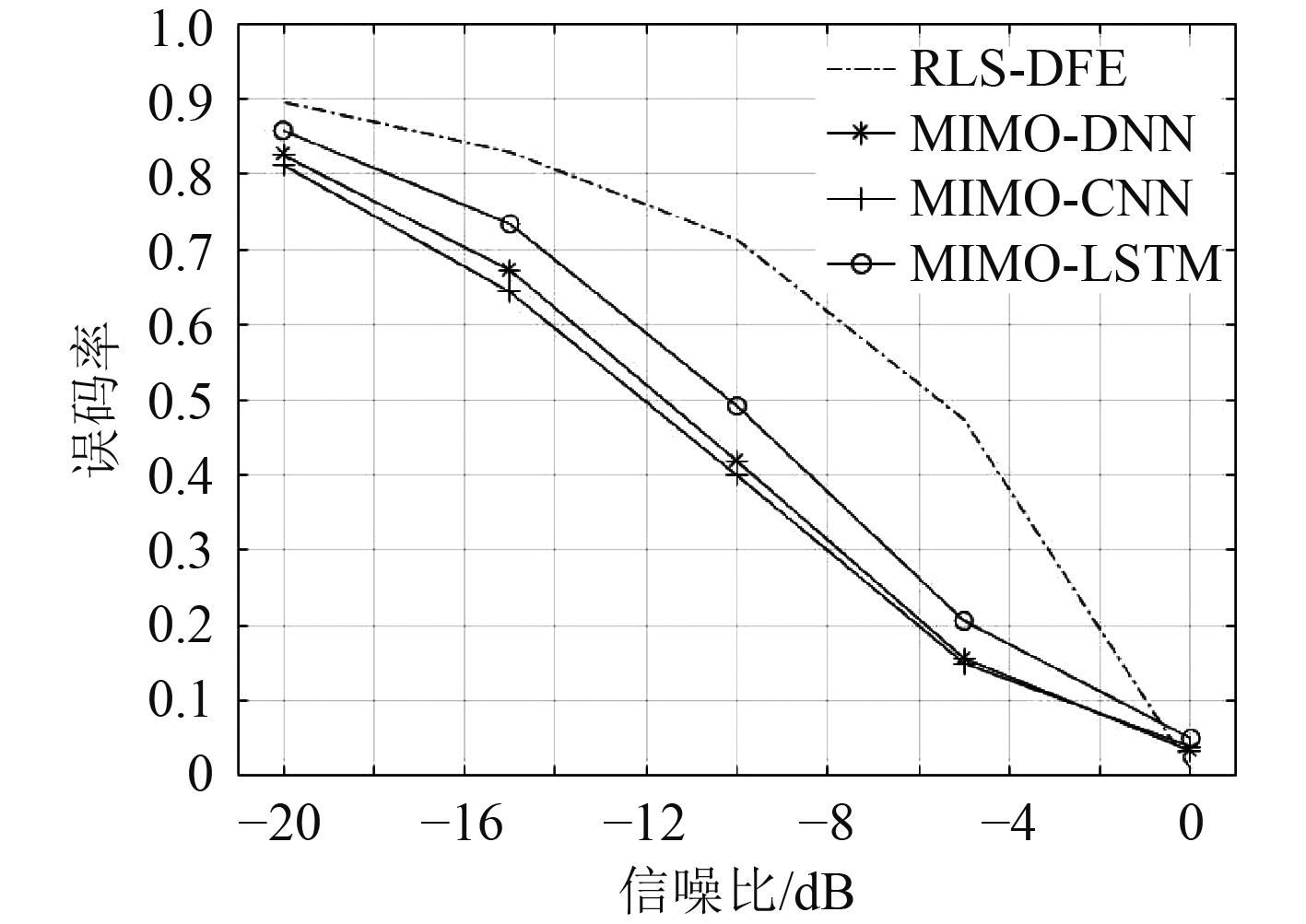
通信系统条件：在信噪比为−20～0 dB的环境下，码元速率 ${f_b} = 2.5\;{\rm{kbps}}$ ，训练序列长度为10000码元，测试长度为15000码元。RLS-DFE信道均常规衡算法及3种基于深度学习网络的均衡算法的误码率（BER）曲线如图9所示。

依据曲线结果，当信噪比低于0 dB时，采用深度学习网络的信道均衡算法误码率均低于传统均衡算法RLS-DFE，且信道均衡算法的误码率都随着信噪比的提高而降低。其中，MIMO-CNN的均衡性能最优，MIMO-DNN次之，对时序更敏感的MIMO-LSTM均衡性能最差，这说明LSTM并不适合单独处理水声信道均衡问题，需要配合其他网络一起使用。同时，MIMO-CNN的误码率始终比MIMO-DNN低，且随着信噪比的增大，两者的误码率逐渐接近。当信噪比为0时，3种算法的误码率均最低，这说明信噪比对均衡算法具有绝对的影响作用。

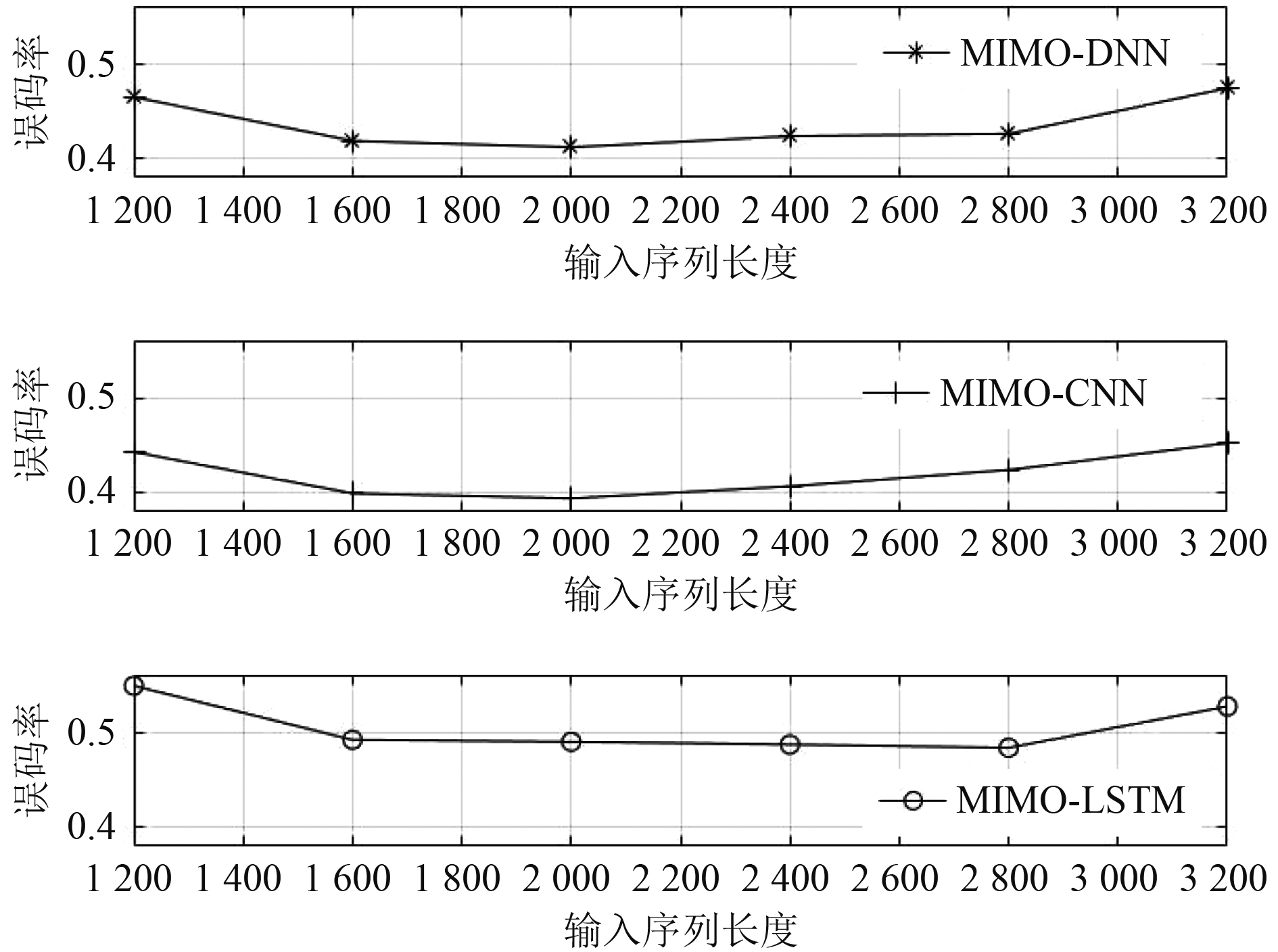
为进一步探索深度学习网络的均衡性能，在信道长度为274码元，信噪比为-10dB条件下研究均衡网络输入序列长度与误码率的关系曲线，如图10所示。

由图可知，基于深度学习的均衡网络性能与输入序列长度并非正相关，输入序列过长反而会导致均衡网络性能下降。输入序列对应的码元长度关系为：

$\begin{aligned}[b] &{{Code\_Length}} = \frac{{{{Input\_Length}}}}{{2{n_R}}}，\\ & 即 Code\_Length = Input\_Length/4 。\end{aligned}$

分析曲线可得知，MIMO-DNN与MIMO-CNN在输入序列长度为2000码元左右，等效约为3.65倍信道长度时误码率最低，均衡性能最佳。MIMO-LSTM在输入序列长度为2400～2800码元之间的误码率低于其他长度范围。3种深度学习均衡网络性能达到最优后，增加或减少输入序列长度都会使误码率提高，因此要设置合理的时间窗长度以提高网络精度，可针对实际情况将上图横坐标进行细化仿真，得到更精细的误码率变化趋势。

4 结　语

本文利用Bellhop获得训练数据集，之后训练3种基于深度学习网络的信道均衡算法，并与传统均衡方法进行比较，最后对实现MIMO信道均衡的3种算法进行性能优劣分析。仿真结果表明，低信噪比环境下，基于深度学习的均衡算法均比常规方法RLS-DFE有更强的信道恢复能力，对信道的补偿作用更佳，且能够有效减弱水声通信中多径时延带来的码间串扰问题。本文算法对比结果表明，最优水声通信信道均衡方法为基于卷积神经网络的均衡算法，且最优的输入序列截取时间窗为2000码元，等效约3.65倍信道长度时误码率最低，均衡性能最佳。