轴承作为舰船装备的核心部件之一,一旦出现故障,如不能及时维修,将会严重影响舰船的战斗力,造成人力物力损失。为了防止滚动轴承因故障而造成一系列损失,因此对设备进行故障诊断并发现设备内部零件的早期故障,根据诊断结果进行视情维修具有重大意义。
结合机器学习算法和原始振动数据进行滚动轴承故障诊断一直是专家学者的研究热点[1]。当设备发生故障时,传感器测得振动数据中时频域信息发生改变,不同故障的特征信息也存在差异[2]。但是通过神经网络等算法提取的特征比较抽象、可解释性弱[3],不利于直观分析原始特征对故障诊断的影响,本文直接选取时域、频域和时频域特征进行分析。在诊断中发现提取到的特征通常会包含干扰信息,如果没有对特征进行筛选,易产生维度灾难和过拟合现象,从而导致模型准确率低[4]。因此本文利用Cat Boost算法在所提取特征中进行筛选,并通过基尼指数快速建立树结构并进行特征排序选取有效特征,并分析不同特征对诊断结果的影响。
Cat Boost(category boosting)是一款梯度提升机器学习库,不需要像其他模型那样进行广泛的数据训练[5],具有高效合理处理类别型特征的优点。本文将Cat Boost算法应用于滚动轴承智能诊断研究中,并将该方法与BP(back propagation)神经网络[6]和支持向量机[7](support vector machine,SVM)算法进行比较,验证该方法的可行性。
1 多特征提取 1.1 时域特征提取时域特征参数分析是指在时域范围内对原始振动信号的统计量参数进行计算[8]。振动信号的时域特征通常提取过程相对简单,可分为无量纲特征和有量纲特征,其中有量纲特征指标对振动信号的异常频率较敏感,与轴承实际的运行工况有关,易受噪声影响;无量纲特征对于早期发生故障或一些危害性不大的故障有较高的敏感性。
本文选择的特征1~特征12为有量纲指标,分别是:最大值、最小值、峰峰值、平均值、平均幅值、均方值、均方根值、方差、峭度、斜度、方根幅值、标准差。以均方值为例,其表示振动信号的二阶矩,可以通过数值大小直接表征信号的能量值。
实际情况中,有量纲指标会因工况变化而受到较大环境干扰。为排除其他干扰因素,选择特征13~特征18为无量纲指标,分别是:波形指标、裕度指标、峰值指标、斜度指标、脉冲指标、峭度指标。本文选取时域特征共18个,其中大部分为原始振动信号的统计量参数。以裕度指标为例,其计算公式如下:
| $ L = \frac{{{x_{{\rm{max}}}}}}{{{{\left(\dfrac{1}{N}\displaystyle\sum\limits_{i = 1}^N {\sqrt {\left| {{x_i}} \right|} } \right)}^2}}}。$ |
式中:
频域特征在频域范围进行提取,通常有频谱分析、包络分析等[9]。频域特征被广泛用于旋转机械的振动信号分析中,相对于时域特征,在频域内对信号进行分析往往更加直观,本文选择的特征19~特征28为频域特征参数,分别是:重心频率、频率方差、均方频率、频域幅值平均值、频域幅值最大值、频域幅值斜度指标、频域幅值峭度指标、均方根频率、频域幅值标准差、频域幅值最小值。以均方频率为例,其计算公式为:
| $ {F_{msf}} = \frac{{\displaystyle\sum\limits_{k = 1}^k {f_k^2s(k)} }}{{\displaystyle\sum\limits_{k = 1}^k {s(k)} }} 。$ |
式中:
频域分析对平稳信号效果较好,对非平稳信号分析不够精确。一些专家学者在时频域分析方面进行了大量研究,经验模态分解方法[10]是由Huang等在1998年提出的一种信号处理方法,该方法基于数据本身的时间特征,无需预设基本函数即可执行信号分解。EMD分解过程的基本步骤是:
对原始信号
| $ {h_1}\left( t \right) = x\left( t \right) - {m_1},$ |
若
得到一阶IMF分量
重复步骤1和步骤2,迭代循环
用
| $ {x_1}\left( t \right) = \sum\limits_{i = 1}^k {{c_i}\left( t \right)} + {r_{k + 1}}\left( t \right),$ |
计算各组各IMF分量和余量的相关系数及能量,相关系数采用皮尔森相关系数[11],
| $ Corr({c_i},{X_j}) = \frac{{\displaystyle\sum\limits_{n = 1}^N {[{c_i}(n) - \widehat {{c_i}}][{X_j}(n) - \widehat {{X_j}}]} }}{{\sqrt {\displaystyle\sum\limits_{n = 1}^N {{{[{c_i}(n) - \widehat {{c_i}}]}^2} \cdot {{[{X_j}(n) - \widehat {{X_j}}]}^2}} } }} ,$ |
能量占比为各IMF分量信号的能量信号与原始振动信号能量的比值,其计算公式如下式:
| $ EnergyRati{o_j}\left( i \right) = \frac{{\displaystyle\sum\limits_{i = 1}^N {{{\left| {{c_i}} \right|}^2}} }}{{\displaystyle\sum\limits_{i = 1}^N {{{\left| {{X_j}} \right|}^2}} }} 。$ |
本文在对不同故障类型的振动数据进行EMD分解时发现,IMF分量数目并不相同,且能量占比随阶数的升高而逐渐减少。为保证所选取的特征参数有意义,本文选择特征29~特征36分别为IMF1~IMF8与原始信号相关系数的大小,选择特征37~特征44分别为IMF1~IMF8所占原始信号的能量占比,若在EMD分解中分量数目不足,则对应的特征输入为0。
2 故障诊断方法Cat Boost[12]是一种基于boosting能够很好地处理类别型特征的梯度提升算法库。其具有两大优势,一是在模型训练过程中自动选择效果较好的特征,避免了人为特征筛选过程;二是计算叶子节点的算法可以避免过拟合现象[13]。在决策树的过程中,可以用基尼指数[14](Gini index)作为评价指标来衡量特征重要性。
基尼指数将变量重要性评分用VIM表示,将Gini指数用GI来表示,假设有m个特征
Gini指数的计算公式为:
| $ G{I_m} = \sum\limits_{k = 1}^{|K|} {\sum\limits_{k' \ne k} {{p_{mk}}{p_{mk\prime }}} } = 1 - \sum\limits_{k = 1}^{|K|} {p_{mk}^2} 。$ |
其中:K为一个系统中有K个类别;
特征
| $ VIM_{jm}^{({\rm{Gini}})} = G{I_m} - G{I_l} - G{I_r},$ |
如果特征
| $ VIM_{ij}^{({\rm{Gini}})} = \sum\limits_{m \in M} {VIM_{jm}^{({\rm{Gini}})}},$ |
假设共有n颗树,那么
| $ VIM_j^{({\rm{Gini}})} = \sum\limits_{i = 1}^n {VIM_{ij}^{({\rm{Gini}})}} 。$ |
最后,把所有求得的重要性评分归一化处理。
| $ VI{M_j} = \frac{{VI{M_j}}}{{\displaystyle\sum\nolimits_{i = 1}^c {VI{M_i}} }}。$ |
在构建决策树的过程中,还有一种较为常见的信息熵法,通过对比2种指标,信息熵的计算相较基尼指数的计算稍慢,信息熵在计算中包括非线性对数函数,基尼指数的计算过程明显简单许多。2种方法对于模型优化来说影响较小,因此本文选择基尼指数作为评价指标。
根据上述选择的评价指标Cat Boost算法的建模步骤为:
步骤1 设置n+1个不同的样本排序方式;
步骤2 初始化用于计算叶子结点i取值的模型Mode0,Mode1,…,Moden;
步骤3 在第t次循环中,建立新树结构Treet,并更新该排序方式下的模型;
1)基于选取的排序方式以及当前模型Moder,估计每一个样本点的梯度大小gradr(i);
2)对每一种可行方案a,建立各自的树结构Treea,计算所有样本基于Treea和排序σr所属的叶子结点,并求解每个叶子结点的所有样本梯度的均值avg(gradr(p))作为该叶子结点样本的梯度的估计值delta(i);
3)构造梯度值损失函数loss(Tc),选取使损失函数取最小值的树结构作为本轮的树模型Treet;
4)更新每种排序策略σr对应的Moder;
步骤4 使用该排序计算Ordered TS,基于树Treet确定每个样本所属的叶子结点,运用基尼指数VIM得到一个将训练集一分为二的所有可能划分中最优的一个;
步骤5 基于样本排序以及模型,估计每一个样本点的梯度值;
步骤6 对于Treet上每一个叶子结点,计算叶子结点的值,即所有属于该叶子点的样本的负梯度均值;
步骤7 更新Mode0。
Cat Boost算法进行特征重要性分析的优点在于不需要额外去做特征选择,因为模型训练的过程中自身已经完成了特征选择,得到了不同特征的评价得分,根据这些得分大小就可得到不同特征对应模型的特征贡献度。
3 工程试验 3.1 数据集来源试验台主要由滚珠轴承、可拆卸轴承座、电机以及调速转置等部分组成。
试验是在试验台所配套的ER-16K系列滚珠轴承上进行的,滚珠个数为9个。该故障试验中轴承损伤是用电火花加工造成的单点损伤,分别在内圈、外圈和滚动体上利用电火花预制了故障。所用加速度传感器竖直安装在待测轴承的轴承座上,采集轴承在不同工作状态下,不同负载和载荷的振动加速度信号,其采样频率为12 kHz。滚珠轴承的转速通过电动机按照需要进行调节,分别在转速为1800 r/min,2400 r/min及3000 r/min等3种工况下,经过放大、滤波后,通过数据采集系统进行信号采集。
每个工况下各设置了3种常见的故障类型,外圈故障(OR)、内圈故障(IR)和滚动体故障(B)以及1个正常状态,总共10类(见表1)。分别采集电机端轴承座(DE)、末端轴承座(FE)和基座(BA)3个相关联位置的振动加速度信号。
|
|
表 1 滚动轴承故障数据分类示意表 Tab.1 Schematic table of rolling bearing fault data classification |
将3种不同工况下不同故障位置的原始信号各选取102400个时间连续的振动值,将连续的1024个振动信号值划分为一组,即每种原始信号分成100组进行时域、频域、时频域信号的特征提取,得到特征矩阵
通过上述计算方法分别提取振动数据的不同维度特征,构建原始的特征子集。再观察不同工况下的数据变化趋势,通过去除对诊断结果影响不大的特征达到减小模型训练时间和数据冗余的效果。在本文所选择的时域、频域、和时频域指标中,不同的特征对模型训练准确度高低存在一定的影响,同时一些特征与其他特征共同输入时可能对模型准确度提高不大且增加训练时间,通过特征选择筛选最佳的特征子集解决以上问题。
特征选择可以在一定程度上优化模型的性能,一是可以减少特征的数量达到降维的效果,使得模型的泛化能力更强,降低过拟合的可能性;二是可以凸显出特征对待解决问题的贡献量,增强对特征参数如时域、频域和时频域参数在滚动轴承故障智能识别方面的理解,为工程实践中选择特征进行监测诊断提供理论依据。
特征选择算法往往会用到评分方法排名和选择特征,比如特征的相关性或其他确定特征重要性的方法。常见故障类型的时域特征、频域特征与正常数据都有较为明显的差别,对于不同组数间除滚动体故障在特征值上与重叠的区间,内圈故障与外圈故障都有较为明显的区分。EMD分解得到时频域特征有一定差别,可以在后续的算法中结合其他特征提升算法精度。同时同一种故障类型在不同转速下的故障特征也有细微差别,可以用来做故障诊断分类的特征输入。对于一些随工况变化特征数值变化较小的特征,考虑将其通过预处理的方式剔除,防止数据在仿真分析中造成时间复杂度的冗余。
考察特征指标的性能时,通常使用敏感性和稳定性。敏感性是指数据特征在正常工况和故障工况下有明显的辨识度,可以反映轴承故障所导致的冲击信号、磨损信号等;稳定性是指在固定工况下一定范围内的特征参数也在一定范围内变化。为量化特征指标的敏感性和稳定性,采用标准差和几何平均数评判各振动参数的离散度。
计算各工况下选取的44维特征的标准差以及每组工况下不同特征的试验数据几何平均数,通过对比得到敏感性较差的特征和稳定性较差的特征,如表2所示。
|
|
表 2 敏感性较差的特征指标 Tab.2 Characteristics with poor sensitivity |
对于敏感性和稳定性表现都差的特征指标,如高阶次的IMF分量所占原始信号的能量比,在两项评价指标中都排在靠后的位置,因此人为筛选并淘汰掉IMF5~IMF8分量所占能量比这4个特征,最终确定提取并保留的特征有40维。
3.3 仿真分析 3.3.1 不同分类方案精度评价与比较将提取到的40维特征代到Cat Boost模型进行验证,选取目前有代表性的主流智能诊断算法BP神经网络和支持向量机算法作为对比,通过对比训练网络的准确度验证Cat Boost模型的有效性,得到的不同算法网络训练准确度如表3所示。
|
|
表 3 五次模型训练准确度 Tab.3 Five times model training accuracy |
为了验证Cat Boost模型对滚动轴承不同工况下故障诊断的可行性,将其与BP和SVM模型进行对比。3种方法的输入数据均采用上述提取的特征,训练模型时采取同一拆分策略的训练集和测试集。其中SVM关键参数选取高斯(rbf)核函数、惩罚系数为C=100。BP神经网络包含2层隐含层,分别有100和50个神经元。3种模型均采用交叉验证方法,随机选择样本中75%的数据为训练数据,余下25%的样本数据为测试样本。BP神经网络利用特征样本进行训练后,识别率为81.44%,使用常规SVM轴承故障诊断方法,经过选取较合适的参数后识别率能够达到94.04%,但是仍然低于本文提出的Cat Boost模型分类结果。
3.3.2 基于Cat Boost模型的特征评价及降维在模型训练过程中,Cat Boost算法利用基尼指数计算40维特征的重要性,并把前20维特征重要性列举如图1所示。

|
图 1 前20维特征重要性排序图 Fig. 1 The importance Ranking diagram of the TOP 20 characteristics |
前20维特征指标中,共包含13个时域特征,6个频域特征,1个时频域特征,但排名靠前的特征指标中,频域特征较多。进一步分析可以得到,峰值可以用来检测振动信号中是否存在冲击,对于滚动轴承的运行,故障的存在会导致滚动体在内圈、外圈中不断产生与正常信号不一致的冲击信号;频域幅值峭度指标也是一个较为关键的特征指标,可以反映振动信号的冲击特性。
本文按照特征指标在重要性排序后的顺序,将不同维度的特征指标作为3种算法的输入,进而得到在相同输入下模型的准确率。不同特征维度下算法对滚动轴承故障诊断的准确度图和Cat Boost模型在特征维度等于10时模型识别准确率的混淆矩阵如图2和图3所示。

|
图 2 不同维度下3种算法的准确度变化曲线 Fig. 2 The accuracy curves of three algorithms under different dimension input |
由图2可以发现对于Cat Boost模型,不同维度的准确率都要优于对比算法,且特征维度在维度较低时就能达到90%左右,在特征维度小于10时随维度的增加,模型的准确率不断提升,当特征维度进一步增大,准确率基本保持不变,维持在99.5%左右。图3中有9个类别分类达到100%准确率,Cat Boost模型在对2和5分类中出现错误,即滚动体故障在1800 r/min和2400 r/min这两类中出现错误,分析原始时两组数据差距较小,提取的特征在面对差距较小时难以通过数值来进行分类。总体而言,Cat Boost模型可以达到期待的准确率。
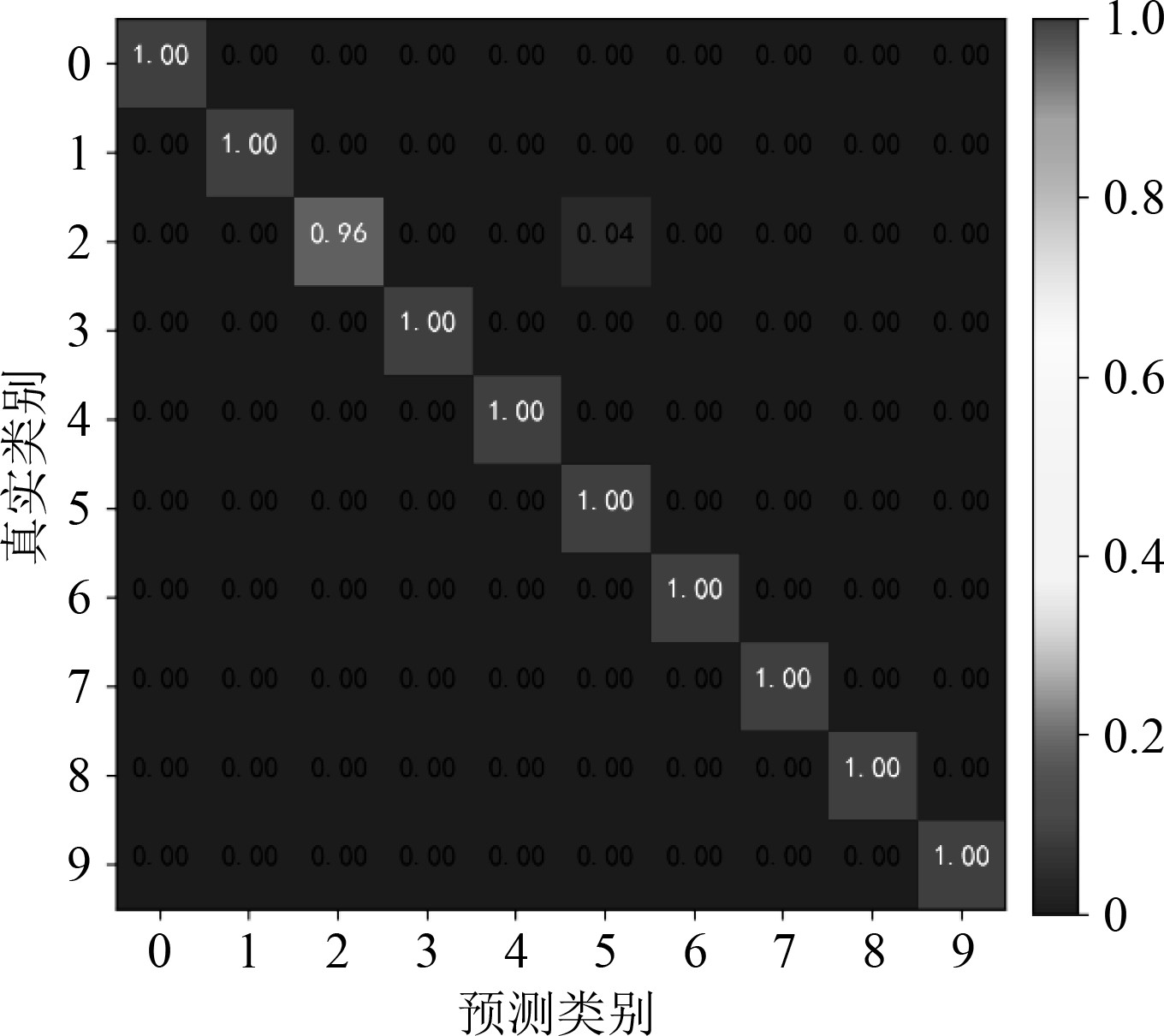
|
图 3 特征维度为10时Cat Boost算法分类的混淆矩阵 Fig. 3 The confusion matrix of Category Boosting classification when the feature dimension is 10 |
本文通过滚动轴承振动信号混合域包括对时域、频域及时频域的特征提取形成初选特征,为接下来的滚动轴承的故障诊断进行了预处理。通过数据分析以及试验可以得出以下结论:
本文选取时域、频域、时频域内较多特征指标,通过检验筛选合适的特征,构造多维特征输入作为滚动轴承精细化故障分类的特征。通过试验结果分析,在Cat Boost模型训练平均准确率可以达到99%以上。该模型的诊断精度高于传统方法,适用于滚动轴承故障的精确诊断;Cat Boost模型中Gini指数的运用可以减少模型算法的时间复杂度,通过阈值的设置,可以更加快速的寻优,建立树结构;基于Cat Boost的特征选择方法提取的特征对于滚动轴承的故障诊断有较好的效果。通过试验结果分析,Cat Boost模型可以有效的将高维特征降维,减少数据冗余的现象,在保证识别准确率的基础上减少模型计算量和训练时间,同时根据特征重要性排序结果给滚动轴承的故障机理提供参考。
| [1] |
吴国文, 田杨阳, 毛文涛. 基于特征融合的滚动轴承在线故障诊断[J]. 控制与决策, 2018: 2–7.
|
| [2] |
李俊, 刘永葆, 余又红. 卷积神经网络和峭度在轴承故障诊断中的应用[J]. 航空动力学报, 2019, 34(11): 2423-2431. DOI:10.13224/j.cnki.jasp.2019.11.014 |
| [3] |
李郅琴, 杜建强, 聂斌, 等. 特征选择方法综述[J]. 计算机工程与应用, 2019, 55(24): 10-19. DOI:10.3778/j.issn.1002-8331.1909-0066 |
| [4] |
崔宇佳, 张一迪, 王培志, 等. 基于多评价标准融合的医疗数据特征选择算法[J]. 复旦学报(自然科学版), 2019, 58(2): 250-255+268. DOI:10.15943/j.cnki.fdxb-jns.2019.02.015 |
| [5] |
苏庆, 林华智, 黄剑锋, 等. 结合CNN和Catboost算法的恶意安卓应用检测模型[J]. 计算机工程与应用, 2021, 57(15): 140-146. DOI:10.3778/j.issn.1002-8331.2004-0385 |
| [6] |
MCCLELLAND J L, RUMELHART D E, Hinton G E. Une nouvelle approche de la cognition : le connexionnisme[J]. Le Débat, 1987, 47(5).
|
| [7] |
CORINNA C, VLADIMIR V. Support-vector networks[J]. Machine Learning, 1995, 20(3).
|
| [8] |
崔立明. 中介轴承寿命预测方法与寿命试验研究[D]. 大连: 大连理工大学, 2016.
|
| [9] |
洪振麒. 基于多特征融合的滚动轴承剩余寿命预测方法研究[D]. 沈阳: 沈阳大学, 2021.
|
| [10] |
周小龙, 杨恭勇, 梁秀霞. 基于EMD重构和SVM的滚动轴承故障诊断方法研究[J]. 东北电力大学学报, 2016, 36(6): 71-6. DOI:10.3969/j.issn.1005-2992.2016.06.014 |
| [11] |
VEER L J, DAI H, VIJVER M J, et al. Gene expression profiling predicts clinical outcome of breast cancer[J]. Nature, 2002, 415(6871): 530-536. DOI:10.1038/415530a |
| [12] |
PROKHORENKOVA L, GUSEV G, VOROBEV A. CatBoost: unbiased boosting with categorical features[C]//Advances in Neural Information Processing Systems, 2018: 6638-6648.
|
| [13] |
姜琦刚, 杨秀艳, 杨长保, 等. 基于CatBoost算法的面向对象土地利用分类[J]. 吉林大学学报(信息科学版), 2020, 38(2): 185-191. DOI:10.19292/j.cnki.jdxxp.2020.02.028 |
| [14] |
GOLDSTEIN B A, POLLEY E C, BRIGGS F B S. Random forests for genetic association studies. [J]. Statistical Applications in Genetics and Molecular Biology, 2011, 10(1).
|
 2022, Vol. 44
2022, Vol. 44
