0 引　言

电网系统是船舶航行的基础功能保障^[1]。为确保船舶电网系统供电的可靠性与不间断性，需定期评估船舶电网系统状态，由此才能及时发现故障与隐患^[2]，根据评估结果进行检修与设备更换，实现船舶电网系统稳定供电。

邢晓敏等^[3]在研究电网状态评估问题时，利用云模型计算评估指标隶属度，并采用D-S证据理论将隶属度转换为信任度，基于最大信任度获取评估结果。但该方法所使用的评估指标过于复杂，导致评估结果产生偏差。毕超超等^[4]在船舶电网状态评估问题中采用伪时序算法，对电网状态评估指标仿真量实施幅值，通过幅值结果的监控获取评估结果。该方法在使用过程中未考虑评估指标的模糊性，导致最终评估结果在特定情况下产生偏差。

针对上述问题，研究基于进化差分算法的船舶电网系统状态评估方法，并通过测试验证该方法的应用性能。

1 船舶电网系统状态评估方法 1.1 基于差分进化算法的评估指标选取

采用文献法与专家咨询法构建船舶电网系统状态评估指标体系^[5]，获取包含8个一级指标与19个二级指标的初始船舶电网系统状态评估指标体系。船舶电网系统状态评估过程中，一般希望最大限度考虑船舶电网系统状态评估指标体系内全部指标，同时所得船舶电网系统状态评估结果可令全部样本处于最显著区域状态，由此完成整体船舶电网系统状态评估过程。但船舶电网系统状态评估过程中，初始船舶电网系统状态评估指标体系内包含的指标维度过多，在实际评价过程中将存在评估过程过于复杂导致效率较差的问题。针对这一问题，采用差分进化算法在初始船舶电网系统状态评估指标体系内进行全局搜索，对初始船舶电网系统状态评估指标体系内所包含的指标进行筛选，构建最终用于评估船舶电网系统状态的指标体系。设船舶电网系统状态评估指标共维，由此可通过 $ X{\text{ = }}\left[ {{x_1},{x_2}, \cdots ,{x_i}} \right]\left( {i = 1,2, \cdots ,19} \right) $ 表示船舶电网系统状态评估指标。全部船舶电网系统状态评估指标数据数量为 $ m $ ，可通过式(1)描述船舶电网系统状态整体评估指标矩阵：

$ {\boldsymbol{X}} = \left[ \begin{array}{*{20}{c}} {x_{11}}, & {x_{12}}, & \cdots , & {x_{1i}} \\ {x_{21}}, & {x_{22}}, & \cdots , & {x_{2i}} \\ { \vdots } & { \vdots } & { \cdots} & \vdots \\ {x_{m1}}, & {x_{m2}}, & \cdots , & {x_{mi}} \end{array} \right]。$

(1)

以 ${\boldsymbol{W}}' = \left[ {{{w'}_1},{{w'}_2}, \cdots ,{{w'}_i}} \right]$ 和 $ {G_m} $ 分别表示各船舶电网系统状态评估指标权重和不同评估指标数据的得分，由此能够得到：

$ G = {\left( {X \times W'} \right)^{\rm{T}}}。$

(2)

式中， $ T $ 表示搜索次数。

以船舶电网系统状态评估指标数据评估获取最大区分度为目的^[6]，令船舶电网系统状态评估指标数据得分的方差达到上限值，公式描述如下：

$ {\hat W^ * } = \arg {\max _W}\left( {{var} \left\{ G \right\}} \right)，$

(3)

式中， $ {var} \left\{ G \right\} $ 表示权重编码的适应度。

为避免差分进化算法陷入局部最优问题，对其进行改进，具体过程描述如下：

步骤1　任意生成权重编码，即 $ {W'_i} = [ {{w'}_1},{{w'}_2}, \cdots , {{w'}_i} ] $ 表示第i个权重编码。

步骤2　在 $ m $ 个权重编码内任意选取e个，分别为 $ {W'_i} $ ， $ {W'_j} $ 和 $ {W'_k} $ ，对三者实施变异处理获取新的权重编码 $ {D_i} $ ，公式描述如下：

$ {D_i} = {W'_i} + S \times {W'_j} - S \times W'，$

(4)

式中， $ S $ 表示缩放因子。

通过 $ m $ 次运行式(4)获取m个新的 $ {D_i} $ 。

步骤3　分别对 $ m $ 个新的 $ {D_i} $ 实施交叉处理，并由其中全部权重编码内选取一个 $ {w'_i} $ 同 $ {D_i} $ 实施交叉处理。

步骤4　确定各 $ {var} \left\{ G \right\} $ ，选择适应度最大的 $ m $ 个权重编码作为新的权重编码集合。

步骤5　循环运行步骤2~步骤5至满足终止要求为止。

步骤6　选择最大的 $ {var} \left\{ G \right\} $ 作为不同船舶电网系统状态整体评估指标的权重。依照权重值对初始船舶电网系统状态评估指标体系内的指标进行筛选。

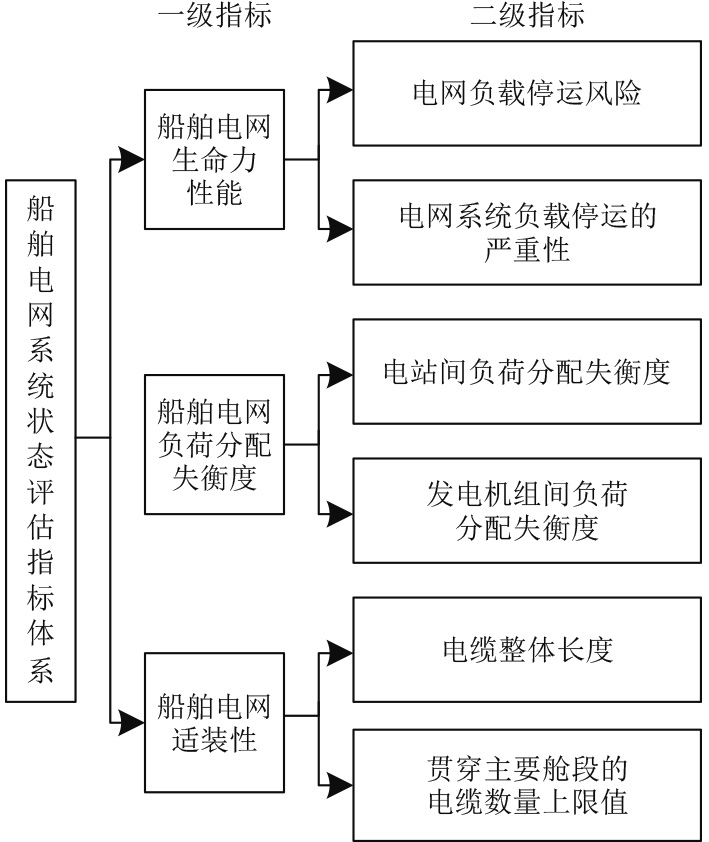
利用差分进化算法筛选船舶电网系统状态评估指标能够最大限度考虑船舶电网系统状态评估指标的数据特征，并防止产生某一重要评估指标被遗漏的问题。通过上述评估指标筛选过程，得到图1所示的船舶电网系统状态评估指标体系。

作为船舶电网系统设计与应用的基础要求，电网系统的生命力要求其在受到损害或形成故障的条件下，最大限度确保较为关键的负载不间断供电。因此船舶电网系统生命力性能可从电网系统负载停运风险与电网系统负载停运的严重性两方面分析，两指标值同船舶电网系统生命力性能呈反比例相关。依照船舶电网系统设置的特性，负荷分配失衡度可通过电站间负荷分配失衡度与发电机组间负荷分配失衡度描述，两指标值同船舶电网系统失衡度呈正比例相关。船舶电网系统的适装性即对其内部元件布设的合理性产生影响，还对船舶结构强度与防灾性能产生影响，所以需对其进行相应约束。适装性可通过电缆整体长度与贯穿主要舱段的电缆数量上限值进行描述，两指标值同船舶电网系统适装性呈反比例相关。

1.2 模糊综合评估

由于船舶电网系统生命力性能负荷分配失衡度在实际计算过程中具有一定模糊性，因此在评估船舶电网系统状态过程中选取模糊综合评估方法，具体评估过程为：

1）确定被评估的船舶电网系统；

2）构建评估指标集 $ X{\text{ = }}\left[ {{x_1},{x_2}, \cdots ,{x_i}} \right] $ ；

3）构建评估结果的评价集 $ P $ ；

4）确定权重集。设定 $ {x_1},{x_2}, \cdots ,{x_i} $ 的权重分别为 $ {w_1},{w_2}, \cdots ,{w_i} $ ，同时符合式(5)标准：

$ \sum\limits_{i = 1}^i {{W_i}} = 1。$

(5)

5）以 $ R = {\left( {{r_{ij}}} \right)_{h \times m}} $ 表示综合评估矩阵，其能够描述 $ X $ 与 $ P $ 的模糊相关性，其中 $ {r_{ij}} $ 表示指标在评估等级 $ {p_j} $ 上的隶属度， $ h $ 和 $ m $ 分别表示评估等级数量和评估指标数量。以令结果归一化为目的，设 $ {r_{ij}} $ 符合 $ \displaystyle\sum\limits_{j = 1}^m {{r_{ij}}} = 1 $ 。

6）利用式(6)实施船舶电网系统状态模糊综合评估运算：

$ \left\{ \begin{gathered} B = W \times R = \left( {{b_1},{b_2}, \cdots ,{b_h}} \right) ，\\ {b_j} = \mathop \vee \limits_{i = 1}^m \left( {{w_i} \wedge {r_{ij}}} \right) 。\end{gathered} \right. $

(6)

7）利用式(7)计算船舶电网系统状态评估结果：

$ \left\{ \begin{gathered} {P_r} = \sum\limits_{j = 1}^h {{\beta _j}{p_j}} ，\\ {\beta _j} = \frac{{{b_j}}}{{\displaystyle\sum\limits_{j = 1}^h {{b_j}} }} 。\end{gathered} \right. $

(7)

2 测试结果与分析

为验证本文基于差分进化算法的船舶电网系统状态评估方法在实际评估船舶电网系统状态时的应用效果，选取某60 m全回转车客渡轮的电网系统为测试对象。测试对象内主要包括电站、电网线路、电网负荷等。电站是测试对象最主要部分，其中包含原动机、发电机配电板与蓄电池等。测试对象内包含2个主电站与1个应急电站，各主电站内分别包含3台三相交流发电机组，不同机组间既能够单机运行，同时还能够进行并联运行。测试对象整体装机容量高达数十万千伏安，为船舶内不同用电设备供电。在测试对象内发电机配电板存在部分故障(并不影响测试对象继续运行)的条件下，采用本文方法对其状态进行评估。

2.1 评价指标信度检验结果

检验本文方法所构建评估指标体系内评估指标信度的主要目的是确定所选取评估指标的可应用性。将本文方法所构建评估指标体系内的3个一级指标分别表示为A1~A3，将6个二级指标分别表示为A11，A12，A21，A22，A31和A32。在检测过程中将Cronbach's α系数作为检测标准，在评估问题研究中，通常将评估指标Cronbach's α系数的标准值设定为0.7，若检测所得Cronbach̓s α系数高于该值，即可表示评估指标信度较高，具有较高可应用性。表1所示为本文方法中所选评估指标的Cronbach̓s α系数值。分析表1能够得到，本文方法所构建的评估指标体系内不同评估指标Cronbach̓s α系数值均高于0.81，且整体评估指标体系的Cronbach̓s α系数值在0.85以上。与评估问题研究中指标Cronbach's α系数的标准值相比，本文方法所构建评估指标体系与其中所包含的6个评估指标的Cronbach̓s α系数值均较高，且差异显著，充分说明本文方法内所构建的评估指标体系内评估指标信度较高，可应用性较强。

2.2 评估过程与结果

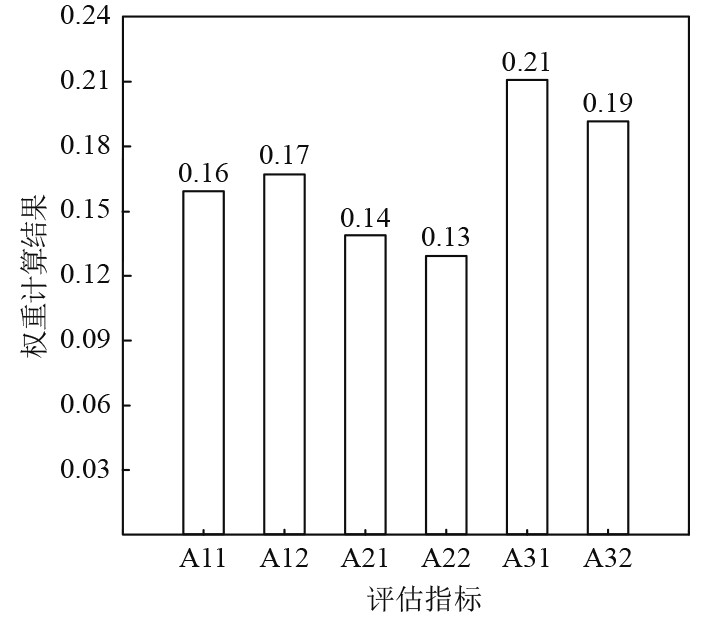
本文方法评估过程中将测试对象状态评估结果划分为四个等级，由高至低分别是严重故障状态(评估结果3~4，测试对象内主要设备产生故障，无法继续运行)、故障状态(评估结果2~3，测试对象内部分设备产生故障，不影响其继续运行)、良好状态(评估结果1~2，测试对象内各设备均无故障，需进行正常维护与检修)、优秀状态(评估结果0~1，测试对象内全部设备功能检测结果均在标准范围内)。采用本文方法计算评估指标权重，所得结果如图2所示。

可知，权重 $ W = \left\{ {0.16,0.17,0.14,0.13,0.21,0.19} \right\} $ 。这表明船舶电网适装性是对于测试对象状态影响最为显著的指标。

式(8)为测试对象的综合评价矩阵：

$ R = \left\{ \begin{gathered} 0.07,0.13,0.37,0.43 \\ 0.15,0.17,0.33,0.35 \\ 0.10,0.18,0.32,0.40 \\ 0.08,0.21,0.36,0.35 \\ 0.13,0.20,0.27,0.40 \\ 0.09,0.16,0.34,0.41 \\ \end{gathered} \right\}。$

(8)

利用式(6)计算得到：

$ B = W \times R = \left( {0.13,0.17,0.29,0.31} \right) 。$

(9)

最后利用式(7)计算能够得到 $ {P_r} $ 值为2.26。与评估结果划分等级进行比较得到，测试对象状态评估结果为故障状态，说明测试对象有部分设备产生故障，虽能够令船舶电网继续运行，但需要对其进行维修与部件更换。这与测试对象实际运行状态相符，由此说明本文方法的准确性。

3 结　语

本文研究基于差分进化算法的船舶电网系统状态评估方法和基于差分进化算法所构建的评估指标体系，采用模糊综合评估方法完成船舶电网系统状态的评估。测试结果显示，本文方法所构建的评估指标体系具有较强应用性，并且利用本文方法能够有效获取船舶电网系统状态评估结果。