凝汽器作为船舶蒸汽动力系统中的主要设备之一,在蒸汽动力循环中起着冷源的重要作用,其运行的动态特性直接影响着整个蒸汽动力循环的效率及稳定性等。因此分析凝汽器的动态特性,可以为整个蒸汽动力循环热效率等的优化提供依据。目前,针对凝汽器的特性,许多学者开展了系列研究。张磊等[1]构建了冷凝器真空偏低的故障树模型,提出探寻冷凝器真空偏低原因的定性方法,并开展冷凝器真空偏低故障的动态仿真,从定性和定量的角度综合诊断船用冷凝器真空下降产生的原因,并给出避免故障的基本措施。张永生等[2]建立了船用小型凝汽器的动态数学模型,可与蒸汽发生器模型、汽轮机模型等一起构成船舶热力系统仿真平台。Vedran Medica-Viola等[3]采用稳态质量守恒定律和能量守恒定律建立了凝汽器数值模型,该数值模型包括4个易于切换的传热系数(HTC)算法,并对算法进行了描述和解释,以某燃煤电厂冷凝器为例进行了验证。郭宏恩[4]建立了核电站表面式凝汽器动态参数模型,采用Adams多步仿真算法对核电凝汽器实时系统进行仿真。
目前,凝汽器的仿真研究大多数都是基于核电站的凝汽器[5-7],关于船舶主凝汽器的研究还是较少。凝汽器及其凝给水系统涉及到汽液两相流、热力学分析、结构强度分析等多个领域,因此,如何针对船舶凝汽器的变工况、变负荷等特点,开展基于多领域物理统一建模的动态特性分析,是当前的难点之一。由于Modelica[8-10]语言在大型复杂多样化物理系统建模上的优势,近年来在多领域物理统一建模与仿真上呈增长趋势。因此,基于Modelica语言,进行船舶凝汽器建模,开展其动态特性分析,可为船舶凝动力系统的优化提供支撑。
本文针对船舶凝给水系统,运用Modelica统一物理建模语言以及Mworks仿真平台等,开发船舶凝汽器的模型库,建立船舶凝汽器的数学模型以及仿真模型等,并研究了其在不同工况下的动态特性,为船舶动力系统的运行优化提供参考。
1 船舶凝给水仿真模型的建立 1.1 船舶凝给水系统的建模原理基于Modelica语言,采用模块化建模方法,将船舶凝给水系统分解为凝汽器、除氧器、给水泵、凝水泵、冷却水泵及管路、阀门等组件。根据凝给水系统的工作原理以及物理方程等,建立凝汽器、除氧器等主要组件的数学模型,且根据热力系统模型库建立凝给水系统的各个组件模型,部分组件模型也可应用于蒸汽动力系统中其他子系统模型。建模流程如图1所示。
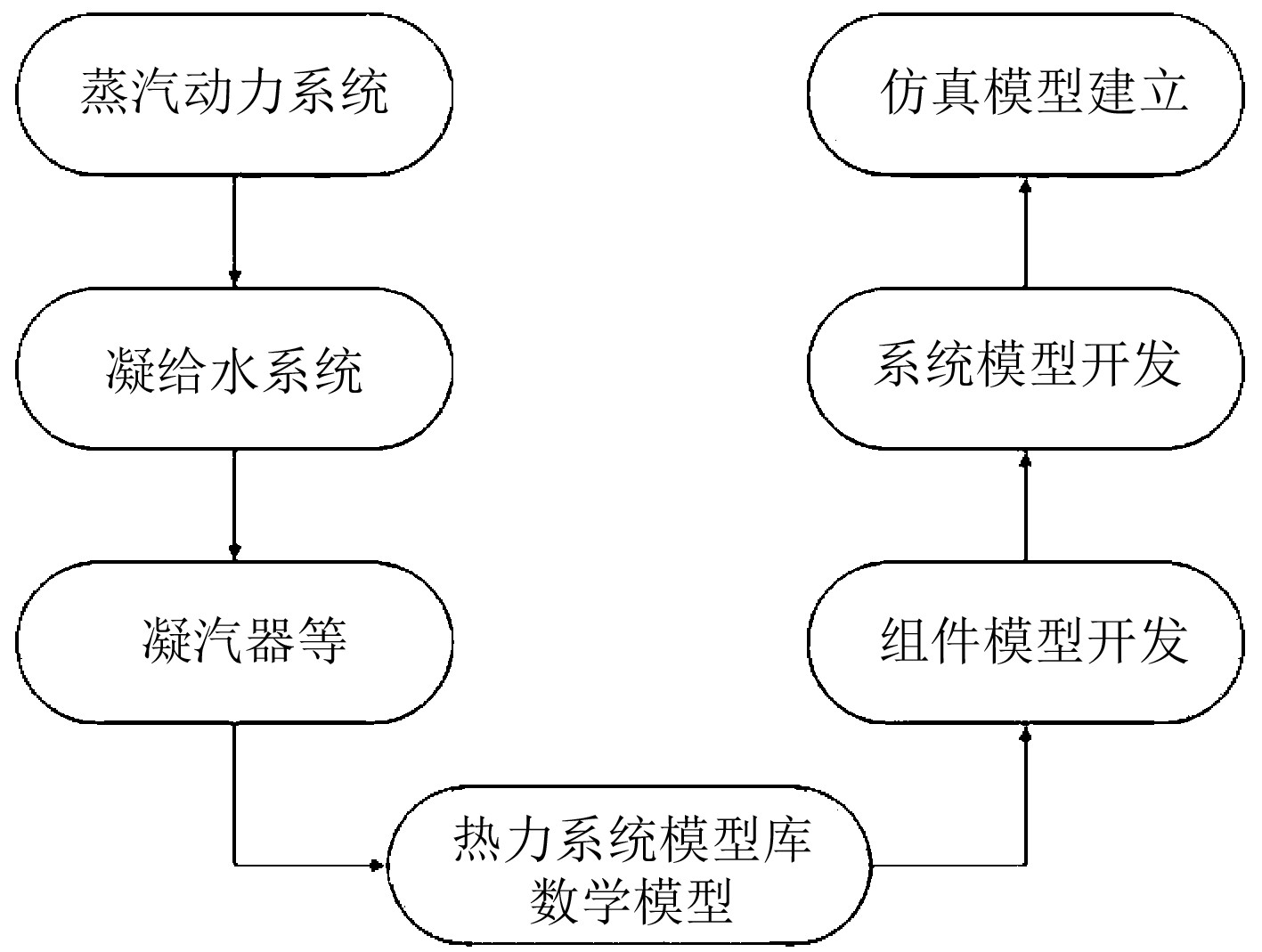
|
图 1 模块化建模原理 Fig. 1 Principle of modular modeling |
凝给水系统是一个包含传热、传质、流动等热力过程的复杂系统,是汽轮机装置的重要组成部分,主要用于冷凝主汽轮机和辅机等排出来的废汽[11]。
某型船用凝给水系统工作原理如图2所示。废汽从汽轮机排出经过冷凝器,同时冷却海水通过离心泵进入冷凝器,将冷凝器中的废汽凝结成水;凝水再通过凝水泵等进入除氧器,经过除氧器除去溶解于凝水的氧气后,经给水泵进入锅炉。
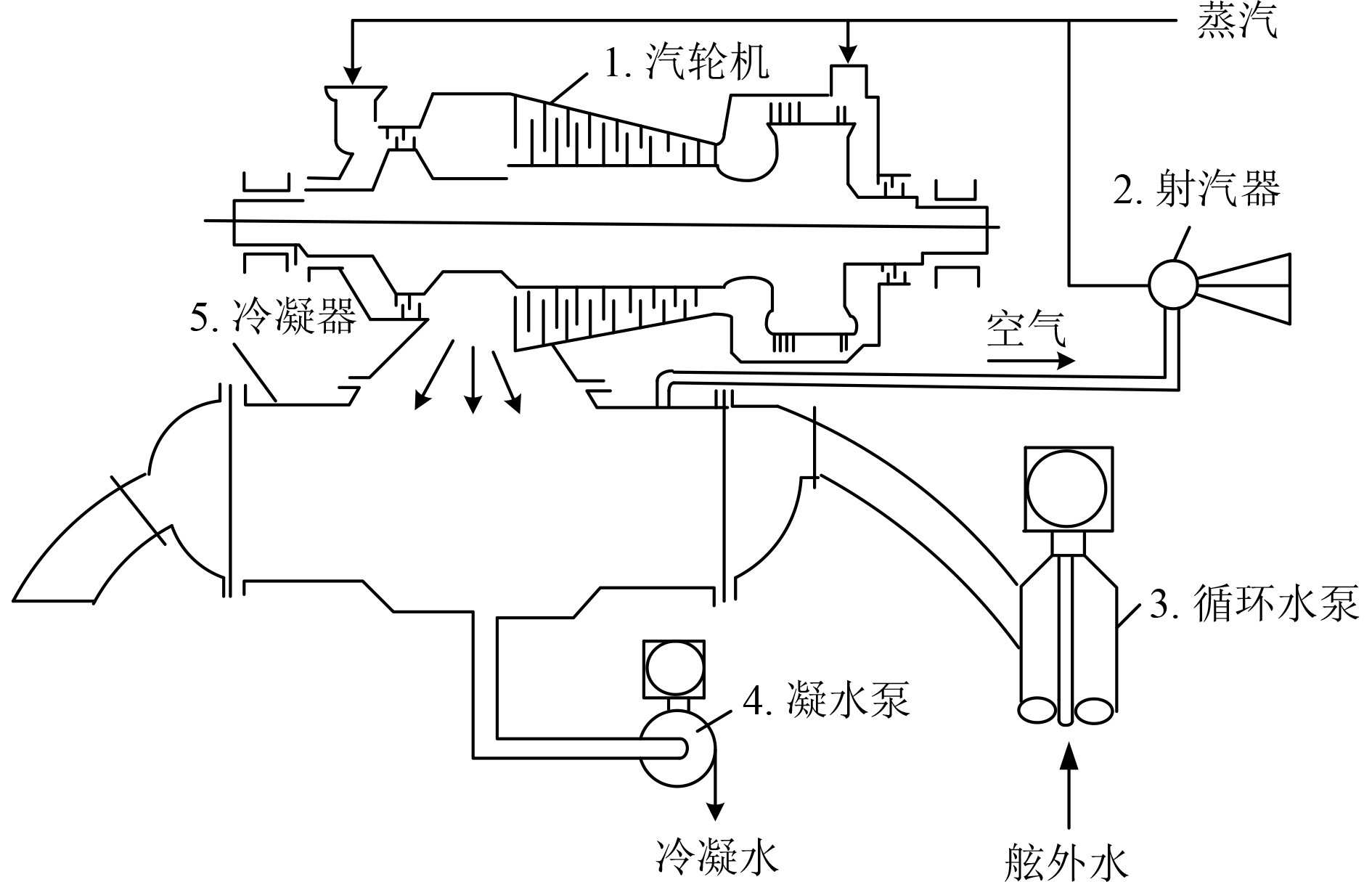
|
图 2 凝给水系统工作原理简图 Fig. 2 Working principle diagram of condensate system |
根据船舶凝汽器的结构组成以及工作原理,将凝汽器分为壳侧蒸汽区和管侧冷却水区两部分。冷却水通过循环水泵进入管侧内流动,蒸汽在壳侧内掠过管外进行凝结放热。
1.3.1 凝汽器壳侧数学模型1)质量守恒定律
| $ {G_i} = {G_{si}} + \sum {{G_{oi}}} - {G_{ci}} 。$ | (1) |
式中:
2)能量守恒定律
| $ {Q_i} + {G_i}{h_i} = {G_{si}}{h_{si}} + \sum {({G_{oi}}{h_{oi}})} - {G_{ci}}{h_{ci}},$ | (2) |
由热平衡方程可知
| $ {Q_i} = {K_i}\Delta {t_i}A,$ | (3) |
凝汽器压力为凝汽器出口焓值所对应的饱和水压力:
| $ p = f({h_i})。$ | (4) |
式中:
1)热平衡方程[12]
| $ {Q_i} = {K_i}\Delta {t_i}A = {G_c}{C_p}({T_{out}} - {T_{in}})。$ | (5) |
式中:
2)对数传热温差
| $ \Delta {T_i} = \frac{{{T_{out}} - {T_{in}}}}{{\ln \dfrac{{{T_m} - {T_{in}}}}{{{T_m} - {T_{out}}}}}} 。$ | (6) |
式中:
假设除氧器内部各部位压力以及温度相等,可根据入口流量、焓值计算出口焓值、流量、压力。
除氧器数学模型:
1)质量守恒方程
| $ \sum {G_{in}} = {G_ {out }} ,$ | (7) |
2)能量守恒方程
| $ \sum {G_{in}}{h_{in}} = {G_{out }} {h_s},$ | (8) |
除氧器压力为除氧器出口焓值所对应的饱和水压力:
| $ p = f({h_s}) $ | (9) |
式中:
针对凝给水系统所涉及的热力系统模型,开发了相对应的管道模型、阀门模型、泵模型、边界模型、工质模型等。
1.5.1 管道数学模型1)质量守恒方程
| $ {G_{in}} = {G_{out}} 。$ | (10) |
式中:
2)能量守恒方程
| $ G_{in}h_{in}= {G_{out}}{h_{out}} 。$ | (11) |
式中:
3)动量守恒方程
假定摩擦阻力发生在管道末端:
| $ \Delta p = p - {p_{out}} - \Delta H\rho g ,$ | (12) |
| $ \Delta p = f\frac{l}{r}\frac{{\rho v\left| v \right|}}{2} 。$ | (13) |
式中:
边界条件是指在求解区域给定变量的值或者是导数随时间变化的规律,边界模型主要分为定常边界和可变边界。针对凝给水系统几个主要输入源,开发相对应的边界模型如表1所示。
|
|
表 1 边界模型 Tab.1 Boundary model |
基于Modelica标准库的前提下,在热力系统模型库中建立控制阀、安全阀、压力传感器、温度传感器、离心泵等组件模块。
2 仿真结果及分析利用所建立的热流系统模型库以及凝汽器、除氧器等主要设备模型,结合Modelica语言标准库,按照凝给水系统工作原理,将各个部件连接起来,搭建船舶凝给水系统模型,如图3所示。
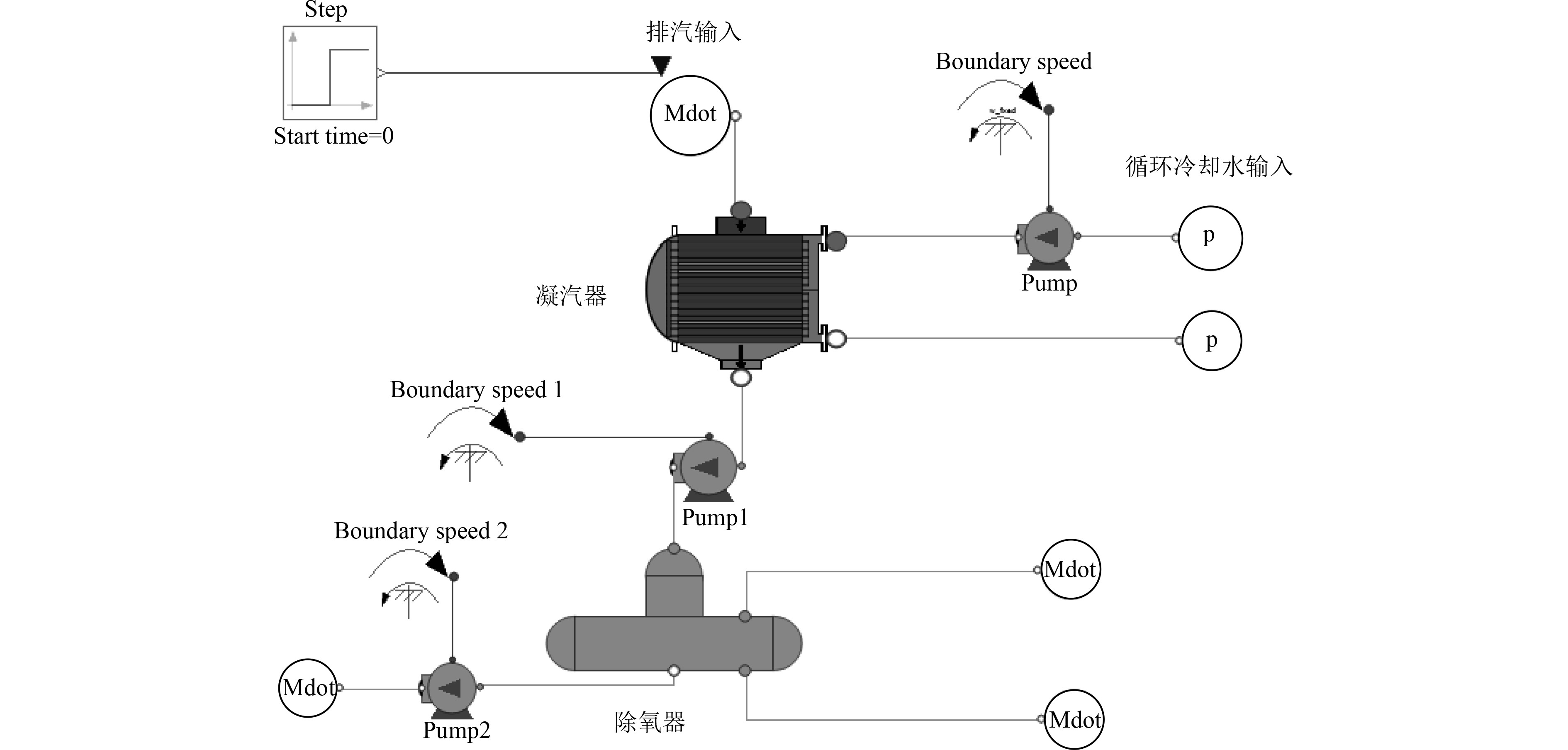
|
图 3 凝给水系统模型 Fig. 3 Condensate system model |
在Mworks平台上运用所建立的凝结水系统模型针对船用凝汽器的额定工况进行仿真,凝结水系统主要参数仿真结果如图4所示。
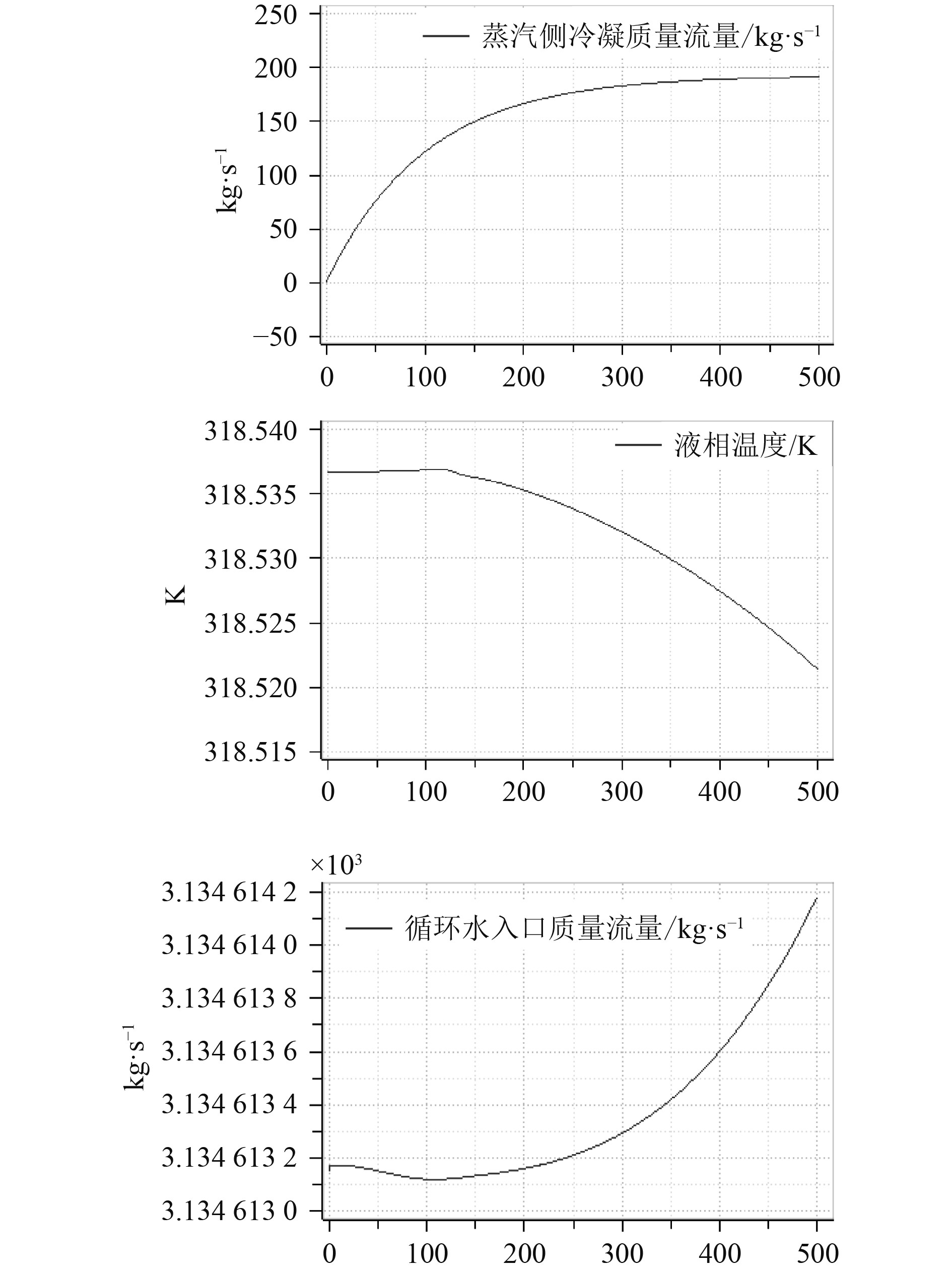
|
图 4 凝汽器主要参数变化情况 Fig. 4 Changes of main parameters of condenser |
由图4可知,凝汽器在额定工况下的运行状态特性与实际运行情况大致相同。与陆地电站凝给水系统不同,船用凝给水系统由于经常在变工况状态下运行,且由于深海与浅海海水压力、温度不同等原因,要保证凝给水系统安全稳定地运行,则及时调控汽轮机排汽量和循环冷却水输入量就显得十分重要。
2.1 汽轮机排汽量的影响为研究汽轮机排汽量对凝给水系统主要参数的影响,假定循环冷却水温度以及入口流量不变的情况下,改变汽轮机排汽量,
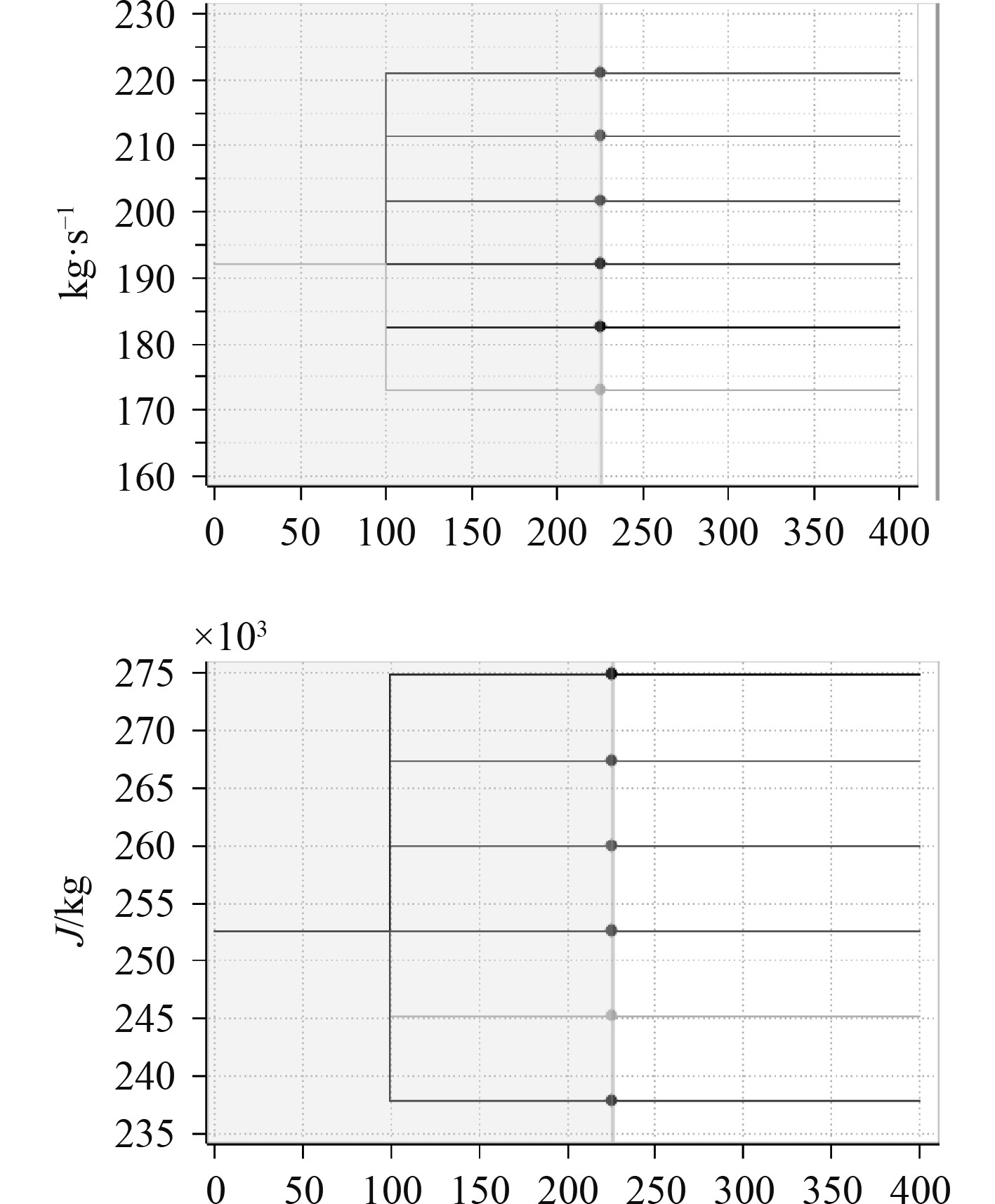
|
图 5 凝汽器内部参数变化情况 Fig. 5 Changes of internal parameters of condenser |
作为凝给水系统另一个主要输入源,循环冷却水流量同样也会对凝汽器造成较大的影响。为研究循环冷却水流量对凝给水系统主要参数的影响,假定汽轮机排汽量以及循环冷却水入口温度不变的情况下,改变循环冷却水流量,
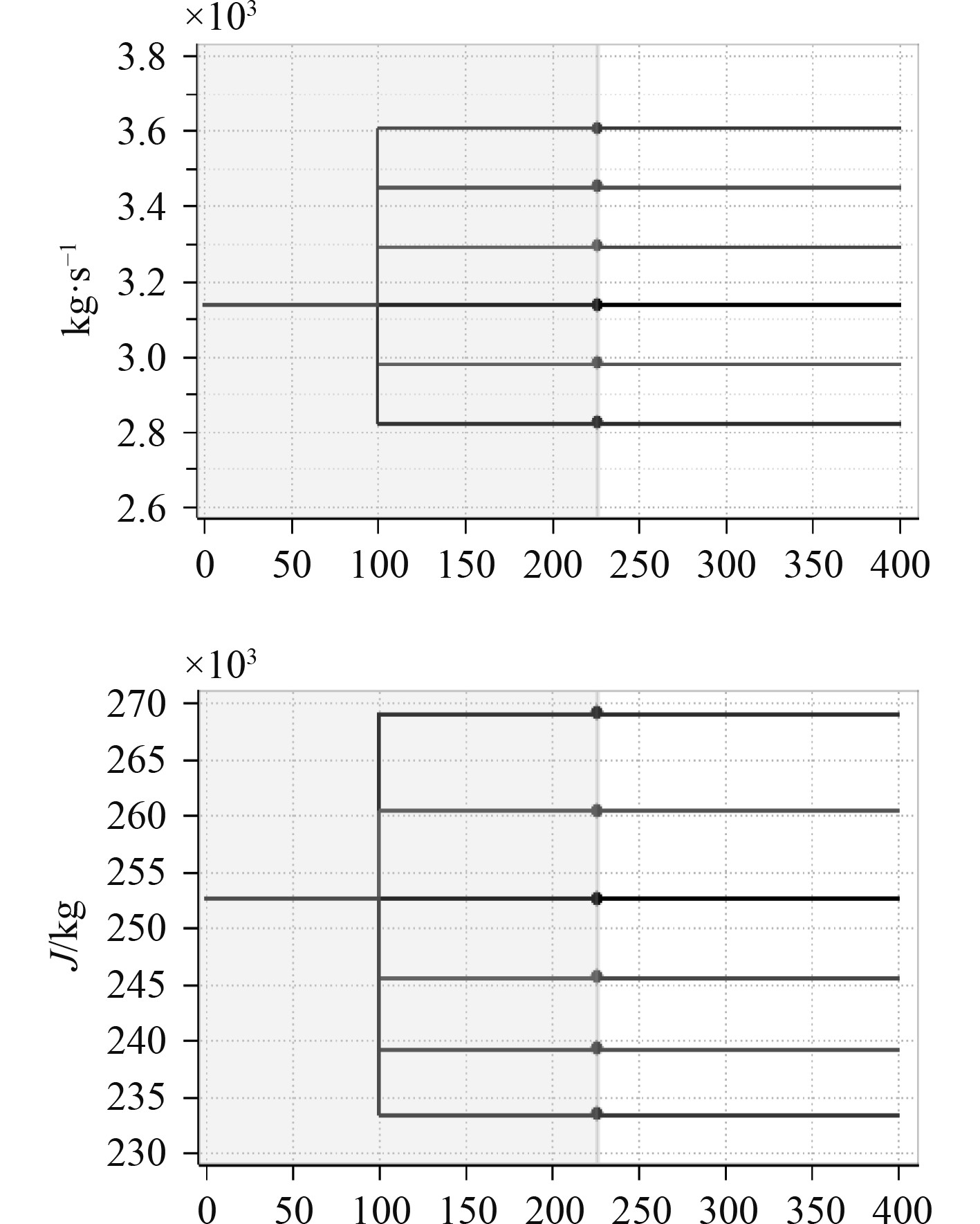
|
图 6 凝汽器内部参数变化情况 Fig. 6 Changes of internal parameters of condenser |
因此,根据凝汽器运行状态曲线,掌握凝汽器排汽量以及循环冷却水流量等主要参数变化情况,及时调控凝给水系统设备的运行状态,能够为船舶蒸汽动力系统安全稳定的运行提供可靠的保证。
3 结 语本文基于多领域物理统一建模语言Modelica与Mworks系统建模仿真平台[13],采用模块化建模思想,建立了船舶凝给水系统模型以及热力系统模型库等,并分析了船舶凝汽器的动态特性。结果表明,建立的仿真模型能够准确地模拟凝汽器运行的参数变化情况,结合实际运行状况,可以为船舶动力系统的运行优化提供参考。与传统建模方法不同,运用Modelica语言所建立的凝给水系统模型通用性高,且所建立的热力系统模型库可扩展性强,可以运用到蒸汽动力系统中其他子系统模型的建模与仿真。
| [1] |
张磊, 曹跃云, 翁雷, 等. 船用冷凝器真空偏低的动态特性分析及故障诊断[J]. 船海工程, 2017, 46(6): 67-71. ZHANG L, CAO Y Y, WENG L, et al. Dynamic characteristic analysis and fault diagnosis of low vacuum of marine condenser[J]. Shipbuilding and Marine Engineering, 2017, 46(6): 67-71. DOI:10.3963/j.issn.1671-7953.2017.06.015 |
| [2] |
张永生, 马运义, 唐滢, 等. 船用凝汽器的数学模型与动态仿真[J]. 舰船科学技术, 2010, 32(10): 101-103. ZHANG Y S, MA Y Y, TANG Y, et al. Mathematical modeland dynamic simulation of marine condenser[J]. Ship Science and Technology, 2010, 32(10): 101-103. DOI:10.3404/j.issn.1672-7649.2010.10.026 |
| [3] |
Vedran Medica-Viola, Branimir Pavković, Vedran Mrzlj-ak. Numerical model for on-condition monitoring of con-denser incoalfired power plants[J]. International Journal of Heat and Mass Transfer, 2018, 117. |
| [4] |
郭宏恩. 核电汽轮机凝汽器运行参数动态特性仿真研究[J]. 中国测试, 2019, 45(8): 55-60. GUO H E. Simulation study on dynamic characteristics of ope-rating parameters of nuclear power turbine condenser[J]. China Test, 2019, 45(8): 55-60. DOI:10.11857/j.issn.1674-5124.2018010080 |
| [5] |
张春秀, 李家富, 蔺杨颖, 等. 核电站凝汽器冷却管防碰摩优化设计[J]. 东方汽轮机, 2021(2): 71-73. ZHANG C X, LI J F, LIN Y Y, et al. Optimal design of anti-collision and friction of condenser cooling pipe in nuclear power plant[J]. Dongfang Steam Turbine, 2021(2): 71-73. DOI:10.13808/j.cnki.issn1674-9987.2021.02.016 |
| [6] |
MATHEWS I, MATHEWS E H, et al. A simulation based prediction model for coal-fired power plant condenser maintenance[J]. Applied Thermal Engineering, 2020, 174. |
| [7] |
陈强, 郭健, 张乃樑, 等. 船体运动对浮动核电站堆内燃料组件结构安全的影响[J]. 兵器装备工程学报, 2019, 40(12): 72-77. DOI:10.11809/bqzbgcxb2019.12.015 |
| [8] |
ZHONG Dawen, MENG Ji’an, QIN Peng, et al. Effect of cooling water flow path on the flow and heat transferin a 660 MW power plant condenser[J]. Science Press, 2019, 28(2).
|
| [9] |
OLIVEIRA M C, ITEN M. Modelling of industrialwat-er circuits with a customised Modelica library[J]. Applied Thermal Engineering, 2020, 169.
|
| [10] |
Schölzel Christopher, Blesius Valeria, Ernst Gernot, et al. An understandable, extensible, and reusable implementation of the Hodgkin-Huxley equations using Modelica[J]. Frontiers in Physiology, 2020.
|
| [11] |
MING L, GUANG M, JIN J P, et al. Application of Modelica/MWorks on modeling, simulation and optimization for electro-hydraulic servo valve system[J]. Theoretical and Applied Mechanics Letters, 2012, 2(6).
|
| [12] |
明媚. 基于Modelica的液压起重机起升系统的多场耦合建模与性能仿真[D]. 上海: 上海交通大学, 2012.
|
| [13] |
朱国情, 程刚, 孙丰瑞. 基于Modelica的船用冷凝系统图形化建模与仿真[C]//第13届中国系统仿真技术及其应用学术年会论文集. Ed. Scientific Research Publishing(SRP), 2011: 217–221.
|
 2022, Vol. 44
2022, Vol. 44
