2. 中国舰船研究院,北京 100192;
3. 航天时代飞鸿技术有限公司,北京 100097
2. China Ship Research and Development Academy, Beijing 100192, China;
3. Aerospace Era Feihong Technology Co., Ltd., Beijing 100097, China
舰船燃气轮机性能不断提升,对压气机性能提出了越来越高的要求。作为压气机叶片设计的基础,二维叶型在很大程度上决定了压气机的总体性能。然而传统叶型可能产生较强的激波并产生流动分离,导致气流损失增大。为了降低损失,近年来发展了可控扩散叶型(controlled diffusion airfoil,CDA)[1-2],这种叶型通过控制气流在吸力面的扩压过程,可以使整个工况条件下发生在吸力面上明显的附面层分离得以消除。大量的叶栅实验研究证明,CDA叶型在设计工况点下的损失更低,低损失的攻角范围更宽,较之常规设计的叶型更高效。
可控扩散叶型是指满足特定表面速度分布的一类叶型,设计可控扩散叶型可以从2个方面进行:正问题设计方法和反问题设计方法。这2种方法都需要反复的迭代调整,耗时长,计算成本高。在针对可控扩散叶型的优化中,需进行叶型参数化设计。以往的参数化方法尽管具有较强的灵活性[3],但并未考虑可控扩散叶型的特点。因此,在可控扩散叶型的优化设计中考虑其速度分布特点进行叶型参数化不仅能确保结果为先进的可控扩散叶型,也能提高优化效率。
舰船燃气轮机的压气机通常处于变工况状态下运行,这就需要叶型在一定的进口攻角范围内,气动性能不出现很明显的恶化,但叶型优化往往是在设计工况参数条件下完成的,在非设计工况,气动性能往往没有改进,甚至可能下降[4-7]。目前,国内外已经围绕燃气轮机压气机叶片优化设计开展了大量的研究。Sanger[8]基于可控扩散叶型最早开展了叶型的优化设计研究。Koller等[9]采用正态分布随机搜索与梯度法相结合的数值最优化方法、流场计算采用势流附面层迭代方法,构成二维叶型优化设计软件。周正贵等[10]开展了混合遗传算法在叶片自动优化设计中的应用研究。以上研究虽提高了叶片在设计工况下的性能,但没有考虑到非设计工况下的叶片性能。刘波等[11]人以叶型总压损失为目标结合数值优化方法对叶型非设计状态下性能进行优化设计。但某些叶型在大攻角下会出现计算不收敛或发散,此时计算出的性能指标意义不大。因此,考虑各个工况点的权重系数和计算状态进行目标函数的设定并以此进行非设计工况下的叶型优化设计,对获得满足舰船燃气轮机宽工况、低损失、高负荷要求的可控扩散叶型具有重要意义。
本文通过采用双圆弧中弧线、多段圆弧厚度分布以及椭圆前缘的定制叶型造型方法快速生成可控扩散叶型,在可控扩散叶型的优化设计中考虑其速度分布特点实现叶型的参数化,并对此叶型进行多工况点的优化设计。通过引入权重系数将多目标优化转化成单目标优化,实现非设计工况下的叶型优化,并引入计算结果状态变量建立优化目标,从而实现可控扩散叶型的多工况气动设计优化。
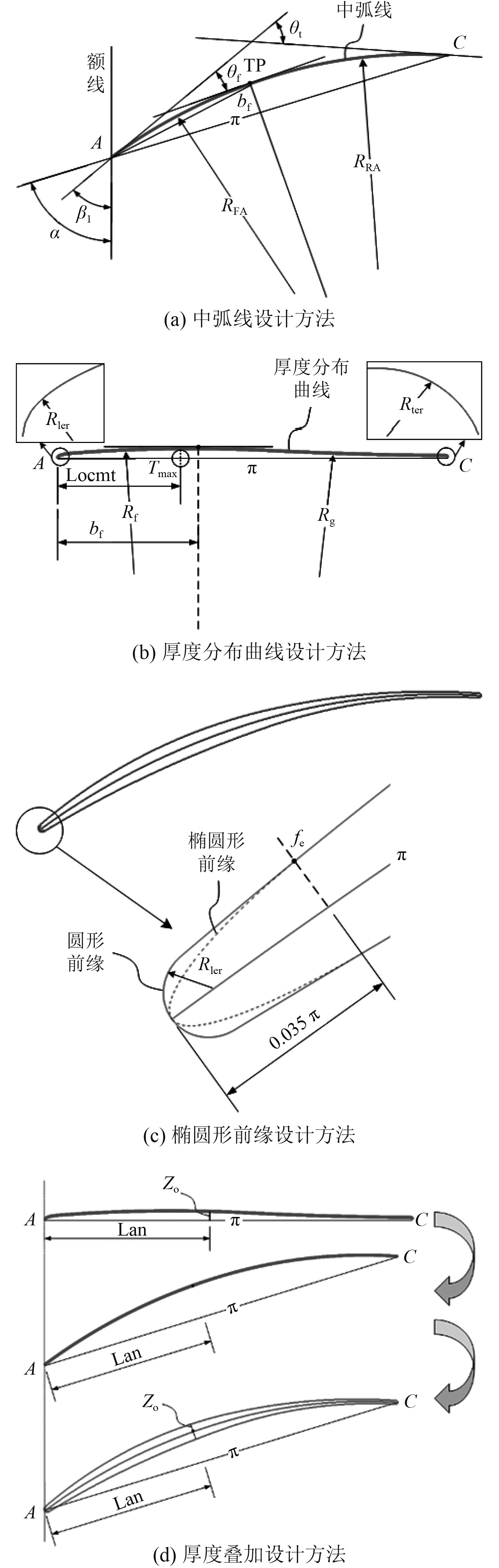
1 基于双圆弧的可控扩散叶型设计方法及分析 1.1 叶型设计方法本文采用中弧线叠加厚度分布的方法进行叶型参数化设计[12-16]。以弦长、栅距、最大厚度、几何进口角和叶型弯角为设计参数,其设计步骤主要包括中弧线造型设计、叶型厚度分布规律设计以及叠加生成型线3个部分[17-21],如图1所示。
|
图 1 叶型设计方法步骤图 Fig. 1 Blade design method step diagram |
1)中弧线造型设计
中弧线由两端相切的圆弧构成,相切点固定在最大挠度点。根据所选取的叶型弦长、进口几何角、叶型弯角、叶栅栅距和叶型最大厚度值,并指定一个初始安装角,即可计算得到前段圆弧的弦长以及弯角,进一步根据弦长确定中弧线前缘点、两段圆弧转接点以及中弧线尾缘点的坐标以及切线斜率,进而得到初始中弧线造型设计。此时中弧线的安装角会发生改变,需要求解出的实际安装角重新代入中弧线造型设计过程进行迭代设计,直至所得到的安装角的变化小于给定误差容限,即可完成中弧线造型设计[22]。
2)厚度分布曲线造型设计
叶型的厚度分布采用多段圆弧相切的方法得到。首先在前缘点、最大厚度点和尾缘点建立圆弧,建立与前缘圆弧和最大厚度圆弧相切的圆弧曲线,然后建立与最大厚度圆弧和尾缘圆弧相切的圆弧曲线,且前后两段圆弧相切。这样便建立起了由前缘圆弧、前段圆弧、后段圆弧和尾缘圆弧构成的叶型厚度分布曲线。光滑的厚度分布规律型线,可使其表面速度分布具有典型的可控扩散叶型表面速度分布特征。
3)椭圆前缘造型设计
为进一步抑制前缘表面气流的过渡膨胀,在设计叶型前缘时,采用有别于传统叶型的椭圆设计。其方法是在以常规方法确定前缘圆弧之后,于叶型厚度曲线上距离前缘点一定长度的位置处作与前缘点相连的椭弧。
4)厚度分布叠加
在厚度分布规律确定以后,将厚度分布沿弦长进行分割,得到一系列的厚度分布数据,然后按照此分割点在弦上的坐标,对中弧线进行划分,在每个中弧线分点上将其对应的厚度数据相应叠加,最终获得叶片吸力面和压力面的型线。
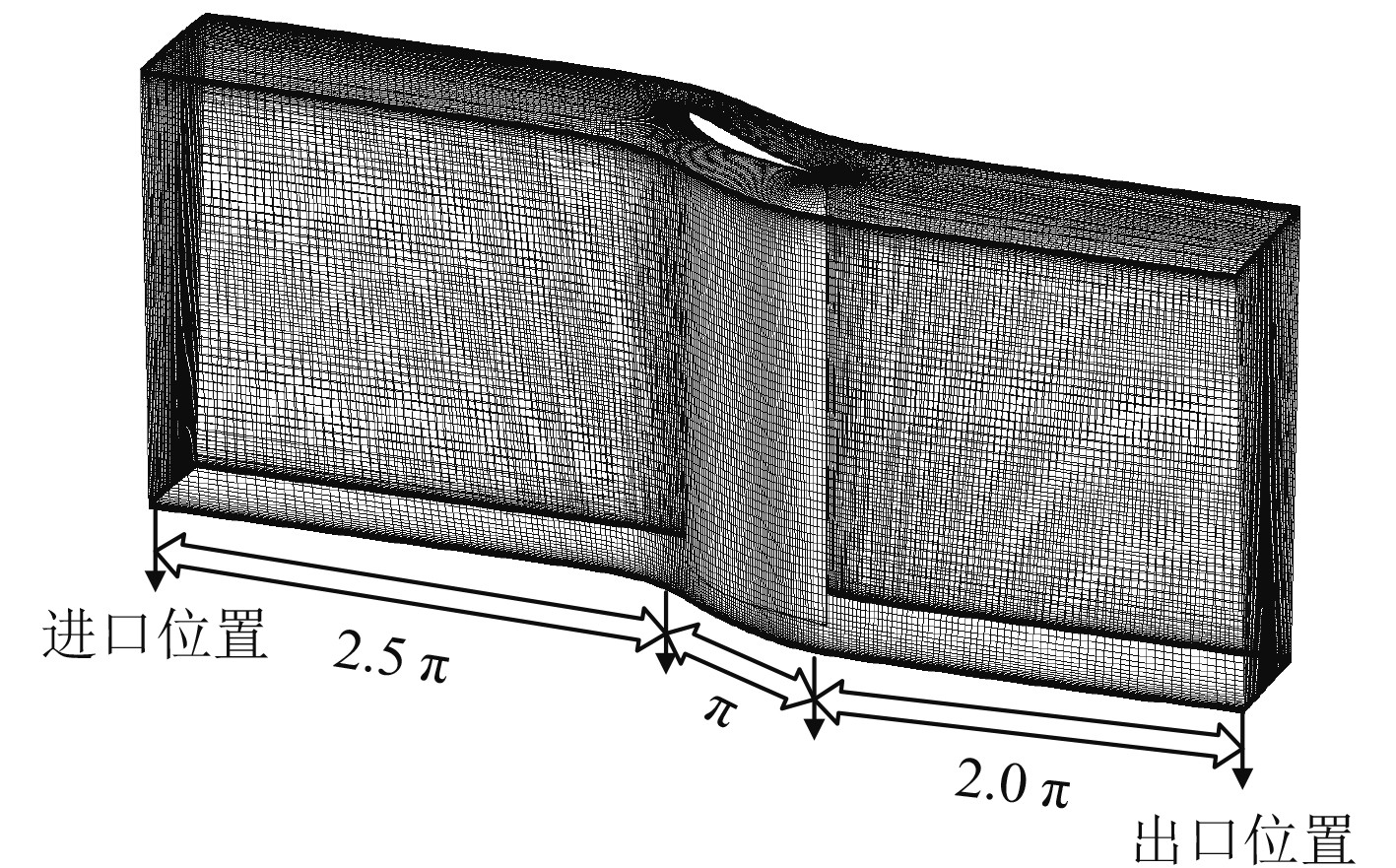
1.2 几何模型采用NUMECA软件对所设计的叶型进行数值计算以获得其气动性能。为保证计算精度,来流入口位于前缘上游2.5倍弦长处,来流出口位于前缘下游2倍弦长处。在周向上,根据叶栅稠度及弦长确定计算域两侧距离。本文建立的单通道计算域如图2所示。
|
图 2 单通道计算域 Fig. 2 Single channel computing domain |
采用NUMECA中的自动网格生成模块AutoGrid5进行网格生成,叶型周围采用O型贴体网格,其余采用H型网格的分块结构化网格。生成整个三维网格数为200万左右。
在Spalart-Allmaras模型中要求y+值为1~10,本文中的全局第1层网格的y+值为分布符合S-A模型标准。其正交性、长宽比、相邻网格尺度的膨胀比以及网格数量均符合网格质量要求。
1.4 边界条件和湍流模型计算域的入口处根据所设攻角与进口气流角给定速度方向、进口总温288.2 K,调节进口总压以保证进口马赫数为0.62,进口湍流粘性为0.00001 m2/s。在计算域的出口给定平均静压为101300 Pa。周向两侧采用周期性边界条件,上下端壁采用绝热固体壁面边界。为了加速收敛,多重网格数设置为3。网格迭代步数设为4000步,收敛准则为全局残差下降5个数量级,质量流量误差不超过1%,压比等量不再波动。数值计算采用中心差分格式,选用Spalart-Allmaras湍流模型。
1.5 数值方法验证使用MAN GHH 1-S1叶型进行数值方法的校核,MAN GHH 1-S1叶型数据来自Steinert和Eisenberg等[23]设计的可控扩散叶型,并对MAN GHH 1-S1叶型设计了一套实验叶栅,进行风洞试验。总流量为20 m3/s,固定进口气流角,通过改变马赫数得到7组不同的试验数据,选取0.62 Ma的试验数据进行研究。MAN GHH 1-S1叶型的几何设计参数如表1所示。
|
|
表 1 MAN GHH 1-S1叶型叶栅设计参数 Tab.1 MAN GHH 1-S1 blade type cascade design parameters |
图3给出了压比与总压损失系数的数值结果与试验结果的对比。结果表明,数值结果与试验结果基本一致,在大的正攻角下计算得到的数值结果相对偏低,总的来看,该数值方法不仅较好校核了叶型的总体性能,而且计算了不同攻角下的叶片表面流动细节并得到较好的验证。

|
图 3 叶型气动性能曲线对比 Fig. 3 Comparison of airfoil aerodynamic performance |
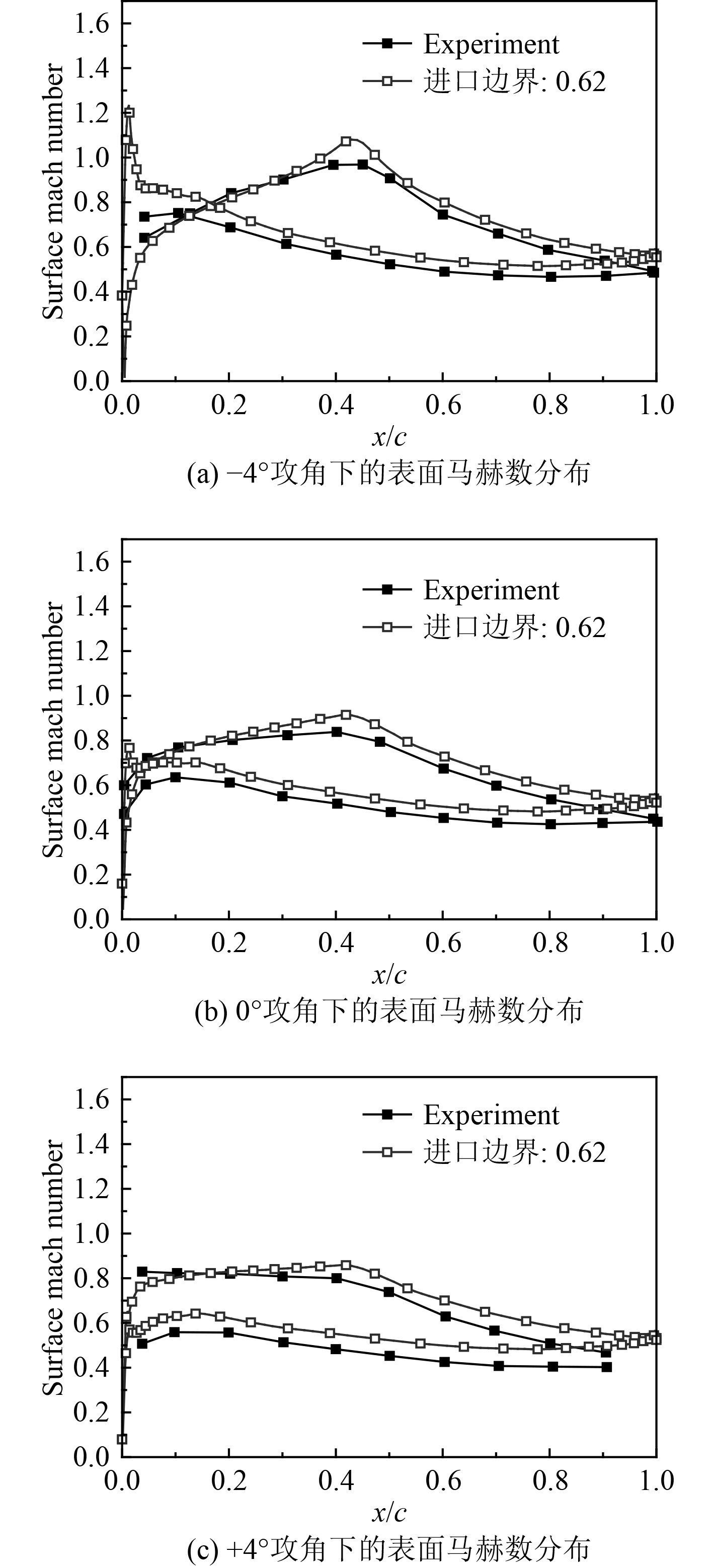
图4给出了在4°,0°和+4°攻角下叶型表面的等熵马赫数分布的对比结果。
|
图 4 不同攻角下表面马赫数分布 Fig. 4 Mach number distribution on the surface under different angles of attack |
上述试验与数值结果的详细对比分析表明,本文所采用的数值计算方法,包括几何模型、网格划分、湍流模型等能有效地进行叶型气动性能计算分析。
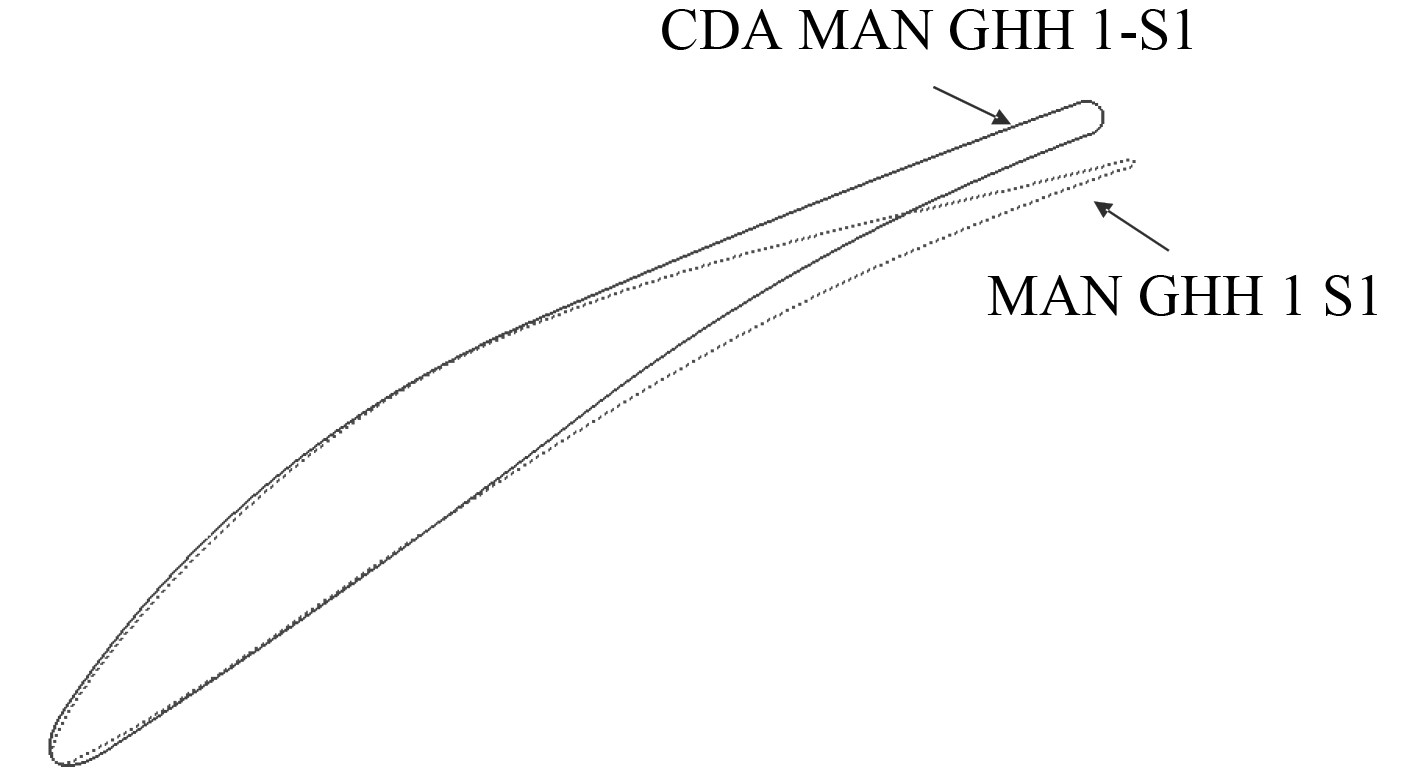
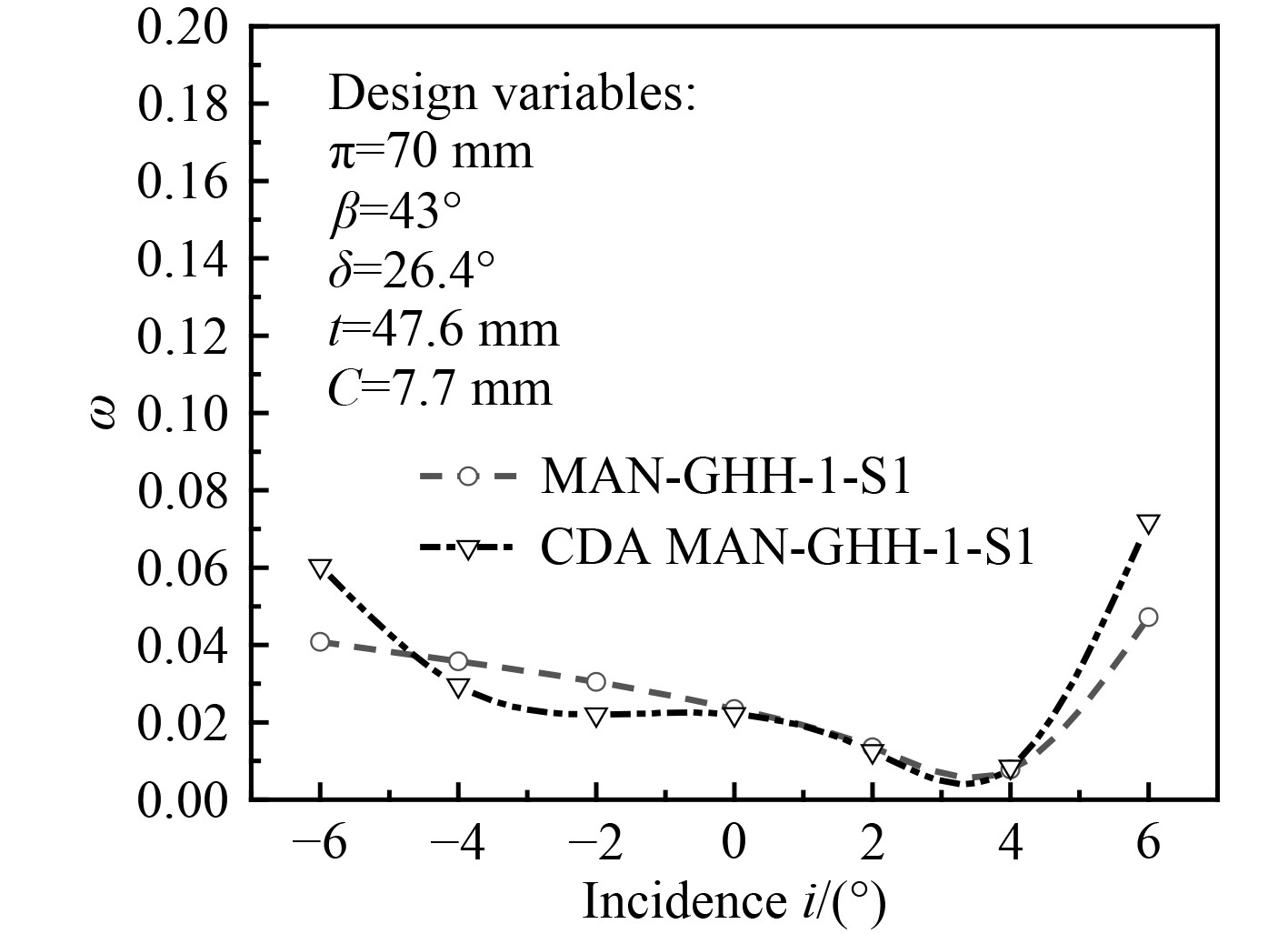
1.6 叶型设计对比基于上述MAN GHH 1-S1叶型的设计参数与试验校核结果,利用本文的叶型设计方法对MAN GHH 1-S1叶型进行改型设计(以下改型后的叶型均称为CDA-MAN GHH 1-S1),以实现考虑其速度分布特点进行叶型参数化,并尽可能保持原有叶型的特点。图5为改型设计后叶型与原始MAN GHH 1-S1叶型的对比。
|
图 5 改型设计叶型对比图 Fig. 5 Blade shape modification design comparison |
图6为叶型经数值计算得到的总压损失系数对比。可知,使用本文可控扩散叶型设计方法改型设计的叶型在设计点下相较于原始叶型有更低的总压损失。同时正攻角下的叶型性能也得到改善,损失系数降低,但负攻角下的损失系数有所上升。
|
图 6 改型设计前后总压损失系数对比 Fig. 6 Comparison of Total pressure loss coefficient before and after modification design |
图7为2种叶型下绝对马赫数的分布。可知,在相同入口马赫数的条件下,改型设计后的叶型在叶型前缘处的临界速度有所降低,叶型吸力面的速度梯度变小,这有助于减小叶型吸力面的气流分离,减少流动损失。

|
图 7 马赫数云图对比 Fig. 7 Mach number cloud map comparison |
设计变量变化范围如表2所示。
|
|
表 2 CDA MAN GHH 1-S1叶型设计变量分布指标 Tab.2 CDA MAN GHH 1-S1 blade shape design variable distribution index |
优化目标函数是叶型优化设计中最为重要的一个组成部分,它决定了叶型优化的方向与结果[24-25]。本文的叶型优化侧重于在较大攻角范围内减小叶型损失,使非设计工况下的叶片性能得到优化。压气机叶型的损失效率/攻角曲线为一个典型的U型曲线,低于某一给定损失系数值得攻角范围即为有效攻角范围,优化时应使该攻角范围越大越好。因此,压气机叶型优化时常给各攻角下的损失系数赋予权重值构成目标函数[20-21],寻优计算目标函数的最小值即为最优的叶型。本文保证马赫数在0.6 左右,并限制叶型的设计参数变化范围在20%之内,所设计的目标函数如下式:
| $ { f = \frac{{5{i_{ - 6}}{\omega _{ - 6}} + 4{i_{ - 4}}{\omega _{ - 4}} + 2{i_{ - 2}}{\omega _{ - 2}} + 0.5{i_0}{\omega _0} + 2{i_2}{\omega _2} + 3{i_4}{\omega _4} + 4{i_6}{\omega _6}}}{{5{i_{ - 6}} + 4{i_{ - 4}} + 2{i_{ - 2}} + 0.5{i_0} + 2{i_2} + 3{i_4} + 4{i_6}}}}。$ |
式中:w为损失系数;i为计算状态变量,下角标表示攻角。i取值分别为−1,0,1,2,其中−1表明计算发散,1表明计算收敛,0表明计算震荡未达到收敛标准,2表明计算发散其他情况。
2.3 试验设计及代理模型直接在数值仿真的基础上开展压气机叶片气动优化,往往需要消耗大量的计算资源。目前发展的先利用DOE试验设计采样,在样本点基础上建立代理模型并进行优化设计的方法,可以有效减少优化迭代中全部调用数值仿真软件导致的计算时间过长问题,被广泛应用于工程结构优化。
拉丁超立方是一种分层的随机抽样的方法,可以以较少的样本点较为均匀在设计空间中采用。本文利用拉丁超立方方法,选取50个水平设计了试验设计矩阵。Kriging代理模型由多项式和随机过程组成,是一种最优线性无偏估计方法。一般的Kriging模型表达式为

|
图 8 马赫数拟合曲面 Fig. 8 Mach number fitting surface |

|
图 9 损失系数拟合曲面 Fig. 9 Loss Coefficient fitting surface |
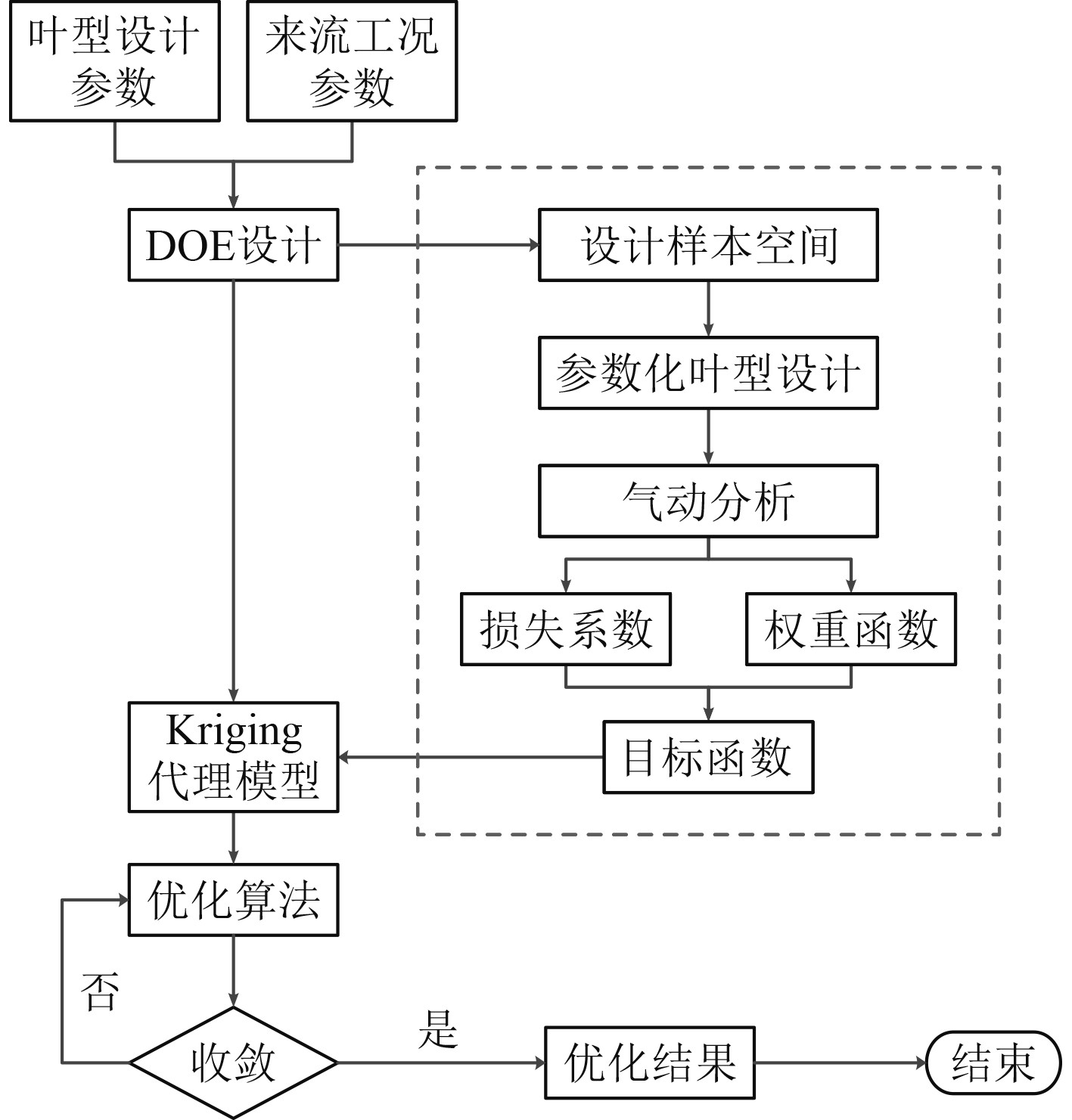
本文以多工况下的损失系数构建多工况优化目标函数,利用多岛遗传算法进行优化设计。图10给出了叶型优化设计流程。在进行寻优计算时,需进行多次的调用集成迭代进行流场分析,计算时间较长。为了提高优化设计效率,在设计优化中引入Kriging近似代理模型,具体流程如下:
|
图 10 优化流程图 Fig. 10 Optimization flow chart |
1)基于本文提出的叶型的参数化设计方法,建立流场分析的集成迭代,获得对设计参数下的响应;
2)确定设计参数与随机变量,利用DOE获取初始样本点,构建Kriging近似代理模型;
3)利用优化算法进行叶型的多工况点稳健性优化体系。
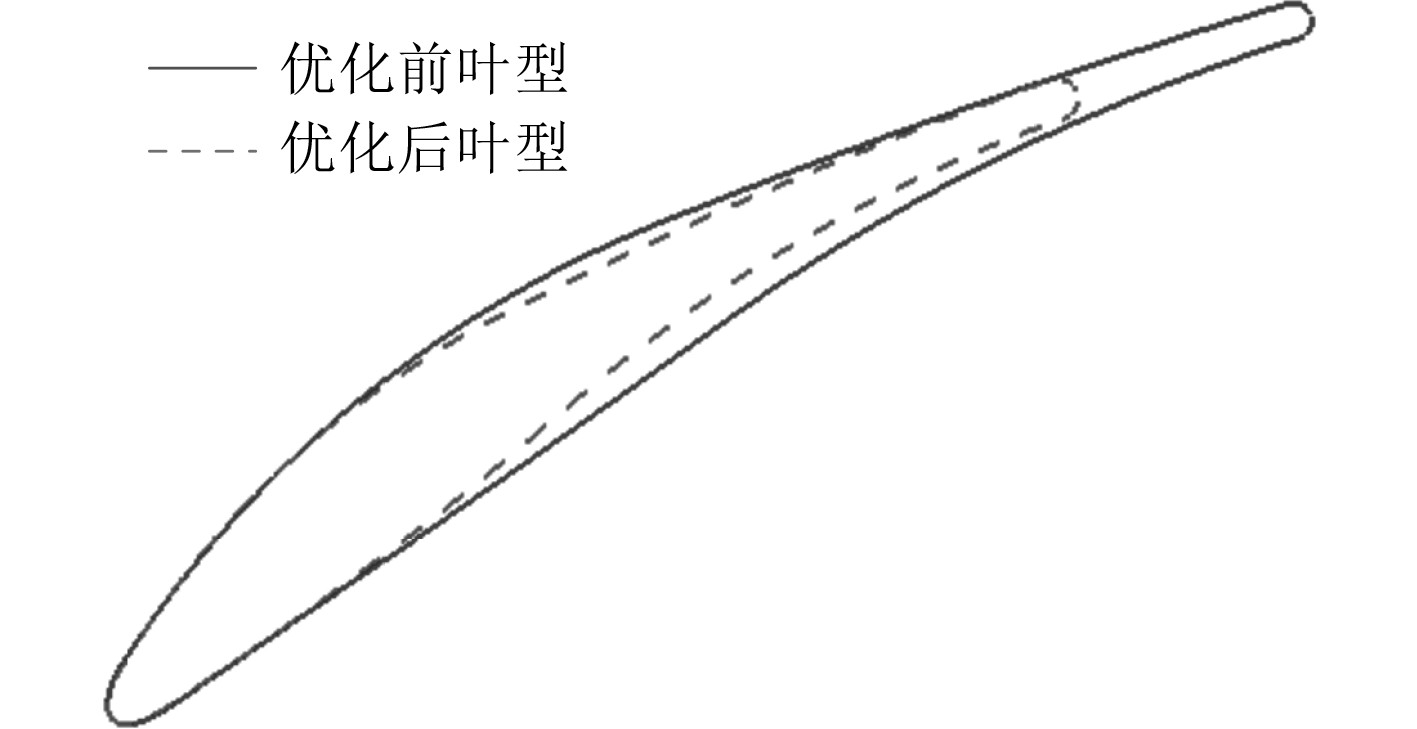
2.5 优化结果 2.5.1 优化前后叶型对比图11为优化前后二维叶型对比图。与原始叶型相比,可以看出优化后叶型参数栅距延长,弦长、几何进口角、弯角及厚度均减小。表3给出了设计变量优化前后的对比。
|
图 11 CDA MAN GHH 1-S1叶型优化前后二维叶型对比 Fig. 11 Comparison two- dimensional blade profile before and after CDA MAN GHH 1-S1 blade profile optimization |
|
|
表 3 设计变量在CDA MAN GHH 1-S1叶型优化前后对比 Tab.3 Comparison of design variables before and after CDA MAN GHH 1-S1 blade shape optimization |
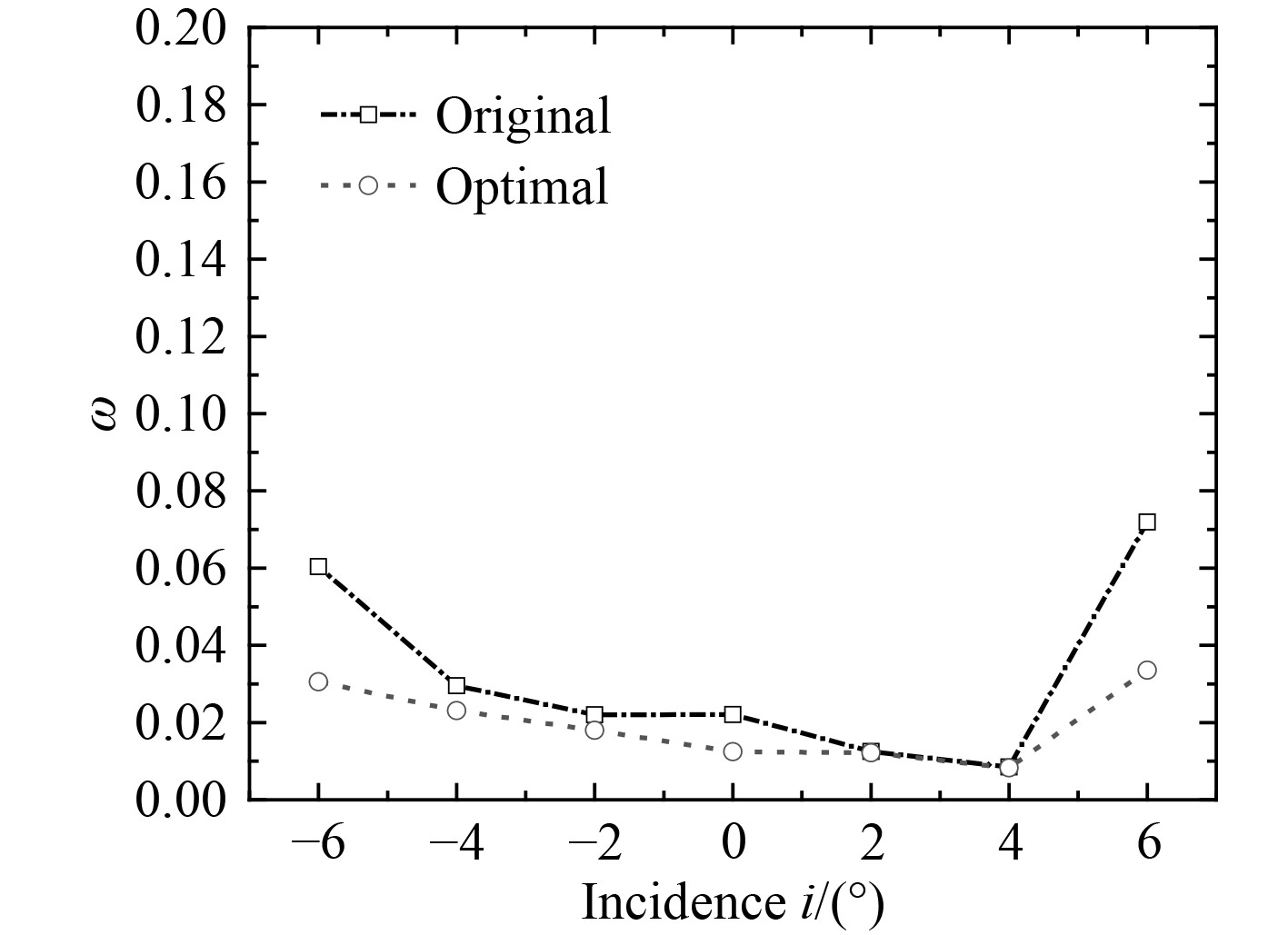
表4给出了优化前后的结果和比较。由分析结果可以看出,在经过叶型优化设计之后,设计点的总压比增大,总压损失系数与优化前相比有了比较明显的下降。
|
|
表 4 CDA MAN GHH 1-S1叶型多工况条件下优化设计前后叶型总压损失系数对比 Tab.4 Comparison of total pressure loss coefficient before and after optimal design of CDA MAN GHH 1-S1 blade profile under multiple conditions |
图13给出了攻角为−6°优化前后相对马赫数等值分布对比图。可知:优化前叶片前缘附近的相对马赫数较大,且变化梯度大,优化后叶片前缘的马赫数明显减小;优化后的相对流速在叶片内部整体分布更加均匀和稳定;原始叶片尾部的流动分离区在优化后得到了很好的改善,损失相对降低,从而提高总压比,降低总损失系数等关键性能指标。
|
图 12 CDA MAN GHH 1-S1叶型优化前后总压损失随攻角变化对比图 Fig. 12 Comparison of total pressure loss with angle of attack before and after CDA MAN GHH 1-S1 blade profile optimization |
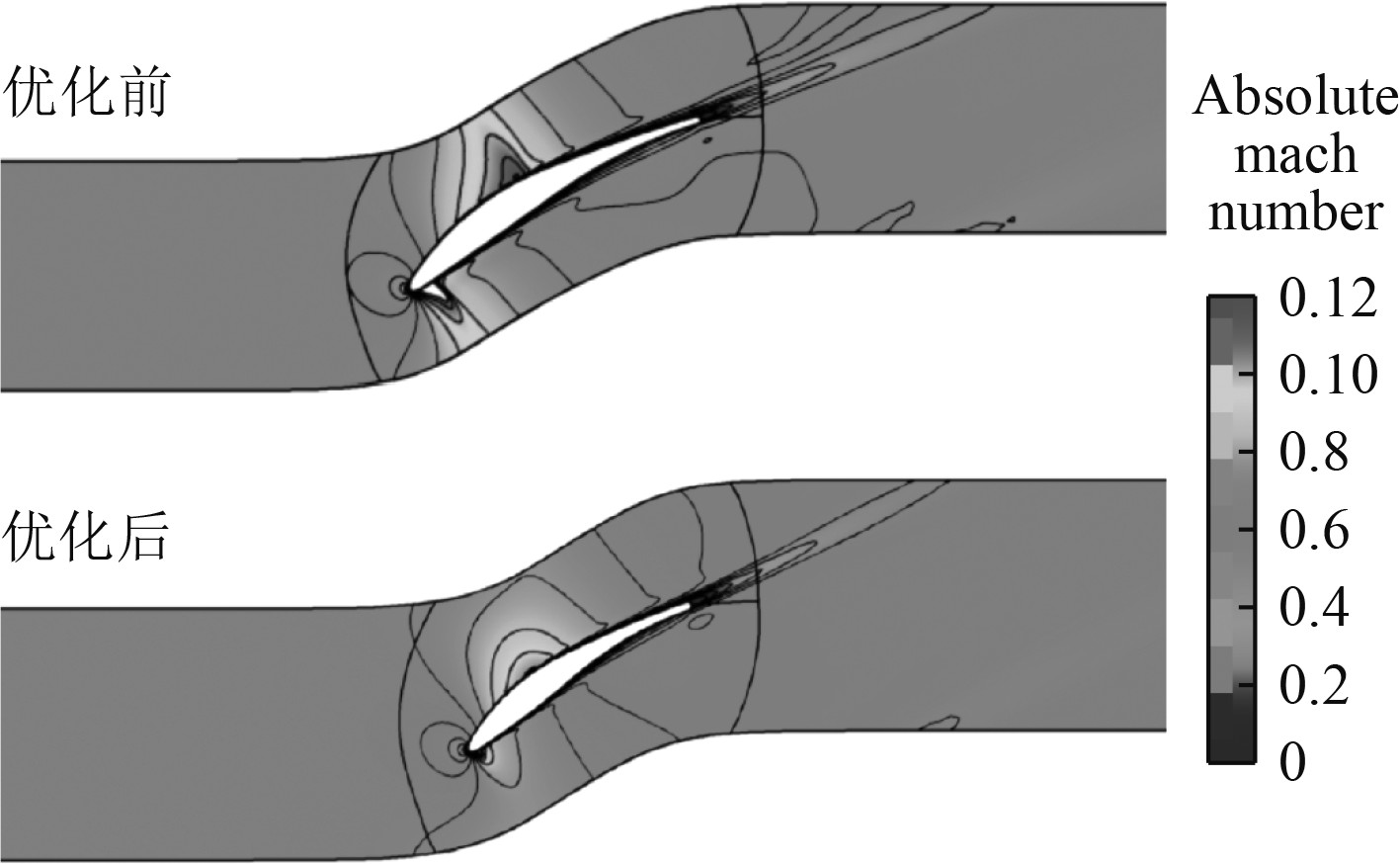
|
图 13 CDA MAN GHH 1-S1叶型优化前后绝对马赫数等值线分布图 Fig. 13 Distribution map of absolute Mach number contours before and after CDA MAN blade profile optimization |
本文通过将叶片气动性能与叶型几何形状参数化结合的CDA定制叶型造型方法对压气机叶片进行多工况点气动设计优化,并通过建立变权重系数的目标函数进行多攻角优化,得出结论如下 :
1)采用双圆弧中弧线、多段圆弧厚度分布以及椭圆前缘参数化方法,能快速生成CDA叶型,建立数值计算方法并进行试验对比验证。
2)基于叶型参数化设计、DOE试验设计、目标函数和近似代理模型建立压气机叶型多工况稳健性设计优化体系,寻优计算获得在多攻角下的宽工况叶型。为考虑结果状态的影响,将权重系数与设计变量相关联,将多目标优化转化成单目标优化,从而大大减少计算工作量,减少优化耗时,实现多工况点的优化。
3)用所建立的优化设计体系对CDA MAN GHH 1-S1叶型优化设计之后,非设计点总压损失系数与优化前相比有了比较明显的下降并使正攻角损失降低4%,实现压气机叶型在非设计工况下气动性能明显提升的优化设计。
| [1] |
钟兢军, 王会社, 王仲奇. 多级压气机中可控扩散叶型研究的进展与展望 第一部分 可控扩散叶型的设计与发展[J]. 航空动力学报, 2001(03): 205-211. ZHONG Jingjun, WANG shehui, WANG zhongqi. progress and prospect of controllable diffusion profile research in multistage compressors part I design and development of controllable diffusion profile[J]. journal of aerospace power, 2001(03): 205-211. DOI:10.3969/j.issn.1000-8055.2001.03.003 |
| [2] |
王会社, 钟兢军, 王仲奇. 多级压气机中可控扩散叶型研究的进展与展望 第二部分 可控扩散叶型的实验与数值模拟[J]. 航空动力学报, 2002(01): 16-22. DOI:10.3969/j.issn.1000-8055.2002.01.002 |
| [3] |
唐志林, 杨岳, 彭波. 罗茨鼓风机圆弧型双叶轮参数化设计[J]. 企业技术开发, 2006(11): 6-8. DOI:10.14165/j.cnki.hunansci.2006.11.002 |
| [4] |
KESKIN A , DUTTA A K , BE STLE D. Modern Compressor Aerodynamic Blading Process Using Multi-Objective Optimization[J]. 2006.
|
| [5] |
BONAIUTI D, ZANGENEH M. On the Coupling of Inverse Design and Optimization Techniques for the Multiobjective, Multipoint Design of Turbomachinery Blades[J]. Journal of Turbomachinery, 2009, 131(2): 021014-021029. DOI:10.1115/1.2950065 |
| [6] |
SAMAD A , KIM K Y . Shape optimization of an axial compressor blade by multi-objective genetic algorithm[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2008.
|
| [7] |
佚名. 航空发动机多学科设计优化技术研究[J]. 中国工程科学, 9(6): 1–96. YI Ming. Research on multidisciplinary design optimization technology of aero-engine. Chinese Engineering Science. 9(6): 1–96. |
| [8] |
SANGER N L . The use of optimization techniques to design controlled diffusion compressor blading[J]. Journal of Engineering for Power, 1982, 105(2).
|
| [9] |
KÜSTERS B, SCHREIBER H A , KÖLLER UD, et al. Development of Advanced Compressor Airfoils for Heavy-Duty Gas Turbines. Part II: Experimental and Theoretical Analysis[C]// International Gas Turbine & Aeroengine Congress. 1999.
|
| [10] |
周正贵, 汪光文. 基于数值优化方法的离心压气机工作轮气动设计[J]. 航空学报, 2006, 27(1): 10-10. ZHOU Zhenggui, WANG Guangwen, Aerodynamic design of centrifugal compressor working wheel based on numerical optimization method. Acta Aeronautica Sinica, 2006(01): 10-15. |
| [11] |
刘波, 周新海, 严汝群, 轴流压气机可控扩散叶型的数值优化设计. 航空动力学报, 1991(01): 9-12+89. LIU Bo, ZHOU Xinhai, YAN Ruqun, Numerical optimization design of controllable diffusion profile of axial compressor. journal of aerospace power, 1991(01): 9-12+89. |
| [12] |
ZHONG J , WANG Z . Development of controlled diffusion airfoils for multistage compressor applications part 1. design and development of controlled diffusion airfoils[C]// Cspe-jsme-asme International Conference on Power Engineering. 2001.
|
| [13] |
RECHTER H, STEINERT W, LEHMANN K. Comparison of Controlled Diffusion Airfoils With Conventional NACA 65 Airfoils Developed for Stator Blade Application in a Multistage Axial Compressor[J]. Journal of Engineering for Gas Turbines & Power, 1985, 107(2): 494-498. |
| [14] |
BEHLKE R F . The Development of a Second-Generation of Controlled Diffusion Airfoils for Multistage Compressors[J]. Journal of Turbomachinery, 1986, 108(1).
|
| [15] |
DUNHAM J . A Parametric Method of Turbine Blade Profile Design[C]// Asme International Gas Turbine Conference & Products Show, 1974.
|
| [16] |
KORAKIANITIS T . Hierarchical Development of Three Direct-Design Methods for Two-Dimensional Axial-Turbomachinery Cascades[J]. Journal of Turbomachinery, 1993, 115(2).
|
| [17] |
SHAHPAR S . Application of the FAITH linear design System to a compressor blade[C]// Isabe, 1999.
|
| [18] |
AMMERER K, MAYER, PAFFRATH, et al. Three-Dimensional Optimization of Turbomachinery Bladings Using Sensitivity Analysis[C]// ASME TURBO EXPO. 2003.
|
| [19] |
Parametric Design of Turbomachinery Airfoils Using Highly Differentiable Splines[J]. Journal of Propulsion & Power, 2015, 20(2): 335-343.
|
| [20] |
LUBENSTEIN J H , ROBIDEAU B A , ROSS A K . Airfoil shape for arrays of airfoils[J]. US, 1984.
|
| [21] |
SHREEVE R P, ELAZAR Y, DREON J W, et al. Wake Measurements and Loss Evaluation in a Controlled Diffusion Compressor Cascade[J]. Journal of Turbomachinery, 1991, 113(4): 591-599. DOI:10.1115/1.2929120 |
| [22] |
西北工业大学. 一种压气机叶型的多工况设计优化方法: CN202111436970.2[P]. 2022-02-11.
|
| [23] |
STEINERT W , EISENBERG B , STARKEN H . Design and Testing of a Controlled Diffusion Airfoil Cascade for Industrial Axial Flow Compressor Application[J]. Journal of Turbomachinery, 1991.
|
| [24] |
SCHNOES M , NICKE E . Exploring a Database of Optimal Airfoils for Axial Compressor Design[C]// Isabe. 2017.
|
| [25] |
FATHI A, SHADARAM A. Multi-Level Multi-Objective Multi-Point Optimization System for Axial Flow Compressor 2D Blade Design[J]. Arabian Journal for Science & Engineering, 2013, 38(2): 351-364. |
 2022, Vol. 44
2022, Vol. 44
