2. 江西制造职业技术学院,江西 南昌 330000
2. Jiangxi Technical College of Manufacturing, Nanchang 330000, China
随着现代移动通信技术的飞速发展,船舶航运朝着智能化以及网络化的方向发展。船舶在海上航行过程中的安全管理变得越来越严格,对船舶的船载航行数据采集系统的可靠性要求也越来越高。本文以移动网络技术为基础,研究移动网络技术在船舶航行数据采集系统中的应用,设计并实现了以移动网络技术为基础的船载航行数据实时采集系统。该系统解决了船舶和船舶之间、设备和设备之间数据传输以及存储难的问题。
1 船舶移动网络技术 1.1 船舶移动网络系统模型和陆地上的高速蜂窝网络相比,船舶海上移动通信网络采用的是窄带宽通信技术,这使得其数据传输速率受到限制,因此如何提升船舶海上移动通信速率是亟需解决的问题。船载基站以及AIS卫星等共同构成了海上移动通信网络。海面上的船载基站通过高塔基站接收无线信号,同时船舶以船载基站作为中继点接入宽带。通过这种中继无线信号的传输模式,可以实现海面上无线信号的覆盖,这样海面上的船舶能够实现类似于陆地上的网络服务。由于船舶在海面上一直处于运动的状态,并且海面上船载基站发射天线采用的是定向天线,因此船舶通过卫星通信将AIS信息发送给海面上的船载基站,以便实时修正定向天线的发射角度。
假设船舶海面移动网络的控制中心拥有大量的计算以及频率资源,并且高塔基站下行以及船载基站上行链路使用不同的频率段。海面上船舶移动网络由网络控制中心统一调控,在信号传输过程中,先把控制信号传递到高塔基站,然后高塔基站再将控制信号分发到每个船载基站中,接着船载基站将网络中心的计算结果分别发送到每个船舶上。为了更好构建船舶海洋通信系统,使用两径放射模型对船舶海上通信的系统增益进行描述,如下式:
| $ {L_{t,r}} = {\left( {\frac{\lambda }{{4{\text{π}} {d_{t,r}}}}} \right)^2}{\left[ {2\sin \left( {\frac{{2{\text{π}} {h_t}{h_r}}}{{\lambda {d_{t,r}}}}} \right)} \right]^2} \text{,} $ | (1) |
式中,λ为载波波长。移动网络的船舶效率通常使用传输速率来衡量。根据香浓理论可以得到海面上船舶移动网络的传输效率,如下式:
| $ {R_{i,j}} = {\log _2}\left( {1 + SIN{R_{i,j}}} \right)\text{,} $ | (2) |
式中,SINRi,j为信号噪声比,其计算如下式:
| $ SIN{R_{i,j}} = \frac{{{P_{i,j}}{L_{i,j}}{{\left| {{h_{i,j}}} \right|}^2}}}{{\displaystyle\sum\nolimits_{\begin{subarray}{l} m = 1 \\ m \ne i \end{subarray}} ^I {\sum\nolimits_{n = 1}^J {{L_{m,j}}{{\left| {{h_{m,j}}} \right|}^2}{p_{m,n}} + {\sigma _n}} } }} 。$ | (3) |
式中:|hi,j|2为容量系数;σn为白噪声系数。
为了扩大船舶移动通信网络的容量,则需要对船舶入网的选择以及海上船载基站的发送功率进行优化。优化过程中,船载基站发送功率的分配主要和负载有关,船舶入网的选择和海上船载基站功率分配的优化问题可以用下式描述:
| $ P = \max \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {{x_{i,j}}{R_{i,j}}} } \text{。} $ | (4) |
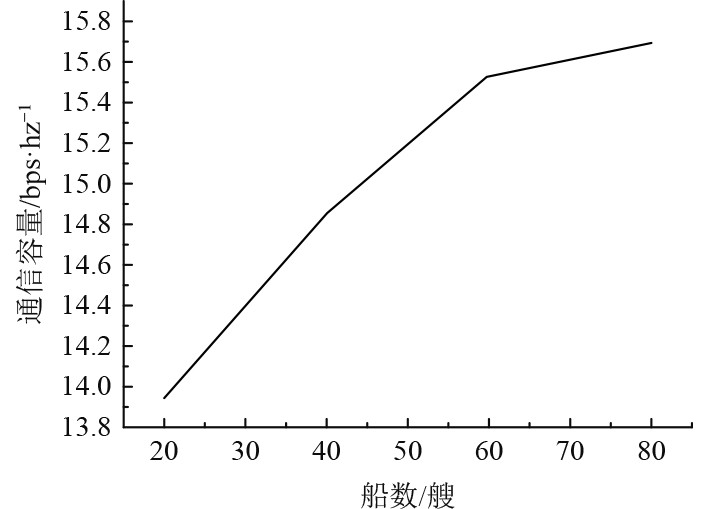
为了解决船载基站功率的优化问题,需要对式(4)进行一定的形变。由于通信容量Ri,j是一种非凸变量,因此使得式(4)为非凸函数。在处理船载基站功率优化问题的时候,需要先将式(4)的非凸函数置换成凸函数。利用对数逼近法将式(4)中的通信容量Ri,j置换成凸变量,然后再将式(4)中的xi,j从整数变量置换成连续变量,对数逼近法可以使用式(5)来描述。式(5)中的θi,j和βi,j的计算方法,分别如式(6)和式(7)所示。通信容量和船舶数量之间的关系,如图1所示。
|
图 1 通信容量和船舶数量之间的关系 Fig. 1 Relationship between communication capacity and number of ships |
| $ \ln \left( {1 + SIN{R_{i,j}}} \right) \geqslant {\theta _{i,j}}\ln \left( {SIN{R_{i,j}}} \right) + {\beta _{i,j}}\text{,} $ | (5) |
| $ {\theta _{i,j}} = \frac{{SIN{R_{i,j}}}}{{1 + SIN{R_{i,j}}}}\text{,} $ | (6) |
| $ {\beta _{i,j}} = \ln \left( {1 + SIN{R_{i,j}}} \right) - \frac{{SIN{R_{i,j}}}}{{1 + SIN{R_{i,j}}}}\ln \left( {SIN{R_{i,j}}} \right)\text{。} $ | (7) |
船舶移动网络的安全容量通常是衡量船舶移动网络物理层安全的重要参数。以单窃听网络模型为例,当信号源A向目标节点B发送信息的时候,存在一个非法的窃听点E,窃听点E会对信号源A发出的信息进行窃取。信号源A和目标节点B之间的信号的传输通道是主信道,信号源A和窃听点E之间的传输通道是窃听信道。假如船舶移动网络传输模型的信道是准静态衰落的,则目标点B和窃听点E对信号的接收可以分别用式(8)和式(9)来表示。
| $ {y_B} = {h_{AB}}{x_A} + {n_B}\text{,} $ | (8) |
| $ {y_E} = {h_{AE}}{x_A} + {n_E}\text{。} $ | (9) |
目标节点B和窃听点E接收信号的信噪比可以分别用式(10)和式(11)来计算。
| $ {\gamma _{Ab}} = \frac{{p{{\left| {{h_{AB}}} \right|}^2}}}{{{\sigma _B}}}\text{,} $ | (10) |
| $ {\gamma _{AE}} = \frac{{p{{\left| {{h_{AE}}} \right|}^2}}}{{{\sigma _E}}}\text{。} $ | (11) |
式中:P为信号源信号的发射功率;|hAB|2为信号源A和目标节点B之间的信道系数;|hAE|2为信号源A和窃听点E之间的信道系数;σB和σE为噪声。船舶移动网络系统的安全速率可以用式(12)来计算。
| $ {C_{AB}} = {\log _2}\left( {1 + \frac{{p{{\left| {{h_{AB}}} \right|}^2}}}{{{\sigma _B}}}} \right) - {\log _2}\left( {1 + \frac{{p{{\left| {{h_{AE}}} \right|}^2}}}{{{\sigma _E}}}} \right)\text{。} $ | (12) |
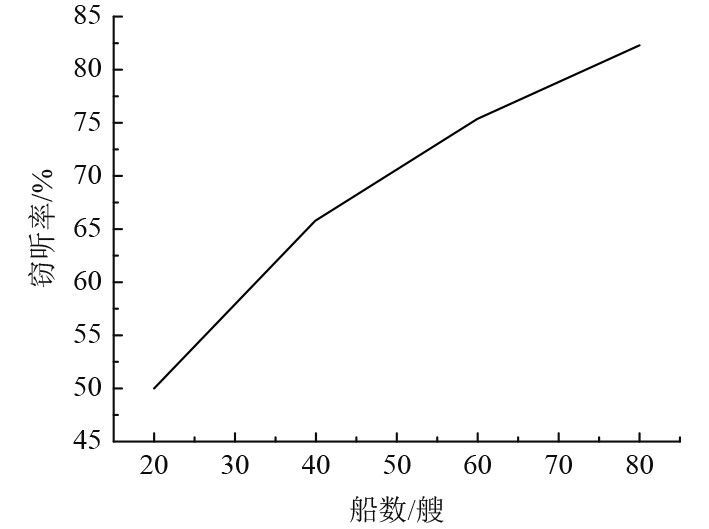
从式(12)中可以看出,船舶移动网络的安全容量是AB之间的传输速率减去AE之间的传输速率,因此当窃听通道的信号传输质量比合法信号通道的传输质量高,则船舶移动网络的安全速率等于0。为了确保船舶移动网络的传输安全性,需要使得合法的信道的传输质量比窃听通道的传输质量高。窃听率和船舶数量之间的关系如图2所示。
|
图 2 窃听率和船舶数量之间的关系 Fig. 2 Relationship between eavesdropping rate and number of ships |
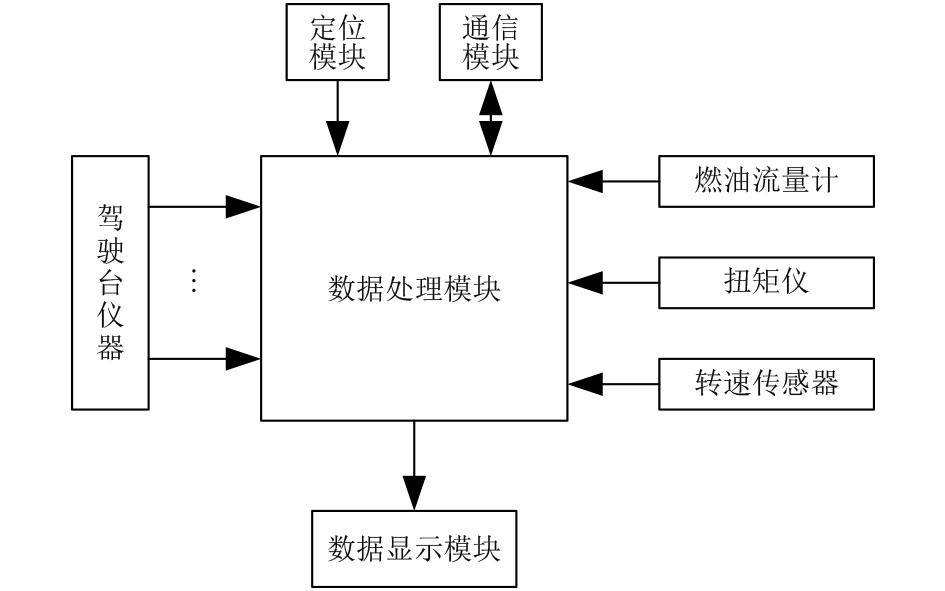
船舶航行数据采集系统是船舶数据采集、显示以及发送的主要载体,是船舶信息检测系统的重要构成部分。本文设计的船舶航行数据采集系统是以单片机为主体,并在单片机的外围完成传感器以及通信信号的处理以及传输,船舶航行数据采集系统结构如图3所示。
|
图 3 船舶航行数据采集系统结构 Fig. 3 Structure of Ship Navigation Data Acquisition System |
从图3可以看出,船舶航行数据采集系统中包含了燃油流量计、转速传感器以及扭矩仪等传感器,船舶数据通信模块采用GPRS通信模块,同时使用北斗模块对船舶的位置、航速等信息进行采集,并利用数据显示模块对相关的数据进行显示,船舶驾驶台仪器可以对船舶航行数据采集系统进行控制。
船舶机舱中的传感器可以对船舶的油耗以及功率等能效数据进行采集,并且能够将采集到的信息传送给单片机的外围设备,完成数据采集和存储任务。船舶航行过程中的油耗可以通过燃油流量计进行计算,但是船舶航行过程中主机的功率无法使用传感器直接进行采集,因此需要通过式(13)进行计算。此外船舶主机的扭矩以及转速,则需要分别通过扭矩仪和转速传感器进行测量。
| $ P = \frac{{M \times n}}{{9550}}\text{。} $ | (13) |
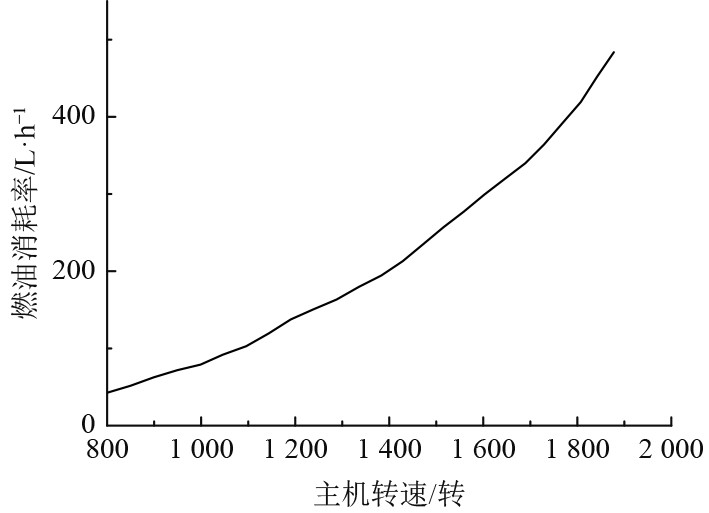
式中:p为船舶主机功率;M为船舶主机扭矩;n为船舶主机转速。船舶燃油消耗是重要的船舶能效指标之一,因此需要使用合适的燃油流量计对船舶航行过程中燃油消耗量进行检测,这样不但可以精确地对船舶能效进行管理,还可以实时掌握船舶燃油消耗的情况。为了确保船舶燃油流量计在测量过程中的精确性,因此船舶燃油流量计在安装到船舶上之前,需要进行波动率的标定,波动率的计算方法如式(14)所示。船舶主机燃油消耗和转速之间的关系如图4所示。
|
图 4 船舶主机燃油消耗和转速之间的关系 Fig. 4 Relationship between fuel consumption and rotational speed of marine main engine |
| $ R = \frac{{\left| {{F_{value}} - {F_{\max }}} \right|}}{{{F_{value}}}} \times 100\% \text{,} $ | (14) |
本文使用的船舶扭矩测量传感器型号为TorqueTrak 10K,该传感器由应变片、发射机以及接收机构成。船舶扭矩仪输出的扭矩信号为电压信号,同时通过AD采样,并将AD采样值转换成实际的扭矩值,实现船舶主机扭矩的测量,数据采集模块的转换方法如式(15)和式(16)所示。
| $ {T_{FS}} = \frac{{{V_{FS}} \times {\text{π}} \times E \times 4 \times \left( {D_0^4 - D_i^4} \right)}}{{{V_{EXC}} \times GF \times N \times 16000 \times \left( {1 + \upsilon } \right) \times {G_{XMT}} \times {D_0}}}\text{,} $ | (15) |
| $ T = {T_{FS}} \times {V_s}\text{。} $ | (16) |
完成船舶航行数据采集系统的设计之后,为了对船舶航行数据采集系统的性能进行验证,对该系统进行船舶定位、航速保持、自动跟踪巡航等测试。船舶能够实现路径精确地跟踪,完全依赖于船舶上导航模块提供的船舶精确的位置信息。
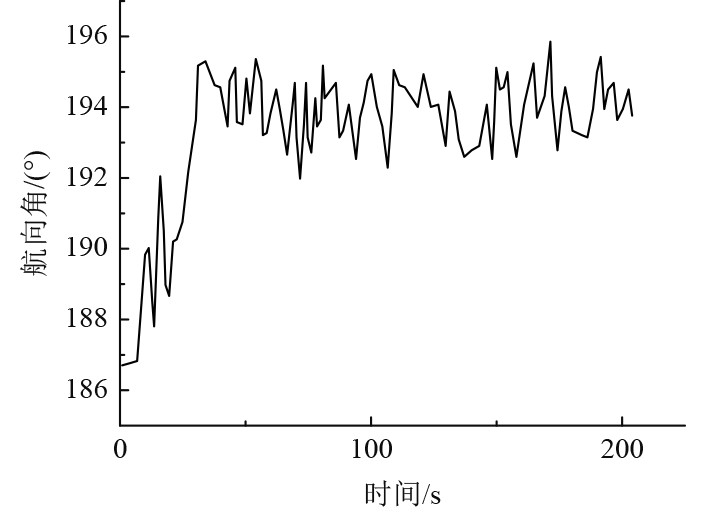
在船舶定位测试过程中,轻微旋转测试船舶使其处于悬停状态,同时通过串口对船舶航向角进行存储,曲线如图5所示。可以看出,随着时间的推移,船舶逐渐处于悬停状态,因此船舶航向角也逐渐趋于稳定,并且随着航向角稳定时间的不断延长,其精度也在不断地提升。利用地磁校准之后的船舶航向角,其精度值在−3°~3°之间,同时考虑到GPRS提供的定位数据,则可以看出船舶导航模块的精度可以满足船舶航行数据采集的精度需求。
|
图 5 船舶航向角随时间变化曲线 Fig. 5 Time varying curve of ship heading angle |
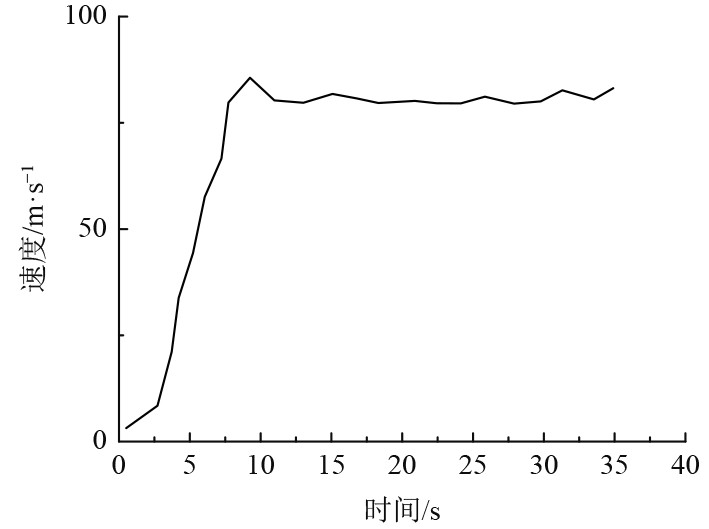
船舶在海面上航行过程中,需要保持一定的航行速度,并且在对航行轨迹进行切换以及悬停的时候,则需要对船舶的航行速度进行调整,因此需要对船舶在海上航行过程中的速度响应进行监测。船载航行数据实时采集系统通过船舶在海面上地理位置的变化,实时解算出船舶的实时速度,并且船舶上的控制系统使用PID控制算法,维持船舶的航行速度不变。本文在测试过程中,预设船舶的航行速度为0.8 m/s,并且利用串口将船舶实时航行的速度存储下来,得到的船舶航行的速度如图6所示。可以看出,船舶在刚开始行驶的时候船舶的速度响应相对比较快,船舶的加速过程大概持续了10 s,10 s之后船舶的速度达到预定值,达到预定航速之后,船舶则保持该速度进行船舶的定速航行。
|
图 6 船舶航行速度随时间变化情况 Fig. 6 Change of ship's sailing speed with time |
随着现代信息技术的快速发展,现代船舶的智能化水平不断提高,这使得船舶上设备的集成度也不断提升。在高集成度设备广泛使用的情况下,船舶在航行过程中产生的各类数据量也以指数级的量级增长。本文以移动网络技术为基础,研究船载航行数据实时采集系统,对船舶航行数据实时采集技术有指导作用。
| [1] |
初秀民, 聂梓熠, 刘怀汉, 等. 航道水沙要素移动测量技术研究综述[J]. 水利水运工程学报, 2022(2): 1-10. |
| [2] |
黄海广, 胡乃军, 仇志金, 等. 基于多源定位数据的实时船舶监控系统设计[J]. 中国海洋大学学报, 2015(45): 122-129. |
| [3] |
项慧慧, 王吉祥, 徐森, 等. 基于无人船的水环境监测物联网研究与设计[J]. 计算机技术与发展, 2022(32): 216-220. DOI:10.3969/j.issn.1673-629X.2022.01.037 |
| [4] |
李学祥, 严新平. 基于在航船舶动态信息的长江航道要素感知方法综述[J]. 水运工程, 2014(12): 31-36. DOI:10.3969/j.issn.1002-4972.2014.12.007 |
| [5] |
侯轶仁, 杨祥国, 陈辉, 等. 内河船舶生活污水排放监测系统设计与实现[J]. 中国航海, 2022(45): 87-93+98. |
| [6] |
沈立, 王海涛, 王凤鸣, 等. 内河运输船舶智能船载终端的设计与应用[J]. 船舶, 2013(24): 61-64. |
| [7] |
顾梦霞. 人工智能的船舶航行数据自动采集系统[J]. 舰船科学技术, 2022(44): 67-70. |
| [8] |
李文华, 张君彦, 林珊颖, 等. 水面自主船舶技术发展路径[J]. 船舶工程, 2019(41): 64-73. |
 2022, Vol. 44
2022, Vol. 44
