由于海上风浪、洋流等各种不确定环境因素的影响,使船舶运动呈现非平稳以及非线性,船舶仅靠自身重力无法在不平稳海况保持稳定运行,当海面处于非平稳状态时船舶容易发生摇荡现象,存在很大的安全隐患。通过对船舶6个自由度方向的姿态预测,进而通过船舶的运动补偿模块进行位姿解算,对船舶运动进行提前补偿调节,保持船舶相对平稳运行,有效保障船上人员的安全。船舶运动姿态预测研究对于保障海上人员的安全意义重大,因此,对船舶运动姿态预测模型精度的优化研究必不可少。
船舶运动姿态的预测模型主要有卡尔曼滤波预报模型[1]、基于时间序列的自回归预报模型[2-3]、灰色理论预报模型[4]、神经网络预报模型[5-6]。但卡尔曼滤波法由于船舶水动力方程难以求解,其预测精度并不理想;基于自回归的预报模型当存在外界因素干扰时,无法达到准确预报;灰色理论预报模型对数据太过依赖,不适用于数据样本过大且波动较大的情况。神经网络由于其独特的数据分析能力,而且适应性强,能够适应非平稳非线性数据,学习能力突出,在船舶运动预测有普遍应用。
但面对船舶运动姿态的复杂性,单一预测模型的准确性往往有待提高,大量实验证明组合的预测模型比单一的预测模型预测精度更高且更稳定。目前,对单一模型的优化主要是通过2种方式提高预测精度,一是利用小波分析、经验模态分解等分解算法对船舶运动数据进行分解[7-9],提高数据的可预测性,分解后分别建立模型预测最后相加,实验证明预测精度得到有效提升;二是利用智能群体算法对预测算法相关参数进行优化[10],可有效提高预测模型在船舶运动姿态的预测精度。
本文通过将2种方式结合,提出一种基于变分模态分解(variational modal decomposition,VMD)和麻雀搜索算法(sparrow search algorithm,SSA)优化门控循环单元(gated recurrent unit ,GRU)的船舶运动姿态预测模型。通过变分模态分解算法对船舶运动姿态数据进行分解,降低数据的非平稳性及非线性,再通过具有全局寻优能力的麻雀搜索算法优化的GRU循环神经网络对各分量分别进行预测,有效提高神经网络的预测精度。将该模型与SSA-GRU以及GRU预测进行实验对比分析,证明该方法可有效提高GRU循环神经网络在船舶运动姿态的预测精度。
1 变分模态分解 1.1 基本原理变分模态分解是一种时频分析方法,通过将多分量信号一次性分解成多个单分量调幅调频信号,避免了迭代过程中遇到的端点效应和虚假分量问题。该方法已被证明能有效处理非线性、非平稳信号。VMD的分解过程即变分问题的求解过程,在该算法中,本征模态函数(intrinsic mode function, IMF)被定义为一个有带宽限制的调幅—调频函数。
在船舶运动姿态数据的处理过程中,VMD是通过将船舶运动姿态的实值输入信号分解为离散数量的子信号,从而降低船舶运动姿态的非平稳和非线性[11]。
1.2 VMD求解步骤步骤1 对于每个模态,通过希尔伯特变换计算相关的分析信号,以便获得单向频谱。
步骤2 通过与调谐到相应估计中心频率的指数混频,将各模态的频谱移至“基带”。
步骤3 通过解调信号的高斯平滑度,即梯度的平方范数来估计带宽。
得到的约束变分问题如下:
| $ \begin{array}{*{20}{c}} {{{\min }_{\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\}}}\left\{ {\displaystyle\sum\limits_k {\left\| {{\partial _t}\left[ {\left( {\delta (t) + \dfrac{j}{{\text{π} t}}} \right)*{u_k}(t)} \right]{e^{ - j{\omega _k}t}}} \right\|} _2^2} \right\}} \text{。}\\ {{\text{ s}}{\text{.t}}{\text{. }}\displaystyle\sum\limits_k {{u_k}} = f} \end{array} $ | (1) |
其中:
步骤4 使用二次惩罚因子和拉格朗日乘子,解决约束问题。
通过利用有限权重下二次罚函数的良好收敛性,以及拉格朗日乘子对约束的严格执行,将约束问题转化为非约束问题,如下式:
| $ \begin{array}{*{20}{c}} {\mathcal{L}\left( {\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\},\lambda } \right): = \alpha \mathop \sum \limits_k \left\| {{\partial _t}\left[ {\left( {\delta (t) + \dfrac{j}{{\text{π} t}}} \right) * {u_k}(t)} \right]{e^{ - j{\omega _k}t}}} \right\|_2^2} +\\ { \left\| {f(t) - \mathop \sum \limits_k {u_k}(t)} \right\|_2^2 + \left\langle {\lambda (t),f(t) - \mathop \sum \limits_k {u_k}(t)} \right\rangle }\text{。}\\[-18pt] \end{array} $ | (2) |
步骤5 利用交替方向乘数法(ADMM)解决变分问题。
通过不断利用式对
| $ u_k^{n + 1} \leftarrow \mathop {\arg \min }\limits_{{u_k}} \mathcal{L}\left( {\left\{ {u_{i < k}^{n + 1}} \right\},\left\{ {u_{i \geqslant k}^n} \right\},\left\{ {\omega _i^n} \right\},{\lambda ^n}} \right)\text{,} $ | (3) |
| $ \omega _k^{n + 1} \leftarrow \mathop {\arg \min }\limits_{{\omega _k}} \mathcal{L}\left( {\left\{ {u_i^{n + 1}} \right\},\left\{ {\omega _{i < k}^{n + 1}} \right\},\left\{ {\omega _{i \geqslant k}^n} \right\},{\lambda ^n}} \right) \text{,}$ | (4) |
| $ {\lambda }^{n+1}\leftarrow {\lambda }^{n}+\tau \left(f-\sum _{k}{u}_{k}^{n+1}\right) \text{,}$ | (5) |
| $ \sum _{k}{u}_{k}^{n+1}-{u}_{k}^{n}{}_{2}^{2}/{u}_{k}^{n}{}_{2}^{2} < \varepsilon \text{。}$ | (6) |
最后得到:
| $ {\widehat{u}}_{k}^{n+1}(\omega )=\dfrac{\widehat{f}(\omega )-\displaystyle\sum _{i\ne k}{\widehat{u}}_{i}(\omega )+\dfrac{\widehat{\lambda }(\omega )}{2}}{1+2\alpha {\left(\omega -{\omega }_{k}\right)}^{2}}\text{,} $ | (7) |
| $ {\omega }_{k}^{n+1}=\dfrac{{\displaystyle\int }_{0}^{\infty }\omega {\left|{\widehat{u}}_{k}(\omega )\right|}^{2}{\rm{d}}\omega }{{\displaystyle\int }_{0}^{\infty }{\left|{\widehat{u}}_{k}(\omega )\right|}^{2}{\rm{d}}\omega }\text{。} $ | (8) |
麻雀搜索算法主要模拟麻雀的觅食行为,寻找全局最优值[12]。麻雀分为发现者和追随者。发现者负责寻找食物并起引导作用,追随者通过追随发现者获得食物。在寻找食物的过程中,为了得到更好的食物,麻雀种群中的成员会一直监视发现者,与发现者竞争或在发现者周围觅食。此外,当麻雀种群意识到捕食者的存在时,会做出反捕食行为。外围的麻雀很容易受到捕食者的攻击,因此需要不断调整自己的位置,以减少受到伤害的可能性。基于麻雀的这些行为,开发了麻雀搜索算法。
步骤如下:
步骤1 参数设定,对适应度进行排序,找到当前最佳适应度个体和最差适应度个体。
步骤2 使用下式更新适应度靠前麻雀(发现者)位置:
| $ X_{ij}^{t + 1} = \left\{ {\begin{array}{*{20}{c}} {X_{i,j}^t \cdot \exp \left(\dfrac{{ - i}}{{\alpha \cdot ite{r_{\max }}}}\right)}\text{,}&{{\text{if }}{R_2} < ST}\text{,} \\ {X_{i,j}^t + Q \cdot L}\text{,}&{{\text{if }}{R_2} \geqslant ST} \text{。} \end{array}} \right.{\text{ }}$ | (9) |
其中:t为当前迭代;j=1,2,…,d;
当
步骤3 使用下式更新适应度靠后麻雀(跟随者)位置:
| $ X_{ij}^{t + 1} = \left\{ {\begin{array}{*{20}{c}} {Q \cdot \exp \left(\dfrac{{x_{{\rm{worst}}}^t - X_{ij}^t}}{{{\beta ^2}}}\right)}\text{,}&{{\rm{if}}{\text{ }}i > n/2}\text{,} \\ {X_p^{t + 1} + |X_{ij}^t - X_p^{t + 1}| \cdot {A^ + } \cdot L}\text{,}&{{\rm{otherwise}}} \text{。} \end{array}} \right. $ | (10) |
式中:
步骤4 使用下式随机更新部分麻雀(警戒者)位置:
| $ X_{ij}^{t + 1} = \left\{ {\begin{array}{*{20}{c}} {X_{{\text{best }}}^t + \beta \cdot\left| {X_{ij}^t - X_{{\text{best }}}^t} \right|}\text{,}&{{\text{ if }}{f_i} > {f_g}} \text{,}\\ {X_{ij}^t + K\cdot\left( {\dfrac{{\mid X_{i,j}^t - X_{{\text{worst }}}^t}}{{\left( {{f_i} - {f_w}} \right) + \varepsilon }}} \right)}\text{,}&{{\text{ if }}{f_i} = {f_g}}\text{。} \end{array}} \right. $ | (11) |
式中:
步骤5 得到当前更新后的位置。
步骤6 如果新位置优于旧位置,更新旧位置。
步骤7 重复进行步骤 4到步骤 6。
步骤8 达到最大迭代次数输出最佳适应度值。
2.2 GRU神经网络模型GRU是循环神经网络的一种[13],该网络模型将长短期记忆神经网络(long-short term memory,LSTM)[14]的输入门、遗忘门、输出门改变为成更新门、重置门,使GRU只需要一个更新门就可以实现数据的遗忘和记忆,训练时间相较于LSTM缩短。LSTM通过门控机制不仅能够记忆过去的信息,并且同时可以选择性的忘记一些不重要信息以及无关信息,从而实现数据的建模。GRU在基于LSTM网络的基础上进行改动,不再保留长期序列同时也减少了梯度问题,提高了网络的训练速度。
GRU内部结构如图1所示。
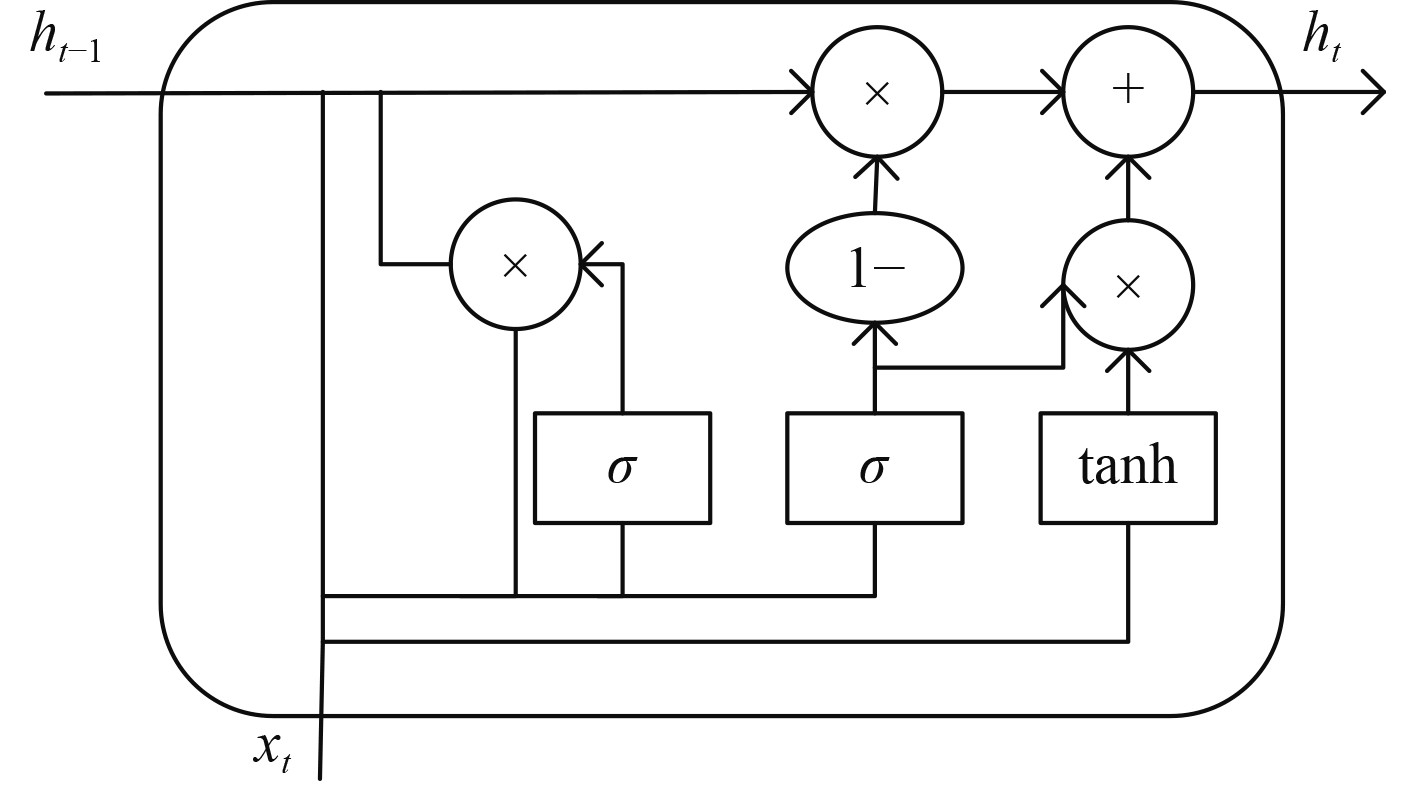
|
图 1 GRU内部结构图 Fig. 1 Internal structure of GRU |
GRU网络的前项传播算法如下:
| $ {z_t} = \sigma \left\{ {{W_z}\left[ {{h_{t - 1}},{x_t}} \right]} \right\}\text{。} $ | (12) |
更新门
| $ {r_t} = \sigma \left\{ {{W_r}\left[ {{h_{t - 1}},{x_t}} \right]} \right\}\text{。} $ | (13) |
GRU不再使用单个的内存单元来存储记忆信息,而是直接利用隐藏单元记录历史状态。利用重置门
| $ {\bar h_t} = \tanh \left\{ {W\left[ {{r_r}{h_{t - 1}},{x_t}} \right]} \right\} \text{。}$ | (14) |
在式(6)中,当
| $ {h_t} = \left( {1 - {z_t}} \right){h_{t - 1}} + {z_t}{\bar h_t} \text{。} $ | (15) |
在最后一步,网络需要计算
利用GRU对时间序列的特殊循环预测性能,同时通过麻雀搜索算法的全局寻优能力对GRU网络进行学习率优化,以提高GRU对船舶运动姿态的预测精度。
步骤如下:
步骤1 初始化。设定麻雀搜索算法的参数及确定GRU网络结构。麻雀搜索算法的参数主要指种群规模,最大迭代次数以及速度取值的范围区间。GRU网络结构指各个网络层神经元节点数及隐含层个数。
步骤2 寻优。将麻雀种群划分为发现者和跟随者,通过不断更新发现者位置以及跟随者位置从而不断更新麻雀种群的全局最优位置,将均方根误差作为适应度函数,选择性对最优位置进行更新,麻雀搜索算法不断进行迭代,当迭代到达最大迭代次数时输出最优值。
步骤3 训练。将步骤2的获得的学习率赋给GRU神经网络,利用船舶运动姿态数据进行训练并预测。
流程如图2所示。

|
图 2 数据散点图 Fig. 2 Scatter diagram of ship data |
由于海上环境的复杂性,船舶运动受到多种不确定因素的影响,单一的预测模型往往无法实现船舶运动姿态的准确预测,因此提出基于分解策略的SSA-GRU预测模型,通过VMD对船舶运动姿态数据进行分解,将非平稳、非线性的船舶运动姿态数据分解为若干个本征模态分量,提高了数据的可预测性,再利用麻雀搜索算法优化的GRU神经网络对各个模态分量进行预测,提高了GRU网络的预测精度。
步骤1 为VMD选取合适的参数:分解个数、惩罚函数;
步骤2 VMD对船舶运动姿态数据进行分解,得到IMF1、IMF2…IMFk等模态分量;
步骤3 对各个模态分量构建SSA-GRU预测模型,完成预测;
步骤4 对模态分量的预测结果进行叠加,得到最终预测结果。
流程如图3所示。

|
图 3 VMD分解结果 Fig. 3 VMD decomposition results |
本文采用风电运维船在浪向角为0°、风速12 m/s、流速2 m/s条件下仿真得到的横摇角、纵摇角、升沉位移数据进行仿真。每种数据总计1000条,采样时间为0.1 s,训练集和测试集的划分为9∶1。数据散点图如图4所示。

|
图 4 数据散点图 Fig. 4 Scatter diagram of ship data |
|
|
表 1 风电运维船主要参数 Tab.1 Main parameters of wind power operation and maintenance ship |
以船舶运动姿态的纵摇角为例,VMD分解个数设置为7,惩罚函数α设置为1000,分解结果见图5所示,得到7个模态分量。同时与经验模态分解(empirical mode decomposition,EMD)分解效果对比,EMD的分解个数由自身的迭代过程解得,对纵摇数据的分解结果见图6。得到6个模态分量和一个res残余分量。一般认为,分解得到的高频分量表示影响船舶运动的外界因素,低频部分表示船舶横摇运动的趋势。从图5和图6可以看出,EMD分解得到的imf2和imf3存在明显的模态混叠现象,而VMD分解得到的各分量模态混叠得到有效避免。同时,从频率方面来看,明显看出VMD分解得到的高频分量变化更具规律性,变化幅值较EMD分解得到的变化幅度更小。表明,VMD对降低船舶运动姿态的非平稳性更具有效性。
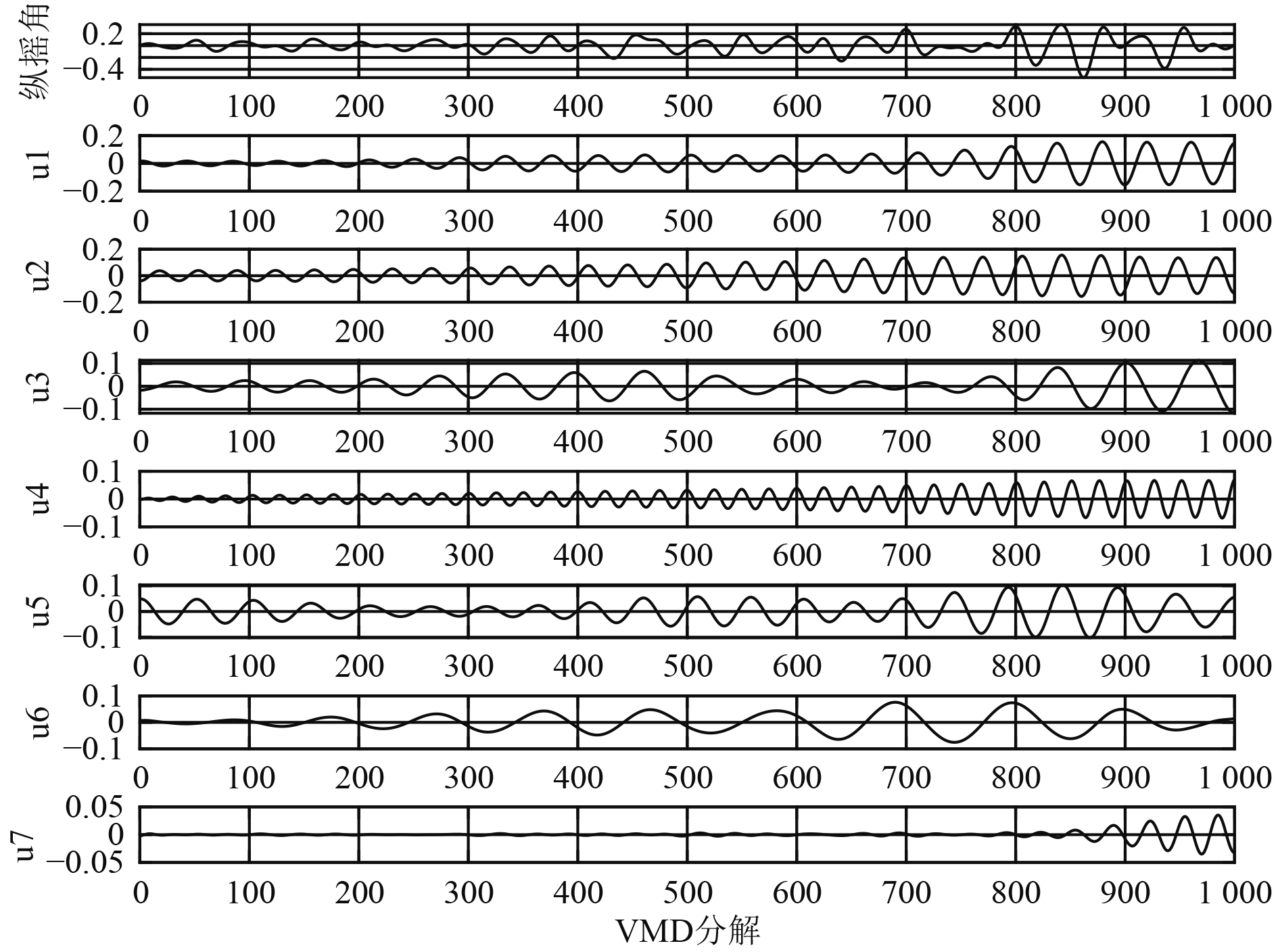
|
图 5 VMD分解结果 Fig. 5 VMD decomposition results |

|
图 6 EMD分解结果 Fig. 6 EMD decomposition results |
仿真前利用下式对各个姿态的数据进行归一化:
| $ {x^\prime } = {\dfrac{{x - \min (x)}}{{\max (x) - \min (x)}}_t}\text{。} $ |
式中:
为了验证提出的VMD-SSA-GRU在船舶运动姿态预测的预测性能,本文同时利用GRU,SSA-GRU,EMD-SSA-GRU预测模型通过对船舶运动姿态的横摇角、纵摇角及升沉位移进行预测,对比预测效果。
算法相关参数设定见表2。
|
|
表 2 参数设定 Tab.2 Parameter setting |
为了有效对结果进行评价,选用均方根误差(root mean squared error,RMSE)以及平均绝对误差(mean absolute error,MAE)作为误差评价指标。公式如下:
| $ {\text{RMSE}} = \sqrt {\dfrac{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{x_i} - {{\hat x}_i}} \right)}^2}} }}{n}} \text{,} $ |
| $ MAE = \frac{1}{n}\mathop \sum \limits_{i = 1}^n \left| {{{\hat x}_i} - {x_i}} \right| \text{。}$ |
对横摇角、纵摇角以及升沉位移的预测结果如图7和表3所示。从图7可知,4个预测模型对船舶运动的横摇角、纵摇角及升沉位移的预测结果与实际数据拟合度皆为可观,但GRU偏离程度最高,SSA- GRU相较于GRU和实际数据拟合度更好,EMD-SSA- GRU和VMD-SSA- GRU对比其他2个模型预测效果更接近于实际数据,而VMD-SSA- GRU相较于另外3个模型拟合度更高。可以证明VMD-SSA- GRU预测模型能够有效提高船舶运动姿态预测的预测精度。
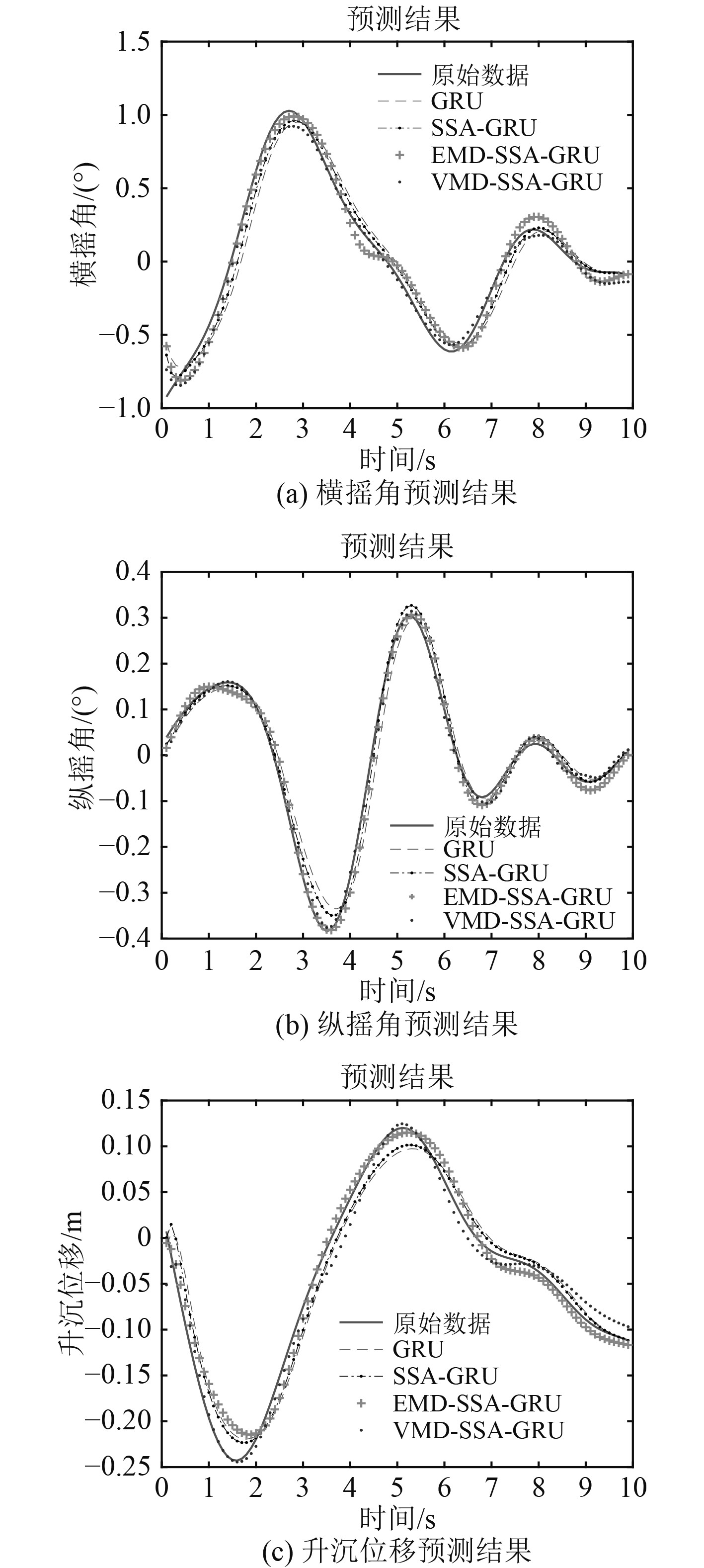
|
图 7 预测结果 Fig. 7 Prediction results |
|
|
表 3 模型预测误差 Tab.3 Model prediction error |
从表3可以看出,在对横摇角、纵摇角及升沉位移的预测中,SSA-GRU相较于GRU预测模型均方根误差以及平均绝对误差均有相应降低,说明了麻雀搜索算法有效提高了GRU网络在船舶运动姿态的预测性能。而通过分解后的预测误差有一定程度的降低,说明分解策略有效降低了船舶运动姿态的非平稳性,提高了数据的可预测性。而VMD-SSA-GRU预测模型在对3组数据的预测中误差均低于EMD-SSA-GRU预测模型的预测误差。证明了提出的预测模型在船舶运动姿态预测的优越性。综上分析,验证了本模型在船舶运动姿态预测的有效性。
5 结 语本文针对船舶运动姿态的非平稳性,提出基于分解策略的SSA-GRU预测模型。该模型通过VMD对船舶运动姿态数据分解,再利用麻雀搜索算法优化的GRU循环神经网络进行预测,有效提高了GRU神经网络在船舶运动姿态的预测精度。同时利用船舶运动姿态的横摇角、纵摇角和升沉位移将本模型与GRU,SSA-GRU,EMD-SSA-GRU进行仿真预测。将结果对比分析证明:提出的模型在横摇角、纵摇角及升沉位移的预测中预测结果和实际数据拟合程度最高,以及预测误差均低于另外3个模型,验证了本模型能够有效用于船舶运动姿态的预测。本文提出的模型不仅适用于船舶的运动姿态预报,同时适用于各个六自由度设备的运动姿态预报。
| [1] |
翁震平, 顾民, 刘长德. 基于二阶自适应Volterra级数的船舶运动极短期预报研究[J]. 船舶力学, 2010, 14(7): 732-740. |
| [2] |
彭秀艳, 赵希人, 高奇峰. 船舶姿态运动实时预报算法研究[J]. 系统仿真学报, 2007(2): 267-271. |
| [3] |
NOVRI, SUHERMI, SUHARTONO, et al. Roll motion prediction using a hybrid deep learning and ARIMA model[J]. Procedia Computer Science, 2018, 144: 251-258. DOI:10.1016/j.procs.2018.10.526 |
| [4] |
沈继红. 灰色系统理论预测方法研究及其在舰船运动预报中的应用[D]. 哈尔滨: 哈尔滨工程大学, 2002
|
| [5] |
YIN J C, ZOU Z J, FENG X. On-line prediction of ship roll motion during maneuvering using sequential learning RBF neuralnetworks[J]. Ocean Engineering, 2013, 61(Mar. 15): 139–147.
|
| [6] |
王国栋, 韩斌, 孙文赟. 基于 LSTM 的舰船运动姿态短期预测[J]. 舰船科学技术, 2017, 39(7): 69-72. |
| [7] |
YIN Jianchuan, PERAKIS A N, WANG Ning. A real-time ship roll motion prediction using wavelet transform and variable RBF network[J]. Ocean Engineering, 2018, 160: 10-19. DOI:10.1016/j.oceaneng.2018.04.058 |
| [8] |
杨震, 王岩, 原新. 一种分解策略的船舶横摇运动姿态在线预报方法[J]. 船舶力学, 2018, 22(8): 915-925. |
| [9] |
张彪, 彭秀艳, 高杰. 基于ELM-EMD-LSTM组合模型的船舶运动姿态预测[J]. 船舶力学, 2020, 24(11): 1413-1421. |
| [10] |
张泽国, 尹建川, 柳成. 基于自适应变异PSO-BP算法的船舶横摇运动预测[J]. 舰船科学技术, 2016, 38(23): 69-73. |
| [11] |
DOMINIQUE, ZOSSO, KONSTANTIN, et al. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing A Publication of the IEEE Signal Processing Society, 2014, 62(3): 531-544. |
| [12] |
XUEJ, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering an Open Access Journal, 2020, 8(1): 22–34.
|
| [13] |
CHO K, MERRIENBOER B V, GULCEHRE C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation[J]. Computer Sci-ence, 2014.
|
| [14] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
 2022, Vol. 44
2022, Vol. 44

