0 引　言

近年来，绿色和智能逐渐成为全球航运业发展的焦点，也是未来技术发展的重要趋势和方向。我国作为航运大国，船舶的绿色技术应用还不完善，智能技术处于初期探索阶段。为明确船舶绿色智能技术未来发展方向和应用路径，以船舶为载体，多方面综合地考虑绿色智能技术的应用成效，开展船舶绿色智能技术应用综合评价研究十分必要，其评价结果为有步骤、可持续地提升船舶绿色智能化水平提供依据。

船舶绿色智能技术应用评价涵盖绿色性、智能性、安全性、经济性，技术性、社会效益性6个方面^[1-3]。其中，对于经济性，技术性、社会效益性这些指标，决策者往往难以给出精确的评价信息，在属性值量化上更适合采用模糊值和随机值表达，因此船舶绿色智能技术应用综合评价是典型的不确定性混合多属性决策问题，使用常规的确定性决策方法或孤立使用随机理论、模糊理论决策方法难以获得客观科学的评价结果。目前对于具有不确定性信息的混合多属性决策问题引起了一些学者的关注，陈小卫等^[4]针对权重已知且属性值为精确实数型、区间型和模糊型的混合型多属性决策问题，提出了一种基于模糊偏序关系的混合型多属性决策方法。张尧等^[5]针对属性值为随机变量、清晰数和模糊数3种信息形式的多属性决策问题，提出了混合占优度及其计算方法，并运用Promethee II对方案排序。王芃等^[6]采用了一种基于混合占优的混合多属性决策方法，并通过计算加权贴进度，推荐了电力行业对用户有序用电的排序方案。上述方法对具有混合不确定性信息的多属性决策问题提供了较好的解决思路，但目前尚未在船舶领域开展应用。因此，将上述不确定性随机决策方法应用于船舶绿色智能技术应用综合评价，为构建科学合理的船舶绿色智能技术应用综合评价方法提供了一种新的解决途径。

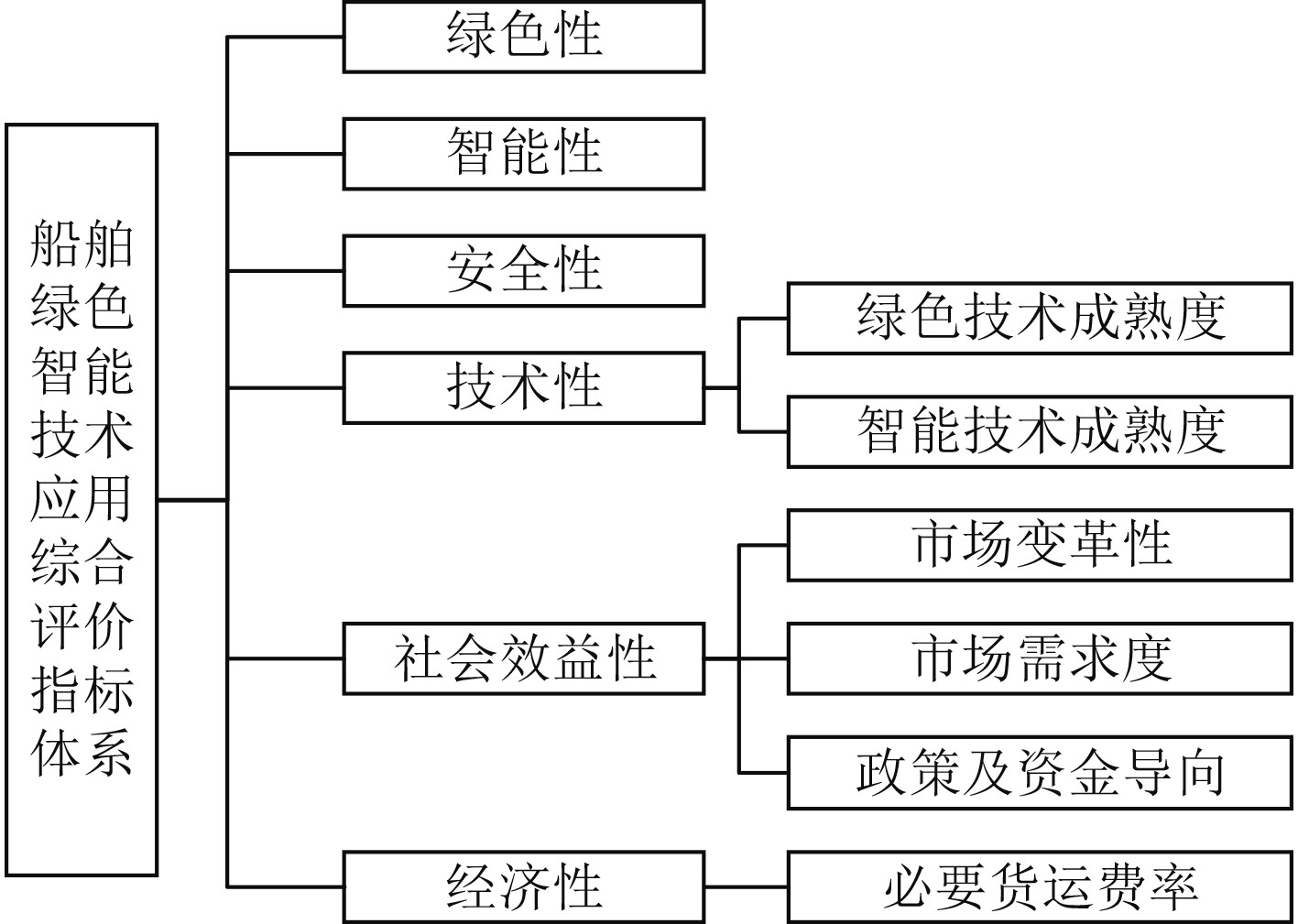
1 船舶绿色智能技术应用综合评价思路

构建船舶绿色智能技术应用综合评价指标体系是开展绿色智能技术应用综合评价的首要问题，船舶绿色智能技术应用综合评价指标如图1所示。

其中，安全性是船舶绿色智能技术应用的前提，可采用综合安全评估（FSA）的方法对技术方案的安全性进行评估。绿色性和智能性为定量指标，其指标及评分方法参照《内河绿色船舶规范》^[7]、《绿色生态船舶规范》^[8]、《智能船舶规范》^[9]及相关研究成果^[10]。而技术性、社会效益性及经济性指标属性值具有不确定性，且指标类型有别。经济性指标下级指标为必要货运费率，为定量指标。技术性下层指标包含绿色技术成熟度、智能技术成熟度，均为定性指标。社会效益性下层指标包括技术变革性、市场需求度、政策及资金导向，均为定性指标。定性指标量化时，应更关注指标的模糊性；定量指标量化时，应重点考虑到其计算参数的随机性。

因此，船舶绿色智能技术应用综合评价的主要思路为：结合现有成果，以图1所示指标体系为依据，重点开展具有模糊性和随机性的指标的量化方法研究，构建科学的不确定性混合多属性决策模型，从而择优推荐船舶绿色智能技术应用方案。

2 综合评价关键指标属性值量化方法

针对技术性、社会效益性、经济性指标，按照定性指标和定量指标的区别，提出相应的量化方法。

2.1 定性指标量化 2.1.1 语言评价集量化

技术性和社会效益性指标为定性指标，对于这类指标，决策者对方案属性值的判断通常很难用一个精确的数字表述出来，具有很强的模糊性。此类问题的处理方法通常是选用模糊值变量和语言评价等级来进行指标评价^[11]。区间型模糊值变量是表达模糊语言信息最为简单有效的形式，因此，本文选用语言评价集S={S₀=很差，S₁=差，S₂=一般，S₃=好，S₄=很好}对技术性和社会效益性指标进行表述，基于区间数的语言短语集的语义表示方法，对[0,1]区间进行均匀划分，从而达到使用区间数近似表达语言评价的目的。语言评价集与区间型模糊值变量的对应关系如表1所示。

2.1.2 模糊语言变量信息集结

对技术性和社会效益性指标进行评价时，考虑到单一的专家评价会导致评价结果存在个人偏好，具有很强的主观性。采用不确定有序加权平均(uncertain ordered weighted averaging, UOWA)算子^[12]能对多个专家的评价意见进行信息集结，充分利用多个专家的意见，从而获得科学合理的定性指标评价结果。

定义1　当 $ a $ ， $ b $ 均为区间数时， $ a = \left[ {{a^L},{a^U}} \right] $ ， $ b = \left[ {{b^L},{b^U}} \right] $ ，则称

$ p(a > b) = \frac{{{\text{min}}\left\{ {{a^U} - {a^L} + {b^U} - {b^L},{\text{max}}({a^U} - {b^L},0)} \right\}}}{{({a^U} - {a^L} + {b^U} - {b^L})}}\text{，} $

(1)

为 $ a > b $ 的可能度。

定义2　 $ {\tilde x_i} = [x_i^L,x_i^U](i = 1,2, \cdots ,n) $ 为一组区间数，若函数UOWA ： $ {\varOmega }^{\text{n}}�\varOmega $ ，满足

$ {\text{UOWA}}\left( {{{\tilde x}_1},{{\tilde x}_2}, \cdots {{\tilde x}_n}} \right) = \sum\limits_{i = 1}^n {{v_i}{{\tilde y}_i}} \text{，}$

(2)

则称UOWA为不确定有序加权平均算子，其中 $ {v_i} $ 为与UOWA算子相关的权重向量，满足 $ {v_i} \in \left[ {0,1} \right],\displaystyle\sum\limits_{i = 1}^n {{v_i} = 1} $ ， $ {\tilde y_i} $ 为区间数 $ {\tilde x_i} $ 按照可能度从大到小排序的一组区间数。

采用UOWA算子进行技术性和社会效益性指标评价信息集结时，按以下步骤进行：

1）假设有s位专家参加评价，得到不同专家对不同指标的评价矩阵为

$ {{\boldsymbol{x}}_{kj}} = \left( {\begin{array}{*{20}{c}} {{x_{11}}}& \ldots &{{{\text{x}}_{1j}}} \\ \vdots & \ddots & \vdots \\ {{x_{s1}}}& \cdots &{{x_{sj}}} \end{array}} \right)\text{，} $

(3)

其中 $ {x_{sj}} $ 为第s位专家对指标的评价区间。

2）由下列公式确定加权向量

$ \begin{split} & v = {\left[ {{v_1},{v_2}, \cdots {v_i}} \right]^{\rm{T}}}\\ & {v_i} = Q\left( {\frac{i}{m}} \right) - Q\left( {\frac{{i - 1}}{n}} \right)\text{，} \end{split} $

(4)

式中，模糊语义量化算子Q由下式计算：

$ Q\left( r \right) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0\text{，}&{r < a} \text{，} \end{array}} \\ {\begin{array}{*{20}{c}} {\dfrac{{r - a}}{{b - a}}}\text{，}&{a \leqslant r \leqslant b}\text{，} \end{array}} \\ {\begin{array}{*{20}{c}} 1\text{，}&{r > b}\text{。} \end{array}} \end{array}} \right. $

(5)

式中： $a,b,c \in \left[ {0,1} \right]$ ，对应模糊语义量化准则：“大多数”，“至少一半”，“尽可能多”的算子Q中参数对分别为（0.3，0.8），（0，0.5），（0.5，1）。

3）对所有专家对同一指标的评价值进行两两比较，获得可能度矩阵 ${\boldsymbol{P}} = {\left( {{p_{ij}}} \right)_{s \times s}}$ ，利用式(6)计算不同指标可能度矩阵的排序向量 $ V = {\left[ {{v_1},{v_2}, \cdots {v_i}} \right]^{\rm{T}}} $ ，并按 $ {v_i} $ 的大小对区间数 $ {\tilde x_i} $ 排序得到 $ {\tilde y_i} $ 。

$ {v_i} = \frac{1}{{m\left( {m - 1} \right)}}\left( {\sum\limits_{j = 1}^m {{p_{ij}} + \frac{m}{2} - 1} } \right)\text{。} $

(6)

4）利用UOWA算子计算各指标的属性值评价结果。

2.2 定量指标量化

经济性的二级指标必要货运费率为定量指标。由于船舶工程项目具有复杂性的特点，计算必要货运费率时会存在部分计算参数具有随机性，难以准确量化，需要估计预测，这类参数的存在最终会导致经济性指标的估计值与实际值存在一定的误差，不符合客观实际。因此经济性在计算时可以采用随机模拟的方法，从而获得合理的结果。

选用船价、燃油价格和绿色智能技术应用成本增量作为经济性计算的不确定参数。

船价和燃油价格是船舶经济性计算最主要的不确定性因素^[13]，船价受经济环境、国家政策、航运市场需求以及船舶建造原材料成本等因素的影响，燃油价格受世界经济、国家政策、航运市场、自然条件等诸多因素影响，均存在不确定性特点，可以通过对上述参数的历史数据进行整理和统计分析，形成频率分布直方图并进行拟合，获得概率分布函数。

在传统的经济性不确定性因素的基础上，增设绿色智能技术应用成本增量，以此衡量绿色智能技术对经济性指标量化结果的影响，提高评价的准确性。由于船舶的绿色智能技术还处于起步阶段，绿色智能技术应用成本增量没有实船数据参考，该部分数据较少，不能确定其准确的概率分布，对于这类参数在进行随机模拟时可以采用符合区间均匀分布的随机变量进行表征。

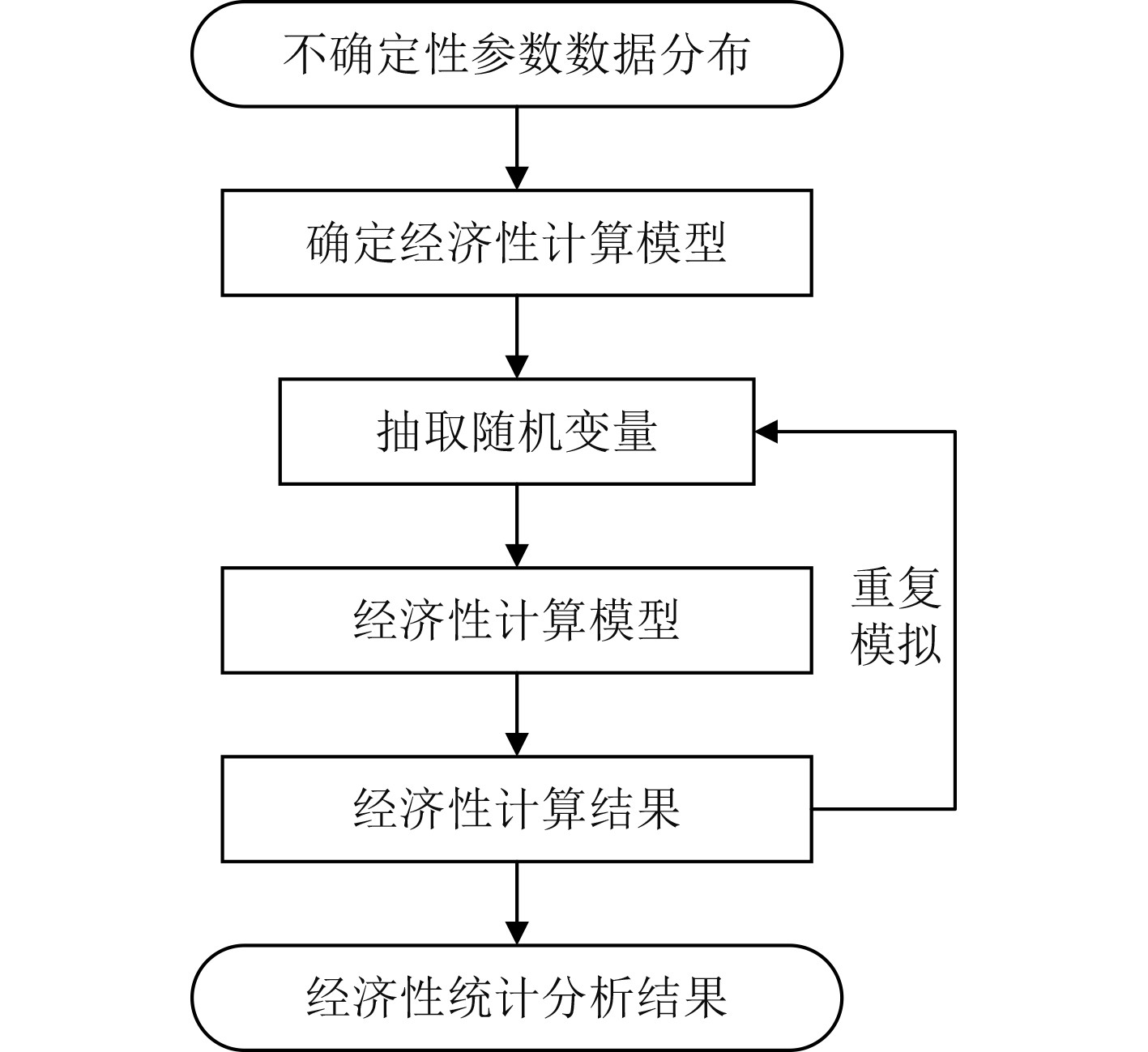
基于上述不确定参数的概率分布结果，通过随机模拟获得必要货运费率的计算结果并拟合出对应的概率分布，即为经济性指标属性值的量化结果，用于后续的决策。图2为经济性随机模拟计算操作流程。

3 不确定性混合多属性决策模型

对于船舶绿色智能技术应用综合评价问题，存在m个绿色智能技术应用方案 ${X_i}\left( {i = 1,2, \cdots ,m} \right)$ ，应首先对各个方案的安全性进行评估，满足安全性要求的方案方可进行后续的评价。开展后续综合评价时，对于n个评价指标 $ {O_j}\left( {j = 1,2, \cdots ,n} \right) $ ，其指标属性值量化方法不同，导致指标属性值的数据类型也不一致，为有效地解决评价信息复杂性和不确定性问题，本文构建了适合船舶绿色智能技术应用方案综合评价的不确定性混合多属性决策模型。

评价模型采用将多指标转化为综合评价指标的总体思想，其决策模型表达为：

$ C{\text{ = }}\sum\limits_{j = 1}^n {{w_j}{D_j}}\text{。} $

(7)

式中： $C = {\left( {{c_{ik}}} \right)_{m \times m}}$ 为综合占优度，表示在考虑所有指标的条件下方案 ${X_i}$ 优于 ${X_k}$ 的综合占优程度； ${w_j}( j = 1,2, \cdots ,n )$ 为指标权重； ${D_j} = {(d_{ik}^j)_{m \times m}}$ 为混合占优度，表示对于某一指标 $ {O_j} $ 方案 ${X_i}$ 优于 ${X_k}$ 的单指标占优程度，可通过进行属性值归一化处理及累计分布函数转化，并基于混合占优准则进行计算。

在式（7）计算所得的综合占优度的基础上，采用改进的偏好顺序结构评估法（Promethee II）方法^[14]计算各方案的净流量，即可实现方案择优。

3.1 属性值归一化方法及累计分布函数

指标类型一般可以分成本型和效益型，为方便后续决策需进行归一化处理并将不同数学形式的属性值统一转化为相应的累计分布函数。

1）绿色性指标

绿色性指标为效益型，其属性值为精确值变量形式，按照式（8）进行归一化处理。

$ x_{ij}' = \frac{{{x_{ij}} - \mathop {\min }\limits_{1 \leqslant i \leqslant m} {x_{ij}}}}{{\mathop {\max }\limits_{1 \leqslant i \leqslant m} {x_{ij}} - \mathop {\min }\limits_{1 \leqslant i \leqslant m} {x_{ij}}}} \text{，}$

(8)

经过归一化处理后精确值的累计分布函数为：

$ {F_{ij}}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0\text{，}&{x < x_{ij}'} \text{，} \end{array}} \\ {\begin{array}{*{20}{c}} 1\text{，}&{x \geqslant x_{ij}'} \text{。} \end{array}} \end{array}} \right.$

(9)

2）智能性指标

智能性指标为效益型，其属性值为精确值变量形式，其归一化方法及累计分布函数与绿色性指标相同。

3）技术性指标

技术性指标为效益型，其属性值为模糊值变量形式，其属性值量化时在[0,1]区间内，无需进行归一化处理，若指标属性值为 $ {x_{ij}} = \left[ {x_{ij}^L,x_{ij}^U} \right] $ ，其累计分布函数为：

$ {F_{ij}}\left( x \right) = \int_{x_{ij}^L}^{x_{ij}^U} {{f_{ij}}} \left( x \right){\rm{d}}x \text{。}$

(10)

4）社会效益性指标

社会效益性指标属性值形式与技术性相同，其累计分布函数形式同式（10）。

5）经济性指标

经济性指标为成本型，其属性值为随机值变量 ${x_{ij}} = {f_{ij}}\left( x \right)$ ，且能够确定其分布的取值范围 $ \left[ {x_{ij}^L,x_{ij}^U} \right] $ ，令 ${x'} = \left( {\mathop {\max }\limits_{1 \leqslant i \leqslant m} {x_{ij}} - x} \right)/\left( {\mathop {\max }\limits_{1 \leqslant i \leqslant m} {x_{ij}} - \mathop {\min }\limits_{1 \leqslant i \leqslant m} {x_{ij}}} \right)$ ，其累计分布函数为：

$\begin{aligned}[b] & {F_{ij}}\left( {{x'}} \right) = \int_0^{{x'}} {\left( {\mathop {\max }\limits_{1 \leqslant i \leqslant m} {x_{ij}} - \mathop {\min }\limits_{1 \leqslant i \leqslant m} {x_{ij}}} \right){f_{ij}}}\text{，} \\ & \left( {\mathop {\max }\limits_{1 \leqslant i \leqslant m} {x_{ij}} - \left( {\mathop {\max }\limits_{1 \leqslant i \leqslant m} {x_{ij}} - \mathop {\min }\limits_{1 \leqslant i \leqslant m} {x_{ij}}} \right){x'}} \right){\rm{d}}x \text{。} \end{aligned}$

(11)

3.2 混合占优度计算

各方案对于某一指标的相对优劣关系可采用混合占优度表示，其计算方法如下式：

$ {d}_{ik}^{j} = \left\{\begin{array}{llllllllllll} \frac{{\text{e}}^{{\displaystyle {\int }_{a}^{b}xd\left({F}_{i}^{j}\left(x\right)\right){\rm{d}}x}}-{\text{e}}^{{\displaystyle {\int }_{a}^{b}xd\left({F}_{k}^{j} \left(x\right)\right){\rm{d}}x}}}{{\text{e}}^{{\displaystyle {\int }_{a}^{b}xd\left({F}_{i}^{j} \left(x\right)\right){\rm{d}}x}}}\text{，}& {F}_{i}^{j}\left(x\right)\text{MD}{F}_{k}^{j}\left(x\right)\text{，}\\ 0\text{，}& {\rm{others}}\text{。}\end{array}\right. $

(12)

其中：X和Y为 $\varOmega \left( {\varOmega = \left\{ {x\left| {x \in \left[ {a,b} \right]} \right.} \right\}} \right)$ 上的随机变量， $ F_i^j\left( x \right) $ 和 $ F_k^j\left( x \right) $ 分别为随机变量X和Y的累积分布函数。MD（mixed-data dominance）统一表示混合占优关系，包括以下3种情况：

1）当且仅当 $ F_i^j\left( x \right) \ne F_k^j\left( x \right) $ ，且 $ {H_1}\left( x \right) = F_i^j\left( x \right) - F_k^j\left( x \right) \leqslant 0 $ ，则称 $ F_i^j\left( x \right) $ 一阶混合占优于 $ F_k^j\left( x \right) $ 。

2）当且仅当 $ F_i^j\left( x \right) \ne F_k^j\left( x \right) $ ，且 $ {H_2}\left( x \right) = \int_a^x {{H_1}\left( y \right)dy} \leqslant 0 $ ，则称 $ F_i^j\left( x \right) $ 二阶混合占优于 $ F_k^j\left( x \right) $ 。

3）当且仅当 $ F_i^j\left( x \right) \ne F_k^j\left( x \right) $ ，且 $ {H_3}\left( x \right) = \int_a^x {{H_2}\left( y \right)dy} \leqslant 0 $ ，则称 $ F_i^j\left( x \right) $ 三阶混合占优于 $ F_k^j\left( x \right) $ 。

3.3 方案择优

基于Promethee II方法分别计算综合优先指标 $C$ 的正流量、负流量及净流量，从而获得各个方案的综合评价结果，比选出综合较优的方案。正流量 $ {\varPhi ^ + }\left( {{X_i}} \right) $ 、负流量 $ {\varPhi ^ - }\left( {{X_i}} \right) $ 和净流量 $ \varPhi \left( {{X_i}} \right) $ 的计算公式如下：

$ {\varPhi ^ + }\left( {{X_i}} \right) = \frac{1}{{m - 1}}\sum\limits_{k = 1}^m {{q_{ik}}}\text{，} $

(13)

$ {\varPhi ^ - }\left( {{X_i}} \right) = \frac{1}{{m - 1}}\sum\limits_{k = 1}^m {{q_{ki}}} \text{，}$

(14)

$ \varPhi \left( {{X_i}} \right) = {\varPhi ^ + }\left( {{X_i}} \right) - {\varPhi ^ - }\left( {{X_i}} \right) \text{。}$

(15)

依据净流量 $ \varPhi \left( {{X_i}} \right) $ 值的大小，对各方案进行排序， $ \varPhi \left( {{X_i}} \right) $ 值越大，说明该方案综合评价结果越优。

4 实例应用 4.1 评价对象

本文以长江7500 t散货示范船作为评价对象。根据技术的安全性要求，初步确定6个绿色智能技术应用方案如表2所示。

4.2 指标属性值量化

依据本文所述的指标量化方法，对各方案的指标进行量化。

4.2.1 绿色性、智能性指标

绿色性指标和智能性指标的属性值结果如表3所示。

4.2.2 技术性、社会效益性指标

针对技术性、社会效益性指标，收集专家对6种方案的技术性、社会效益性二级指标的评价结果，并以模糊语义量化准则为“大多数”，采用UOWA算子对专家评价信息集结，获得技术性、社会效益性指标二级指标属性值，并采用简单平均加权法计算技术性、社会效益性指标属性值，其属性值结果如表4所示。

4.2.3 经济性指标

1）船价的确定

收集长江干散货船的造价数据，并通过公式 $ P = \dfrac{{{P_0}}}{{DWT}} $ 转化为均吨位造价。其中，P为估算船舶的造价， $ {P_0} $ 为已知船舶造价， $ DWT $ 为已知船舶载货量。将转化后的船舶均吨位造价进行整理和统计分析，其概率分布服从对数正态分布，概率分布函数为：

$ f\left( x \right) = \frac{1}{{0.01x\sqrt {2\text{π} } }}{e^{{\text{ - }}\frac{{{{\left( {\ln x - 0.2} \right)}^2}}}{{{\text{0}}{\text{.0002}}}}}} \text{。}$

(16)

2）燃油价格

对燃油价格的历史数据进行整理和统计分析，拟合的概率分布为Weibull分布，其概率分布函数为:

$ f\left( x \right) = \frac{{2.85}}{{488.33}}{\left( {\frac{x}{{488.33}}} \right)^{2.85 - 1}}{e^{ - {{\left( {\frac{x}{{488.33}}} \right)}^{2.85}}}} \text{。}$

(17)

3）绿色智能技术成本增量

考虑到绿色智能技术的应用，这部分数据通过调研，确定不同方案所带来的成本增量区间如表5所示。

4）必要运费率的计算

船舶的必要货运费率按照下式计算：

$ RFR = \frac{{AAC}}{Q} = \frac{{\left( {P - L} \right) * \left( {\frac{A}{P},i,n} \right) + L * i + Y}}{Q} \text{。}$

(18)

式中： $RFR$ 为必要运费率，元/t； $AAC$ 为平均年费，元； $P$ 为船舶投资金额，元； $\left( {\dfrac{A}{P},i,n} \right)$ 为资金回收因数； $L$ 为残值； $i$ 为基准收益率，%；Y为年营运费用，元； $Q$ 为年运输总量，t。

5）计算结果

通过输入计算参数并进行随机模拟，获得经济性计算结果的相关统计参数，并拟合出概率分布函数，拟合必要概率分布图如图3所示，其概率分布的相关参数如表6所示。

4.3 多属性决策

根据本文所述多属性决策模型。通过式（7）计算综合占优度。其中，指标权重通过专家调查获得，绿色性、智能性、经济性、技术性、社会效益性的指标权重向量为：[0.24，0.22，0.20，0.18，0.16，混合占优度根据式（12）计算获得。综合占优度计算结果如下式：

$ {\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 0 & {0.0166} & {0.0304} & {0.0314} & {0.0722} & {0.0707} \\ {0.0030} & 0 & {0.0331} & {0.0229} & {0.0746} & {0.0618} \\ {0.0369} & {0.0527} & 0 & {0.0114} & {0.0470} & {0.0478} \\ {0.0423} & {0.0465} & {0.0169} & 0 & {0.0626} & {0.0624}\\ {0.0811} & {0.0969} & {0.0485} & {0.0599} & 0 & {0.0252}\\ {0.0680} & {0.0730} & {0.0485} & {0.0485} & {0.0149} & 0 \end{array}} \right]。$

(19)

根据式（13）～式（15），计算各方案的正流量、负流量和净流量，如表7所示。

得到各方案的排序结果为：方案4>方案5>方案3>方案1>方案6>方案2，为此，选择方案4为推荐方案。7500 t散货示范船实际采用柴电混合动力系统，并取得CCS智能船舶i-ship（M, Es, I）认证符号。可见，本文择优推荐的7500 t级散货船绿色智能技术应用方案与工程实际吻合，研究提出的综合评价方法具有可行性和有效性。

5 结　语

针对船舶绿色智能技术应用评价指标众多、且部分指标属性值具有模糊性和随机性的问题，本文提出了不确定性指标的量化方法，考虑了指标的模糊性和随机性，使量化结果更符合实际；构建了混合多属性决策模型，有效地处理具有精确值变量、模糊值变量和随机值变量的混合多属性决策问题，为全面客观地综合评价船舶绿色智能技术应用提供了技术支持。同时应用本文评价方法推荐的长江7500 t散货示范船绿色智能技术应用方案与工程实际吻合，验证了方法的有效性。