振动控制技术一直是船用设备环境适应性领域的重点研究对象,根据“从振源削减振动传递”准则[1],精密设备与振源间安装弹性元件是最为重要的技术手段之一。但随着导航、测量等船用精密设备集成化、敏感度的提升,对低频振动提出了更高的要求[2-4],因此,降低低频振动量级、提升全频带减振效果就显得尤为重要。
具有高静刚度、低动刚度的准零刚度系统相比传统减振系统,可以达到大承载能力下具备小动刚度的效果,因此受到了国内外诸多研究人员的广泛关注。最为典型的结构形式是2个倾斜弹簧和1个垂直弹簧并联组合[5-6]。Carrella等[7]应用金属螺旋弹簧与永磁铁,组合成一种准零刚度系统。Xu等[8]应用永磁铁设计出一种具有低动刚度、高静刚度的低频准零刚度隔振器。Huang等[9]应用金属弹簧和屈曲梁结构,提出了纯结构型准零刚度设计方法。苏攀等[10]研究了准零刚度系统的工作原理,并设计了低频系统反馈控制方案。以上方法的负刚度机构多为机械弹簧或永久磁力弹簧,具有刚度小、不可调、正刚度和负刚度叠加困难等缺陷,现阶段未见将电磁弹簧与碟型硅氟橡胶相结合的报道。
本文应用电磁弹簧提供大负刚度力,并将其与碟型硅氟橡胶弹簧的正刚度力直接线性数值叠加,消除低频振动放大现象,实现减振器的零动刚度效果,提高船用精密设备的振动环境水平。
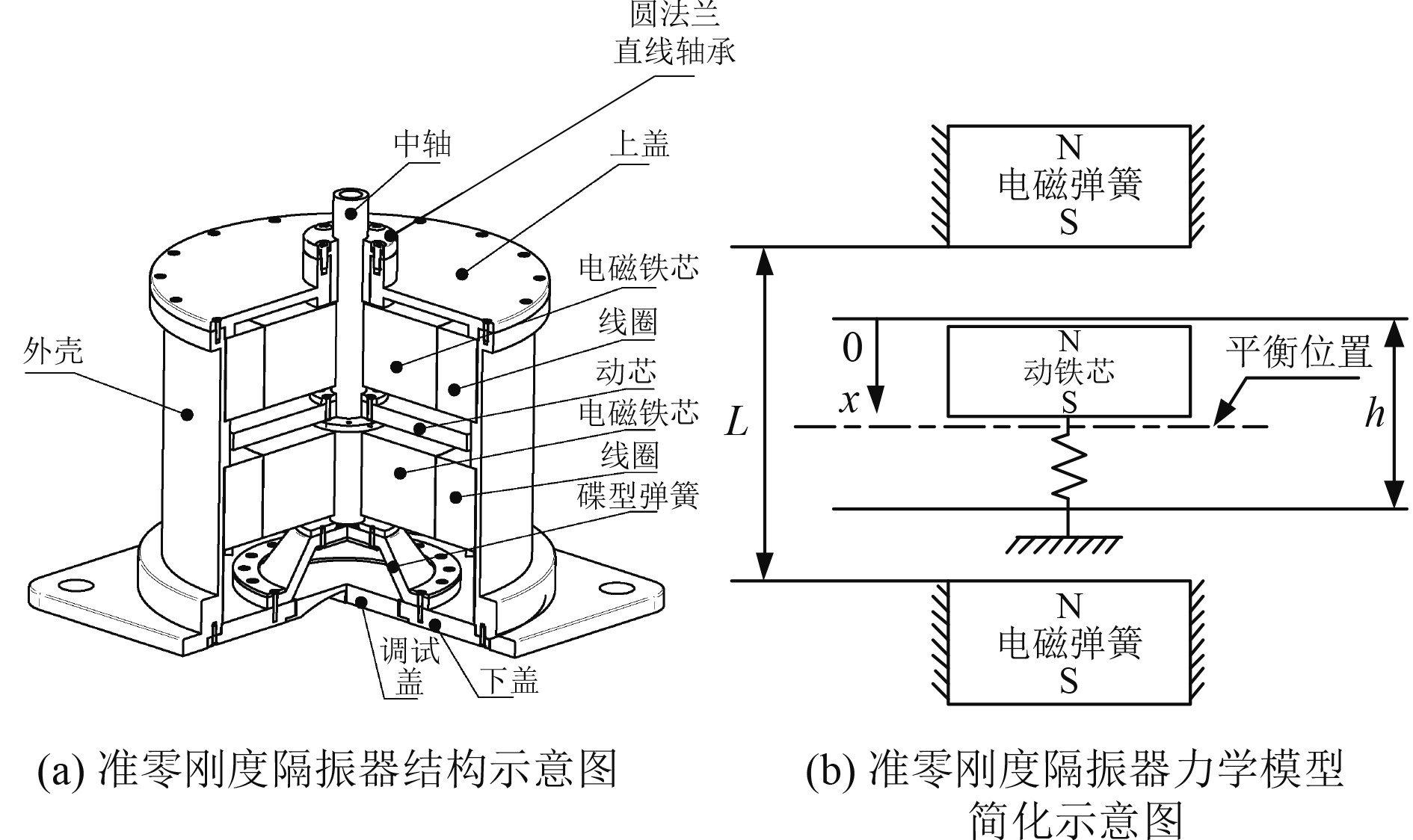
1 准零刚度隔振器机理分析 1.1 准零刚度隔振器力学模型基于准零刚度原理,以碟型硅氟橡胶提供正刚度,电磁弹簧提供负刚度,并联组合形成一种适用于船用精密设备减振的准零刚度隔振器,其结构如图1(a)所示。电磁弹簧由线圈和铁芯组成,2个相同的电磁弹簧在动芯两侧对称放置,且顶端有圆法兰直线轴承作为导向。等效简化减振器力学模型,如图1(b)所示。
|
图 1 准零刚度隔振器示意图 Fig. 1 Diagram of quasi-zero stiffness vibration isolator |
电磁铁间距为
| $ {f}_{m} =\frac{{\mu }_{0} · {N}^{2} · A·{i}^{2}}{2} · \left[\frac{1}{{\left(0.5 \times \left(L-h\right) + x \right)}^{2}} - \frac{1}{{\left(0.5 \times \left(L + h\right) - x\right)}^{2}}\right]\text{。} $ | (1) |
式中:
| $ f = kx + \frac{{\mu }_{0} · {N}^{2} · A · {i}^{2}}{2} · \left[\frac{1}{{\left(0.5 \times \left(L - h\right) + x\right)}^{2}} - \frac{1}{{\left(0.5 \times \left(L + h\right) - x\right)}^{2}}\right]\text{。} $ | (2) |
式中,
| $ \mathop f\limits^ \wedge = \mathop x\limits^ \wedge + \dfrac{{{{\left( {\mathop i\limits^ \wedge } \right)}^2}}}{2}\left[ {\dfrac{1}{{{{\left( {0.5 \times \left( {\alpha - 1} \right) + \mathop x\limits^ \wedge } \right)}^2}}} - \dfrac{1}{{{{\left( {0.5 \times \left( {\alpha + 1} \right) - \mathop x\limits^ \wedge } \right)}^2}}}} \right] \text{,}$ | (3) |
对上式求导,可得系统无量纲刚度为:
| $ \mathop K\limits^ \wedge = 1 - \frac{{{{\left( {\mathop i\limits^ \wedge } \right)}^2}}}{4}\left[ {{{\left( {0.5 \times \left( {\alpha - 1} \right) + \mathop x\limits^ \wedge } \right)}^{ - \frac{3}{2}}} + {{\left( {0.5\left( {\alpha + 1} \right) \times - \mathop x\limits^ \wedge } \right)}^{ - \frac{3}{2}}}} \right] \text{,}$ | (4) |
令
| $ {\mathop I\limits^ \wedge _{qzs}} = {\left( {\dfrac{{{\alpha ^3}}}{2}} \right)^{0.25}} \text{。}$ | (5) |
假定

|
图 2 平衡位置处无量纲电流与力和刚度的关系示意图 Fig. 2 Diagram of the relation of current to force and stiffness at equilibrium position |
由结果可知,电流的增加会使系统的非线性特性增强。在平衡位置处,若电流小于
为使运算更为简便,可将系统无量纲力进行泰勒展开,令
|
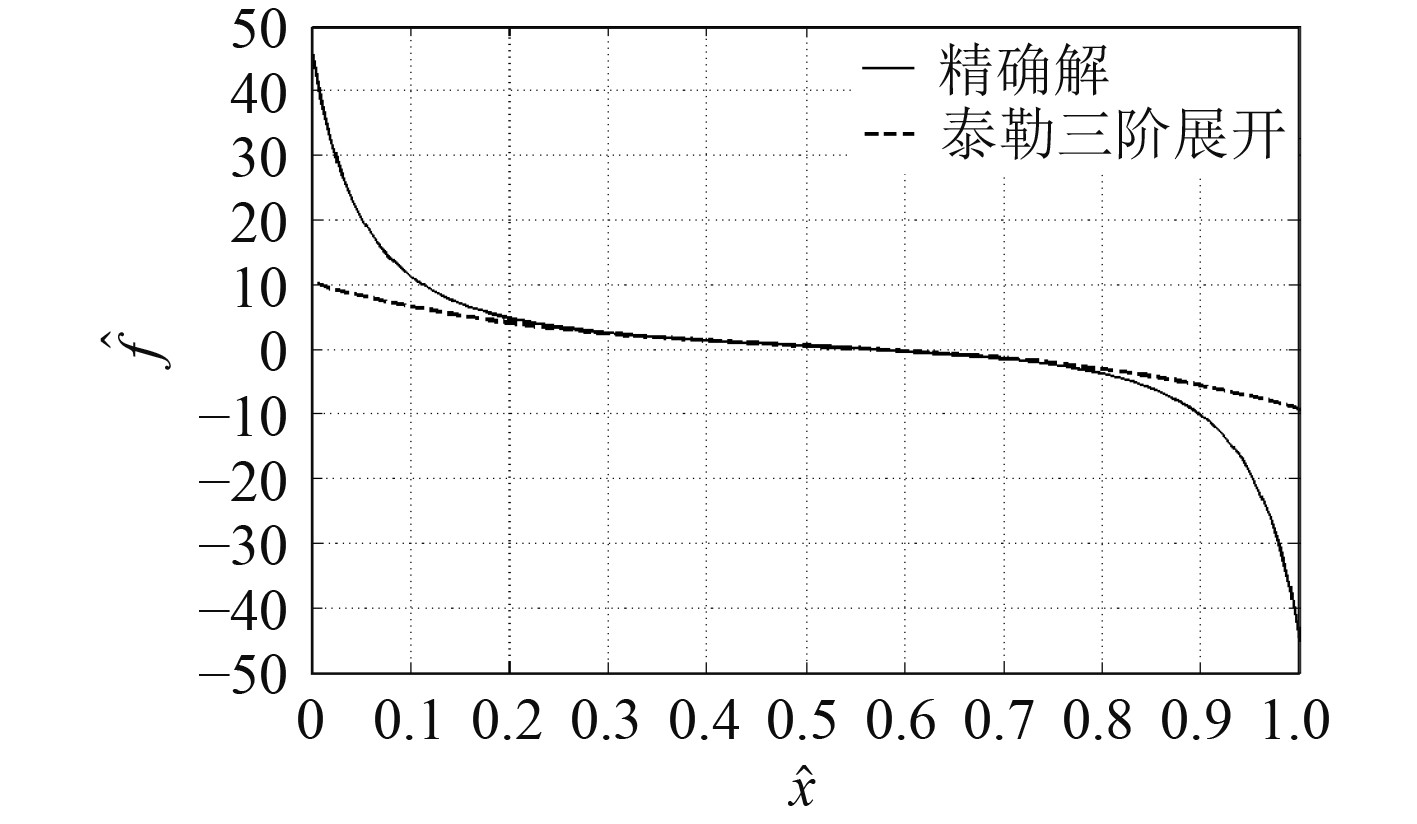
图 3 三阶泰勒展开与精确解对比关系示意图 Fig. 3 Diagram of the relation of third order Taylor expansion compared with exact result |
| $ \mathop f\limits^ \wedge = - 7.6\mathop y\limits^ \wedge - 47.8{(\mathop y\limits^ \wedge )^3} \text{。}$ | (6) |
由图3可知,在平衡位置附近,应用三阶泰勒级数展开的方式与精确解误差很小,在远离平衡位置处,误差较大,因此三阶泰勒展开方式可用来分析平衡位置附近的力学分析。
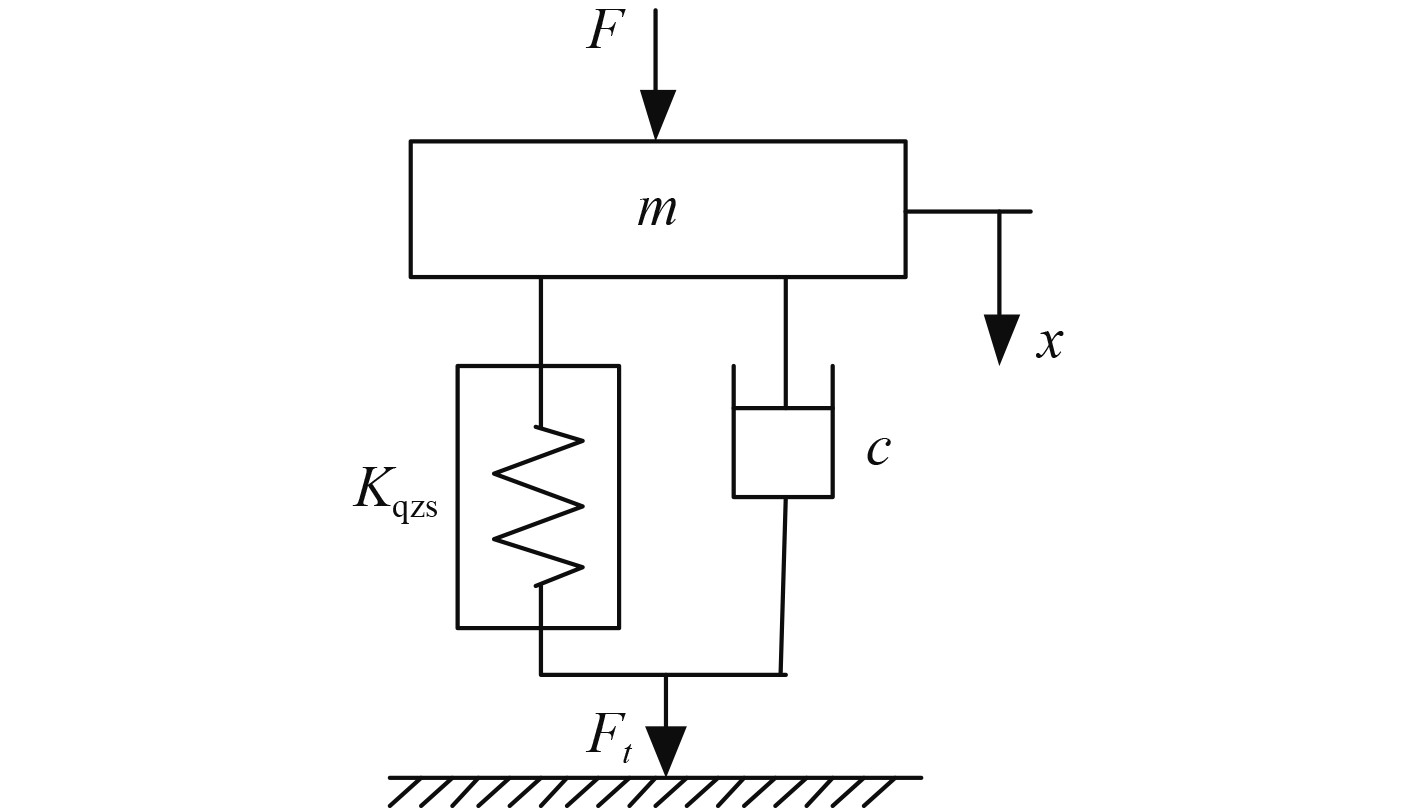
1.2 准零刚度系统幅频特性在外界载荷激励的作用下,准零刚度系统力学示意图如图4所示。基于前文泰勒展开结果,系统无量纲动力学方程可表示为:
|
图 4 准零刚度系统力学模型示意图 Fig. 4 Schematic diagram of mechanical model of quasi-zero stiffness system |
| $ {\left( {\mathop y\limits^ \wedge } \right)^{\prime \prime }} + \xi (\mathop y\limits^ \wedge )' + 7.6\mathop y\limits^ \wedge + 47.8{\left( {\mathop y\limits^ \wedge } \right)^3} = \mathop F\limits^ \wedge \cos (\varOmega \tau )。$ | (7) |
式中:
若振动激励条件为线性时,系统的解可表示为:
| $ \mathop y\limits^ \wedge = a\cos (\varOmega \tau ) + b\sin (\varOmega \tau )\text{,} $ | (8) |
对上式进行求导,得
| $ {\left( {\mathop y\limits^ \wedge } \right)^\prime } = - a\varOmega \sin (\varOmega \tau ) + b\varOmega \cos (\varOmega \tau ) \text{,}$ | (9) |
若振动条件为非线性的,系统的解可表示为:
| $ \mathop y\limits^ \wedge = a(\tau )\cos (\varOmega \tau ) + b(\tau )\sin (\varOmega \tau )\text{,} $ | (10) |
假定非线性条件下的振动速度与线性条件的振动速度形式相同,可得:
| $ {\left( {\mathop y\limits^ \wedge } \right)^\prime } = - a(\tau )\varOmega \sin (\varOmega \tau ) + b(\tau )\varOmega \cos (\varOmega \tau ) \text{,}$ | (11) |
对式(10)求导可得:
| $ \begin{aligned}{\left( {\mathop y\limits^ \wedge } \right)^\prime } = &a'(\tau )\cos (\varOmega \tau ) - \varOmega a(\tau )\sin (\varOmega \tau ) + \\ &b'(\tau )\sin (\varOmega \tau ) + \varOmega a(\tau )\cos (\varOmega \tau )\text{,}\end{aligned} $ | (12) |
由式(11)和式(12)可得:
| $ a'(\tau )\cos (\varOmega \tau ) + b'(\tau )\sin (\varOmega \tau ) = 0\text{,} $ | (13) |
系统解的二阶导可表示为:
| $ \begin{aligned}{\left( {\mathop y\limits^ \wedge } \right)^{\prime \prime }} = & - \varOmega a'(\tau )\sin (\varOmega \tau ) - {\varOmega ^2}a(\tau )\cos (\varOmega \tau ) +\\ &\varOmega b'(\tau )\cos (\varOmega \tau ) - {\varOmega ^2}b(\tau )\sin (\varOmega \tau )\text{。}\end{aligned} $ | (14) |
将式(11)和式(14)代入式(7)可得:
| $ \begin{array}{l}\mathrm{cos}(\varOmega \tau )(\xi {a}^{\prime }(\tau )-{\varOmega }^{2}a(\tau )+7.6a(\tau )+\varOmega {b}^{\prime }(\tau )+\xi \varOmega b(\tau )-\stackrel{\wedge }{F})+\\ \mathrm{sin}(\varOmega \tau )·(\xi {b}^{\prime }(\tau )-\varOmega {a}^{\prime }(\tau )- \xi \varOmega a(\tau )-{\varOmega }^{2}b(\tau )+7.6b(\tau ))+\\ 47.8{a}^{3}(\tau ){\mathrm{cos}}^{3}(\varOmega \tau )+143.4{a}^{2}(\tau )b(\tau )\mathrm{sin}(\varOmega \tau ){\mathrm{cos}}^{2}(\varOmega \tau )+ \\ 143.4a(\tau ){b}^{2}(\tau ){\mathrm{sin}}^{2}(\varOmega \tau )\mathrm{cos}(\varOmega \tau )+47.8{b}^{3}(\tau ){\mathrm{sin}}^{3}(\varOmega \tau )=0。\end{array} $ | (15) |
组合式(13)和式(15)可得:
| $ \left\{ {\begin{aligned} a'(\tau ) = & - 143.4{a^2}(\tau )b(\tau )/(8\varOmega ) + 0.5\xi a(\tau ) +\\ &143.4{b^3}(\tau )/(8\varOmega ) - 0.5\varOmega b(\tau ) + 3.8b(\tau )/\varOmega\text{,} \\ b'(\tau ) =& - 143.4a(\tau ){b^2}(\tau )/(8\varOmega ) + 0.5\varOmega a(\tau ) - 3.8a(\tau )/\varOmega -\\ &143.4{a^3}(\tau )/(8\varOmega ) - 0.5\xi b(\tau ) + 0.5{{\mathop F\limits^ \wedge \mathord{\left/ {\vphantom {{\mathop F\limits^ \wedge } \varOmega }} \right. } \varOmega }} \text{。} \end{aligned}} \right. $ | (16) |
为简化上式,将
| $ \left\{\begin{array}{llll}{r}^{\prime }=(-r\xi \varOmega +\stackrel{\wedge }{F}\mathrm{sin}(\theta ))/(2\varOmega )\text{,}\\ {\theta }^{\prime }=(-143.4{r}^{3}-30.4r+4r{\varOmega }^{2}+4\stackrel{\wedge }{F}\mathrm{cos}(\theta ))/8r\varOmega \text{。}\end{array}\right. $ | (17) |
对于平衡点处,令式(17)等于0,根据
| $ \dfrac{{{r^2}{{(143.4{r^2} - 4{\varOmega ^2} + 30.4)}^2}}}{{16{{(\mathop F\limits^ \wedge )}^2}}} + \dfrac{{{\xi ^2}{r^2}{\varOmega ^2}}}{{{{(\mathop F\limits^ \wedge )}^2}}} = 1\text{。} $ | (18) |
橡胶材料在应变较小时可视为弹性材料,因此可应用经验公式法创建其数学模型。该方法考虑到结构形态、约束面积、硬度等问题,能够较为准确地反映橡胶材料的力学特性,并使试验成本有较大程度降低。综合考虑形状、预紧力、材料等因素,本文以式(19)创建橡胶动弹性模量,并与试验对比,以此验证该方法的正确性。
| $ \begin{split}{E}_{t}=&{K}_{G}\times {K}_{P}\times {K}_{M}\times {E}_{0}=\dfrac{{A}_{总}}{{A}_{自由}}\times \\ &\left(\dfrac{A+\Delta A}{A}\times \dfrac{h+\Delta h}{h}\right)\times \left({e}^{\dfrac{Hs}{100}}-1\right)\times {e}^{(0.02Hs-0.4)}\text{。}\end{split} $ | (19) |
式中:
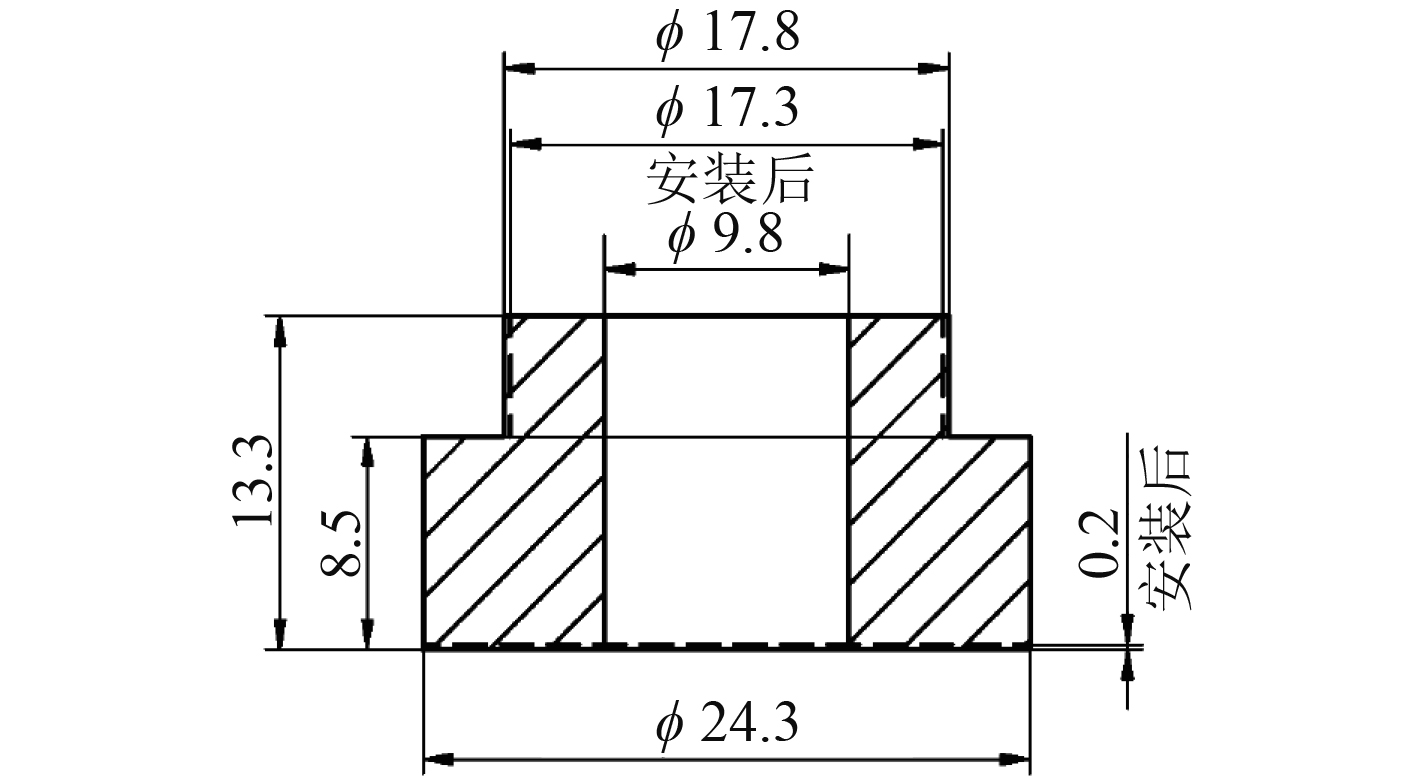
|
图 5 橡胶垫尺寸示意图 Fig. 5 Rubber pad dimensions |
材料硬度变化时,基于Abaqus进行固有频率数值计算,并与试验进行对比,结果如表1所示。
|
|
表 1 固有频率数值解与试验结果对比 Tab.1 Comparison of numerical solution of natural frequency with experimental results |
由表1结果可知:橡胶硬度在不超过40时,橡胶材料公式建模方法的数值解与试验结果较为相吻合,当橡胶硬度大于50时,该方法误差达到0.157。因此,在硬度低于50时,该方法具精度较高,并可较大程度的降低材料建模工作量。
2.2 碟型橡胶弹簧力-位移关系碟型橡胶弹簧相比柱形橡胶弹簧,具有更大的运动行程,并且具有更高的稳定性,是工程中常见的结构形式。本文碟型弹簧尺寸和边界条件如图6(a)所示,基于本文橡胶材料公式建模方法,碟型弹簧取不同硬度值时,计算力与位移关系结果如图6(b)所示。
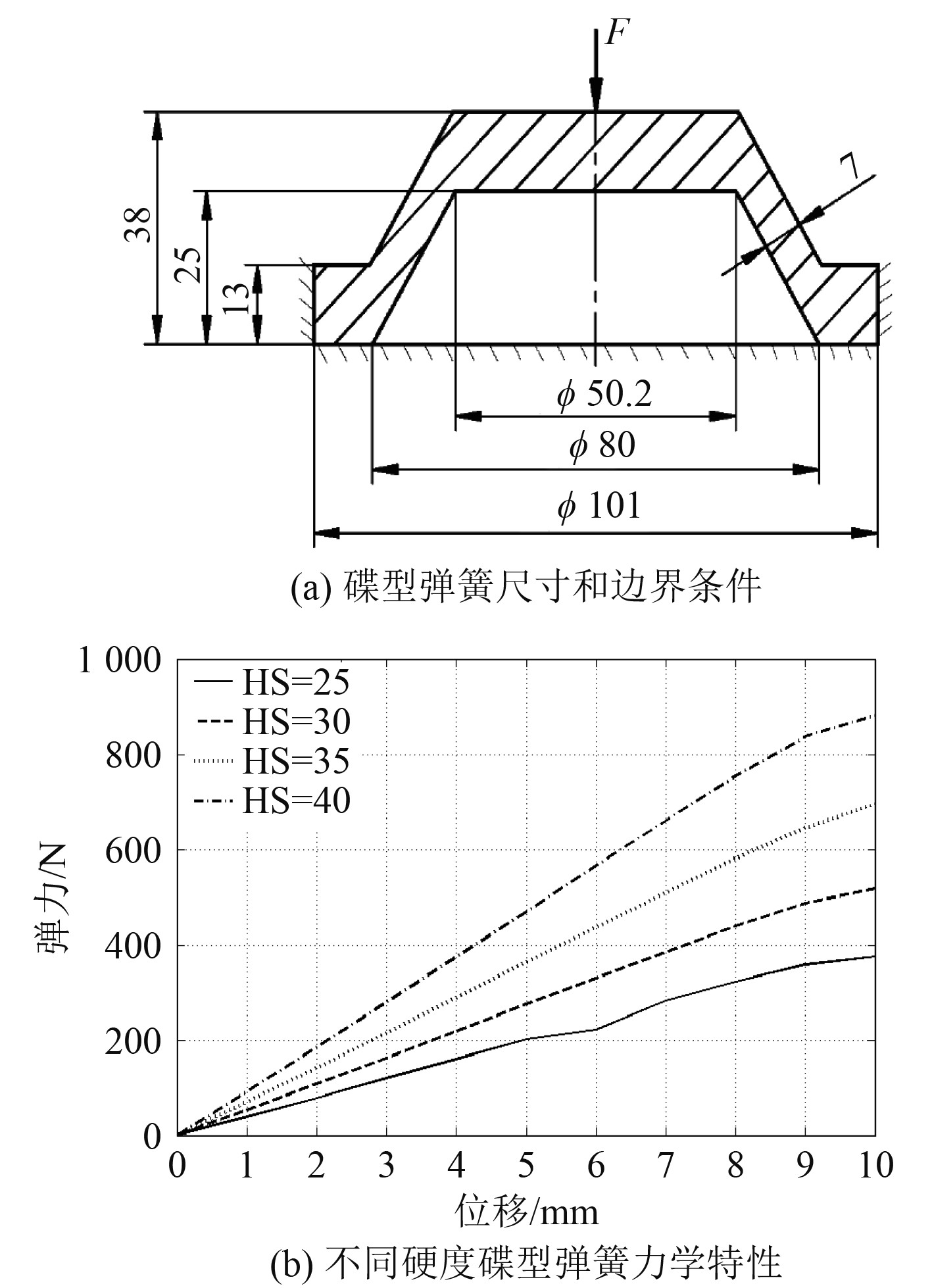
|
图 6 橡胶碟型弹簧尺寸和力学特性结果图 Fig. 6 The dimensions and mechanical properties of rubber disc spring |
由结果可知,随着橡胶材料硬度的增加,弹簧的弹力有明显提升。对于本文弹簧结构,当位移小于9 mm时,弹簧力与位移呈线性关系,大于9 mm时,为非线性关系,而力学特性为线性的碟型弹簧,更易实现准零刚度效果,因此本文采用硬度为30的碟型橡胶,设定最大位移为8 mm。当压缩4 mm时,弹力为218 N,因此设定单个额定承载为21.8 kg。
3 负刚度电磁力计算和准零刚度的实现 3.1 电磁力计算方法验证负刚度力的精确计算是准零刚度隔振器成功设计的基础。本文准零刚度隔振器主要部件为轴对称结构,因此在电磁力计算时可转化为1/2截面积的2D问题,如图7(a)所示。该方法可显著减小计算量。为验证该法的正确性,设置上下磁铁半径为60 mm,磁铁间距14 mm,线圈匝数2000,电流0.1A,基于MAXWELL计算电磁力数值解,并与式(1)解析解对比验证,结果如图7(b)所示。
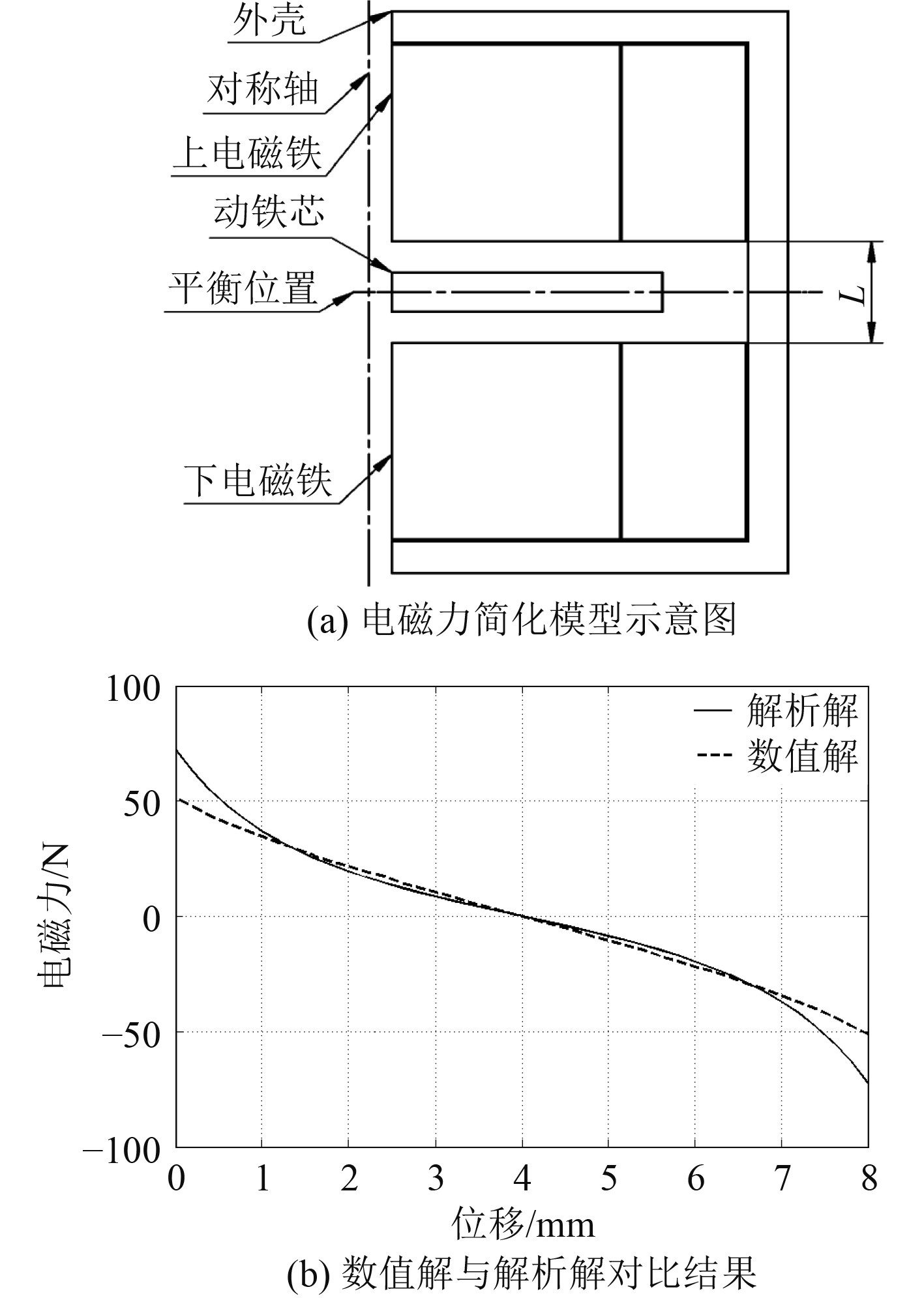
|
图 7 电磁力计算方法验证结果 Fig. 7 The verification result diagram of electromagnetic force calculation method |
由结果可知,4 mm处为平衡位置,动铁芯在偏离平衡位置±3 mm以内时,数值解与解析解几乎重合,在超过±3 mm时,数值解与解析解具有一定误差。船舶振动条件多为谐响应和随机振动,其振幅均在此范围内,因此该方法精度可靠,适用于隔振器设计时的数值计算。
3.2 隔振器参数对电磁负刚度力影响磁铁间距、动芯材料、线圈电流等是电磁弹簧的重要参数,本文计算以上3种参数变化时的系统负刚度力,研究不同参数对负刚度力的影响规律。平衡位置处位移为0,计算结果如图8所示。
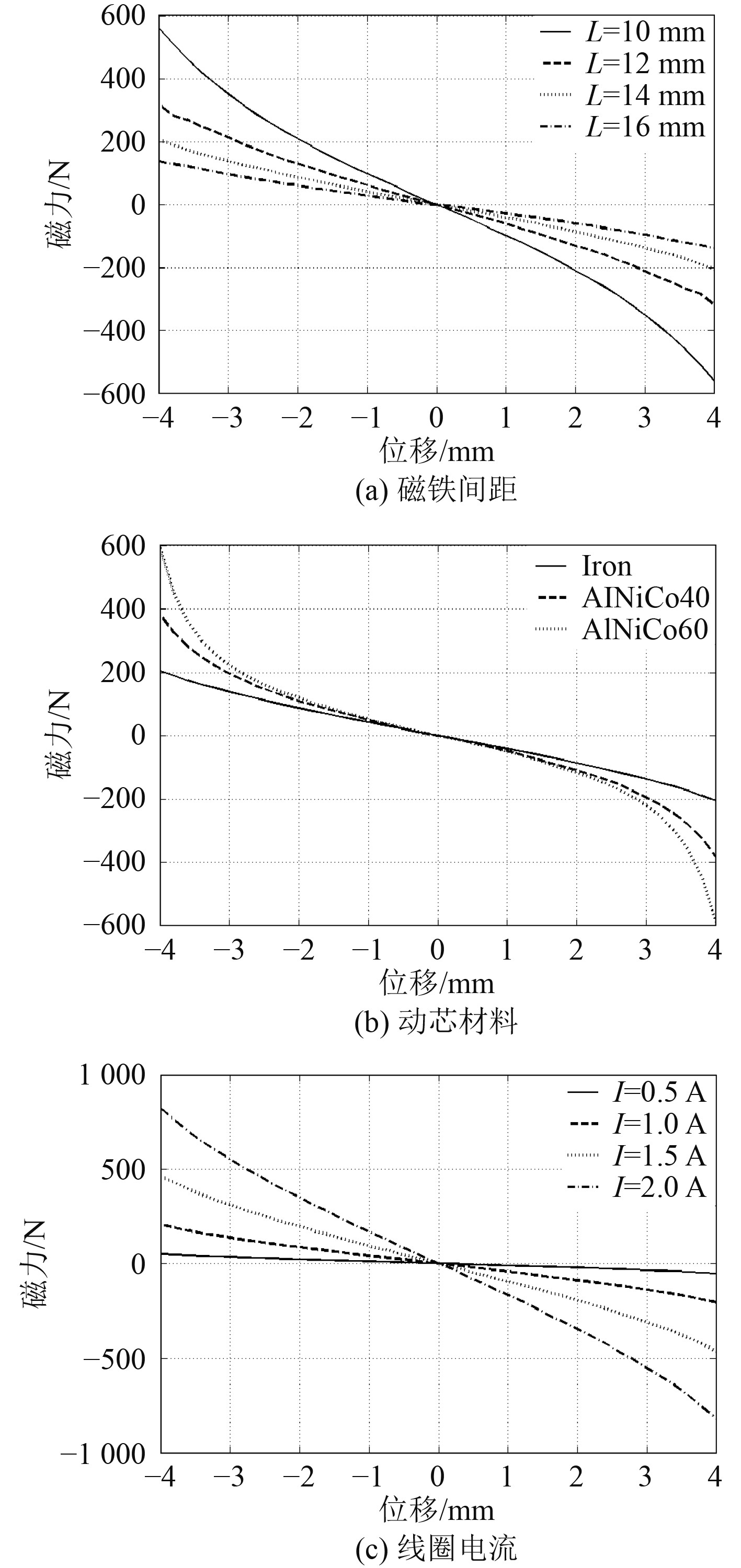
|
图 8 不同参数对电磁负刚度力影响结果 Fig. 8 The effect of different parameters on electromagnetic negative stiffness force |
由图8(a)可知,随着磁铁间距的增大,负刚度力将有较大程度的缩减,因此在保证设备稳定安全的前提下,应尽量减小磁铁间距,以获得最大的负刚度力。本文动铁芯行程为8 mm,因此将磁铁间距设定为14 mm,既可提供较大的负刚度力,又可避免动铁芯与磁铁磕碰。由图8(b)可知,动芯为铁时,负刚度力偏小,但整体趋势为线性,当动铁芯为铝镍钴永磁材料时,负刚度力较大,但在远离平衡位置时呈现明显的非线性,且磁性越强,非线性越显著,不利于准零刚度的实现,因此本文动芯材料为铁。由图8(c)可知,线圈电流的增加会显著提升负刚度力值,且整体呈现为近似线性,因此负刚度力可通过电流进行调节。
3.3 准零刚度的实现与减振效果计算通过前文分析,得到了正刚度力和负刚度力的趋势均近似线性,因此可直接叠加来实现准零刚度。本文碟型橡胶弹簧材料硬度为30,根据式(1),计算出可抵消正刚度力时的电流值约为1.17 A。根据以上条件,计算橡胶碟型弹簧正刚度力和电磁负刚度力,并将两者数值叠加,得到准零刚度系统的力与位移的关系。在此基础上,通过修改Abaqus脚本文件,将组合力输入系统中进行振动计算,振动条件为0~16 Hz幅值为1 mm,16~60 Hz幅值为1 g,得到结果如图9所示。
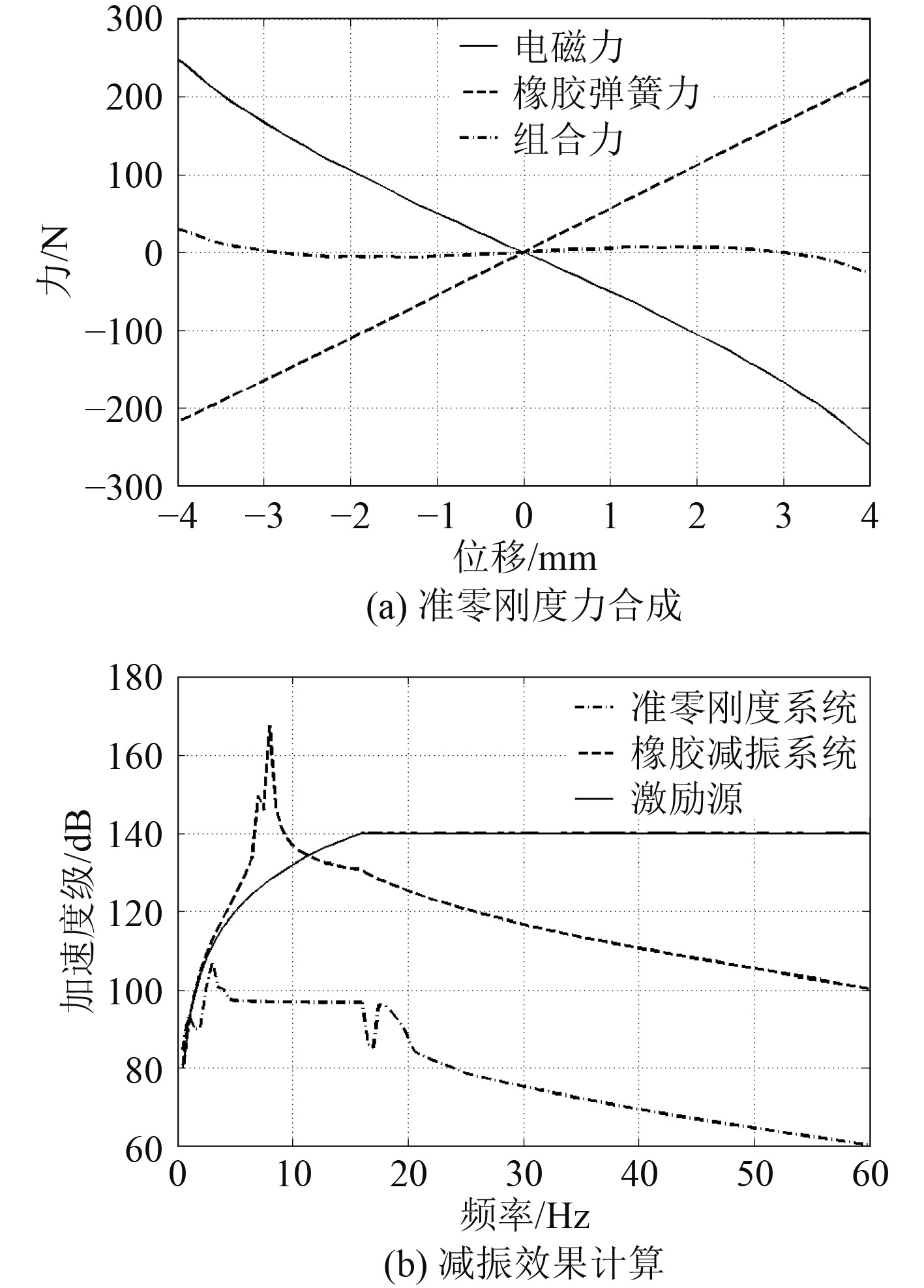
|
图 9 准零刚度的实现与减振效果图 Fig. 9 Realization of quasi-zero stiffness and vibration reduction effect diagram |
由图9(a)结果可知,弹簧正刚度与电磁负刚度叠加后,在平衡位置±3 mm内,组合力较小,在大于3 mm时,组合力最大约为18 N。由图9(b)可知,本文准零刚度隔振器工作时,低频无任何放大现象,在0~3 Hz频段,系统响应略小于激励源,在3~60 Hz频段,减振效果相比传统减振系统有约40 dB的提升,适用于船用精密设备的减振设计。
4 结 语基于麦克斯韦电磁原理研究了准零刚度时系统的电流值,并推导了系统幅频特性方程。通过对比分析数值结果、试验值、解析解,得到橡胶材料的准确建模方法和隔振器电磁力计算方法。在此基础上,计算橡胶硬度对弹簧弹力的影响,以及磁铁间距、动芯材料、线圈电流值等对负刚度力的影响规律,通过合理组合,得到以下结论:
1)在行程为±4 mm时,碟型弹簧、电磁弹簧产生的刚度力均为近似线性,依据该优势,可直接进行数值叠加,准零刚度更易实现,因此在设计时应让两者均向线性靠近;
2)电磁铁间距对电磁负刚度力影响较大,在保证动铁芯不与磁铁磕碰前提下,减小磁铁间距可提高负刚度力的大小;
3)动芯材料为永磁材料时,可提高负刚度力,但整体力学特性呈现明显的非线性,不利于准零刚度的实现,因此动芯应规避此类材料;
4)本文准零刚度隔振器可达到全频带无振动放大效果,且在大于3 Hz时,相对于传统橡胶减振器,可使减振效果提高约40 dB,适用于船用精密设备的减振设计。
| [1] |
CREMER L, HECKL M, UNGAR E E. Structure-borne Sound [M]. Second Edition. Berlin: Springer-Verlag, 1988.
|
| [2] |
王汀, 于沛, 李晶. 振动条件下平台惯导系统误差抑制技术研究[J]. 振动与冲击, 2019, 38(15): 6. WANG Ting, YU Pei, LI Jing. Study on error suppression technology of platform Inertial Navigation system under vibration condition[J]. Shock and Vibration, 2019, 38(15): 6. |
| [3] |
党建军, 罗建军, 万彦辉. 挠性捷联惯组振动环境下适应性及导航精度分析[J]. 弹箭与制导学报, 2010, 30(1): 4. DANG Jianjun, LUO Jianjun, WAN Yanhui. Adaptability and navigation accuracy analysis of flexible strapdown inertial navigation group under vibration environment[J]. Journal of Arrows and Guidance, 2010, 30(1): 4. |
| [4] |
赵钟磊. 磁存储设备的振动冲击电磁主动控制技术的研究[D]. 西安: 西安电子科技大学, 2002.
|
| [5] |
李东海, 赵寿根, 何玉金, 等. 含有时滞控制的准零刚度隔振器的隔振性能研究[J]. 西北工业大学学报, 2018, 36(6): 8. LI Donghai, ZHAO Shougen, HE Yujin, et al. Research on vibration isolation performance of quasi-zero stiffness vibration isolator with time delay control [J]. Journal of Northwestern Polytechnical University, 2018, 36(6): 8. |
| [6] |
刘琪, 李占龙, 王建梅, 等. 准零刚度低频隔振技术的研究进展[J]. 机械强度, 2021. LIU Qi, LI Zhanlong, WANG Jianmei. Research progress of quasi-zero stiffness low frequency vibration isolation technology [J]. Journal of Mechanical Strength, 2021. |
| [7] |
CARRELLA A, BRENNAN M J, WATERS T P, et al. On the design of a high-static-low-dynamic stiffness isolator using linear mechanical springs and magnets[R]. In special Issue: Euromech Colloquium 483, Geometrically Non-linear Vibrations of Structures, 2008.
|
| [8] |
XU D, YU Q, ZHOU J, et al. Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic[J]. Journal of Sound and Vibration, 2019, 332(14): 3377-3389. |
| [9] |
HUANG X, LIU X, SUN J, et al. Vibration isolation characteristics of a nonlinear isolator using Euler buckled beam as negative stiffness corrector: A theoretical and experimental study[J]. Journal of Sound & Vibration, 2020, 333(4): 1132-1148. |
| [10] |
苏攀, 吴杰长, 刘树勇, 等. 准零刚度振动系统反馈控制动态特性及试验研究[J]. 船舶力学, 2020, 24(4): 11. SU Pan, WU Jiechang, LIU Shuyong. Dynamic characteristics and experimental study of feedback control for quasi-zero stiffness vibration system[J]. Journal of Ship Mechanics, 2020, 24(4): 11. |
 2022, Vol. 44
2022, Vol. 44
