2. 江苏科技大学 环境与化学工程学院,江苏 镇江 212100
2. School of Environment and Chemical Engineering, Jiangsu University of Science and Technology, Zhenjiang 212100, China
波浪能装置的工作海域经常会遇到大洋环流,潮汐等引起的流的影响,波流混合后改变了原有波浪场的流场特征。波浪能装置俘获的能量来自于波浪场水质点运动的动能和势能,流对原波浪场的改变间接影响装置浮体的动态响应特征,并进而影响PTO的波能转换。因此,流对波浪能装置的影响本质是波流相互作用问题。Gudmestad[1]论述了波流相互作用对海洋结构物设计、工作的重要性;李玉成[2-3]、王涛[4]、Tambroni N.[5]和Crisan D.[6]等分别采用能量守恒、波作用守恒及实验观测等方法对波流混合特征进行了探讨,研究结果均显示流对波浪的波形和波谱等有显著地影响。
目前对波浪能装置的研究主要考虑装置在波浪中的运行特性[7-9]。然而,在实际工程应用中,流的影响不可忽视。本文针对这一问题,通过建立的波流多场耦合数值水槽模型,开展铰接多浮体波浪能装置的动态响应和波能俘获特性研究,更全面掌握波浪能装置在复杂海况下的工作性能,并有效指导装置的设计。
1 铰接多浮体式波浪能装置模型的建立本文以铰接多浮体式波浪装置为研究对象,如图1所示。该装置由2节尺寸、质量分布相同的水平圆柱型浮体和2组参数一致的PTO(Power Take-off,能量提取)单元及锚索组成。2组PTO单元由浮体上下两侧对称安装的2组粘性PTO阻尼器组成,安装在2节浮体之间,并将2节浮体连接在一起。浮体在波浪激励下做多自由度运动,PTO阻尼器通过浮体的相对运动将波浪能提取出来。

|
图 1 铰接多浮体式波浪能装置原理示意图 Fig. 1 Configuration schematic of the articulated multi-body floating WEC |
与其他波浪能转换系统相比,该类型装置具有能量转换效率高、穿浪性好、海况水深适应性好的显著优势。最有代表性的是英国开发的Pelamis筏式波浪发电系统[10]及McCabe Wave Pump(MWP)波力装置等[11]。
1.1 浮体运动模型装置稳定运行时的纵向通常与波浪传播方向一致,此时,浮体表现为纵摇、垂荡和纵荡三自由运动。假定流体无粘、不可压缩且无旋,浮体的动力学方程可以表示为:
| $ \left\{ \begin{gathered} \left( {{m^{\left( n \right)}} + {A_X}^{\left( n \right)}} \right) \cdot {{x''}^{\left( n \right)}}\left( t \right) = {F_X}^{\left( n \right)}\left( t \right) \text{,} \\ \left( {{m^{\left( n \right)}} + {A_Z}^{\left( n \right)}} \right) \cdot {{z''}^{\left( n \right)}}\left( t \right) = {F_Z}^{\left( n \right)}\left( t \right)\text{,} \\ \left( {{J_{yy}}^{\left( n \right)} + {J_{Ayy}}^{\left( n \right)}} \right) \cdot {{\theta ''}^{\left( n \right)}}\left( t \right) = {M^{\left( n \right)}}\left( t \right)\text{。} \\ \end{gathered} \right. $ | (1) |
式中:
通过对浮体运动和浮体之间几何关系的分析,可以推导出如下几何关系式:
| $ \left\{ \begin{gathered} {z^{\left( 2 \right)}}\left( t \right) - {z^{\left( 1 \right)}}\left( t \right) = \dfrac{1}{2}\left( {L + l} \right) \cdot \left[ {\sin {\theta ^{\left( 1 \right)}}\left( t \right) + \sin {\theta ^{\left( 2 \right)}}\left( t \right)} \right]\text{,} \\ {x^{\left( 2 \right)}}\left( t \right) - {x^{\left( 1 \right)}}\left( t \right) = \dfrac{1}{2}\left( {L + l} \right) \cdot \left[ {\cos {\theta ^{\left( 2 \right)}}\left( t \right) + \cos {\theta ^{\left( 1 \right)}}\left( t \right)} \right] \text{。} \\ \end{gathered} \right. $ | (2) |
铰接浮体在波浪上的运动取决于式(1)和式(2)。波浪力、PTO阻尼力、浮体的附加质量及附加质量转动惯量等通过数值模拟的方式求解。
1.2 PTO俘能计算模型2组PTO单元采用线粘性阻尼器,其瞬时转换功率计算如下:
| $ {\tilde P_{PTO}} \approx 2C{v^2}_c \approx 2C{R^2}{\left( {{{\dot \theta }^{\left( 2 \right)}} - {{\dot \theta }^{\left( 1 \right)}}} \right)^2}\text{。} $ | (3) |
式中:
将瞬时转换功率在一个运动周期、或运动周期整数倍的时间内取平均值,即为装置的波浪能转换功率:
| $ {\bar P_{PTO}} = \dfrac{1}{T}\int_{{t_0}}^{{t_0} + T} {\left[ {2C{R^2}{{\left( {{{\dot \theta }^{\left( 2 \right)}} - {{\dot \theta }^{\left( 1 \right)}}} \right)}^2}} \right]} {\rm{d}}t\text{。} $ | (4) |
式中:
本文数值仿真在STAR-CCM+平台上进行,采用线性波假设,浮体幅值、PTO功率的计算分析基于Matlab/Simulink软件。图2为数值仿真计算域,尺寸为150 m× 100 m× 50 m。圆柱形浮体长10.0 m,半径1.0 m,静吃水1.2 m,PTO阻尼系数C为1.0×105 N·s/m,波流参数参考中国黄海沿海水域海况[12],波高选取为1.2 m,选取正向流(波流同向)和逆向流(波流反向)2种代表性流向。本文采用的数值仿真方法已在文献[13]中获得验证。

|
图 2 仿真计算域 Fig. 2 Simulating calculation region |
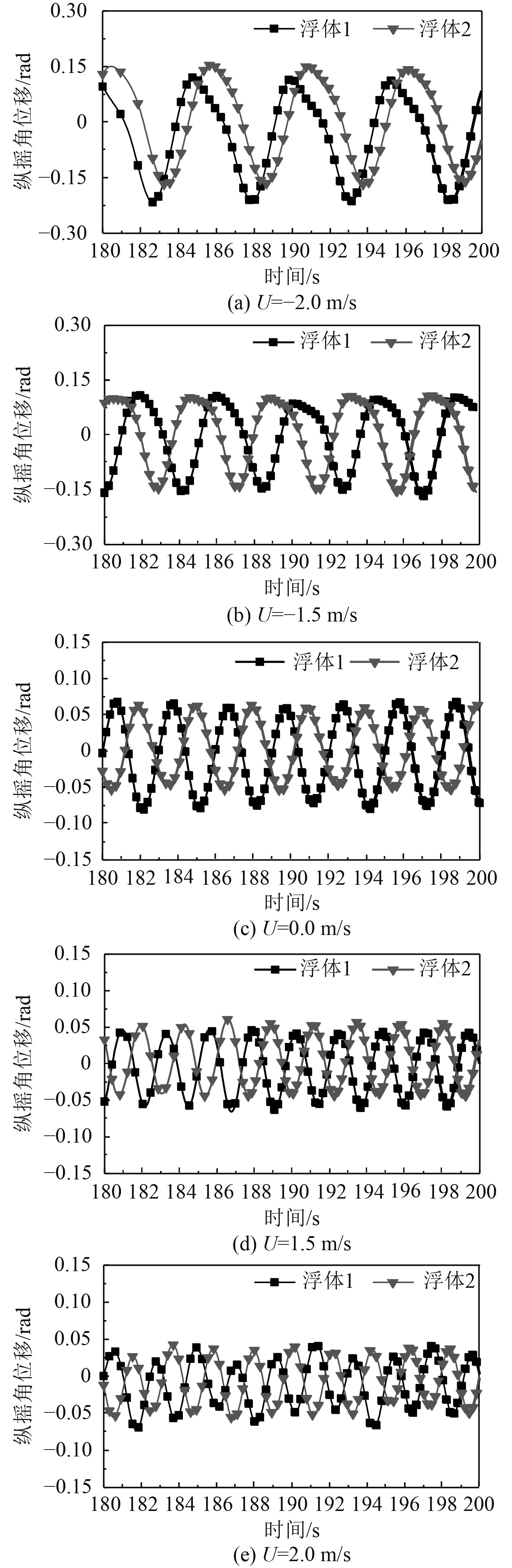
图3为波浪周期T=3.0 s,波高H=1.2 m,典型流速下(+指正向流,−指逆向流)的浮体纵摇运动时域曲线。图4和图5分别为浮体纵摇运动周期和幅值在不同入射波浪周期Tw条件下随流的变化曲线(其中,因2节浮体运动幅值近似,将纵摇运动幅值定义为2节浮体相对于平衡位置时最大位移的平均值)。
|
图 3 典型流速下,浮体纵摇运动时域曲线(T=3.0 s,H=1.2 m) Fig. 3 Time-domain curves of pitching motion of buoys at typical currents (T=3.0 s,H=1.2 m) |
|
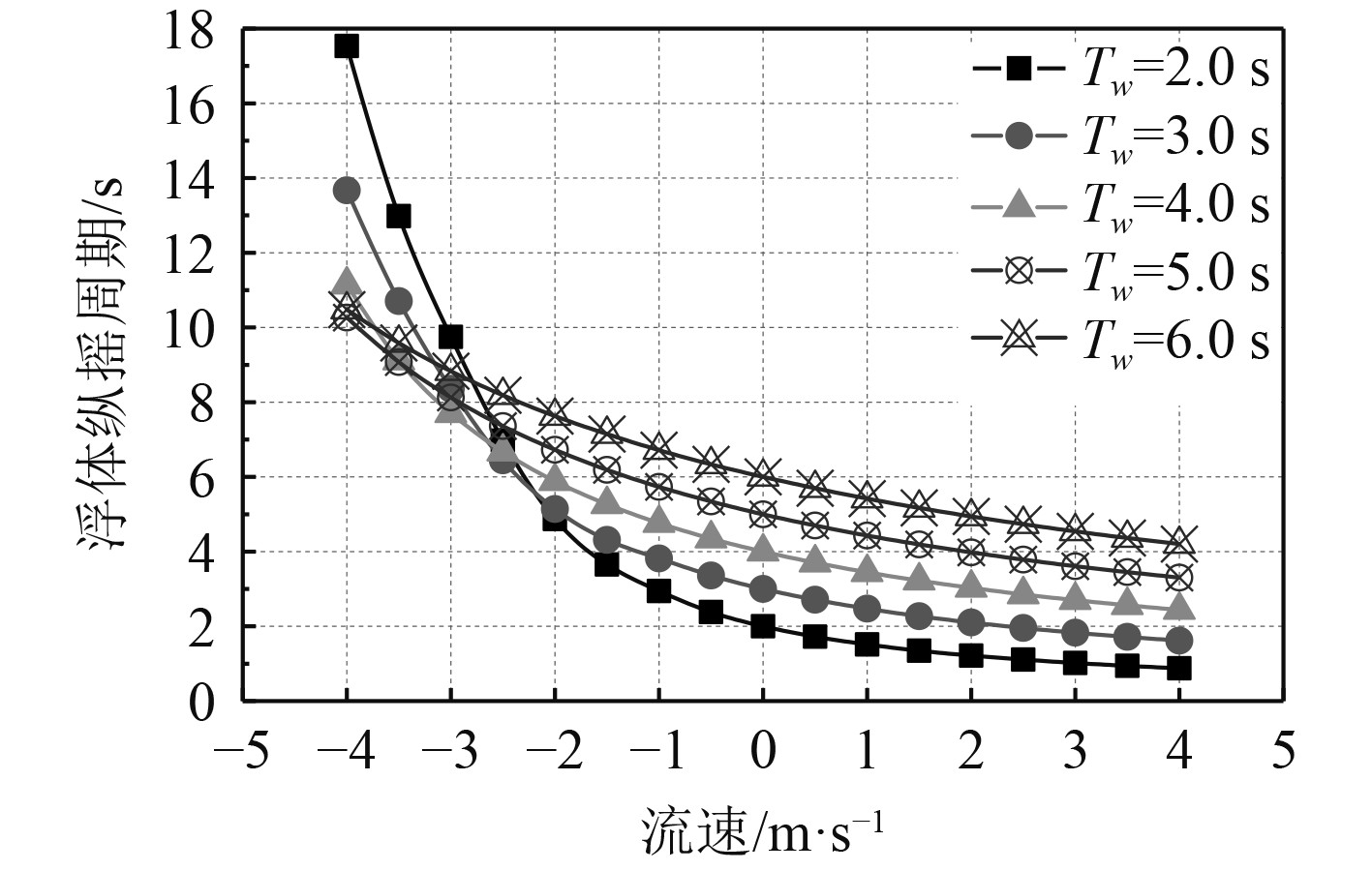
图 4 浮体纵摇运动周期随流变化曲线 Fig. 4 The period of pitching motion of buoys with current |
|
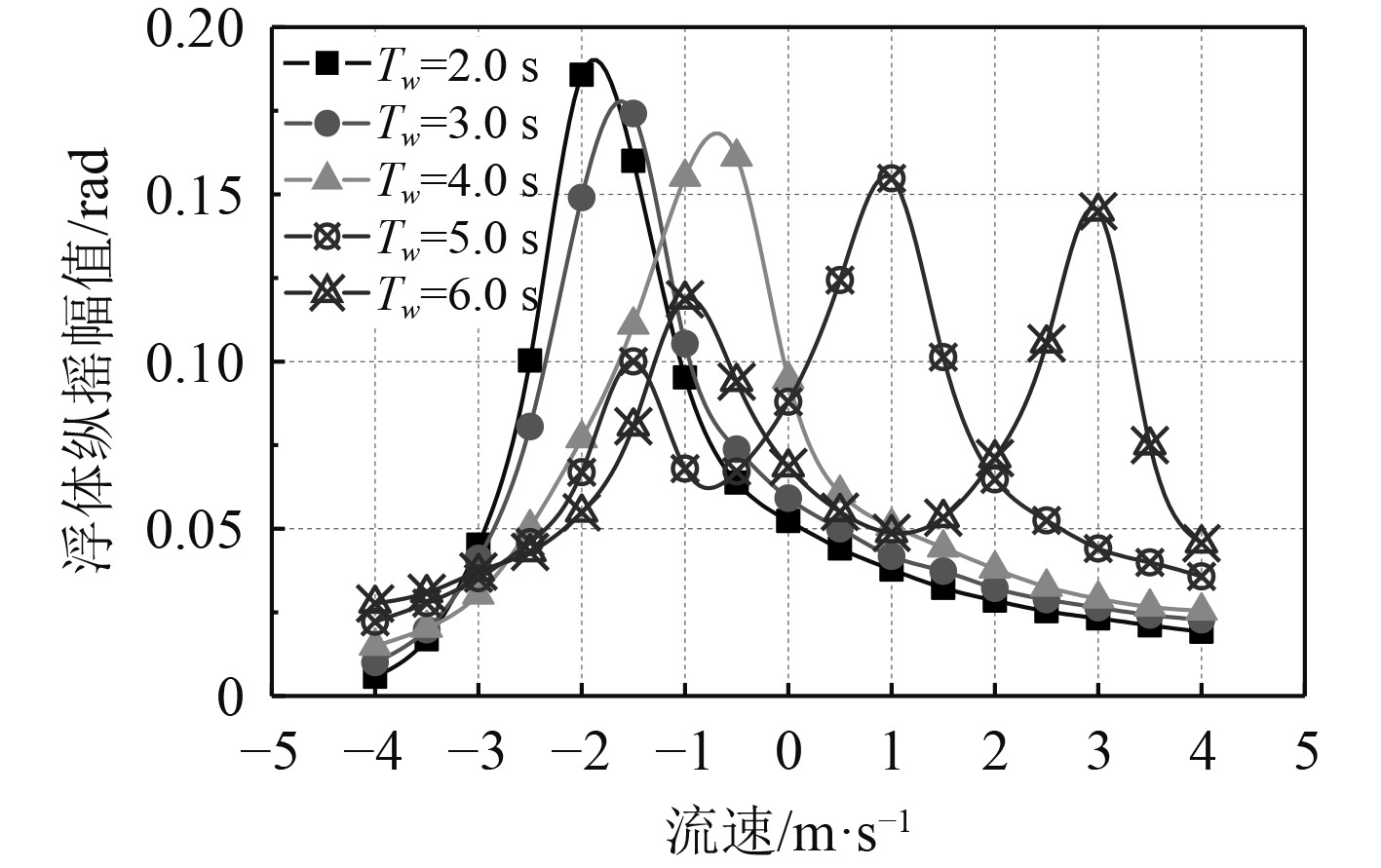
图 5 浮体纵摇运动幅值随流变化曲线 Fig. 5 The amplitude of pitching motion of buoys with current |
通过图3可以看到,在线性波条件下,浮体纵摇运动近似于线性简谐振动系统,在流的影响下,浮体纵摇运动的非线性增强。由图4可知,在流速−4~4 m/s范围内时,在各个入射波浪周期工况内,浮体的运动周期均持续减小。
由图5可以看到,波浪周期为2.0 s,3.0 s和4.0 s时,浮体纵摇幅值随流速变化的曲线为单峰曲线,且峰值均出现在逆向流工况下。波浪周期为5.0 s和6.0 s时,浮体纵摇幅值随流速变化的曲线为双峰曲线,其中,最高峰值出现在正向流工况下,次高峰值出现在逆向流工况下。
为了更深入分析装置运动响应特征,根据图4和图5得到浮体纵摇峰值所对应的特征参数,如表1所示。
|
|
表 1 浮体纵摇运动峰值特征参数 Tab.1 Characteristic parameters of peak pitching of buoy |
分析表1可知,随着波浪周期的增大,浮体纵摇运动峰值所对应的流速也持续增大,且在该流速下,浮体的纵摇周期均在4.5 s左右,这也是浮体的固有纵摇运动周期,此时,浮体纵摇运动达到共振。
当浮体固有纵摇运动周期小于波浪周期时,在逆向流工况下,由于波流混合后流场的波浪幅值明显增大,使得浮体纵摇运动也会出现一个较大值,即出现次高峰值,随后幅值随着浮体纵摇周期的持续增大而减小。
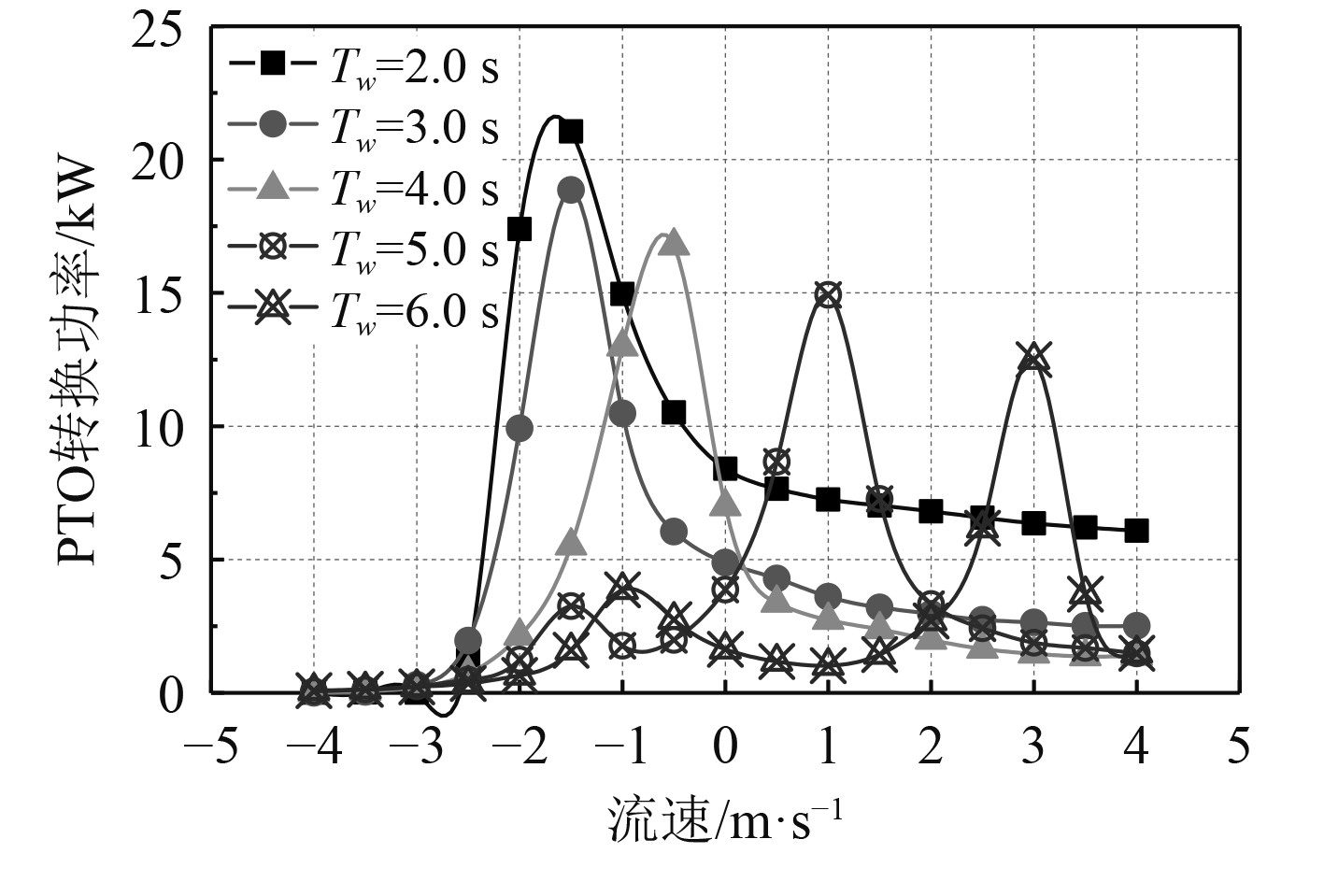
2.2 流对装置波浪能转换功率的影响PTO单元转换的能量来自于波浪能转换而来的浮体运动的机械能,波浪能转换功率取决于2节浮体间的相对纵摇角位移、浮体运动频率及PTO线性阻尼系数,计算得到装置的波能转换功率随流变化的曲线如图6所示。
|
图 6 装置波浪能转换功率随流变化曲线 Fig. 6 The wave energy conversion power of WEC with current |
由图6可知,与流对浮体纵摇幅值的影响特征相似,当浮体固有纵摇运动周期小于波浪周期时,功率曲线表现为双峰曲线,最高峰值出现在浮体共振处,次高峰值出现在逆向流工况的纵摇幅值较大处。当浮体固有纵摇运动周期大于波浪周期时,功率曲线为单峰曲线,峰值出现在浮体共振处。
3 结 语波流混合对原流场的改变影响波浪能装置的工作性能。本文通过建立三维数值水槽对波流混合条件下的铰接多浮体式波浪能装置进行仿真,揭示了流对装置的浮体动态响应特征和俘能规律,全面阐释了装置在复杂波流混合海况下的工作性能。
| [1] |
GUDMESTAD O T, KARUNAKARAN D.. Wave current interaction[J]. Advances in Underwater Technology, Ocean Science and Offshore Engineering, 1990, 26: 81-110. |
| [2] |
LI Y. C. Wave-current interaction[M]. Handbook of Coastal and Ocean Engineering, Houston, 1990, 3: 703−726.
|
| [3] |
李玉成. 波浪与水流共同作用下波浪要素的变化[J]. 海洋通报, 1984, 3: 3-14. LI Yu-cheng. Changes of wave characteristics under coaction of wave and currents[J]. Marine Science Bulletin, 1984, 3: 3-14. |
| [4] |
王涛, 李家春. 波作用量守恒原理在波流相互作用中的应用[J]. 力学学报, 1996, 28(3): 281-290. WANG Tao, LI Jia-chun. Application of conservation law of wave action flux to wave current interaction[J]. Acta Mechanica Sinica, 1996, 28(3): 281-290. DOI:10.3321/j.issn:0459-1879.1996.03.004 |
| [5] |
TAMBRONI N, BLONDEAUX P, VITTORI G.. A simple model of wave-current interaction[J]. Journal of Fluid Mechanics, 2015, 775: 328-348. DOI:10.1017/jfm.2015.308 |
| [6] |
CRISAN D, HOLM D D, STREET O D. Wave-current interaction on a free surface [J]. Studies in Applied Mathematics, 2020.
|
| [7] |
SOLANKI V M. Design and development of ocean wave energy power generation system[J]. International Journal of Engineering and Technical Research, 2021, 10(3): 2. |
| [8] |
GOMES M, SALVADOR H, MAGNO F, et al.. Constructal design applied to geometric shapes analysis of wave energy converters[J]. Defect and Diffusion Forum, 2021, 407: 147-160. DOI:10.4028/www.scientific.net/DDF.407.147 |
| [9] |
崔天宇, 赵江滨, 周建林, 等. 双浮筒式波浪能发电装置的浮体运动及水动力性能分析[J]. 舰船科学技术, 2018(10): 99-104. CUI Tian-yu, ZHAO Jian-bin, ZHOU Jian-lin, et al.. Research on motion and hydrodynamic performance of the float in twin-pontoons wave energy converter[J]. Ship Science and Technology, 2018(10): 99-104. DOI:10.3404/j.issn.1672-7649.2018.10.019 |
| [10] |
REDDY K S, PRAJWAL K S, SATWIK T, et al. A review on the gradiation towards pelamis wave energy converter[C]// 2020 4th International Conference on Trends in Electronics and Informatics (ICOEI), 2020.
|
| [11] |
WANG L, RINGWOOD J V. Geometric optimization of a hinge-barge wave energy converter [C]// 13th European Wave and Tidal Energy Conference, 2019.
|
| [12] |
谢冬梅, 陈永平, 张长宽. 东中国海波浪分布特征研究[J]. 水运工程, 2012(11): 14-21. XIE Dong-mei, CHEN Yong-ping, ZHANG Chang-kuan. On wave distribution of the East China Sea[J]. Port and Waterway Engineering, 2012(11): 14-21. DOI:10.3969/j.issn.1002-4972.2012.11.003 |
| [13] |
LI B, SUI F F, YANG B S. An efficient multi-factor geometry optimization based on motion analysis and resonance response for hinged double-body floating wave energy converter[J]. Science Progress, 2020, 103(3): 1-24. |
 2022, Vol. 44
2022, Vol. 44
