2. 武汉第二船舶设计研究所,湖北 武汉 430064
2. Wuhan Second Ship Design and Research Institute, Wuhan 430064, China
随着我国对海洋资源的开发力度增大,各式各样的水下检测装置显著增多,其中锚固基础在维持水下检测装置在位稳定性方面发挥极大的作用。重力锚作为一种锚固基础,主要通过自身重力以及锚体与海底淤泥之间所产生的吸力来锚固设备。由于重力锚具有较强的适应性,一些位于复杂地质条件下的装置常常用其进行锚固,如海洋温差发电结构,张力腿式风电结构等[1-2]。但由于重力锚的大小和形式取决于其所要锚固结构物以及水底土质,到目前为止,针对重力锚尚未形成一套成熟的理论框架以及设计标准。因此,在将满足指标的重力锚主体尺寸确定后,往往都需要对其结构强度进行有限元分析[3-4]。
国内外学者针对适用于不同环境下的重力锚进行了结构设计以及有限元模拟研究。徐保照等[5]针对南海钙质砂土质条件下根据规范初步设计了重力锚尺寸,通过采用有限元计算了重力锚的水平承载力,并与规范给出的重力锚设计原则以及相关计算公式的结果进行比较,发现2个结果一致,验证了有限元模型的可靠性。李飒等[6]在室内物理模型试验的基础上,结合有限元软件,对重力锚在钙质土上的水平承载过程进行了模拟,对有限元计算结果进行了可靠性验证,并进一步对其承载机理进行了深入分析。认为在可能安装重力锚的位置上,由于海底条件不同,需要提出不同的设计方案。韩森等[7]提出一种计算锚泊系统静回复力的方法用来优化布锚夹角并满足锚泊线的强度要求。Taylor等[8]介绍了海洋热能转换器安装所需锚的设计解决方案,根据环境条件选择拖曳嵌入锚或者重力锚,并讨论了它们的尺寸选择。闫宏生等[9]运用有限元软件Abaqus对重力锚在黏土中的水平承载力进行模拟计算,并通过模型试验对比验证了结果的可靠性。根据实际海底地质情况和理论计算,杨鹏等[10]设计了钢筋混凝土重力锚,使重力锚在实际施工过程中可以提供200 t以上的锚抓力。
本文根据锚体实际工作环境、锚体需提供的抗拔力大小以及锚体重量要求等约束条件,对所需重力锚进行主体尺寸设计,运用大型有限元分析软件Abaqus对所设计的重力锚结构在2种复杂工况下的强度进行校核。同时,通过相关力学理论验算,验证其设计合理性和安全性。
1 重力锚结构有限元模型的建立 1.1 几何建模根据场地的工程地质条件及系泊缆载荷等参数,按照相关规范要求以及工程经验,对所需的重力锚进行设计计算,确定设计图纸。其具体的环境条件以及技术指标数据见表1。
|
|
表 1 重力锚技术指标数据 Tab.1 Gravity anchor technical indicator data |
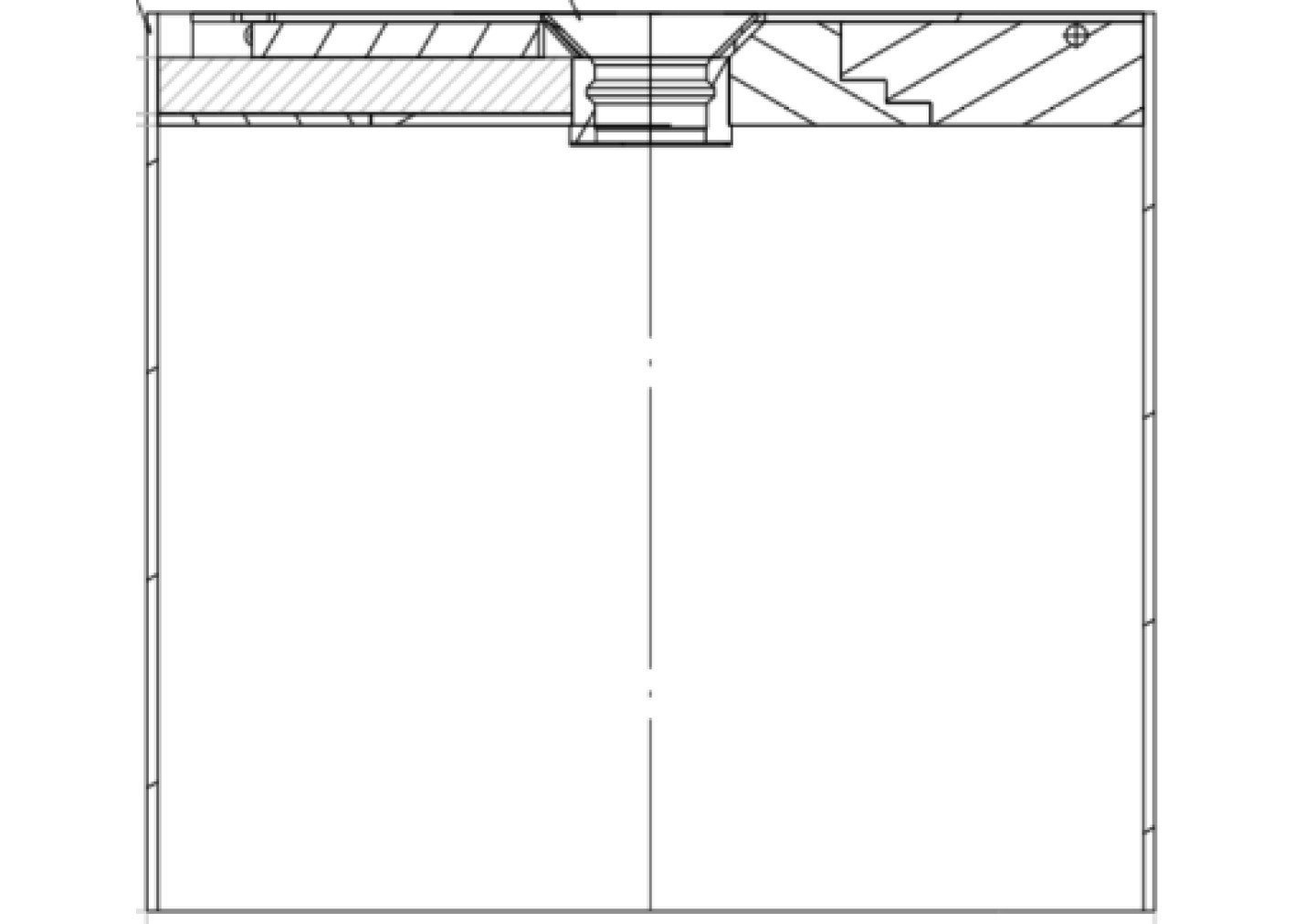
满足上述技术指标的重力锚总体设计方案如图1所示。
|
图 1 筒状重力锚总体设计方案二维平面图 Fig. 1 Two-dimensional plan of the overall design of the cylindrical gravity anchor |
通过材料力学特性及其经济性比较综合考虑,重力锚的各部件材质已选取完成,其相应材质的许用应力、弹性模量、泊松比详细数据如表2所示。
|
|
表 2 重力锚材料参数 Tab.2 Material performance parameters of gravity anchor |
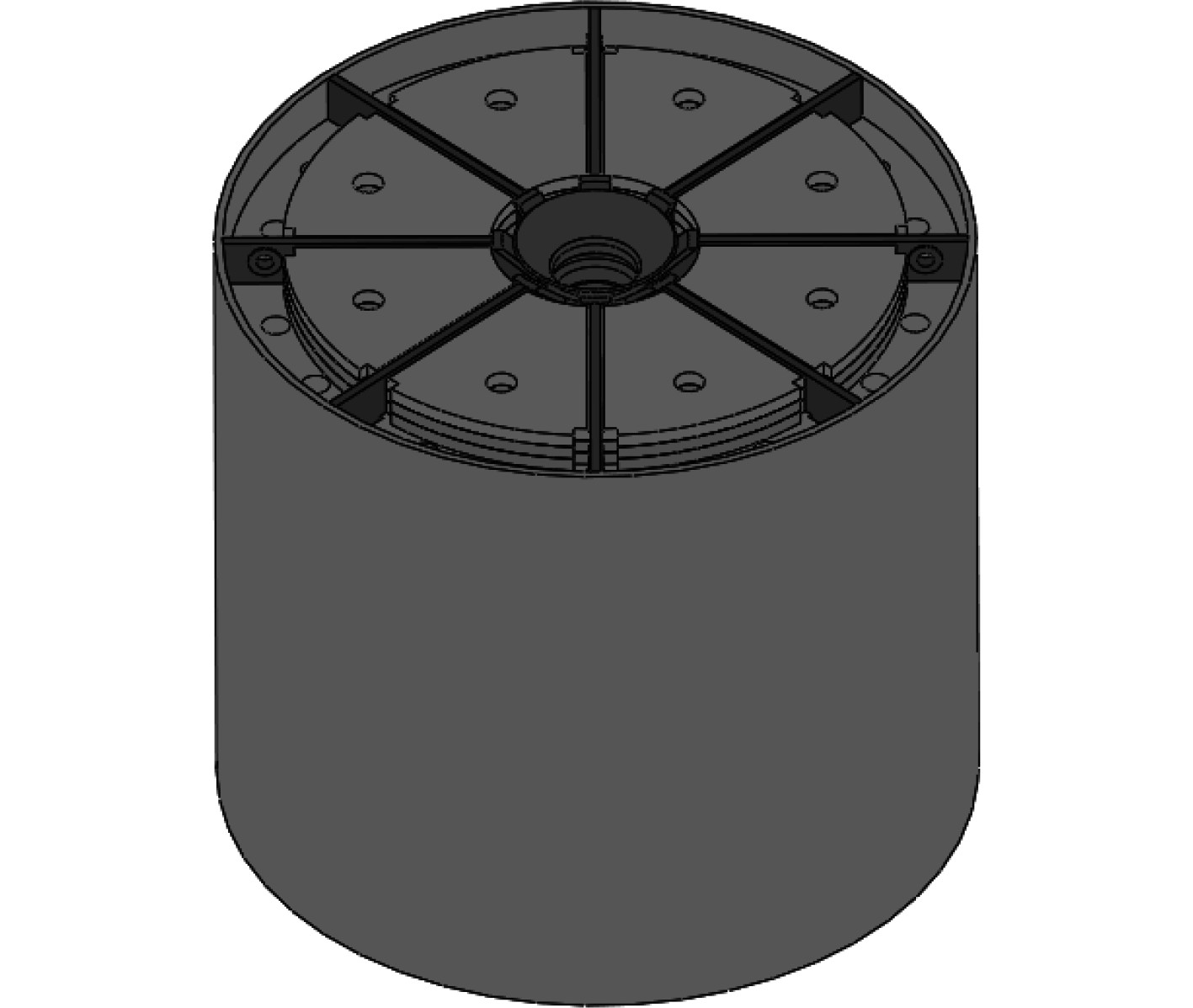
按照重力锚二维设计图纸,建立三维结构静力分析模型,如图2所示。
|
图 2 重力锚实体模型 Fig. 2 Solid model of gravity anchor |
遴选重力锚工作状态下最具代表性的2种工况进行有限元分析,其具体工况的描述如表3所示。
|
|
表 3 重力锚2种计算工况 Tab.3 Gravity anchor two calculation conditions |
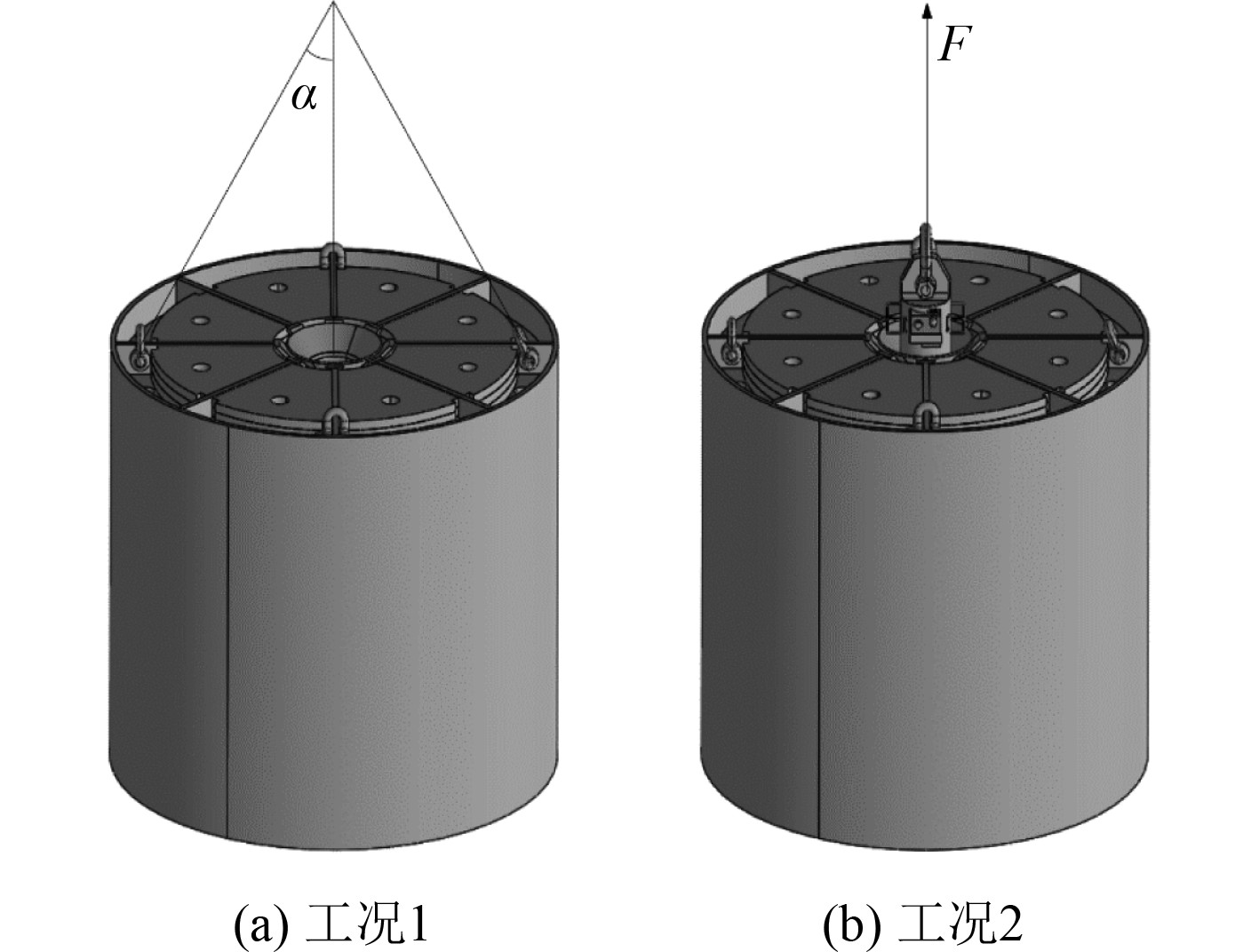
对于工况1(见图3(a)),起吊点在锚中心位置的正上部,它和卸扣之间通过桁架单元进行连接,忽略桁架的变形,对其进行刚体约束。桁架与竖直方向的夹角а=10°,20°。将起吊点的3个方向位移进行固定,释放桁架所在面内的旋转自由度,固定剩余2个旋转自由度。吊耳孔洞直径为100 mm,厚度为60 mm,其在筋板上的位置为距离筋板顶部130 mm,距离裙板内圆壁250 mm。卸扣在垂直对称面方向的移动和3个转动自由度固定,考虑到接触收敛的困难性,先忽略卸扣材料的变形,将其进行刚体约束。卸扣外柱面与吊耳内圆面设置接触,法向硬接触,切向给0.1的摩擦系数(钢材与钢材的摩擦系数),消除刚体移动,卸扣直径取90 mm。锚的对称面沿法线方向固定,其具体边界条件的设置如图4所示。
|
图 3 2种复杂工况示意图 Fig. 3 Schematic diagram of two complex working conditions |

|
图 4 工况1下边界条件设置 Fig. 4 Boundary conditions setting under working conditions 1 |
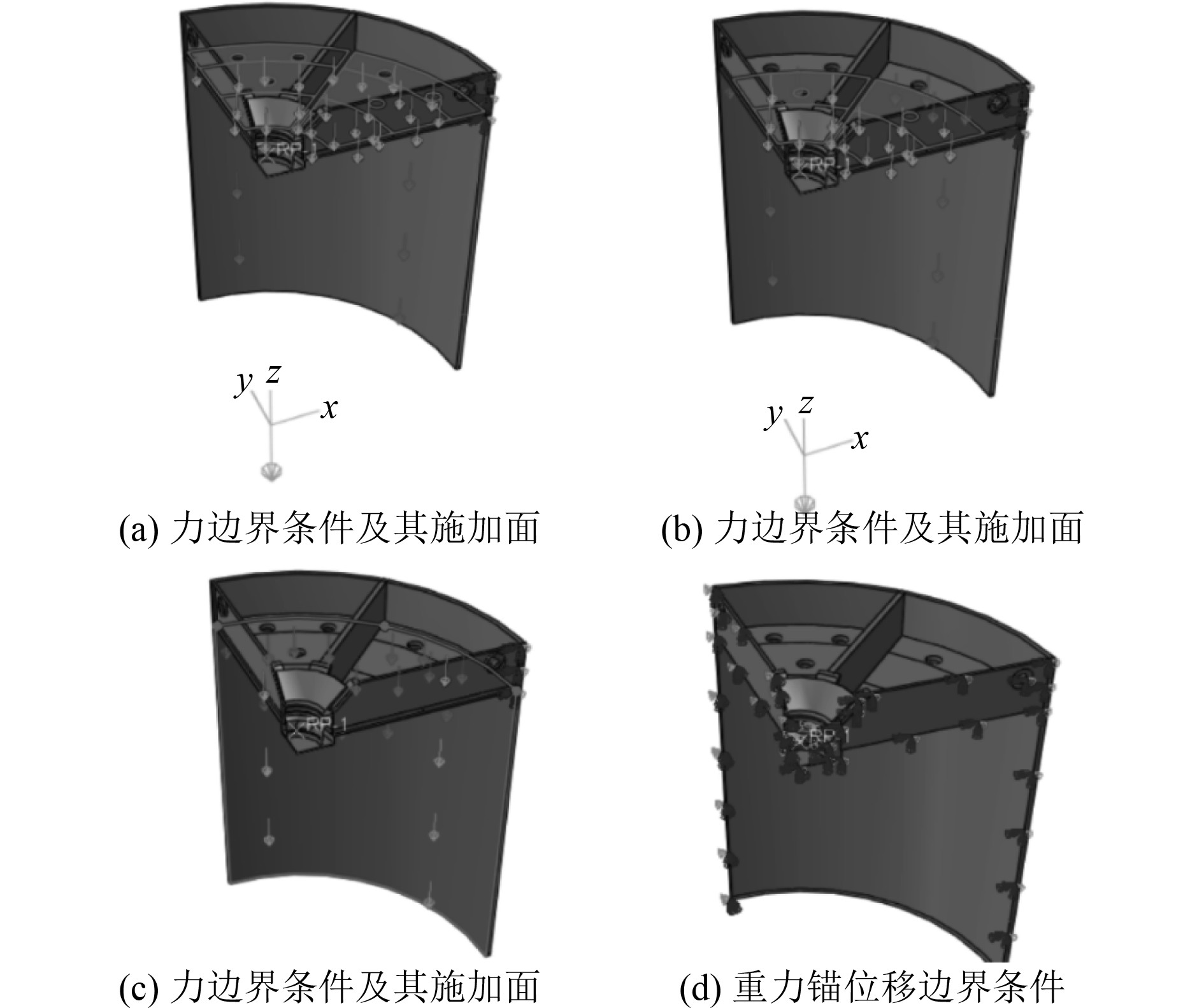
对于工况2(见图3(b)),在带有卡牙的装置上施加竖直向上的力F,起吊点仍在锚中心位置,通过卡牙装置与应急解脱装置接口装置内壁接触,通过摩擦力带动整个锚体。因此,卡牙与接口内壁设置法向硬接触,切向接触为无摩擦力接触。卡牙设置为刚体。由于在水下工作,整个重力锚的浮重约为60 t。按照要求起锚力小于等于120 t,设置安全系数1.5,需保证整个锚体结构在180 t起锚力下仍安全,因此需要在重力锚的裙板上施加120 t的力。同时约束锚体对称面法线方向的位移,在底板上施加竖直方向的均布载荷,在底板以下的裙板上施加切向均布载荷,如图5所示。
|
图 5 工况2下边界条件设置 Fig. 5 Boundary conditions setting under working conditions 2 |
针对工况1,考虑到几何模型以及载荷的对称性,只取整个模型的1/4进行建模分析计算。重力锚锚体使用三维8节点全积分单元C3D8单元进行离散,大部分区域的网格尺寸为20 mm,吊装孔以及应急解脱装置解锁接口部位局部加密,网格尺寸为5 mm,模型单元数共计93513,节点数总计132994,有限元网格模型如图6所示。

|
图 6 工况1下重力锚有限元模型 Fig. 6 Finite element model of gravity anchor under working conditions 1 |
针对工况2,依然考虑到几何模型以及载荷的对称性,只取整个模型的1/4进行建模分析计算。卡牙使用整个模型,卡牙单元采用三维8节点减缩积分体单元 C3D8R,锚体部分使用C3D8单元,大部分区域的网格尺寸为15 mm,应急解脱装置解锁接口部位局部加密,网格尺寸5 mm,模型单元数共计175932,节点数总计334415,有限元网格模型如图7所示。

|
图 7 工况2下重力锚有限元模型 Fig. 7 Finite element model of gravity anchor under working conditions 2 |
有限元应力分析采用MISES等效应力进行判断,针对工况1,当吊绳与竖向夹角为20°时,求解得到的整体结构以及各部件的MISES应力云图如图8所示。
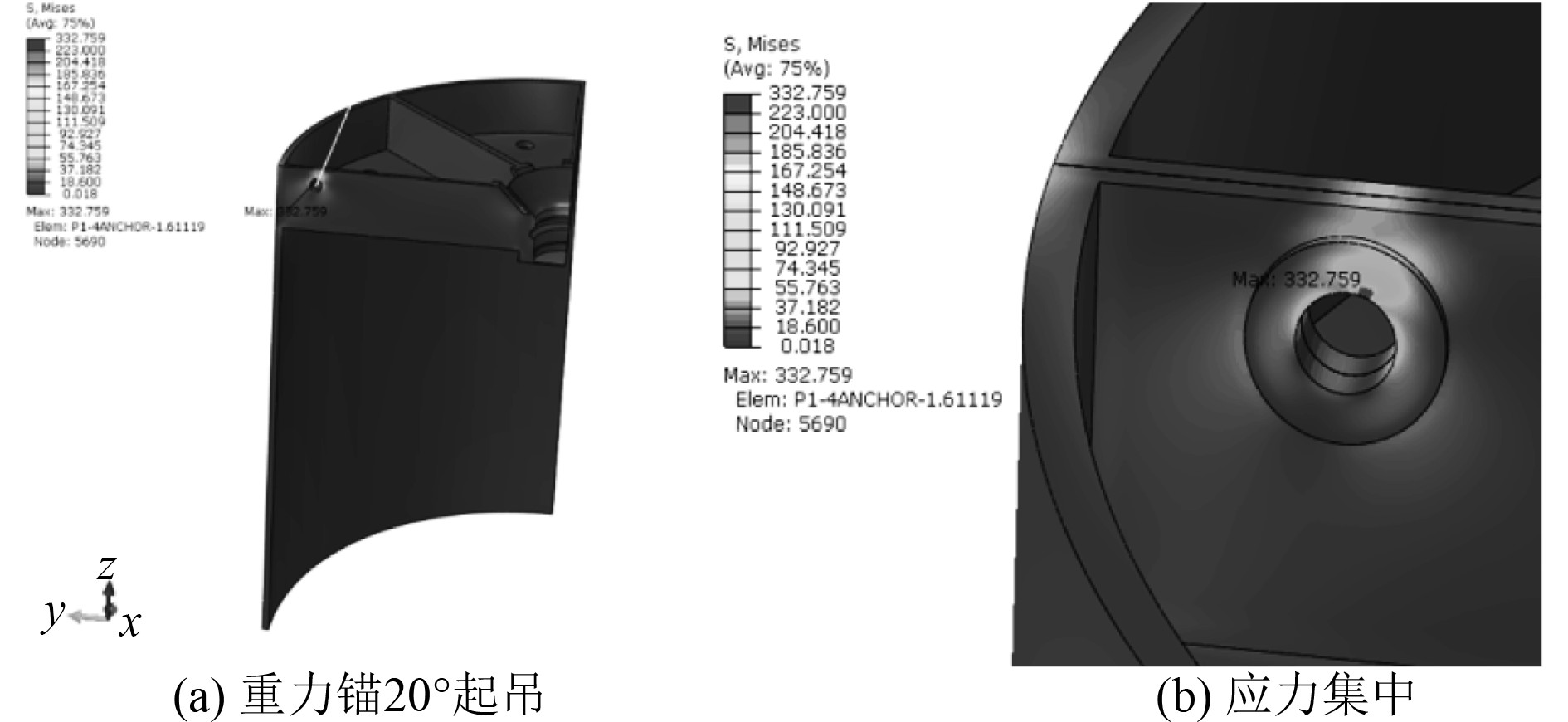
|
图 8 重力锚20°起吊工况的Mises应力分布和应力集中部位 Fig. 8 Mises stress distribution under 20° lifting condition of gravity anchor and stress concentration part |
当吊绳与竖向夹角为10°时,求解得到的整体结构以及各部件的MISES应力云图如图9所示。根据计算结果可知,重力锚的Mises应力最大值大于钢板设计允许值,其中大于材料设计允许值(223.3 MPa)的区域如图8(b)和图9(b)所示。从等效应力云图可以看出,应力超过 223.3 MPa 的区域仅位于卸扣与吊耳很小的接触区域处,因此,可以划为峰应力(peak stress),其允许极限值为670 MPa,此值大于最大Mises应力,因此结构满足工况1要求。

|
图 9 重力锚10°起吊工况的Mises应力分布和应力集中部位 Fig. 9 Mises stress distribution under 10° lifting condition of gravity anchor and stress concentration part |
针对工况2,其计算结果如图10所示。可以看出,在应急解脱装置与筋板上面板的接触部位有应力集中,此应力集中局部的 Mises应力依然小于材料的屈服强度。针对直接施加压力,同时约束底板竖直位移的情况,重力锚上最大应力远小于材料屈服强度,满足工况2要求。
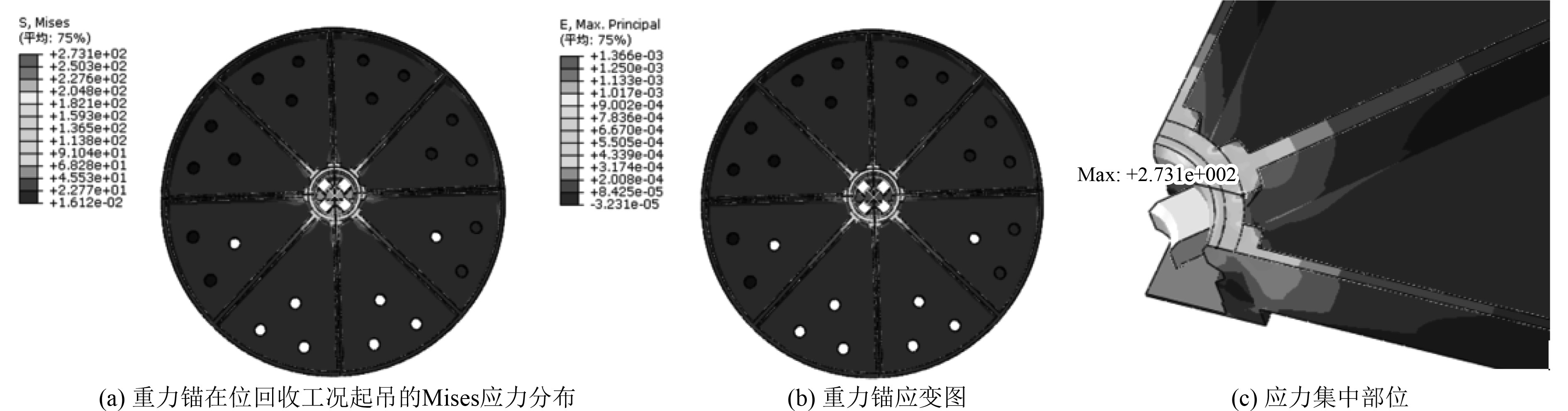
|
图 10 工况2计算结果 Fig. 10 Result of conditions 2 |
在吊装过程中,整个重力锚为竖直起吊状态。吊绳与竖直方向的角度为а。吊耳结构强度可按下式简化公式计算:
| $ \sigma = \frac{{{F_Z}}}{{(B - d)t}} \leqslant \left[ \sigma \right] = \frac{{{\sigma _s}}}{{{n_s}}}。$ | (1) |
式中:
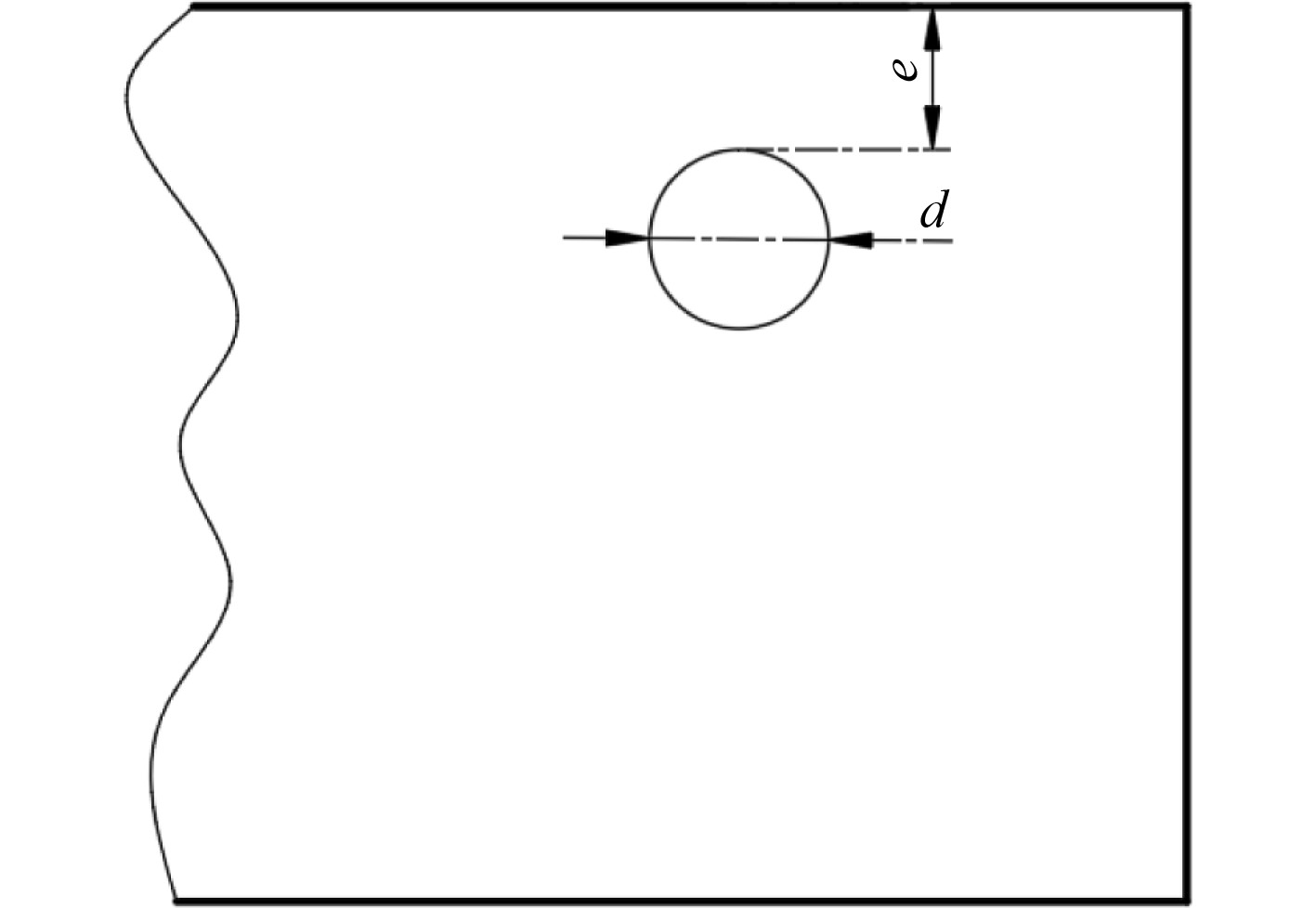
|
图 11 吊耳孔示意图 Fig. 11 Schematic diagram of the ear hole |
重力锚筋板的吊耳孔承受垂向力
| $ \tau = \dfrac{{{F_Z}}}{{2\left(e + \dfrac{d}{8}\right)t}} \leqslant \dfrac{{{\tau _{_S}}}}{{{n_s}}} = \dfrac{{(0.6\sim 0.8){\sigma _s}}}{{{n_s}}} $ | (2) |
式中:
本文针对筒状重力锚的整体结构进行强度分析,通过有限元软件Abaqus分析重力锚在2种代表性工况下的受力情况。根据分析结果可知,吊装工况下,重力锚上吊耳与销钉接触的部位应力最大,最大应力值为332.7 MPa,其余部位应力值均低于此处,因此,在施工过程中需要对吊耳孔周围进行加厚,从而提高该结构的强度。而在位回收工况下,在支撑筋板与应急解脱装置的接触部位应力最大,最大应力值为273.1 MPa,其余部位应力值均低于此处。为安全起见,在两者接触部位加一块面板,加大接触面积,从而降低应力。最后通过理论公式推导,围绕重力锚结构强度和剪切破坏强度2个方面,对重力锚上吊耳进行强度校核。通过对重力锚的整体构型进行优化设计,找出符合要求的设计方案,为工程实践提供理论基础和设计参考。
| [1] |
叶邦全. 海洋工程用锚类型及其发展综述[J]. 上海造船, 2012(3): 1-7. |
| [2] |
SCLAVOUNOS P D, LEE S, DIPIETRO J. Floating offshore wind turbines: tension leg platform and taught leg buoy concepts supporting 3~5 MW wind turbines[R]. Proc European Wind Energy Conference EWEC, 2010: 20–23.
|
| [3] |
李怀亮, 黄山田, 王晓飞, 等. 重力锚水平承载力特性的有限元分析[J]. 中国港湾建设, 2016, 36(1): 6-9. |
| [4] |
竺新文. 重力锚室内模型试验及数值模拟研究[D]. 天津: 天津大学, 2016.
|
| [5] |
徐保照. 钙质土中锚固基础设计研究[D]. 天津: 天津大学, 2014.
|
| [6] |
李飒, 竺新文, 李怀亮, 等. 水平荷载作用下重力锚室内模型试验及数值模拟分析[J]. 中国海上油气, 2018, 30(2): 152-157. |
| [7] |
韩森, 贾宝柱, 孙文正, 等. 多点锚泊定位系统布锚夹角的影响及优化分析[J]. 中国舰船研究, 2018, 13(5): 61-67. |
| [8] |
TAYLOR R J. Interaction of anchors with soil and anchor design[R]. Technical Note of Naval Civil Engineering Laboratory, California, 1982: 1–50.
|
| [9] |
闫宏生, 刘鹏飞, 孟祥伟, 等. 深水重力锚黏土质水平承载机理研究及数值模拟[J]. 中国造船, 2021, 62(3): 222-230. DOI:10.3969/j.issn.1000-4882.2021.03.020 |
| [10] |
杨鹏, 陈世海, 蒋岩, 等. 重力锚在“世越”号打捞中的应用[J]. 世界海运, 2017, 40(9): 7-10. |
 2022, Vol. 44
2022, Vol. 44
