水空两用装备可显著增强水下优势、区域存在以及影响力,是提升海军作战能力的重要手段之一。
水空两用装备是指既能水下潜航、又可在空中飞行的新概念特种装备,集成空中和水下2种航行器的能力,即飞机空中快速飞行能力和潜艇潜水隐藏能力。水空两用装备虽优势明显,但推进问题是严重制约其发展的重大关键性问题。
在目前已问世的水空两用装备中,以电动机作为动力源的推进方式主要包括螺旋桨推进(约70%)和扑翼式推进(约20%);以发动机作为动力源的推进方式主要包括喷气式推进(约20%)、火箭推进(约10%)和螺旋桨推进(约70%)。
由此可见,螺旋桨是目前水空两用装备推进技术的主要方式,也是最实用的形式,能完成多次水/空2种不同介质间的运动切换。早在19世纪70年代,高效螺旋桨设计就备受国内外学者青睐。William[1]在1878年率先提出叶素理论,这一理论考虑了螺旋桨的旋转效应,反映了气流经过桨叶的绕流特征,成为螺旋桨设计的基本理论之一。Gold-Stein[2]提出螺旋桨涡流理论,奠定了螺旋桨设计的理论基础。Black等[3]提出带冠螺旋桨的设计思想,并且进行带冠螺旋桨的性能试验。Larrabee[4]提出最小诱导损失螺旋桨的设计方法。Eppler等[5]提出螺旋桨设计的逆方法。
由于水与空气间的密度相差近800倍,用于水中的螺旋桨和用于空气中的螺旋桨具有不同的设计方法,纵观国内外螺旋桨方面的设计研究[6-11],目前尚未形成统一的解决方案。
本文以NACA4412翼型为研究对象,采用程序设计方法开展水空两用螺旋桨的快速设计研究,最终形成一种在水中和空中效率均较高的高效推进螺旋桨设计方法,采用与相关文献以及试验数据的比较来校核该快速设计方法的可靠性。
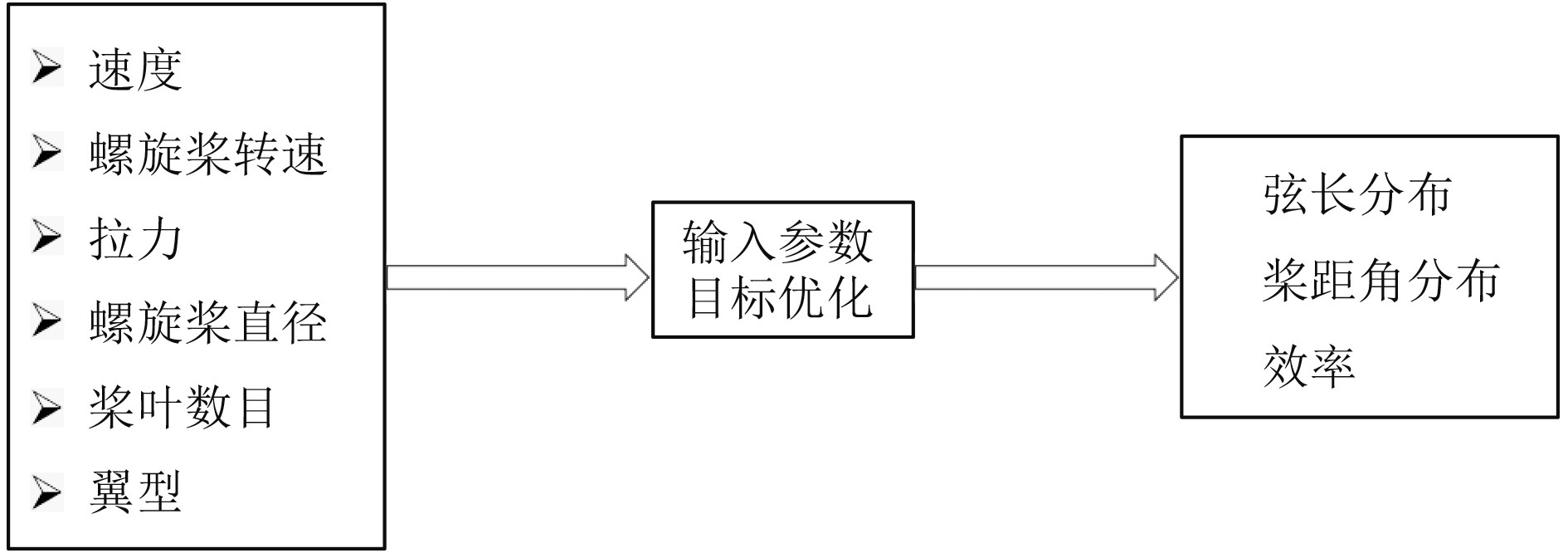
1 设计原理根据给定的飞行速度、螺旋桨转速、拉力、螺旋桨直径、桨叶数、翼型,能够计算出最大效率时的螺旋桨几何特性,包括桨叶的弦长分布、桨距角分布与效率。最高效率螺旋桨的能量损失是最小的,如果沿桨叶径向的所有翼型都在最大效率(最大升阻比)攻角工作,那么螺旋桨的效率是最高的。因此,程序设计目标函数为每个翼段尽可能工作在最大升阻比攻角工况,使整个螺旋桨工作效率达到最大值。采用Matlab程序设计方法进行螺旋桨设计,设计流程如图1所示。
|
图 1 螺旋桨设计流程 Fig. 1 Propeller design process |
设计过程中,对于公式的编程及设计程序的流程主要采用的是微分思想。整个设计过程中需解决如下所面临的技术问题,才能实现水空两用螺旋桨的快速设计:
1)1个难点:拉格朗日积数的确定;
2)3个修正:速度修正,雷诺数修正,马赫数修正;
3)3个基本公式:进距比,功率,螺旋桨效率;
4)1个关键循环:最优量寻找。
对于拉格朗日积数K的确定,采用下列公式进行计算:
| $ \frac{T}{{4\rho {\text{π}} {V^2}}} = \int_{R - {R_h}}^R {({K_1} + K_1^2)} {k_p}r{\rm{dr}},$ | (1) |
| $ {K_1} = \dfrac{K}{{1 + {{\left(\dfrac{V}{{\varOmega r}}\right)}^2}{{\left(1 + K\right)}^2}}}。$ | (2) |
式中:T为给定的力;ρ为流体密度;kp为纠正因子;V为来流速度;Ω为螺旋桨转速;r为该翼段所在位置。
对于3个修正,采用下式计算:
| ${\mathop V \limits^{\frown}}_{e}=\sqrt{1+{\left(\dfrac{{\xi }_{i}}{\lambda }\right)}^{2}\mathrm{cos}{\alpha }_{i}} ,$ | (3) |
| $ {R}_{e\xi }={R}_{e}\cdot {{\mathop V \limits^{\frown}}_{e}}\cdot b ,$ | (4) |
| $ {M}_{a\xi }={M}_{a}\cdot {\mathop V \limits^{\frown}}_{e} 。$ | (5) |
式中:λ为前进比;ξi为第i个截面的无量纲坐标;αi为第i个截面的诱导攻角;b为无量纲弦长。
3个主要基本公式中,进距比、功率、螺旋桨效率可采用下式计算:
| $ J = \frac{V}{{{n_s}D}},$ | (6) |
| $ P = 2{\text{π}} {n_s}M,$ | (7) |
| $ \eta = \frac{{TV}}{P}。$ | (8) |
式中:ns为螺旋桨转速;D为螺旋桨直径;M为螺旋桨转矩。
对于最优量的寻找,采用下式计算:
| $ B = \frac{{8\text{π} }}{n} \cdot \frac{{{\xi _i}{k_p}\tan {\alpha _i}\sin \delta }}{{{C_{l,\max }} - {C_{d,\max }}\tan \delta }}。$ | (9) |
式中:n为桨叶数目;δ为修正速度与螺旋桨旋转平面间的夹角;Cl, max和Cd, max分别为最大升力系数与最大阻力系数;B为计算所的无量纲弦长,与b间不同的是,b为人为设定值,B为b设定后的计算结果,通过比较两者之差,寻找绝对值最小的情况下,对应的弦长、桨距角、最大攻角、最大升力系数以及最大阻力系数,将此参数用于螺旋桨效率的计算。
2 可靠性验证采用Matlab程序进行编程计算,并进行界面优化设计。为验证程序设计的可靠性,Matlab程序与参考文献[12]中2种工况下的数据进行综合对比分析,输入参数分别如表1和表2所示,2种验证工况结果比较如表3所示,程序设计结果与参考文献数据结果最大误差不超3%。
|
|
表 1 输入参数(程序精度验证工况1) Tab.1 aaaaa |
|
|
表 2 输入参数(程序精度验证工况2) Tab.2 aaaaa |
|
|
表 3 程序精度验证工况结果分析 Tab.3 aaaaa |
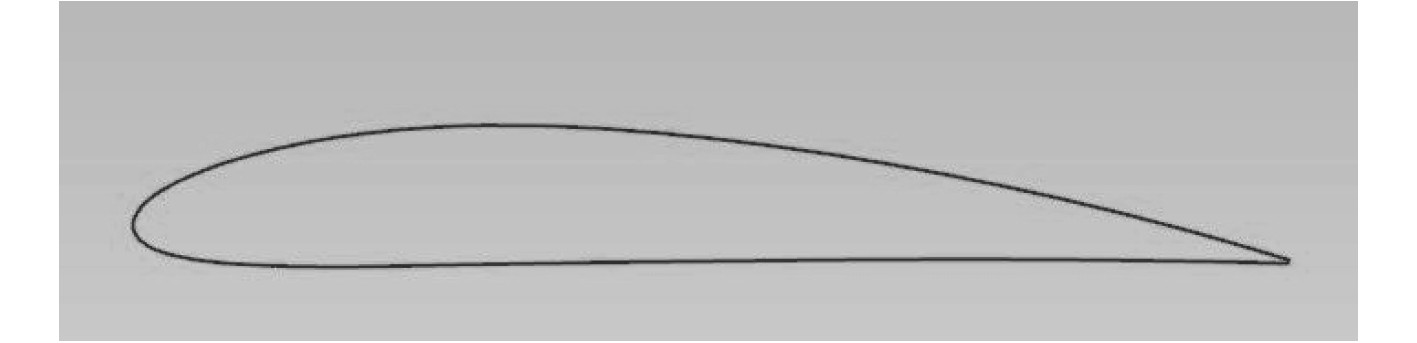
通过Matlab程序开展螺旋桨空中工况计算,螺旋桨桨叶采用NACA4412翼型,几何形状如图2所示,输入参数如表4所示,对应计算流程如图3所示。所采用的计算方法为,在Matlab程序首次结果的基础之上,采用曲线拟合后,再次进行计算。计算过程,螺旋桨做分段处理,所得到的结果为离散结果,通过曲线拟合使结果变光顺。开展程序首次计算结果与光顺优化后的结果对比分析,首次螺旋桨效率计算结果为0.76,光顺优化后的为0.77。弦长和扭角分布如图4所示。
|
图 2 NACA4412翼型 Fig. 2 NACA4412 airfoil |
|
|
表 4 输入参数(螺旋桨设计空中工况) Tab.4 aaaaa |

|
图 3 螺旋桨空中工况计算流程(Matlab程序方法) Fig. 3 Calculation flow of propeller air condition (Matlab program method) |

|
图 4 螺旋桨空中工况计算结果(弦长和扭角) Fig. 4 Calculation results of propeller air condition (chord length and torsion angle) |
由Matlab程序进行螺旋桨水中工况计算时,所输入参数如表5所示。螺旋桨为智能变体形式,在空中状态时为空中使用螺旋桨;在水下航行时,水中螺旋桨尺寸与空中不同,尺寸有所减小,部分桨叶在机械结构驱动下缩回至根部桨叶空隙中。采用Matlab程序方法对螺旋桨进行水中工况设计的计算流程如图5所示。在螺旋桨进行水中工况计算时,桨尖部分去掉,留下桨根部分,仅截取水中使用的数据,在实际操作过程中,未截取部分代表已经缩回至桨根空隙中。通过计算,水中螺旋桨效率值为0.97,此时未考虑相关损失,如轴承摩擦损失等。
|
|
表 5 输入参数(螺旋桨设计水中工况) Tab.5 aaaaa |

|
图 5 螺旋桨设计水中工况计算流程(Matlab程序方法) Fig. 5 Calculation process of propeller design underwater working conditions (Matlab program method) |
对前文设计的单排螺旋桨,其效率已高于0.7,通过参考文献[1]可知,与相同桨叶数目的单排螺旋桨相比,对转桨的气动特性的变化趋势与其基本相同,由于对转桨前后排桨叶间的相互影响,同一工况下的扭矩和功率均低于单桨,推力和效率则高于单桨。由推进效率和消除惯性力矩方面考虑,对转桨具有一定优势。
通过该设计成果,在风洞开展高效推进装置空中构型性能评估试验,所采用的对转螺旋桨桨叶数目为前6后4。试验研究过程,涉及轴系包括天平体轴系、模型体轴系、风轴系。天平体轴系:正阻力与X轴正方向相反,其余分量按照右手螺旋定则确定。模型体轴系:原点位于螺旋桨桨盘中心,X轴与螺旋桨转轴重合并指向前,Y轴垂直X指向上,Z轴垂直于YOX平面,指向符合右手定则。风轴系:原点与模型体轴系相同,X轴指向来流,Y轴垂直X轴指向上,Z轴垂直于YOX平面,指向符合右手定则。图6为螺旋桨三维图。

|
图 6 螺旋桨三维图 Fig. 6 Three-dimensional drawing of propeller |
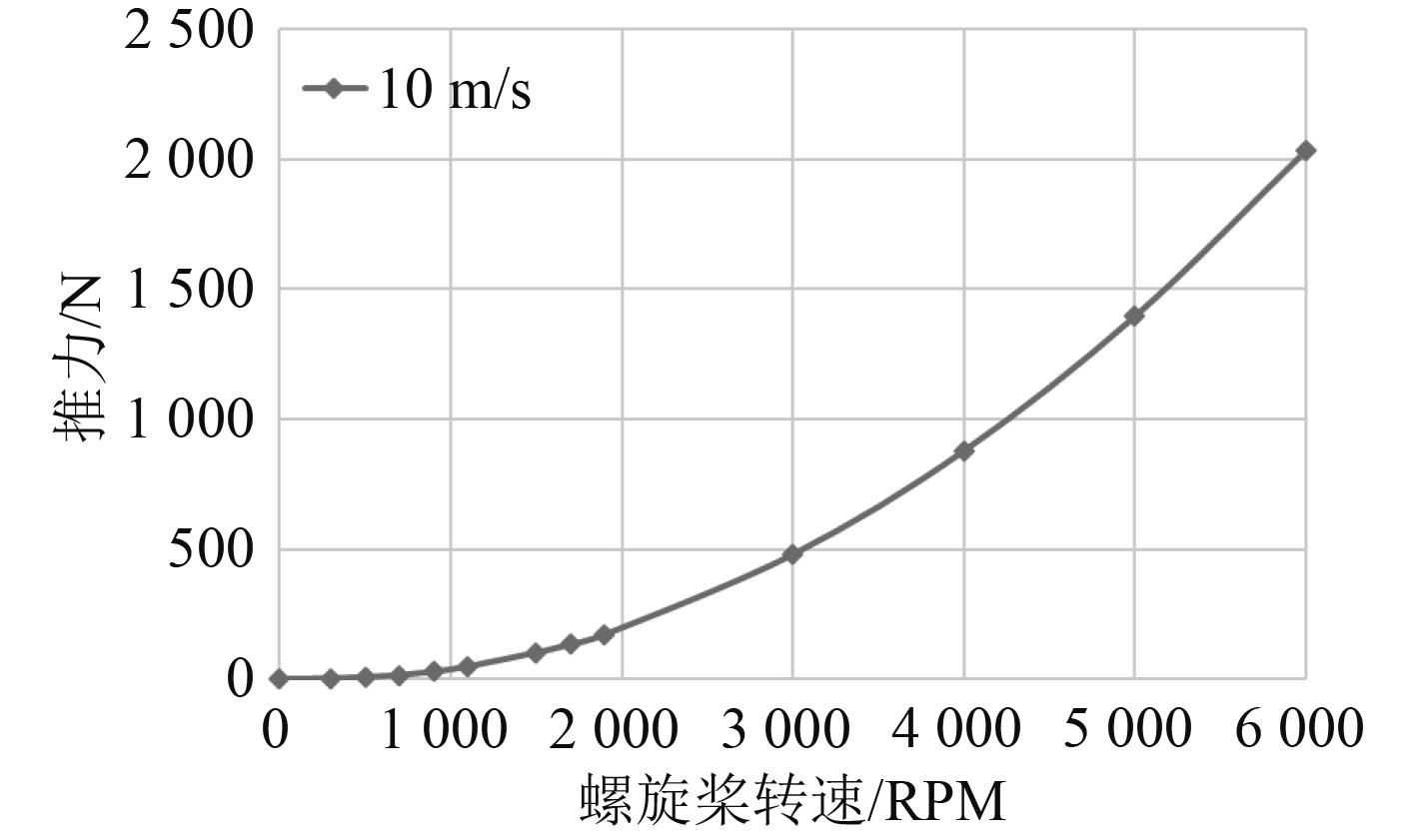
试验中,对转螺旋桨的效率计算按照下式进行,得出的效率为0.75。图7给出了风速为10 m/s的情况下对转螺旋桨转速与推力间的函数关系。
|
图 7 对转螺旋桨推力与转速之间的关系 Fig. 7 Relationship between thrust and rotational speed of counter-rotation propeller |
| $ \eta = \frac{{FV}}{P},$ | (10) |
| $ P = {P_{rated}}\varepsilon 。$ | (11) |
其中:Prated为电机额定功率,值为30 kW;ε为损失系数,取值为0.9;
本文得到的主要结论如下:
1)基于动量叶素理论以及XFOIL翼型升阻力快速计算程序,给出一套水空两用螺旋桨快速设计方法,通过与文献结果对比分析,说明该程序可靠。
2)开展水空两用对转螺旋桨风洞试验研究。试验中螺旋桨采用程序设计结果,根据单排螺旋桨与对转螺旋桨间的关系,单排螺旋桨设计结果可应用于对转螺旋桨设计中,并且可得出较高的推进效率。
| [1] |
蔡明轩. 对转螺旋桨级间气动干涉研究 [D]. 南京: 南京航空航天大学, 2018.
|
| [2] |
GOLDSTEIN. On the vortex theory of screw propellers [C] // Proceedings of the Royal Society, London, 1929: 440−465.
|
| [3] |
BLACK D M, WAINAUSKI H S. Shrouded propellers: a comprehensive performance study [R]. Pennsylvania: AAIA 5th Annual Meeting and Technical Display Philadelphia, 1968.
|
| [4] |
LARRABEE E E. Practical design of minimum induced loss propellers [R]. SAE Preprint 790585, 1979.
|
| [5] |
EPPLER R, HEPPERLE M. A procedure for propeller design by inverse methods [C] // Proceedings of the International Conference on Inverse Design Concepts in Engineering Science (ICIDES). Austin TX: ICIDES, 1984: 445−460.
|
| [6] |
AKKERMANS R A D, STUERMER A, DELFS J W. Active flow control for interaction noise reduction of contra-rotating open rotors[J]. AIAA Journal, 2016, 1413-1423. |
| [7] |
杨路春, 杨晨俊, 李学斌. 基于多目标进化算法和决策技术的螺旋桨优化设计研究[J]. 中国造船, 2019, 3(60): 55-66. DOI:10.3969/j.issn.1000-4882.2019.03.006 |
| [8] |
王广东, 杨丽, 余建星. 基于改进进化算法的螺旋桨设计方法研究[J]. 船舶工程, 2004, 26(2): 20-23. DOI:10.3969/j.issn.1000-6982.2004.02.007 |
| [9] |
王晓强, 龚正琦. 水下螺旋桨技术发展现状与展望[J]. 中国水运, 2021, 4(25): 74-76. DOI:10.13646/j.cnki.42-1395/u.2021.04.025 |
| [10] |
余龙, Drukenbrod M, Greve M. 基于CFD技术的导管螺旋桨自动优化设计技术研究[J]. 水动力学研究与进展A辑, 2013, 4(28): 438-444. |
| [11] |
曾志波, 刘登成, Kuiper G. 桨叶剖面空泡形态发展特性研究[J]. 水动力学研究与进展A辑, 2018, 1(33): 9-16. DOI:10.16076/j.cnki.cjhd.2018.01.002 |
| [12] |
项松, 王吉, 张利国, 等. 一种高效率螺旋桨设计方法[J]. 航空动力学报, 2015, 1(30): 136-141. DOI:10.13224/j.cnki.jasp.2015.01.019 |
 2022, Vol. 44
2022, Vol. 44
