2. 中国舰船研究设计中心,湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
操纵性是船舶非常重要的特性之一,特别是对于水下航行器。舵翼结构是其流线型结构中较为明显的突出部位,尾舵在转动过程中与其周围的海水发生相互作用,在舵附近形成时空非均匀流场,海水给舵及周围的潜艇结构施加非均匀分布的脉动载荷,激起其结构振动,向三维半空间中的海水中辐射声波,在转舵过程中表现为瞬态非平稳噪声。
转舵过程中舵噪声研究涉及流—固—声耦合系统的结构振动与声辐射,较为复杂,目前尚无法进行解析求解,通常采用数值计算仿真方法。针对流固声耦合下的计算,齐贺阳[1]通过结合STAR CCM+与Abaqus联合仿真计算不同来流速度下锥柱组合结构的流激噪声; 冯亮等[2]采用单向耦合对比了艇壳体在水流作用下的流噪声以及艇壳体与水流耦合下的流激噪声。目前国内专家针对潜艇尾舵噪声进行了一些研究,屈铎等[3]基于CFD 大涡模拟及Lighthill 声类比理论对不同舵角下的舵翼结构流场和声场进行了模拟,结果显示舵角的增大使得声压级变大但增大幅值减小,且涡流是产生流噪声的原因;董仁义等[4]则基于Lilley声功率计算公式针对流体在舵叶转动时的声辐射规律进行了研究,并对舵叶设计给出建议。研究并未考虑到流固耦合下的影响。
本文基于Fluent及结构FEW,采用双向流固耦合方法计算舵转动引起的舵结构动态响应,然后以有限元计算得到的结构振动作为激励源,用边界元方法计算海水中的声辐射,针对不同转舵函数下舵翼转舵过程引起的振动辐射效应进行对比分析。本文仿真计算流程如图1所示,其中流固耦合计算流程如图2所示。
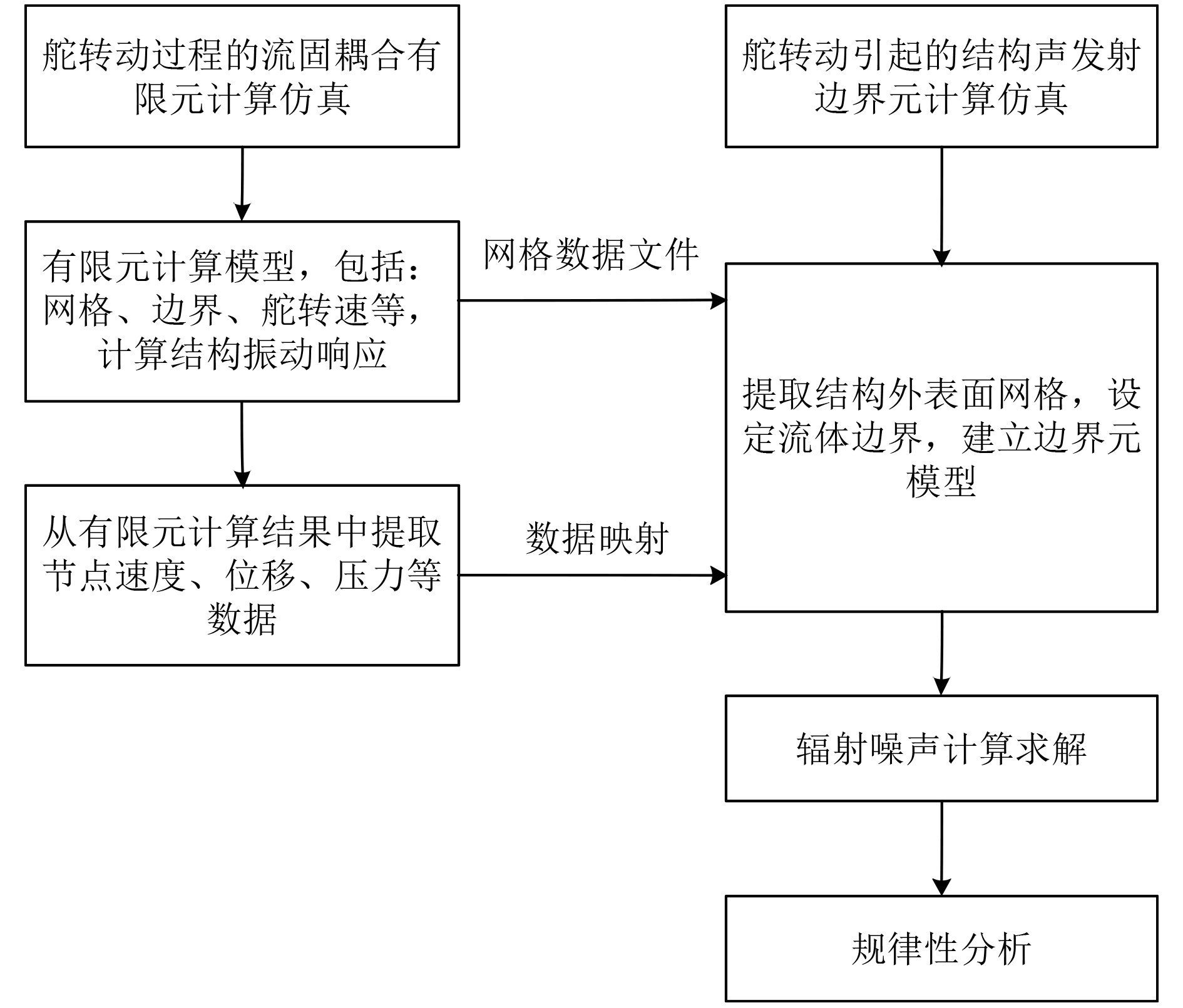
|
图 1 仿真计算流程 Fig. 1 Simulation calculation process |
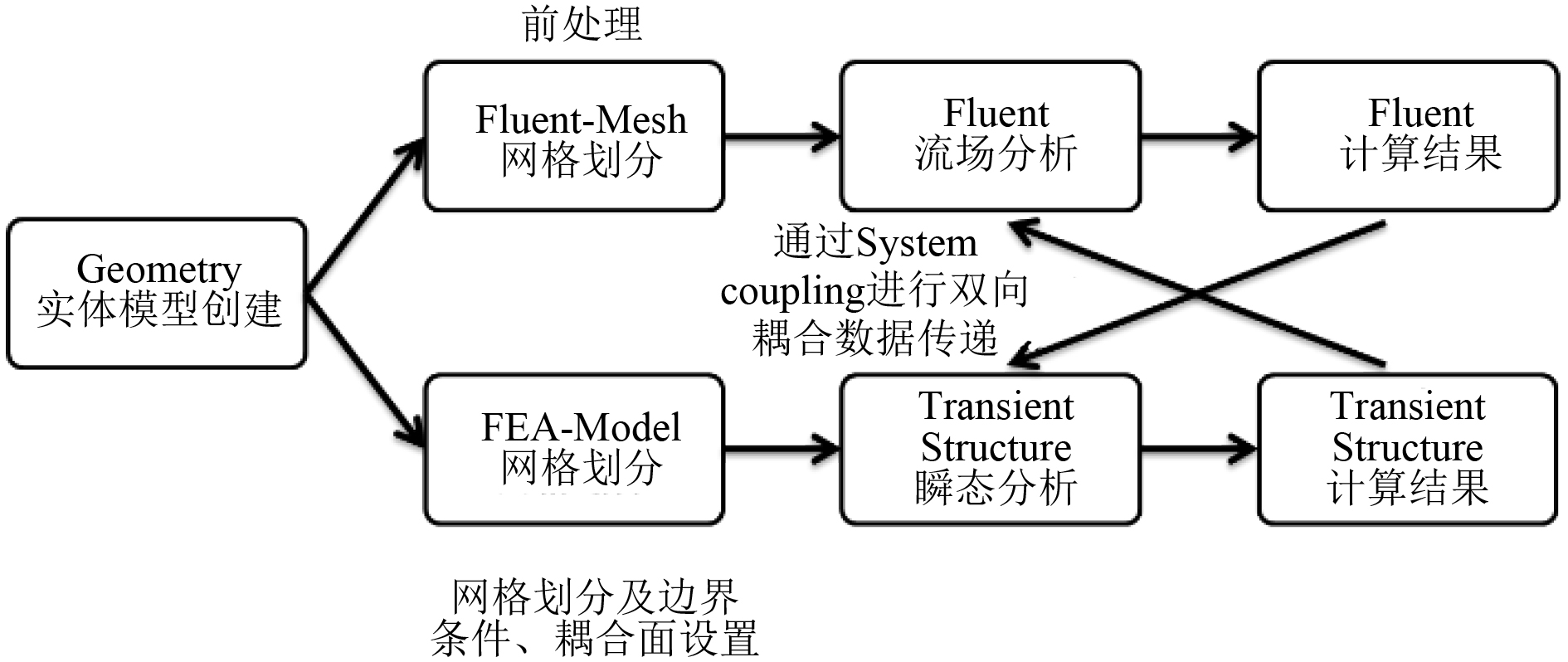
|
图 2 舵转动过程流固耦合计算流程 Fig. 2 Fluid-solid coupling calculation process of rudder rotation |
流体遵守质量守恒、动量守恒和能量守恒定理,因此其基本控制方程可由下列方程[5]表示:
质量守恒方程
| $ \frac{{\partial {\rho _f}}}{{\partial t}} + \frac{{\partial ({\rho _f}u)}}{{\partial x}} + \frac{{\partial ({\rho _f}v)}}{{\partial y}} + \frac{{\partial ({\rho _f}w)}}{{\partial z}} = 0。$ | (1) |
式中:u,v、w是速度矢量U在x,y和z方向上的分量。
动量守恒方程
| $ \frac{{\partial {\rho _f}u}}{{\partial t}} + {\rm{div}}({\rho _f}uu - {\tau _f}) = {f_f}。$ | (2) |
式中:
由牛顿第二定律可以建立固体域的控制方程:
| $ {\rho _s}{\ddot d_s} = {\rm{div}}({\sigma _s}) + {f_s} 。$ | (3) |
式中:
流固耦合方法分为直接求解法以及分离求解法。直接求解法同时求解流体和固体控制方程,而分离求解法则分别求解流体和固体,需要通过耦合交界面进行数据的传递。
直接求解法控制方程:
| $ \left[ {\begin{array}{*{20}{c}} {{A_{ff}}}&{{A_{fs}}} \\ {{A_{sf}}}&{{A_{ss}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta X_f^k} \\ {\Delta X_s^k} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{B_f}} \\ {{B_s}} \end{array}} \right] 。$ | (4) |
式中:系统矩阵
分离求解法满足下列方程:
| $ \left\{ {\begin{array}{*{20}{c}} {{q_f} = {q_s}} \\ {{T_f} = {T_s}} \\ {{d_f} = {d_s}} \\ {{\tau _f}{n_f} = {\tau _s}{n_s}} \end{array}} \right. $ | (5) |
式中:q为热流量;T为温度;d为位移;
本文采用分离求解法中的双向耦合。考虑双向交换数据,除考虑流体对结构的影响外,还考虑结构变形对流场的影响。
1.2 边界元法声学边界元方法是计算声学中常用的方法[6-8]。与声学有限元相比,它具有更强的灵活性和直观性。本研究主要采用直接边界元法,对翼舵的辐射噪声噪声进行分析。边界元求解方程为:
| $ {\boldsymbol{{B}}}p={\boldsymbol{C}}{v_n} $ | (6) |
式中:B,C为边界元法的系数矩阵;p为节点声压向量;vn为节点法向速度向量。
2 计算模型 2.1 计算几何仿真计算对象为翼后舵,主要特征参数如表1所示。
|
|
表 1 主要特征参数 Tab.1 Main characteristic parameters |
|
图 3 舵翼模型 Fig. 3 Model of the rudder wing |
针对3种转舵函数对翼舵转动时的流场及噪声响应进行仿真分析,分别为均匀速度转舵函数
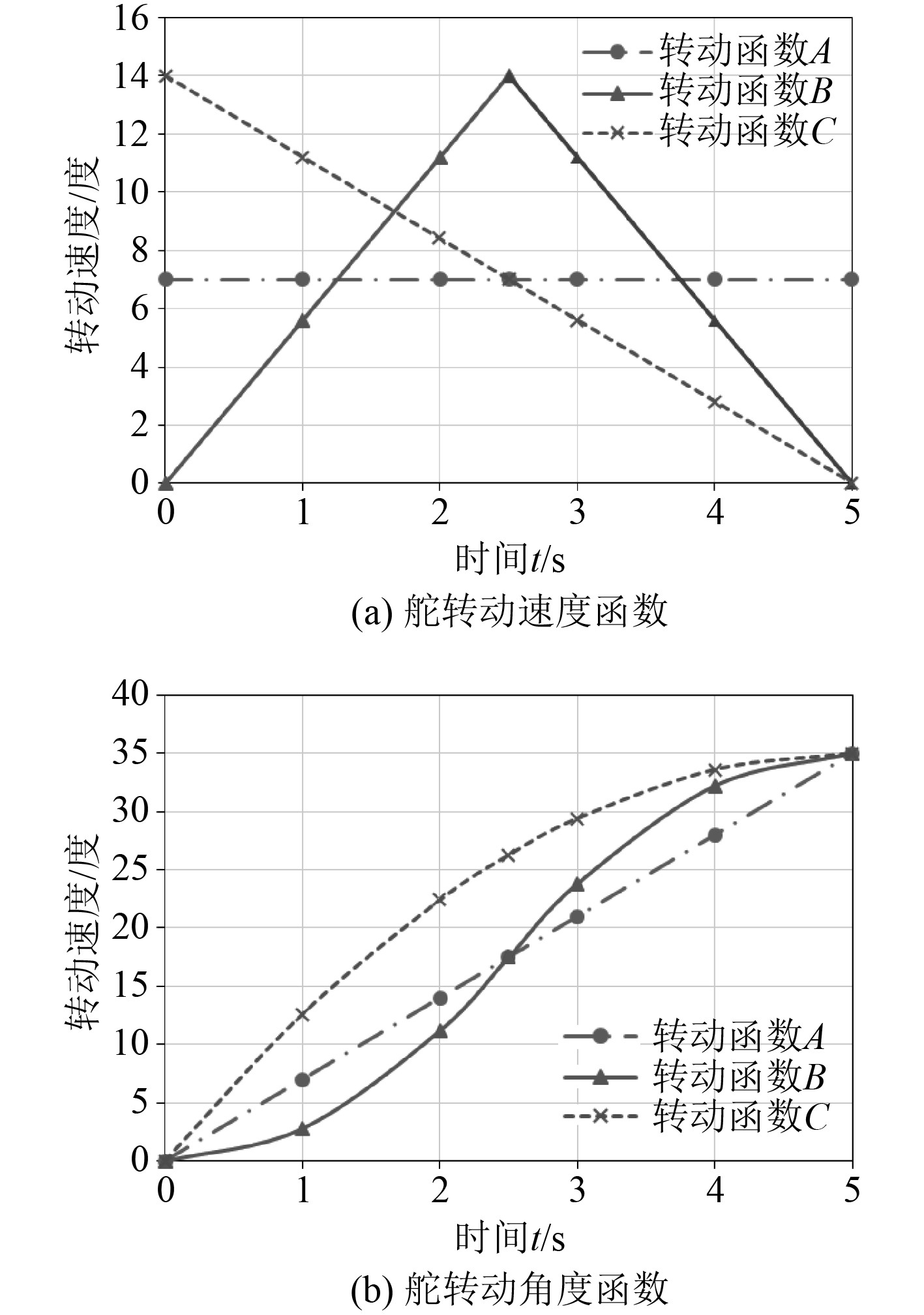
|
图 4 舵转动函数 Fig. 4 Rudder rotation function |
| $ \begin{array}{l} {{\dot \theta }_A}(t) = {\text{7}},\;\;\;\;\;\;0 \leqslant t \leqslant 5\;{\rm{s}} ,\\ {{\dot \theta }_B}(t) = \left\{ {\begin{array}{*{20}{c}} 14 \times t/2.5,&0 \leqslant t < 2.5\;{\rm{s}} ,\\ 28 - 14 \times t/2.5,&2.5\;{\rm{s}} < t \leqslant 5\;{\rm{s}} ,\end{array}} \right. \\ {{\dot \theta }_C}(t) = {\text{14}} - {\text{7}} \times t/2.5,\;\;\;\;\;\;\;\;\;0 \leqslant t \leqslant 5\;{\rm{s}}。\end{array} $ | (7) |
在流固耦合有限元计算中,对翼舵结构分别施加转动角度函数
| $ \begin{array}{l}{\theta }_{A}(t)=7t,\quad \quad 0\leqslant t\leqslant 5\;{\rm{s}},\\ {\theta }_{B}(t)=\left\{ \begin{array}{ll}7\times {t}^{2}/2.5,& 0\leqslant t < 2.5\;{\rm{s}},\\ 28\times t-7\times {t}^{2}/2.5-35,& 2.5\leqslant t\leqslant 5\;{\rm{s}},\end{array}\right.\\ {\theta }_{C}(t)=14t-3.5\times {t}^{2}/2.5\text{,}\quad \quad 0\leqslant t\leqslant 5\;{\rm{s}}。\end{array} $ | (8) |
针对每种转动函数分析舵转动时的噪声响应,需取典型角度并且在该角度临近的一个小区间下对舵转动过程进行流固耦合数值计算及噪声分析,具体实现方法为:取5个典型角度0°,9°,19°,29°,34°,在3种转舵函数下,分别计算该角度下舵转动0.1s的流固耦合响应过程,并将该0.1 s的结构响应结果导入LMS Virtual声学模块进行噪声分析。计算工况如表2所示。
|
|
表 2 工况设置 Tab.2 operation setting |
依据翼舵几何模型,建立翼舵结构的有限元模型,并在翼舵的有限元模型基础上,建立翼舵结构周围的流域模型。流体域模型如图5所示。为保证来流均匀和尾流的充分发展,流体域大小为20 m×10 m×16 m(X×Y×Z),且翼舵结构距离入口、出口均大于3倍舵宽,距离上下边界均大于2倍舵高,距离Y方向边界均大于2倍舵的厚度。

|
图 5 流体域模型 Fig. 5 Fluid domain model |
图6为舵结构网格模型,翼和舵表面网格数量为114826单元;流体域均采用非结构化网格进行离散,共有238297个单元。

|
图 6 舵结构网格模型 Fig. 6 Rudder structure grid model |
采用Fluent进行流体仿真计算,在有限元计算模型基础上对翼舵Solid结构进行抑制,针对流体域进行网格划分,网格共24万。采用SST-omega湍流模型,该模型在湍流粘度定义中考虑了湍流剪切应力的运输过程,适用于翼型绕流问题的计算。采用网格变形成转舵过程网格运动。
2.3.3 流固耦合设置选择翼舵结构所有的面作为流固耦合交界面,进行固体瞬态求解器与流体瞬态求解器计算数据的双向传递。如图7所示,在翼结构的下端设置固定约束,定义舵局部坐标系及旋转轴,并施加旋转位移。求解时间设置为0.1 s,计算时间步长为0.001 s。

|
图 7 模型Transient structual设置 Fig. 7 Model Transient structual setting |
基于导入的尾舵结构网格,定义声学包络网格,网格如图8所示。采用直接边界元法进行计算。定义X,Y,Z平面场点网格,和圆形指向性场点网格,如图9所示。声学计算需导入结构的流固耦合计算数据,使用其结构表面的加速度数据,同时定义结构网格至声学包络网格的数据映射,通过傅里叶变换,将时域数据变换为频域数据。

|
图 8 声学包络网格(舵角19°) Fig. 8 Acoustic envelope grid ( rudder angle 19° ) |

|
图 9 场点网格 Fig. 9 Field point grid |
针对A转舵函数,提取翼舵结构A1~A4工况、0.05 s的应力云图与加速度云图,如图11所示。对比可以发现,结构响应与舵的转动角度有关。随着转舵角度递增,结构应力及加速度也越大。因为舵转动角度越大,其在流体的速度方向投影面积越大,受流体冲击的响应也就越大。而舵典型位置的加速度曲线图都有共同特征,舵转动初期,加速度波动较大,后趋于稳定。
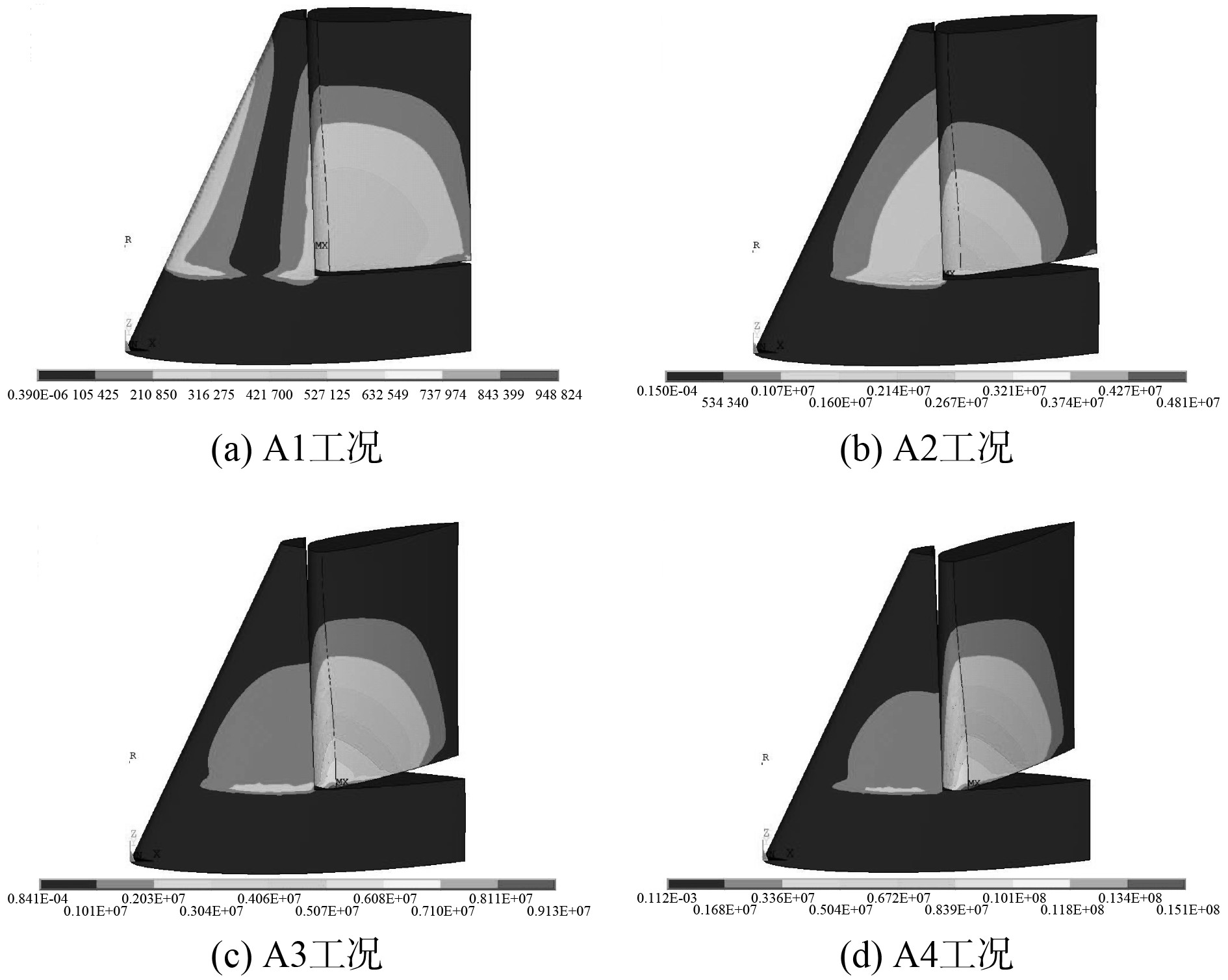
|
图 10 应力云图(0.05 s) Fig. 10 Stress cloud diagram (0.05 s) |

|
图 11 加速度云图(0.05 s) Fig. 11 Acceleration cloud diagram (0.05 s) |
针对不同转舵函数对比,选取A2,B2,C2工况进行加速度、结构图以及流场对比,如图12所示。可以发现,结构响应与舵转动的角速度有关。舵转动的角速度越大,结构的应力和加速度也越大。舵转动的角速度越大,在其瞬时对流场产生的扰动越大,结构的响应也越大。

|
图 12 应力与加速度云图(0.05 s) Fig. 12 Stress and acceleration nephogram (0.05 s) |
以3种转动函数A,B,C转舵时,舵1在0°,9°,19°,29°,34°时刻的辐射声功率曲线如图13~图15所示。可以看出,3种转动函数下的声功率曲线的形态基本一致,最大声功率基本出现在40 Hz时,且都随着角度的增大而增大。
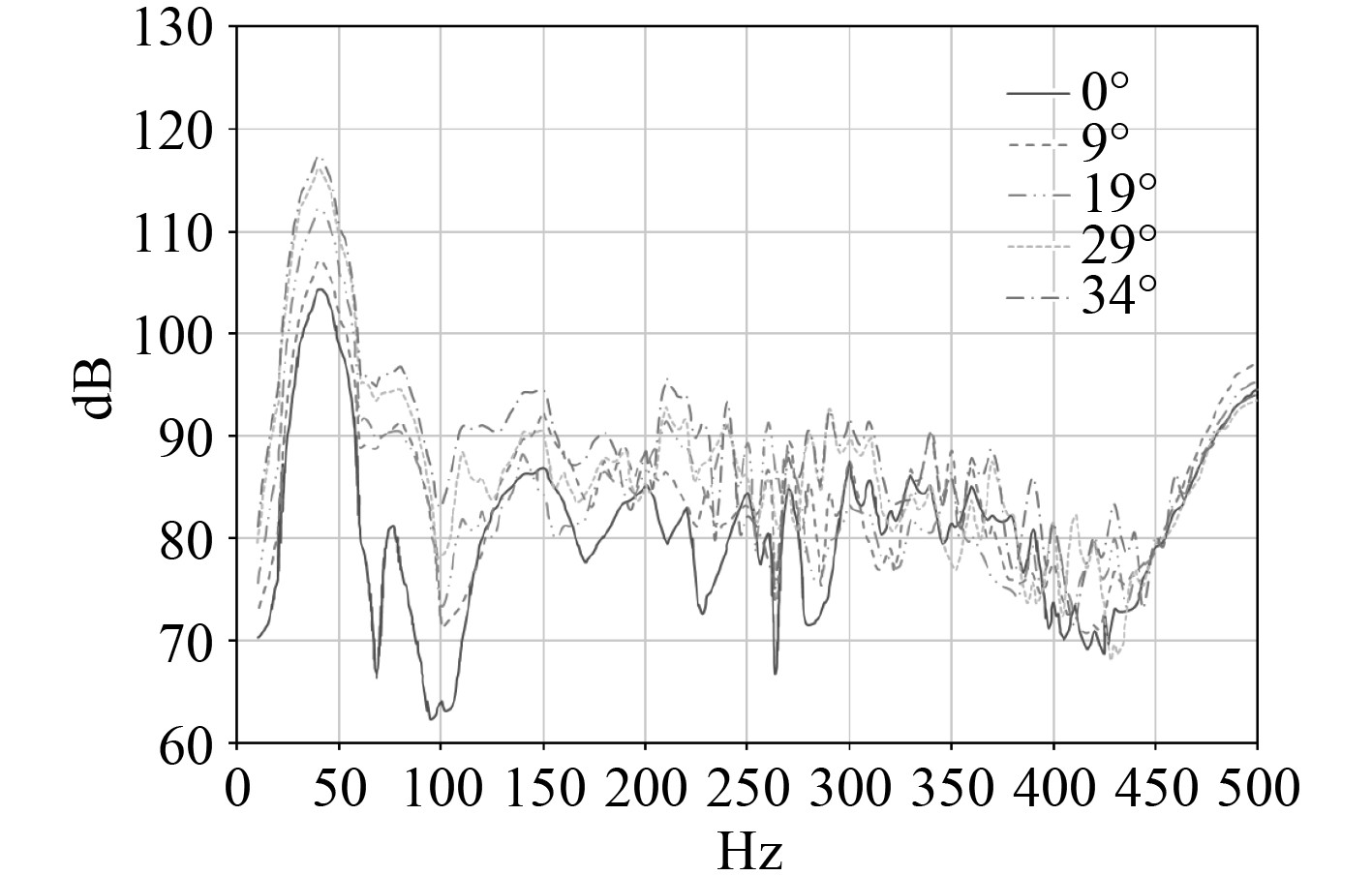
|
图 13 不同转舵角下辐射声功率图(转舵函数A) Fig. 13 Radiation sound power diagram at different rudder angles ( rudder function A ) |
由于转动函数B在0°时的转速和转角都很小,因此声功率曲线较为特殊,且整体偏低。
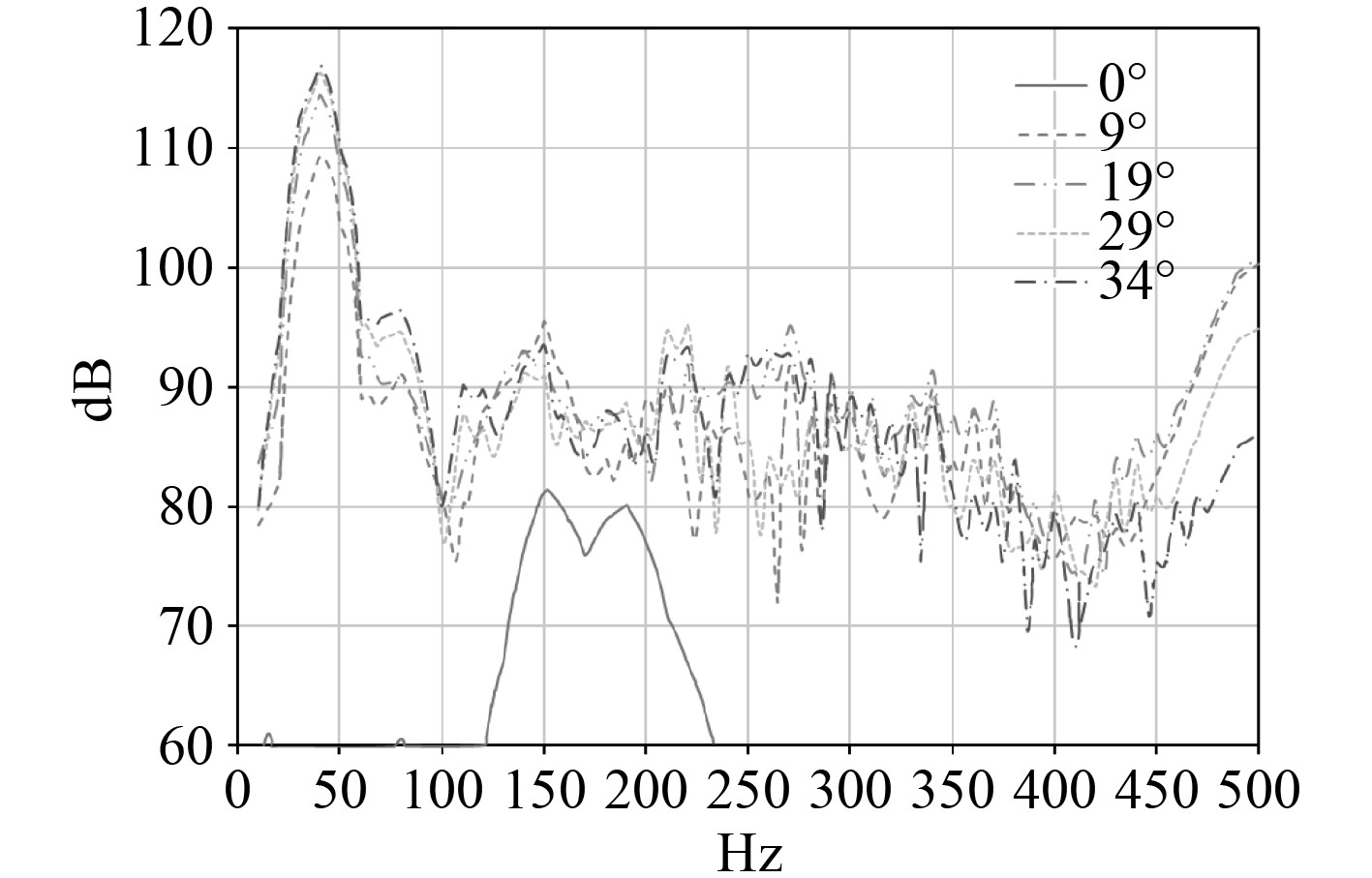
|
图 14 不同转舵角下辐射声功率图(转舵函数B) Fig. 14 Radiated sound power at different rudder angles ( rudder function B ) |
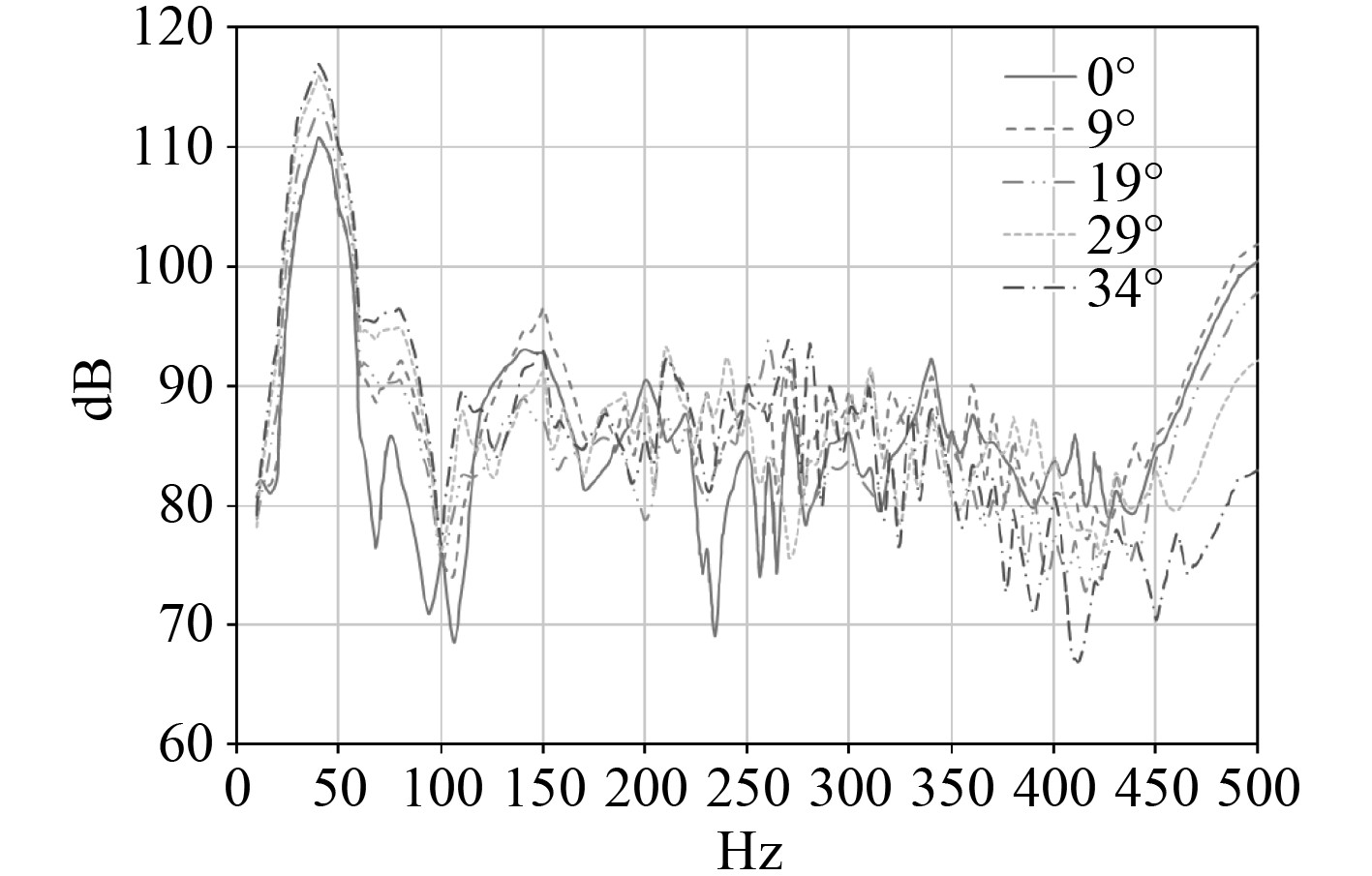
|
图 15 不同转舵角下辐射声功率图(转舵函数C) Fig. 15 Radiated sound power at different rudder angles ( rudder function C ) |
A,B,C等3种转动函数下,最大辐射声功率与角度关系如图16所示。可以看出,除0°之外,转动函数B在不同舵角的声功率与转动函数C的声功率基本一致,整体比转动函数A要大。因此,对于舵翼结构,在设计转舵函数时,匀速转舵产生的声辐射功率较低。
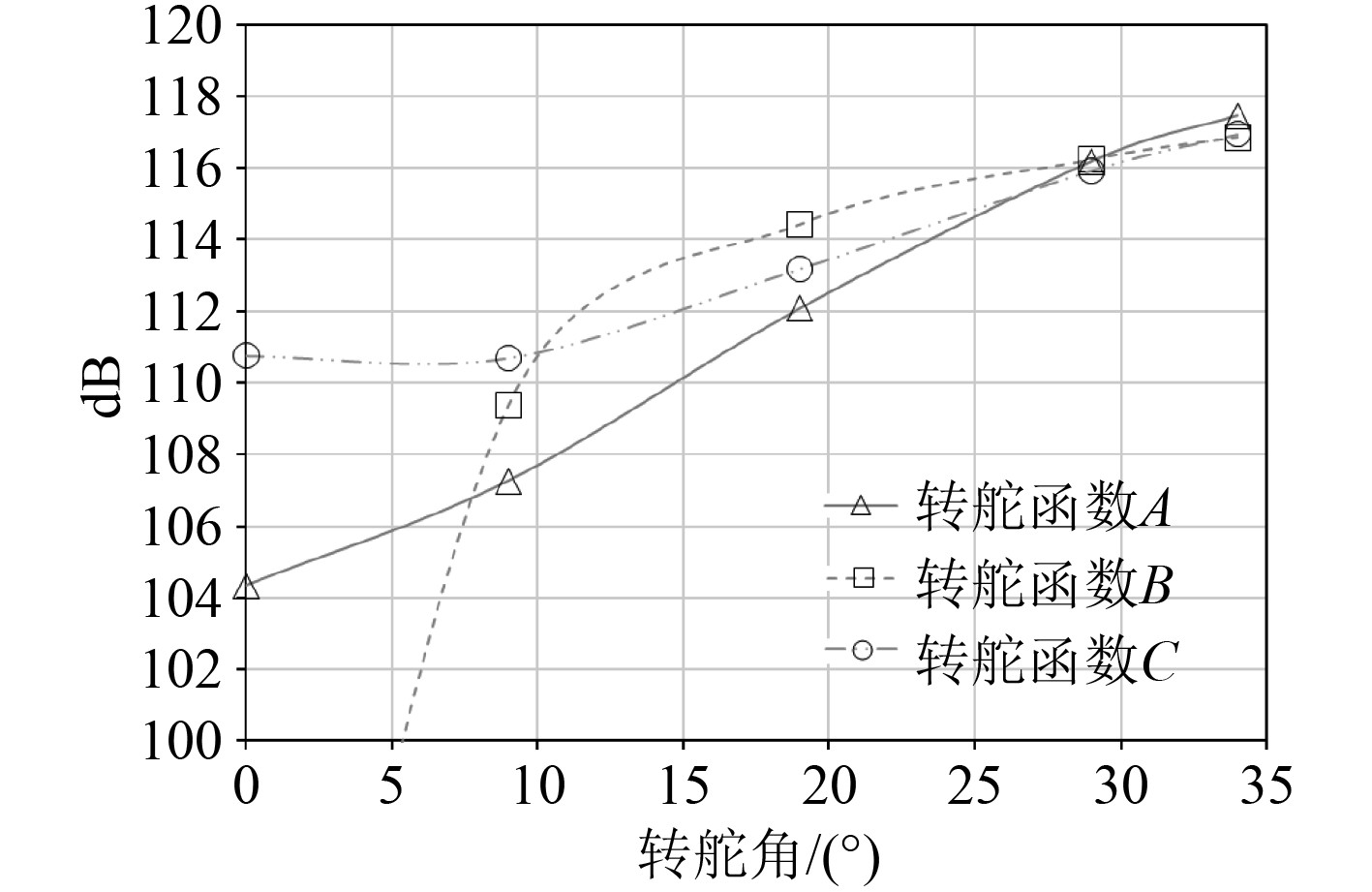
|
图 16 不同转舵函数下最大辐射声功率对比图 Fig. 16 Comparison of maximum radiated sound power under different rudder functions |
以3种转动函数A,B,C转舵时,舵在0°,9°,19°,29°和34°时刻的声辐射效率曲线如图17~图19所示。

|
图 17 不同转舵角下最声辐射效率对比图(转舵函数A) Fig. 17 Comparison of the most acoustic radiation efficiency at different rudder angles ( rudder function A ) |
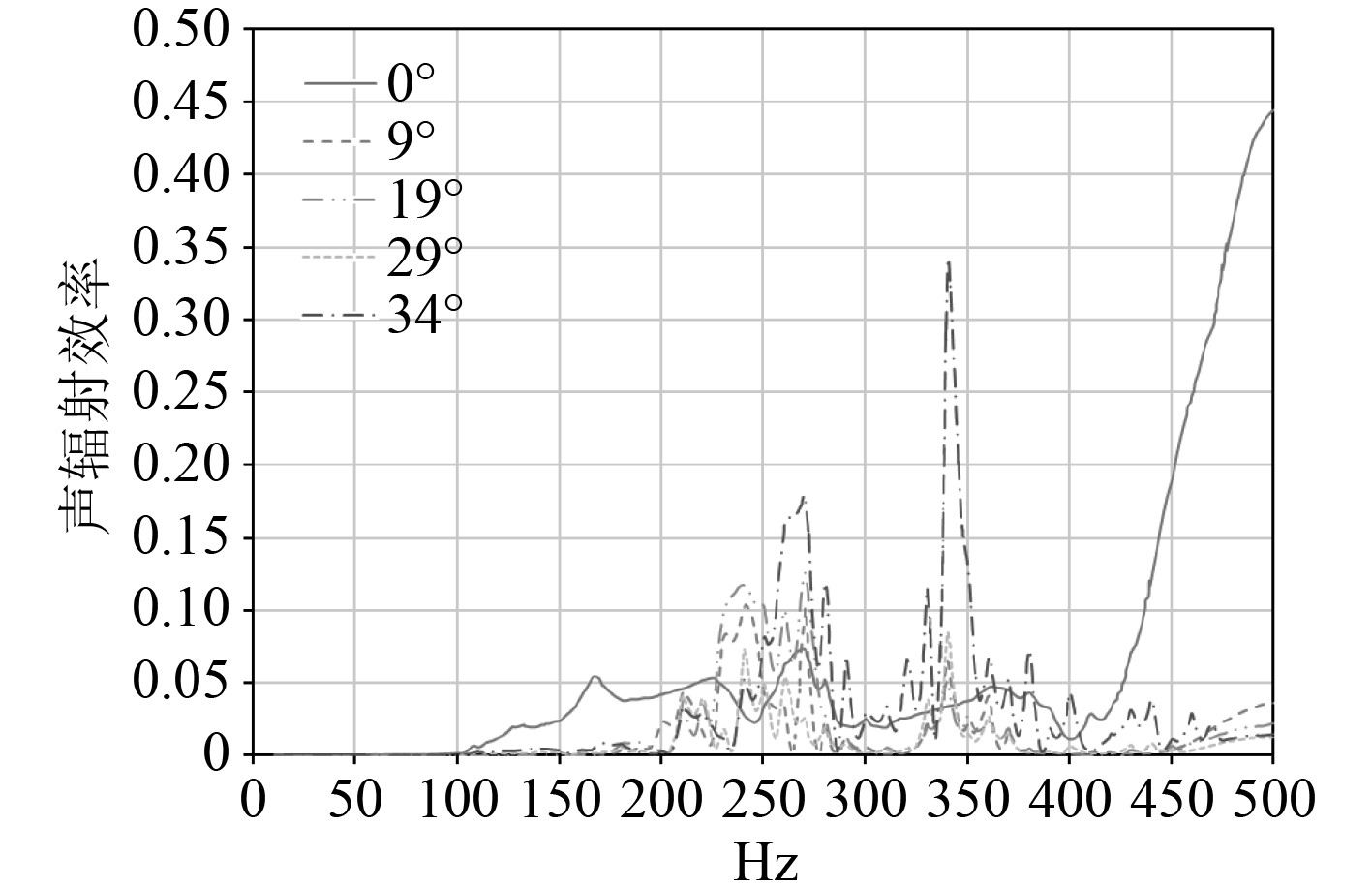
|
图 18 不同转舵角下最声辐射效率对比图(转舵函数B) Fig. 18 Comparison of the most acoustic radiation efficiency at different rudder angles ( rudder function B) |
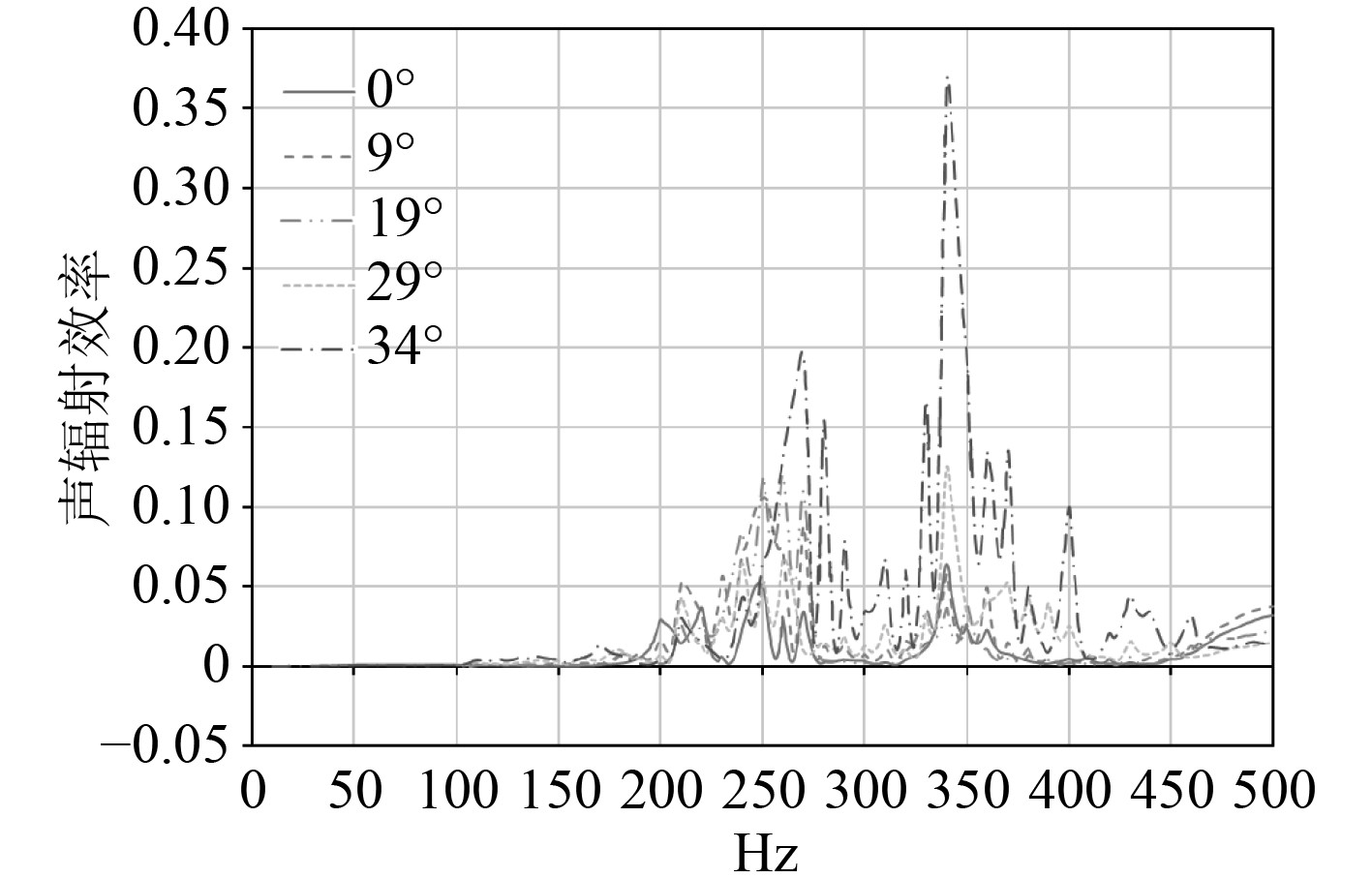
|
图 19 不同转舵角下最声辐射效率对比图(转舵函数C) Fig. 19 Comparison of the most acoustic radiation efficiency at different rudder angles ( rudder function C) |
在转动函数B中,0°和34°的声辐射效率较高,19°的较低;转动函数C中,34°的声辐射效率较高,0°的较低。其共同点都是转速较低,则声辐射效率较高,反之,转速较高,则声辐射效率较低。
舵在转动函数C下转角19°时声辐射功率最大,最大声辐射效率基本出现在340 Hz左右,其值约0.37。
在转动函数A中,由于其转速不变,各角度的声辐射效率基本一致。
3.2.3 声指向性分析舵1结构的指向性图的极坐标系规定如下:以俯视图(Z平面)为坐标平面,转轴为原点,右方向(X方向)为半径方向,逆时针方向(右手系)为转角方向。以舵转动19°为例,其声指向性极坐标系如图20所示。
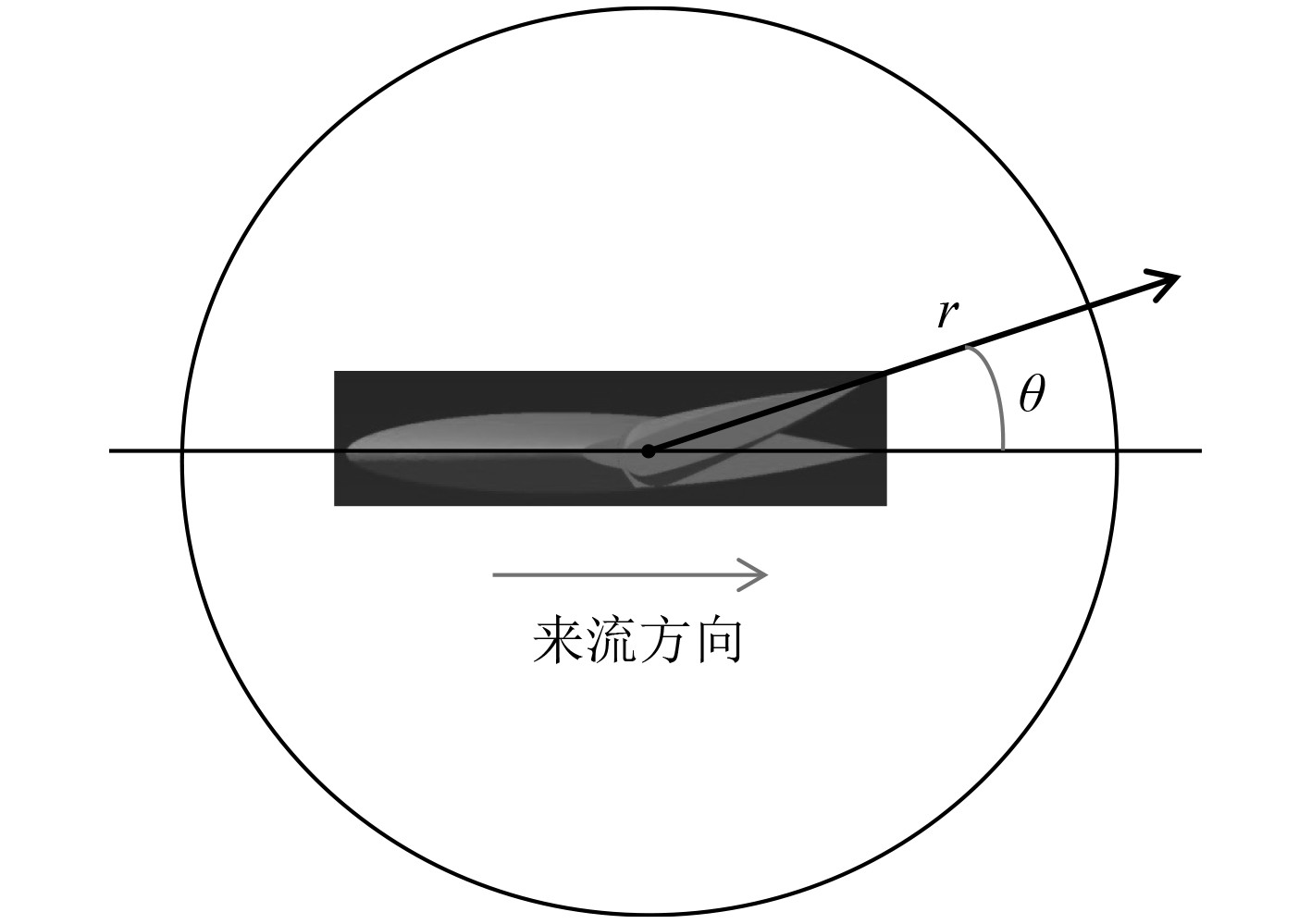
|
图 20 舵转动19°示意图 Fig. 20 Schematic diagram of the rudder rotation of 19° |
由于舵结构转动过程中声功率的最大值出现在40 Hz,因此分析舵40 Hz下的声指向性,图21为对应于转动函数A下4个角度的指向性图。
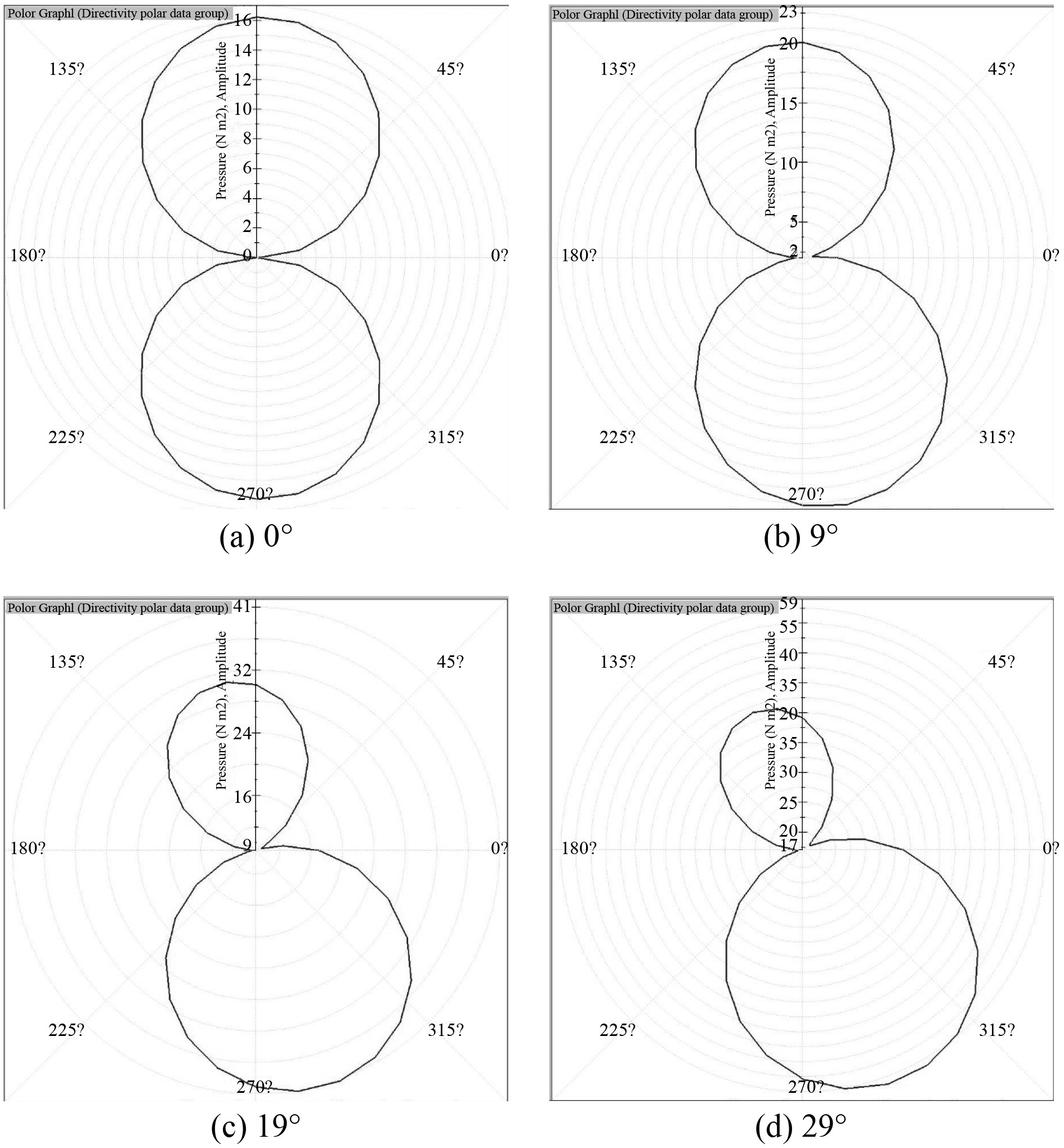
|
图 21 舵在转动函数A下0°,9°,19°,29°转角时的40 Hz声指向性(声压单位:Pa) Fig. 21 40 Hz acoustic directivity (sound pressure unit: Pa) at 0°, 9°, 19°, and 29° angles under the rotating function A |
从图中可以看出,在翼舵的2个翼面周围的流体中,声压呈现近似圆形的等值线分布,且随着舵的转动而移动,保持与翼舵面相切。若规定受到来流冲击的翼面为正面,另一面为背面,则随着角度的增大,正面和背面翼面产生的声压逐渐增大,对于3种不同的转舵函数而言,该规律是一致的。
4 结 语本文采用双向流固耦合方法计算方法,通过对舵翼结构在不同转舵速度函数的仿真计算,通过流固耦合计算得到如下结论:
1)在流固耦合计算的初期,结构响应较为剧烈,即结构加速度与应力均较大,但在后期流固耦合振动渐渐稳定,整体加速度与应力值均急剧减小;
2)翼舵结构在小范围运动下,对流场影响很小,即流速及压强分布保持稳定;
3)对比3种不同转舵函数下,不同工况的结构应力响应可以发现,随着转舵角度递增,结构应力及加速度也增大;而舵典型位置的加速度曲线图都有共同特征:舵转动初期,加速度波动较大,后趋于稳定声辐射效率总体上会随着声音频率的增大而增大。
通过声学分析可以得到如下结论:
1)3种转动函数的最大声功率基本出现在40 Hz时,且都随着角度的增大而增大;
2)40 Hz附近,转动函数C所对应的声功率整体上是最大的,转动函数B除0°时的声功率较小外,其余角度的声功率整体上比转动函数A大。因此匀速转舵产生的声辐射功率较低;
3)转速较低时,声辐射效率较高;转速较高时,声辐射效率较低;
4)40 Hz声压主要分布于舵的2个翼面,且随着舵的转动而转动,并随着角度的增大,背面压力相对于正面压力逐渐增大。
| [1] |
齐贺阳. 基于联合仿真水下航行器流激噪声的数值模拟[D]. 大连: 大连理工大学, 2020.
|
| [2] |
冯亮, 刘宝柱, 刘明. 潜艇流噪声与流激噪声有限元仿真建模研究[J]. 声学与电子工程, 2019(3): 20-23. |
| [3] |
屈铎, 张振海, 楼京俊. 不同舵角的舵翼结构涡量及流噪声特性分析[J]. 舰船科学技术, 2018, 40(11): 40-44. QU duo, ZHANG Zhenhai, LOU Jingjun. Analysis of vorticity and flow noise characteristics of rudder-wing under different rudder angles[J]. Ship Science and Technology, 2018, 40(11): 40-44. |
| [4] |
董仁义, 吴崇健, 张京伟. 基于Lilley宽带声源模型的舵叶流噪声数值模拟研究[J]. 船海工程, 2009, 38(5): 24-26+31. DONG Renyi, WU Chongjian, ZHANG Jingwei. Study on numerical simulation of flow noise about rudder based on Lilley Broad-bound noise source model[J]. Ship & Ocean Engineering, 2009, 38(5): 24-26+31. DOI:10.3963/j.issn.1671-7953.2009.05.006 |
| [5] |
张晓明. 基于Ansys Workbench的流固耦合室内供水管道振动特性研究[D]. 西南大学, 2018.
|
| [6] |
Dowell Earl H. Aero elasticity of plates and shells[M]. Noordhoff International Publishing, The Netherlands, 1975.
|
| [7] |
CHEN L H, SCHWEKERT D G. Sound radiation from an arbitrary body[J]. Journal of Acoustical Society of America, 1963, 35: 1626-1632. DOI:10.1121/1.1918770 |
| [8] |
BARON M L, MCCORMICK J M. Sound radiation from submerged cylindrical shells of finite length[J]. ASME. Trans. Ser., 1963, B87: 393-405. |
 2022, Vol. 44
2022, Vol. 44
