2. 武汉理工大学 交通与物流工程学院,湖北 武汉 430063
2. School of Transportation and Logistics Engineering, Wuhan University of Technology, Wuhan 430063, China
双体船因其具有优良的操纵性、横稳性、耐波性、快速性以及宽大的甲板面积等优点,在军用和民用方面均得到大量的应用[1-3]。船舶阻力与流场分析是进行双体船设计首要予以保证的,在工程设计中,计算流体力学是研究船舶阻力等水动力学特性的一个重要方法[4-5]。国内外学者也进行了一系列研究,其中包含双体船在不同负载条件下的船模水池实验分析、基于米切尔Michell瘦船理论的一种小水线面双体船SWATH兴波阻力分析,基于CFD的穿浪双体船耐波性预报、影响双体船阻力计算的流场CFD因素探讨等[6-9]。通过调研文献可知,如何准确计算船舶黏性流场、自由液面处理方法及流场网格处理技术仍是船舶阻力计算的重点。本文采用CFD数值仿真法,分析双体船在波浪中运动的状况,并实验对比模拟的准确性。
1 控制方程与自由液面法本文主要分析双体船运动阻力与流场特性,船舶在运动过程中包含可压缩的空气与不可压缩水,为混合两相流场变化。因此在进行船体运动流场数值分析时,采用能计算流体黏性效应的雷诺平均Navier-Stokes方程,其中RANS 方程包括连续方程与动量方程,两方程可表示为[10-11]:
| $ \left\{ \begin{gathered} \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho v) = 0,\\ \frac{\partial }{{\partial t}}(\rho v) + \nabla \cdot (\rho {v^2}) = - \nabla p + \nabla \cdot \tau + \rho g + F 。\\ \end{gathered} \right. $ | (1) |
式中:
式(1)中的剪应力
| $ \tau = \mu \left[ {(\nabla v + \nabla {v^T}) - \frac{2}{3}(\nabla \cdot v)I} \right]。$ | (2) |
式中:
由于双体船是在含有空气与水2种介质的流场中运动,其自由液面变化将对船体阻力及运动姿态造成影响,因此在数值计算过程中应用流体自由液面法(VOF)来处理该运动问题。VOF方法是将流场计算区域划分成多个网格区域,并对各个区域定义出二相流场函数,此函数值介于0~1之间,代表每个区域内2种介质的比例,其方程可表示为:
| $ \frac{{\partial {\alpha _q}}}{{\partial t}} + v \cdot \nabla {\alpha _q} = 0。$ | (3) |
式中:
在应用VOF方法处理自由液面问题时,首先定义计算区域流场的自由液面条件为
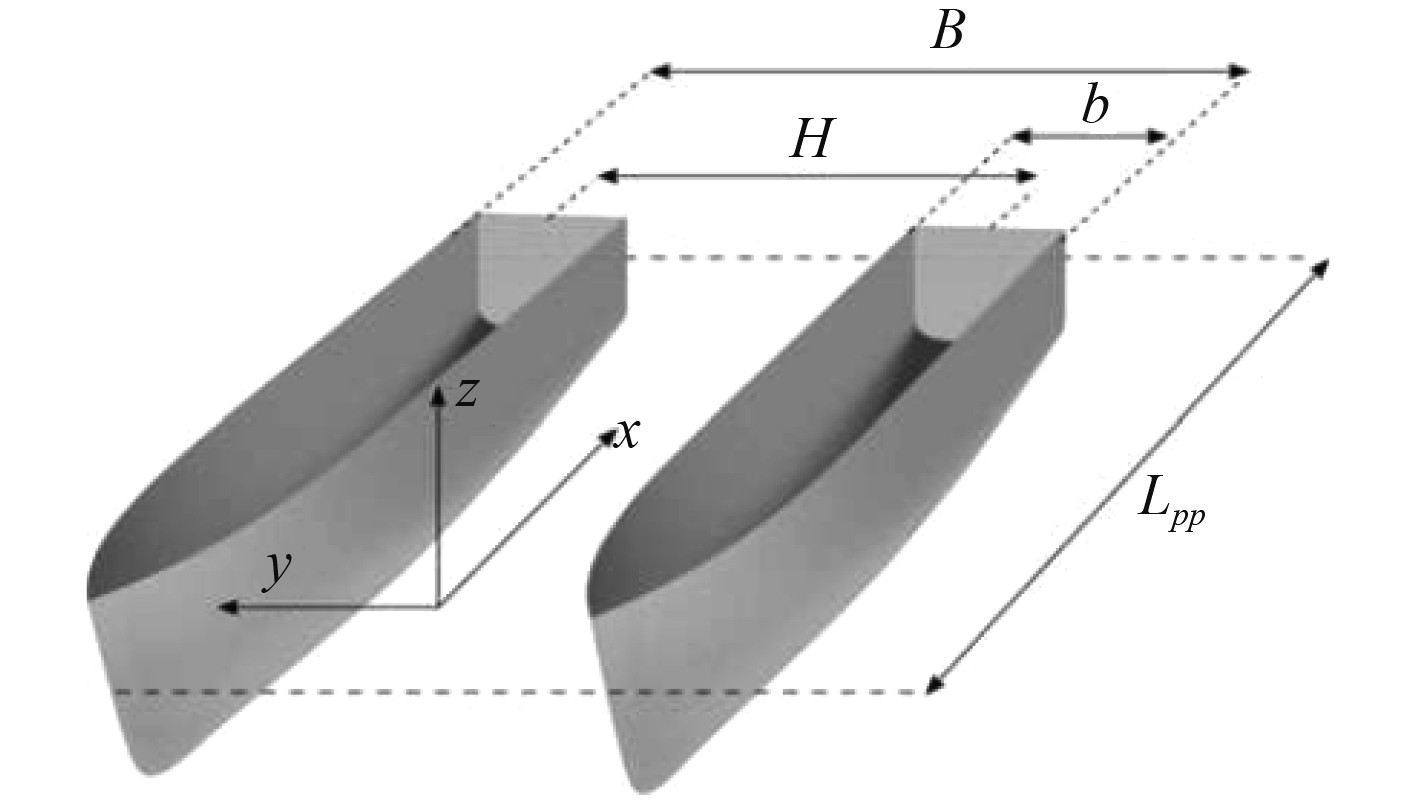
双体船模型如图1所示。其主要尺寸船长Lpp=3.00 m、船宽B=0.94 m、单船体船宽b = 0.24 m、吃水T=0.15 m,排水量为0.087 t,3种船体间距变化H/Lpp分别为0.167,0.233与0.300。船体运动流场数值计算过程中,将同时以前述3种船体间距变化及傅汝德数Fr= 0.25~0.75的不同流场速度进行数值计算,以探讨不同船体间距变化对其运动流场的影响。采用Broglia等[12]所发表的双体船模型阻力实验结果与本文的数值仿真结果进行比较,进而验证数值模拟方法对双体船运动阻力计算的准确性。
|
图 1 双体船模型 Fig. 1 Model of catamaran |
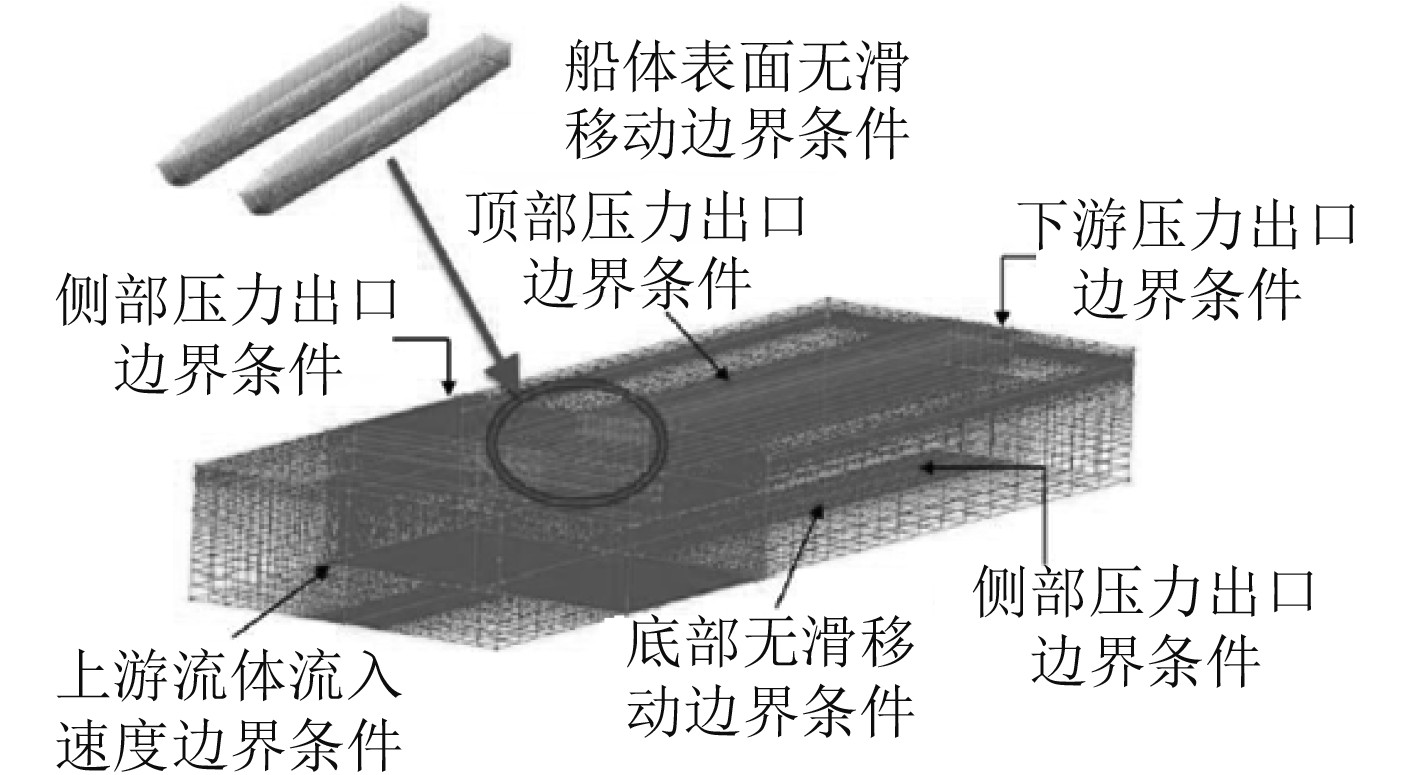
模型网格划分及其边界条件设置如图2所示。考虑到计算区域两侧与底部边界条件对船体周围流场的影响,为同时达到减少网格数量及边界条件对船体流场干扰的目标,计算区域长度设置为6倍船长、宽度为11倍船宽、计算区域自由液面至底部距离为10倍船体吃水高度,自由液面至计算区域顶部距离为1倍船体吃水高度。构建的相对运动流场计算区域网格,分为包缚船体的网格区块及不包含船体的网格区块两部分,用于调整网格的品质,包缚船体的网格区块使用精密网格,不包含船体的网格区块则使用粗网格,以减少网格数量节省计算时间。此外,在相对运动计算区域边界条件设定上,顶部、下游边界及两侧边界均设为压力出口边界条件,上游边界配合流体相对运动速度与方向设定为流体入口边界条件,而船体表面与计算区域底部则设定为无滑移边界条件。
|
图 2 固定姿态模型网格划分及其边界条件设置 Fig. 2 Mesh generation and boundary condition setting of fixed attitude |
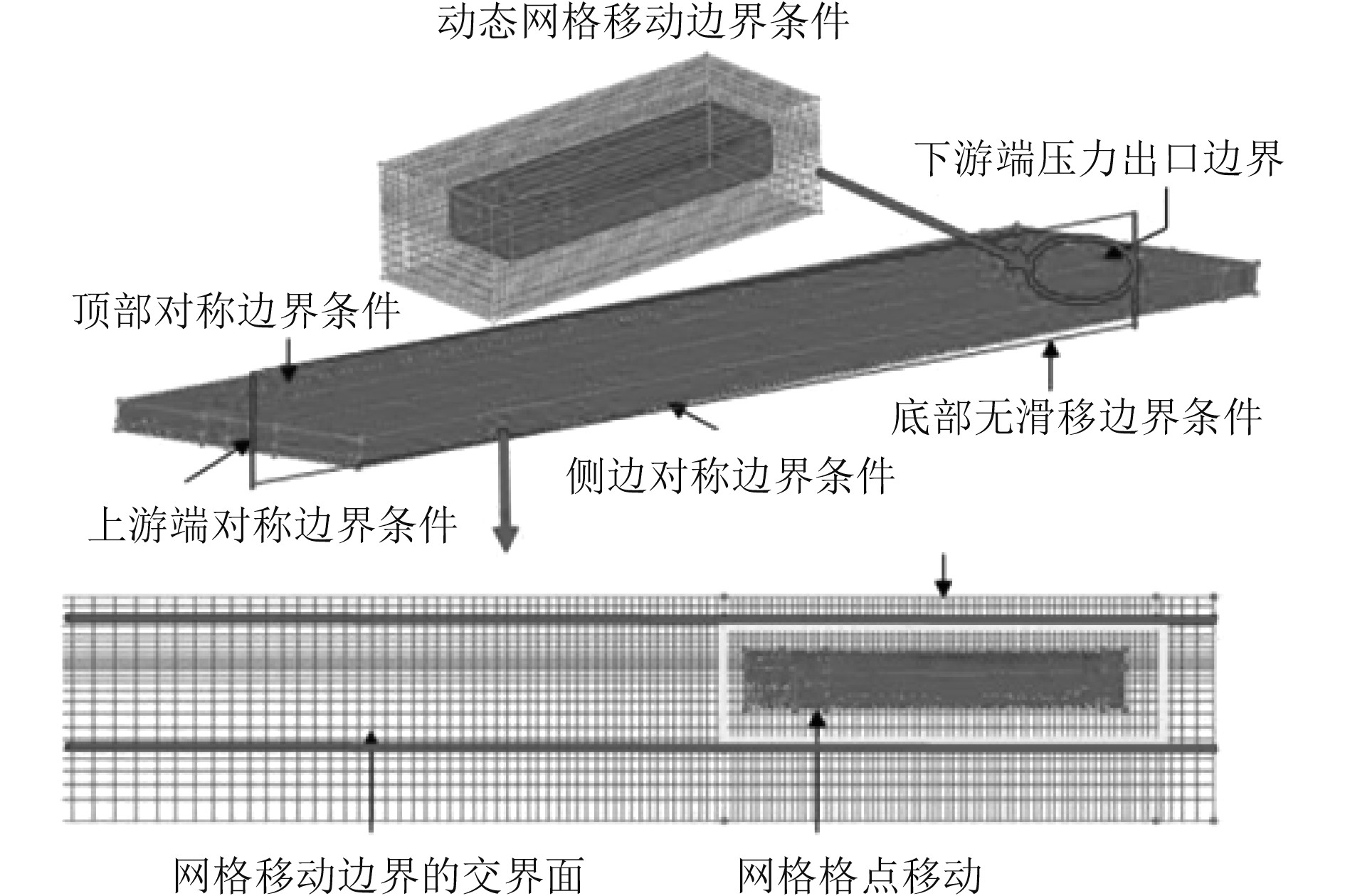
在进行双体船绝对运动流场计算时,采用网格滑移技术进行分析,将船体姿态固定,并以固定速度进行船体运动流场模拟,因此在计算区域尺寸大小的设置上,为减少计算区域边界与动态网格之间流场的交互作用影响,将计算区域宽度设定为40倍船宽,而长度则由于船体前进运动所需的移动距离,将其设定为46倍船长,自由液面至计算区域顶部的高度设定为3倍吃水。绝对运动流场计算区域网格,分为船体运动网格区块、船体重建网格区块以及外计算区域网格区块3个部分,其中在船体运动网格区块以一个网格区块包缚船体,有利于调整网格数量与品质;而船体重建网格区块,则是为了满足在模拟船体前进时能在此区域进行网格压缩及拉伸。此外,上述二者以外的区域则为完全静止的外计算区域网格区块,此区域可配合其他网格区块完成船体绝对运动流场计算。在计算区域边界条件设定方面,因为在绝对运动流场上游边界并不产生相对入流,故设定为对称边界条件。而船体在运动时由于对计算区域顶部边界影响较小,因此将其设定为对称边界条件。另外计算区域左右两侧也设定为对称边界条件,计算区域底部设定为无滑移边界条件,下游端边界则设定为压力出口边界条件,其整体计算区域边界条件设定如图3所示。
|
图 3 绝对运动模型网格划分及其边界条件设置 Fig. 3 Mesh generation and boundary condition setting of absolute motion |
双体船总阻力分为摩擦阻力、黏性阻力及兴波阻力,其中黏性阻力与雷诺数相关、兴波阻力与傅汝德数有关,两者合称为剩余阻力。由船体周围自由液面高度随不同傅汝德数产生的变化,可判断船型及航速对兴波阻力的影响。图4为双体船在傅汝德数Fr=0.50,Fr=0.75情况下,配合不同船体间距H/L=0.167,H/L=0.233及H/L=0.300所得到的船体周围自由液面高度变化。从图中可以看出双体船在进行水平运动时,靠近船首2侧及船尾后方均有较高的自由液面陇起,即船首与船尾均出现散波波形特征,且在两船体之间会产生由2个独立船体衍生出的散波组合波形,此组合波形也会造成自由液面陇起。另外,在船体外侧与两船体间所形成的陇起波峰外型像英文字母W,该波形具有随船体间距或傅汝德数增加而逐渐变大的趋势。比较各个算例的 W波形也可发现,在船速不变、船体间距变大的情况下,W波形的中间自由液面陇起位置,有向船尾方向延伸的趋势,这将迫使两船体间所形成自由液面的波谷位置逐渐移动到船尾处。由此可知双体船的两船体间距将对其周围自由液面波形变化产生极大的影响,并直接影响其航行时所受的兴波大小。

|
图 4 双体船周围自由液面高度变化仿真结果 Fig. 4 Simulation results of free liquid level change around catamaran |
数值仿真进行结果验证,参考Broglia 等[12]所提供的实验数据资料。图5为双体船在傅汝德数Fr= 0.50,Fr=0.75情况下,配合不同船体间距H/L=0.167,H/L = 0.233及H/L=0.300 所得到的船体周围自由液面高度变化的实验结果。可以看出,自由液面高度变化趋势与数值仿真结果相一致。

|
图 5
双体船周围自由液面高度变化实验结果
Fig. 5
|
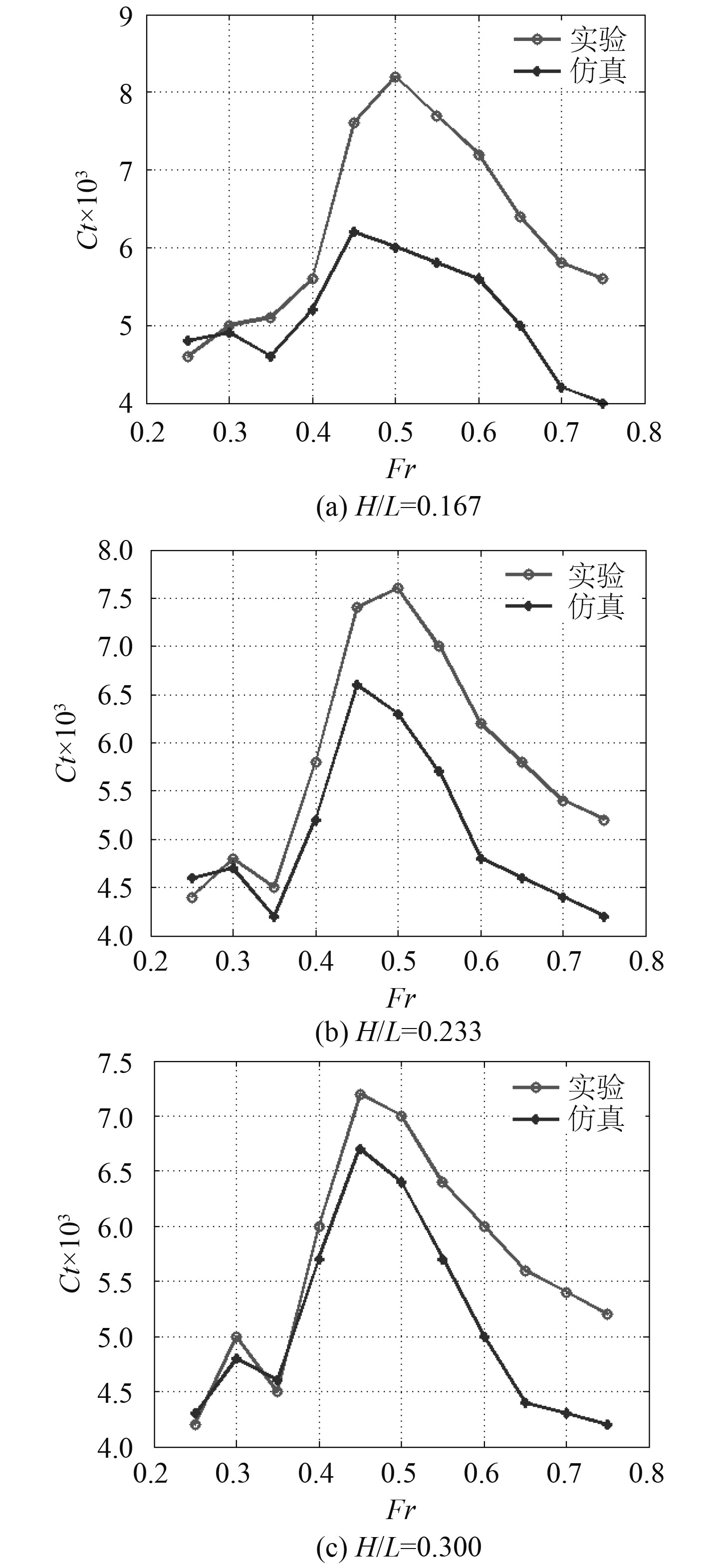
文献[12]中的实验数据是以船体总阻力系数呈现,本文数值仿真结果与实验值对比如图6所示。可以看出,在不同的船体间距变化下,两者的阻力系数变化趋势相近,但当傅汝德数变大时,数值模拟与实验结果的差异逐渐增大,此状况在船体间距较小时尤其明显。原因可能是仿真过程中采用相对运动计算模式,并未采用六自由度计算模式。从图4也可看出,当两船体间距越小、傅汝德数越大,造成的自由液面陇起与凹陷也越大,这表示船体纵摇与起伏运动非常明显,因此在目前计算模式下船舶阻力会产生较大差异。
|
图 6 总阻力系数随傅汝德数变化对比结果 Fig. 6 Comparison of total resistance coefficient with Froude number |
船体固定姿态绝对运动流场计算是模拟船体在设定船速、固定航向上的平移运动,此运动模式与船体实际运动方式相近。为进行该运动模式计算,将应用滑移网格解决包缚船体的网格区块因随船体移动而与外部流场网格所产生的网格交错问题。滑移网格可控制指定的网格区块在特定方向进行运动,而此网格区块在运动过程中,其邻近的结构性网格可进行重建与移除,而不会改变流场计算域大小或增加网格数。除上述优点外,应用此种网格模式处理二相流问题时,可保持较佳的自由液面高变化连续性。
图7为在绝对运动计算模式下,船体间距H/L= 0.167的双体船在静水中以速度3.798 m/s进行水平动态运动时,船体周围自由液面高度与流场网格变化,其中图7左半部分为船体周围流场波形变化,右半部分为船体在不同模拟时刻的位移量变化与利用滑移网格处理后的船体网格区块外流场网格变化。从图中可看出,在船体刚开始运动时(t = 0.25 s),船体周围的波形变化尚未稳定,而当运动时间至t = 1.5 s时,船体周围流场波形已逐渐稳定。

|
图 7 绝对运动状态下船体流场波形与网格变化 Fig. 7 Waveform and grid change of ship flow field in absolute motion |
船体在水面上运动不可能维持固定姿态,在其运动过程中,将随着船速增大而产生明显的俯仰与起伏运动,为使船舶运动的数值模拟更接近实况,在完成固定船体姿态的相对运动及绝对运动计算模式比较与验证后,进一步增加船体六自由度计算模式,探讨俯仰与起伏运动对船舶运动阻力的影响。图8分别为傅汝德数Fr = 0.25,Fr = 0.50时的双体船(船体间距 H/L= 0.167)在不同模拟时刻船体周围自由液面变化情况,由于此计算模式船体姿态并不固定,因此船体本身运动会使其周围自由液面高度呈现周期性的变化。

|
图 8 船体俯仰与起伏绝对运动下的自由液面变化 Fig. 8 Free liquid level change under absolute motion of hull pitching and heave |
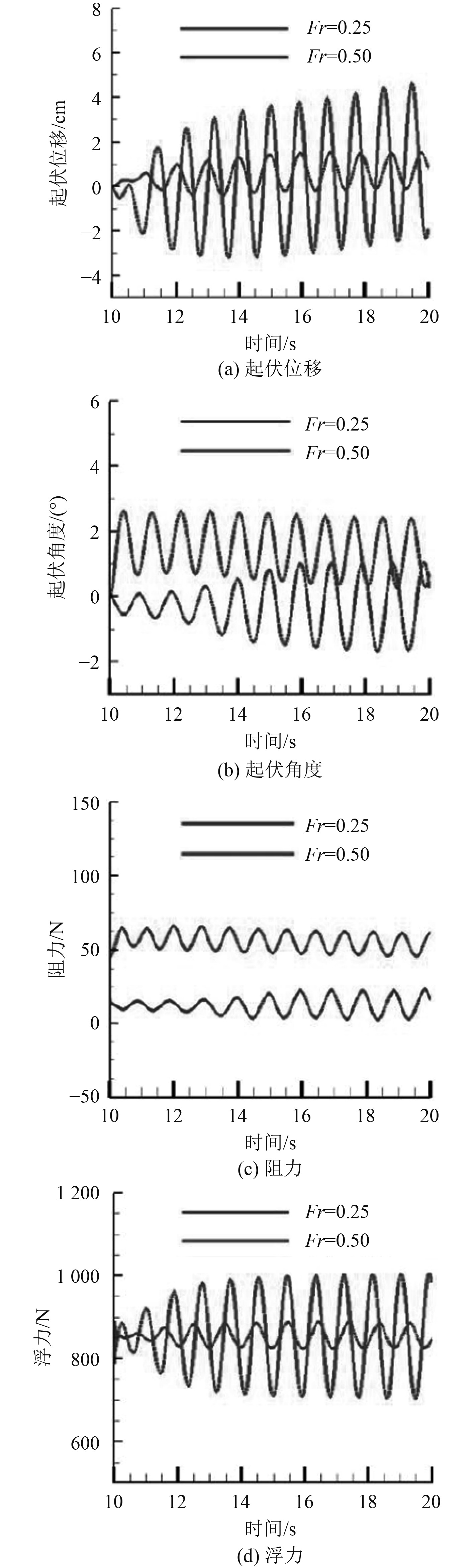
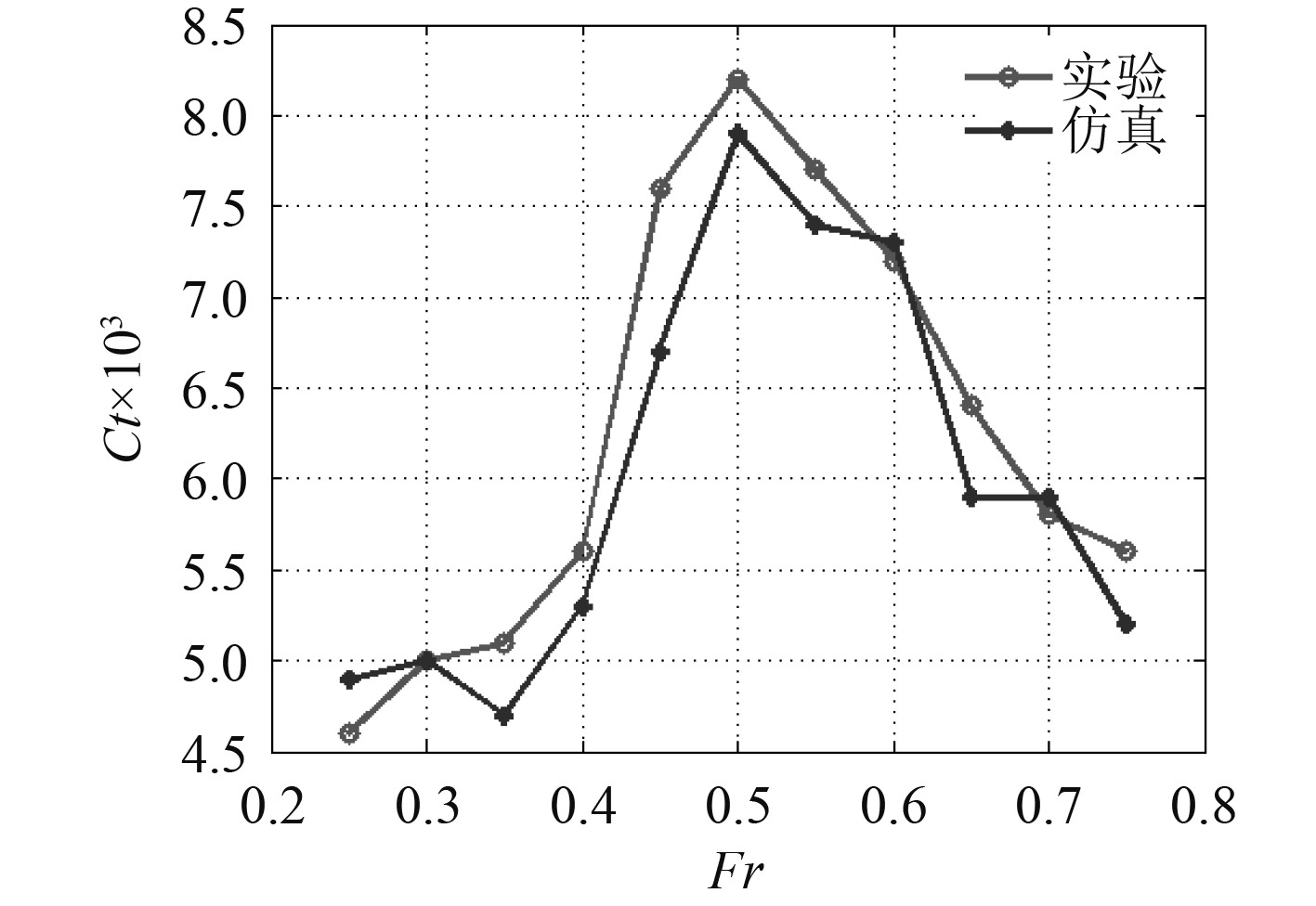
图9为不同傅汝德数下的俯仰起伏参数变化,其中图9(a)和图9(b)为双体船在不同航速与不同模拟时刻的俯仰与起伏变化。从图中可看出,傅汝德数越大则船体的起伏位移与俯仰角越大,并呈周期性变化趋势。在傅汝德数较大的模拟算例,其船体起伏与俯仰周期较小、频率较快。图9(c)和图9(d)为双体船在不同航速与不同模拟时刻的阻力与浮力变化,而此阻力变化趋势及周期性与图9(a)和图9(b)的结果相呼应,由图9(c)和图9(d)可以看出,在模拟过程中船体起伏与俯仰均会造成浮力变化,当浮力大于船体重力时,船体将产生向上加速度,而当船体所受重力大于浮力时,船体将产生向下加速度,此现象均说明数值模拟结果与船舶运动物理特性相吻合。另外,为验证应用此计算模式的准确性,将船体间距H/L = 0.167时的数值模拟与实验阻力值进行比较,如图10所示。可以看出,采用船体仰俯、起伏相对运动流场模拟结果与实验结果吻合度较好,当傅汝德数变大时,该计算模式所得的阻力系数比相对运动计算模式所得的阻力系数更接近实验值。
|
图 9 不同傅汝德数下的俯仰起伏参数变化 Fig. 9 Changes of pitch fluctuation parameters under different Froude number |
|
图 10 总阻力系数随傅汝德数变化对比结果 Fig. 10 Comparison of total resistance coefficient with Froude number |
为探讨双体船在波浪中运动的船体阻力变化,构建数值造波水槽,以研究波浪对船体作用的物理机制。数值波浪水槽的构建,除了在上游边界须能正确造出模拟所需的水波波形外,下游边界则通常须具备良好的消波能力,方能避免来自下游边界的反射波干扰。因此在完成前述各项流场计算模式验证后,通过改变计算域上、下游边界条件的设定,进行船体受波浪作用的相对运动流场计算模式测试。船体的运动环境为水深 1.50 m,水波特性为波长 1.50 m、振幅 0.10 m、周期 1.387 s 的深水波。前述上、下游边界条件设定为上游端以Stokes 三阶波的速度场加上船体对流体的相对运动速度为入流边界条件,模拟固定速度的船体顶浪运动,下游端则采延伸疏网格配置,配合深水域及压力出口的边界条件设定,以达消波功能。模拟算例分3阶段进行,其中第1阶段(0~2000Δt;Δt= 0.01 s)为船体固定不动,进行相对运动流场模拟,待观察船体向上作用力(浮力)接近船体重量时,再进行第2阶段(2000Δt~4000Δt;Δt= 0.005 s)含括船体起伏与俯仰运动的模拟计算,然后在4000Δt (Δt = 0.0025 s)之后,在上游边界导入前进水波以进行第3阶段的船体在波浪中运动的数值模拟。
图11为进行起伏与俯仰运动的双体船在有相对入流无波浪与有波浪无相对入流测试条件的流场对比图。由图11右半部分的模拟结果可知,随着模拟时间增加,上游端进入的水波逐渐接近船体,使计算域自由液面在不同模拟时刻呈现不同的变化,而相对于右半部分的模拟结果,左图不含波浪运动的流场模拟,则只有在船体周围附近才能观察到自由液面变化。从图中也可发现,包括波浪运动的模拟算例所造成的船体阻力变化幅度比不包括波浪运动的模拟算例大,其原因是在包含波浪运动的模拟算例中,自由液面下的流体分子在受波浪影响后,将使其在波浪前进的方向出现往复运动产生周期性的变化所致。在不包含波浪运动的模拟算例中,由于仅有相对入流的作用,而有较小的阻力变化。

|
图 11 船体受波浪影响下的自由液面变化 Fig. 11 Free liquid level change of ship hull affected by waves |
本文所构建的双体船数值模拟流场分析模式,能有效分析船体几何变化对船舶流场及阻力的影响。双体船的两船体间距对其周围自由液面波形变化产生极大的影响,并直接影响其航行时所受的兴波阻力大小。运用船体六自由度计算模式可接近船舶运动实况,加入波浪运动后船体阻力变化的数值计算结果接近实船的阻力测量值,验证了该方法的有效性。本文成果可为未来船型开发设计与流场阻力预测提供参考。
| [1] |
冯萌萌. 基于CFD的小水线面双体船多目标优化[D]. 大连: 大连理工大学, 2016.
|
| [2] |
HAASE M. Energy-efficient large medium-speed catamarans: Hull form design by full-scale CFD simulations[J]. Ship Technology Research, 2016, 63(2): 133-134. DOI:10.1080/09377255.2016.1208974 |
| [3] |
熊文海, 周振路, 陈力. 基于细长体理论的小水线面双体船操纵性预报[J]. 中国航海, 2007(4): 9-12. XIONG W H, ZHOU Z R, CHEN L. Maneuverability forecast of SWATH based on slender body theory[J]. China Navigation, 2007(4): 9-12. DOI:10.3969/j.issn.1000-4653.2007.04.003 |
| [4] |
NAJAFI A, ALIMIRZAZADEH S, SEIF M S. RANS simulation of interceptor effect on hydrodynamic coefficients of longitudinal equations of motion of planing catamarans[J]. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 2014, 37(4): 1-19. |
| [5] |
王晓燕, 李婷婷. 基于CFD的双体船航行阻力研究[J]. 舰船科学技术, 2016, 38(10): 4-6. WANG X Y, LI T T. Research on navigation resistance of catamaran based on CFD[J]. Ship Science and Technology, 2016, 38(10): 4-6. |
| [6] |
HAJIABADI A, SHAFAGHAT R, MOGHADAM H K. A study into the effect of loading conditions on the resistance of asymmetric high-speed catamaran based on experimental tests[J]. Alexandria Engineering Journal, 2017, 57(4): 1713-1720. |
| [7] |
刘军, 易宏. 小水线面双体船兴波阻力特性研究[J]. 武汉理工大学学报:交通科学与工程版, 2010, 34(1): 117-121. LIU J, YI H. Study on wave-making resistance characteristics of small waterplane catamaran[J]. Journal of Wuhan University of Technology:Traffic Science and Engineering Edition, 2010, 34(1): 117-121. |
| [8] |
胡晓峰. 基于CFD的穿浪双体船耐波性预报技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
|
| [9] |
邓锐, 黄德波, 于雷, 等. 影响双体船阻力计算的流场CFD因素探讨[J]. 哈尔滨工程大学学报, 2011, 32(2): 141-147. DENG R, HUANG D B, YU L, etal. Discussion on CFD factors affecting the calculation of catamaran resistance[J]. Journal of Harbin Engineering University, 2011, 32(2): 141-147. DOI:10.3969/j.issn.1006-7043.2011.02.002 |
| [10] |
COFFEY T, MCMULLAN R J, KELLEY C T, et al. Globally convergent algorithms for nonsmooth nonlinear equations in computational fluid dynamics[J]. Journal of Computational & Applied Mathematics, 2001, 152(2): 69-81. |
| [11] |
王福军. 计算流体动力学分析-CFD软件原理与应用[M]. 清华大学出版社, 2004.
|
| [12] |
BROGLIA R, JACOB B, ZAGHI S, et al. Experimental investigation of interference effects for high-speed catamarans[J]. Ocean Engineering, 2014, 76(12): 75-85. |
 2022, Vol. 44
2022, Vol. 44
