2. 中国船舶集团有限公司系统工程研究,北京 100094
2. Systems Engineering Research Institute, CSSC, Beijing 100094, China
水下航行体是海洋工程领域的重要装备,航行体在水下直航时受到的阻力对其水动力特性有较大影响[1]。现有研究多考虑光滑表面航行体的动力学特性,少有对粗糙表面水下航行体的直接数值分析研究。本文基于SUBOFF水下航行体模型,对光滑表面及粗糙表面水下航行体的水动力特性开展数值分析。利用计算流体动力学方法对光滑SUBOFF模型进行数值计算,并与美国的Taylor水池试验结果对比,验证计算方法的有效性。基于验证有效的数值方法分析水下航行体直航时的阻力特性,同时计算不同航速下表面粗糙航行体阻力,并与光滑SUBOFF模型阻力进行对比分析粗糙表面模型的阻力特性。
1 计算模型与方法 1.1 几何模型计算模型选用SUBOFF标准模型,即缩尺比为24,艇长4.356 m,计算模型尺寸如图1所示。其中突出体宽为5 mm,考虑凸出高为2 mm以及1 mm两种情况。为考虑航行体光滑表面与粗糙表面的差异,在对表面光滑航行体进行水下直航阻力计算,并参考试验结果,验证航行体水下直航计算方法的有效性。
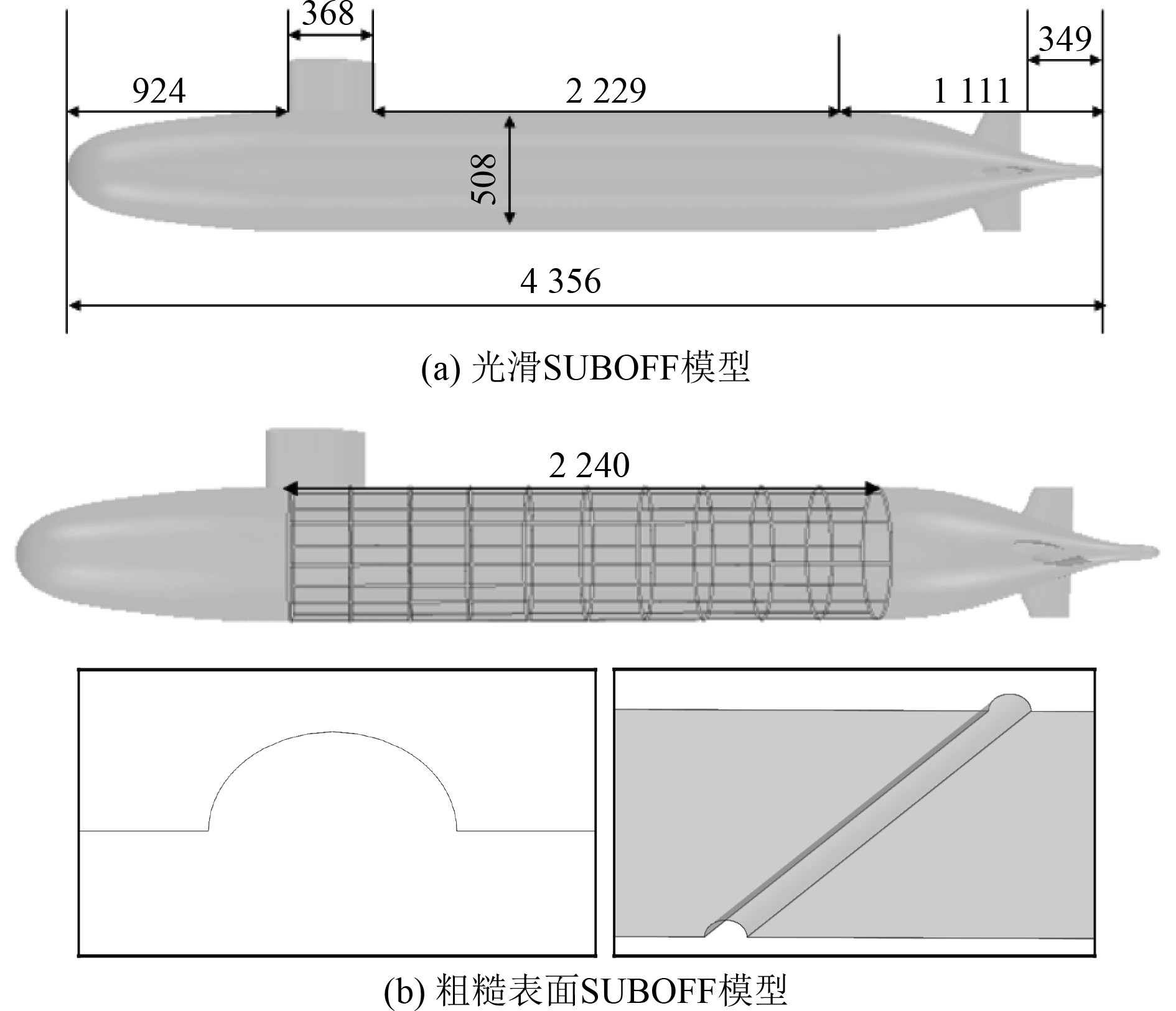
|
图 1 光滑和粗糙表面SUBOFF模型几何示意图 Fig. 1 SUBOFF model with smooth and rough surface |
航行体水下直航时处于高雷诺数运动状态,属于不可压缩流体问题,应满足一般粘性控制Navier-Stokes方程。由于水下航行体问题涉及高雷诺数,因此本系统还需满足湍流方程。这些均属于流体控制方程[2],所用到的方程如下:
1)质量守恒方程
航行体水下直航遵循质量守恒,结合欧拉描述的粘性不可压缩流体所得方程如下:
| $ \dfrac{{\partial \rho }}{{\partial t}} + \dfrac{{\partial (\rho u)}}{{\partial x}} + \dfrac{{\partial (\rho v)}}{{\partial y}} + \dfrac{{\partial (\rho w)}}{{\partial z}} = 0 。$ | (1) |
其中:ρ为流体的密度;t为时间;u,v与w为速度矢量在笛卡尔坐标系中3个坐标方向上的分量大小。
2)动量守恒方程
航行体水下直航时应满足牛顿第二定律,所用到动量方程结合流体力学可描述为流体微团动量与力的对应关系。结合水下直航时的流体流动特性,可以推导得到流体质点在三维笛卡尔坐标系 x,y,z 轴上的动量守恒方程为:
| $\begin{aligned}[b] & {\dfrac{{\partial (\rho u)}}{{\partial t}} + \nabla \cdot (\rho u\vec u) = - \dfrac{{\partial \rho }}{{\partial x}} + \dfrac{{\partial {\tau _{xx}}}}{{\partial x}} + \dfrac{{\partial {\tau _{yx}}}}{{\partial y}} + \dfrac{{\partial {\tau _{zx}}}}{{\partial z}} + {F_x}} ,\\ & {\dfrac{{\partial (\rho v)}}{{\partial t}} + \nabla \cdot (\rho v\vec u) = - \dfrac{{\partial \rho }}{{\partial y}} + \dfrac{{\partial {\tau _{xy}}}}{{\partial x}} + \dfrac{{\partial {\tau _{yy}}}}{{\partial y}} + \dfrac{{\partial {\tau _{zy}}}}{{\partial z}} + {F_y}} ,\\ & {\dfrac{{\partial (\rho w)}}{{\partial t}} + \nabla \cdot (\rho w\vec u) = - \dfrac{{\partial \rho }}{{\partial z}} + \dfrac{{\partial {\tau _{xz}}}}{{\partial x}} + \dfrac{{\partial {\tau _{yz}}}}{{\partial y}} + \dfrac{{\partial {\tau _{zz}}}}{{\partial z}} + {F_z}} 。\end{aligned} $ | (2) |
3)湍流模型
在考虑水下航行体阻力计算时,由于该问题涉及高雷诺数,故需选取合适的湍流模型进行后续研究,结合前人研究选用k-ω湍流模型进求解,湍动能k和耗散率ω的输运方程如下:
| $ \begin{aligned} & {\dfrac{\partial }{{\partial t}}(\rho k) + \dfrac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \dfrac{\partial }{{\partial {x_j}}}\left( {{{{\varGamma }}_k}\dfrac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} + {S_k}} ,\\ & {\dfrac{\partial }{{\partial t}}(\rho \omega ) + \dfrac{\partial }{{\partial {x_i}}}\left( {\rho \omega {u_i}} \right) = \dfrac{\partial }{{\partial {x_j}}}\left( {{{{\varGamma }}_\omega }\dfrac{{\partial \omega }}{{\partial {x_j}}}} \right) + {G_\omega } - {Y_\omega } + {S_\omega }} 。\end{aligned} $ | (3) |
式中:Sk与Sω为自定义源;Gk为k的产生项;Gω为ω的产生项;ω为耗散率;Yk和Yω分别为k和ω的耗散;Γk和Γω为k和ω的有效扩散;k为湍动能。
1.3 计算模型根据计算模型的尺寸选择较为合适的计算域,数值模拟通过划分高质量网格进行参数的离散。其中,网格质量对计算结果的精确度、流场的捕捉影响很大。在计算几何的复杂流动现象时,网格划分是数值计算分析的重要步骤[3]。
本文的计算域设置为方形(见图2),航行体尾部流场尺寸约为2倍艇长,航行体艏部流场和四周流场尺寸设置为1倍艇长。在图2中,L表示为航行体艇长。计算域左侧设置为速度入口边界条件,给定一定的流速。航行体表面设置为壁面。流场右侧设置为压力出口,计算域其余位置设置为对称平面[4]。通过改变速度进口的不同流速来模拟航行体以不同航速直航。
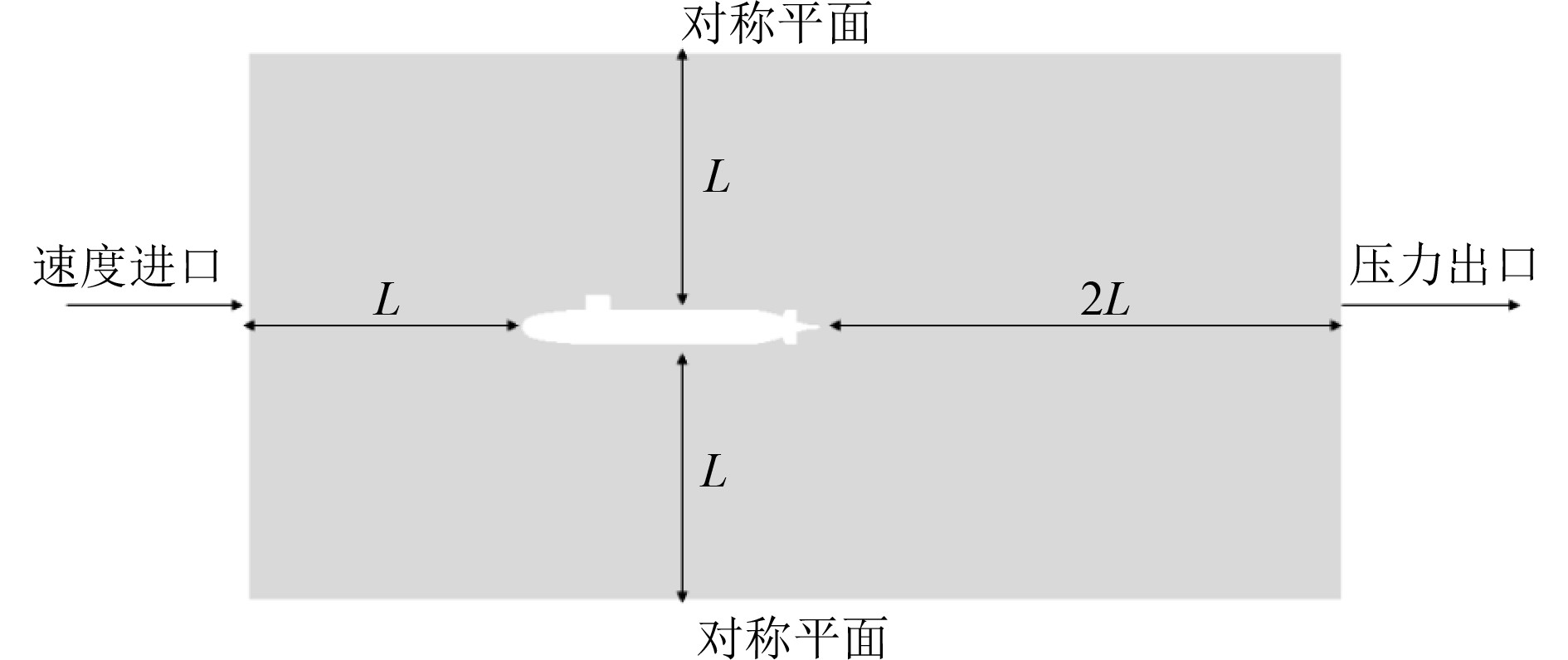
|
图 2 计算域示意图 Fig. 2 Computational domain |
为准确描述流场的流动细节,对主附体附近及其尾流等流动复杂区域的网格进行局部加密,采用SST k-ω湍流模型模拟粘性底层流动和湍流流场,本文采用壁面函数法来解决水下航行体壁面与流体的相互作用,选用全y+壁面函数,在划分边界层网格时,保证y+>30,以实现高保真数值模拟。
2 计算方法验证 2.1 SUBOFF标准模型阻力验证用切割体网格生成器生成整齐的非结构网格,并用棱柱层网格生成器生成所需的边界层网格,并对航行体表面及计算域表面网格进行加密。对航行体四周网格进行局部加密,并对围壳、尾部十字舵再次进行网格加密,保证计算域网格过渡均匀,以提高计算效率及计算精度。生成网格256万,如图3所示。
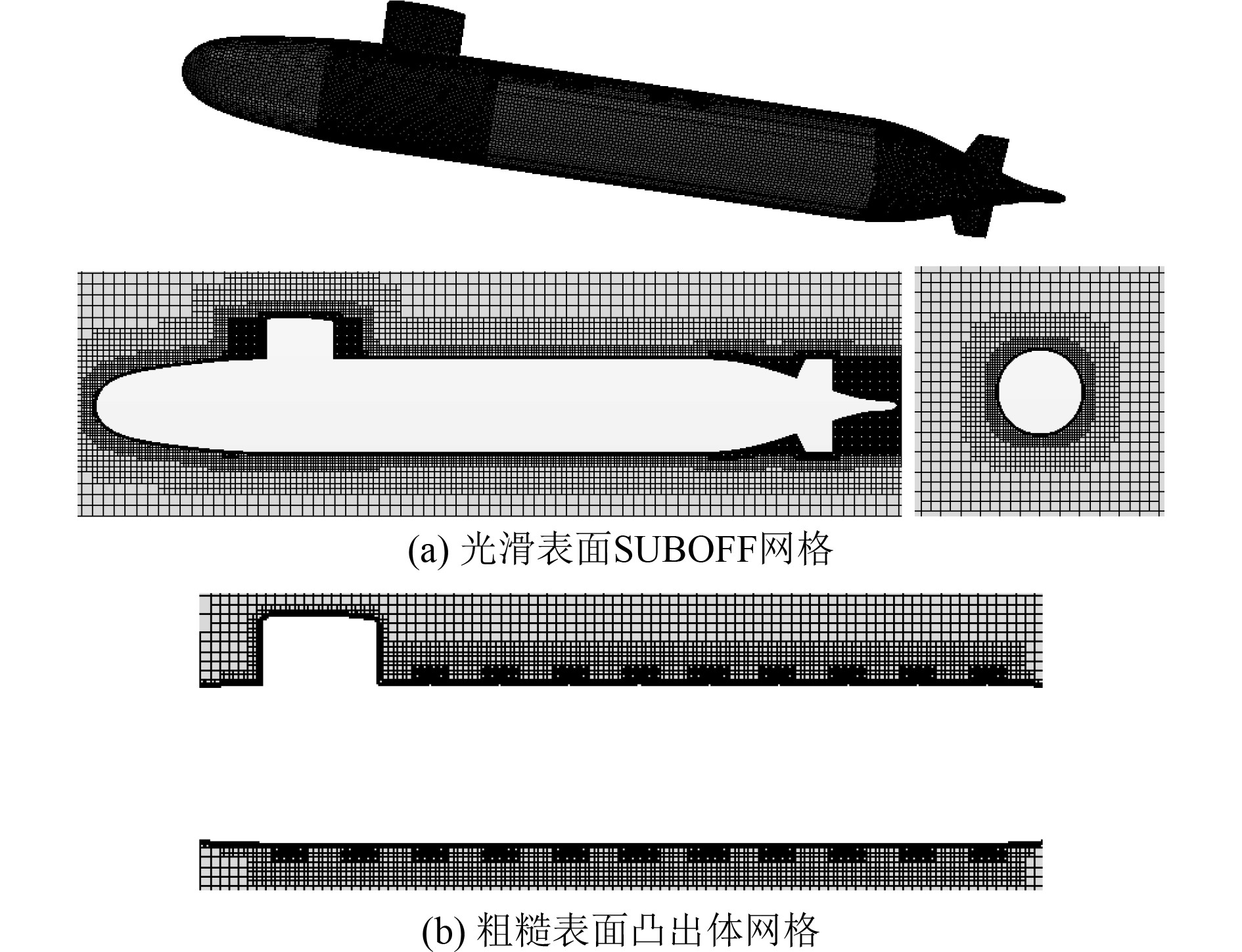
|
图 3 SUBOFF计算网格 Fig. 3 Computational mesh for SUBOFF |
湍流模型选用SST k-ω模型,边界层选用壁面函数法,采用分离流求解器对该水下航行体进行定常数值模拟,边界层设置为5层,增长比例为1.5,对流项采用二阶格式[4]。
为探究不同航速下的阻力特性,在计算域速度入口边界给定对应的速度。计算后与泰勒水池的实验值进行比较,如表1所示。其中v为航速(来流速度),F为模型受到的总阻力。可以看出数值结果略小于实验结果,但偏差均在7%以内。造成这一偏差的原因可能是实验中存在的自由液面影响,当航速较高时引起自由表面兴波,使得阻力增大。此外,阻塞效应、艇表面粗糙度、来流湍流等因素也可能是使得实验结果偏大的影响因素[9]。可见,本文计算方法合理。
|
|
表 1 SUBOFF模型计算与实验数据对比 Tab.1 Comparison of numerical results and experimental data |
为减小网格的影响,划分3种尺寸网格进行分析。通过对网格进行加密划分,划分为160万个网格,256万个网格,260万个网格。如图4所示,模拟所得的结果与实验值比拟很好,且计算结果随网格增加收敛。结合许锦宇[4]、李永坤[9]用STAR-CCM+模拟结果综合考虑,选取对网格数为256万的计算结果进行阻力性能分析。
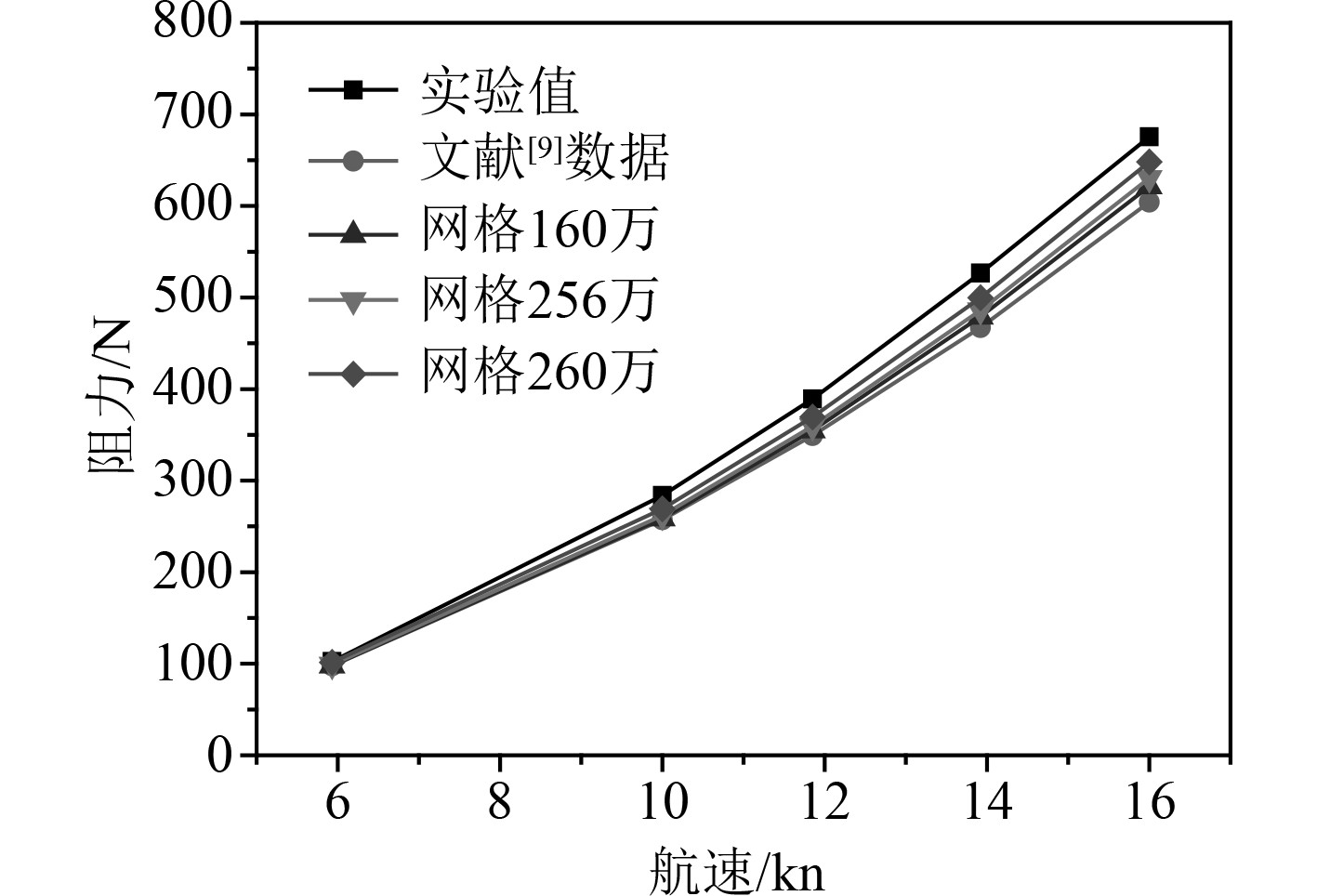
|
图 4 不同网格计算得到的阻力随航速变化结果 Fig. 4 Numerical results from different mesh |
综上所述,所选用的算例设置是合理可靠的,后续研究粗糙表面模型的水动力特性可采用上述设置进行流场仿真计算。
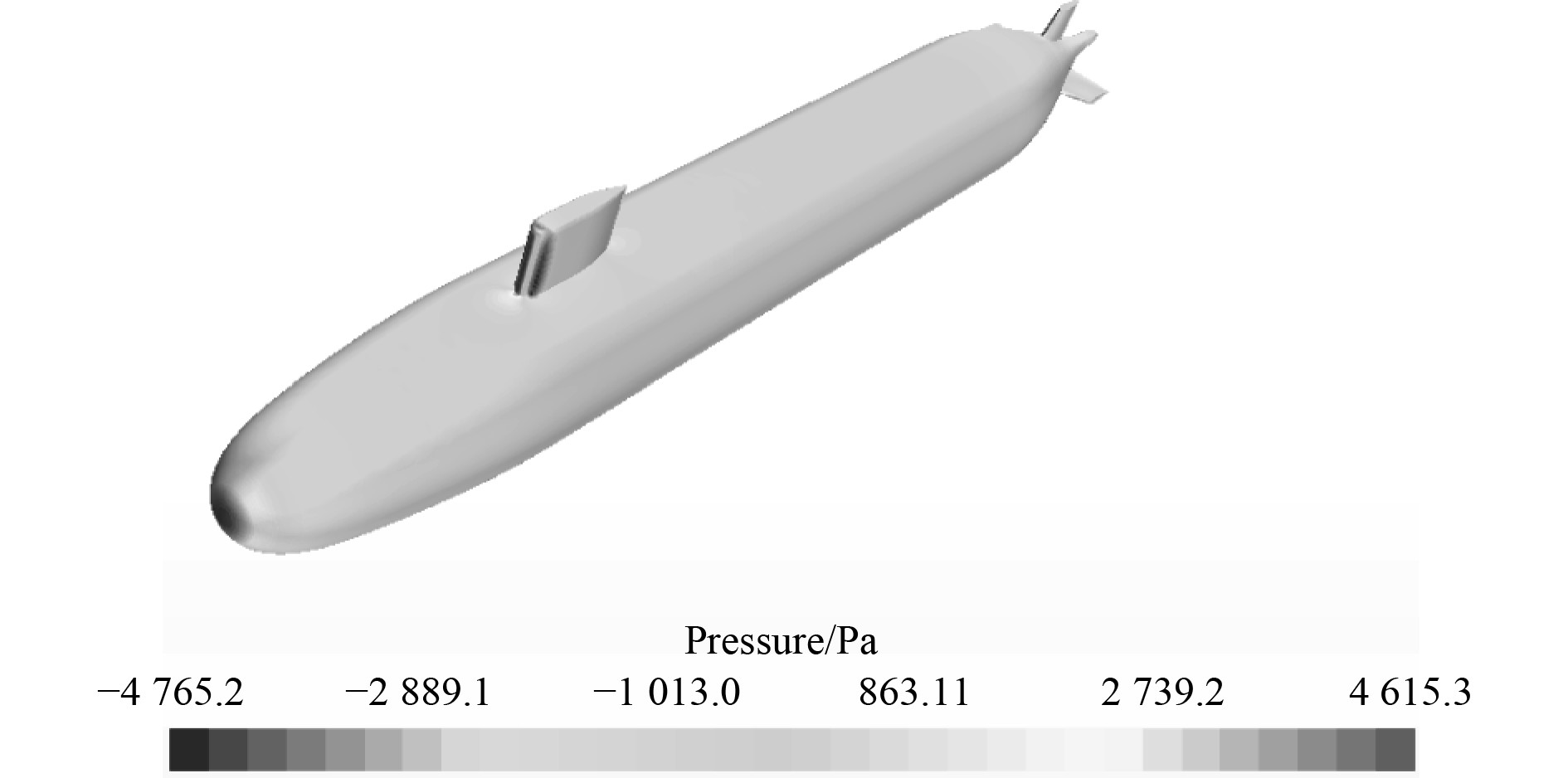
3 计算结果与分析 3.1 压力分布特性对光滑表面水及粗糙表面水下航行体在流场中不同剖面的压力分布进行研究,航行体以5.93 kn直航时表面压力分布云图如图5和图6所示。从不同剖面的压力云图可见,航行体部分区域出现了压力集中,部分区域受到的压力较大。
|
图 5 航速5.93 kn光滑表面SUBOFF压力云图 Fig. 5 Pressure contour of SUBOFF with smooth surface at 5.93 kn |

|
图 6 航速5.93 kn粗糙表面SUBOFF压力云图 Fig. 6 Pressure contour of SUBOFF with tough surface at 5.93 kn |
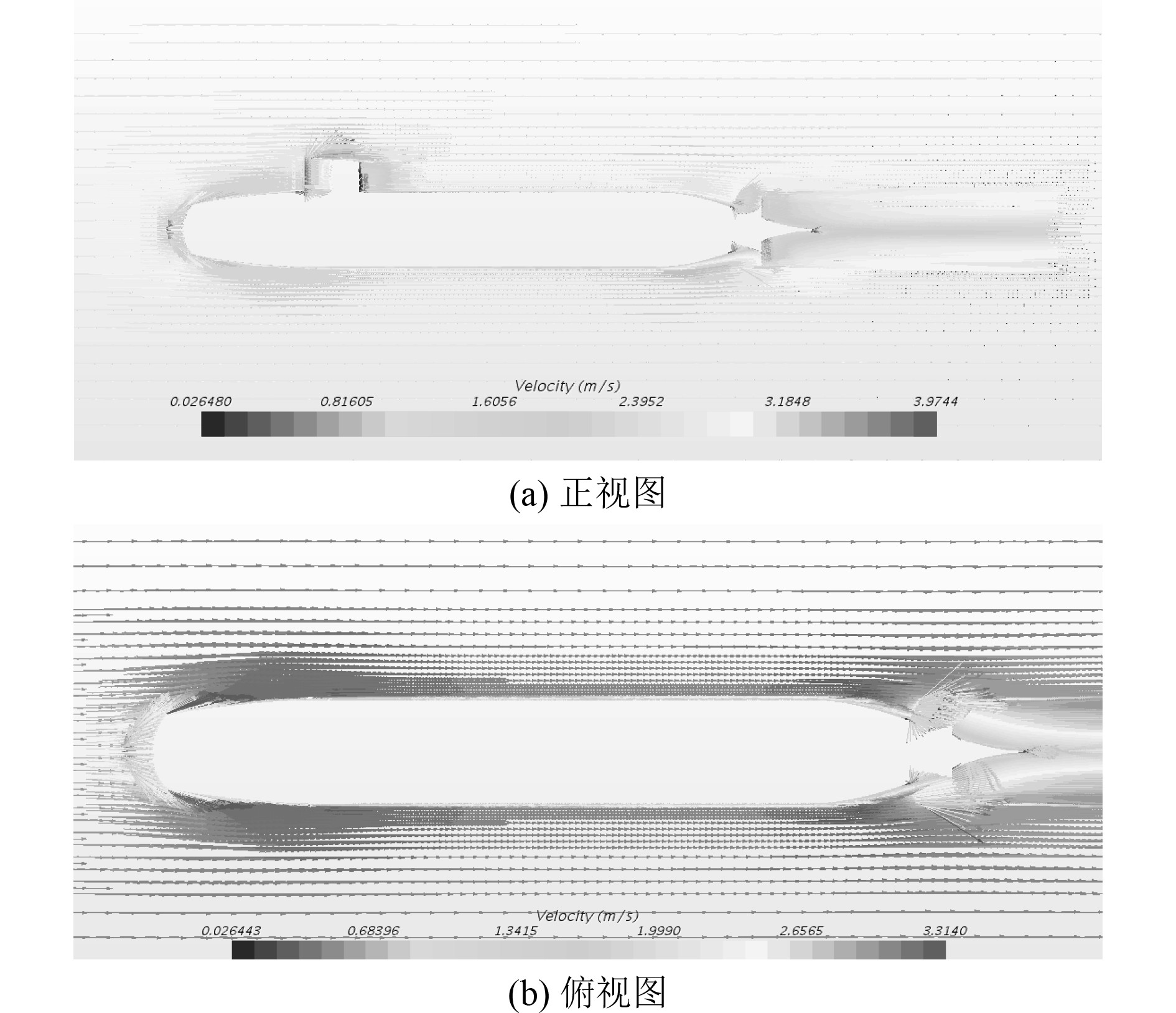
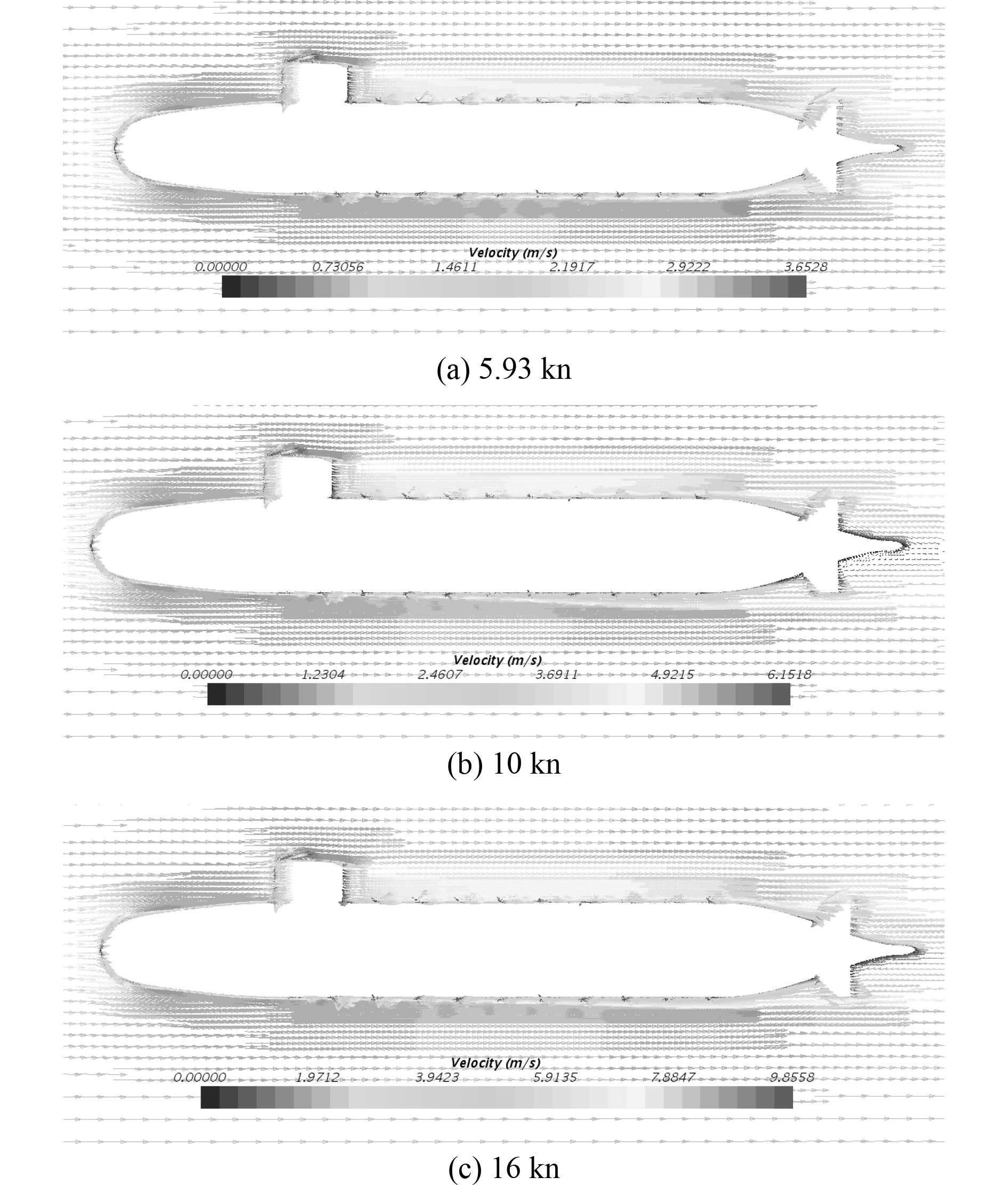
对光滑水下航行体附近的速度流场进行研究,图7为水下航行体航速为5.93 kn时航行体中纵剖面在流场中的速度矢量图。不同航速下粗糙航行体的流场速度分布情况如图8所示。
|
图 7 航速5.93 kn光滑表面SUBOFF速度矢量图 Fig. 7 Velocity vector of SUBOFF with smooth surface at 5.93 kn |
|
图 8 不同航速下粗糙表面SUBOFF速度矢量图 Fig. 8 Velocity vector of SUBOFF with tough surface |
从图中可以看到,在光滑表面的SUBOFF模型四周,流体能较好流过表面,而在流经粗糙表面SUBOFF模型时,会在凸出体周围产生较强烈的扰动,带来压力的较大变化,由此会对航行体阻力产生影响。
3.3 不同航速下对比分析通过模型SUBOFF换算实尺度SUBOFF阻力,包括两部分,光滑表面SUBOFF航行体阻力以及粗糙表面航行体凸出体引起的阻力。
采用模型阻力换算实尺度模型应符合雷诺相似准则,但由此预估实尺度模型航速不具有参考价值,考虑到阻力系数在实际航行过程中变化较小,直接以仿真得到的阻力系数换算所需航速实尺度航行体阻力。已知模型SUBOFF湿表面积为6.375 m2,粗糙表面凸出体面积为0.238 m2;实尺度凸出体总面积为44.913 m2(凸出高度2 mm)及 37.873 m2 (凸出高度1 mm),其不同航速下光滑表面及粗糙表面航行体阻力系数如表2所示。
|
|
表 2 粗糙表面与光滑表面航行体阻力系数比较 Tab.2 Resistance coefficient of tough surface and smooth surface |
由表3可知,光滑表面航行体的总阻力比粗糙表面(2 mm)航行体的总阻力小8%~10%,光滑表面航行体的总阻力比粗糙表面(1 mm)航行体的总阻力小7%~10%。
|
|
表 3 粗糙表面与光滑表面航行体水动力性能比较 Tab.3 Resistance of tough surface and smooth surface |
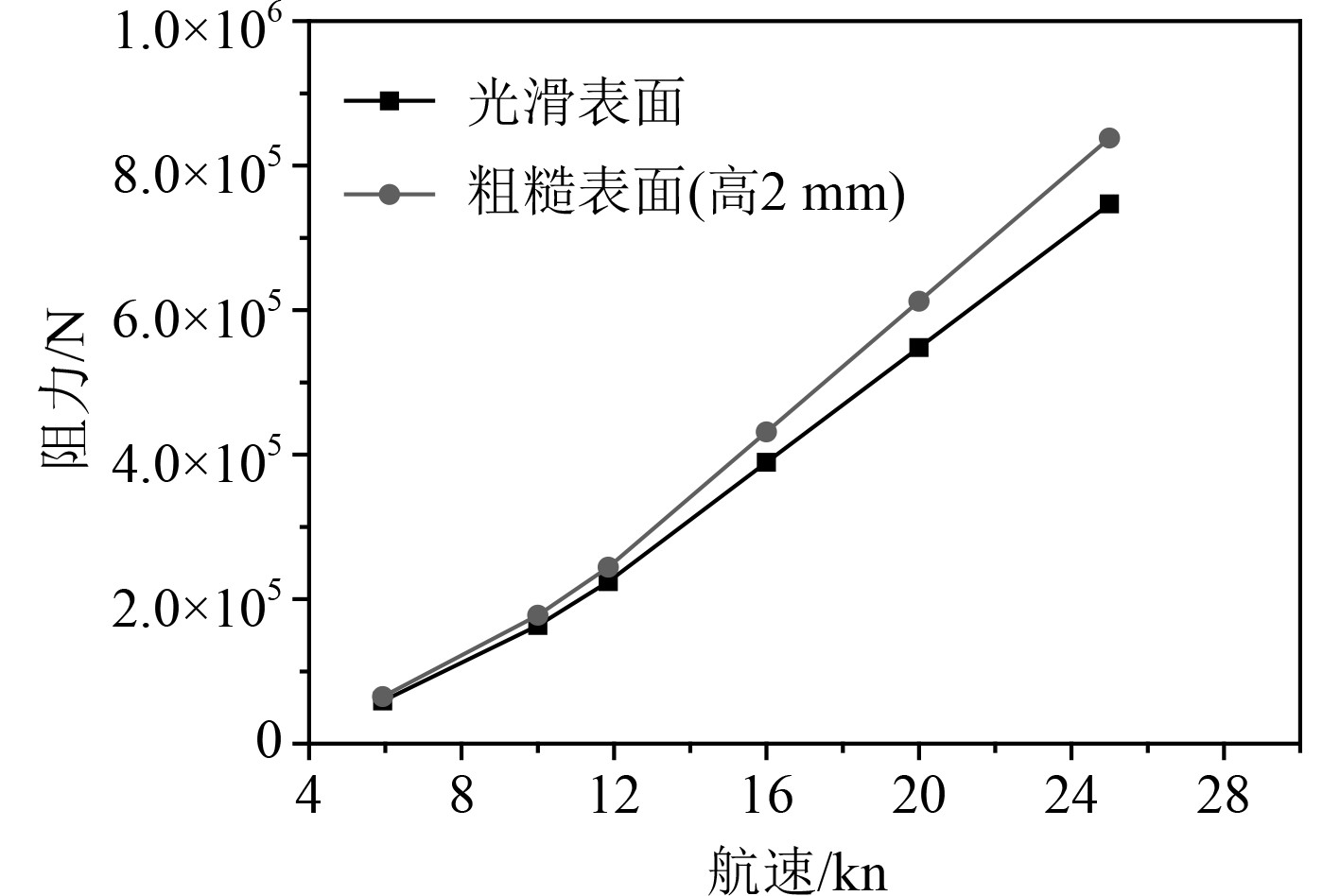
通过上述计算数据可以拟合外插得到20 kn和25 kn阻力结果,其中光滑航行体阻力值为548149.36(20 kn),746904.06(25 kn),粗糙表面(高度2 mm)航行体阻力值为612088.00(20 kn),837917.85(25 kn),可到不同航速下阻力变化如图9所示。
|
图 9 不同航速下光滑表面和粗糙表面SUBOFF阻力对比 Fig. 9 Comparison of resistance of SUBOFF with tough surface and smooth surface |
由图9可知,直航速度对阻力特性影响较大。由不同阻力与航速的对应关系可得到不同阻力下SUBOFF模型航行速度曲线如图10所示。

|
图 10 不同阻力下光滑表面和粗糙表面SUBOFF航行速度对比 Fig. 10 Comparison of velocity of SUBOFF with tough surface and smooth surface |
从图10可知,同样阻力情况下,光滑表面航行体将能够以更快的速度航行,当粗糙表面(2 mm)航行体航速为20 kn时,光滑航行体航速可达到21.6 kn。
4 结 语本文对光滑表面和粗糙表面的SUBOFF模型航行性能进行了数值研究,所采用的数值计算方法与泰勒水池的实验值比较最大偏差小于7%。经过对水下航行体阻力性能的模拟,发现相较于光滑表面航行体,粗糙表面航行体阻力有所增加。光滑表面航行体的总阻力比高度2 mm的粗糙表面航行体的总阻力小8%~10%,比高度1 mm的粗糙表面航行体的总阻力小7%~10%。当同样阻力情况下,高度2 mm粗糙表面航行体航速为20 kn时,光滑航行体航速可达到21.6 kn。
| [1] |
王玉婷, 向先波, 王瑟. 基于CFD和直接计算技术的航行器阻力系数算法研究[J]. 中国科技论文, 2016, 11(19): 2164-2168. DOI:10.3969/j.issn.2095-2783.2016.19.003 |
| [2] |
王庆旭. 三体滑行艇阻力和稳定性研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [3] |
FLORIAN R. Menter. Improved Two-Equation k-ω Turbulence Models for Aerodynamic Flows. NASA Technical Memorandum 103975. 1992.
|
| [4] |
许锦宇. 作业型AUV总体设计与水动力性能分析[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [5] |
SAVITSKY D. Hydrodynamic design of planing hulls[J]. Marine Technology, 1964, 1(1): 71-95. |
| [6] |
GHASSEMI H, KOHANSAL AR. Higher order boundary element method applied to the hydrofoil beneath the free surface[C]// Proceedings of the 28th International Conference on Ocean, Offshore and Engineering. Honolulu, Hawaii USA: [s. N. ], 2009.
|
| [7] |
苏玉民, 陈庆童, 沈海龙, 等. 基于 CFD 技术和 2.5D 理论的滑行艇水动升力计算[C]第十五届中国海洋(岸)工程学术讨论会论文集. 214-218.
|
| [8] |
陈庆童. 滑行艇在高速航行时横向水动力的数值计算[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [9] |
李永坤. 全系统水下航行体流固耦合计算及水动力噪声计算[D]. 大连: 大连理工大学, 2020.
|
 2022, Vol. 44
2022, Vol. 44
