现代大型船舶的系统性、功能性不断提升,在提高性能的同时也使得船舶机械设备的复杂程度越来越高。以船舶动力系统为例,现代大型船舶的动力系统发展方向是高功率、大马力,柴油发动机的功率不断提升,齿轮箱、螺旋桨等关键部件的故障率也不断提高。因此,为了提高大型船舶的可靠性,降低经济损失,进行船舶关键机械部件的故障预测具有十分深远的意义。
船舶机械设备故障预测的核心是建立合理的故障预测模型,由于船舶机械设备的运行环境较为恶劣,在海浪等外界干扰作用力下,机械设备运行过程中受到振动、冲击载荷,这些因素可能会导致船舶机械设备的各种故障。因此,在建立机械设备故障预测模型时,需要充分考虑机械故障的非线性、不确定性、动态时变性等。
本文结合HSMM隐马尔科夫模型进行船舶机械设备故障预测模型的搭建,从HSMM的原理出发,利用模态分解的机械设备信号处理技术,实现了船舶机械故障演化预测模型的建立。
1 SMM马尔科夫模型和HSMM隐马尔科夫模型介绍SMM马尔科夫模型和HSMM隐马尔科夫模型是2种较为常用的预测模型。其中,隐马尔科夫模型能够针对动态过程的时间序列进行分类,识别时序下的故障信号;隐马尔科夫模型HSMM是在SMM的基础上引入时间概率函数,能够显著提高故障诊断的精度[1]。
HSMM隐马尔科夫模型的原理如下:
假设任意
| $ P\left( {{Q_t} = {S_i},t = 1,2,...,i} \right) \text{。} $ |
假设系统在时间t的状态只与t-1时刻的状态有关,可以得到一个一阶马尔科夫链,表示为:
| $ P\left( {{Q_{t - 1}}} \right) = P\left( {{Q_t} = {S_i}\left| {{Q_{t - 1}} = {S_j}} \right.} \right) \text{。} $ |
定义条件概率公式为:
| $ P\left( {{Q_t} = {S_i}\left| {{Q_{t - 1}} = {S_j}} \right.} \right) = {a_{ij}} \text{,} i > 1,j > 1 \text{。} $ |
条件概率解释为系统从t−1时刻的状态
若该系统的任意状态都是可切换的,则可以得到系统的状态转移矩阵如下:
| ${\boldsymbol{ M}} = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{}&{{a_{1N}}} \\ {{a_{21}}}&{{a_{22}}}&{}&{{a_{2N}}} \\ {...}&{...}&{...}&{...} \\ {{a_{N1}}}&{{a_{N2}}}&{}&{{a_{NN}}} \end{array}} \right] 。$ |
马尔科夫模型SMM示意图如图1所示。
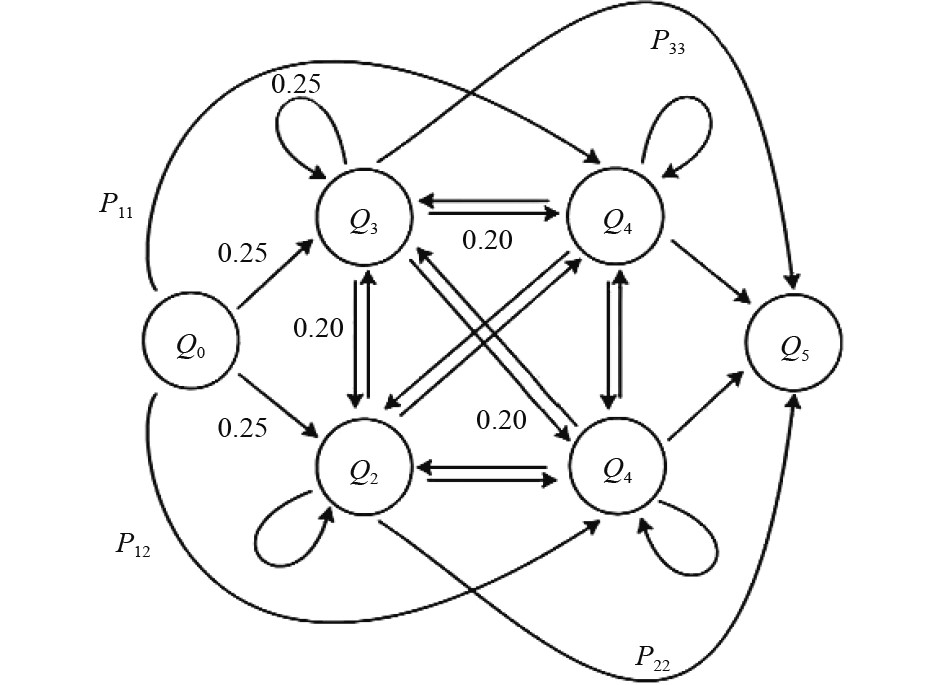
|
图 1 马尔科夫模型SMM示意图 Fig. 1 Schematic diagram of Markov model SMM |
假设系统的t时刻状态不仅与t-1时刻的状态有关,也与m个历史状态有关,表示为:
| $ P\left( {{Q_t}} \right) = P\left( {{Q_t} = {S_i}\left| {{Q_{t - 1}} = {S_j} \cup ...{Q_m} = {S_m}} \right.} \right) \text{,} $ |
则称该模型为m阶马尔科夫模型。
定义隐马尔科夫模型为:
| $ P\left( D \right) = {\left( {{a_{ij}}} \right)^d}\left( {1 - {a_i}_j} \right),i < N \text{。} $ |
式中,d为时间单元的个数。
隐马尔科夫模型示意图如图2所示。
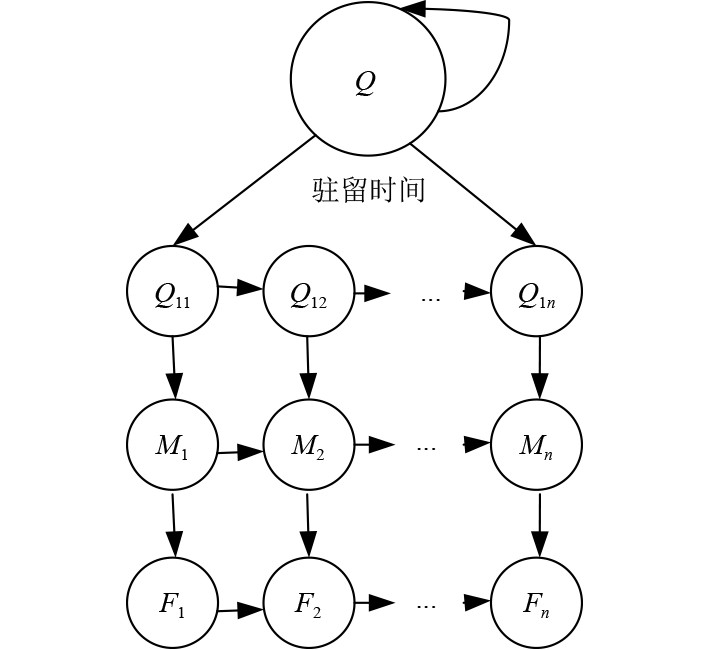
|
图 2 隐马尔科夫模型示意图 Fig. 2 Schematic diagram of hidden markov model |
可知,模型的关键结构参数如下:
1)
2)M为系统所有可能出现的观测符号数,记为
3)F为隐马尔科夫模型状态转换的概率,用
本文基于HSMM隐马尔科夫模型研究船舶机械故障诊断方法,其基本思路是提取设备运行信号的特征向量,将信号的特征向量作为HSMM模型的输入,然后利用RBF神经网络算法进行HSMM模型的训练,建立对应各个信号状态的模型库。最后,利用模型库进行船舶设备运行状态信号的故障预测。
模型库的输入信号为未知状态的信号特征向量,进行状态识别之前需要使用Viterbi算法[2]计算向量的对数似然率,利用似然率来表征当前输入向量与模型库中向量的相似程度。
基于HSMM的船舶机械故障预测与识别流程如图3所示。
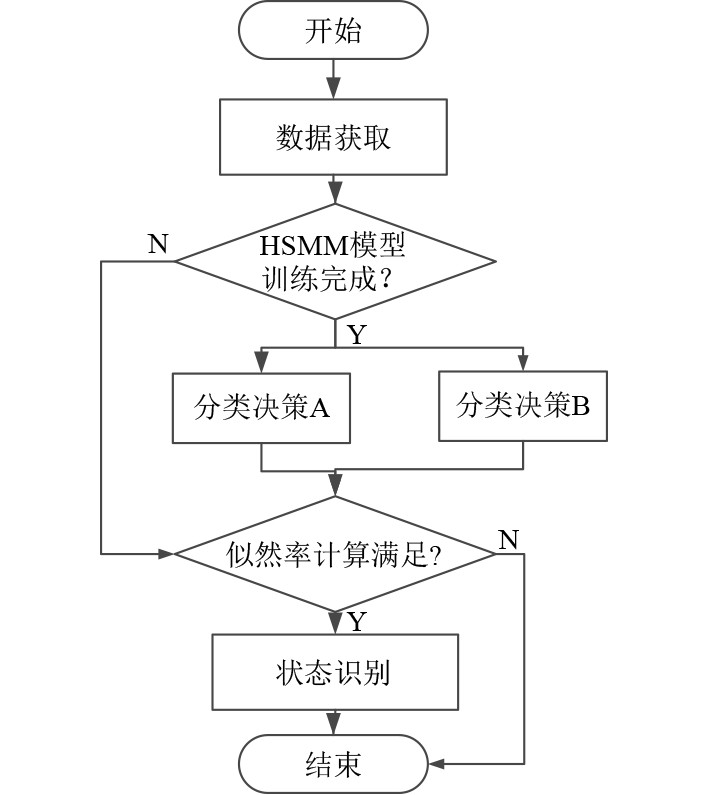
|
图 3 基于HSMM的船舶机械故障预测与识别流程图 Fig. 3 Flow chart of ship machinery fault prediction and identification based on HSMM |
船舶机械设备故障预测的输入信号包括时域信号和频域信号2种,信号的预处理包括数据的噪声抑制、模态分解、异常数据判断等。
针对不同频域下的船舶机械设备故障信号,进行基于变分模态分解(VMD)的预处理,假设机械设备故障信号
步骤 1 建立固有模态函数
| $ h\left( t \right) = \left( {\delta \left( t \right) + \frac{j}{{\text{π} \sqrt 2 t}}} \right)\cdot{u_k}\left( t \right) \text{,} $ |
式中:
步骤 2 进行固有模态函数的高斯变换:
| $ \varGamma \left( t \right) = \left[ {\left( {\delta \left( t \right) + \frac{j}{{\text{π} \sqrt 2 t}}} \right) \cdot {u_k}\left( t \right)} \right]{e^{ - jwt}} \text{,} $ |
步骤 3 进行信号的模态调制:
| $ \left\{ \begin{aligned} &\min \left\{ {\sum\limits_k^{} {\left| {\frac{\partial }{{\partial t}}} \right.} } \right.\left( {\delta \left( t \right) + \frac{j}{{\text{π} \sqrt 2 t}}} \right) \cdot {u_k}\left( t \right){w_k}\left( t \right),\\ &\sum\limits_k^{} {{u_k}\left( t \right) = f\left( t \right)} 。\end{aligned} \right. $ |
式中:
步骤 4 引入拉格朗日算子
| $\begin{aligned}[b] & B({u_k}\left( t \right),{w_k}\left( t \right)) =\\ & \lambda \left( t \right) \cdot \min \left. {\left\{ {\sum\limits_k^{} {\left| {\frac{\partial }{{\partial t}}} \right.} } \right.\left( {\delta \left( t \right) + \frac{j}{{\text{π} \sqrt 2 t}}} \right) \cdot {u_k}\left( t \right){w_k}\left( t \right)} \right\} \text{。} \end{aligned}$ |
基于变分模态分解算法的信号预处理流程图如图4所示。
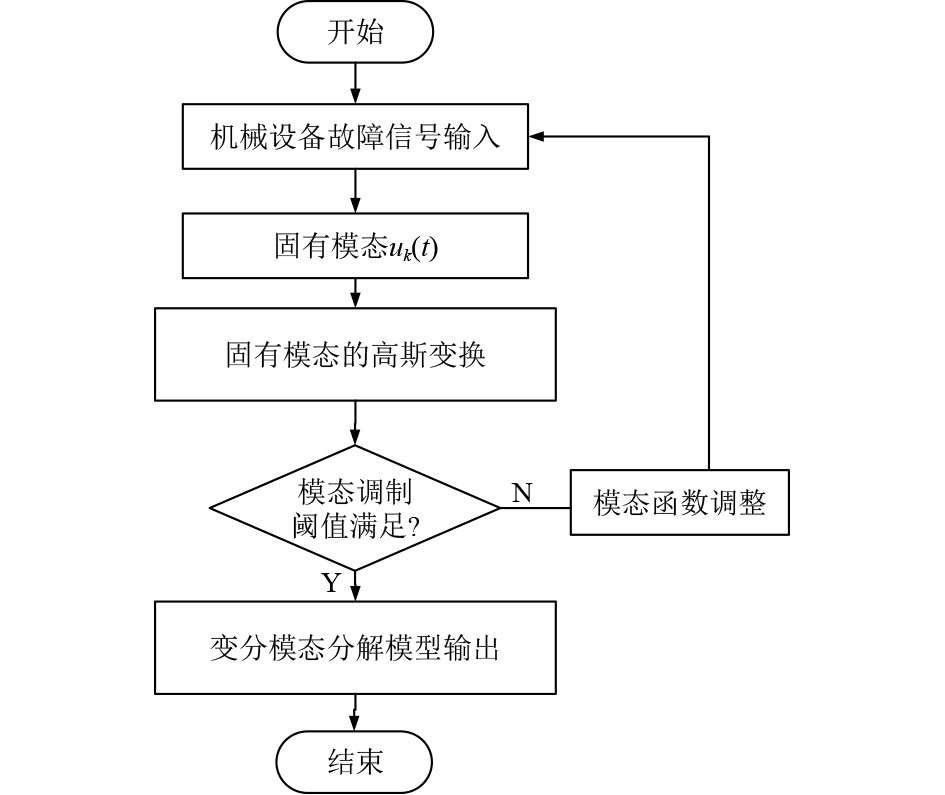
|
图 4 基于变分模态分解算法的信号预处理 Fig. 4 Signal preprocessing based on variational modal decomposition algorithm |
本文结合Matlab平台建立了船舶机械故障演化预测模型,并利用模型进行故障信号的仿真预测,采集的输入信号包括故障信号
| $ {f_1}\left( t \right) = \frac{1}{{\sqrt {2\text{π} \rho } }}\exp \left[ {\frac{{{{\left( {t - a} \right)}^2}}}{{2{\rho ^2}}}} \right] \text{,} $ |
式中:
噪声信号的瑞利分布概率密度函数为:
| $ {f_1}\left( t \right) = \frac{t}{{{b^2}}}\exp \left[ {\frac{{{{\left( {t - 1} \right)}^2}}}{{2{b^2}}}} \right],t > 0 \text{。} $ |
式中:b为瑞利分布系数[4],t的均值为
机械设备故障噪声信号曲线,如图5所示。
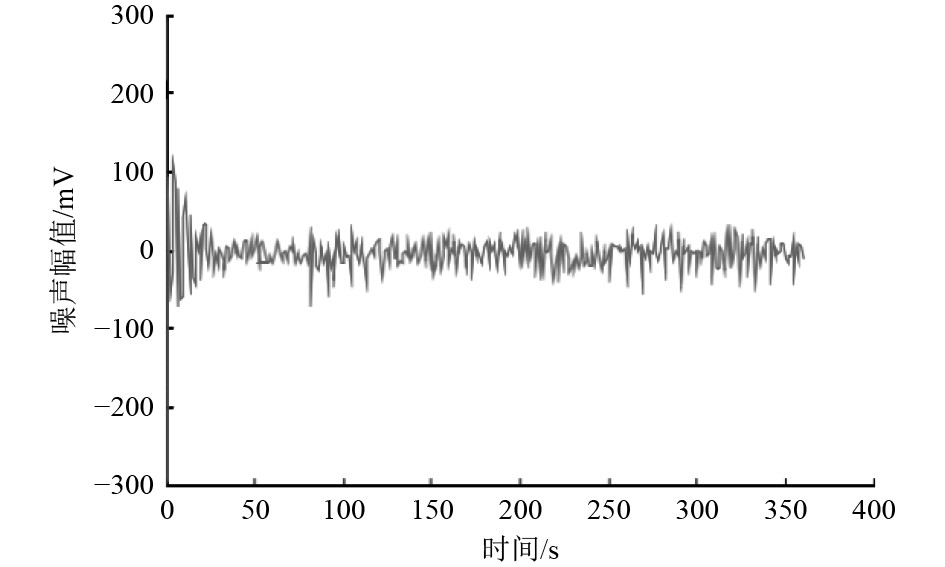
|
图 5 机械设备故障噪声信号的采样曲线 Fig. 5 Sampling curve of mechanical equipment fault noise signal |
将故障信号
本文以不同位置船舶动力系统齿轮箱的齿轮故障信号为输入,得到该HSMM模型下的不同位置齿轮故障预测统计如图6所示。
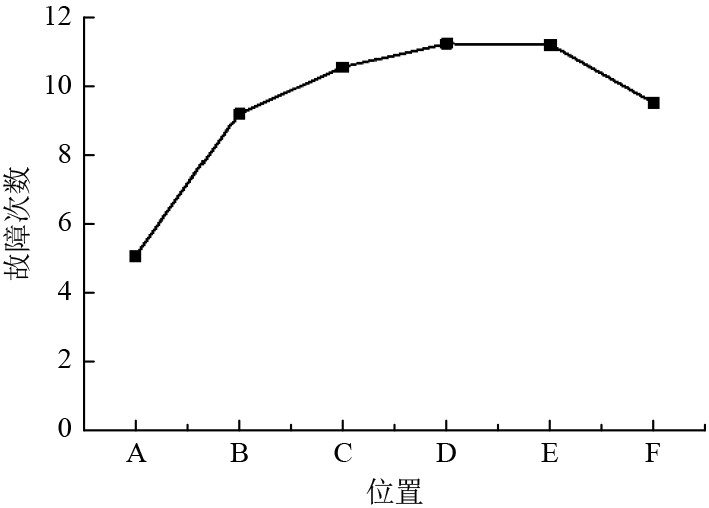
|
图 6 HSMM模型下的船舶齿轮故障预测统计 Fig. 6 Prediction statistics of ship gear faults based on HSMM model |
船舶机械设备故障的识别与预测对于提高船舶的可靠性有重要的意义。本文使用HSMM隐马尔科夫模型建立了船舶机械设备故障预测模型,并结合变分模态分解技术和Matlab平台,进行船舶机械故障预测的仿真。
| [1] |
杨志强, 朱家伟. 基于高斯混合隐马尔科夫模型的自由换道识别[J]. 计算机系统应用, 2022, 31(8): 388-394. YANG Zhi-qiang, ZHU Jia-wei. Free lane change recognition based on Gaussian mixture hidden Markov model[J]. Computer System Application, 2022, 31(8): 388-394. |
| [2] |
李丹, 赵荣阳. 基于隐马尔科夫模型的水声传感器位置稳定性模型研究[J]. 电脑与电信, 2022(5): 1-4. LI Dan, ZHAO Rong-yang. Study on position stability model of underwater acoustic sensor based on hidden Markov model[J]. Computer and Telecommunications, 2022(5): 1-4. DOI:10.15966/j.cnki.dnydx.2022.05.008 |
| [3] |
余楠, 晋玉星. 基于隐马尔科夫模型的激光主动成像图像分割方法[J]. 激光杂志, 2022, 43(2): 105-109. YU Nan, JIN Yu-xing. Image segmentation method of laser active imaging based on hidden Markov model[J]. Laser Journal, 2022, 43(2): 105-109. |
| [4] |
王越, 康志文. 一种改进的基于隐马尔科夫模型地图匹配算法[J]. 信息技术与信息化, 2021(3): 103-106. WANG Yue, KANG Zhi-wen. An improved map matching algorithm based on hidden Markov model[J]. Information Technology and Informatization, 2021(3): 103-106. DOI:10.3969/j.issn.1672-9528.2021.03.034 |
 2022, Vol. 44
2022, Vol. 44
