2. 广西市场科技职业技术学院,广西 南宁 530009
2. Guangxi Vocational College of Marketing Science and Technology, Nanning 530009, China
船舶为人类开发利用海洋资源提供了高效安全的途径。海上主动避碰是船舶领域重要的研究方向之一,主动避碰技术是确保船舶可以安全地完成航行任务的重要保障。船舶在海上航行过程中,其周围环境十分复杂,不断受着风浪等因素的干扰,同时还要面对突然出现的各类障碍物带来的碰撞危险。如果船舶上没有一套有效的主动避碰系统,这些障碍物很有可能会给船舶带来灾难性的后果。本文研究海上船舶多目标侧向主动避碰算法,对船舶主动避碰技术的发展起积极促进作用。
1 船舶海上制导系统 1.1 船舶海上路径规划设计船舶在海上的制导系统主要包括:1)基于现有的电子海洋地图,获得电子地图中已有的障碍物,对船舶航行的起始点到终点的航行路径进行初步规划,同时获得相应的航路点,以避开这些已知的障碍物;2)使用船舶的控制系统对船舶航行的速度、位置以及姿态等参数进行实时调整,完成船舶的安全航行,并绘制出船舶实际航行路径。
本文基于势流法对船舶的路径进行规划。在势流法中,当流体从起始点流向目的点时会绕开路径上的障碍物,因此可以以势流理论为基础,构建出存在障碍物的情况下流体的流动模型。因为势场是标量场,因此可以将势场看作是笛卡尔变量,如下式:
| $ \varPhi = \varPhi \left( {x,y} \right) \text{,} $ | (1) |
| $ \nabla \varPhi = q\text{。} $ | (2) |
势的梯度被称为流,因此流是速度势的一种,并不属于力势。势能满足连续性方程,即拉普拉斯方程,如下式:
| $ {\nabla ^2}\varPhi = 0\text{。} $ | (3) |
获得方程的相关边界值之后,则可以使用面元法对式(3)进行求解。在实际求解过程中,物体的表面不可以存在交叉流动,因此可以使用neumann条件,如下式:
| $ \nabla \left( {\varPhi + {\varPhi _\infty }} \right) \cdot n = 0\text{,} $ | (4) |
除此之外,物体的流速会随着距离的变大而不断衰减,如下式:
| $ \mathop {\lim }\limits_{r \to \infty } \left( {\nabla \varPhi - \nu } \right) = 0\text{,} $ | (5) |
根据叠加理论,则可以得到:
| $ {\nabla ^2}\varPhi = \sum\limits_{k = 1}^n {{c_k}{\nabla ^2}{\varPhi _k} = 0} \text{。} $ | (6) |
面元法的解均分布于物体的表面,并且每个基本解都可以使得连续方程成立,同时每个解也满足连续方程的边界条件。根据叠加原理可以得到,满足连续方程基本解的组合也能够满足方程的连续性。
在实际应用中,通常使用圆柱绕流作为一种替代方案,对船舶的路径进行规划。将均匀流以及势偶极子进行叠加,则可以获得这种圆柱绕流。基于相互垂直的2个偶极子可以对任意方向的流进行解算。假设需要解决的基础解的数量为n,则可以得到:
| $ {a_{i1}}{\mu _1} + \cdots + {a_{in}}{\mu _n} + {b_i} = 0\text{。} $ | (7) |
式中:μn为偶极子的数值;bi为目标流的数值;ain为单位强度的偶极子的数值。进行简化,如式(8)所示。其中,A为影响因子矩阵。
| $ {\boldsymbol{A}}\mu = - b\text{。} $ | (8) |
偶极子由势场和流函数构成,可以通过流函数进行制导,流函数如下:
| $ \varPsi \left( r \right) = \sum\limits_{i = 1}^n {{\mu _i}\Psi \left( {r - {r_i},{n_i}} \right) + {\Psi _t}\left( {r - {r_t}} \right)} \text{。} $ | (9) |
式(9)域中的流函数中存在一个标量值Ψ,并且Ψ=Ψ(r)。同时式(9)中的Ψt(rt)为目标产生的流函数。偶极子产生的流函数如式(10)所示,源产生的流函数如式(11)所示。基于这些流函数,则可以获得船舶航行的流线,最终实现路径规划。
| $ {\varPsi _d}\left( {d,n} \right) = \frac{{{d_1}{n_2} - {d_2}{n_1}}}{{4\text{π} {{\left\| d \right\|}^2}}}\text{,} $ | (10) |
| $ {\varPsi _s}\left( d \right) = \frac{{\arctan \left( {{d_1},{d_2}} \right)}}{{2\text{π} }}\text{。} $ | (11) |
当船舶在海上航行过程中,需要追踪识别一个正在海面上移动的物体,并且没有该物体下一步运动的信息时,则需要使用目标寻迹算法。目标寻迹算法可以保持船舶在执行任务过程中维持稳定的航行速度以及航行方向,目标寻迹算法的控制方程为:
| $ \mathop {\lim }\limits_{t \to \infty } \left[ {{p^n}\left( t \right) - p_t^n\left( t \right)} \right] \text{,} $ | (12) |
式中,pn为船舶的位置。
船舶在海面上航行过程中,可以使用视线制导法进行目标循迹的制导控制。航行速度为:
| $ U\left( t \right) = \left\| {v\left( t \right)} \right\| = \sqrt {x{{\left( t \right)}^2} + y{{\left( t \right)}^2}} \geqslant 0\text{。} $ | (13) |
转向和角度存在一定的关系,如下式:
| $ \chi \left( t \right) = \arctan 2\left( {y\left( t \right),x\left( t \right)} \right),x\left( t \right) \in \left[ { - \text{π} ,\text{π} } \right]\text{。} $ | (14) |
当船舶通过pk和pk+1两个航路点,并且将航路点pk作为坐标系的原点时,则x轴的旋转角度可以用式(15)表示。船舶在该坐标下的计算方法如下式:
| $ \alpha \left( t \right) = \arctan 2\left( {{y_{k + 1}} - {y_k},{x_{k + 1}} - {x_k}} \right)\text{,} $ | (15) |
| $ \varepsilon \left( t \right) = {R_p}{\left( {{\alpha _k}} \right)^{\rm{T}}}\left( {{p^n}\left( t \right) - p_k^n} \right) = {\left[ {s\left( t \right)\quad e\left( t \right)} \right]^{\rm{T}}}\text{。} $ | (16) |
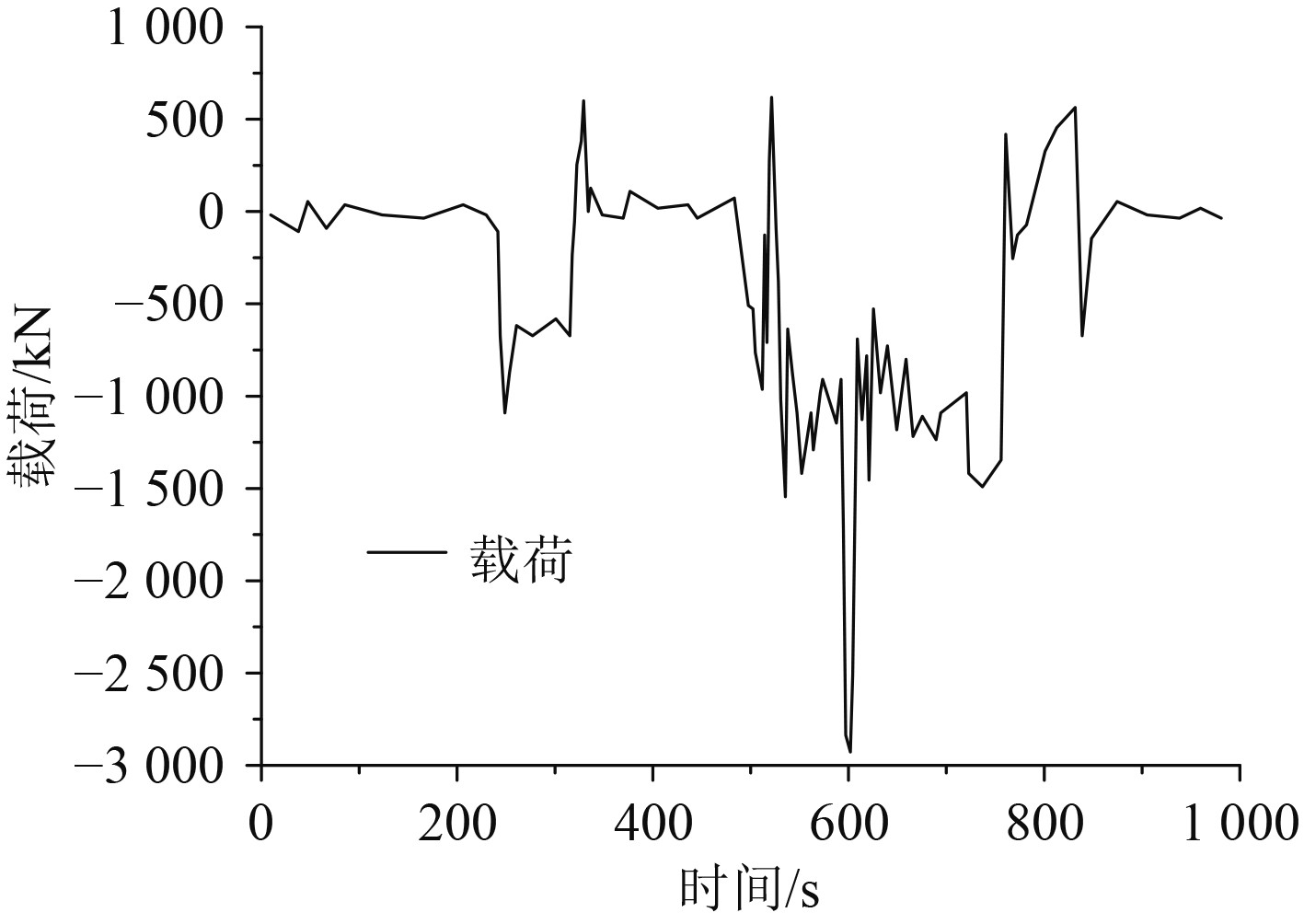
式中,Rp(αk)的计算公式如式(17)所示。最终则可以得到船舶沿着路径的距离以及追踪误差,如式(18)和式(19)所示。当追踪误差e(t)=0时,则表示船舶航迹收敛。船舶航行过程中受到的载荷随时间变化如图1所示。
|
图 1 船舶在航行过程中受到的载荷随时间变化情况 Fig. 1 The change of load on the ship with time during navigation |
| $ {R_p}\left( {{\alpha _k}} \right) = \left[ {\begin{array}{*{20}{c}} {\cos \left( {{\alpha _k}} \right)}&{ - \sin \left( {{\alpha _k}} \right)} \\ {\sin \left( {{\alpha _k}} \right)}&{\cos \left( {{\alpha _k}} \right)} \end{array}} \right]\text{,} $ | (17) |
| $ s\left( t \right) = \left[ {x\left( t \right) - {x_k}} \right]\cos \left( {{\alpha _k}} \right) + \left[ {y\left( t \right) - {y_k}} \right]\sin \left( {{\alpha _k}} \right)\text{,} $ | (18) |
| $ e\left( t \right) = - \left[ {x\left( t \right) - {x_k}} \right]\sin \left( {{\alpha _k}} \right) + \left[ {y\left( t \right) - {y_k}} \right]\cos \left( {{\alpha _k}} \right)\text{。} $ | (19) |
船舶在海面上的视觉目标定位方法,大多数以扩展卡尔曼滤波器为基础。由于在海上的作业环境复杂,船舶周围的海洋环境是一种非线性的强噪声系统,因此基于神经网络技术对船舶周围的目标进行检测定位。
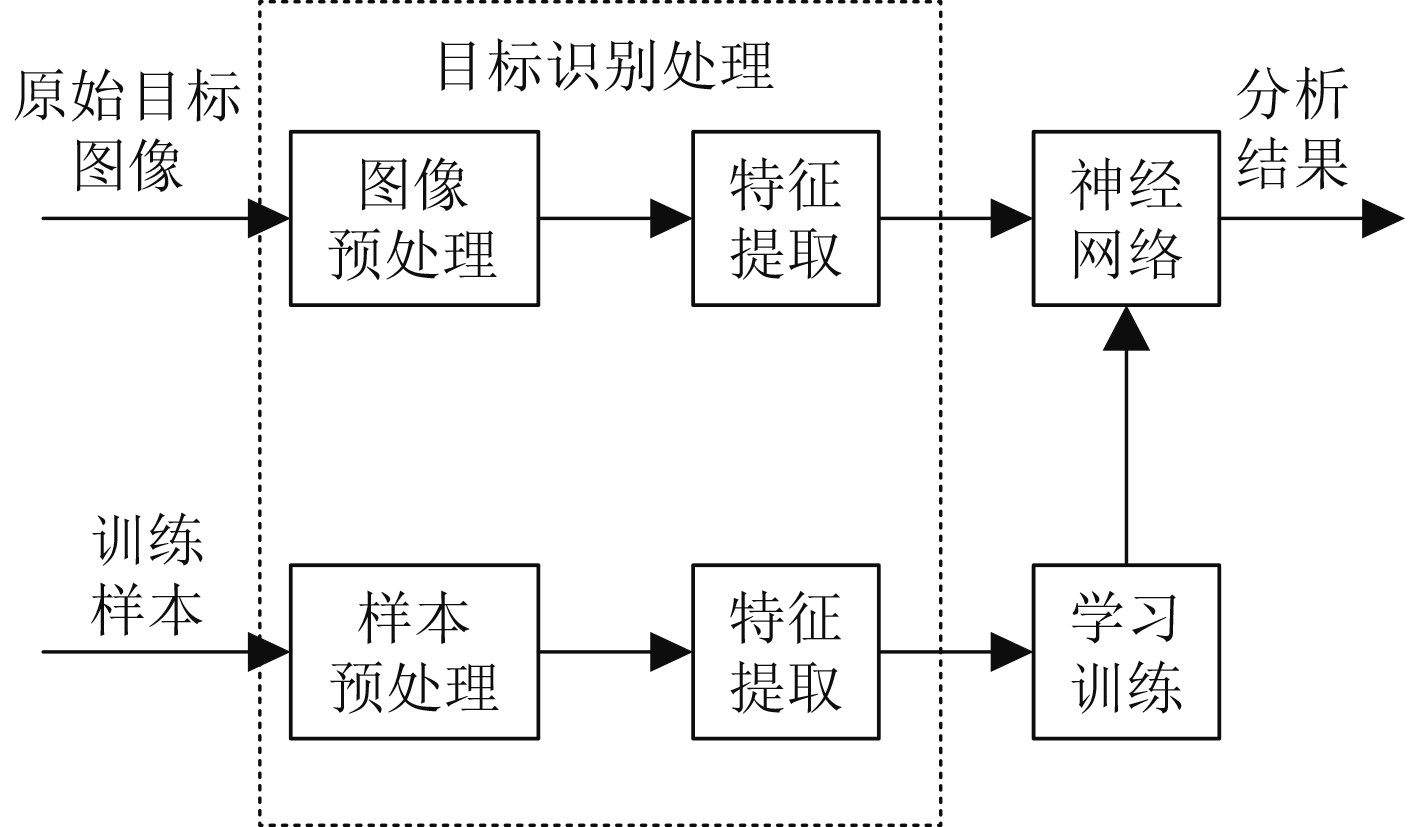
多个神经网络一起构成了船舶的视觉子神经网络,由于船舶的视觉神经网络是基于目标的形状以及目标所处的位置所生成的,因此对船舶的每个视觉子神经网络的结构进行简化,这样可以增加整个视觉传感系统的泛化能力,提升输出的精度。同时也可以通过增加船舶的子神经网络来完善船舶的视觉网络系统,以提升船舶对目标的定位能力。基于神经网络的船舶目标检测系统的结构如图2所示。
|
图 2 基于神经网络的船舶目标检测系统结构 Fig. 2 Structure of ship target detection system based on neural network |
模糊神经网络由模糊控制以及神经网络共同构成,由于模糊神经网络的设计方式不同,因此可以获得多种模糊神经网络。船舶神经网络在进行信息融合的过程中,利用信息融合模块,可以清晰地对跟踪的目标进行描述识别。规则层的数学模型如公式(20)所示,输出层的数学模型如式(21)所示。
| $ {y_i} = 1 - {\left[ {\prod\limits_{j = 1}^n {{{\left( {1 - {x_j}} \right)}^{{\omega _{ij}}}}} } \right]^{{q_i}}}\text{,} $ | (20) |
| $ {y_i} = {\left[ {\prod\limits_{j = 1}^n {{{\left( {{x_j}} \right)}^{{\omega _{ij}}}}} } \right]^{{p_i}}}\text{。} $ | (21) |
式中,yi为目标的识别概率。输入层和规则层之间数据传输权值的计算式为:
| $ {\omega _{ki}}\left( {t + 1} \right) = {\omega _{ki}}\left( t \right) - \eta \frac{{\partial E}}{{\partial {\omega _{ki}}}}\text{,} $ | (22) |
| $ \frac{{\partial E}}{{\partial {\omega _{ki}}}} = - \sum\limits_{\alpha = 1}^S {\left[ {\sum\limits_{j = 1}^M {\left( {\hat F_j^\alpha - F_j^\alpha } \right)} } \right]\frac{{R_k^\alpha {P_k}}}{{1 - R_k^\alpha }}} \ln \left( {X_i^\alpha } \right)\text{。} $ | (23) |
规则层中模糊推理的参数计算方法如下:
| $ {P_k}\left( {t + 1} \right) = {P_k}\left( t \right) - {\eta _p}\frac{{\partial E}}{{\partial {P_k}}}\text{,} $ | (24) |
| $ \frac{{\partial E}}{{\partial {P_k}}} = - \sum\limits_{\alpha = 1}^S {\left[ {\sum\limits_{j = 1}^M {\left( {\hat F_j^\alpha - F_j^\alpha } \right)} {q_i}\left( {1 - F_j^\alpha } \right)} \right]\frac{{R_k^\alpha }}{{\left( {1 - R_k^\alpha } \right){P_k}}}\ln \left( {R_k^\alpha } \right)} \text{。} $ | (25) |
规则层到输出层之间数据传输的权值计算方法如下:
| $ {C_{jk}}\left( {t + 1} \right) = {C_{jk}}\left( t \right) - \eta \frac{{\partial E}}{{\partial {C_{jk}}}}\text{,} $ | (26) |
| $ \frac{{\partial E}}{{\partial {C_{jk}}}} = \sum\limits_{\alpha = 1}^S {\left( {\hat F_j^\alpha - F_j^\alpha } \right){q_i}\left( {1 - F_j^\alpha } \right)\ln \left( {1 - R_k^\alpha } \right)} \text{。} $ | (27) |
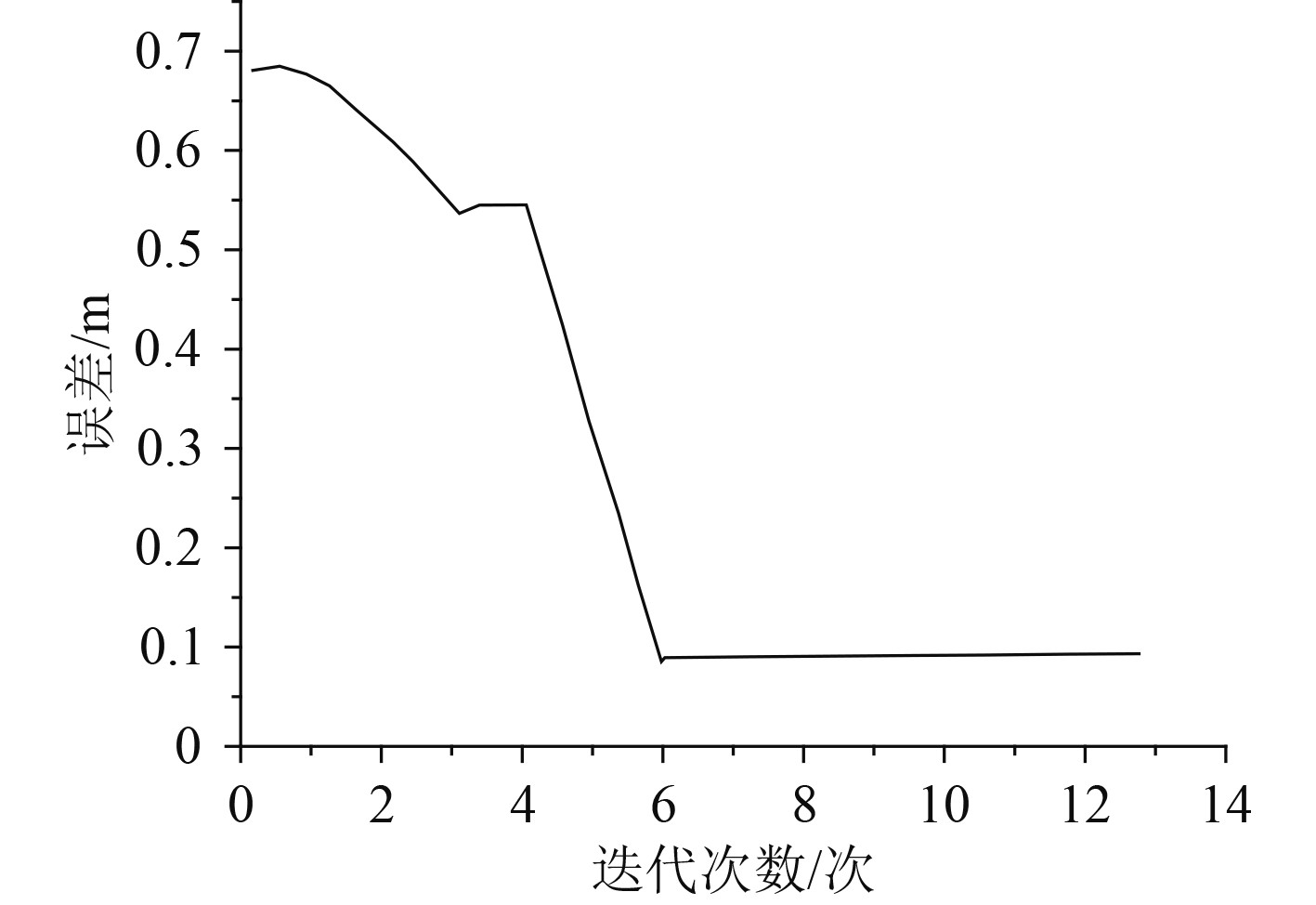
输出层中模糊推理的参数计算方法如式(28)和式(29)所示。神经网络的计算误差随迭代次数的变化情况如图3所示。
| $ {q_j}\left( {t + 1} \right) = {q_j}\left( t \right) + {\eta _q}\frac{{\partial E}}{{\partial {q_j}}}\text{,} $ | (28) |
| $ \frac{{\partial E}}{{\partial {q_j}}} = \frac{1}{{{q_j}}}\sum\limits_{j = 1}^M {\left( {\hat F_j^\alpha - F_j^\alpha } \right)\left( {1 - F_j^\alpha } \right)\ln \left( {1 - F_j^\alpha } \right)} \text{。} $ | (29) |
|
图 3 训练误差随迭代次数的变化曲线 Fig. 3 Curve of training error changing with iteration times |
海面上的船舶可以从已有的电子海图中得到航线上静态障碍物的各类信息,并利用这些障碍物的信息对船舶的全程航线进行规划,最终规划出安全的全局航线。由于船舶无法通过自身携带的电子航海图实时地获得航线上障碍物信息,这就导致海面上新添加的静态障碍物或者动态障碍物会对船舶的安全航行产生影响。
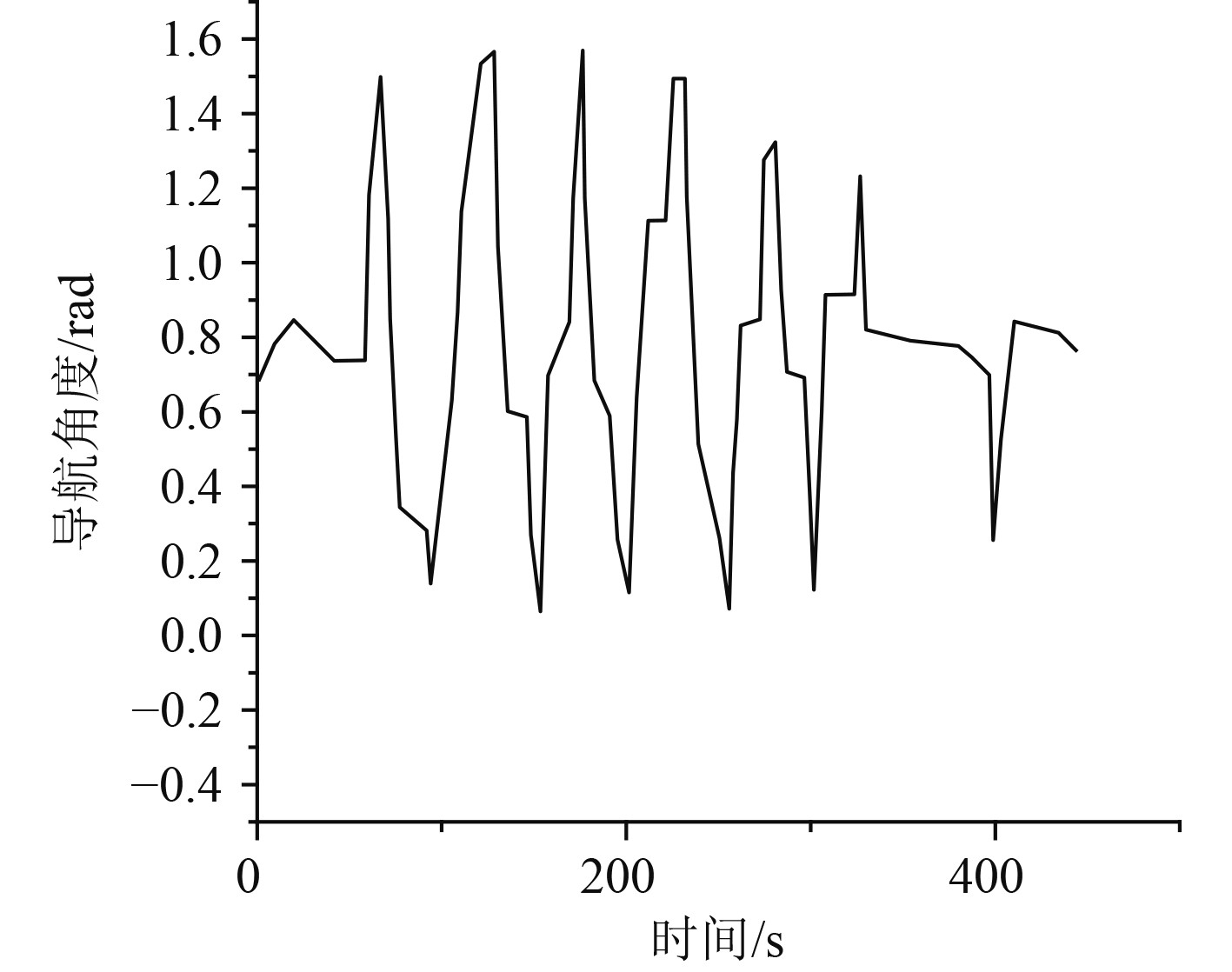
在对船舶进行避碰仿真实验的过程中,设置探测器最大的识别距离为220 m,海面上障碍物的膨胀系数为π/36,目标的波动距离为150 m。通过建立封闭式的障碍物区域对船舶的主动避碰算法进行仿真验证。船舶以航向稳态模型生成的导航角度为基础进行航行,同时船舶的航向稳态模型是构建在最优航向角之上的,因此船舶在海面上航行过程中可以避免局部最优,而实现航线全局最优,导航角度随时间变化曲线如图4所示。
|
图 4 导航角度随时间变化曲线 Fig. 4 Navigation angle curve with time |
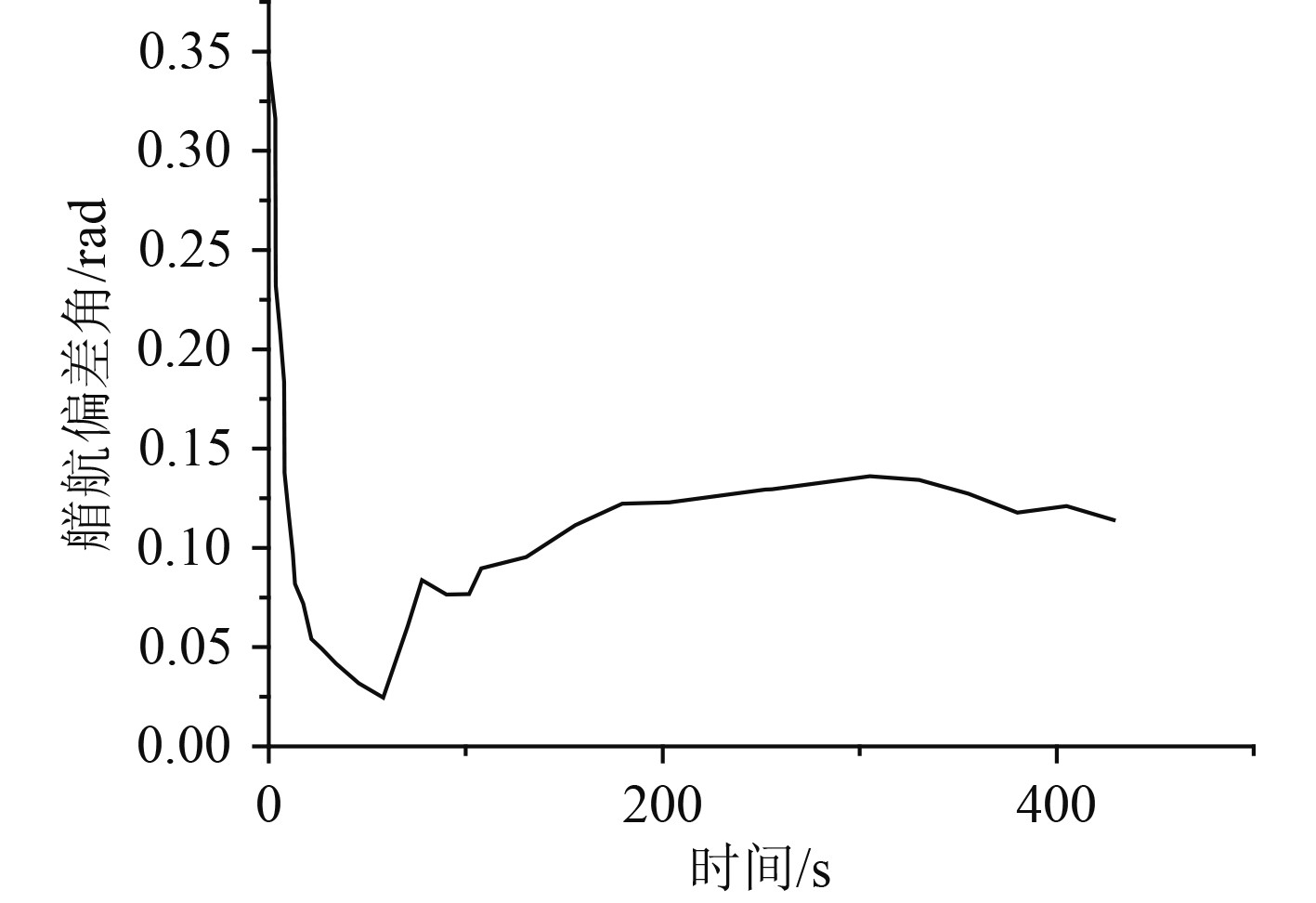
基于计算机技术的仿真测试环境下,由于船舶在航行过程中没有周围环境的干扰因素,因此船舶首向的变化受到导航角度的影响。本文引入首向偏差角来描述船舶避碰算法的稳定性,首向偏差角的计算方法如式(30)所示。船舶在封闭式的障碍物区域避碰仿真测试中,船舶首向偏差角变化情况如图5所示。
| $ {\bar \theta _{delta}} = \frac{1}{N}\sum\limits_{t = 1}^N {\left| {\theta _{delta}^t} \right|} \text{。} $ | (30) |
|
图 5 首向偏差角随时间变化曲线 Fig. 5 Time varying curve of yaw deviation angle |
为了保证船舶在海面上安全航行、降低航运成本、减少船员人数,以节能安全为目标,朝着高速、大型、高度智能化的方向发展。船舶主动避碰系统是船舶自动化研究中的重点问题。船舶在海面上的碰撞事故,不但会威胁到船员的生命财产安全,还会造成燃油泄漏等问题,从而影响到海洋环境。本文对船舶在海面上多目标侧向主动避碰算法进行研究,有助于船舶避碰技术的发展。
| [1] |
时继潮, 郝卓然, 徐娜, 等. 船舶自适应避碰系统设计[J]. 计算机与数字工程, 2019, 47(4): 1010-1013. |
| [2] |
喻伟, 张国庆, 陈海键. 分道通航制水域船舶的安全航行与避碰研究[J]. 广州航海学院学报, 2020, 28(3): 56-60. DOI:10.3969/j.issn.1009-8526.2020.03.012 |
| [3] |
路俊维, 马林霏, 陶智. 海上极端恶劣环境下舰船避碰系统设计[J]. 舰船科学技术, 2021, 43(18): 52-54. LU Jun-wei, MA Lin-fei, TAO Zhi. Design of ship collision avoidance system in extremely harsh environment at sea[J]. Ship Science and Technology, 2021, 43(18): 52-54. |
| [4] |
李美菊. 基于单片机的船舶主动避碰系统设计[J]. 舰船科学技术, 2015, 37(2): 160-163. LI Mei-ju. Design of ship collision avoidance system based on micro controller unit[J]. Ship Science and Techonogy, 2015, 37(2): 160-163. DOI:10.3404/j.issn.1672-7649.2015.02.035 |
| [5] |
丁志国, 张新宇, 王程博, 等. 基于驾驶实践的无人船智能避碰决策方法[J]. 中国舰船研究, 2021, 16(1): 96-113. |
| [6] |
茅云生, 彭伟, 向祖权, 等. 基于目标干扰意图识别的无人艇避碰算法[J]. 大连海事大学学报, 2021, 47(2): 26-34. |
| [7] |
贺益雄, 李丽玲, 胡惟璇, 等. 开阔水域直航船自主避碰决策方法[J]. 武汉理工大学学报, 2021, 45(5): 994-999. |
| [8] |
宋利飞, 杨远鹏, 徐凯凯, 等. 面向无人艇的船舶主动干扰意图识别模型[J]. 大连海事大学学报, 2022, 48(1): 73-82. |
| [9] |
曹海. 人工免疫算法的船舶避碰智能策略研究[J]. 舰船科学技术, 2016, 38(2): 10-12. |
| [10] |
范云生, 苏辉, 王国峰, 等. 无人水面艇自主航行能力测试技术与应用[J]. 大连海事大学学报, 2020, 46(3): 38-49. FAN Yun-sheng, SU Hui, WANG Guo-feng, et al. Testing technology and its application of autonomous navigation ability for unmanned surface veicle[J]. Journal of Dalian maritime University, 2020, 46(3): 38-49. DOI:10.16411/j.cnki.issn1006-7736.2020.03.005 |
 2022, Vol. 44
2022, Vol. 44
