0 引　言

由于船舶航行时，通常需要依据船舶自身的控制系统控制船体沿航线运动，若船舶航行时航线出现拥堵，系统会自动做出避碰举动，导致船舶航线出现异常点轨迹，若不对其展开深度数据挖掘^[1-2]，会直接影响船舶后期航行轨迹，导致船舶出现偏离航道情况。因此，提出基于船舶航行时的船舶避碰行为，对船舶航线上的异常轨迹点实施必要的数据动态挖掘，就显得尤为重要。

文献[3]提出一种多步骤船舶轨迹聚类方法。该方法压缩了船舶轨迹数据，并匹配了轨迹点。根据计算的距离相似性，完成了轨迹数据的聚类挖掘。但该方法挖掘异常轨迹点时容易受噪声影响，其挖掘准确率有待完善。文献[4]提出了基于改进K中心点聚类的船舶典型轨迹自适应挖掘算法，以轨迹点作为聚类对象,分析船舶的航速、航向特征并对轨迹点进行压缩。将分段均方根误差引入K中心点聚类算法，实现了轨迹数据自适应提取。但该方法在挖掘过程中的耗时有待完善。

为了提升船舶轨迹异常数据动态挖掘的效果，本文提出面向船舶避碰的异常轨迹点数据动态挖掘方法，利用小波去噪算法进行船舶异常轨迹点数据的去噪。结合长短期记忆网络构建船舶异常轨迹点的数据动态挖掘模型，实现异常轨迹点数据的挖掘。

1 轨迹异常点数据特征提取 1.1 船舶避碰危险程度分析

船舶在避碰过程中，行动领域的界限需要建立在船舶碰撞危险程度上。首先将船舶航行运行状态划分成碰撞会遇以及非碰撞会遇2种状态。受船吸现象影响，碰撞会遇通常是指当两船最小安全会遇距离小于船长的2倍时，产生的船舶会遇局面，而非碰撞会遇指的是碰撞会遇之外的船舶会遇情况，该种情况不意味船舶之间无碰撞风险，只是碰撞程度较为不同。

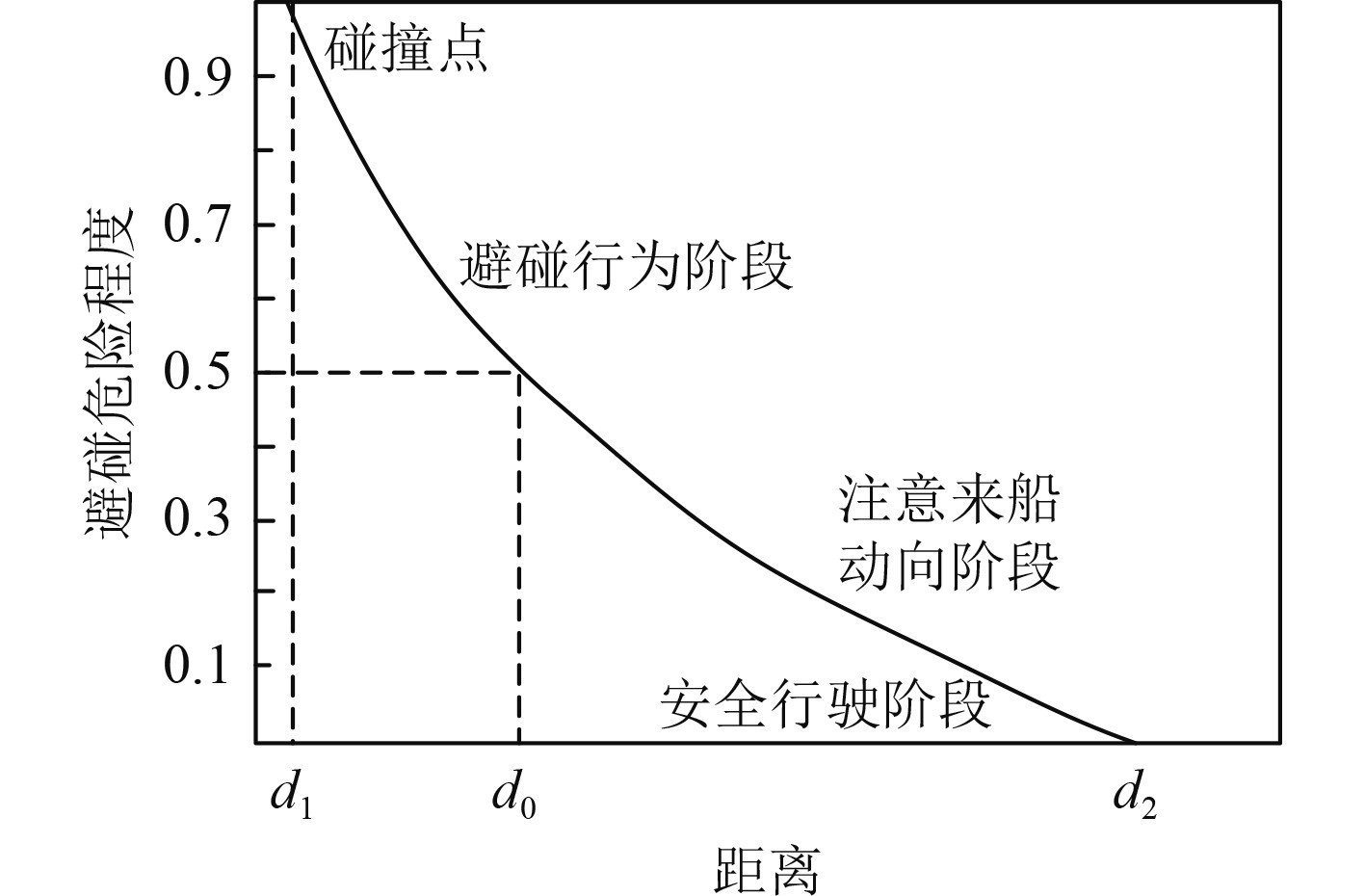
基于上述分析结果，获取船舶行驶时碰撞危险程度曲线图，如图1所示。

基于上述确定的船舶行驶避碰危险程度曲线，结合船舶行驶过程中会遇目标船只对本船的威胁程度变化，设定权重系数为 $ \alpha $ ，待定系数为 $ \ \beta $ ，获取船舶避碰危险程度数学表述形式，结果如下式：

$ CRI=\left\{\begin{array}{ll}1\text{，}&\left(d\leqslant {d}_{1}\right)，\\ \mathrm{min}\left(1,\alpha {e}^{\prime }\right), & \left({d}_{1} < d\leqslant {d}_{2}\right)，\\ 0,&\left(d > {d}_{2}\right)。\end{array}\right. $

(1)

式中： $ {d_1} $ 为船舶避碰时的碰撞距离； $ {d_2} $ 为注意距离； $ d $ 为目标船只至本船只距离； $ e^{\prime} $ 为船舶避碰危险系数函数。

1.2 轨迹异常点数据去噪

基于对船舶行驶避碰危险程度分析结果，在船舶异常轨迹点数据动态挖掘前，确定船舶发生避碰时的危险程度，采集异常轨迹点的运行数据，并基于小波阈值去噪算法对采集数据展开去噪处理，获取完整的船舶异常轨迹点数据集合。

异常数据中的噪声能量则会在映射完成后整体分布于数据信号的小波域中，导致小波分解后信号稀疏大于噪声系数。这时在数据的小波尺度上建立一个阈值门限 $ \chi $ ，当获取的小波系数低于该阈值门限时，即可确定该小波系数是噪声引起的，可立刻对其展开处理，实现数据噪声去除。具体去噪流程如下：

1）小波分解

设定原始船舶异常轨迹点数据信号为 $ f\left( t \right) $ ，选取合适的小波函数以及分解层数，对含有噪声的数据信号实施正交小波变换，过程如下：

$ F\left( w \right) = {\phi _{j,k}}\frac{1}{{\sqrt a }}\int_{ - \infty }^\infty {f\left( t \right) \cdot \delta \frac{{\left( {t - \varepsilon } \right)}}{a}{\rm{d}}t} 。$

(2)

式中： $ F\left( w \right) $ 为数据信号的小波变换结果； $ {\phi _{j,k}} $ 为数据信号的尺度 $ {\rm{d}}t $ 分解系数； $ f\left( t \right) $ 为原始数据信号； $ \delta \dfrac{{\left( {t - \varepsilon } \right)}}{a} $ 为小波函数。

2）建立小波阈值函数

选取合适的去噪阈值 $ \chi $ 建立阈值函数，对不同尺度的小波系数实施阈值处理，获取信号的估计小波系数值，并基于计算结果使小波系数估计值无限接近无噪声数据信号的小波变换系数。

由于传统阈值函数有软阈值函数与硬阈值函数2种，表述形式如下式：

$ \left\{ {\begin{array}{*{20}{l}} {y{{\hat \phi }_{j,k}} = \left\{ {\begin{array}{*{20}{c}} {\phi _{j,k}},&\left| {{\phi _{j,k}}} \right| \geqslant \chi，\\ 0,&\left| {{\phi _{j,k}}} \right| < \chi 。\end{array}} \right.} \\ {r{{\hat \phi }_{j,k}} = \left\{ {\begin{array}{*{20}{c}} {{\rm{sgn}}} \left( {{\phi _{j,k}}} \right)\left( {\left| {{\phi _{j,k}}} \right| - \chi } \right),&\left| {{\phi _{j,k}}} \right| \geqslant \chi，\\ 0,&\left| {{\phi _{j,k}}} \right| < \chi 。\end{array}} \right.} \end{array}} \right. $

(3)

式中： $ y{\hat \phi _{j,k}} $ 为硬阈值函数； $ r{\hat \phi _{j,k}} $ 为软阈值函数； $ {{\rm{sgn}}} \left( {{\phi _{j,k}}} \right) $ 为符号函数。建立新的阈值去噪函数，过程如下式：

$ x{\hat \phi _{j,k}} = \left\{ {\begin{array}{*{20}{c}} {{\rm{sgn}}}& \left( {{\phi _{j,k}}} \right){{\left( {{\phi _{j,k}}^2 - {\chi ^2}} \right)}^{1/2}},\left| {{\phi _{j,k}}} \right| \geqslant \chi ，\\ 0,&\qquad\quad\qquad\qquad\quad\,\, \left| {{\phi _{j,k}}} \right| < \chi 。\end{array}} \right. $

(4)

式中， $ x{\hat \phi _{j,k}} $ 为建立的新阈值函数。

3）完成信号去噪重构

通过对小波分解层级低频系数以及阈值函数计算出的分解系数估计值，对数据信号开展小波逆变换，完成数据信号的重构，实现船舶异常轨迹点运行数据的去噪处理

2 船舶异常轨迹点数据动态挖掘 2.1 异常轨迹点特征提取

由于轨迹数据是船舶一系列时间变化下的时空数据点，数据中包括船舶航速、加速度、航向以及转角、曲率等参数。因此设定船舶航行时，轨迹点 $ {P_i} $ 与上一轨迹点 $ {P_{i - 1}} $ 之间的距离为 $ d\left( {{P_i},{P_{i - 1}}} \right) $ ，以此计算船舶在异常轨迹点的航速和加速度，结果如下：

$ \left\{ {\begin{array}{*{20}{c}} {{v_i} = \dfrac{{d\left( {{P_i},{P_{i - 1}}} \right)}}{{{t_i} - {t_{i - 1}}}}}，\\ {{\varphi _i} = \dfrac{{{v_i} - {v_{i - 1}}}}{{{t_i} - {t_{i - 1}}}}} 。\end{array}} \right. $

(5)

式中： $ {v_i} $ 为船舶在异常轨迹点的航速； $ {\varphi _i} $ 为加速度； $ {t_i} $ 为船舶移动值异常轨迹点状态； $ {t_{i - 1}} $ 为上一时刻状态。

在船舶航行时，当前轨迹点与后一时刻轨迹之间的连线夹角为航向，转角则为连续2个轨迹点航向之间的变化，而转角率则是连续轨迹点转角变化与时间的比值，航向、转角以及转角率特征提取结果如下：

$ \left\{ \begin{gathered} {\zeta _i} = \arctan \left( {X,Y} \right)，\\ X = \cos \left( {{\gamma _i}} \right) \cdot \sin \left( {{\eta _i} - {\eta _{i - 1}}} \right)，\\ Y = \cos \left( {{\gamma _{i - 1}}} \right) \cdot \sin \left( {{\gamma _i}} \right) - \sin \left( {{\gamma _{i - 1}}} \right) \cdot \cos \left( {{\gamma _i}} \right) \cdot \sin \left( {{\eta _i} - {\eta _{i - 1}}} \right)。\\ \end{gathered} \right. $

(6)

$ \left\{ \begin{gathered} {\iota _i} = {\zeta _{i - 1}} - {\zeta _i} ，\\ {\omega _i} = \frac{{{\iota _i} - {\iota _{i - 1}}}}{{{t_i} - {t_{i - 1}}}} 。\\ \end{gathered} \right. $

(7)

式中： $ {\zeta _i} $ 为船舶在异常轨迹点的航向； $ {\iota _i} $ 为转角值； $ {\omega _i} $ 为转角率； $ \arctan \left( {X,Y} \right) $ 为轨迹点位置； $ \left( {{\gamma _i},{\eta _i}} \right) $ 为坐标精度。船舶航行时，曲率为轨迹点两点之间的直线距离比值，通常正常轨迹点的曲率要低于异常点曲率，获取流程如下：

$ {q_i} = \frac{{d\left( {{P_i},{P_{i - 1}}} \right) + d\left( {{P_i},{P_{i + 1}}} \right)}}{{d\left( {{P_i},{P_{i + 1}}} \right)}}。$

(8)

式中， $ {q_i} $ 为船舶异常轨迹点曲率值。

2.2 建立数据动态挖掘模型

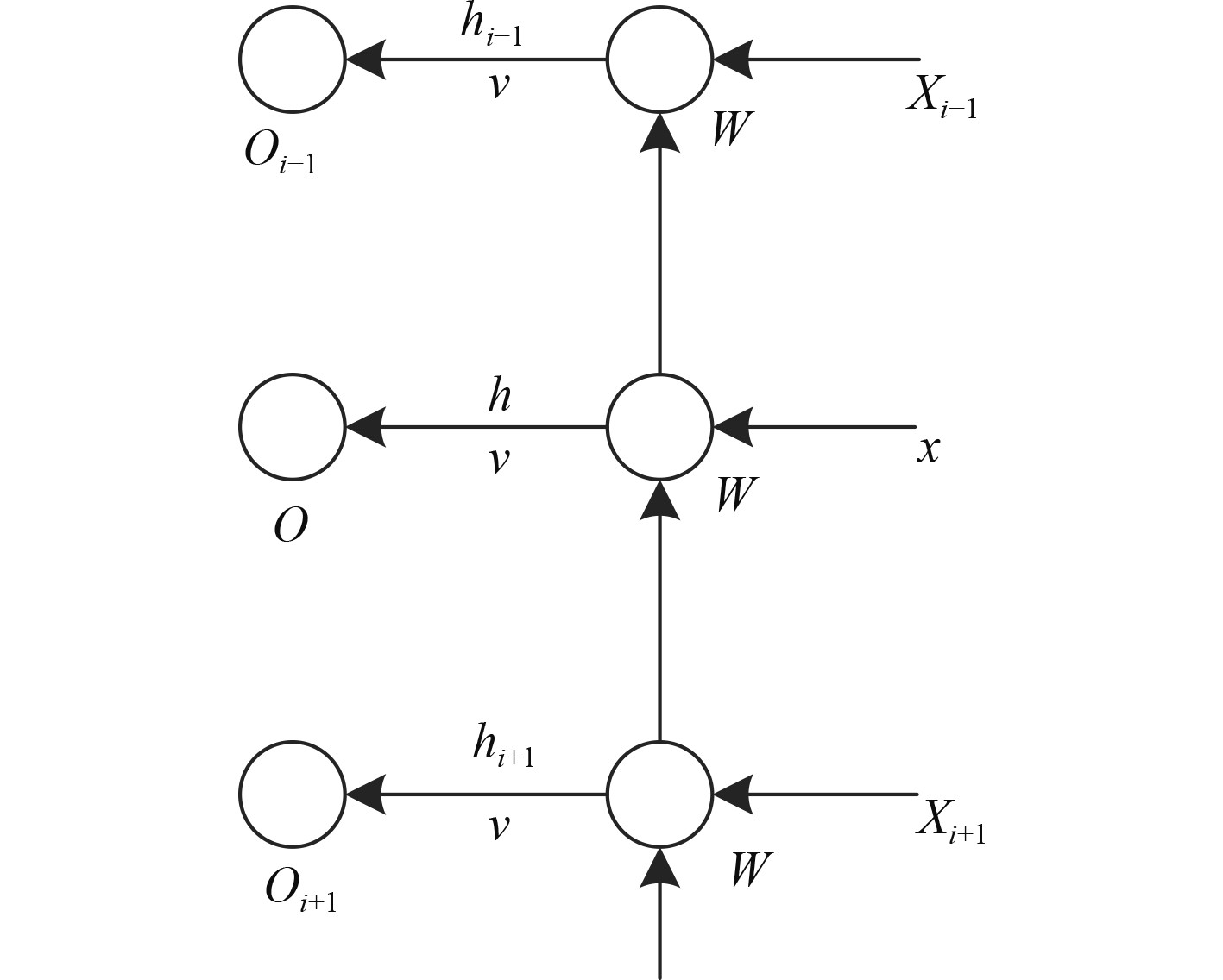
基于上述提取的船舶异常轨迹点各项特征值，结合长短期记忆神经网络构建船舶异常轨迹点的数据深度动态挖掘模型，并将提取的特征值作为模型输入值，输入构建的挖掘模型中，通过模型输出结果实现船舶异常轨迹点的数据动态挖掘。长短期记忆神经网络的具体结构如图2所示。

可知，长短期记忆网络是由输入向量 $ x $ 、隐含层 $ h $ 以及输出层组成的，每个层级都存在若干节点，层级权重表述成 $ U,V $ 形式。基于上述神经网络结构分析结果，设定网络激活函数为 $ a,b $ ，以此计算神经网络输出层输入权值以及输出层的输出结果，过程如下：

$ \left\{ {\begin{array}{*{20}{l}} {{r_t} = a\left( {U{x_t} + W{r_{t - 1}}} \right)}，\\ {{o_t} = b\left( {V{r_t}} \right)} 。\end{array}} \right. $

(9)

式中： $ {r_t} $ 为神经网络隐含层输出层输入权值； $ {o_t} $ 为输出层的输出结果。

由于长短期记忆神经网络能够有效保存历史数据，获取数据的时间序列特征，因此设定船舶异常轨迹点形式轨迹为 $ K = \left( {{\kappa _1},{\kappa _2}, \cdots ,{\kappa _{i - 1}},{\kappa _i}} \right) $ ，长短期记忆模型为 $ L $ ，以此构建船舶异常轨迹点的数据深度动态挖掘模型，过程如下：

$ {K_{\hat y}} = L\left( {{\kappa _1},{\kappa _2}, \cdots ,{\kappa _{i - 1}},{\kappa _i}} \right)，$

(10)

式中， $ {K_{\hat y}} $ 为建立的船舶异常轨迹点数据深度动态挖掘模型。

完成模型建立后，设定提取的异常轨迹点特征有 $ n $ 个，随机选取 $ m $ 个特征展开变异处理，对模型输入特征实施重新赋值，结果如下：

$ \left\{ {\begin{array}{*{20}{l}} {0 \leqslant c \leqslant \mu \left( {{p_{\max }} - {p_i}} \right)}，\\ {{p_{ic}} = {p_i} + \theta \cdot c} 。\end{array}} \right. $

(11)

式中： $ \mu $ 为变异因子； $ c $ 为随机生成输入值数量； $ {p_{\max }} $ 为最大输入特征向量； $ \theta $ 为约束条件； $ {p_{ic}} $ 为特征向量重新赋值结果。

最后将重新赋值后的轨迹点异常数据特征值放入建立的深度挖掘模型中，基于模型的输出结果，确定船舶异常轨迹点异常动态类型，完成船舶异常轨迹点的异常轨迹点数据动态挖掘。

3 实　验 3.1 实验结果及分析

分别采用面向船舶避碰的异常轨迹点数据动态挖掘方法（本文方法）、多步骤船舶轨迹聚类方法研究与实现（文献[3]方法）、基于改进K中心点聚类的船舶典型轨迹自适应挖掘算法（文献[4]方法）进行测试。

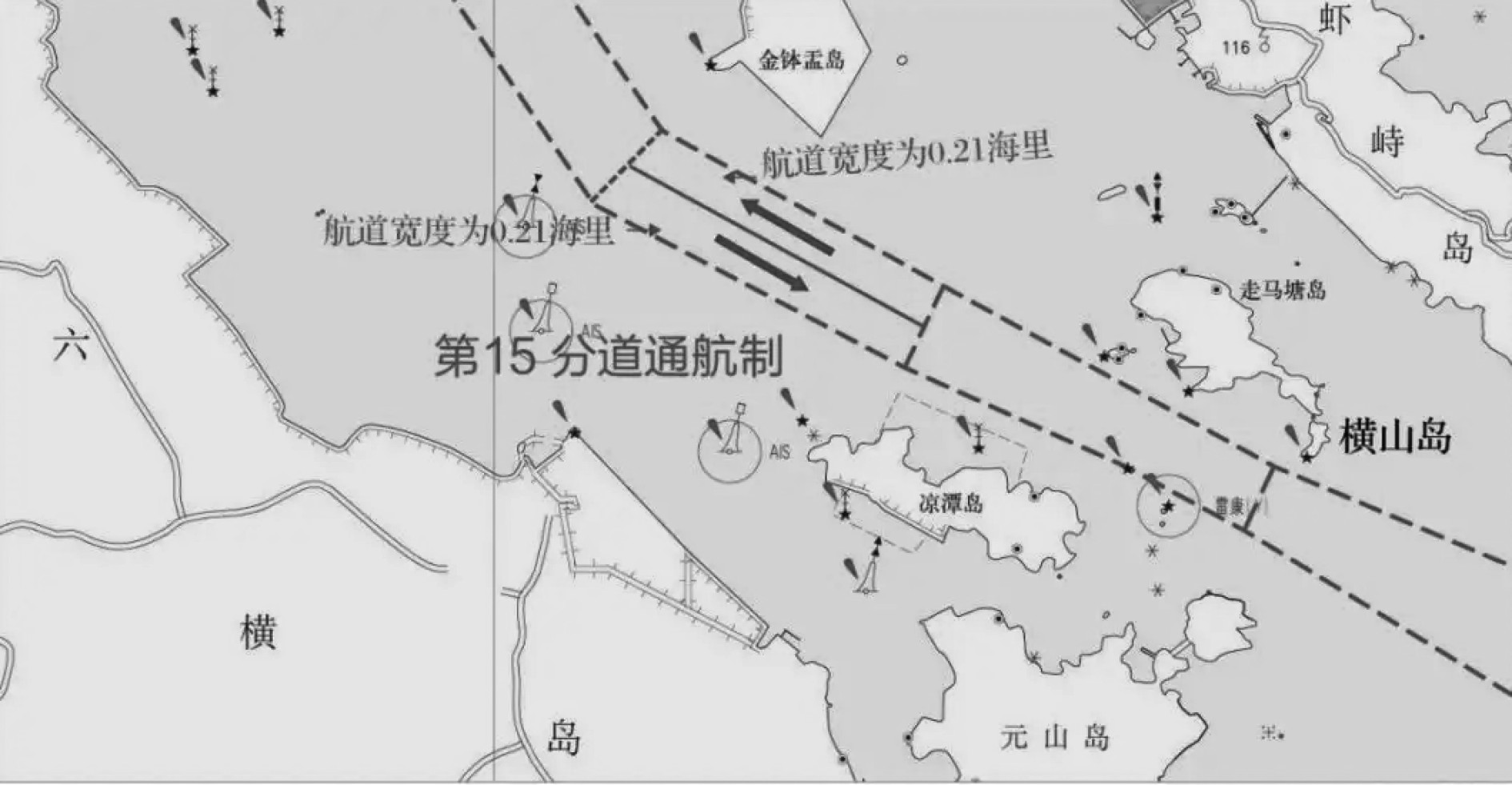
选取某地港口主航道作为本次测试实际环境，测试过程将2021年8月1日至9月1日期间内船舶航行数据作为样本数据集合，并在其中随机选取50条船舶避碰轨迹路线。将实际环境输入到Matlab仿真平台中输出仿真数据，建立异常轨迹点的数据样本测试集合，以此验证上述3种方法在异常轨迹点数据动态挖掘时的有效性。实际航线环境如图3所示。

1）挖掘性能测试

基于本文方法、文献[3]方法以及文献[4]方法开展数据动态挖掘时，将准确率和误检率以及平均挖掘时间作为数据动态挖掘方法的挖掘性能评价标准，测试上述3种方法在异常数据动态挖掘时，不同挖掘方法的挖掘性能。

设定异常轨迹点数据动态挖掘时，准确率为Accuracy，误检率为 $ {\text{noise factor}} $ ，以此获取评价标准计算过程，结果如下：

$ \left\{ \begin{gathered} {\text{Accuracy = }}\frac{{TP}}{{TP + FN}}，\\ {\text{noise factor = }}\frac{{FP}}{{FP + TP}} 。\\ \end{gathered} \right. $

(12)

式中： $ TP $ 为正确挖掘出的异常数据动态类型； $ FN $ 为数据异常类型的正确挖掘结果； $ FP $ 为错误挖掘结果。不同异常轨迹数据动态挖掘方法的挖掘准确率、误检率测试结果如图4所示。

不同方法在数据动态挖掘时的平均挖掘时间，如表1所示。

分析可知，在开展数据动态挖掘时，本文方法检测出的准确率、误检率以及平均挖掘时间都优于文献[3]方法以及文献[4]方法的测试结果。本文方法在数据动态挖掘前，充分分析了船舶避碰状态并且及时的对采集的数据实施噪声剔除，所以该方法在数据动态挖掘时的，挖掘准确率、误检率以及挖掘时间都优于其他方法。

2）挖掘效果测试

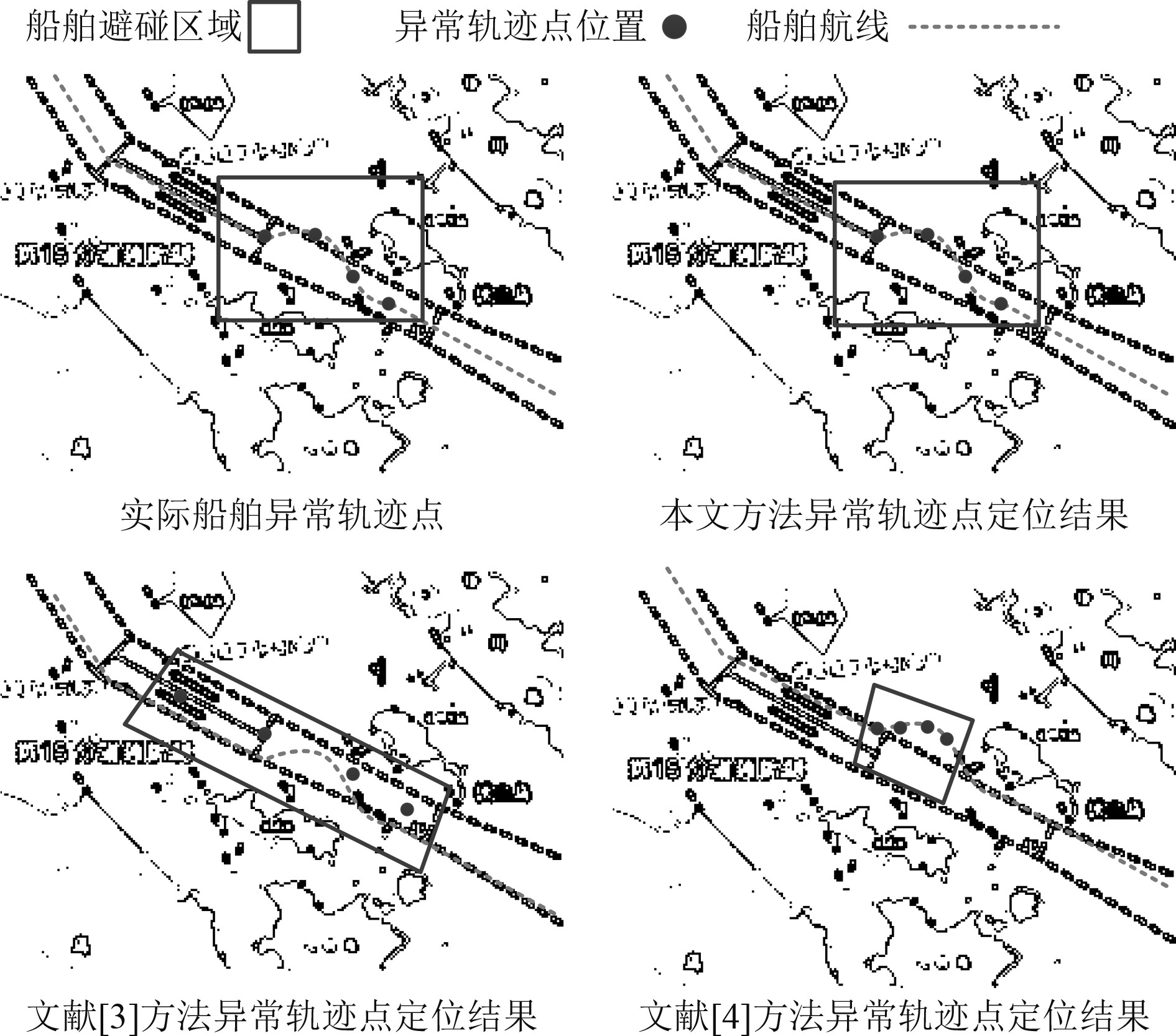
基于上述挖掘性能检测结果，将3种不同的数据挖掘方法实际应用到船舶异常轨迹点数据动态挖掘当中，通过对异常轨迹点定位结果的验证，验证不同挖掘方法实际数据挖掘效果，结果如图5所示。

可知，本文方法能够在船舶异常轨迹点数据动态挖掘时，有效地完成异常轨迹点的精准定位，且划分的船舶避碰区域与实际船舶避碰区域一致，由此可证明本文方法在船舶异常轨迹点数据动态挖掘时，挖掘效果好。

4 结　语

船舶异常轨迹点数据挖掘是当前的重要研究课题，针对传统数据挖掘方法中存在的问题，提出面向船舶避碰的异常轨迹点数据动态挖掘方法。该方法基于船舶避碰行为分析结果，采集异常轨迹点数据，通过数据的去噪结果完成异常轨迹点参数特征的提取。最后通过建立的异常轨迹点数据深度挖掘模型，实现对船舶避碰异常轨迹点数据动态挖掘。