随着计算机技术的迅速发展,计算机辅助设计与制造(CAD/CAM)技术在制造业中的应用范围越来越广,在提升产品设计质量、缩短产品开发周期等方面发挥着重要作用。传统的CAD/CAM开发模式是一种正向开发,从提出设计需求,到设计迭代、部件生产装配到产品发货,每一个环节都需要投入大量的成本和精力。逆向工程是从成熟的产品出发,利用三维扫描、CAD/CAM快速成型等方式,直接得到新产品。这种技术有助于提高产品的设计水平,目前在船舶等行业有重要的应用。
在逆向工程中,三维模型的逆向重建技术是其中的关键。利用计算机扫描仪获取的产品三维数据以数据点云的形式存储在计算机中,三维模型的重建包括数据预处理、特征提取、曲线与曲面重建等。本文介绍逆向三维重建技术的现状,对逆向三维建模中的数据特征提取进行详细研究。
1 船舱三维建模与逆向工程技术的研究现状逆向三维重构技术从产品出发,利用计算机视觉技术、测量技术获取初步模型点云,然后利用模型重构和特征提取算法获取最终模型,最后利用CAE系统实现快速加工和生产。
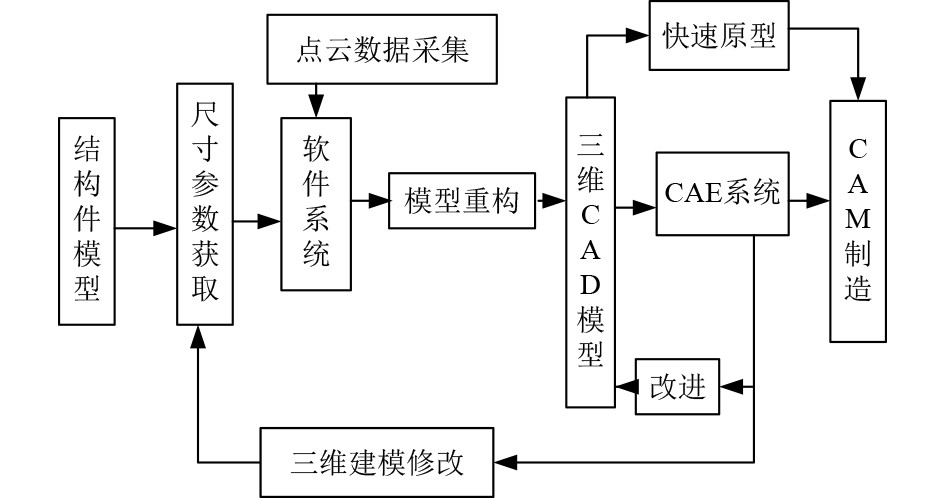
逆向三维重构技术的原理如图1所示。
|
图 1 逆向三维重构技术的原理图 Fig. 1 Schematic diagram of reverse 3D reconstruction technology |
逆向三维重构的关键技术包括:
1)数字化测量[1]
逆向三维重构的关键是模型点云粒子数据的获取,传统的获取方式以三坐标测量仪为主,这种测量方式尽管精度较高,但效率相对较低,且被测产品的尺寸受到限制,对于船舶这种大型结构件难以实现。数字化测量技术利用扫描仪和计算机视觉设备,直接对产品进行扫描,不仅不会受到产品外型尺寸的限制,数据获取的效率也非常高。目前,工业摄像机配合OPENGL图像处理设备已经成为逆向三维重构的主流手段。
2)加工一体化
加工一体化是利用CAD/CAM系统,在三维模型重构完成后进行快速的加工和制造,系统可以根据结构件的外型特性实现刀具轨迹、参数的设计,并直接生成GM代码和数控加工程序。加工一体化能够显著提升产品的生产效率。
2 基于粒子计算的船舱三维数据特征提取系统设计 2.1 船舱三维粒子数据的离散特性点云粒子数据是三维扫描生成的粒子数据,能够精确描述某一产品外型的关键点和产品表面的关键几何信息。从粒子数据中提取出产品的外型关键特征,并根据这些特征生成特征线、特征面,这一过程是实现三维重构的关键[2]。
本文使用的粒子算法是一种基于离散导数估算的方法,该方法利用离散导数和微分几何理论,对几何特性进行离散化,估算出曲线的几何特性。
离散导数的定义为:
| $ {y_i} = {f_d}\left( {{x_i}} \right) \text{,} {x_i} \in \left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\} \text{。} $ |
其在点
| $ y_k^\prime = f_d^\prime \left( {{x_i}} \right) = \frac{{\displaystyle\sum\limits_{j = k - {m_1}}^{k + {m_1}} {\left( {{x_j} - {x_k}} \right)} \left( {{y_j} - {y_k}} \right)}}{{\displaystyle\sum\limits_{j = k - {m_1}}^{k + {m_1}} {{{\left( {{x_j} - {x_k}} \right)}^2}} }} \text{。} $ |
相对应的,其在点
| $ y_k^{(n)} = f_d^{(n)}\left( {{x_k}} \right) = \frac{{\displaystyle\sum\limits_{j = k - {m_n}}^{k + {m_n}} {\left( {{x_j} - {x_k}} \right)} \left( {y_j^{(n - 1)} - y_k^{(n - 1)}} \right)}}{{\displaystyle\sum\limits_{j = k - {m_n}}^{k + {m_n}} {{{\left( {{x_j} - {x_k}} \right)}^2}} }} 。$ |
定义好离散导数后,需要利用累积弦长对粒子数据
| $ {t_i} = \frac{{\displaystyle\sum\limits_{j = 1}^{n - 1} {\left| {{p_j}} \right|} }}{{\displaystyle\sum\limits_{j = 1}^{n - 1} {\left| {{p_{j + 1}} - {p_j}} \right|} }},2 \leqslant i \leqslant j \leqslant n \text{。} $ |
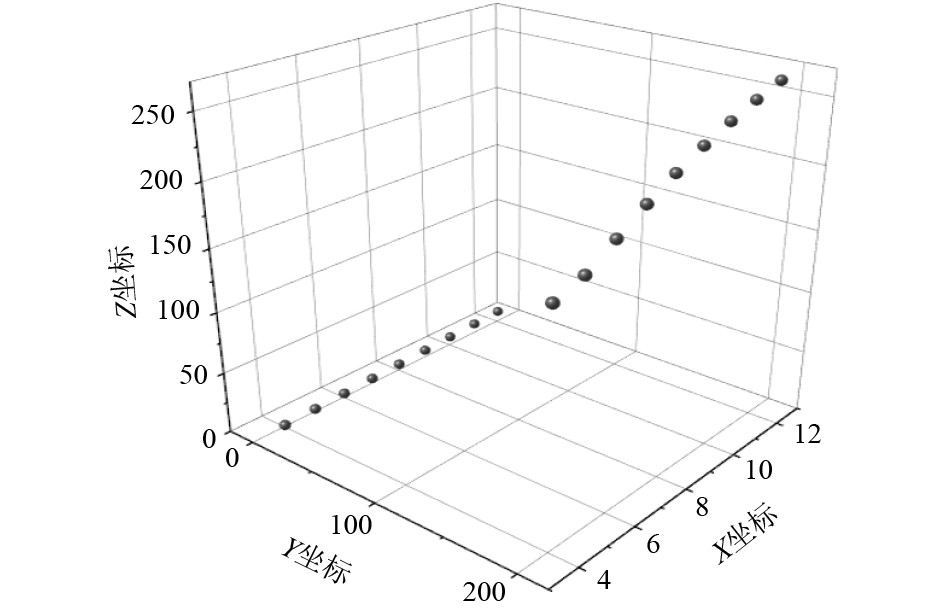
利用累积弦长和离散导数可以判断点云粒子数据中曲线与曲面的不连续性,比如法向量不连续、曲率不连续等,图2为空间点云粒子数据的法向量不连续示意图。
|
图 2 空间点云粒子数据的法向量不连续示意图 Fig. 2 Diagram of normal vector discontinuity of spatial point cloud data |
针对船舱的三维重构进行研究时,重点对粒子数据的曲率特性进行分析,粒子数据的曲率定义是指以采样点为中心的邻域范围切平面曲率。粒子数据的曲率特性包括:
1)曲率表征曲线的弯曲程度
曲线越弯曲,对于其切向力的方向变化就越快,定义采样点的曲线为:
| $ \lambda \left( s \right) = \frac{{\Delta \varphi }}{{\Delta s}} \text{。} $ |
式中:
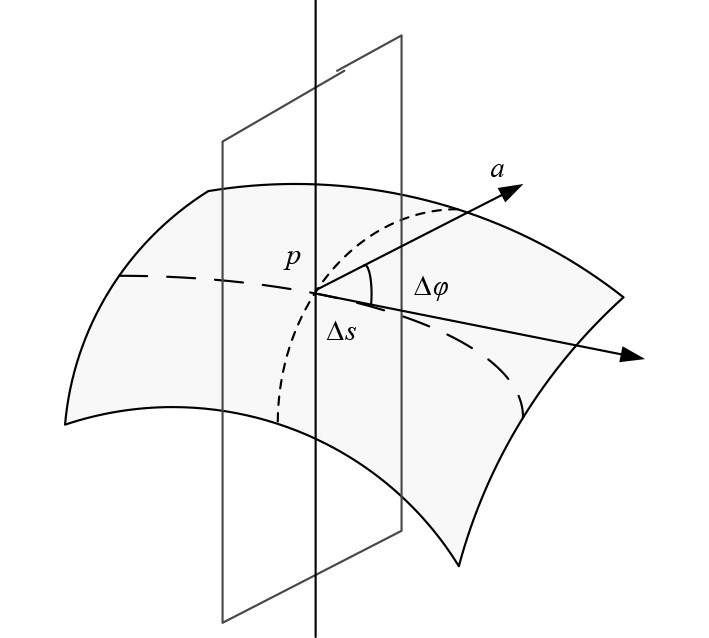
|
图 3 空间点云粒子数据的曲率示意图 Fig. 3 Curvature diagram of space point cloud particle data |
2)曲面的表示形式
对于点云粒子数据的曲面描述主要有2种,参数坐标形式:
| $ \left\{ \begin{gathered} x = x\left( {u,v} \right),\\ y = y\left( {u,v} \right),\\ z = z\left( {u,v} \right) 。\\ \end{gathered} \right. $ |
向量形式:
| $ \vec {\boldsymbol{S}} = \vec {\boldsymbol{S}}\left( {u,v} \right) = \left\{ {x\left( {u,v} \right),y\left( {u,v} \right),z\left( {u,v} \right)} \right\} 。$ |
在船舱三维数据特征提取过程中,使用的算法为LOF粒子检测算法,该算法的核心是对每个粒子对象赋予离群因子,根据离群因子判断该粒子的孤立程度,LOF值越大,粒子数据是异常数据的可能性越高。
LOF粒子检测算法的关键参数:
1)第K距离
粒子数据P的
2)可达距离
粒子q与粒子对象p的可达距离定义为:
| $ rea = \max \left( {k - dis\left( p \right),p = 0,1,...,n} \right) \text{。} $ |
3)离群因子
粒子p局部区域的离散状态,定义为:
| $ LOF\left( p \right) = \frac{1}{{\left( {\dfrac{{\displaystyle\sum\limits_{p = 1}^n {rea\left( p \right) - \left( {k - {\rm{dis}}\left( p \right)} \right)} }}{n}} \right)}} \text{。} $ |
利用LOF粒子算法能够提高船舱点云数据的拟合精度,剔除异常粒子数据。
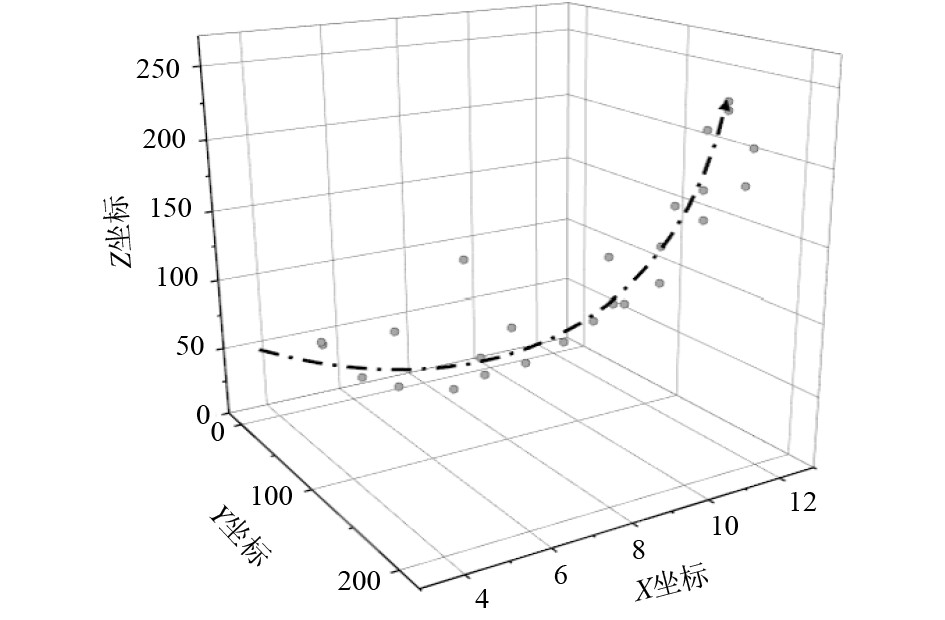
图4为基于LOF粒子算法的点云数据拟合示意图。
|
图 4 基于LOF粒子算法的点云数据拟合示意 Fig. 4 Sketch map of point cloud data fitting based on LOF particle algorithm |
图中使用的拟合曲线主要有:
1)Bezier曲线
Bezier曲线由可伸缩的线段和节点组成,定义如下:
| $ B\left( t \right) = \sum\limits_{i = 1}^n {{B_{i,n}}\left( t \right)} \text{,} $ |
式中,n为Bezier曲线的阶数,其基函数[3]为:
| $ {B_{i,n}}\left( t \right) = \frac{n}{{i\left( {i - t} \right)}}{t^2}{\left( {1 - t} \right)^{n - 2}} \text{。} $ |
2)NURBS样条曲线
NURBS样条曲线是非均匀曲线的一种,其定义为:
| $ f\left( t \right) = \frac{{\displaystyle\sum\limits_{i = 1}^n {{p_{i,n}}\left( t \right){N_{i,k}}\left( t \right)} }}{{\displaystyle\sum\limits_{i = 0}^n {{w_i}{N_{i,k}}\left( t \right)} }} \text{,} $ |
式中,
3)B-Spline曲线
| $ f\left( t \right) = \sum\limits_{i = 0}^n {{s_i}{S_{i,k}}\left( t \right),\;\;0 \leqslant t \leqslant 1} \text{,} $ |
其中,
本文针对船舱的三维模型重构进行相应的计算机系统开发,利用C++仿真语言和OpenGL开源图形库,在Windows环境下进行船舱三维数据特征提取系统的设计与开发。
船舱三维数据特征提取系统的具体配置如表1所示。
|
|
表 1 三维数据特征提取系统的具体配置表 Tab.1 Specific configuration table of 3D data feature extraction system |
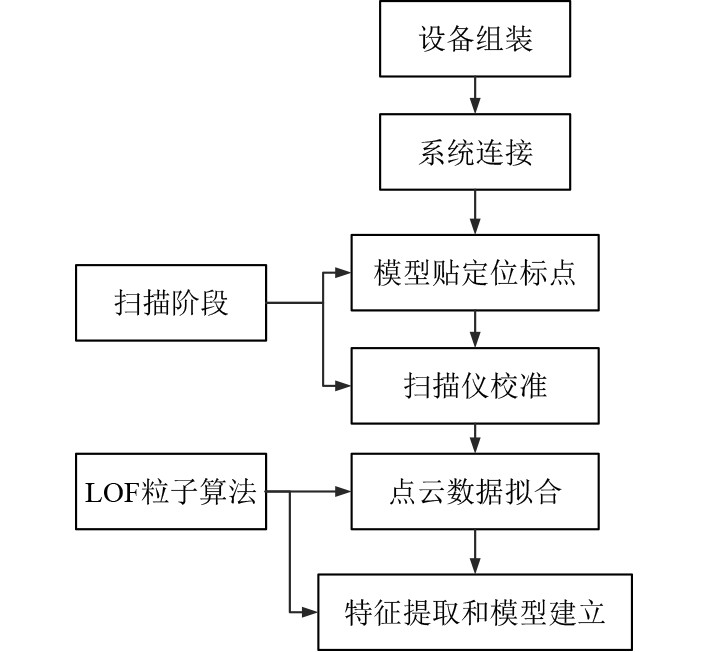
船舱三维数据特征提取系统的工作流程如图5所示。
|
图 5 船舱三维数据特征提取系统的工作流程 Fig. 5 Workflow of cabin 3D data feature extraction system |
| [1] |
刘界鹏. 基于三维激光扫描的房屋尺寸质量智能化检测方法[J]. 建筑科学与工程学报, 2022, 39(4): 71-80+3-4. LIU Jie-peng. Intelligent detection method of building size and quality based on 3D laser scanning[J]. Journal of Building Science and Engineering, 2022, 39(4): 71-80+3-4. |
| [2] |
朱明芳. 基于底面特征匹配的钢结构桥梁虚拟预拼装[J]. 北京测绘, 2022, 36(2): 168-172. ZHU Ming-fang. Virtual pre assembly of steel structure bridges based on bottom feature matching[J]. Beijing Surveying and Mapping, 2022, 36(2): 168-172. |
| [3] |
蒋心学, 唐飞笼, 杨迪. 机载三维激光点云数据分类数学模型[J]. 激光杂志, 2021, 42(7): 142-146. JIANG Xin-xue, TANG Fei-long, YANG Di. Mathematical model of airborne three-dimensional laser point cloud data classification[J]. Laser Journal, 2021, 42(7): 142-146. DOI:10.14016/j.cnki.jgzz.2021.07.142 |
 2022, Vol. 44
2022, Vol. 44
