伴随着雷达系统的快速发展,阵列天线作为其电磁波收发装置的核心备受关注。如何通过对天线单元幅相激励的综合来实现所需天线阵列方向图,一直是研究的热点[1]。由于天线系统应用需求及环境的复杂化,传统的天线综合技术往往显得乏力,而基于仿生技术的各类优化算法的方向图综合技术得到了极大的发展,如遗传算法(genetic algorithm,GA)、模拟退火算法(simulated annealing, SA)、粒子群算法(particle swarm optimization, PSO)等。在这些优化算法中,Storn等[2]在1997年提出的差分进化算法(differential evolution, DE)以其卓越的性能得到广泛关注[3]。其具有运算步骤简单、收敛迅速、善于解决多变量问题等优点,已广泛应用于机械设计[4]、材料研究[5]、通信系统[6]以及各种天线阵方向图综合方面[7-13]。
本文将该算法应用于阵列天线宽波束综合和低副瓣综合两类问题。在此两类应用问题中,DE算法不需要初值信息,可以快速、高效地找到最优解,是传统优化算法不可比拟的。
1 设计目标本文介绍2个算法实例,分别实现平面矩形阵列天线的宽波束方向图综合和低副瓣方向图综合。
宽波束天线阵列形式:矩形阵列;单元数22×6,水平单元数22个,垂直单元数6个;水平和垂直间距均为0.5 λ;水平方向实现宽波束扇形扫描,扫描范围–45°~45°。
低副瓣天线阵列形式:矩形阵列;单元数20×8,水平单元数20个,垂直单元数8个;水平和垂直间距均为0.5 λ;水平辐射方向图实现低副瓣–30 dB性能。天线增益因幅度加权,下降不能超过1 dB。
2 优化设计模型及其求解算法算法设计模型分3个部分:第1部分为通用的DE优化算法模型及求解过程;第2部分为针对宽波束方向图综合所设计的目标函数及其求解过程;第3部分为针对低副瓣方向图综合所设计的目标函数及其求解过程。
2.1 差分进化算法差分进化算法是一个并行直接搜索方法。它的每一代采用NP个D维参数向量作为种群,种群个数NP不随最小化优化过程变化,初始种群随机选择并包含整个参数变量空间。DE算法通过2个不同的个体向量相减产生差分向量,将差分向量赋予权值后与第3个向量相加,即产生变异向量
| $ {{{X}}_{i,G}}, i = 1,2 \ldots NP\text{。} $ | (1) |
式中:
工程设计采用策略如下:
变异:对于目标向量
| $ {{V}_{i,G}} = {X_{r2,G}} + F({X_{r2,G}} - {X_{r3,G}})\text{。} $ | (2) |
式中:
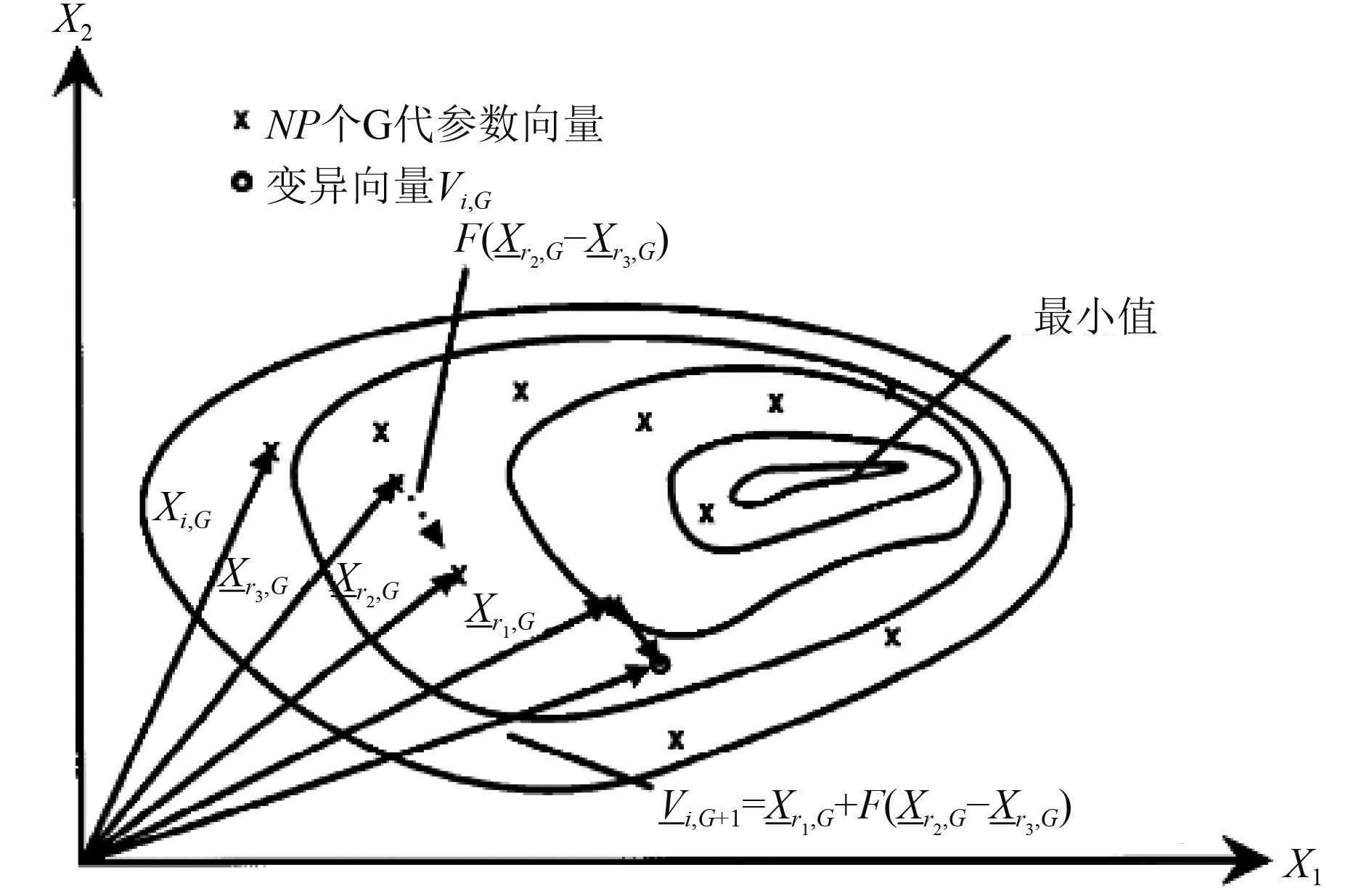
|
图 1 二维DE算法变异过程示例 Fig. 1 Two-dimensional differential evolution algorithm mutation process example |
交叉:第i个变异向量
| $ {{{U}}_{{{ji,}}G}} = \left\{ \begin{aligned}&{{{V}}_{{{ji,}}G}},\;\;\;{\rm{if}}\; {\rm{rand}}\left( j \right) \leqslant CR\;\; {\rm{or}}\;\; j = k\text{,}\\ &{X_{{{ji,}}G}},\;\;\;{\rm{else}},\end{aligned}\right. j=1\sim {{D}}\text{。}$ | (3) |
需要说明的是,式(3)中k是随机生成的正整数,且k∈[1, D]。这样保证能够至少有D个更新到
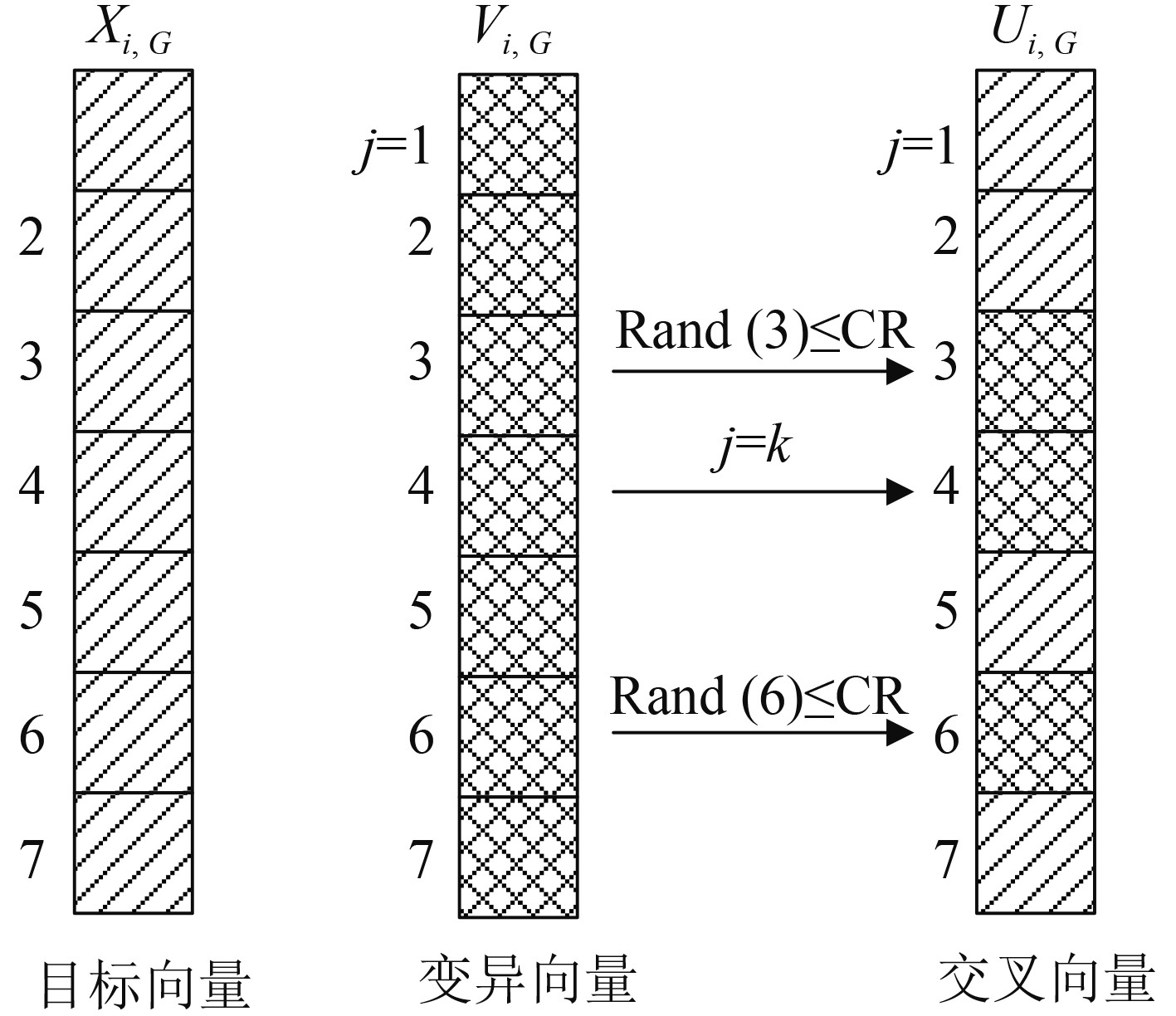
|
图 2 七维参数变量生成交叉向量示意图 Fig. 2 Schematic diagram of generating cross-vectors with seven-dimensional parametric variables |
选择:选择过程比较简单,采用贪婪策略。即将目标向量和交叉向量分别代入目标函数中,比较哪个更小,取更小的向量作为下代目标向量
| $ {X_{{{i,}}G + 2}} = \left\{\begin{aligned} &{U_{{{i,}}G}},\;\;\;{\rm{if}}\; {{f}}\left( {{U_{{{i,}}G}}} \right) \leqslant f( {{X_{{{i,}}G}}})\text{,} \\ &{{{X_{{{i,}}G}},\;\;\; {\rm{else}}} }\text{。} \end{aligned}\right. $ | (4) |
基本DE差分算法的Matlab伪代码其停止准则可以是给定的最大进化代数,最大的函数计算次数,或者满足给定的速度要求等。计算步骤如下所示[12]:
步骤1 设置DE算法的基本参数:尺度因子F,交叉概率CR,种群规模NP,求解参数个数D,求解参数值域范围[Xmin, Xmax],求解代数Gmax等。
步骤2 初始化种群
步骤3 开始DE算法核心操作。依次循环进行变异、交叉、选择操作,直到完成收敛条件。
步骤4 算法返回所达到收敛条件后的最小目标函数值,以及所对应的参数变量值。
2.2 宽波束目标函数虽然所处理的问题为矩形平面阵,但问题只涉及到水平面一个平面的优化。因此,问题最终归结到一维方向图乘积定理。本问题不考虑天线互耦影响,天线单元方向图采用理想点源形式。天线采用一般形式,
| $ AF = \sum\nolimits_{i = 2}^N {{I_n}} \exp \left( {jk\left( {{Z_n} - {Z_1}} \right)\cos \theta + j{\varphi _n}} \right)。$ | (5) |
已知天线单元幅度、相位和坐标分布,就可以计算出阵列的方向图,即AF=AF(
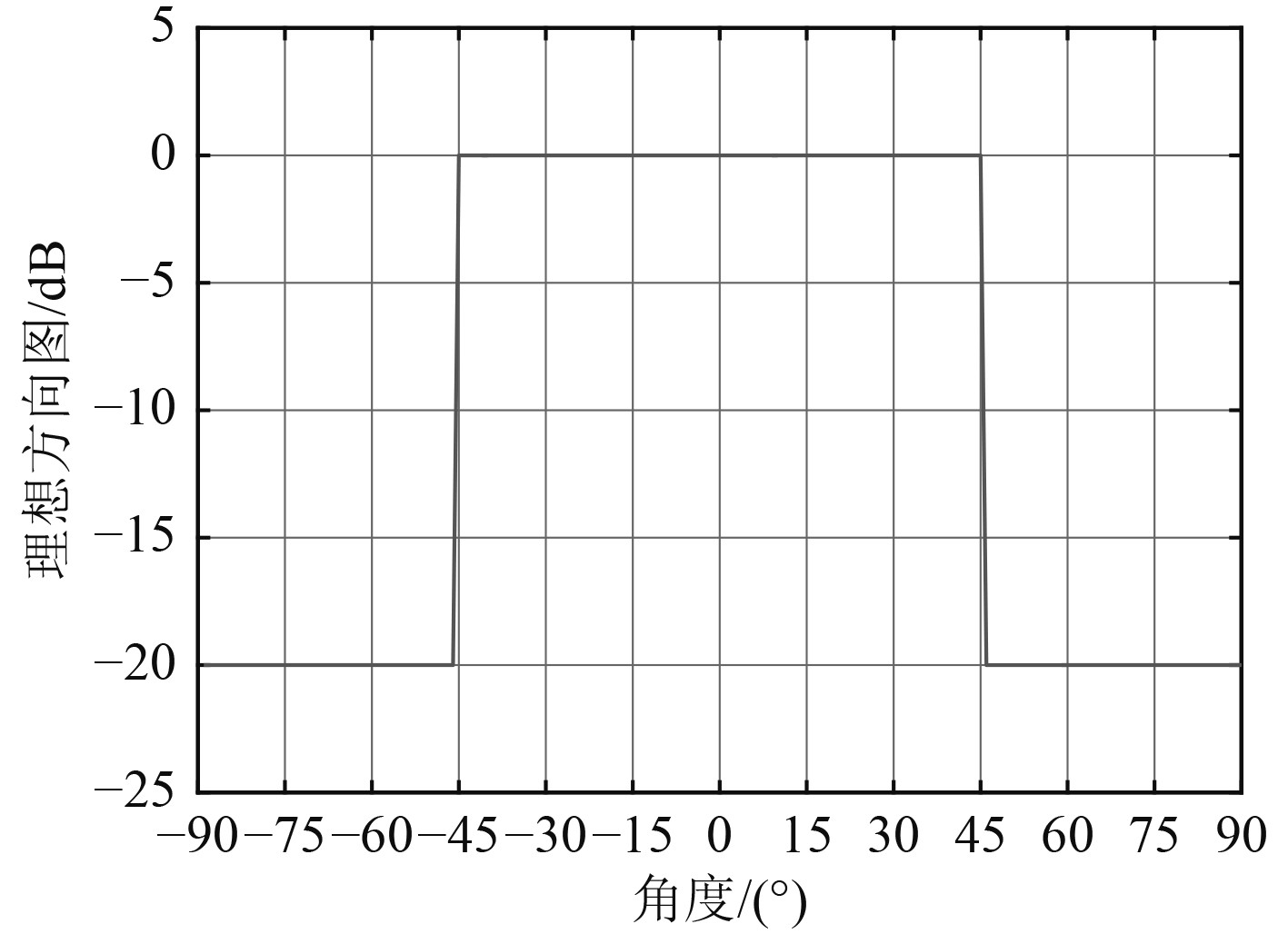
根据设计目标可知,要求天线方向图在–45°~45°实现宽波束等功率辐射,如图3所示。此类方向图的实现可以有先验知识作为参考,详见文献[13]。先验的知识为:天线的幅度和相位分布具有中心对称的特性。可以利用这一特性减小阵列天线优化变量,增加天线优化的效率。
|
图 3 理想方向图 Fig. 3 Ideal pattern |
天线优化的目标:主瓣区(–45°~45°)等功率辐射;副瓣区(–90°~–55°)和(55°~90°)优于–20 dB;优化时阵列天线的增益不能下降太多。用数学公式将最小化目标函数表达下式:
| $ \begin{split}DES1 = &\left| {0 - \min \left( {AF\left( { - {{45}^ \circ }\text{~}{{45}^ \circ }} \right)} \right)} \right|\text{,} \\ DES2 =& \left| { - 20 - \max \left( {AF\left( { - {{90}^ \circ }\text{~}{{55}^ \circ }} \right)} \right)} \right| +\\ &\left| { - 20 - \max \left( {AF\left( {{{55}^ \circ }\text{~}{{90}^ \circ }} \right)} \right)} \right| \text{,}\\ DES3 =& - Dir\text{,}\\ DES =& \alpha * DES1 + \beta * DES2 + \gamma * DES3\text{。} \end{split} $ | (6) |
其中:
优化阵列天线的副瓣电平为阵列天线设计的传统且最常用的设计,目标函数建立比较简单。首先只要已知

|
图 4 等幅同相方向图 Fig. 4 Equal-amplitude in-phase pattern |
传统优化副瓣电平SLL的目标函数易优化为等副瓣特性。等副瓣Chebyshev特性在进行阵列天线功分馈电网络设计的时候,会引起尾部电流突变而增加馈电网络的设计难度。因此,在设计天线副瓣电平时,常常采用Taylor综合方法。在这里对副瓣电平采用优化算法进行优化时,除了要综合考虑幅度加权后对天线阵列增益的影响外,还要考虑到馈电网络的设计有无问题。所以本文引入对天线方向图1/u变化的控制,使得阵列天线电流变化更加的缓和、单调。
天线优化的目标:阵列副瓣电平SLL≤–30 dB,远区副瓣电平差值DIFF=–5 dB,天线增益减小不超过1 dB。用数学公式将最小化目标函数表达如下式:
| $ \begin{split}& DES1 = \left| {{\text{ - 3}}0 - \max \left( {SLL} \right)} \right|\text{,}\\ &DES2 = \left| {\max \left( {DIFF\left( { - 5} \right) - SLL} \right)} \right|\text{,} \\ &DES3 = - Dir\text{,} \\ &DES = \alpha * DES1 + \beta * DES2 + \gamma * DES3\text{。}\end{split} $ | (7) |
其中:
设计结果及分析分2个部分进行说明。第1部分为阵列天线宽波束等功率辐射方向图的设计结果及分析;第2部分为阵列天线低副瓣方向图的设计结果及分析。
3.1 宽波束设计阵列天线水平单元数为22个,由先验知识可以知道此类方向图的幅度与相位分布呈中心对称分布。强制设置中心2个天线单元幅度为1、相位为0,则剩余优化变量个数为20个:10个幅度参数变量和10个相位参数变量。
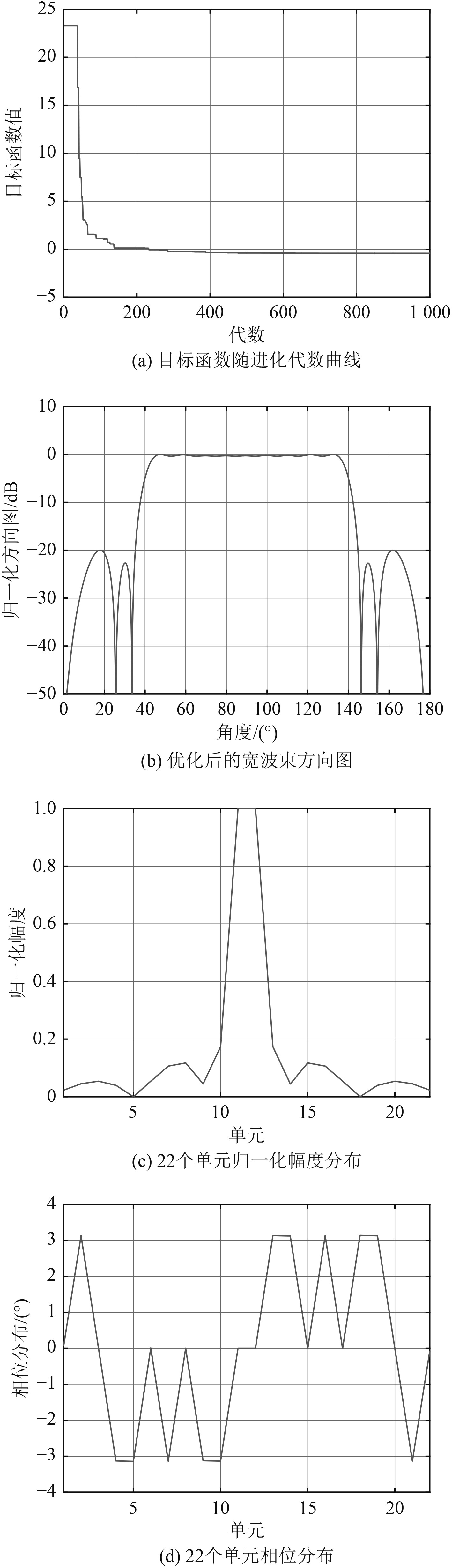
从优化的结果来看,差分进化即使采用基本的方法,优化20个变量,无需提供初值信息,效果依然很好。从图5(a)可以看出,DE在第40代左右进化迅速,快速收敛。在500代左右已经找到全局最优解,目标函数达到最小值。图5(b)为目标函数最小值情况下的对应的水平面–45°~45°内等功率全向辐射方向图。–45°~45°角度内归一化方向图平稳,副瓣区低于–20 dB,达到优化设计要求。图5(c)为22个单元的归一化幅度分布。由先验知识可知(Woodward-lawson抽样法则),其分布呈中心对称,故可用在优化中减少优化变量。图5(d)为22单元的相位分布。相位分布很有特点,相位为0,pi,–pi等3个位置。这样的优化结果也与Woodward-lawson抽样综合法则相一致。
|
图 5 采用差分进化算法优化宽波束方向图 Fig. 5 Optimizing wide beam patterns using differential evolution algorithm |
阵列天线水平单元数为20个,由先验知识可以知道此类方向图的幅度分布同样呈中心对称分布。强制设置中心2个天线单元幅度为1,则剩余优化变量个数为9个幅度变量。
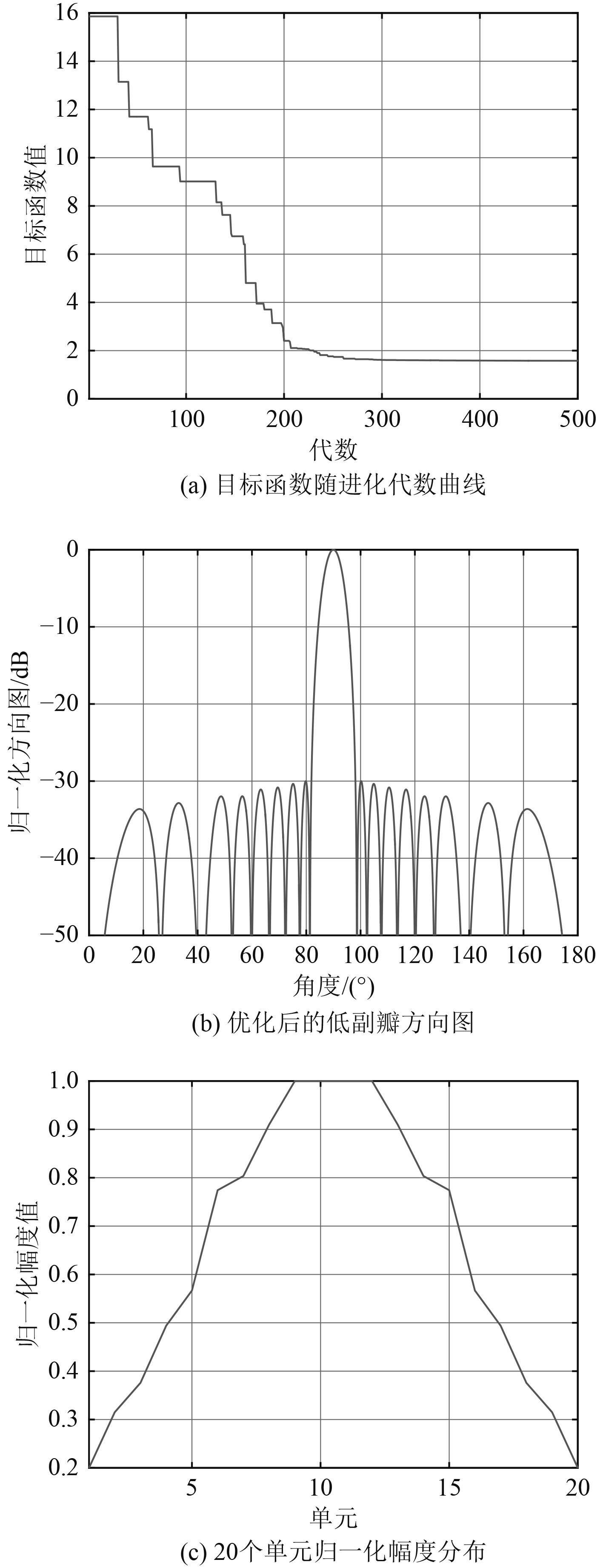
在低副瓣优化设计过程中,由于只需优化幅度分布,变量个数减少,其优化过程更快。从图6(a)可以看出,DE优化算法在300代之后,已经基本收敛,目标函数值不再减小。算法在前200代进化明显,进行了快速的收敛。图6(b)为优化后的低副瓣方向图。副瓣低于–30 dB,且由于对副瓣电平进行控制,副瓣电平不再是类似chebyshev形式的等副瓣特性,而是依次呈一定落差(1/u)特性的副瓣电平,差值DIFF目标控制在5 dB。图6(c)为优化所得到的归一化幅度分布曲线。幅度分布特性呈单调特性。根据优化后的天线点源的幅度和相位,仿真阵列天线增益为12.311 3 dB。而对间距为半个波长,20个点源的阵列天线理论值为13 dB,使用优化算法造成阵列天线增益减小了0.688 7 dB,满足阵列天线增益变化小于1 dB的目标。
|
图 6 采用差分进化算法优化低副瓣方向图 Fig. 6 Optimizing low sidelobe patterns using differential evolution algorithm |
本文基于基础差分进化算法,对2个工程实例进行优化设计,实现了宽波束等功率辐射方向图和低副瓣(副瓣可控)阵列方向图2个算例。基于这2个算例,可以看到差分进化算法不需要初值信息,依然能够快速找到全局最优解。另外,差分进化算法程序简单,执行效率非常高。因此,这种随机性全局最优化进化算法很适合在以后的工作中运用。
| [1] |
ZHANG Fan, ZHANG Fu-shun, ZHAO Gang, et al. Pattern analysis and synthesis of the conformal antennas array[J]. Jounal of Xidian University, 2010, 37(3): 496-501. |
| [2] |
STORN R, PRICE K V. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces[J]. J Global Optim, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 |
| [3] |
LIU Ruo-chen, JIAO Li-cheng, LEI Qi-feng, et al. New differential evolution constrained optimization algorithm[J]. Jounal of Xidian University, 2011, 38(1): 47-53. |
| [4] |
ROGALSKY T, DERKSEN R W, KOCABIYIK S. Differential evolution in aerodynamic optimization[C]//Proc 46th AnnuConfof Can Aeronaut Space Inst. Montreal: Candian Aeronautics and Space Institute, 1999: 29–36.
|
| [5] |
JOSHI R, SANDERSON A C. Minimal representation multisensory fusion using differential evolution[J]. IEEE Trans onSyst Man CybernA, Syst Humans, 1999, 29(1): 63-76. DOI:10.1109/3468.736361 |
| [6] |
STORN R. On the usage of differential evolution for function optimization [C]//Proc Biennial Conf North AmerFuzzyInf Process Soc. Berkeley: IEEE, 1996: 519–523.
|
| [7] |
MASSA A, PASTORINO M, RANDAZZO A. Optimization of the directivity of a monopulse antenna with a subarrayweightingby a hybrid differential evolution method[J]. IEEE Antennas Wireless PropagLett, 2006(5): 155-158. |
| [8] |
CHEN Y, YANG S, NIE Z. The application of a modified differential evolution strategy to some array pattern synthesis problems[J]. IEEE Trans on Antennas Propag, 2008, 56(7): 1919-1927. DOI:10.1109/TAP.2008.924713 |
| [9] |
GUO Jing-li, LI Jian-ying. Pattern synthesis of conformal array antenna in the presence of platform using differential evolution algorithm[J]. IEEE Trans on Antennas Propag, 2009, 57(9): 2615-2621. DOI:10.1109/TAP.2009.2027046 |
| [10] |
LIN C, QING A, FENG Q. Synthesis of unequally spaced antenna arrays by using differential evolution[J]. IEEETrans on Antennas Propag, 2010, 58(8): 2553-2561. DOI:10.1109/TAP.2010.2048864 |
| [11] |
FAN Yu, JIN Rong, GENG Jun-ping, et al. A hybrid optimized algorithm based on differential evolution and genetic algorithm and its applications in pattern synthesis of antenna arrays[J]. Acta Electronica Sinica, 2004, 32(12): 1997-2000. |
| [12] |
张立, 基于差分进化算法的天线优化设计[D]. 西安: 西安电子科技大学, 2011.
|
| [13] |
汪茂光, 吕善伟, 刘瑞祥, 阵列天线分析与综合[M]. 西安: 西安电子科技大学, 1995.
|
 2022, Vol. 44
2022, Vol. 44
