2. 大连测控技术研究所,辽宁 大连 116018
2. Dalian Scientific Test and Control Technology Institute, Dalian 116018, China
舰船的辐射噪声是水下目标被动探测的信息源,是水声设备进行被动目标探测、识别和定位的基础,直接影响到自身的隐蔽能力和武器装备性能的发挥。通过实际测量发现,舰船的辐射噪声场具有明显指向性,随着方位的变化而变化。因此,采用传统的单极子模型来模拟舰船辐射噪声往往不能将其声场特性准确描述,如若再利用点声源建模结果进行预报,声场特性将与实际情况差异更大。
对于舰船水下辐射声场特性的研究,一直以来受到学者们的重视。Sascha Merz等[1-2]建立水下低频声源辐射解析模型和有限元/边界元模型,将水下声源建模为一端半球一端圆锥体的有限长加肋圆柱壳,并利用亥姆霍兹积分方程得到模型结构辐射声压的表达式。Seol等[3-4]对螺旋桨噪声进行数值研究,对比多极子声源声场,总结出螺旋桨流噪声主要是由偶极子声源引起。近年来,国内学者此方面问题的研究逐渐增多。相敬林[5-6]根据舰船不同部位辐射噪声具有明显不同的功率谱特征这一特点,将舰船视为体积声源,对不同航速下舰船辐射噪声沿船舶纵向的分布特性及其变化进行了研究。罗建[7-8]在相敬林研究基础上,将舰船沿纵向分布的噪声源简化为中部、后部和尾部3个主要亮点,研究了舰船作为体积目标辐射噪声的重构模型和重构方法。张永坤等[9]根据波动方程求得螺旋桨流场声压与偶极子运动关系,对比舰船螺旋桨空化气泡的体积脉冲,对螺旋桨空泡噪声及非空泡噪声进行预报。孟春霞[10]建立了在船舶的首部、中后部和尾部,由若干强度不同的多极子声源构成的船舶辐射噪声源的体积模型描述船舶水下辐射噪声场。
本文基于势函数的球面多极子级数展开方法,建立参数化点源模型,将声场表示为空间共点的不同阶次多极子叠加的形式,并对单极子和偶极子的声场传输特性进行仿真,对比分析单极子与偶极子声场传播损失。
1 多极子声场势函数的数学表示为了描述水下声源的方向特性,基于势函数的球面多极子级数展开方法,建立参数化点源模型。为了论证利用这种模型的可行性,设有一个在无界均匀空间中的谐波声源,该声源无形状限制,尺寸有限。选择声源内任意一点
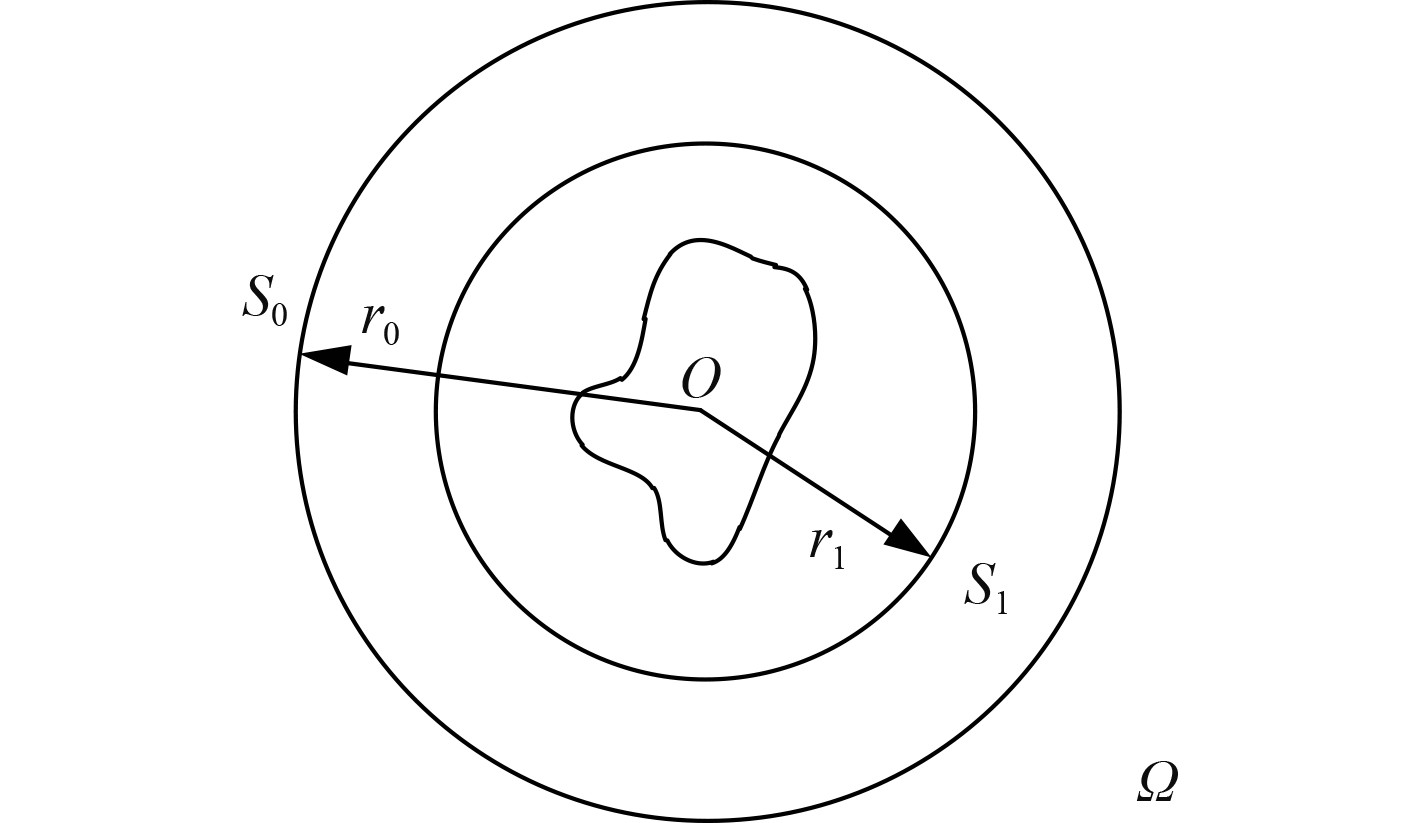
|
图 1 模型示意图 Fig. 1 Model diagram |
以
| $ \tilde P({r_0},\theta ,\varphi ,t) = i\omega {\rho _0}\tilde \psi ({r_0},\theta ,\varphi ){e^{ - i\omega t}} ,$ | (1) |
其中,
起始的声源在
| $ \Delta \psi (M) + {k^2}\psi (M) = 0,M \in \varOmega ,$ | (2) |
且在边界
| $ \Delta \psi (M) = \tilde \psi (M),M \in {S_0}。$ | (3) |
其中,
| $ \psi (R,\theta ,\varphi ) = \sum\limits_{n = 0}^\infty {\sum\limits_{m = - n}^n {{C_{nm}}h_n^{(1)}(kR)P_n^{|m|}(\cos \theta ){e^{im\varphi }}} } 。$ | (4) |
辐射位于球坐标系的中心,
| $ \psi (R,\theta ,\varphi ) = \dfrac{i}{k}\sum\limits_{n = 0}^L {\displaystyle\sum\limits_{m = - n}^n {{D_{nm}}\displaystyle\int\nolimits_{ - \infty }^\infty {H_m^{(1)}(r\xi ){e^{b|z|}}P_n^{|m|}(b/ik)\frac{{\xi {\rm{d}}\xi }}{b}} } } 。$ | (5) |
其中,
根据声源产生机理的不同,可以将声源分为单极子、偶极子和四极子。其发声机制和辐射特性描述如下:
1)单极子
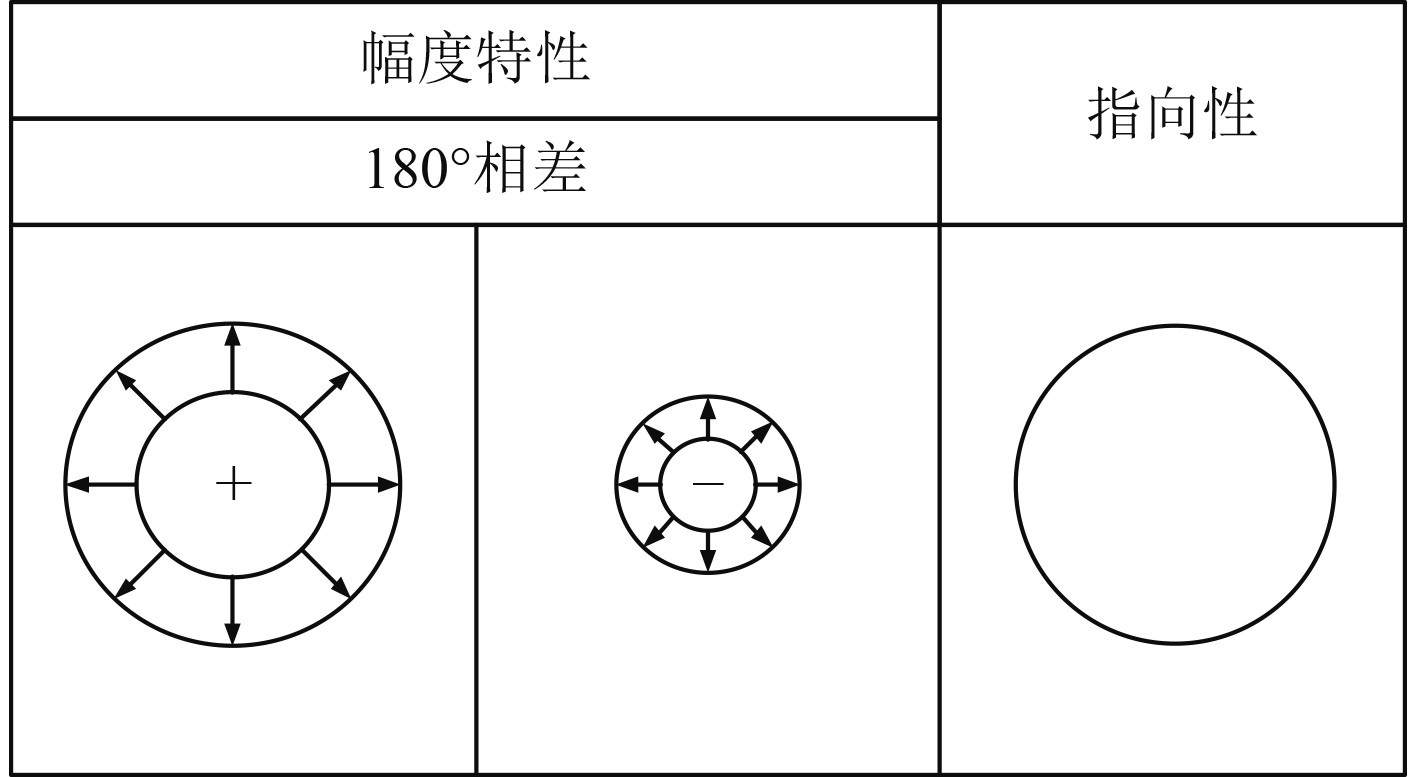
单极子声源表面各点沿径向做均匀、同振幅、同相位的涨缩振动,形成球对称声场。其辐射声压的大小只与观测点的距离有关,可以用下式描述这种运动特性:
| $ {p_M}(r,t) = \frac{{{\rho _0}}}{{4{\text{π}} r}}\frac{{{\rm{d}}V}}{{{\rm{d}}t}}。$ | (6) |
单极子的辐射特性和指向性如图2所示。
|
图 2 单极子声源辐射特性及其指向性 Fig. 2 Radiation characteristics and directivity of monopole sound source |
2)偶极子
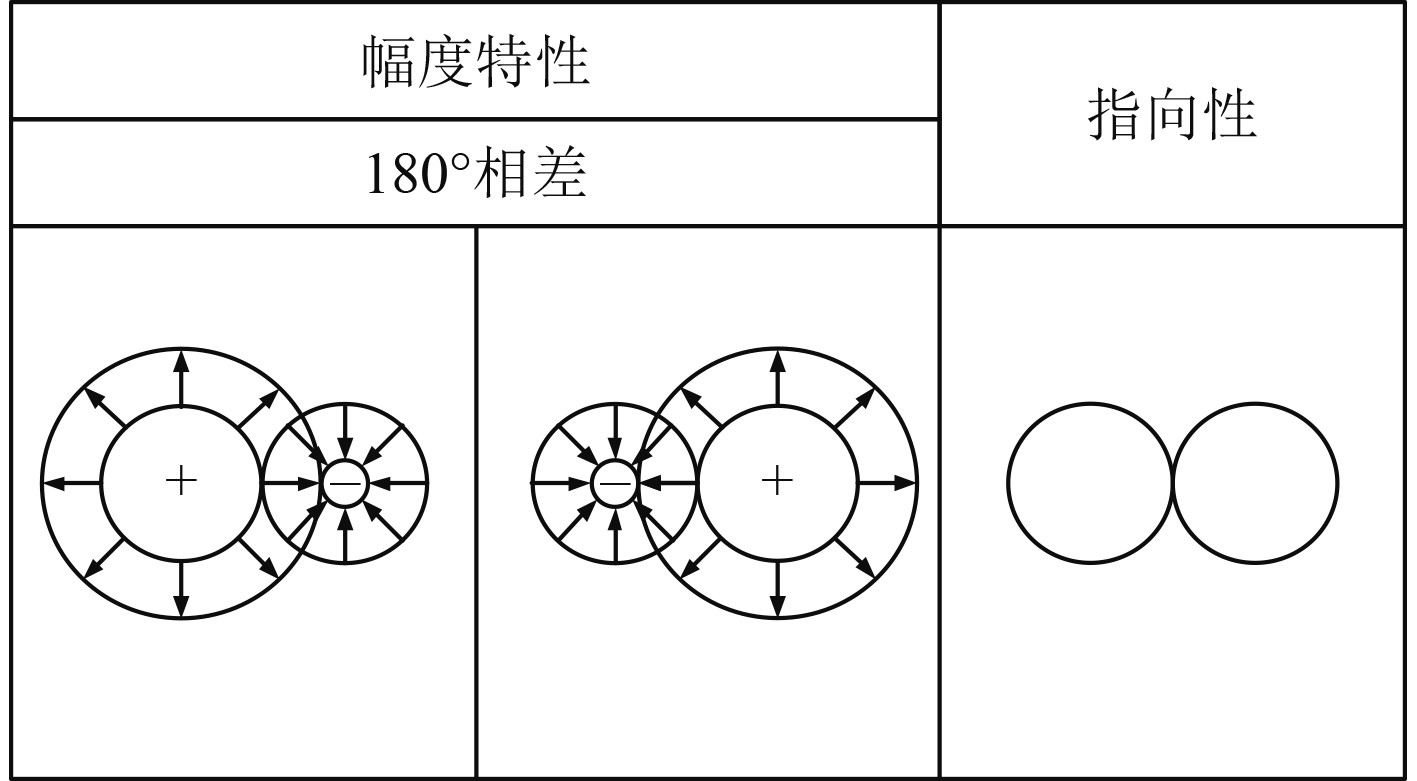
偶极子由2个相距很近、振幅相同而相位相反的单极子组成。偶极子的净流量为零但是动量变化却不为0。这导致沿着偶极矩方向作用力最大而垂直于偶极矩方向作用力为0。这样的特性导致其辐射指向性成“8”形。偶极子一般在流速较高的条件下产生,其产生的声压辐射可以表述为:
| $ {p_D}(r,t) = \frac{{b\cos \theta }}{{{c_0}}}\frac{{{\rm{d}}{p_M}}}{{{\rm{d}}t}}。$ | (7) |
可以看出,偶极子辐射声场与观测点和声源之间的夹角有关。当夹角为90°时,两点源的声波幅值相等,相位相反,声压被抵消。而在180°方向上,声波得到叠加增强。偶极子的辐射特性和指向性如图3所示。
|
图 3 偶极子声源辐射特性及其指向性 Fig. 3 Radiation characteristics and directivity of dipole sound source |
3)四极子
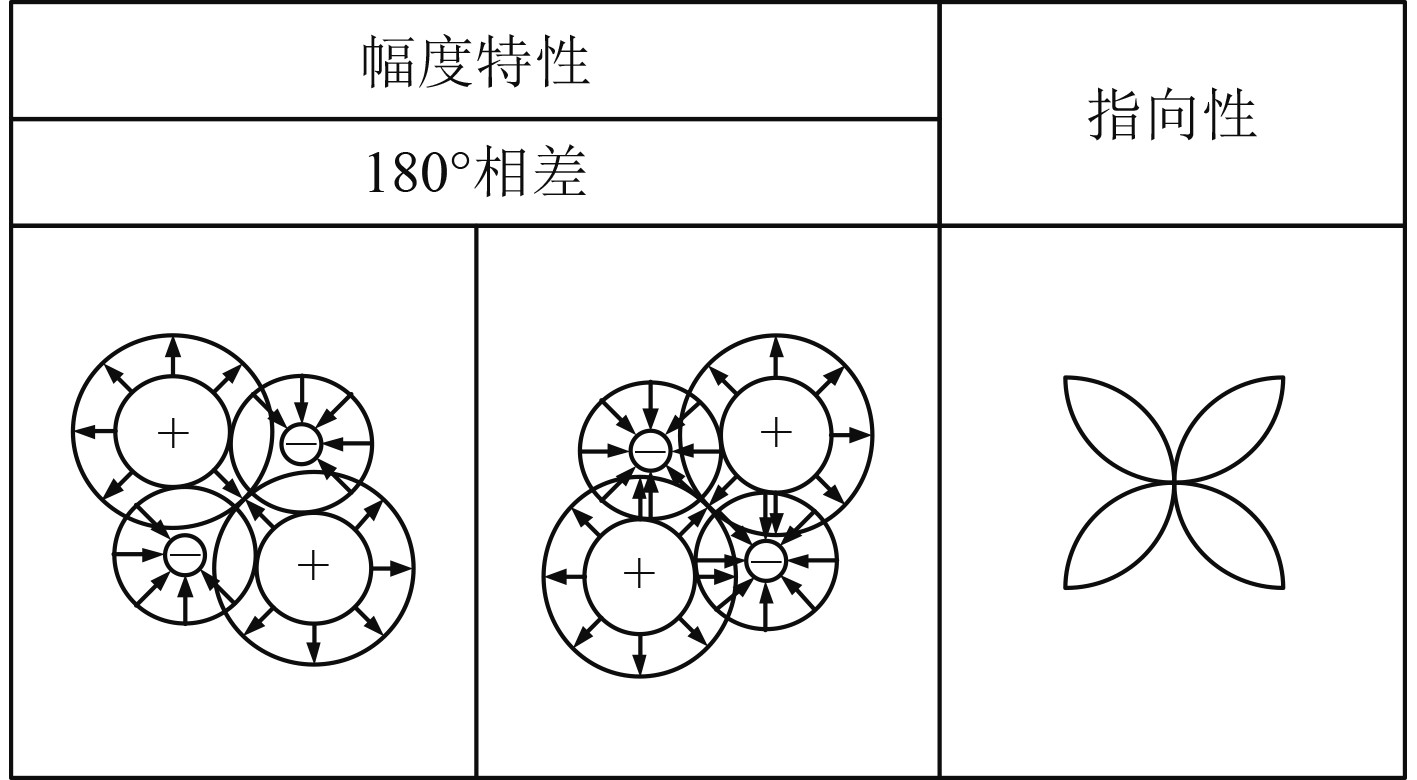
四极子由2个相距较近、振幅相同而相位相反的偶极子组成,按照组成的方式不同可以分为横向偶极子和纵向偶极子,横向偶极子辐射功率高于纵向偶极子,其辐射声压可以表述为:
| $ {p_Q}(r,t) = \frac{{b\cos \theta }}{{{c_0}}}\frac{{{\rm{d}}{p_D}}}{{{\rm{d}}t}} 。$ | (8) |
四极子的辐射特性和指向性如图4所示。
|
图 4 四极子声源辐射特性及其指向性 Fig. 4 Radiation characteristics and directivity of quadrupole sound source |
以典型的Pekeris波导为参照,对单极子和偶极子的声场结构进行仿真研究。仿真计算所设置的波导环境由60 m深,声速1 500 m/s的均匀海水层和声速1 800 m/s,密度2.7 g/cm3,吸收系数0.1 dB/wavelength的液态海底构成。首先,对声源在海面处(5 m深)和接收点在海底处(50 m深)的情况进行仿真,对比单极子和水平偶极子传播损失衰减曲线。设声压观测方向为沿X轴方向,此时两极子在Y轴上的y偶极子在X轴观测方向上声压为0,因此讨论的是两极子在X轴上的x偶极子。声场仿真结果如图5所示。
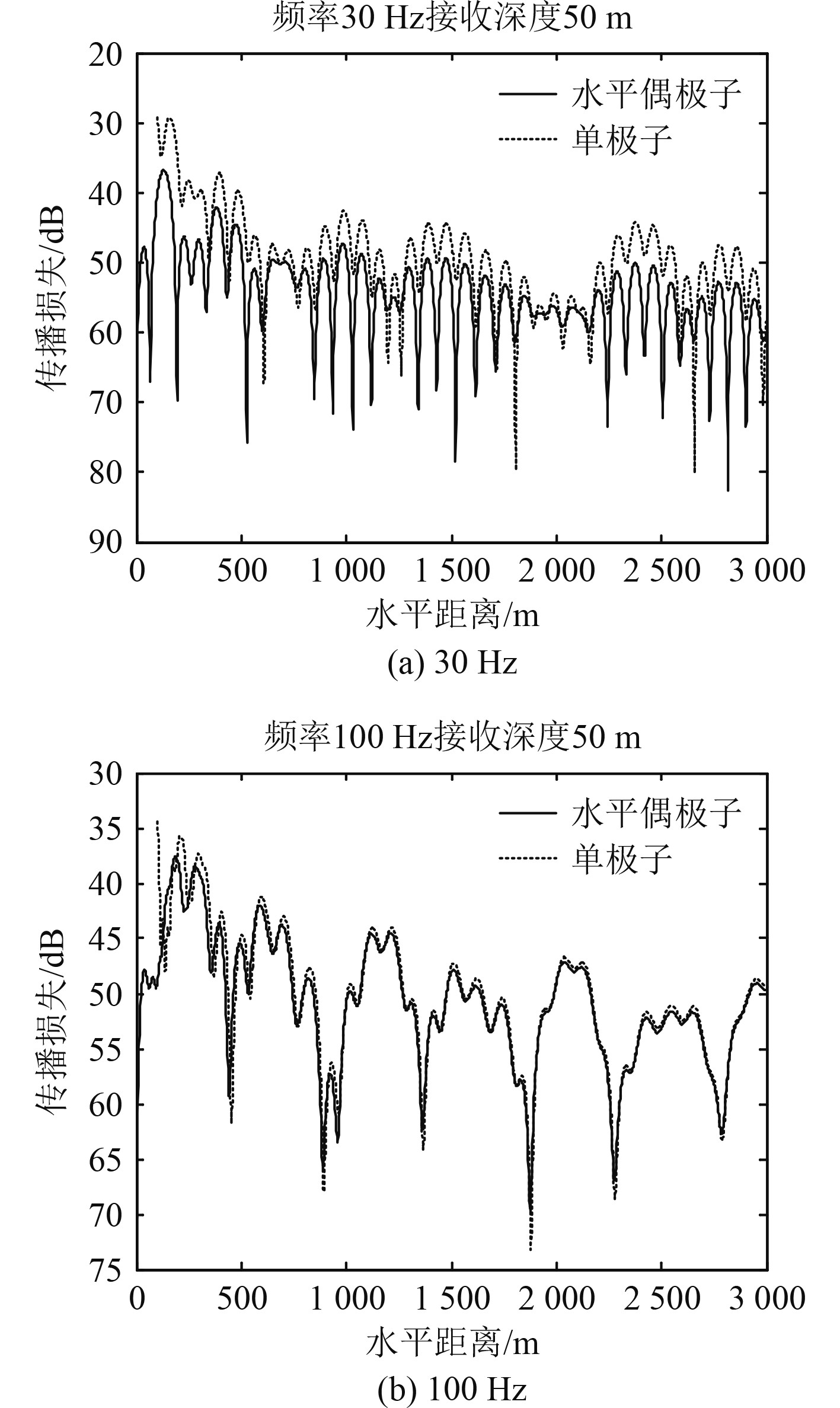
|
图 5 不同频率下水平偶极子声场传播损失仿真 Fig. 5 Simulation of propagation loss of horizontal dipole sound field at different frequencies |
通过上述对比看出,海洋声学参数相同情况下,2种极子传播损失的变化趋势相同,衰减规律相同。由于存在声场相互抵消,水平偶极子源声场强度小于单极子源声场强度。随着频率的增高,信号的衰减变快,传播损失随之变大。
设观测点与声源之间存在一定的正横距离,对不同正横距离下水平偶极子传播损失进行仿真研究。
图6为30 Hz和100 Hz条件下水平偶极子与单极子传播损失随距离变化对比图。从传播损失曲线可以发现,水平偶极子的声场是具有指向性的。
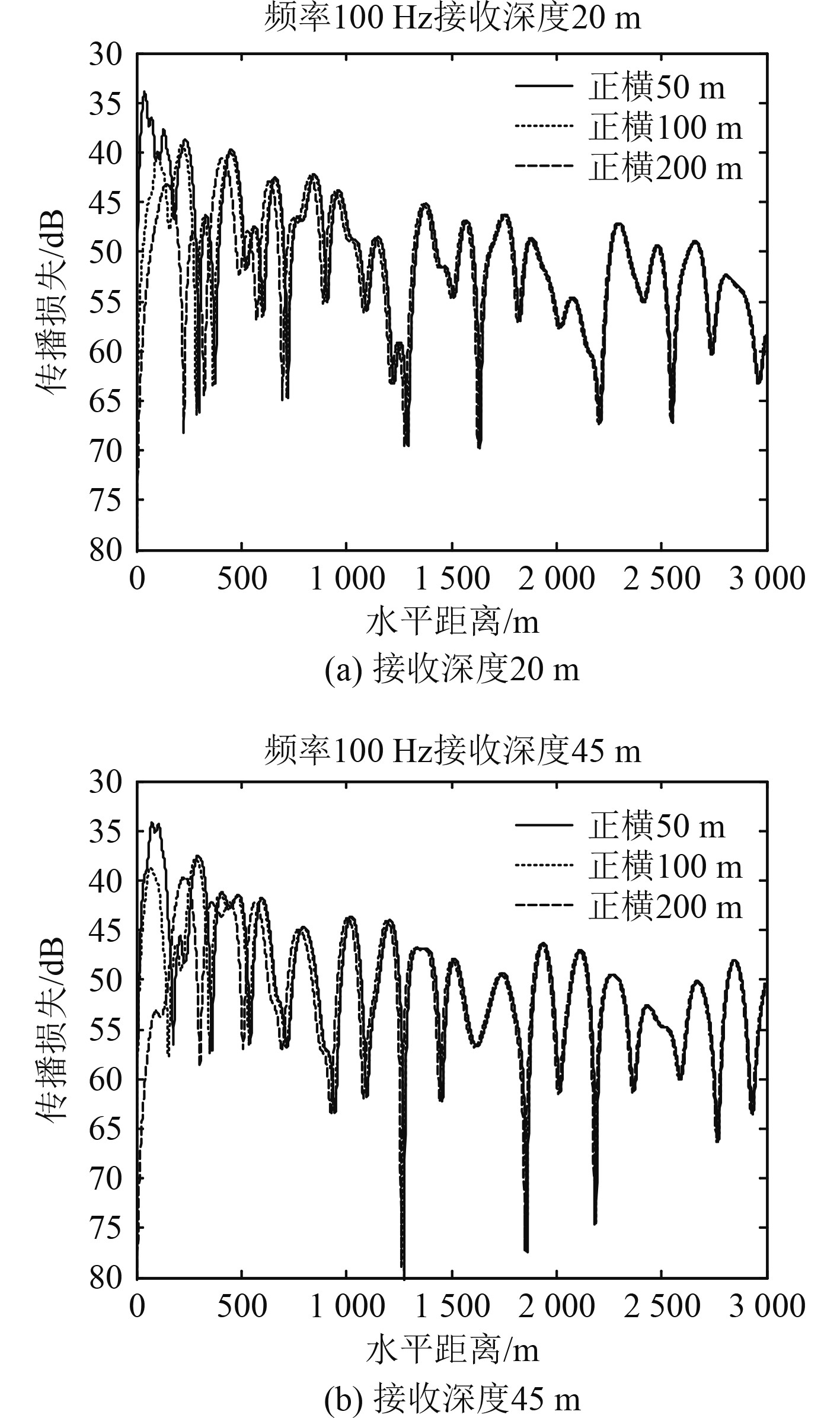
|
图 6 100 Hz水平偶极子不同正横距离声场仿真 Fig. 6 Simulation of horizontal dipole sound field at different transverse distances at 100 Hz |
由于声信号是在海洋信道这一特定环境中进行传播,其随机复杂的特性使得声场的指向性发生了畸变。相同接收深度条件下,距离较近时,偶极子声源与观测点之间的夹角
垂直偶极子为拥有一个垂直轴的z偶极子。设接收深度20 m(此时
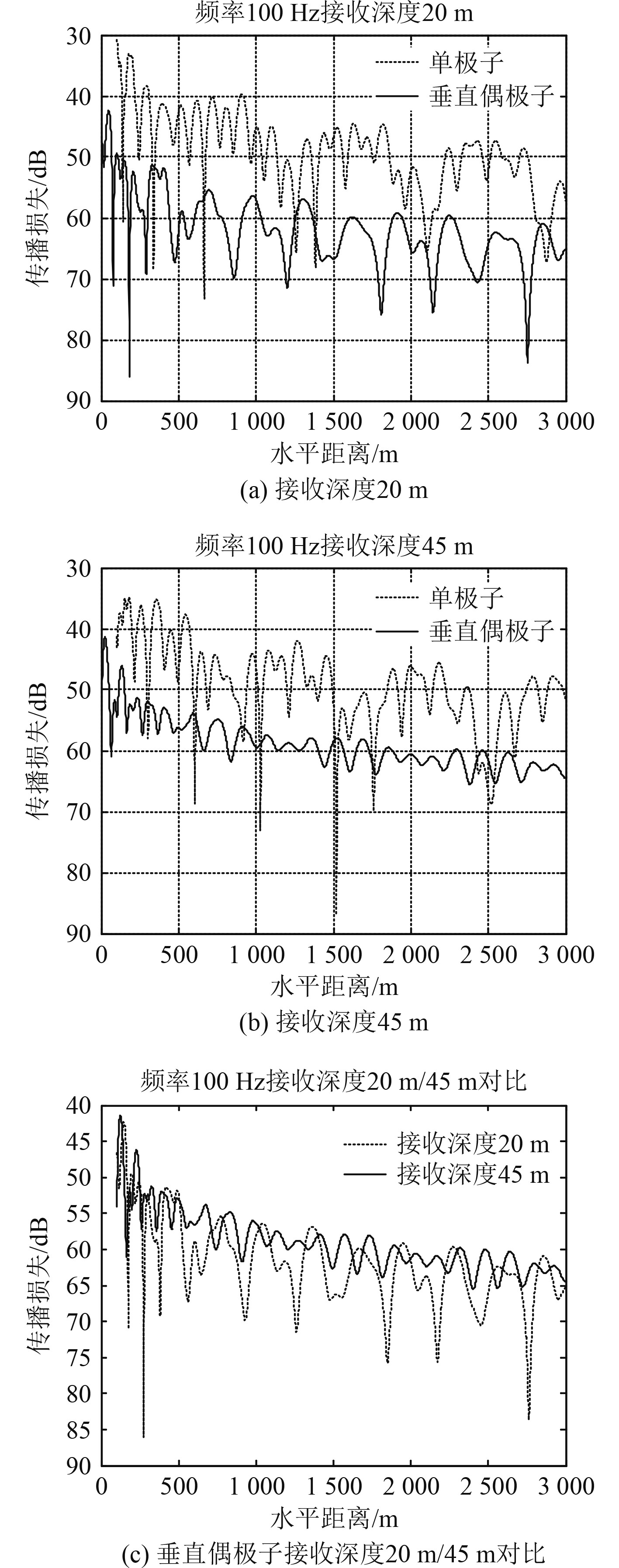
|
图 7 f=100 Hz垂直偶极子不同接收深度声场仿真 Fig. 7 Simulation of vertical dipole sound field at different acceptance depths at 100 Hz |
保持垂直偶极子声源深度不变,更改接收深度为45 m,得到声场仿真结果如图7(b)所示。可以看到,改变接收深度后夹角
垂直偶极子声场在近距离上表现出偶极子的方向特性,原因在于改变水平距离时,当声源深度和接收深度的值不同时,相对于偶极子方向特性轴来说,接收器的方向是变化的,这就影响了声场势函数的幅度值。
3.3 不同类型偶极子声场衰减规律对比设水平偶极子声源、垂直偶极子声源与接收深度相同,均为20 m,保持其他参数不变。仿真计算30 Hz与100 Hz情况下,3种极子声场的传播损失对比图,此时声场观测方向为沿着X轴方向。
对比图8中不同极子传播损失曲线,能够得到水平偶极子具有与单极子相同的衰减规律,而垂直偶极子与前两者相比衰减更快,传播损失更大。
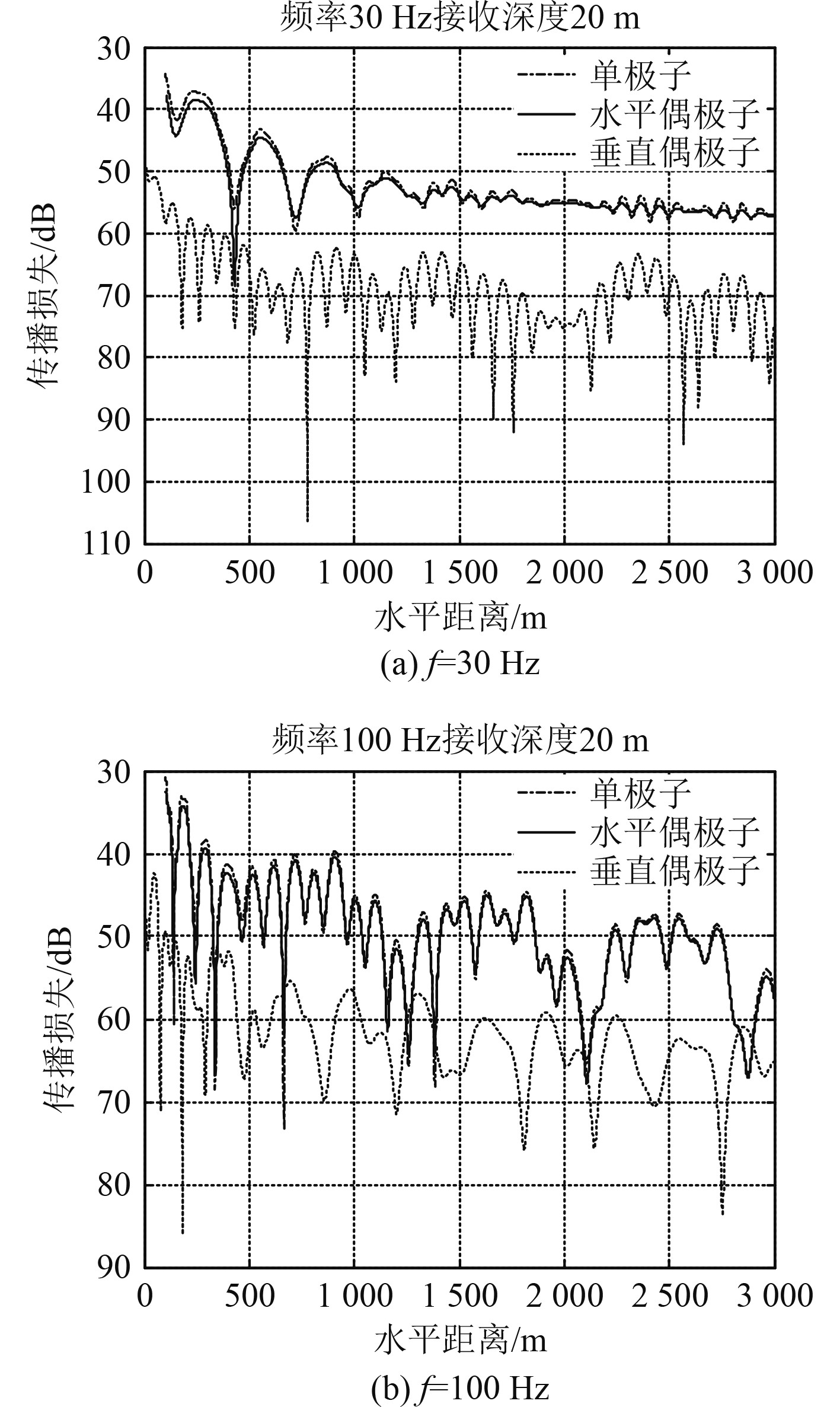
|
图 8 不同频率下3种极子衰减规律对比 Fig. 8 Comparison of attenuation laws with different frequencies |
本文给出了多极子声场势函数的数学表示,可以令空间共点的不同阶多极子叠加表示指向性声源声场,且仿真模拟了单极子及2种偶极子声源在典型波导环境中的声场特性。通过分析,可以得到以下结论:1)海洋声学参数相同的情况下,单极子与水平偶极子的传播损失随距离变化的趋势相同,衰减规律相同。而垂直偶极子与前两者相比,衰减更快。2)偶极子声源声场随夹角
| [1] |
SASCHA M, KESSISSOGLOU N. Influence of resonance changer parameters on the radiated sound power of a submarine[J]. Acoustics Australia, 2009, 37(1): 12-17. |
| [2] |
SASCHA M, SEBASTIAN O. Development of coupled FE/BE models to investigate the structural and acoustic responses of a submerged vessel[J]. Journal of Computational Acoustics. 2007, 15(1), 23-47.
|
| [3] |
SEOL H, JUNG B, SUH J C, et al. Prediction of non-cavitating underwater propeller noise[J]. Journal of Sound and Vibration, 2002, 257(1): 131-156. DOI:10.1006/jsvi.2002.5035 |
| [4] |
SEOL H Development of hybrid method for the prediction of underwater propeller noise[J]Journal of Sound and Vibration, 2005, 288(2): 345-360.
|
| [5] |
相敬林, 刘勋. 舰船作为体积声源的源强度谱纵向分布特性[J]. 探测与控制学报, 2002, 24(2): 5-17. XIANG J L. LIU X. The longitudinal distribution of source intensity spectrum of ship-radiated noise[J]. Journal of Detection & Control, 2002, 24(2): 5-17. DOI:10.3969/j.issn.1008-1194.2002.02.002 |
| [6] |
刘勋, 相敬林, 周越, 等. 作为体积目标的船舶声辐射纵向分布特征的研究[J]. 西北工业大学学报, 2000, 18(3): 409-412. LIU Xun, XIANG Jinglin, ZHOU Yu, et al. Research on longitudinal distribution characteristics of the radiated noise of a ship as a volume object[J]. Journal of Northwestern Polytechnical University, 2000, 18(3): 409-412. DOI:10.3969/j.issn.1000-2758.2000.03.018 |
| [7] |
罗建, 湛雅倩, 马定坤. 舰船多辐射声源近距离通过特性的仿真[J]. 应用声学, 2008, 27(2): 108-112. LUO Jian, ZHAN Yaqian, MA Dingkun. Simulation of Short-distance-through-signature considering multi-radiation sources of a ship[J]. Applied Acoustics, 2008, 27(2): 108-112. DOI:10.3969/j.issn.1000-310X.2008.02.005 |
| [8] |
罗建, 赵亚磊, 黄仁可. 作为体积目标的舰船辐射噪声建模[J]. 数字海洋与水下攻防. 2018, (1): 38–42. LUO Jian, ZHAO Yalei, HUANG Renke. Modeling of ship-radiated noise as volume targets[J]. Digital Ocean & Underwater Warfare. 2018(1): 38–42. |
| [9] |
张永坤, 熊鹰, 赵小龙. 螺旋桨无空泡噪声预报[J]. 噪声与振动控制, 2008, 28(1): 44-47. ZHANG Yongkun, XIONG Ying, ZHAO Xiaolong. Prediction of prediction of propeller non-cavitations noise[J]. Noise and Vibration Control, 2008, 28(1): 44-47. DOI:10.3969/j.issn.1006-1355.2008.01.013 |
| [10] |
孟春霞. 船舶辐射噪声源简化模型[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
 2022, Vol. 44
2022, Vol. 44
