船舶电力推进系统处于制动工况时,为了让船体迅速停航,需要使推进电机带动的螺旋桨减速至零或减速至零后继续反转,该过程制动时间短、能量回馈大。当制动产生的再生能量经过逆变器反并联二极管整流回馈到中间直流侧时,由于直流侧电容要求的容值有限,当船体迅速制动时,回馈电能不能被电容完全吸收,会引起与直流侧并联的电容两端电压上升[1],因此为了保证船舶电力推进系统的正常工作,回馈的再生能量需要消耗和利用。船舶再生能量再利用的方法包括:超级电容储能法、飞轮储能法、四象限整流回馈法、并网回馈法等[2]。本文采用基于LCL滤波器的并网回馈法,相对其他方法虽然该方法控制器较为复杂,但其装置体积较小,成本较低有很大的应用前景[3-4]。传统船舶再生能量并网逆变控制器采用比例多谐振控制(proportional multiple resonant controller, PMR)和比例积分控制(proportional integral, PI)。这2种控制方法能满足船舶再生能量并网的基本要求,且控制参数易整定,控制成本适宜[4]。但是这2种典型的控制器对船舶电网侧扰动和谐波的抑制能力有限,当船舶电网测出现扰动时,会增加并网电流中的谐波,为此设计一种基于LCL自抗扰(active disturbance rejection control, ADRC)控制策略的控制器。该控制策略相较于传统并网逆变器控制增加系统的稳定性,使得其对并网电流谐波的抑制能力大大提高,并对电网侧电压的波动和畸变有一定的抗干扰能力。
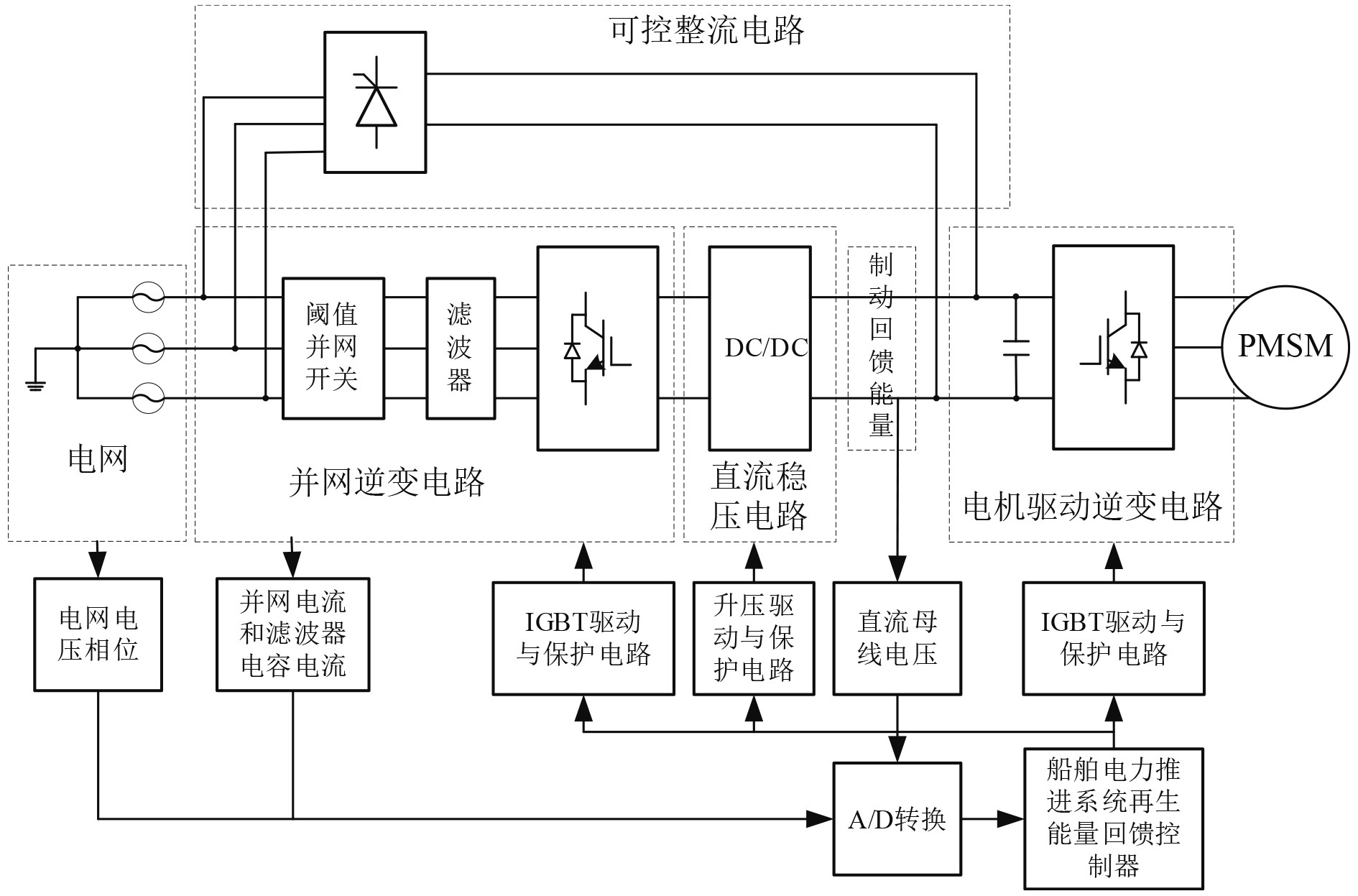
1 船舶再生能量并网逆变系统设计和分析如图1所示,船舶再生能量并网逆变控制系统的总体结构由测量电路、驱动和保护电路、控制电路构成。测量电路需要测量出电网相位、并网电流和滤波器电容电流,直流母线电压等;并网逆变电路、升压直流电路、推进电机逆变电路有驱动电路提供开关驱动信号;保护电路实现控制电路与驱动电路隔离保护。控制电路实现对船舶再生能量的并网回馈控制和电机驱动控制。
|
图 1 船舶再生能量并网逆变控制系统 Fig. 1 Ship regenerative energy grid-connected inverter control system |
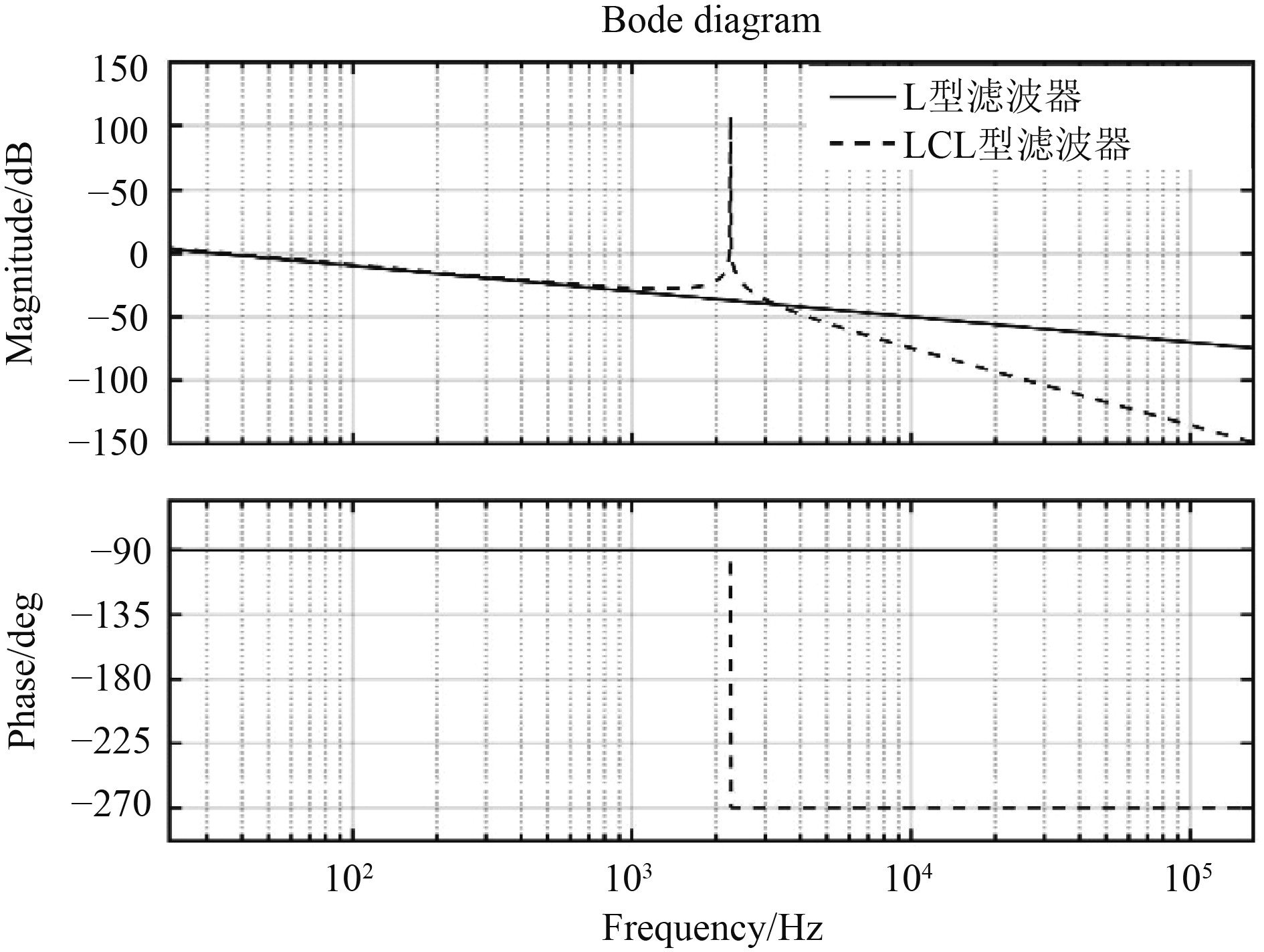
由于船舶再生能量并网逆变器通常采用脉冲宽度调制(pulse-width modulation, PWM)技术,该技术运用等效原理利用方波模拟正弦波输出,因此造成逆变器输出电压中存在大量的高频开关谐波。标准的船舶电网电压为正弦波,含大量开关谐波的逆变器输出电压若直接并入船舶的电网会增加并网电流的谐波,影响船舶电网电压品质。为此,本文采取在逆变器与电网之间安装适当的输出滤波器对输出电压进行滤波去除高频开关谐波[5]。目前市场上输出滤波器主要有RC型、L型和LCL型3种,但在船舶并网逆变系统主要使用后2种。LCL型滤波器中滤波电容C起到了为高频谐波电流提供旁路的作用,减小了通过
|
图 2 两种滤波器的频率特性 Fig. 2 Frequency characteristics of the two filters |
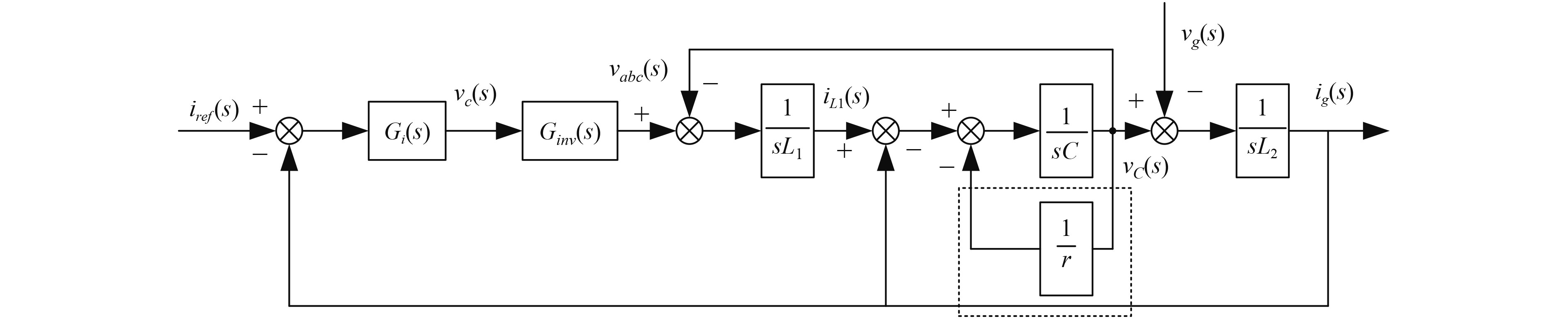
文献[6-7]表明,滤波电容两端并联电容更为有效。如图3所示,在原有的控制系统框图中给滤波电容两端并联一个阻值为r的电阻(虚线框内)。其中
|
图 3 船舶并网逆变控制系统框图 Fig. 3 Block diagram of ship grid-connected inverter control system |
由于并联一个真实电阻会带来的额外的能量损耗,因此采用滤波器有源阻尼,需要对船舶并网逆变控制系统框图进行等效变换。如图4所示,通过等效变换把电阻分离出来,成为滤波器电容电流反馈传递函数

|
图 4 船舶并网逆变控制系统等效框图 Fig. 4 Equivalent block diagram of ship grid-connected inverter control system |
滤波器电容电流反馈传递函数中
LCL滤波器的传递函数如式(1)所示,如果根据该传递函数设计的ADRC控制器为3阶ADRC控制器。但高阶ADRC控制的工程应用价值不高,因此需要对式(1)进行降阶。采用
| $ {G}_{LCL}=\frac{{I}_{out}}{{U}_{in}}=\frac{1}{{{L}_{1}{L}_{2}Cs}^{3}+({L}_{1}+{L}_{2})s},$ | (1) |
| $ {G}_{LCL}=\frac{{I}_{out}}{{U}_{in}}\approx \frac{1}{({L}_{1}+{L}_{2})s}。$ | (2) |
降阶后LCL两电平并网逆变器的电网电流在dq旋转坐标下的状态方程为:
| $\begin{split} \frac{{\rm{d}}}{{\rm{d}}t}\left[\begin{array}{c}{i}_{gd}\\ {i}_{gq}\end{array}\right]&=-\frac{1}{{L}_{1}+{L}_{2}}\left[\begin{array}{c}{v}_{gd}\\ {v}_{gq}\end{array}\right]+\\ &\left[\begin{array}{cc}0& {\omega }_{0}\\ {-\omega }_{0}& 0\end{array}\right]\left[\begin{array}{c}{i}_{gd}\\ {i}_{gq}\end{array}\right]+\frac{1}{{L}_{1}+{L}_{2}}\left[\begin{array}{c}{v}_{d}\\ {v}_{q}\end{array}\right]。\end{split}$ | (3) |
其中:
以d轴和q轴分别构造一阶ADRC控制器。以d轴一阶ADRC控制器构造为例。通过式(3)可以得出:
| $ \dot{{i}_{gd}}=-\frac{1}{{L}_{1}+{L}_{2}}{v}_{gd}+{\omega }_{0}{i}_{gq}+\frac{1}{{L}_{1}+{L}_{2}}{v}_{d},$ | (4) |
由于船舶并网逆变系统在运行过程存在干扰,假设干扰为R(t),并令
| $ \dot{{i}_{gd}}=-b{v}_{gd}+{\omega }_{0}{i}_{gq}+R\left(t\right)+\left(b{-b}_{0}\right){v}_{d}+{b}_{0}{v}_{d} 。$ | (5) |
把式(5)中等式右侧的前4项表示并网系统中存在的总扰动量,可得出:
| $ {f}_{d}=-\frac{1}{{L}_{1}+{L}_{2}}{v}_{gd}+{\omega }_{0}{i}_{gq}+R\left(t\right)+\left(b{-b}_{0}\right){v}_{d}。$ | (6) |
根据式(5)和式(6),可得出:
| $ \dot{{i}_{gd}}={f}_{d}+{b}_{0}{v}_{d}。$ | (7) |
设状态变量
| $ \left\{\begin{split} &\left[\begin{array}{c}\dot{{x}_{d1}}\\ \dot{{x}_{d2}}\end{array}\right]={\boldsymbol{A}}\left[\begin{array}{c}{x}_{d1}\\ {x}_{d2}\end{array}\right]+{\boldsymbol{B}}{v}_{d}+{\boldsymbol{E}}{h}_{d},\\ &{y}_{d}={\boldsymbol{C}}\left[\begin{array}{c}{x}_{d1}\\ {x}_{d2}\end{array}\right]。\end{split}\right. $ | (8) |
其中:
图7为一阶线性ADRC结构框图,其中LSEF为线性误差反馈控制器,LESO为线性扩张观测器。根据式(8)和图5可以设计一阶线性ADRC控制器。

|
图 5 一阶线性ADRC结构框图 Fig. 5 First order linear ADRC block diagram |
|
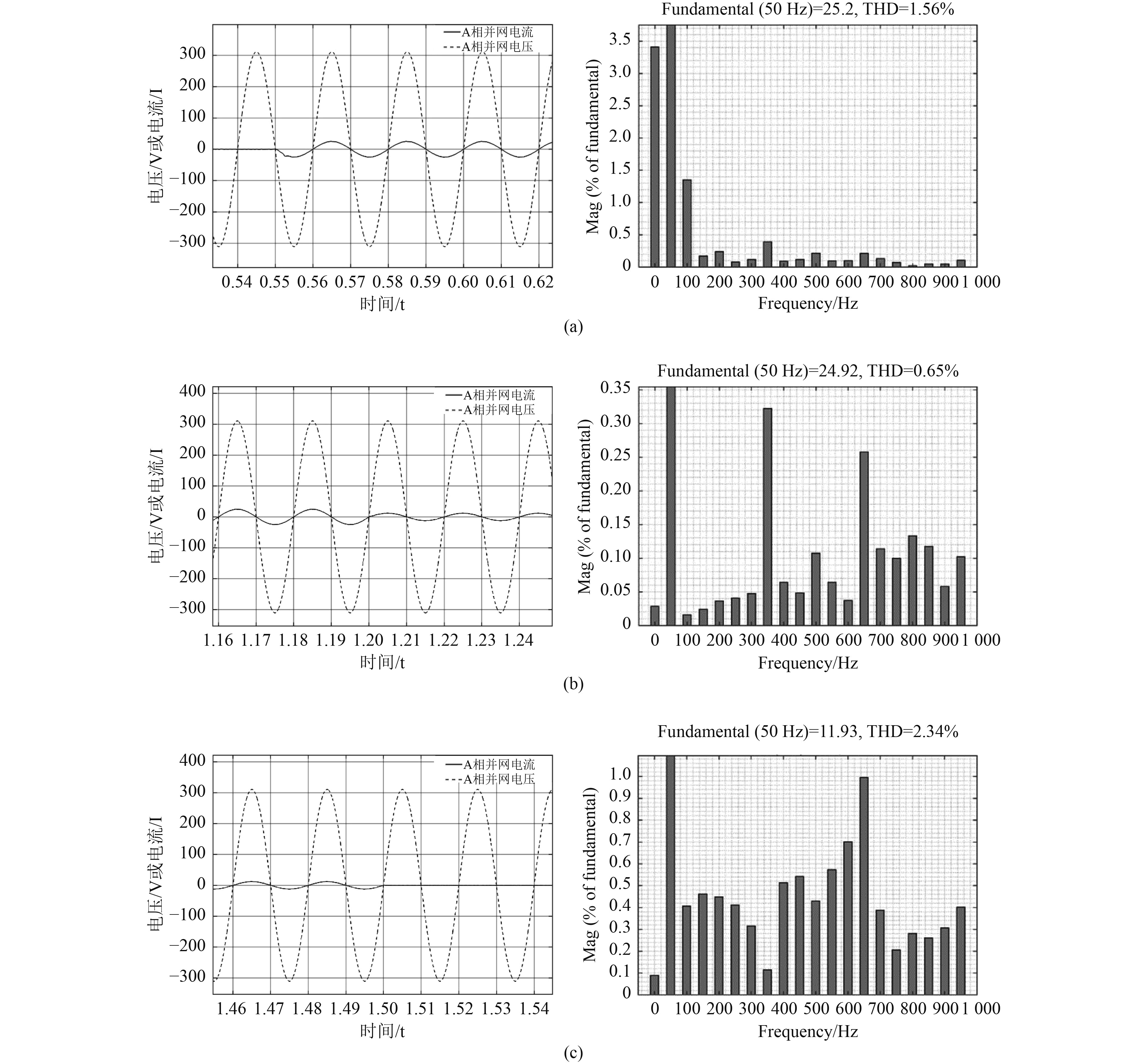
图 7 船舶制动能量回馈仿真结果 Fig. 7 Simulation results of ship braking energy feedback |
用
| $ \left\{\begin{split} &\left[\begin{array}{c}\dot{{z}_{d1}}\\ \dot{{z}_{d2}}\end{array}\right]={\boldsymbol{A}}\left[\begin{array}{c}{z}_{d1}\\ {z}_{d2}\end{array}\right]+{\boldsymbol{B}}{v}_{d}+{\boldsymbol{L}}({x}_{d1}-{z}_{d1}),\\ &\widehat{y}={C}_{z}\left[\begin{array}{c}{z}_{d1}\\ {z}_{d2}\end{array}\right]。\end{split}\right. $ | (9) |
其中:
| $ \left\{\begin{split} &\dot{{z}_{d}}=\left[\begin{array}{cc}-{\beta }_{1}& 1\\ -{\beta }_{2}& 0\end{array}\right]{z}_{d}+\left[\begin{array}{cc}{b}_{0d}& {\beta }_{1}\\ 0& {\beta }_{2}\end{array}\right]\left[\begin{array}{c}{v}_{d}\\ {y}_{d}\end{array}\right],\\ &\widehat{y}=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]{z}_{d}。\end{split}\right. $ | (10) |
线性状态误差反馈控制环节LESF的表达式为
| $ {u}_{0}={k}_{p}({i}_{dref}-{z}_{d1}) 。$ | (11) |
根据带宽法设计ADRC控制器的参数可得:
并网逆变控制类型分为电压控制和电流控制,其中电流控制分为dq旋转坐标系下的电流控制和
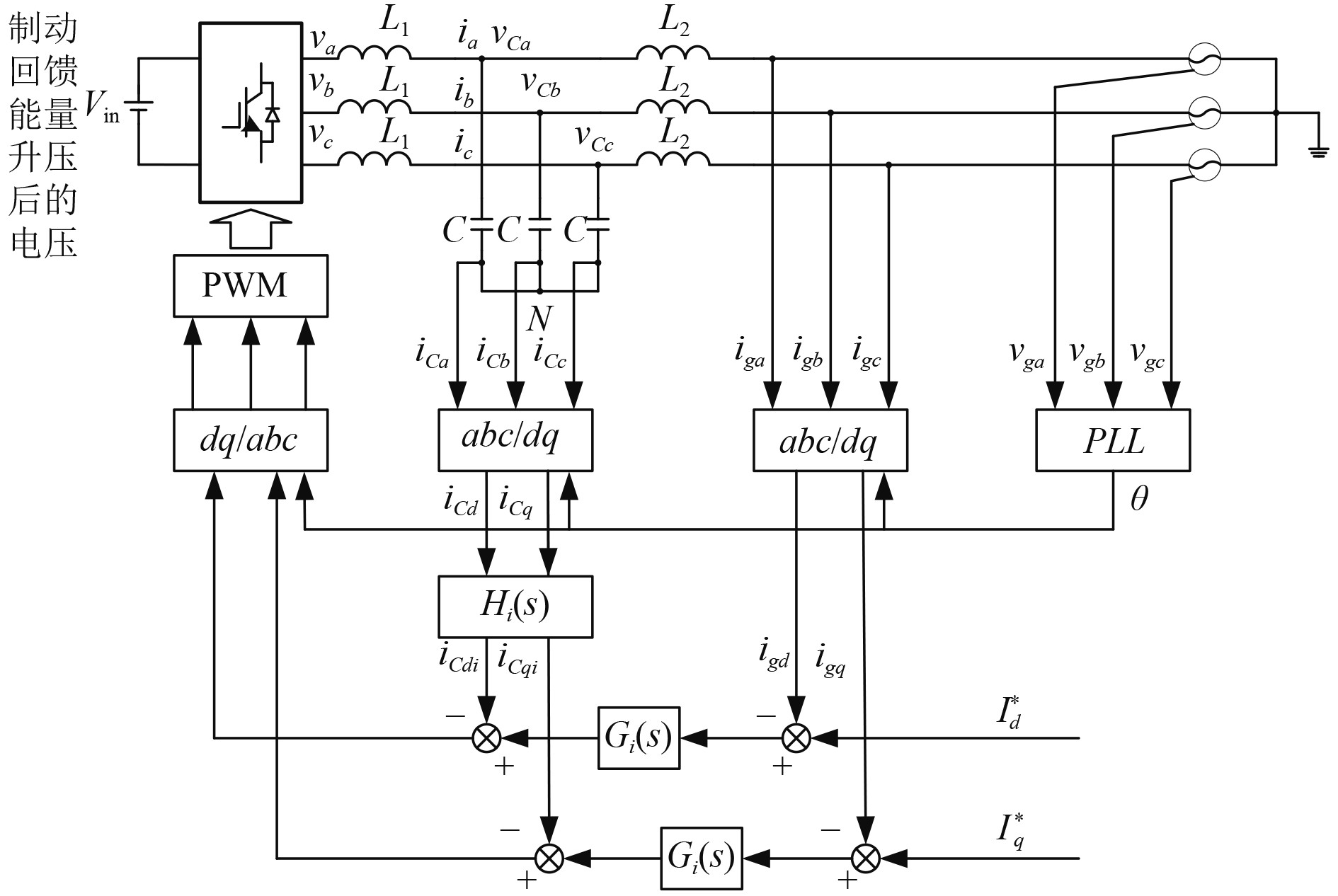
|
图 6 三相LCL型并网逆变器控制结构图 Fig. 6 Control structure diagram of three-phase LCL type grid-connected inverter |
仿真从时间0 s开始,在0~0.5 s内电机处在正常运行状态,此区间时间内直流母线侧电压稳定,并网阈值开关断开,可控三相整流器工作正常。0.5 s时,电机开始制动,制动回馈能量通过逆变器回馈到直流母线侧,直流母线上的电压开始升高,0.55 s时直流母线上的电压超过阈值电压后,并网阈值开关闭合,此时并网控制器开始工作。图7(a)左为船舶开始并网反馈能量时并网电流与并网电压仿真图,此时并网电流与并网电压相位相同且稳定。由于船舶电机制动回馈能量功率不恒定,因此并网电流需要可以调节,以满足可以快速使直流母线侧电压降低到额定电压值,图7(b)左中并网电流值有25 A降低到12 A,实现了并网功率的调节。图7(c)左中,1.5 s时刻由于直流母线侧电压降低到阈值电压,并网阈值开关闭合,并网回馈结束。
根据船级社规范要求,船舶电网的并网电流谐波畸变率(total harmonic distortion, THD)不能超过5%。图7(a)右为并网开始时并网电流THD分析,此时THD为1.56%。图7(b)右为并网稳定时并网电流THD分析,此时THD为0.65%。图7(c)右为并网电流变换时并网电流THD分析,此时THD为2.34%。通过对比可以得出本文设计船舶电力系统制动能量并网回馈仿真模型符合船级社规范要求。
4 结 语针对船舶电力推进系统制动时回馈能量的处理问题,本文对比总结各种船舶制动能量回馈利用的方法,选择基于ADRC控制器的LCL并网逆变回馈的控制策略。首先进行控制系统的设计,确定控制系统的结构。该结构实现了当直流侧存在大量再生能量时进行并网回馈电网,回馈完成后并网回馈结束。然后分析系统对控制系统进行降阶处理,根据ADRC控制的特点把系统模型误差当作内扰,利用扩张状态观测器进行补偿。另外,采用有源阻尼前置回馈的方法处理LCL型滤波的谐振尖峰。最后,根据系统设计和数学模型分析对其仿真。仿真结果表明,设计的系统在并网开始时和并网电流调节时都能够很好实现船舶再生能量的并网回馈,并网时并网电流THD分析满足设计要求。因此,该控制策略对于实现提高船舶能源利用率具有很好的实用价值。
| [1] |
何孝祖. 永磁同步电机再生能量回馈并网优化研究[D]. 株洲: 湖南工业大学, 2020.
|
| [2] |
曾宏宇. 船舶电力推进系统能量回馈过程研究与分析[D]. 北京: 中国舰船研究院, 2017.
|
| [3] |
高善诚. 基于复合型无源控制器弱电网LCL并网逆变器研究[D]. 武汉: 湖北工业大学, 2020.
|
| [4] |
JO H R, KIM Y J, LEE K B. LCL-filter design based on modulation index for grid-connected three-level hybrid anpc inverters[J]. Journal of Electrical Engineering & Technology, 2021, 16(3):
|
| [5] |
靖震. 船舶新能源LCL型并网逆变器控制策略研究[D]. 武汉: 武汉理工大学, 2018.
|
| [6] |
阮新波, 王学华, 等. LCL型并网逆变器的控制技术[M]. 北京: 科学出版社, 2015.
|
| [7] |
HE Y, WANG X, RUAN X, et al, Capacitor-current proportional-integral positive feedback active damping for LCL-type grid-connected inverter to achieve high robustness against grid impedance variation[J]. IEEE, 2019,34, (12): 12423–12436.
|
| [8] |
龙文浩. 光伏并网系统模型降阶研究[D]. 合肥: 合肥工业大学, 2020.
|
| [9] |
马明, 廖鹏, 蔡雨希, 等. LCL并网逆变器的自抗扰控制策略[J]. 高电压技术, 2021, 47(6): 2223−2231. MA Ming, LIAO Peng, CAI Yuxi, et al. Active disturbance rejection control strategy for lcl grid-connected inverter [J]. High Voltage Technology, 201, 47(6): 2223−2231. |
| [10] |
王福豹. 降阶自抗扰控制器参数整定[D]. 北京: 华北电力大学(北京), 2020.
|
 2022, Vol. 44
2022, Vol. 44

