柴油机凭借其性能优良在现代舰船动力装置中得到广泛应用,目前广泛使用的柴油机调速器是基于PID 控制算法构建的。文献[1]研究模糊自适应PID控制算法调节柴油机转速,在调速实时性方面得到了提升;文献[2]基于改进粒子群算法对PID控制器进行优化,减小了超调量,缩短了调节时间;文献[3] 建立径向基神经网络PID(RBF-PID)调速系统改善柴油机调速系统,在超调量与波动比方面都有很大的改善。目前对柴油机调速问题的主流研究方向是针对PID控制器的控制性能的优化与改进,对模型的不确定性与控制过程抗干扰性方面的研究较少,而外部干扰存在不确定性,常常导致系统运行效果达不到设计时预期的性能,甚至无法保证系统稳定性。鲁棒控制理论因其全面考虑系统模型参数不确定性和外部扰动不确定性因素,为开发控制器提供了更加可靠的理论基础,成为工业控制研究的热点,在精度控制和改善系统抗干扰性方面有着广泛的应用。文献[4] 针对航天惯性制导测试过程中单轴转台控制问题引入鲁棒控制算法,抗干扰性能优于传统PID 控制器,系统稳定性有了明显改善;文献[5]将鲁棒控制算法用于四旋翼飞行器姿态控制,稳定性有了很大的提升,并且在响应速度和姿态准确度方面有了改进;文献[6]将鲁棒控制理论应用于柔性机械手臂的控制领域,在控制精度尤其是抵抗外部干扰方面有了重大的改进;文献[7]应用鲁棒控制理论于重型商用车自动循迹控制方面,显著提升轨迹跟踪精度。
随着线性矩阵不等式(LMI)及凸优化等数学理论的发展,尤其是Matlab软件中LMI工具箱的推出,为鲁棒控制问题的分析与求解提供更加便捷的数学工具。
本文借助Matlab/Simulink仿真环境及PA-6型柴油机非线性机理模型,定量分析模型二次稳定性。建立
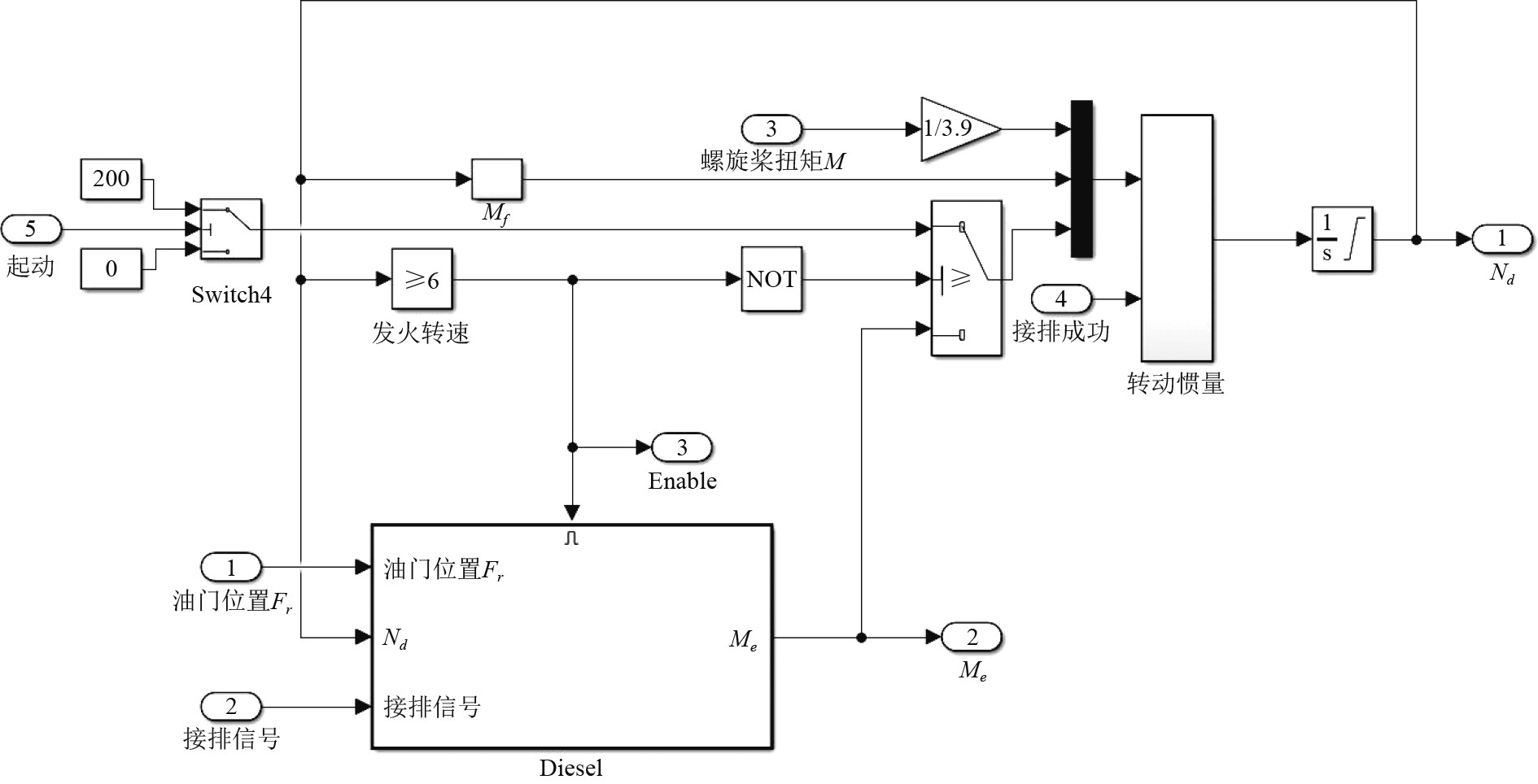
柴油机本体与喷油泵所构成的系统是典型的非线性系统,根据PA-6型柴油机技术资料建立了非线性机理模型,如图1所示。
|
图 1 柴油机非线性机理模型 Fig. 1 Nonlinear mechanism model of diesel engine |
柴油机模型稳定运转后,选取系统稳态工作点,对其进行局部线性化建模,得到系统状态空间表达式:
| $ \left\{\begin{aligned}&\dot{x}={\boldsymbol{A}}x+{\boldsymbol{B}}u,\\ &y={\boldsymbol{C}}x。\end{aligned}\right. $ | (1) |
式中:
| $ \begin{array}{c}{\boldsymbol{A}}=\left[\begin{array}{cc}\begin{array}{cc}-0.0093& 0.0102\\ 0& -2\end{array}& \begin{array}{cc}0& 0\\ 0& 100\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}-10& -100\\ 1& 0\end{array}\end{array}\right],\\{\boldsymbol{ B}}=\left[\begin{array}{c}\begin{array}{cc}0& -0.0011\\ 0& 0\end{array}\\ \begin{array}{cc}1& 0\\ 0& 0\end{array}\end{array}\right],\\ {\boldsymbol{C}}=\left[\begin{array}{cccc}1& 0& 0& 0\end{array}\right]。\end{array}$ | (2) |
显然,通过近似和简化得到的系统模型与实际系统存在偏差,即模型的不确定性,为确保系统不会因模型不确定性而影响其稳定性,在设计控制器前需进一步对不确定系统进行鲁棒稳定性分析。
由于系统主要受到摩擦力影响,经分析,摩擦力矩与柴油机转速间存在近似线性关系:
| $ {M}_{f}={k}_{f}{N}_{d}。$ | (3) |
式中:
式(3)表明,在柴油机运转时,摩擦力矩会随柴油机转速而变化,使得柴油机从某一稳态向另一稳态过渡过程中,系统系数矩阵会产生变化,也因此带来了系统模型的不确定性。
以上不确定性系统可表示为:
| $ \stackrel{~}{G}={G}_{0}+\mathrm{\Delta }\left(\delta \right)。$ | (4) |
式中:
| $ \left\{ \begin{aligned} &\dot{x}={\boldsymbol{A}}\left(\delta \right)x+{\boldsymbol{B}}u,\\ &y={\boldsymbol{C}}x。\end{aligned}\right. $ | (5) |
| $ A\left(\delta \right)={A}_{0}+\mathrm{\Delta }\left(\delta \right)。$ | (6) |
对额定转速下所有稳态工作点进行线性化,得到式中误差矩阵
由二次稳定性定义可知,若存在对称正定矩阵
| $ {{\boldsymbol{A}}}^{{\rm{T}}}\left(\delta \right){\boldsymbol{P}}+{\boldsymbol{P}}A\left(\delta \right) < 0 $ | (7) |
成立,则系统为二次稳定的。
借助Matlab中LMI工具箱的quadstab函数进行分析,求取对称正定矩阵
| $ {\boldsymbol{P}}=\left[\begin{array}{cccc} 0.0779& -0.0001& -0.0001& 0.0013\\ -0.0001& 0.4456&0.5825& 1.8752\\ -0.0001& 0.5825&2.3692& 11.2293\\ 0.0013& 1.8752& 11.2293& 120.6625\end{array}\right]。$ | (8) |
此时,
结果表明,系统
鲁棒控制是建立在状态反馈控制的控制理论,其本质是通过优化算法得到增益
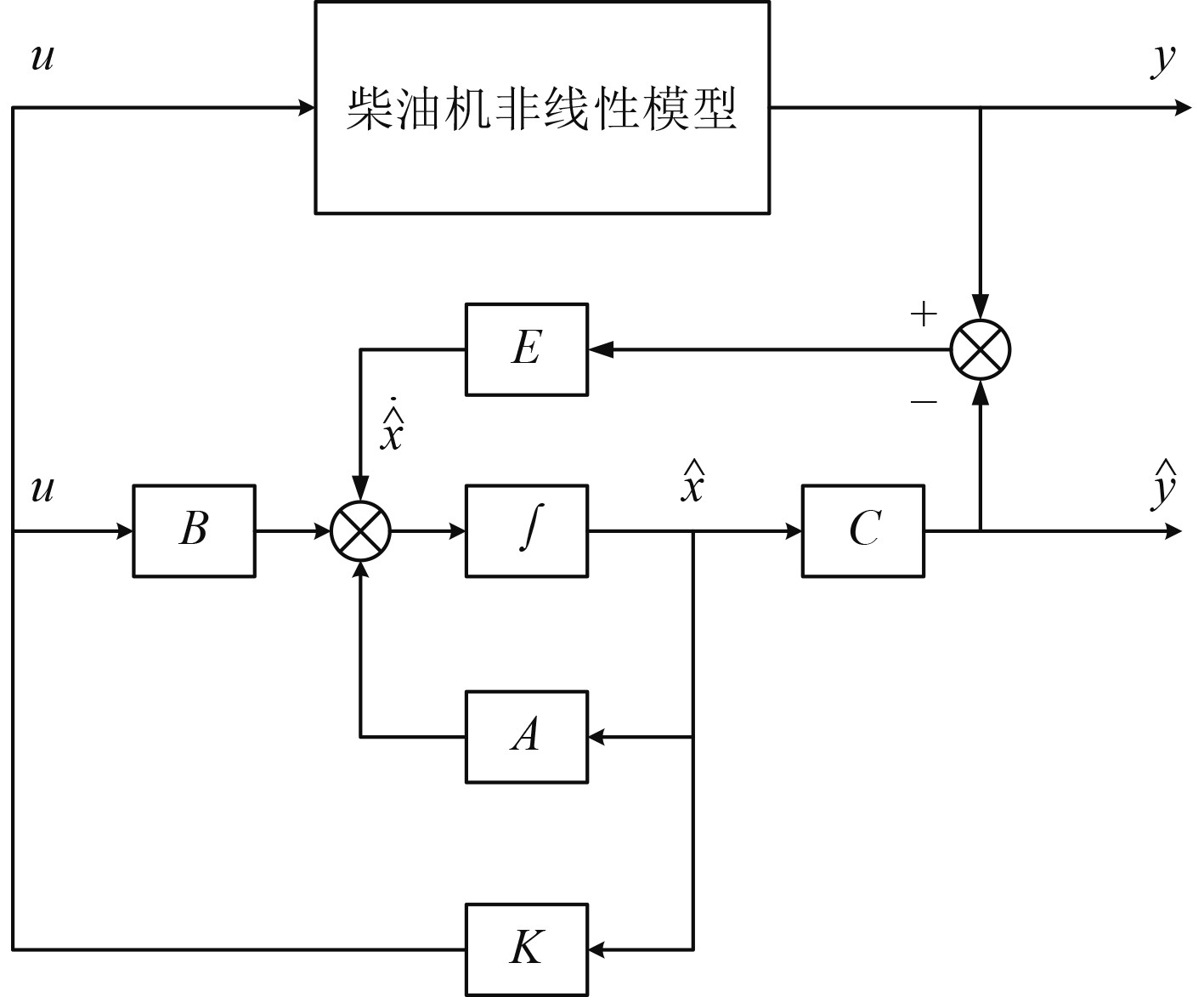
柴油机状态观测器结构如图2所示。
|
图 2 柴油机系统状态观测器结构图 Fig. 2 Structure diagram of diesel system state observer |
状态重构本质是对系统状态向量进行估计的过程,所以系统状态完全能观测是系统状态可重构的前提条件。通过观测器结构图可得:
| $ \dot{\widehat{x}}={\boldsymbol{A}}\widehat{x}+{\boldsymbol{B}}u+{\boldsymbol{E}}(y-\widehat{y})。$ | (9) |
式中:
| $ \dot{\widehat{x}}{\boldsymbol{=A}}\widehat{x}+{\boldsymbol{B}}u+{\boldsymbol{EC}}(x-\widehat{x}),$ | (10) |
则
| $ \dot{\widehat{x}}-\dot{x}={\boldsymbol{A}}\widehat{x}+{\boldsymbol{B}}u+{\boldsymbol{EC}}\left(x-\widehat{x}\right)-\left({\boldsymbol{A}}x-{\boldsymbol{B}}u\right) ,$ | (11) |
| $ (\dot{\widehat{x}}-\dot{x})=({\boldsymbol{A}}-{\boldsymbol{EC}})(\widehat{x}-x)。$ | (12) |
从式(12)可以看出,重构状态向量与原系统状态向量之差构成微分方程,其解形式为:
| $ \widehat{x}-x=\Delta x\left(t\right)={e}^{\left({\boldsymbol{A}}-{\boldsymbol{EC}}\right)\left(t-{t}_{0}\right)}\Delta x\left({t}_{0}\right),$ | (13) |
若
| $ \underset{t\to \infty }{\rm{lim}}\Delta x\left(t\right)=\underset{t\to \infty }{\rm{lim}}{e}^{({\boldsymbol{A}}-{\boldsymbol{EC}})(t-{t}_{0})}\Delta x\left({t}_{0}\right)=0,$ | (14) |
从而
| $ \underset{t\to \infty }{\rm{lim}}(\widehat{x}-x)=0,$ | (15) |
即当
加入状态观测器后,系统(1)可改写为:
| $ \left\{\begin{aligned} &\dot{\widehat{x}}=({\boldsymbol{A}}-{\boldsymbol{EC}})\widehat{x}+{\boldsymbol{B}}u+Ey,\\ &\widehat{y}={\boldsymbol{C}}\widehat{x}。\end{aligned}\right. $ | (16) |
此时,控制输入为:
| $ u=K\widehat{x} 。$ | (17) |
| $ {\boldsymbol{E}}={\left[\begin{array}{cccc}27.991& 33592& -7323.9& 2929.6\end{array}\right]}^{{\rm{T}}} 。$ | (18) |
作为舰船推进主动力装置的柴油机,其调速控制是典型的系统跟踪控制,令系统输出
| $ e\left(t\right)=r-y\left(t\right),$ | (19) |
误差
| $ q\left(t\right)=\int e\left(\tau \right){\rm{d}}\tau =\int [r-y(\tau \left)\right]{\rm{d}}\tau,$ | (20) |
求导数后有:
| $ \dot{q}\left(t\right)=e\left(t\right)=r-y\left(t\right)=-{\boldsymbol{C}}x+r。$ | (21) |
将重构的状态向量
| $ \left\{\begin{aligned} &\dot{\widehat{x}}=({\boldsymbol{A}}-{\boldsymbol{EC}})\widehat{x}+{\boldsymbol{B}}u+{\boldsymbol{E}}y,\\ &\dot{q}=-{\boldsymbol{C}}x+r\approx -{\boldsymbol{C}}\widehat{x}+r,\\ &\widehat{y}={\boldsymbol{C}}\widehat{x}。\end{aligned}\right. $ | (22) |
对各系数矩阵进行增广处理:
| $ \left\{\begin{array}{c}\widetilde{{\boldsymbol{A}}}=\left[\begin{array}{cc}{\boldsymbol{A}}-{\boldsymbol{EC}}& 0\\ -{\boldsymbol{C}}& 0\end{array}\right],\\ \widetilde{{\boldsymbol{B}}}=\left[\begin{array}{c}{\boldsymbol{B}}\\ 0\end{array}\right],\\ \widetilde{{\boldsymbol{C}}}=\left[\begin{array}{cc}{\boldsymbol{C}}& 0\end{array}\right]。\end{array}\right. $ | (23) |
则系统的状态空间形式为:
| $ \left \{ \begin{aligned} &\left[ \begin{array}{c}\dot{\widehat{x}}\\ \dot{q}\end{array} \right]=\left[ \begin{array}{cc}{\boldsymbol{A}}-{\boldsymbol{EC}} 0\\ -{\boldsymbol{C}} 0\end{array} \right]\left[ \begin{array}{c}\widehat{x}\\ q\end{array} \right]+\left[ \begin{array}{c}{\boldsymbol{B}}\\ 0\end{array} \right]u+\left[ \begin{array}{c}{\boldsymbol{E}}y\\ r\end{array} \right],\\ &\;\widehat{y}=\left[ \begin{array}{cc}{\boldsymbol{C}} 0\end{array} \right]\left[ \begin{array}{c}\widehat{x}\\ q\end{array} \right]。\end{aligned} \right. $ | (24) |
同时,控制律
| $ \stackrel{~}{K}=\left[\begin{array}{cc}{K}_{1}& {K}_{2}\end{array}\right],$ | (25) |
控制输入
| $ u=\stackrel{~}{K}\left[\begin{array}{c}\widehat{x}\\ q\end{array}\right]=\left[\begin{array}{cc}{K}_{1}& {K}_{2}\end{array}\right]\left[\begin{array}{c}\widehat{x}\\ q\end{array}\right]={K}_{1}\widehat{x}+{K}_{2}q。$ | (26) |
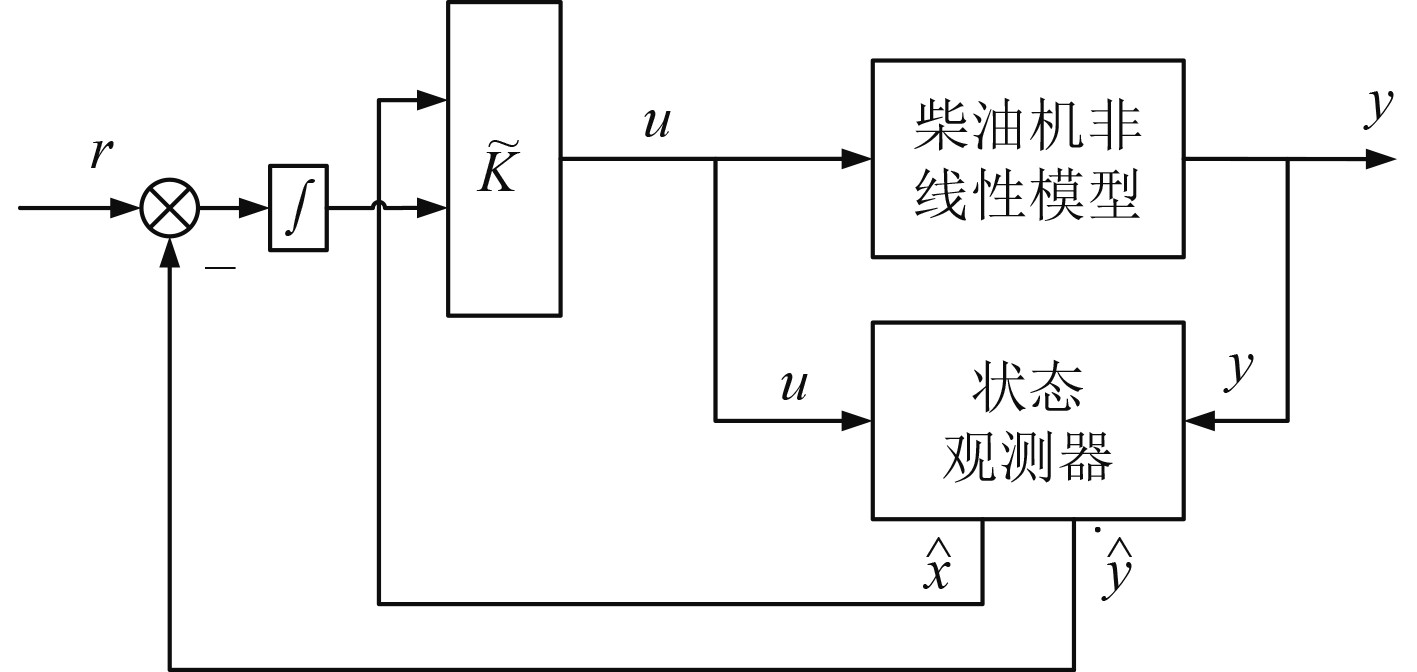
则控制系统结构框图如图3所示。
|
图 3 柴油机调速系统跟踪控制结构框图 Fig. 3 Diesel speed control system tracking control structure block diagram |
跟踪控制系统构建完成,进而设计鲁棒控制律
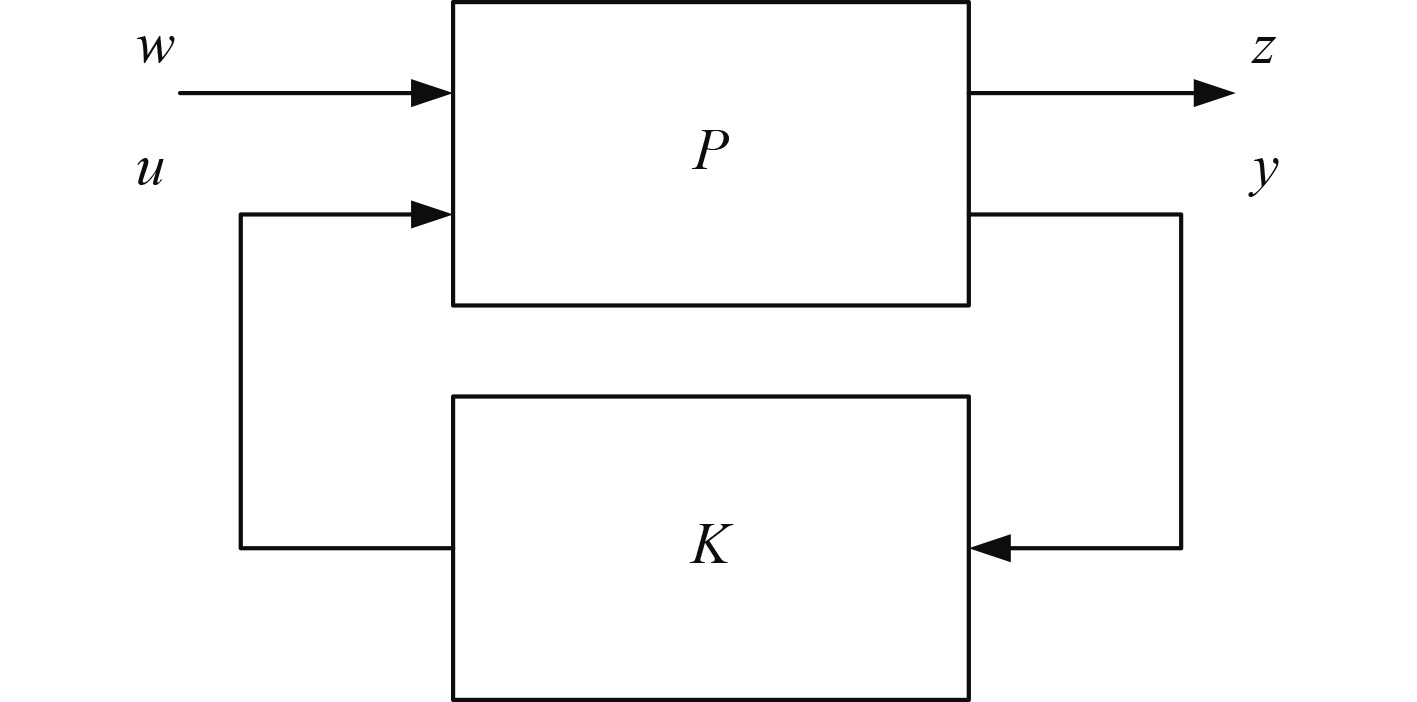
设计鲁棒
|
图 4 广义系统双端子图 Fig. 4 Two terminal graph of singular system |
图中
| $ \left\{\begin{aligned} &\dot{x}=Ax+{B}_{1}w+{B}_{2}u,\\ &z={C}_{1}x+{D}_{11}w+{D}_{12}u,\\ &y={C}_{2}x+{D}_{21}w+{D}_{22}u。\end{aligned}\right. $ | (27) |
对于任意扰动
| $ {\int }_{0}^{\infty }\left({\sum }_{1}^{n}{q}_{i}{x}_{i}^{2}+\rho {u}^{2}\right){\rm{d}}t < {\int }_{0}^{\infty }{w}^{2}{\rm{d}}t 。$ | (28) |
式中,
若理想被控输出对扰动
| $ z={C}_{1}x+{D}_{12}u ,$ | (29) |
同时令:
| $ \left\{ \begin{aligned} &{C}_{1}=\left[\begin{array}{c}{\rm{diag}}\left(sqrt\right(q\left)\right)\\ {0}_{1\times m}\end{array}\right],\\ &{D}_{12}=\left[\begin{array}{c}{0}_{n\times 1}\\ \sqrt{\rho }\end{array}\right]。\end{aligned}\right. $ | (30) |
其中,
设计控制器
| $ {‖{T}_{wz}\left(s\right)‖}_{\infty } < 1,$ | (31) |
满足上述2个条件的控制器
显然,通过关系式(31)计算得到的控制器并不唯一。进一步将控制输入
| $ \left\{ \begin{aligned} &\dot{x}=(A+{B}_{2}K)x+{B}_{1}w,\\ &z={(C}_{1}+{D}_{12}K)x+{D}_{11}w。\end{aligned}\right. $ | (32) |
同时限定闭环传递函数
| $ {‖{T}_{wz}\left(s\right)‖}_{\infty } < \gamma,$ | (33) |
化简得:
| $ {‖{T}_{wz}\left(s\right)‖}_{\infty }={‖{(C}_{1}+{D}_{12}K){[sI-(A+{B}_{2}K\left)\right]}^{-1}{B}_{1}+{D}_{11}‖}_{\infty } < \gamma ,$ | (34) |
求解式(34),得系统(27)的
控制器
定理1 对系统(27),存在一个状态反馈
| $ \left[\begin{array}{ccc}AX+{B}_{2}W+{\left(AX+{B}_{2}W\right)}^{{\rm{T}}}& {B}_{1}& {({C}_{1}X+{D}_{12}W)}^{{\rm{T}}}\\ {B}_{1}^{{\rm{T}}}& -I& {D}_{11}^{{\rm{T}}}\\ {C}_{1}X+{D}_{12}W& {D}_{11}& -{\gamma }^{2}I\end{array}\right] < 0 。$ | (35) |
进而可行解
| $ K={W}^{*}{\left({X}^{*}\right)}^{-1}。$ | (36) |
通过定理1得到线性矩阵不等式(35),使设计
将重构的参数矩阵代入系统(27),设加权参数
| $ \stackrel{~}{K}=\left[\begin{array}{ccc}\begin{array}{cc}-0.7505& 0\end{array}& 0& \begin{array}{cc}0& 0.2\end{array}\end{array}\right]。$ | (37) |
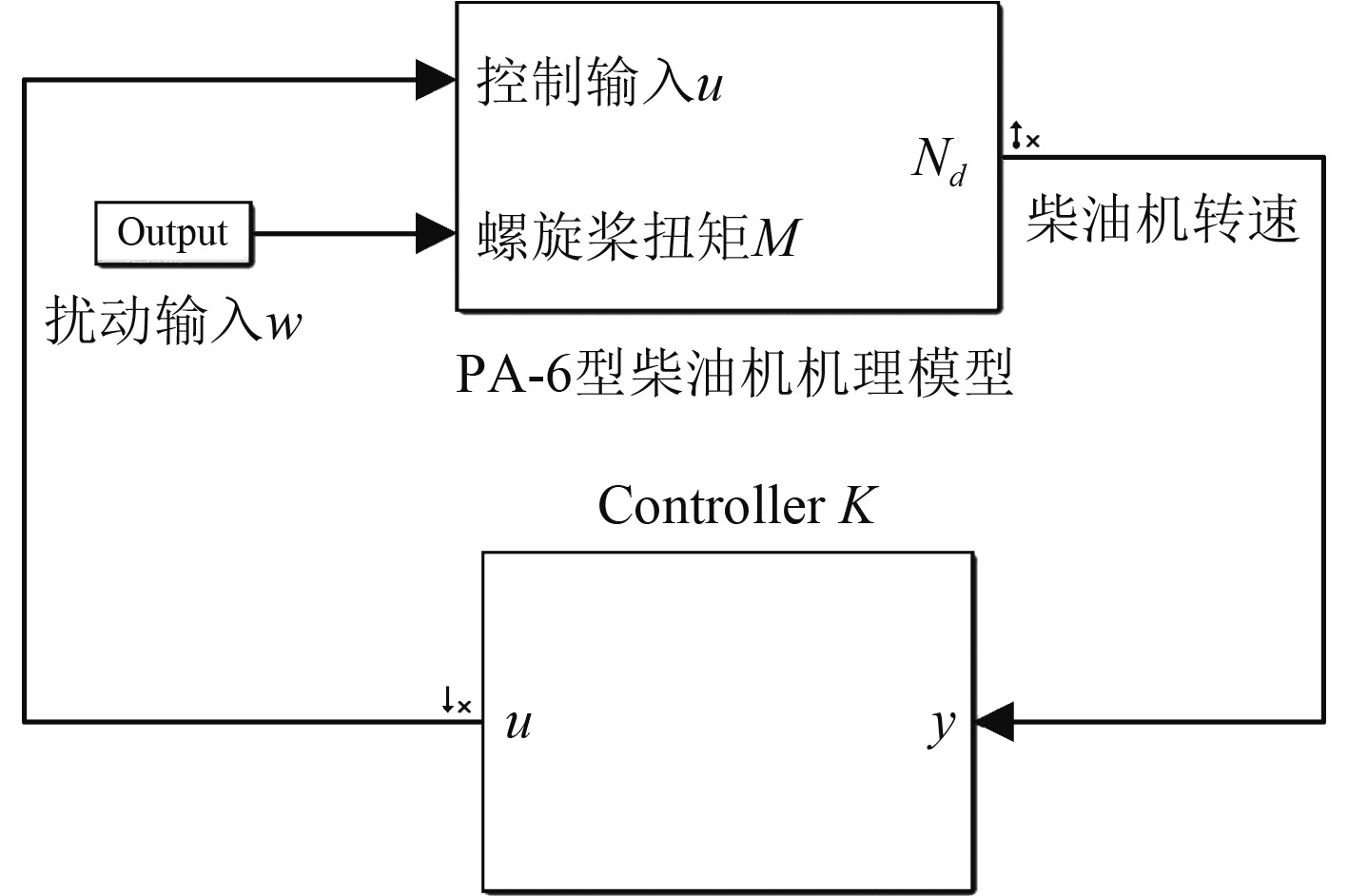
借助Matlab/Simulink仿真平台进行实验,编写M-File计算控制律。构建柴油机调速系统,如图5所示。
|
图 5 Simulink控制系统图 Fig. 5 Control system diagram by Simulink |
仿真实验分为3个部分,考察控制器在阶跃信号、柴油机空载运转、带载运转时转速调节情况。
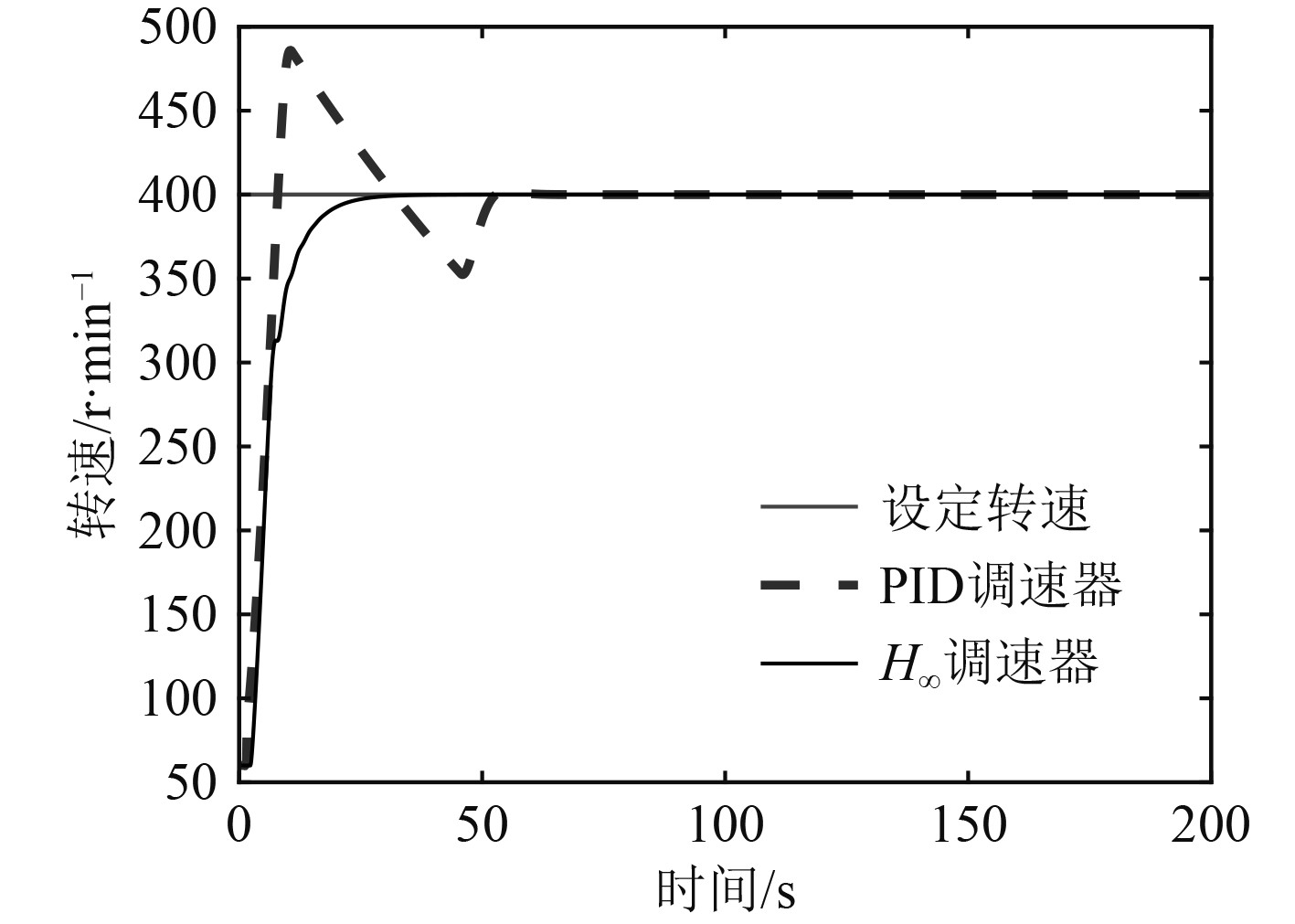
5.1 阶跃响应设定转速为
|
图 6 阶跃响应曲线图 Fig. 6 Diagram of step response curve |
响应曲线揭示2种调速器均可使柴油机转速稳定在设定转速,PID控制器超调明显,调节时间约为50 s,而
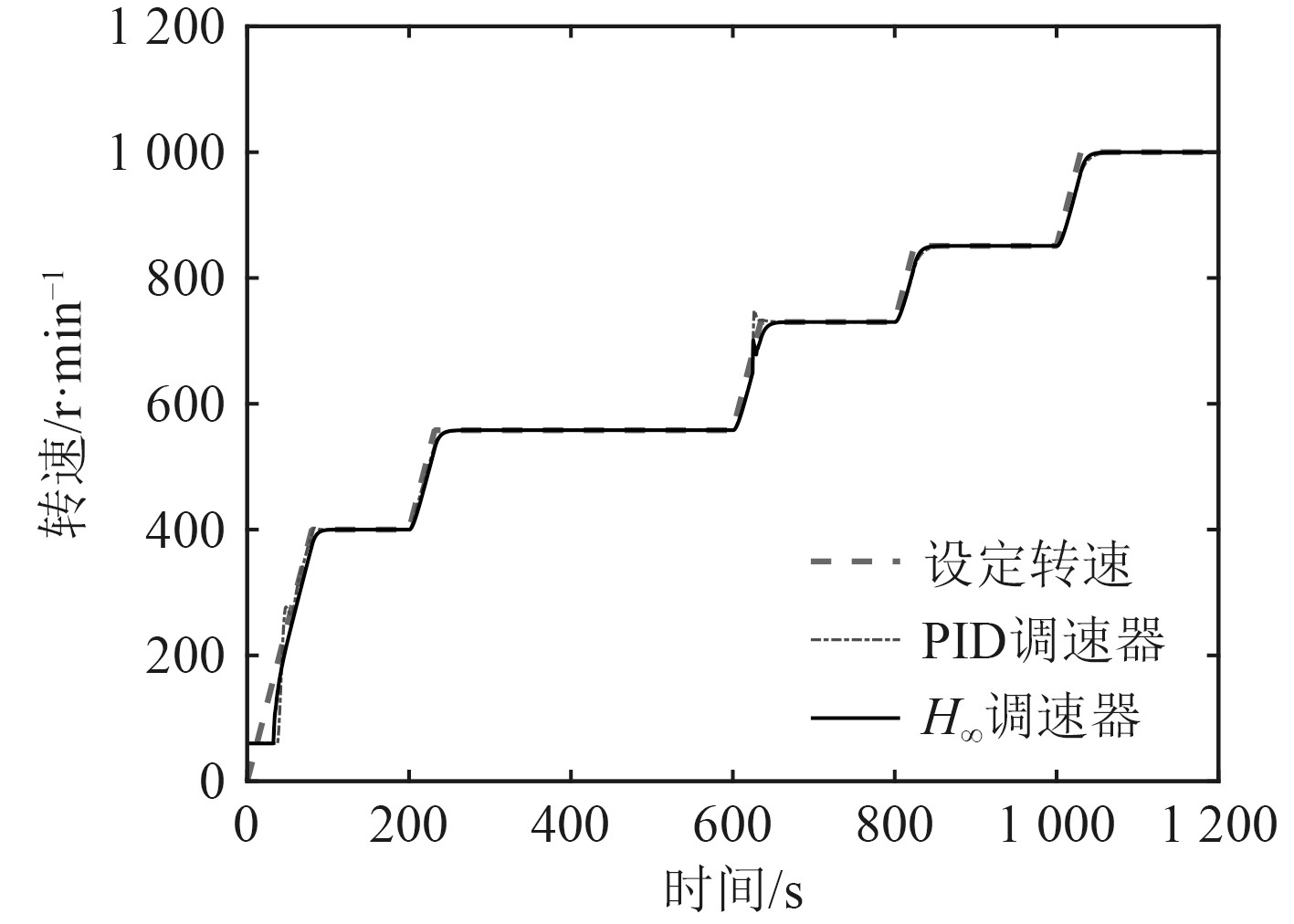
调速曲线如图7所示。
|
图 7 柴油机空载运转曲线图 Fig. 7 Diagram of diesel engine operation curve without load |
两控制器在连续调速过程中均能够使柴油机运行平稳,表现出良好的控制性能。PID控制器运行时存在微小超调量。
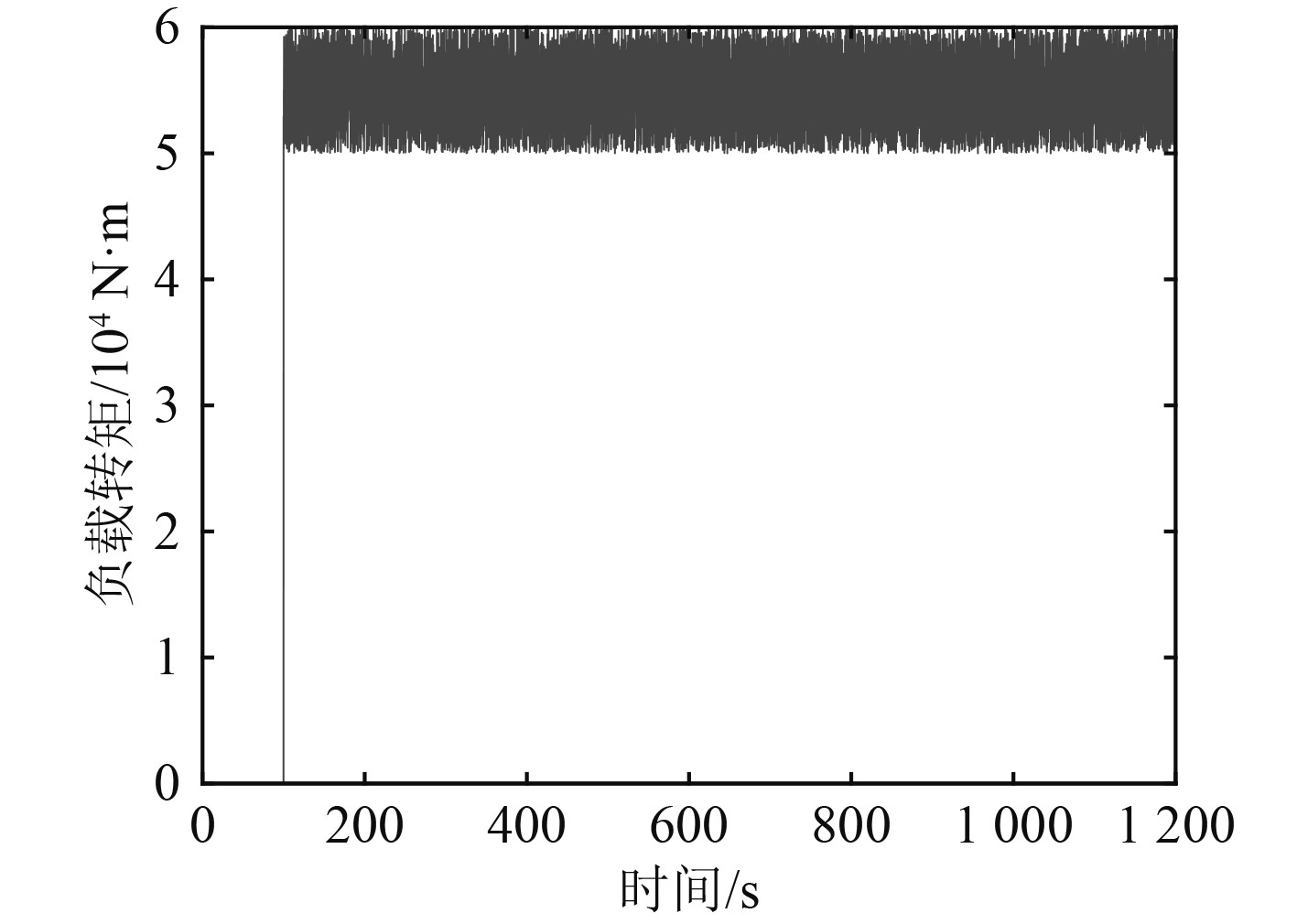
5.3 柴油机带载运转设定当柴油机稳定运行后,模拟舰船实际航行,给柴油机加额定负载,同时附加强烈的随机扰动。负载扭矩如图8所示。带负载状况下连续调速曲线如图9所示。
|
图 8 负载扭矩曲线图 Fig. 8 Diagram of load torque curve |
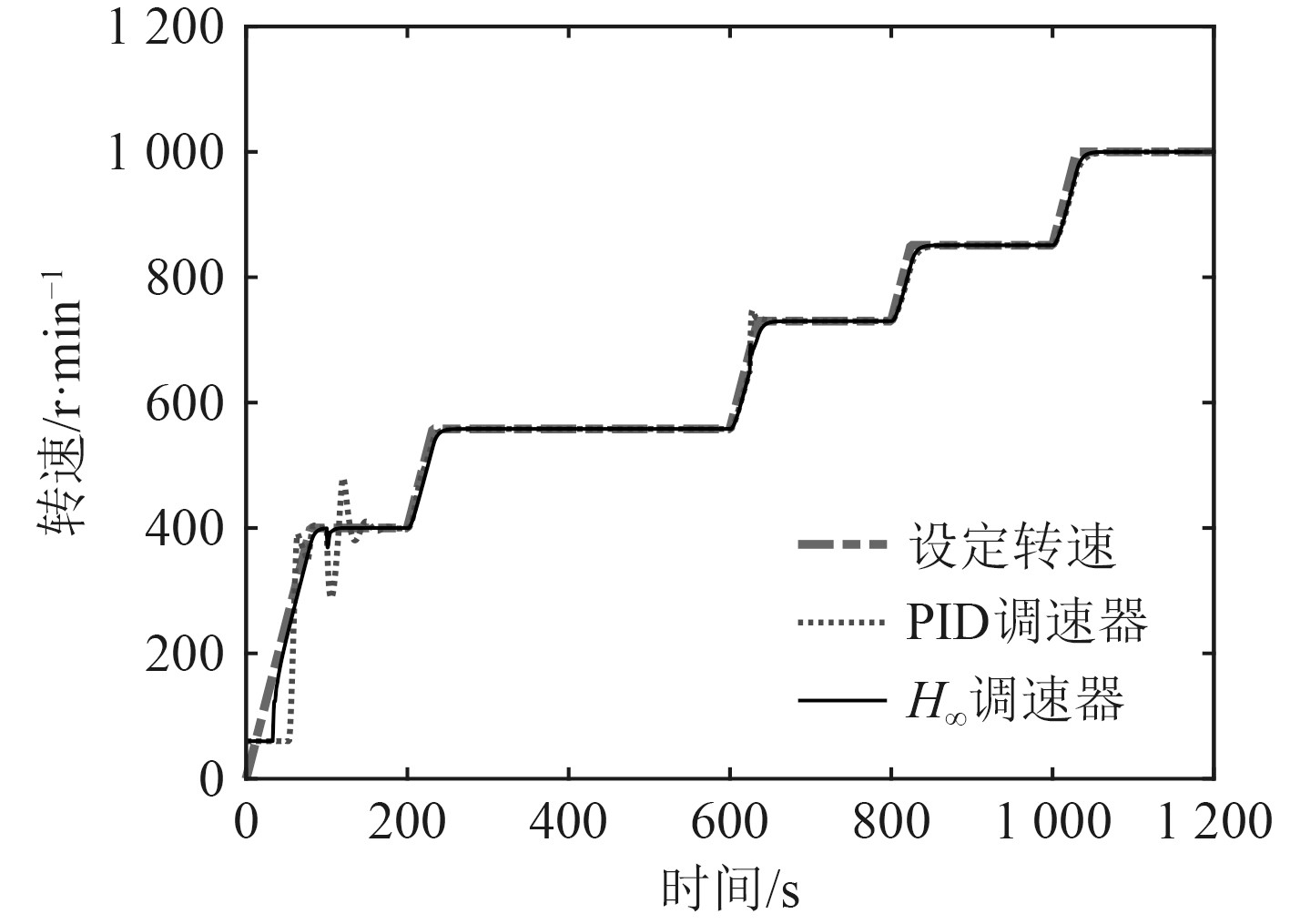
|
图 9 柴油机带负载运转曲线图 Fig. 9 Diagram of diesel engine operation curve with load |
可以看出,当系统带负载的瞬间,PID调速器出现明显波动,且经过较长调节时间后稳定。
| [1] |
束长健, 曾洁, 邹娟, 等. 基于模糊自适应PID控制的柴油机调速模型仿真研究[J]. 铁道机车与动车, 2020(1): 9-12. |
| [2] |
贾波凯. 基于改进粒子群算法的柴油机调速策略研究[D]. 北京: 中国舰船研究院, 2019.
|
| [3] |
李宗营, 马传杰, 杨传雷, 等. RBF神经网络对STC柴油机调速系统性能改善研究[J]. 应用科技, 2018, 45(5): 102-107. |
| [4] |
任伟杰, 麻恒进, 孟凡军. 基于鲁棒控制理论的单轴转台动态性能研究[J]. 航空精密制造技术, 2021, 57(3): 24-28+32. DOI:10.3969/j.issn.1003-5451.2021.03.007 |
| [5] |
尚冠宇, 孙童真. 采用自适应观测器的共轴多旋翼无人机鲁棒控制[J]. 电光与控制, 2021, 28(6): 85-89. DOI:10.3969/j.issn.1671-637X.2021.06.019 |
| [6] |
GOUBEJ M, et al.. Employing finite element analysis and robust control concepts in mechatronic system design-flexible manipulator case study[J]. Applied Sciences, 2021, 11: 3689. DOI:10.3390/app11083689 |
| [7] |
董晴, 季学武, 刘玉龙,等. 基于LPV/H_∞鲁棒控制的重型商用车自动循迹[J/OL]. 清华大学学报(自然科学版): 1-9 [2021-08-10].
|
 2022, Vol. 44
2022, Vol. 44
