船舶主动式升沉补偿装置作为一项关键技术,在海上油气开采、物资运输、风机安装修建、港口装卸等方面有着广泛的应用。船舶进行吊装作业时,货物随着船舶上下升沉运动无法保持一个稳定的状态,从而严重影响一些需要定位精确、环境稳定下才能进行的海上作业,船舶装备和船员人身安全面临严重的安全隐患。因此为保证吊装作业在升沉方向上的平稳可靠,对升沉补偿技术进行研究就成为十分迫切的需要[1]。
由于主动式升沉补偿装置具有复杂的机械执行机构以及涉及液压传动,从而导致升沉补偿控制系统具有时滞性特点[2]。另外船舶运动中海况多变,风、浪、流等外界干扰对系统有很大的影响,受模型参数摄动使得完全基于模型的控制方法难于实现[3]。文献[4]采用预测模糊控制克服了系统的时滞问题并且一定程度上提高了升沉补偿效率,但是该控制方法对模型的依赖性程度高,在海况和模型变化的情况下控制效果存在缺陷。
自抗扰控制技术(active disturbance rejection control,ADRC)[5-6]由韩京清提出,是对经典PID技术的继承与发展,自抗扰控制算法安排过渡环节解决经典PID中快速性与超调之间的矛盾,并且通过扩张状态观测器和非线性误差反馈控制率实时估计和补偿扰动。自抗扰控制对强干扰系统和模型不确定的系统具有较好的控制效果,并且其具有算法容易实现、抗扰能力强、不依赖精确系统模型等优点,所以将ADRC控制器应用于大惯性、非线性、强干扰和大时滞性的船舶主动式升沉补偿控制系统具有重要的研究意义。ADRC技术已经在船舶动力定位系统、航向舵角控制等领域有所应用[7-9]。本文将ADRC控制器应用于主动式升沉补偿控制系统,提高系统的响应性能和鲁棒性,并通过建立模型进行仿真分析。
1 升沉补偿系统数学模型 1.1 系统描述对系统进行建模是控制系统仿真研究的首要环节,也是控制系统静动态特性研究的基础。主动式升沉补偿控制系统是一套主要由机械执行、液压传动和控制部分组成的机电液一体化的现代化装备。为了提高液压传动系统效率,应尽量减少中间环节数量及传递的功率损失。从能源消耗的角度考虑,将液压二次调节驱动系统选为主动式升沉补偿系统中的驱动装置。
本文研究的主动式升沉补偿操作系统是基于海洋船用起重设备进行的。升沉补偿船舶通过安装动力定位系统保持了水平面上基本的稳定状态,系统已经获得了船舶升沉设备吊装点实时综合升沉运动信号,不考虑负载的摆动,考虑主动式升沉补偿系统所具有的时滞性与所处的强干扰环境进行系统控制研究。
1.2 建立液压驱动单元数学模型工作母船在进行海上吊装作业时,起重设备通过钢丝绳索进行货物装卸与过驳,将钢丝绳索视为刚体,在实际吊装过程中不考虑其受力过程中产生的微小伸缩形变以及升沉过程中的最大张力。卷筒作为机械执行机构的终端环节,通过正反旋转从而实现伴随船舶升沉运动所产生的升沉速度与位移的补偿。
吊装绳索张力方程为:
| $ T = EA\varepsilon \text{。} $ | (1) |
式中:
卷筒模型方程为:
| $ G(s) = \dfrac{r}{i} \text{。}$ | (2) |
式中:
液压二次调节驱动系统主要由恒压油源装置单元、二次控制单元和执行单元3部分组成。液压二次调节驱动系统基本的工作原理是:控制阀的流量改变变量缸杆的位移,从而改变斜盘角度的大小,进而改变系统的排量,最终调节系统的输出转矩及转速[10-11]。
一般电液伺服系统的伺服比例阀的传递函数通常用二阶环节表达:
| $ {G_v}(s) = \dfrac{{Q(s)}}{{I(s)}} = \dfrac{{{K_v}}}{{\dfrac{1}{{\omega _v^2}}{s^2} + \dfrac{{2{\xi _v}}}{{{\omega _v}}}s + 1}} \text{。}$ | (3) |
式中:
由连续性方程可知,变量液压缸的流量为:
| $ {Q_{\rm{f}}} = {A_{\rm{r}}}\dfrac{{{\rm{d}}Y}}{{{\rm{d}}t}} + {C_{{\rm{tp}}}}{p_{\rm{v}}} + \dfrac{{{V_{\rm{t}}}}}{{4{\beta _{\rm{e}}}}}\dfrac{{{\rm{d}}{p_{\rm{v}}}}}{{{\rm{d}}t}} \text{。}$ | (4) |
式中:
变量液压缸的力平衡方程为:
| $ {p_v}{A_r} = m\dfrac{{{{\rm{d}}^2}Y}}{{{\rm{d}}{t^2}}} + {B_k}\dfrac{{{\rm{d}}Y}}{{{\rm{d}}t}} + KY + F \text{。}$ | (5) |
式中:
斜盘受力方程为:
| $ F = \dfrac{{{J_{\rm{s}}}}}{{L_{\rm{s}}^2}}\dfrac{{{{\rm{d}}^2}Y}}{{{\rm{d}}{t^2}}} + \dfrac{{{B_{\rm{s}}}}}{{L_{\text{s}}^2}}\dfrac{{{\rm{d}}Y}}{{{\rm{d}}t}} + \dfrac{{{K_{\rm{s}}}}}{{L_{\rm{s}}^2}}Y \text{。}$ | (6) |
式中:
液压二次元件排量方程为:
| $ V = \dfrac{{{V_{\max }}}}{{{\gamma _{\max }}}}\gamma \approx \dfrac{{{V_{\max }}}}{{{Y_{\max }}}}Y \text{。}$ | (7) |
式中:
对卷筒绳索收放过程进行力学分析,可得到力矩平衡方程为:
| $ M - Tr = J{\theta _{\rm{m}}}\dfrac{{{{\rm{d}}^2}\varphi }}{{{\rm{d}}{t^2}}} + {B_{\rm{m}}}\dfrac{{{\rm{d}}\varphi }}{{{\rm{d}}t}} \text{。}$ | (8) |
式中:
自抗扰控制器的核心思想是通过采用“观测+补偿”的方法对非线性、大时滞、强不确定性的系统对象进行控制,消除系统误差,并且利用扩张状态观测器对系统内外扰动进行实时估计,将所有其他项忽略的模型与外界的扰动(噪声)统一为总扰动,并在反馈中给予补偿从而抑制扰动的影响,进一步提高控制器的动态响应性能。自抗扰控制技术因其对具体模型的要求低以及良好的抗干扰能力特点而广泛应用于工业界。
自抗扰控制器主要由跟踪微分器(TD)、扩张状态观测器(ESO)和非线性状态误差反馈控制率(NLSEF)3个主体部分构成。以二阶系统为例,其基本结构如图1所示[12]。

|
图 1 二阶自抗扰控制器基本结构 Fig. 1 The basic structure of two order ADRC |
1)跟踪微分器主要起到对输入信号进行处理、过渡的作用。针对升沉补偿系统而言,TD可以对船舶升沉速度进行跟踪并且输出光滑、连续的信号,解决传统PID控制存在的响应速度与与超调之间的矛盾。适用于二阶系统的自抗扰控制器离散算法为[13]:
| $ \left\{\begin{split} & {x_1}(k + 1) = {x_1}(k) + h{x_2}(k) \text{,} \\ & {x_2}(k + 1) = {x_2}(k) + hfh \text{,} \\ & fh = fhan({x_1}(k) - x(k),{x_2}(k),r,{h_0}) \text{。} \\ \end{split} \right.$ | (9) |
其中:
| $ \left\{\begin{array}{l}d=r{h}_{0}{}^{2};\;{a}_{0}={h}_{0}{x}_{2}\text{,}\\ y={x}_{1}+{a}_{0}\text{,}\\ {a}_{1}=\sqrt{{d}^{2}+8d\left|y\right|}\text{,}\\ {a}_{2}={a}_{0}+sign(y)\dfrac{({a}_{1}-d)}{2}\text{,}\\ a=({a}_{0}+y-{a}_{2}){S}_{y}+{a}_{2}\text{,}\\ {S}_{y}=({\rm{sign}}(y+d)-{\rm{sign}}(y-d))/2\text{,}\\ {S}_{a}=({\rm{sign}}(a+d)-{\rm{sign}}(a-d))/2\text{,}\\ fhan=-r(a/d-{\rm{sign}}(a)){S}_{a}-r{\rm{sign}}(a)\text{。}\end{array} \right.$ | (10) |
式中:
2)扩张状态观测器(ESO)是自抗扰控制器设计中最重要的部分,其原理是将未建模或者未知模型部分与外界的扰动(噪声)统一为总扰动,通过扩张出一个新的状态变量,进而对系统内外扰动进行实时估计,并进行补偿。考虑二阶系统,其离散化公式如下[13]:
| $ \left\{\begin{split} & e(k) = {z_1}(k) - y(k) \text{,}\\ & {z_1}(k + 1) = {z_1}(k) + h\left\{ {{z_2}(k) - {\beta _1}e(k)} \right\} \text{,}\\ & {z_2}(k + 1) = {z_2}(k) + h\left\{ {{z_3}(k) - {\beta _2}fal(e(k),{\alpha _1},\delta )} \right\} \text{,} \\ & {z_3}(k + 1) = {z_3}(k) - h{\beta _3}fal(e(k),{\alpha _2},\delta ) \text{。} \end{split} \right.$ | (11) |
式中:
3)状态误差反馈控制率是对信号误差反馈进行非线性组合,从而构成系统的控制量,为了使误差反馈更有效率,通常情况下选择2个不一样的非线性函数进行组合,形成一个新的更优化的控制率。其公式如下[13]:
| $ \left\{\begin{split} & {e_1} = {x_1}(k) - {z_1}(k) \text{,}\\ & {e_2} = {x_2}(k) - {z_2}(k) \text{,}\\ &{u_0} = {k_1}fal({e_1},n{\alpha _1},\delta ) + {k_2}fal({e_2},n{\alpha _2},\delta ) \text{,}\\ &u = {u_0} - {z_3}/b \text{。} \end{split} \right.$ | (12) |
式中:
1)船舶模型参数
采用开源的挪威科技大学开发的船舶仿真器(MMS)提供的供给船[14]船舶模型作为工作母船进行升沉补偿控制系统仿真设计。其中船舶模型参数如表1所示。
|
|
表 1 船舶模型参数 Tab.1 Ship model parameters |
2)主动升沉补偿系统参数
主动升沉补偿系统采用液压二次调节驱动系统,其具体参数如表2所示。
|
|
表 2 液压二次调节驱动系统参数 Tab.2 Parameters of hydraulic secondary regulation drive system |
3)ADRC控制器参数整定
ADRC的参数较多,其中TD中的积分步长
根据深海船舶装备的实际工作环境和特点,针对目前主动式升沉补偿控制系统存在的时滞性、工作环境存在干扰等问题,通过仿真分析,对比ADRC与传统的PID控制对于干扰和时滞系统的控制效果。为了分析控制系统的抗干扰性能如何,给入系统一个幅值大小为1的正弦信号,对升沉补偿控制系统进行控制研究,在第7 s的时候给定一个大小为100的脉冲干扰,并对系统进行仿真分析,结果如图2所示。

|
图 2 ADRC VS PID控制干扰系统仿真结果 Fig. 2 Simulation results of ADRC vs PID control disturbance system |
针对系统存在的时滞性,研究PID控制和ADRC对于延迟系统的动态响应性能,并对系统进行仿真分析。以一个单位为1的阶跃信号作为系统输入,以升沉补偿控制系统作为被控对象,在系统延迟0.2 s,0.4 s和0.8 s的情况下进行仿真分析,结果如图3所示。

|
图 3 ADRC VS PID控制时滞系统仿真结果 Fig. 3 Simulation results of ADRC vs PID control time-delay system |
图2和图3分别为ADRC控制和传统的PID控制针对干扰系统和时滞系统进行的仿真分析。从图2可以看出,控制系统面对突然外来干扰信号时,PID控制在干扰处有明显的波动起伏,瞬时误差较大,而ADRC控制在面对干扰时变化平稳,曲线与其他无干扰处基本一致,说明与传统的PID控制系统相比,自抗扰控制面对干扰系统时能更快的趋于稳定,能够对干扰进行准确估计并且消除误差,具有良好的抗干扰能力。
从图3可以看出,针对时滞系统PID控制效果并不理想。图3(a)中,当系统的时滞为0.2 s时,PID控制虽然有超调但是一段时间后基本可以保持系统稳定,随着延迟时间增加到0.4 s,系统的超调量和调节时间逐渐增大,以至最后0.8 s时系统不再稳定并且出现发散现象。与PID相比,ADRC控制时滞系统到达稳定状态时调节时间短并且没有超调现象,系统的鲁棒性能更好,说明在时滞系统中自抗扰控制相较于传统PID控制具有更好的动态响应性能。
3 主动式升沉补偿数值模拟自抗扰控制在应对具有时滞性和干扰作用的系统时,表现出良好的鲁棒性与抗干扰能力。因此将ADRC应用于主动式升沉补偿控制系统,并对其结果进行仿真分析。海洋环境下海况是复杂多变的,不同的海况环境下风、浪、流等外界干扰对系统模型的参数均有很大影响,因而控制系统的模型不确定,从而导致一般的控制算法面对多变海况环境时控制效果很差。
选择将6级海况环境作为主动式升沉补偿控制系统的研究对象,调节出一组效果良好的自抗扰控制器参数,并在不改变ADRC参数的情况下进行4级和5级海况数值模拟研究。针对每级海况存在的只有海浪环境、有风有浪环境和风浪流三者兼具的3种情况,分析自抗扰控制器在参数不变、环境改变情况下的控制效果。
海况设置中,风的方向选择与船首尾成45°夹角;默认波浪是由海风而引起的,设置海风的方向和波的方向相同;选取海流流方向为30°。方向参数与六级海况设置相同。对应的海况等级参数如表3所示。
|
|
表 3 海况等级参数 Tab.3 Sea state parameters |
对不同海况不同环境下的具有延迟环节的升沉补偿系统进行系统仿真分析,补偿效率如表4所示。单一波浪、波浪和风耦合以及风浪流耦合3种环境下的补偿效果分别如图4~图6所示。随着海况等级增加,船舶上下升沉的位移也会变大,船舶运动也会更加剧烈。可以看出:6级海况风浪流全耦合环境下,升沉补偿精度可达0.02 m,并且在不改变控制器参数的情况下在同环境的4级、5级海况补偿中自抗扰控制具有更高的补偿精度,说明在满足6级海况环境下的自抗扰控制更能满足低海况环境下的高精度补偿;针对单一波浪、波浪和风耦合、风浪流耦合3种不同情况下自抗扰控制效率均能维持在高精度范围且与风浪流耦合环境下补偿效率高度接近,说明在满足风浪流耦合环境下的自抗扰控制在其他组合的环境下同样高效适用。使用同一套参数在不同的海况环境下自抗扰控制均取得了令人满意的深沉补偿效果,由此可以看出自抗扰所具有的优越性。
|
|
表 4 自抗扰控制主动升沉补偿效率 Tab.4 Active heave compensation efficiency of ADRC |
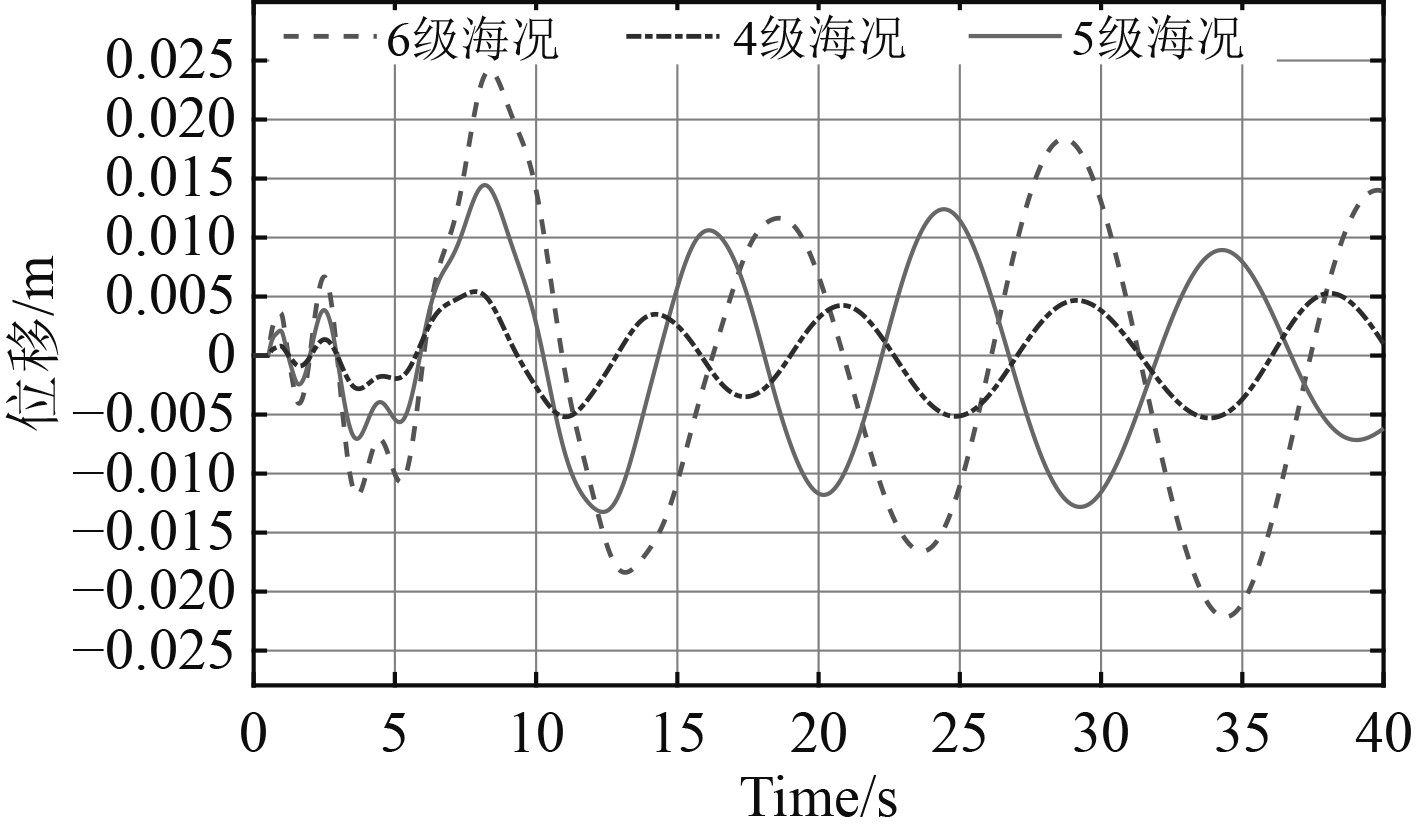
|
图 4 只有波浪环境下补偿效果 Fig. 4 Heave compensation effect only in wave environment |
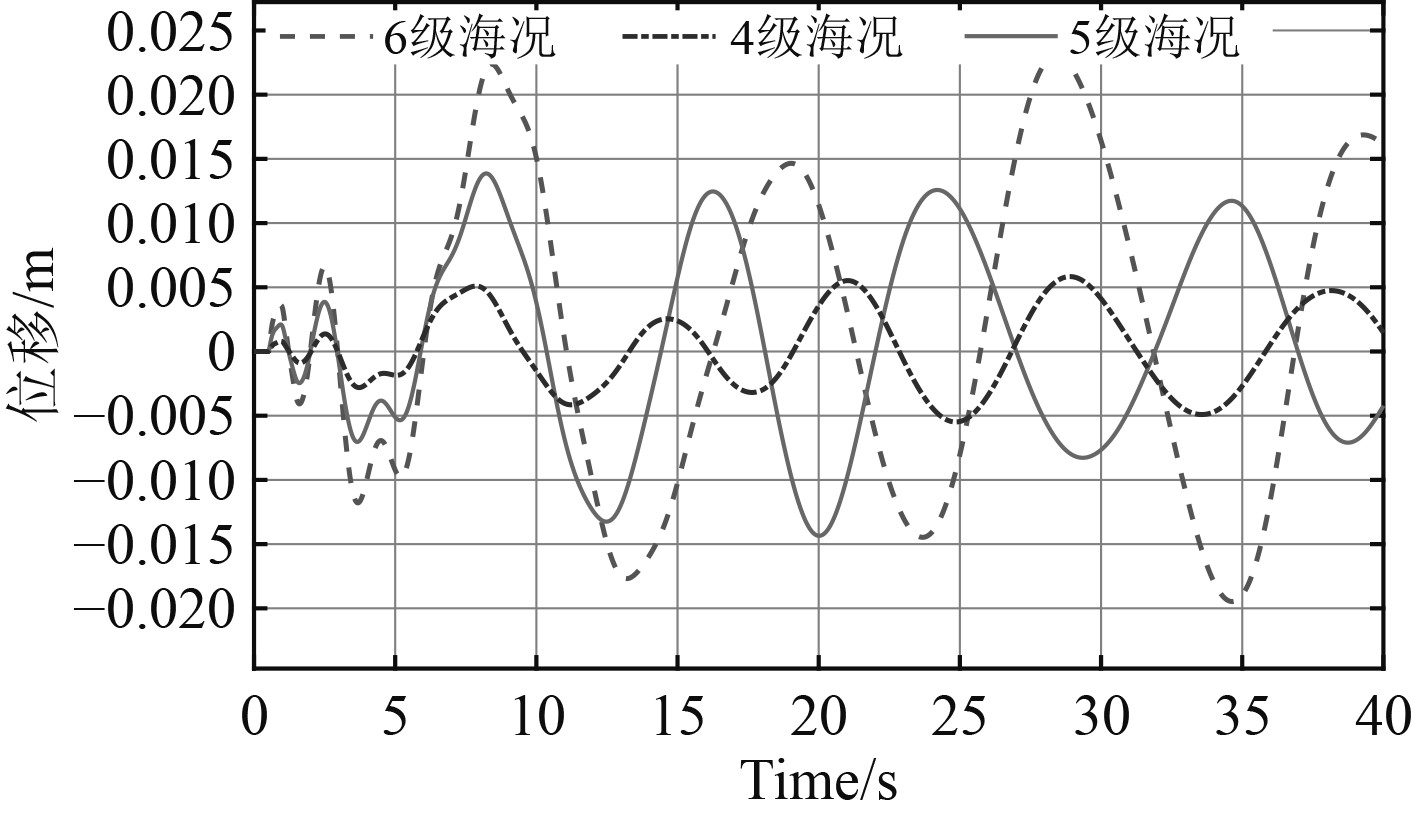
|
图 5 波浪和海风环境下升沉补偿效果 Fig. 5 Heave compensation effect in wave and wind environment |

|
图 6 风浪流耦合情况下补偿效果 Fig. 6 Heave compensation effect in wind wave current coupling environment |
本文针对海上船舶主动式升沉补偿系统具有的时滞性与干扰性的特点,提出将针对上述环境仍具有很好控制效果的ADRC技术用于船舶升沉补偿控制系统,从而提高升沉补偿系统的动态响应性能。
1)对液压二次调节驱动系统进行理论分析并对主动式升沉补偿系统进行数学建模;介绍自抗扰控制器的原理和组成,并进一步给出自抗扰控制器3个模块的理论设计过程。
2)通过仿真分析,验证ADRC和传统PID控制针对干扰系统和时滞系统的控制效果。根据结果可知,ADRC控制针对系统出现的干扰,因其具有良好的抗干扰能力,从而在面对干扰系统时变化更加平稳,恢复稳定的速度也更快;在针对具有时滞环节的控制系统时,自抗扰控制展现出良好的稳定跟踪性能,响应速度快以及没有超调现象。
3)对自抗扰控制效果进行案例分析。以6级海况为母船工作环境,考虑海风、海浪和海流三者耦合情况下,在环境改变参数不变的情况下进行仿真分析。从结果可以看出,升沉补偿效率达到99%。仿真结果表明,自抗扰控制效果取得满意效果,显示出将其应用于船舶升沉补偿系统中的优势,为升沉补偿系统下一步更深层次的研究奠定了基础,具有良好的工程应用价值导向。
| [1] |
段玉响, 任政儒, 周利. 主动式升沉补偿技术研究现状和发展趋势[J]. 舰船科学技术, 2020, 42(21): 76-82. DUAN Yu-xiang, REN Zheng-ru, ZHOU Li. Research status and development trend of active heave compensation technology[J]. Ship Science and Technology, 2020, 42(21): 76-82. |
| [2] |
吴汪洋, 刘贤胜, 等. 船用起重机主动升沉补偿系统时延的实时控制研究[J]. 液压与气动, 2021, 45(4): 167-174. WU Wang-yang, LIU Xian-sheng, et al. Research on real-time control of time delay of active heave compensation system of marine crane[J]. Hydraulic and Pneumatic, 2021, 45(4): 167-174. DOI:10.11832/j.issn.1000-4858.2021.04.025 |
| [3] |
李荣辉, 等. 欠驱动水面船舶航迹跟踪自抗扰控制[J]. 大连海事大学学报, 2013, 39(2): 5-8. LI Rong-hui, et al. Automatic disturbance rejection control for track tracking of underactuated surface ships[J]. Journal of Dalian Maritime University, 2013, 39(2): 5-8. DOI:10.3969/j.issn.1006-7736.2013.02.002 |
| [4] |
周利, 等. 主动式升沉补偿控制系统及运动预报[J]. 华中科技大学学报(自然科学版), 2021, 49(3): 98-104. ZHOU Li, et al. Active heave compensation control system and motion prediction[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2021, 49(3): 98-104. |
| [5] |
韩京清. 从PID技术到“自抗扰控制”技术[J]. 控制工程, 2002(3): 13-18. HAN Jing-qing. From PID technology to "Auto disturbance rejection control" technology[J]. Control Engineering, 2002(3): 13-18. DOI:10.3969/j.issn.1671-7848.2002.03.003 |
| [6] |
韩京清. 控制理论——模型论还是控制论[J]. 系统科学与数学, 1989(4): 328-335. HAN Jing-qing. Control theory -model theory or cybernetics[J]. Systems Science and Mathematics, 1989(4): 328-335. |
| [7] |
楼梦瑶. 基于运动预测的ROV主动升沉补偿控制系统研究[D]. 上海: 上海交通大学, 2020.
|
| [8] |
赵顺利. RBF神经网络优化自抗扰在船舶航迹控制中的应用[D]. 大连: 大连海事大学, 2020.
|
| [9] |
张淑艳, 谢园. 自抗扰技术在船舶动力系统控制中的应用[J]. 舰船科学技术, 2020, 42(6): 106-108. ZHANG Shu-yan, Xie Yuan. Application of auto disturbance rejection technology in ship power system control[J]. Ship Science and Technology, 2020, 42(6): 106-108. |
| [10] |
段玉响. 海上吊装主动式升沉补偿与防摆控制系统研究[D]. 镇江: 江苏科技大学, 2021.
|
| [11] |
王旭辉. 船用起重机的升沉与减摇控制研究[D]. 大连: 大连理工大学, 2021.
|
| [12] |
廖薇, 等. 电驱动海洋绞车主动升沉补偿自抗扰控制系统[J]. 中国机械工程, 2018, 29(24): 2999-3008. LIAO Wei, et al. Active heave compensation auto disturbance rejection control system for electric driven marine winch[J]. China Mechanical Engineering, 2018, 29(24): 2999-3008. DOI:10.3969/j.issn.1004-132X.2018.24.015 |
| [13] |
HAN Jingqing. From PID to Active Disturbance Rejection Control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906. DOI:10.1109/TIE.2008.2011621 |
| [14] |
PEREZ T, SMOGELI O, FOSSEN T, et al. An overview of the marine systems simulator (MSS): A simulink toolbox for marine control systems[J]. Modeling, Identification and Control, 2006, 27(4): 259-275. DOI:10.4173/mic.2006.4.4 |
| [15] |
韩京清. 自抗扰控制技术——估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008.
|
 2022, Vol. 44
2022, Vol. 44
