2. 海洋石油工程(青岛)有限公司,山东 青岛 266555
2. Offshore Oil Engineering (Qingdao) Co., Ltd., Qingdao 266555, China
海洋立管在水下油气的开采项目中主要负责连接水上平台与水下井口,担任十分重要的角色。海洋立管在工作期间会承受波浪、海流和地震等复杂的环境荷载作用,在来流的作用下,立管后部两侧会产生泄放的漩涡,漩涡脱落会对立管产生周期性的力,使立管发生复杂的简谐振动。当结构振动频率和固有频率接近时,就会引发外载荷与结构的共振,发生“锁定”现象,严重时结构还会发生灾难性的破坏[1-3]。因此,涡激振动是导致海洋立管发生疲劳破坏的主要原因。随着深海海洋石油项目的发展,单根立管已不能满足需求,由多根立管组合形成的立管群得到了广泛应用,由于立管在串联时两立管间尾流会产生相互作用,结构振动会十分多变,加速结构疲劳寿命缩短。因此对串联立管进行涡激振动特性研究,分析其振动特性,对海洋油气开发的技术理论具有重要意义。
梁鹏[4]采用Ansys/CFX针对大雷诺数串联双立管绕流和流固耦合,基于物理模型分析串联立管在不同雷诺数和间距下双立管的受力情况,结果表明当两立管间距较大时可以采取圆柱绕流的方法代替流固耦合来模拟立管受力结果。郭晓玲等[5]研究了串联两圆柱不同间距比和质量比对下游圆柱运动响应的影响,研究表明间距比和质量比会导致锁定区间的变化,体现了双圆柱干涉作用对涡激振动的影响。Ryu S[6] 应用有限体积法(FVM)对一对相邻圆柱的流体动力系数进行了研究,结果表明由于圆柱之间间隔的变化,可以用5种不同的漩涡脱落模型描述流体动力系数的变化。廖俊与景思睿[7]采用表面涡方法,研究了不同排列方式对双圆柱在高雷诺数条件下水动力响应的影响规律,并将数值模拟结果与实验数据进行了比较,研究结果清楚描述了双圆柱绕流的流动状况。王晓凯等[8]针对小尺寸串联双圆柱进行二维仿真研究,研究得到在间距比L/D=4的条件下,上下游圆柱“锁定”区间一致且相互干涉作用较小,串联圆柱的尾涡脱落模式随Ur增大会发生显著变化。武磊等[9]采用基于Open FOAM自主开发的求解器,研究在阶梯流下不同浸没长度串联排列的双立管涡激振动,发现随着浸没长度的增加,下游立管由于受到上游立管的尾流作用,其漩涡泄放得到进一步加强。
早期大部分关于涡激振动的研究主要集中在质量比较大的圆柱上,均忽略圆柱的顺流向振动,仅针对横流向振动进行研究,涉及到尾流干涉下考虑双自由度的小尺寸圆柱研究相对较少。因此,本文应用 Fluent 软件加入求解结构振动的代码,写入自定义函数UDF中与流动控制方程耦合,选取SST
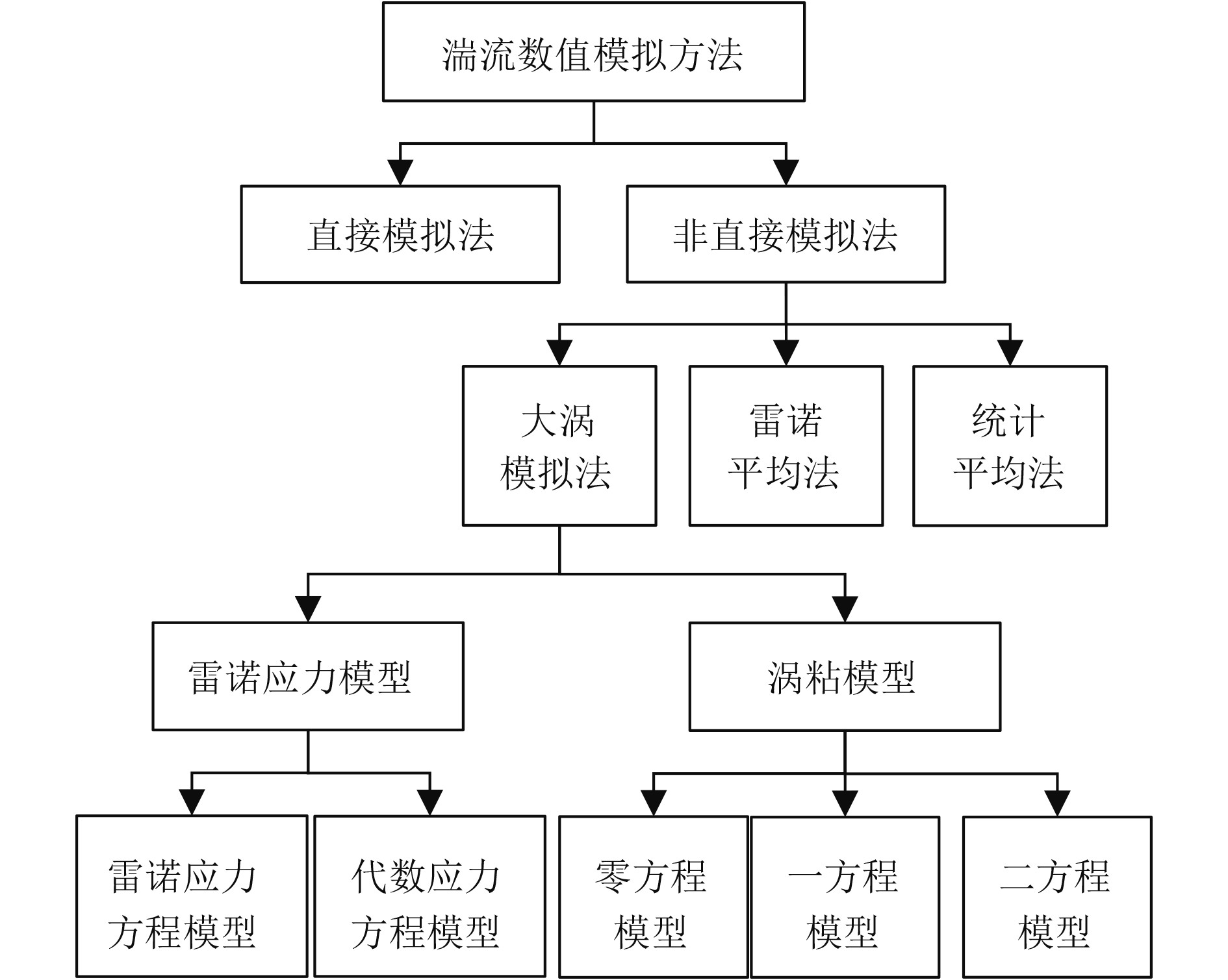
图1表示湍流数值模拟的模型分类,数值湍流模拟主要有直接模拟法、大涡模拟法和雷诺平均法,后者由涡粘模型和雷诺应力模型组成,而涡粘模型又可以进一步分为零方程、一方程与二方程模型。
|
图 1 湍流模型分类 Fig. 1 Classification of turbulence models |
本文应用基于雷诺平均法的SST
对一个随机信号进行周期性分析时,需要将信号从时域变换到频域,变换得到的频谱中每个频率都对应信号的一个周期谐波分量。FFT为快速傅里叶变换,傅里叶变换的定义为:
| $ F\left(\omega \right)={{\displaystyle\int_{-\infty }^{+\infty } }}f\left(t\right){e}^{-j\omega t}{\rm{d}}t。$ | (1) |
其中:
对于二维不可压均匀粘性牛顿流体,控制方程是连续性方程和 Navier-Stokes 方程:
| $ \nabla \cdot u = 0,$ | (2) |
| $ \frac{{\partial u}}{{\partial t}} + (u \cdot \nabla )u = - \nabla p + \frac{{{\nabla ^2}u}}{{Re}}。$ | (3) |
式中:
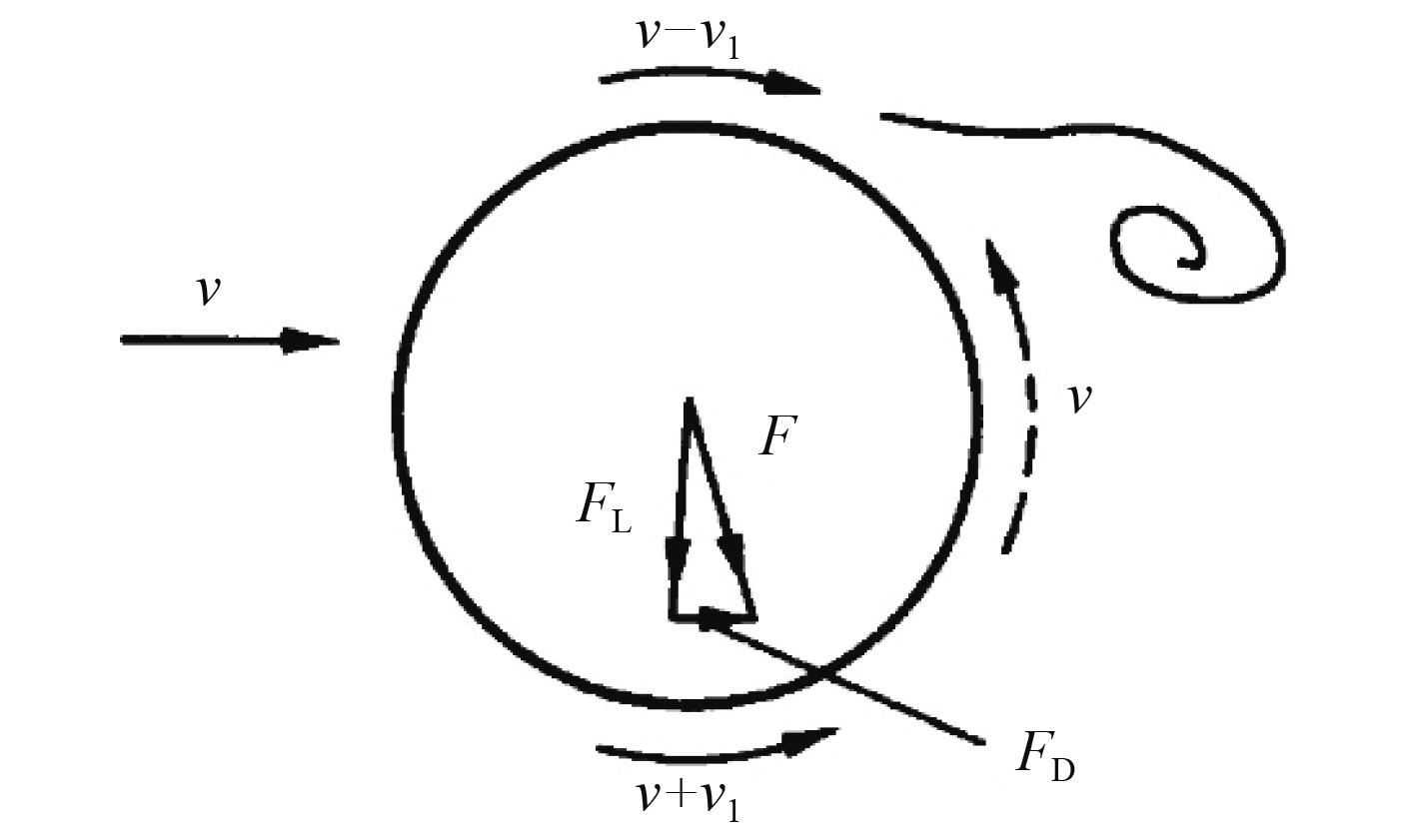
如图2所示,对于不可压缩流体来说,当圆柱体尾部两侧出现周期性交替脱落的漩涡时,速度变化将会引起压强的改变。由于漩涡脱落导致圆柱产生压力差从而形成顺流向的阻力(FD)和垂直于来流方向的升力(FL),其表达式分别为:
|
图 2 漩涡泄放对圆柱体作用力 Fig. 2 The force of circular cylinder given by vortex discharge |
| $ {F_L}{\text{ = }}\frac{1}{2}{C_L}\rho {U^2}{D^2},$ | (4) |
| $ {F_D}{\text{ = }}\frac{1}{2}{C_D}\rho {U^2}{D^2}。$ | (5) |
式中:CL为升力系数,CD为曳力系数;ρ为流体密度,kg·m−1;U为流体流速,m·s−1;D为圆柱结构直径,m。
斯特劳哈数St是衡量物理模型时引入的相似性准则,在考虑具有特征频率的圆周运动时需要使用St定义,主要是由流体流经的结构的特征尺寸和雷诺数大小决定的。
| $ {s_t} = \frac{{{f_s} \cdot D}}{u}。$ | (6) |
式中:fs为漩涡脱落频率,Hz;D为圆柱直径,m;u为来流速度,m/s。
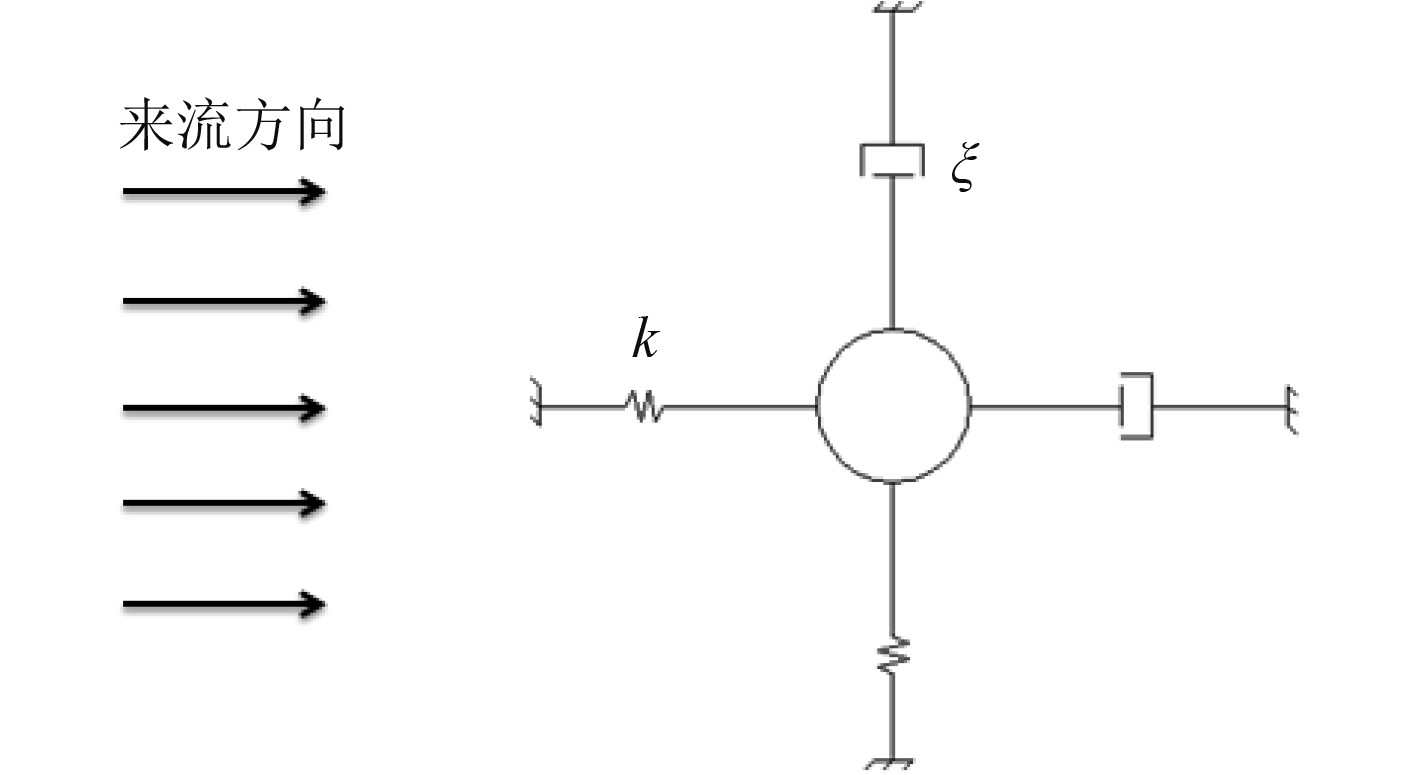
立管振动模型可以简化为双自由度质量-阻尼-弹簧系统。振动模型的控制方程为:
| $ m\frac{{{{\rm{d}}^2}x}}{{{\rm{d}}{t^2}}} + c\frac{{{\rm{d}}x}}{{{\rm{d}}t}} + kx = {F_D}(t),$ | (7) |
| $ m\frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{t^2}}} + c\frac{{{\rm{d}}y}}{{{\rm{d}}t}} + ky = {F_L}(t)。$ | (8) |
式中:m为圆柱质量,kg ;x,y分别为圆柱顺流向位移与横流向位移,m;c为结构阻尼系数;k为系统刚度系数;FD(t)为圆柱所受顺流向阻力,N;FL(t)为圆柱所受横流向升力,N。
|
图 3 圆柱振动模型 Fig. 3 Cylindrical vibration model |
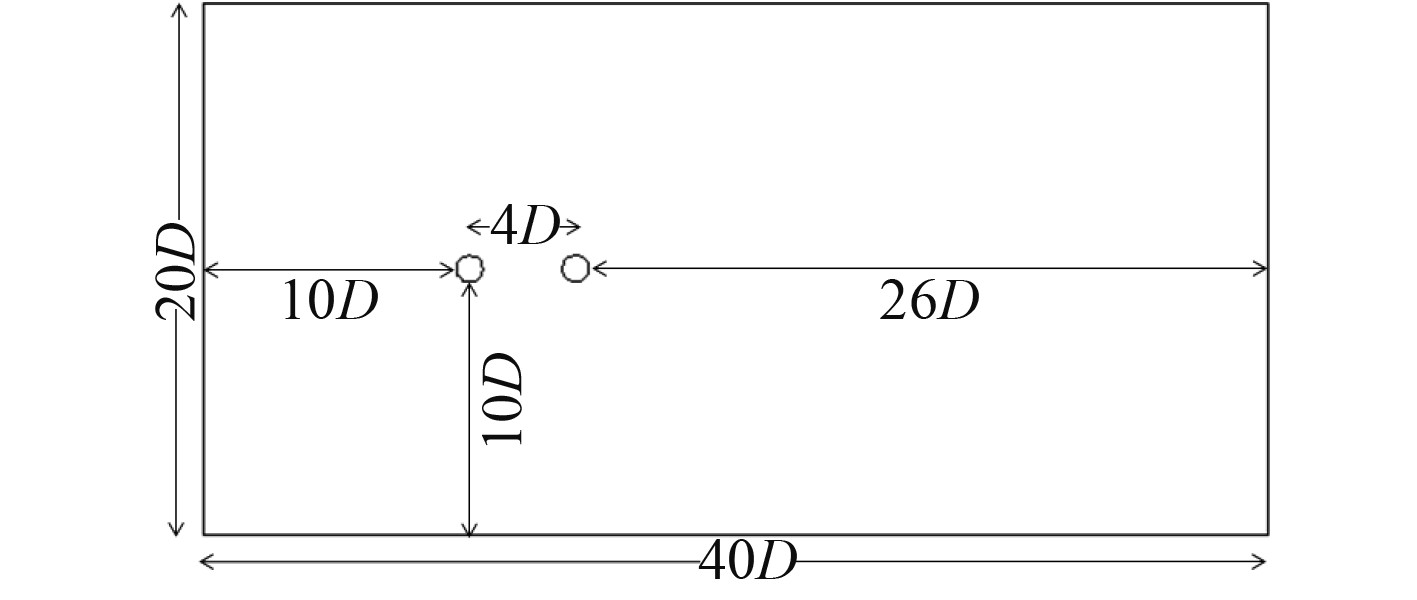
根据Prasanth[10]对流场网格划分的研究结果,在流场区域在能够满足尾流区长度和整体高度要求时,边界效应将不再影响圆柱结构的涡激振动响应。因此将整个流场区域大小设置为40D(长)×20D(宽),计算域如图4所示。其中圆柱直径D=0.02 m,下游圆柱尾流区域长度为26D。基于Overset-Mesh技术对流场计算域进行网格划分。计算域由矩形背景网格和2个环形部件网格组成,如图5所示。网格类型均为结构化四边形网格,并且对圆柱附近和漩涡泄放脱落形成的尾流区域周围的网格进行加密处理。
|
图 4 圆柱串联排列计算区域几何模型 Fig. 4 Geometric model of calculation area of tandem cylinders |

|
图 5 网格划分 Fig. 5 Mesh generation |
选取圆柱直径D=0.018 m,质量比m*=1.77,阻尼比ξ=0.003,自振圆频率ω/Hz=10.6。
|
|
表 1 圆柱模型基本参数 Tab.1 Basic parameters of cylindrical model |
边界条件设定:入流面采用速度边界(Velocity-inlet);出流面采用压力边界(Pressure-outlet);上下对称面边界均选择使用对称边界条件(Symmetry);圆柱表面采用边界条件(Wall);湍流通过湍流强度及水力直径定义;湍流模型采用SST
为验证本文所建计算模型的可靠性,在雷诺数Re=200条件下分别进行单圆柱和间距比S/D=3及S/D=4下串联双圆柱绕流数值模拟。应用Fluent软件将前处理划分的网格进行初始化设置,同时根据网格相对运动需要小于嵌套网格最小长度尺寸的要求确定迭代时间步长为0.01 s。
如表2和表3所示,将所得升力系数Cl、阻力系数
|
|
表 2 单圆柱绕流结果对比 Tab.2 Comparisons of flow results of single cylinder |
|
|
表 3 双圆柱绕流结果对比 Tab.3 Comparisons of flow results for two tandem cylinders |
基于上述数值模型,对在约化速度Vr=1.0~15.0的范围内,圆心间距比S/D=3.0,4.0,5.0的串联双圆柱立管涡激振动响应特性开展研究。
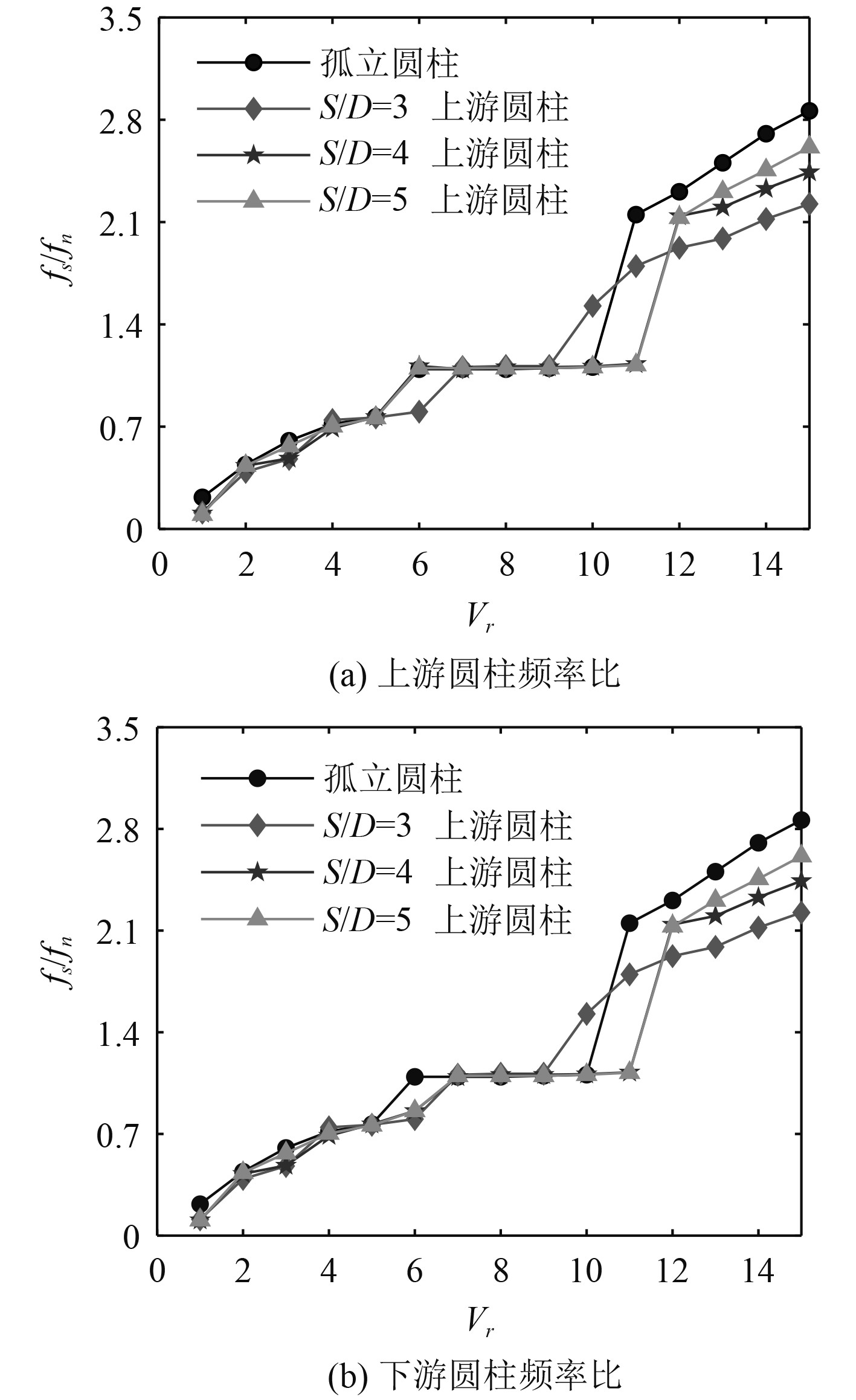
3.1 频率响应图6为不同间距比下两串联圆柱频率比与约化速度之间的关系,观察发现间距比的变化将导致串联圆柱“锁定”区间的差异。当S/D=3时,上下游两圆柱的“锁定”区间均为Vr=7-9,当S/D=4与S/D=5时,串联两圆柱的“锁定”区间范围增大,上游圆柱的“锁定”区间变为Vr=6-11,下游圆柱“锁定”区间则为Vr=7-11,存在一定滞后性。在约化速度较低时,不同间距比的曲线趋势相同,而当Vr>11后差异开始逐渐体现,上下游两圆柱的频率比均明显小于孤立圆柱,同时频率比随着间距比的增大而呈现上升趋势。此外,在同一间距比时上游圆柱与下游圆柱频率比几乎相同。
|
图 6 不同间距比和约化速度下的频率比 Fig. 6 Frequency ratios under different spacing ratios and reduced velocities |
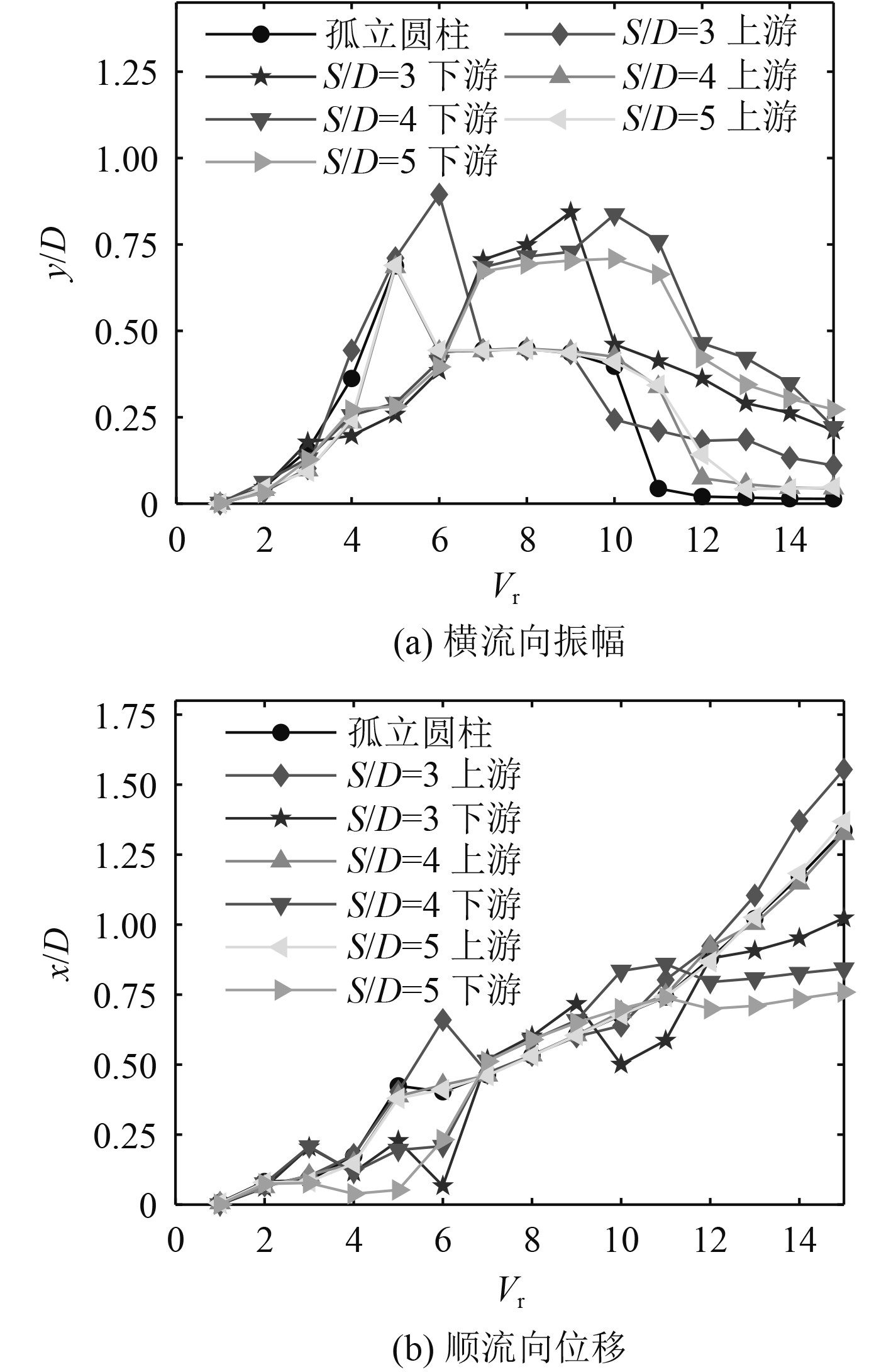
图7为不同间距比下串联两圆柱无量纲位移振幅与约化速度之间的关系曲线。由于受到上游圆柱干涉效应的影响,可以观察到下游圆柱的“锁定”区间会出现滞后现象,即下游圆柱的振幅峰值要滞后于上游圆柱,并且当上下游圆柱均进入“锁定”区间后,下游圆柱横流向振幅将远大于上游圆柱。在S/D=3时上游圆柱的横流向振幅显著大于孤立圆柱和其他两种间距比下的振幅,随着间距比的不断增大,下游圆柱的存在对上游圆柱的影响逐渐减小,可以看到S/D=4与S/D=5时上游圆柱的振幅曲线基本一致,因此可将S/D=4视为临界间距比,在S/D≥4后间距比的改变对于干涉效应的影响将显著减弱。
|
图 7 不同间距比和约化速度下的位移幅值 Fig. 7 Displacement response under different spacing ratios and reduced velocities |
串联两圆柱顺流向位移在“锁定”区间前后会有一些波动,但总体上与单个孤立圆柱相似,呈现出持续上升的趋势。由图7(b)可以看出,当Vr>11进入高约化速度范围后,上游圆柱位移幅值要比孤立圆柱大,下游圆柱位移幅值会比孤立圆柱小。这是由于下游圆柱流动干涉效应的影响,上游圆柱沿顺流向受到的来流冲击作用得到提升,由于上游圆柱的遮蔽抵抗作用,来流对下游圆柱的冲击将远远小于孤立圆柱时的情况,上游圆柱对下游圆柱起到了抗冲击的保护作用,因此两圆柱之间顺流向位移幅值会有差异。
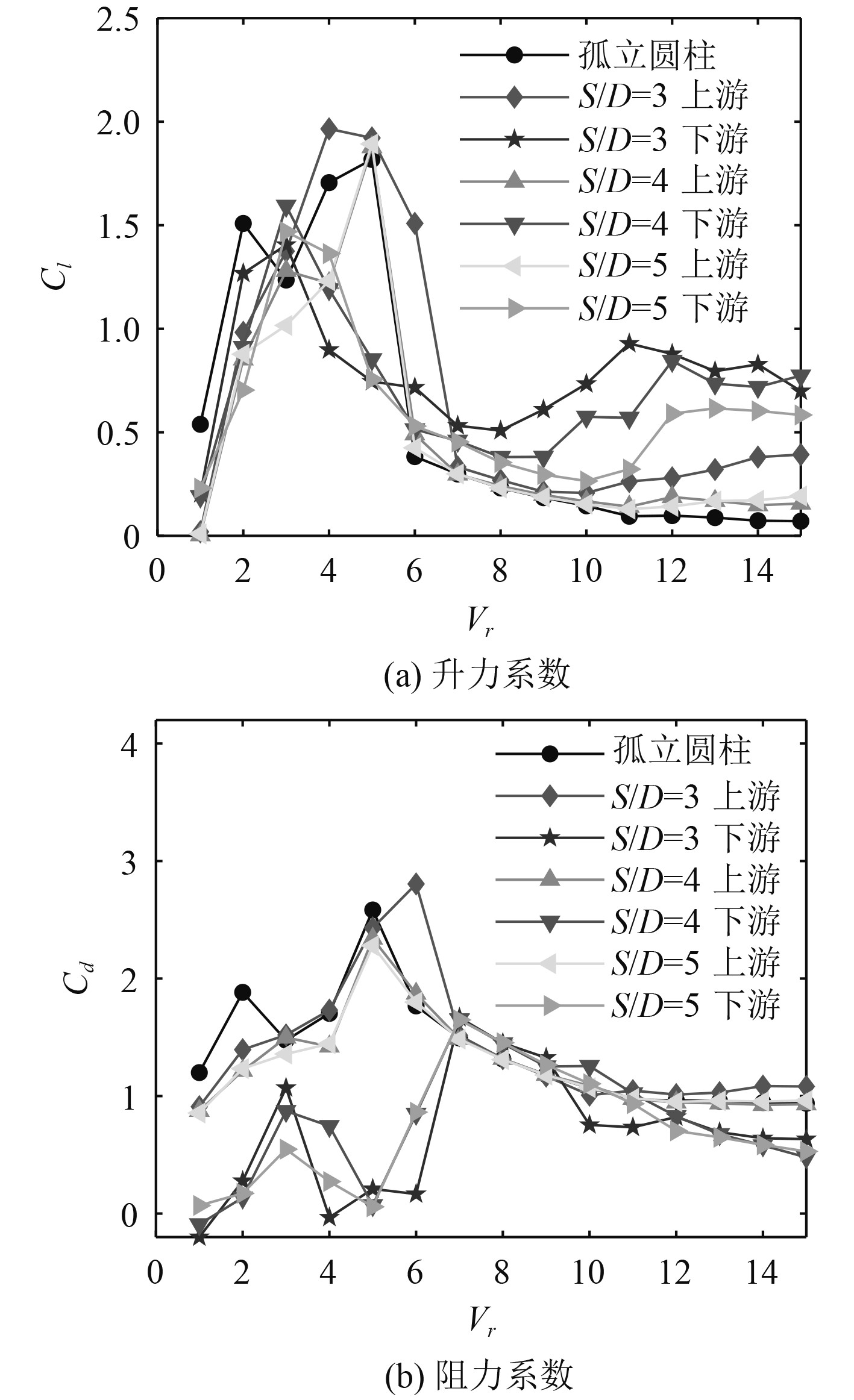
3.3 受力特性串联两圆柱在不同间距比下的受力情况随约化速度变化关系如图8所示。观察分析可得升力系数与间距比呈负相关,随着间距比增大,圆柱的升力系数呈现递减趋势,上游圆柱的升力系数在高约化速度范围内均显著大于下游圆柱。同时由于流动干涉效应的影响,串联两圆柱的升力系数均大于孤立圆柱,间距比的增大会导致升力系数减小,这说明两圆柱间的干涉效应一直存在,但干涉影响会随着间距比的增大而持续减弱。
|
图 8 不同间距比和约化速度下的升阻力系数 Fig. 8 Lift-drag coefficients under different spacing ratios and reduced velocities |
串联两圆柱的阻力系数曲线之间存在明显差异,在来流速度相对较小时,下游圆柱的阻力系数明显小于上游圆柱,当进入“锁定”区间后两圆柱的阻力系数差距逐渐缩小,甚至会短暂出现上游圆柱小于下游圆柱的现象,随着约化速度继续增大,涡激振动离开“锁定”区间后,下游圆柱的阻力系数将再次小于上游圆柱并趋于稳定。此外,上游圆柱的阻力峰值始终大于下游圆柱,间距比增大会导致峰值的不断减小。
3.4 运动轨迹图9表示不同间距比下串联圆柱质心运动轨迹的变化情况。可以看出,当S/D=3时串联两圆柱运动的规律性均较差,因为在此间距比下两圆柱间的流动干涉效应最为强烈。当S/D=4时,上游圆柱在“锁定”区间内开始呈现“8”字形的运动轨迹,但其运动周期性不明显,这是因为随着间距比的增大,下游圆柱对上游圆柱的影响逐渐减小。当S/D=5时,上游圆柱的“8”字形朝向会出现偏转,即圆柱在两个流向上的振动相位会出现偏差,产生了在孤立圆柱时会出现的“相位开关”现象,“8”字形轨迹变得更加标准,同时圆柱运动的周期性得到提升,运动轨迹变得更加简单、具有明显规律性。

|
图 9 不同间距比和约化速度下的圆柱运动轨迹 Fig. 9 Trajectories of cylinders under different spacing ratios and reduced velocities |
相比于上游圆柱,下游圆柱的轨迹呈现多样化的特点,在S/D=3时随Vr的增大,下游圆柱的运动轨迹在 “水滴”形、“新月”形等之间转换,不同轨迹交织重合。圆柱运动的周期性较差使得轨迹相对杂乱,这是由于上游圆柱流动干涉的作用较为强烈,因此导致下游圆柱频繁出现不稳定非周期性运动。随着间距比的不断增大,两圆柱间的干涉效应影响逐步减弱,串联圆柱的运动轨迹朝着简单、规律的态势不断演变。
4 结 语1)当S/D=3时,上游、下游两圆柱的“锁定”区间均为Vr=7-9,当S/D=4与S/D=5时,两圆柱的“锁定”区间范围增大,上游圆柱的“锁定”区间为Vr=6-11,下游圆柱则为Vr=7-11,存在一定滞后性。
2)在S/D=3时上游圆柱的横流向振幅要明显大于孤立圆柱和其他两种间距比时的情况,可知在本次模拟中S/D=3时下游圆柱对上游圆柱的干涉影响最强,随着间距比增大下游圆柱对上游圆柱的影响不断减小,可将S/D=4视为临界间距比,在S/D≥4后间距比的变化对于干涉效应的影响相对较弱。
3)间距比的增大会导致升力系数相应减小。在高约化速度范围内上游圆柱的升力系数均显著大于下游圆柱。在来流速度较小时,上游圆柱的阻力系数明显小于下游圆柱,当进入“锁定”区间后两圆柱的阻力系数差距缩小,随着约化速度持续增大,上下游圆柱的阻力系数均趋于稳定。
4)在S/D=3时,串联两圆柱的运动规律性较差,S/D=4时上游圆柱在“锁定”区间内开始出现“8”字形的运动轨迹,S/D=5时上游圆柱的“8”字形朝向会出现偏转,轨迹变得更加标准。下游圆柱的轨迹呈现多样化的特点,圆柱运动的周期性较差。
| [1] |
周守为, 李清平, 朱海山, 等. 海洋能源勘探开发技术现状与展望[J]. 中国工程科学, 2016, 18(2): 19–31. ZHOU Shouwei, LI Qingping, ZHU Haishan , et al. The current state and future of offshore energy exploration and development technology[J]. Chinese Engineering Science. 2016, 18(2), 19–31 |
| [2] |
吴林强, 张涛, 徐晶晶, 等. 全球海洋油气勘探开发特征及趋势分析[J]. 国际石油经济, 2019, 27(3): 29-36. WU Linqiang, ZHANG Tao, XU Jingjing, et al. Characteristics and trends of global offshore oil and gas exploration and development[J]. International Petroleum Economics, 2019, 27(3): 29-36. |
| [3] |
TONG X. G. , ZHANG G. Y. , WANG Z. M. , et al. Distribution and potential of global oil and gas resources[J]. Petroleum Exploration and Development Online, 2018, 45(4).
|
| [4] |
梁鹏, 黄泽平, 魏泽东. 基于全相似的串联双立管大雷诺数涡激振动研究[J]. 船海工程, 2015, 44(1): 145-149. LIANG Peng, HUANG Zeping, WEI Zedong. Study on vortex-induced vibration of the tandem risers under high reynolds[J]. Ship & Ocean Engineering, 2015, 44(1): 145-149. DOI:10.3963/j.issn.1671-7953.2015.01.037 |
| [5] |
郭晓丽, 唐国强, 刘名名, 等. 低雷诺数下串联双圆柱涡激振动的数值研究[J]. 振动与冲击, 2014, 33(4): 60-69. GUO Xiaoli, TANG Guoqiang, LIU Mingming, et al. Numerical investigation on vortex-induced vibration of twin tandem circular cylinders under low Reynolds number[J]. Journal of Vibration and Shock, 2014, 33(4): 60-69. |
| [6] |
RYU S, LEE S B, LEE B H, et al. Estimation of hydrodynamic coefficients for flow around cylinders in side-by-side arrangement with variation in separation gap[J]. Ocean Engineering, 2009, 36(9-10): 672-680. DOI:10.1016/j.oceaneng.2009.03.001 |
| [7] |
廖俊, 景思睿. 高雷诺数下双圆柱绕流的数值模拟[J]. 水动力学研究与进展(A辑), 2001(1): 101–110. LIAO Jun, JING Sirui. Numerical simulation of flow around an cylinder at high reynolds number[J]. Journal of Hydrodynamics. 2001(1): 101–110. |
| [8] |
王晓凯, 娄敏. 尾流干涉下串联圆柱涡激振动数值模拟研究[J]. 石油机械, 2021, 49(1): 72-79. WANG Xiaokai, LOU Min. Numerical simulation on the vortex-induced vibration of tandem cylinders under wake interference[J]. China Petroleum Machinery, 2021, 49(1): 72-79. DOI:10.16082/j.cnki.issn.1001-4578.2021.01.011 |
| [9] |
武磊, 赵伟文, 万德成. 不同浸没长度下串列双立管涡激振动数值模拟[J]. 海洋工程, 2020, 38(3): 52–61. WU Lei, ZHAO Weiwen, WAN Decheng. Numerical simulations on vortex-induced vibrations (VIV) of two tandem risers with different submerged lengths[J]. Ocean Engineering, 2020, 38(3): 52–61. |
| [10] |
PRASANTH T K, BEHARA S, SINGH S P, et al. Effect of blockage on vortex-induced vibrations at low Reynolds numbers [J]. Journal of Fluids & Structures, 2006, 22 (6–7) : 865–876.
|
| [11] |
BRAZA M, CHASSAING P, HAMINH H. . Numerical study and physical analysis of the pressure and velocity fields in the near wake of a circular cylinder[J]. Fluid Meth, 1986, 165: 79-130. |
| [12] |
MENDES P A, BRANCO F A. Analysis of fluid-structure interaction by an arbitrary lagrangian-eulerian finite element formulation[J]. International Journal for Numerical Method in Fluids, 1990, 30: 897-919. |
| [13] |
MENEGHINI J R, SALTARA F, SIQUEIRA C L R, et al. Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangement[J]. Journal of Fluids and Structures, 2001, 15(2): 327-350. DOI:10.1006/jfls.2000.0343 |
| [14] |
刘景伟, 郭海燕, 赵婧. 等直径串列双圆柱体绕流的数值模拟[J]. 中国海洋大学学报(自然科学版), 2013, 43(12): 92-97. LIU J W, GUO H Y, ZHAO J. Numerical simulation of flow around two tandem circular cylinders of equal diameter[J]. Periodical of Ocean University of China, 2013, 43(12): 92-97. DOI:10.16441/j.cnki.hdxb.2013.12.015 |
| [15] |
于定勇, 刘洪超, 王昌海. 不等直径串列双圆柱体绕流的数值模拟[J]. 中国海洋大学学报(自然科学版), 2012, 42(Z2): 160-165. YU D Y, LIU H C, WANG C H. Numerical simulation of viscous flow past two tandem circular cylinders of different diameters[J]. Periodical of Ocean University of China, 2012, 42(Z2): 160-165. DOI:10.16441/j.cnki.hdxb.2012.z2.025 |
 2022, Vol. 44
2022, Vol. 44
