UUV集群攻击目标问题是指对UUV集群系统下达一个具体侦察或探测任务时,在一定的约束条件下(如UUV总数守恒、目标依赖关系匹配等),UUV集群的主控台根据具体分配任务的复杂度、各UUV的位置和UUV数量对任务进行分配,使得系统的总目标最优或者系统的某个指标最优,从而提高执行任务效率。
目前UUV集群系统使用的任务分配方法主要有市场机制法和图论法等。近年来,专家学者开始研究生物群体智能,并映射到集群控制研究中,提出了群智能算法。例如多目标猫群优化、灰狼算法[1]、多目标蚁群优化[2]、多目标人工蜂群算法等。吕洪莉[3]针对多区域海底地形勘察问题提出一种基于多个蚁群的多目标优化算法,该算法解决了多UUV从不同位置出发对多区域进行侦察和探测的任务分配问题。Mirjalili等[1]在2014年提出了一种新型群体智能化优化算法,灰狼算法(grey wolf optimizer,GWO)。GWO通过模拟灰狼群体捕食行为,基于狼群群体写作的机制来达到优化的目的。GWO算法结构简单、需调节的参数少,容易实现,但传统灰狼算法并未考虑全局与局部搜索的协调配合以及未考虑位置更新的权重问题。张阳等[4]采用指数规律收敛因子减小策略来提高灰狼算法的求解精度。游达章等[5]将灰狼优化算法中的线性收敛因子转变为非线性收敛因子,并将粒子群与灰狼优化算法结合,将改进算法运用到机器人路径规划中。林梅金等[6]提出了一种基于反余弦函数收敛因子变化和变异策略的新型灰狼优化算法。以上文献都针对灰狼算法中的收敛因子进行了非线性改进,但是没有考虑GWO算法后期搜索多样性的缺失,算法陷入局部最优的问题。本文针对以上2个问题对GWO进行改进,提出改进收敛因子以余弦规律减小和引入动态权重的改进灰狼算法,并基于改进灰狼算法设计UUV集群攻击目标的方法。
狼群围捕猎物的行为具有自主认知、严密分工、分布式、协作性,化整为零和聚零为整的灵活战术,以及对环境的适应性等优点,改进灰狼优化算法能够以较大的概率快速找到最优解,其并行性可以在同一时间从多个点出发进行搜索,点与点之间互不影响,从而提高其效率。本文将狼群行为理论和灰狼算法引入到UUV集群任务分配问题中,基于狼群行为机制对UUV集群攻击目标问题进行数学建模,包括约束条件,攻击目标收益、攻击目标代价以及总代价函数,设计基于改进灰狼算法的UUV集群任务分配的方法。为了验证方法的可行性和优越性,进行集群侦察和攻击目标2种仿真,并针对同一侦察场景分别采用了GWO,GA和IGWO算法进行仿真。
1 UUV集群任务分配问题建模狼群围捕猎物行为机制包括游动搜索、接近包围和围捕攻击,以及行为更新等智能行为。狼群围捕猎物的行为机制借鉴到UUV集群侦察与攻击多目标任务分配问题中,本文基于狼群围捕猎物的行为机制对UUV集群任务分配问题进行研究。
选用一个五元组描述UUV集群任务分配:
| $ \{ P,U,T,C,S\} {\text{。}}$ | (1) |
式中:
建立的约束条件有:
| $ \sum\limits_{i = 1}^N {num({P_i})} = M {\text{,}}$ | (2) |
| $ num({P_i}) \geqslant \min num({P_r}),{P_r} \in P {\text{,}}$ | (3) |
| $ Pfinal = \left\{ {{P_2},{P_1}, \cdots ,{P_j},{P_i}, \cdots ,{P_n}} \right\} {\text{。}}$ | (4) |
式中:
建立的目标收益函数如下:
| $ benefit = dense + sp \times \left(value \times \sum\limits_{i = 1}^k {hur{t_i}} \right) {\text{。}}$ | (5) |
式中:
| $ damage = {d_1} + {d_2} + {d_3} + {d_4} {\text{。}}$ | (6) |
式中:
| $ {d_3} = \sqrt {{{({x_{UUV}} - {x_P})}^2} + {{({y_{UUV}} - {y_P})}^2}} {\text{。}}$ | (7) |
式中:
基于狼群行为机制的UUV集群攻击目标分配模型的目标函数可以定义为:
| $ price = damage - benefit {\text{。}}$ | (8) |
式中,目标收益
1)灰狼算法
在灰狼算法中,存在社会等级,头狼
灰狼通过以下公式逐渐包围猎物:
| $ \vec D = \left| {\vec C \cdot {{\vec X }_p}(t) - \vec X (t)} \right| {\text{,}}$ | (9) |
| $ \vec X (t + 1) = {\vec X _p}(t) - \vec A \cdot \vec D {\text{。}}$ | (10) |
式中:t为当前迭代次数;
| $ \vec A = 2\vec \alpha \cdot \vec {{r_1}} - \vec \alpha ,\vec C = 2 \cdot \vec {{r_2}} {\text{。}}$ | (11) |
式中:
其他狼
| $ {\vec D _\alpha } = \left| {{{\vec C }_1} \cdot {{\vec X }_\alpha } - \vec X } \right|,{\vec D _\beta } = \left| {{{\vec C }_2} \cdot {{\vec X }_\beta } - \vec X } \right|,{\vec D _\delta } = \left| {{{\vec C }_3} \cdot {{\vec X }_\delta } - \vec X } \right| {\text{,}} $ | (12) |
| $ {\vec X _1} = {\vec X _\alpha } - {\vec A _1} \cdot ({\vec D _\alpha }),{\vec X _2} = {\vec X _\beta } - {\vec A _2} \cdot ({\vec D _\beta }),{\vec X _3} = {\vec X _\delta } - {\vec A _3} \cdot ({\vec D _\delta }) {\text{,}}$ | (13) |
| $ \vec X (t + 1) = \frac{{{{\vec X }_1} + {{\vec X }_2} + {{\vec X }_3}}}{3}{\text{。}} $ | (14) |
式中:
2)改进灰狼算法
群体智能算法在迭代过程中均有全局搜索和局部搜索2种搜索方式,全局和局部搜索需要较好的协调,否则算法会陷入局部最优或收敛性能降低。全局搜索能力强能够使保持算法种群的多样性从而避免算法陷入局部最优,局部搜索能力强可以确保精确的进行局部搜索,加速算法的收敛。GWO作为群智能算法之一也要均衡两者,其中收敛因子就是与全局和局部搜索相关的值,GWO中
在GWO算法中,狼群个体主要跟随最优解
针对这些问题,本文提出改进收敛因子减小规律和引入动态权重的方式改进传统灰狼算法(improve grey wolf optimizer,IGWO)。
1)收敛因子以余弦规律减小的策略
本文提出一种让
| $ \alpha = 2 \times (1 - t/T) {\text{,}}$ | (15) |
| $ \alpha = \left\{ \begin{gathered} {\alpha _f} + ({\alpha _i} - {\alpha _f}) \times \frac{{1 + {{\left| {\cos ((t - 1){\text{π}} /(T - 1))} \right|}^n}}}{2},t \leqslant \frac{1}{2}T {\text{,}} \\ {\alpha _f} + ({\alpha _i} - {\alpha _f}) \times \frac{{1 - {{\left| {\cos ((t - 1){\text{π}} /(T - 1))} \right|}^n}}}{2},\frac{1}{2}T < t \leqslant T {\text{。}} \\ \end{gathered} \right. $ | (16) |
式中:

|
图 1 收敛因子变化图 Fig. 1 Change of convergence factor |
原始的收敛因子在迭代过程中线性减小,改进后的因子图像是一条余弦规律减小的曲线,在初期减小的速率较慢,收敛因子可以长时间保持在较大值,从而提高搜索效率,后期收敛因子减小的速率较快,可以提高算法的精度,从而有效地平衡了GWO算法的全局与局部搜索的更离。
2)引入自适应移步方法与改进适应度值的动态比例权重策略
受差分进化算法与文献[7]的启发,引入了自适应移步方法与改进适应度值的动态比例权重策略。文献[7]提出了一种基于适应度值的比例权重表达式可能会出现分母为0的情况,所以在文献[7]的基础上,对其他狼更新位置的公式继续改进,在学习率的公式中再引入一个极小的常数
| $\begin{split} {W_1} &= \frac{{\left| {{X_1}} \right|}}{{\left| {{X_1}} \right| + \left| {{X_2}} \right| + \left| {{X_3}} \right| + \rho }}, {W_2} = \frac{{\left| {{X_2}} \right|}}{{\left| {{X_1}} \right| + \left| {{X_2}} \right| + \left| {{X_3}} \right| + \rho }},\\ {W_3} &= \frac{{\left| {{X_3}} \right|}}{{\left| {{X_1}} \right| + \left| {{X_2}} \right| + \left| {{X_3}} \right| + \rho }}{\text{。}} \end{split}$ | (17) |
| $ X(t + 1) = \frac{{{X_1} \cdot {W_1} + {X_2} \cdot {W_2} + {X_3} \cdot {W_3}}}{3}\left(1 - \dfrac{t}{T}\right) + {X_1}\frac{t}{T} {\text{。}}$ | (18) |
式中:
3)改进灰狼算法步骤
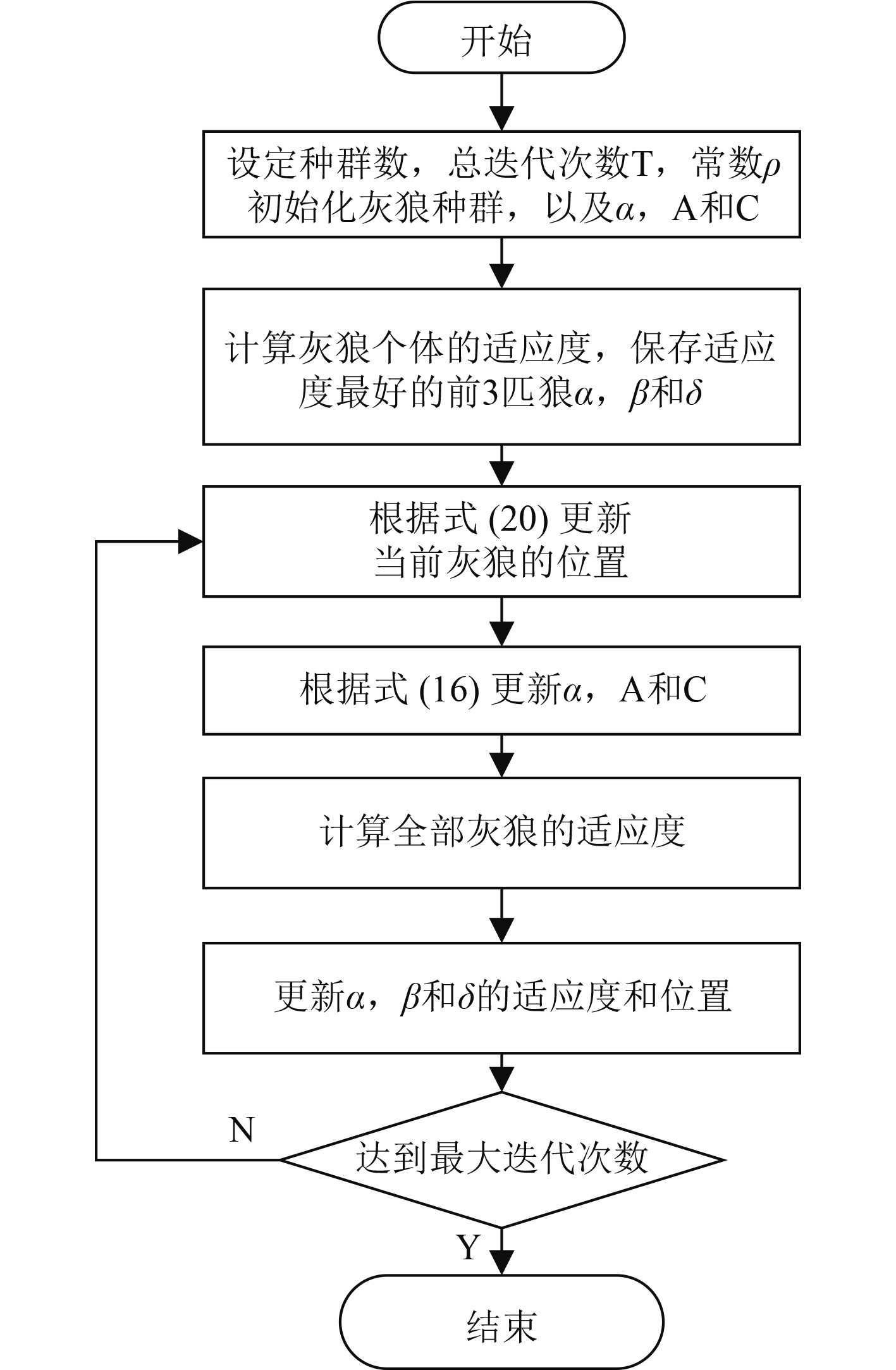
结合所有的改进策略,本文提出的改进灰狼算法流程图如图2所示。
|
图 2 改进灰狼算法流程图 Fig. 2 Flow chart of IGWO |
基于UUV集群攻击目标的数学模型,本文提出UUV集群攻击目标的方法。根据现有的信息生成地图,将N个目标信息标记在地图上并初始化UUV;对要攻击目标进行优先级排序;头UUV分配目标;头UUV根据获得的目标优先级列表来向从UUV分配目标,从UUV向头UUV汇报的目标函数值,头UUV进行汇总,得到目标总代价值

|
图 3 基于改进灰狼算法的UUV集群攻击目标流程图 Fig. 3 Flow chart of research on cluster attack of multi-UUV based on improve grey wolf optimizer |
仿真试验以UUV集群为仿真对象,选取
|
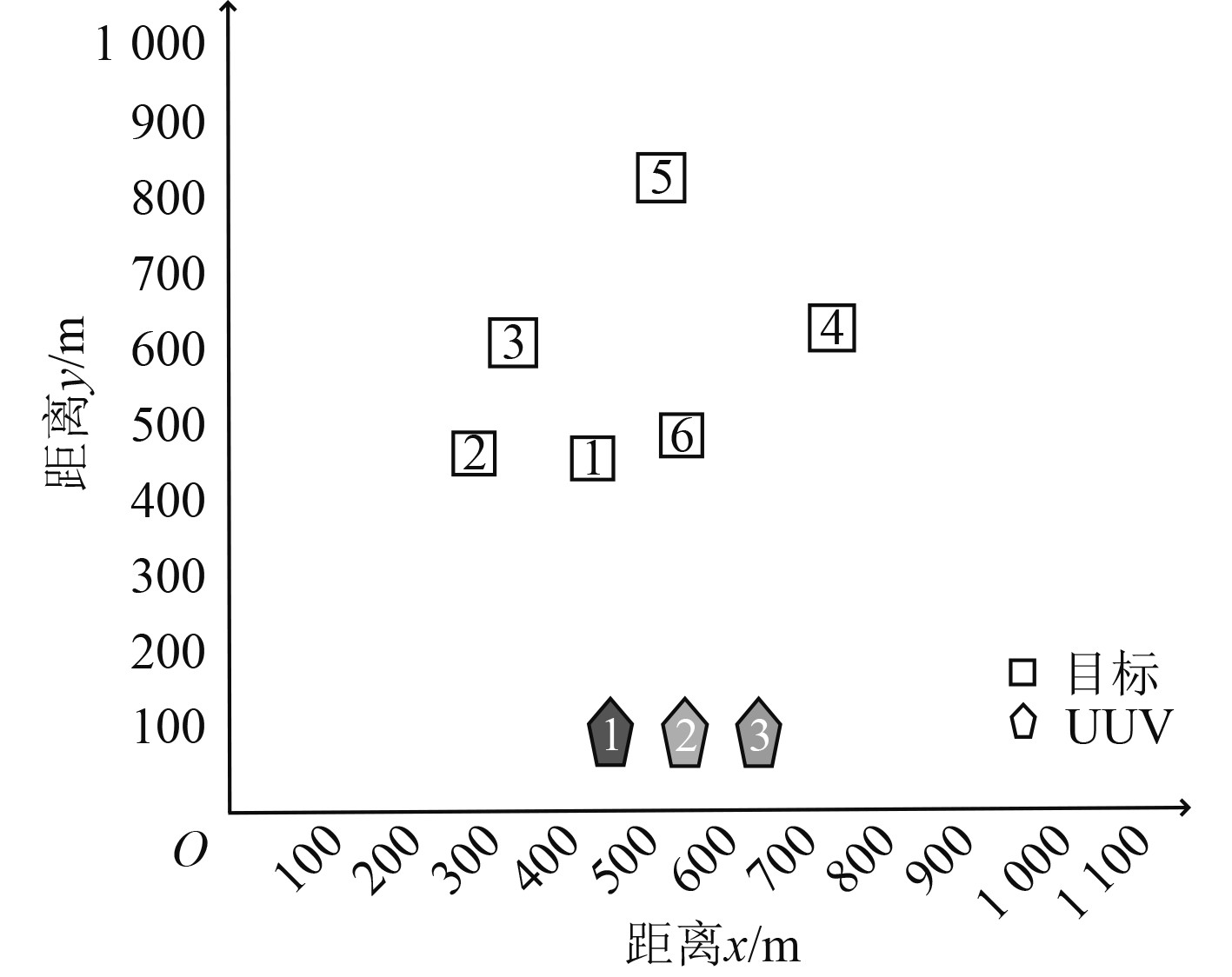
图 4 初始分布图 Fig. 4 Initial distribution |
3艘侦察型UUV起始位置在图下方呈一字排开坐标分别为
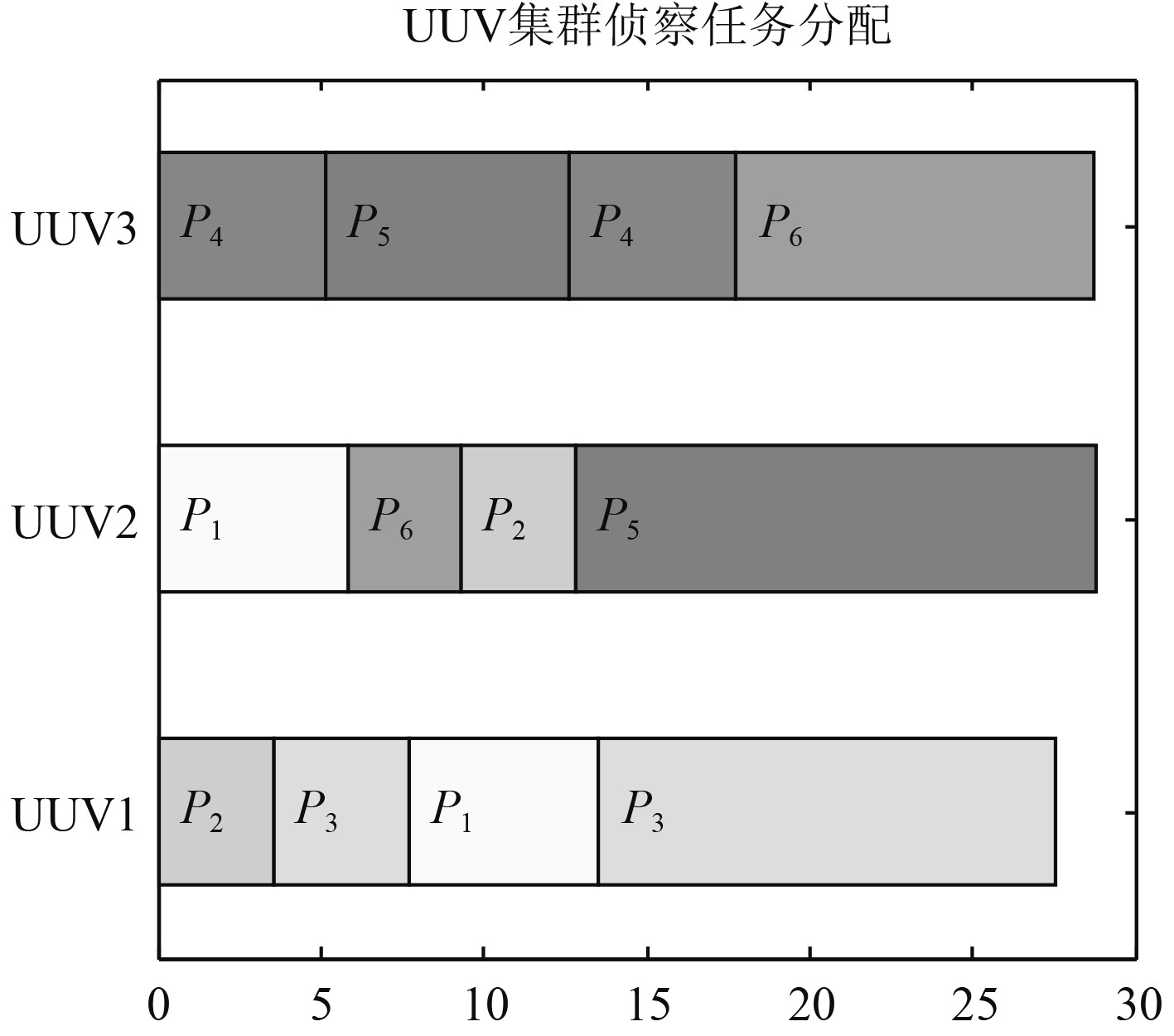
依据总代价函数,利用改进灰狼优化算法,得到最终图5的UUV集群侦察目标分配结果。为了更加直观表示分配结果,基于图5得到图6所示的分配结果示意图,再将每个UUV侦察的目标进行汇总得到表1。由表1可知,每个UUV被分配的目标数较为均衡符合预想。
|
图 5 UUV集群侦察目标分配结果 Fig. 5 Distribution result and convergence curve diagram |

|
图 6 UUV集群侦察目标分配结果示意图 Fig. 6 Distribution result diagram |
|
|
表 1 UUV集群侦察目标分配情况表 Tab.1 Distribution result |
设定每个UUV只能攻击一个目标,根据不同目标的价值高低分配的UUV数量也不同。仿真试验选取

|
图 7 初始分布情景 Fig. 7 Initial distribution |
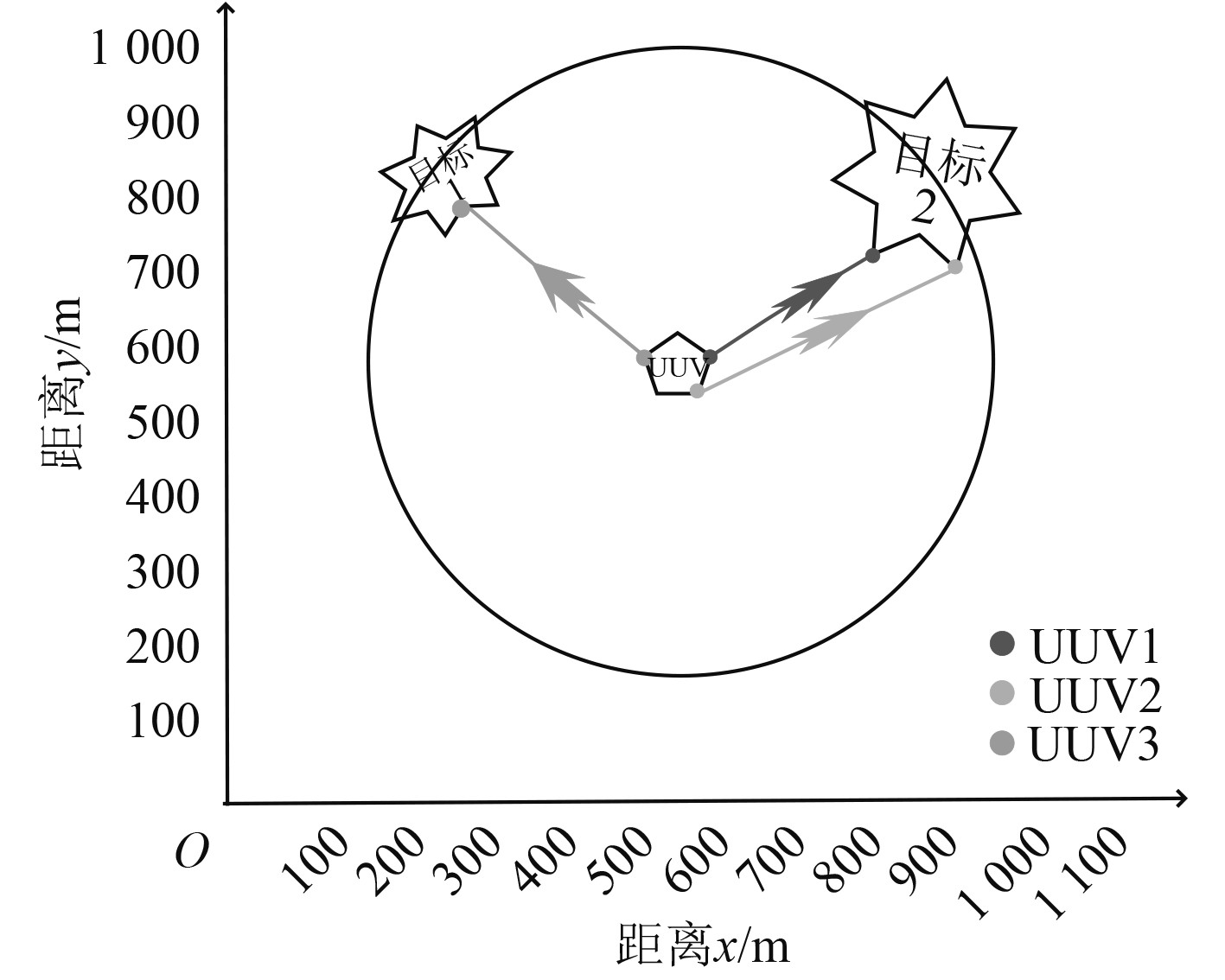
目标1和目标2分别为低价值和高价值目标,3个攻击型UUV放置在
|
图 8 UUV集群攻击目标分配结果 Fig. 8 Distribution result and convergence curve diagram |
基于图8得到图9所示的UUV集群攻击目标分配结果示意图,再将结果汇总得到表2。如图9所示,UUV1和UUV2去攻击了目标2,UUV3独自攻击了目标1。在距离相同的条件下,分配攻击高价值目标的UUV较多,分配攻击低价值目标的UUV较少,符合预期目标。
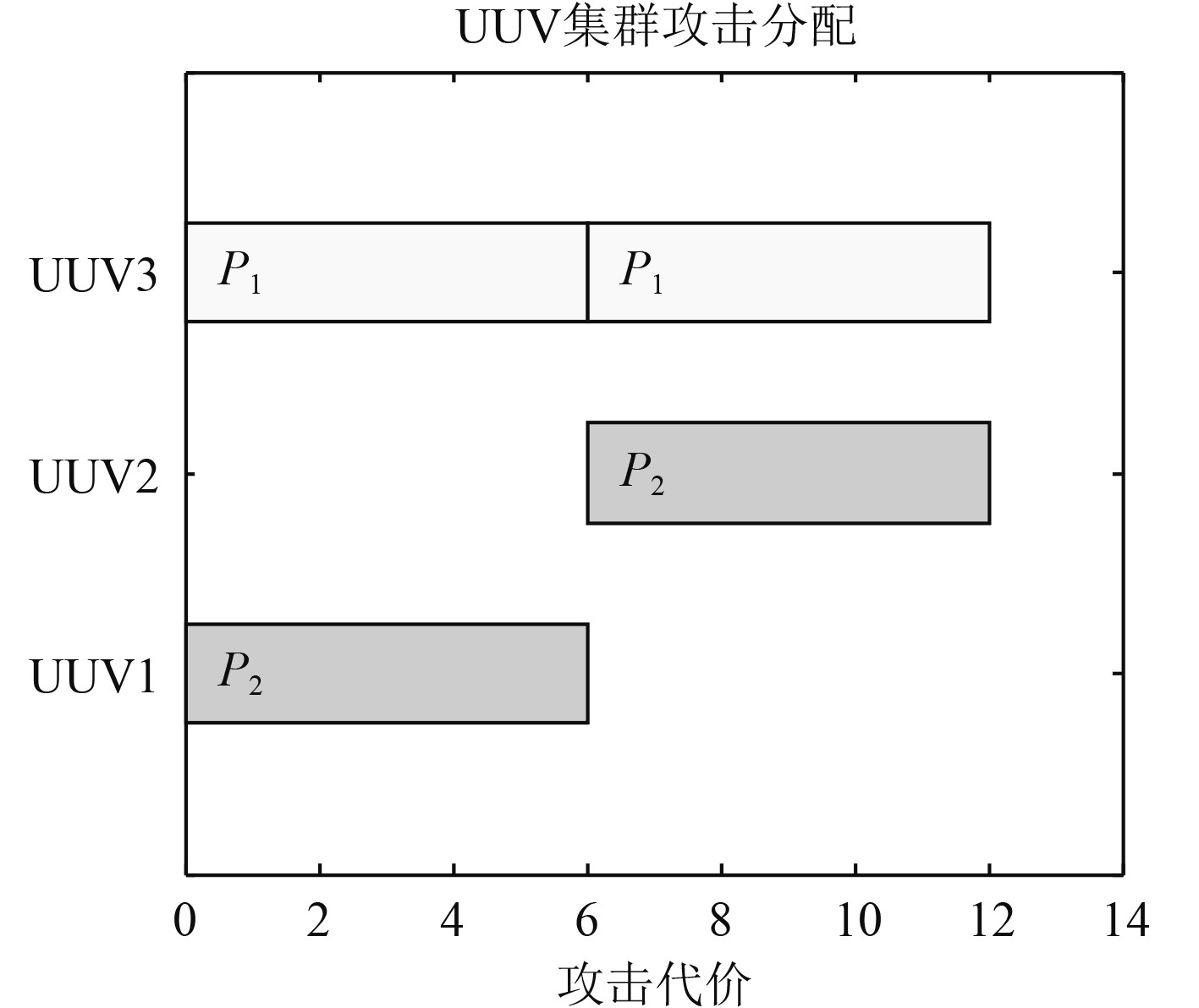
|
图 9 分配结果示意图 Fig. 9 Distribution result diagram |
|
|
表 2 UUV集群攻击目标分配情况表 Tab.2 Distribution result |
在原来仿真条件基础上,增加目标的数量到12个为原来目标数的2倍,分别采用灰狼算法(GWO)、遗传算法(genetic algorithm,GA)和改进灰狼算法(IGWO)进行仿真。遗传算法是一种高效率,并行性强,全局搜索的优化算法。仿真结果如图10所示,3种算法得到的最优值结果(即完成任务最短时间)分别为61.59,62.07和60.97 min,单次仿真结果不能得出看出哪者更优的结论,接下来进行多次仿真再统计比较3种算法得到的最优解。

|
图 10 GWO,GA和IGWO集群侦察任务分配对比图 Fig. 10 Distribution result |
由图10可知,3种算法得到的最优值结果分别为61.591,62.067和60.975 min,单次仿真结果不能得出哪个更优的结论,所以进行多次仿真再统计比较2种算法得到的最优解。为了更加清楚地对比结果,将3种算法得到的分配情况进行汇总得到表3,V表示最优值,单位为min,T表示第几次仿真。
|
|
表 3 UUV集群侦察目标分配情况对比表 Tab.3 Distribution result |
GWO得到的最短时间为61.516 min,GA得到的是62.128 min,IGWO得到的是61.138 min。综上说明,IGWO算法比GWO和GA算法能够更好对UUV集群侦察目标任务分配的问题进行求解,提高多UUV系统的资源利用率和系统的工作效率。
4 结 语狼群攻击围捕目标行为机制有很多优点,基于狼群理论提出的优化算法寻优效率高。本文将狼群行为理论引入到UUV集群任务分配问题中,解决UUV集群侦察与攻击多任务目标的问题。基于狼群行为机制对UUV集群攻击目标问题进行数学建模,包括约束条件,攻击目标收益、攻击目标代价以及总代价函数;针对传统灰狼算法未考虑全局与局部搜索的协调配合以及未考虑位置更新的权重问题进行改进,提出改进收敛因子以余弦规律减小和引入动态权重的改进灰狼算法设计基于改进灰狼算法的UUV集群任务分配的方法。为了验证方法的可行性和优越性,利用Matlab进行侦察和攻击目标分配仿真,并针对同一场景分别采用GWO、GA和IGWO三种算法对比仿真。结果表明,IGWO算法比GWO和GA算法能够更好对UUV集群侦察目标任务分配的问题进行求解,提高UUV系统的资源利用率和系统的工作效率。
| [1] |
SEYEDALI M, SEYED M M. Grey Wolf Optimizer[J]. Advances in Engineering Software, 2014: 46–61.
|
| [2] |
SEYEDALI M. Multi-objective ant lion optimizer: a multi objective optimization algorithm for solving engineering problems[J] Springer, 2016(45) 46–61.
|
| [3] |
吕洪莉. 面向多目标优化的多AUVs群体协同任务分配[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [4] |
张阳, 周溪召. 求解全局优化问题的改进灰狼算法[J]. 上海理工大学学报, 2021(43): 73-82. DOI:10.13255/j.cnki.jusst.20200331002 |
| [5] |
游达章, 等. 一种改进灰狼优化算法的移动机器人路径规划方法[J]. 机床与液压, 2021, 49(11): 1-6. |
| [6] |
林梅金, 等. 改进收敛因子和变异策略的灰狼优化算法[J]. 佛山科学技术学院学报(自然科学版), 2021, 39(3): 1-6. DOI:10.13797/j.cnki.jfosu.1008-0171.2021.0031 |
| [7] |
郭振洲, 刘然, 拱长青, 等. 基于灰狼算法的改进研究[J]. 计算机应用研究, 2017(12): 3603-3606. |
 2022, Vol. 44
2022, Vol. 44
