UUV水下搜索问题建模与仿真

引用本文

刘志浩, 刘彦伯, 黄波. UUV水下搜索问题建模与仿真. 舰船科学技术, 2022, 44(22): 63-68 复制到剪切板

LIU Zhi-hao, LIU Yan-bo, HUANG Bo. Modeling and analysis of underwater search for UUV. Ship Science and Technology, 2022, 44(22): 63-68 复制到剪切板

UUV水下搜索问题建模与仿真

刘志浩, 刘彦伯, 黄波

海军潜艇学院，山东青岛 266000

收稿日期: 2022-04-01.

作者简介: 刘志浩(1991-)，男，博士，讲师，研究方向为水下无人装备技术与运用

摘要: 当前通常利用潜艇搜索模型计算研究UUV的搜索能力，然而UUV等小型水下平台在能源及尺度方面受限，其声呐数量较少且配置位置相对受限，若不加区分的采用潜艇搜索模型，将忽略UUV搜索扇面对搜索能力的约束，进而影响搜索能力的计算。本文基于搜索论相关内容，给出随机搜索中相对速度的计算方法，确定相对速度方向的概率分布，区分首部声呐和舷侧声呐提出了搜扫宽度的计算方法，从而建立一种针对UUV或其他受搜索扇面影响较大的水下平台搜索模型，并针对巡逻线搜索和随机搜索两类典型问题对模型进行仿真验证。仿真结果表明模型可靠，相关结论可应用于UUV搜索问题的研究，也可应用于其他具有相似特点的水下机动平台搜索问题。

关键词: UUV 搜索模型搜扫宽度巡逻线搜索随机搜索

Modeling and analysis of underwater search for UUV

LIU Zhi-hao, LIU Yan-bo, HUANG Bo

Naval Submarine Academy, Qingdao 266000, China

Abstract: The research on UUV search ability depends on submarine search model now. Compared to large underwater platform such as submarine, due to the limit of scale and energy for UUV, the sonar was more less, and the position deployed was limited. If the omnidirectional detecting model was used for UUV, the constraint of detecting sector and deployed position will be ignored, so the conclusion on the search ability for UUV will be inaccurate. In this paper, based on the study of search theory, the calculation method of relative velocity in random search was gave, the probability distribution of relative velocity direction was established. The search width of sonar also was calculated by distinguishing between bow-sonar and side-sonar. Then the search model of UUV was established, and underwater platforms whose search ability was affected by detecting sector were also suitable for this model. The model was simulated combined with line search and random search. The results shown it was accurate and reliable, so the model can be applied to the study of UUV search abilities and other platforms with similar characteristics.

Key words: UUV search model search width line search random search

0 引　言

UUV在水下搜索的军事行动中具有非常广泛的应用，凭借低成本、高隐蔽等特性，可以在敏感区域或危险区域执行反潜跟踪、区域警戒、反水雷等任务，与潜艇及反潜水面舰艇等有人兵力密切配合，提升水下体系作战能力^[1-2]。

当前UUV水下搜索问题的研究，大多基于相对成熟的潜艇搜索模型展开，尚未有针对UUV特性而专门建立的搜索模型^[3]。从平台搭载的传感器来看，UUV与潜艇均依赖声呐水下搜索，但考虑平台性能和尺度差异，潜艇等大型平台能源及空间相对充沛，可以于不同位置配置多套声呐，进而可以将平台的探测范围等效为一个以声呐作用距离为半径的圆，即可认为潜艇是全向搜索的。而UUV由于能源及传感器布置空间相对有限，通常于特定位置搭载相对较少的声呐，若仍将其等效为全向搜索，忽略探测扇面角的影响，则显然不满足UUV的实际情况，从而对其搜索能力的计算产生影响。综合调查REMUS，Bluefin，Hugin等系列典型UUV的声呐载荷，根据搜索探测用声呐布置位置的不同，大体可以分为首部声呐和舷侧声呐，且两类声呐的探测扇面关于UUV轴线纵对称^[4-5]。布置位置的差异及扇面角的不同显然使UUV的探测范围也随之变化，因此有必要综合考虑相关因素，建立适于UUV特性的搜索模型，从而便于更好地开展UUV水下搜索问题的研究。

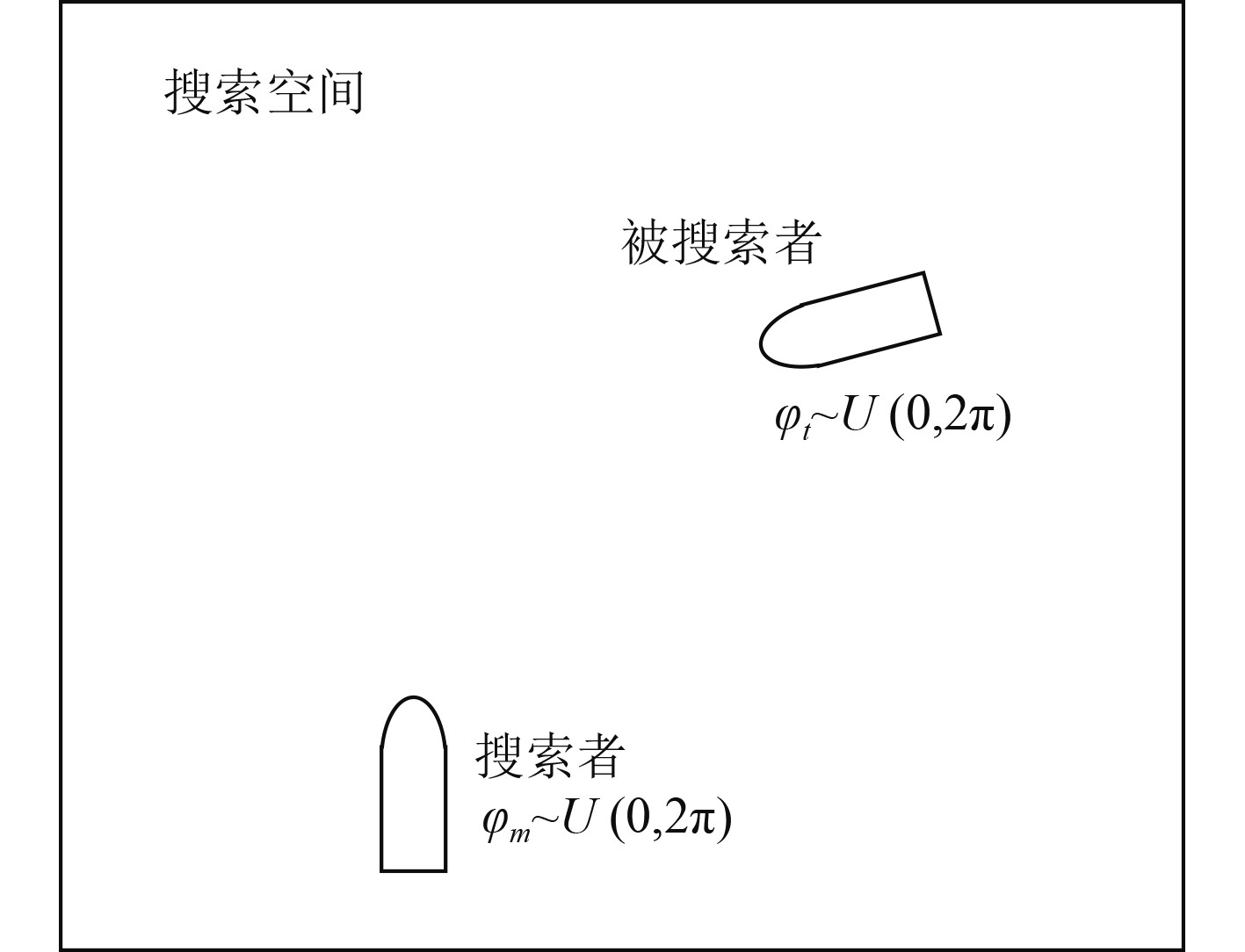
1 UUV随机搜索中的数学模型

随机搜索是一种典型搜索方式，也是分析其他类型搜索问题的重要依据。如图1所示，随机搜索指的是搜索者和目标在一定区域内可能采取任意航向的搜索过程^[6-7]。这种搜索过程通常适用于已知目标存在于某一区域、但其具体运动路径未知的搜索问题。

图 1 随机搜索方式示意图 Fig. 1 Diagram of random search

基于搜索论的相关结论，随机搜索总的发现概率为：

$P\left( t \right) = 1 - \exp \left( { - \frac{{VWt}}{A}} \right)。$

(1)

式中： $V$ 为相对运动的速度； $W$ 为搜扫宽度； $A$ 为搜索区域的面积。在UUV搜索中使用该模型时，易存在的问题是假定传感器全向作用，即简单的将 $W$ 等效为传感器作用距离的2倍，但考虑到声呐布置位置和扇面角的实际影响，这种假设显然难以成立，因此有必要针对不同情况进行分析。

1.1 相对搜索速度的确定

在随机搜索中，令UUV航速为 $U$ ，目标航速为 $V$ ，考虑搜索者 ${\varphi _m}$ 和目标航向 ${\varphi _t}$ 均符合 $\left[ {0,2\pi } \right)$ 的均匀分布，令二者的航向差为 $\Delta \varphi$ ，则

$\begin{split} F\left( {\Delta \varphi } \right) =& P\left( {{\varphi _m} - {\varphi _t} \leqslant \Delta \varphi } \right) =\\ &\left\{ {\begin{array}{*{20}{l}} {\dfrac{{{{\left( {2{\text{π}} + \Delta \varphi } \right)}^2}}}{{8{{\text{π}} ^2}}}}，&{\Delta \varphi \in \left( { - 2{\text{π}} ,0} \right)}，\\ {1 - \dfrac{{{{\left( {2{\text{π}} - \Delta \varphi } \right)}^2}}}{{8{{\text{π}} ^2}}}}，&{\Delta \varphi \in \left[ {0,2{\text{π}} } \right)} 。\end{array}} \right. \end{split}$

(2)

取微分后有

$f\left( {\Delta \varphi } \right) = F'\left( {\Delta \varphi } \right) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{2{\text{π}} + \Delta \varphi }}{{4{{\text{π}} ^2}}}}，&{\Delta \varphi \in \left( { - 2{\text{π}} ,0} \right)}，\\ {\dfrac{{2{\text{π}} - \Delta \varphi }}{{4{{\text{π}} ^2}}}}，&{\Delta \varphi \in \left[ {0,2{\text{π}} } \right)} 。\end{array}} \right.$

(3)

显然 $f\left( {\Delta \varphi } \right)$ 是关于 $\Delta \varphi = 0$ 对称的，考虑到 $\Delta \varphi$ 的定义，显然有

$\begin{array}{*{20}{c}} {f\left( {\Delta \varphi } \right) = \dfrac{1}{{2{\text{π}} }}}&{\Delta \varphi \in \left[ {0,2{\text{π}} } \right)}。\end{array}$

(4)

式（4）表明 $\Delta \varphi$ 也是符合均匀分布的，因此相对运动速度 ${V_s}$ 在 $\left[ {0,2\pi } \right)$ 内的均值可表示为：

$\begin{split}{\overline{V}}_{s}=&{\displaystyle{\int _{0}^{{2{\text{π}} }}}f\left(\Delta \phi \right)\sqrt{{U}^{2}+{V}^{2}-2UV\mathrm{cos}\Delta \phi }{\rm{d}}\Delta \phi }=\\ &\dfrac{\sqrt{{U}^{2}+{V}^{2}}}{{\text{π}} }\displaystyle\int_{0}^{\text{π}} \sqrt{1-\dfrac{2UV}{{U}^{2}+{V}^{2}}\left[2{\mathrm{cos}}^{2}\dfrac{\Delta \phi }{2}-1\right]}{\rm{d}}\Delta \phi =\\ &\dfrac{2\left(U+V\right)}{{\text{π}} }{\displaystyle\int_{-\tfrac{{\text{π}} }{2}}^{0} \sqrt{1-\dfrac{4UV}{{\left(U+V\right)}^{2}}{\mathrm{sin}}^{2}\alpha }{\rm{d}}\alpha } =\\ &\dfrac{2\left(U+V\right)}{{\text{π}} }{E}_{\mathrm{II}}\left(\dfrac{4UV}{{\left(U+V\right)}^{2}}\right)。\end{split}$

(5)

式中： $\alpha {\text{ = }}\dfrac{{\Delta \varphi - {\text{π}} }}{2}$ ； ${E}_{\mathrm{II}}$ 表示第二类完全椭圆积分。

1.2 搜扫宽度的确定

前文已证 $\Delta \varphi$ 为均匀分布，图2为以 $U$ 为 $y$ 轴建立坐标系，令 $V$ 的方向为 $\varphi$ ， ${V_s}$ 的方向为 $\ \beta$ ，令 $k = U/V$ 。

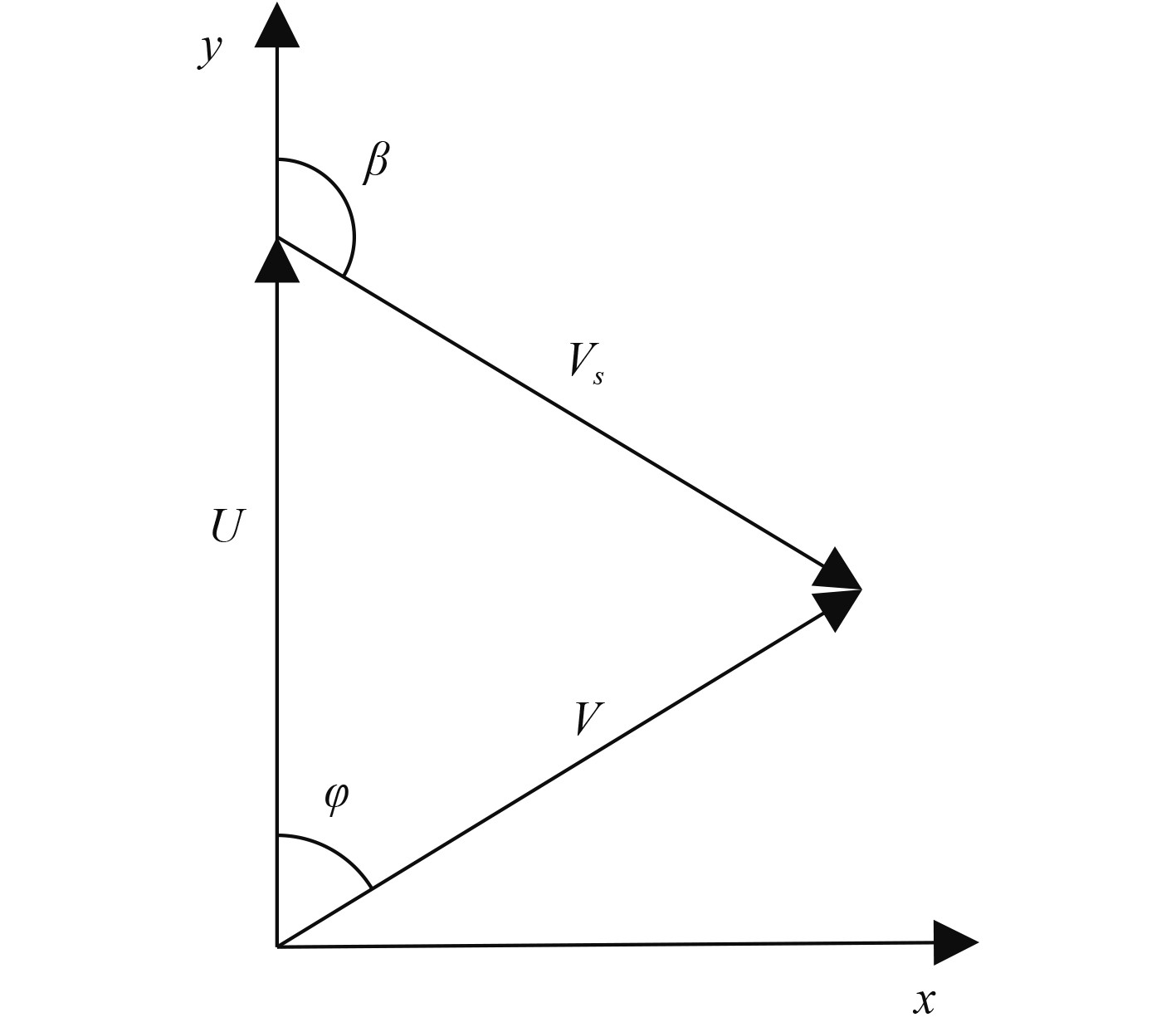
图 2 坐标系建立方法示意图 Fig. 2 Establishment of coordinate

考虑对称性，仅讨论 $\varphi \in \left[ {0,\pi } \right)$ 。当 $k > 1$ 即 $U > V$ 时，显然 $\ \beta$ 始终指向 $y < 0$ 区域，此时

$\begin{split} {F_1}(\beta ) =& P\left\{ {\arctan \frac{{\sin \varphi }}{{\cos \varphi - k}} \leqslant \beta } \right\} =\\ &\frac{{\arccos \left( {{K_2} - {K_1}} \right) - \arccos \left( {{K_2} + {K_1}} \right)}}{\text{π} } 。\end{split}$

(6)

式中： ${K_1} = \sqrt {{{\cos }^2}\beta \left( {{k^2}{{\cos }^2}\beta - {k^2} + 1} \right)}$ ； ${K_2} = k - k{\cos ^2}\beta$ ； $\ \beta \in \left( {\arccos \dfrac{{ - \sqrt {{k^2} - 1} }}{k},\text{π} } \right)$ 。

当 $k = 1$ 即 $U = V$ 时，此时 ${V_s}$ 相当于割以 $U$ 为半径的圆的弦，进而有 $\ \beta = \dfrac{{{\text{π}} + \varphi }}{2}$ ，因此有

$\begin{array}{*{20}{c}} {{F_2}\left( \beta \right) = \dfrac{{2\beta - {\text{π}} }}{{\text{π}} }}，&{\beta \in \left[ {\dfrac{{\text{π}} }{2},{\text{π}} } \right)} ，\end{array}$

(7)

当 $k > 1$ 即 $U < V$ 时，此时 $\ \beta$ 在 $\left[ {0,\pi } \right)$ 内分布，因此有

${F_3}\left( \beta \right) = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{\arccos \left( {{K_2} + {K_1}} \right)}}{{\text{π}} }}，&{\beta \in \left[ {0,\dfrac{{\text{π}} }{2}} \right)} ，\\ {\dfrac{{\arccos \left( {{K_2} - {K_1}} \right)}}{{\text{π}} }}，&{\beta \in \left[ {\dfrac{{\text{π}} }{2},{\text{π}} } \right)} 。\end{array}} \right.$

(8)

对上述分布函数 $F\left( \beta \right)$ 取微分后可确定 $k$ 取值不同情况下 $\beta$ 的概率密度函数，也可用于离散化求取某一范围内相对运动方向的分布概率，从而可确定平均搜扫宽度的值。

1.2.1 仅配置首部声呐时搜扫宽度的确定

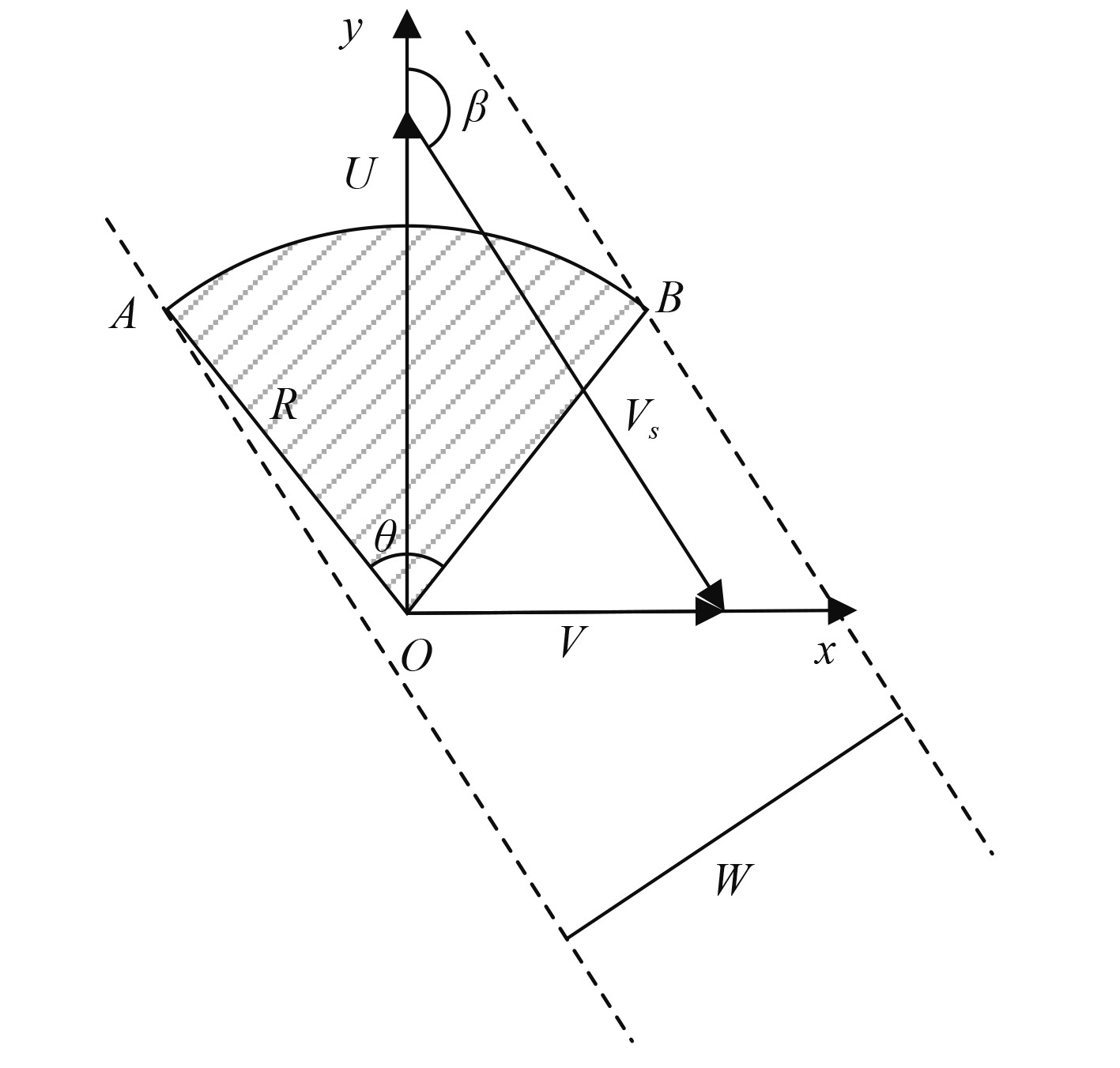
根据文献[8]，搜扫宽度基于横向距离的积分确定，而横向距离指的是在距离最近点处搜索者和目标之间的距离。由此，当仅配置首部声呐时，如图3所示。令声呐作用距离为 $R$ ，声呐扇面角为 $\theta$ 。显然， $W$ 等于搜索扇面沿 $\ \beta$ 方向投影的长度，且受 $\ \beta$ 和 $\theta$ 取值影响。

图 3 首部声呐搜扫宽度确定方法示意图 Fig. 3 Daigram of bow sonar search width

若 $\theta \leqslant {{\text{π}} \mathord{\left/ {\vphantom {{\text{π}} 2}} \right. } 2}$ ，则当 $\ \beta \in \left[ {0,{\theta \mathord{\left/ {\vphantom {\theta 2}} \right. } 2}} \right]$ 时， $W$ 等于弦 $AB$ 构成线段沿 $\ \beta$ 方向的投影长度，因此

${W_1} = 2R\sin \frac{\theta }{2}\cos \beta，$

(9)

当 $\ \beta \in \left[ {{\theta \mathord{\left/ {\vphantom {\theta 2}} \right. } 2},{{\left( {{\text{π}} - \theta } \right)} \mathord{\left/ {\vphantom {{\left( {{\text{π}} - \theta } \right)} 2}} \right. } 2}} \right]$ 时， $W$ 等于线段 $AO$ 沿 $\ \beta$ 方向的投影长度，因此

${W_2} = R\sin \left( {\beta + \frac{\theta }{2}} \right) ，$

(10)

当 $\ \beta \in \left[ {{{\left( {{\text{π}} - \theta } \right)} \mathord{\left/ {\vphantom {{\left( {{\text{π}} - \theta } \right)} 2}} \right. } 2},{{\left( {{\text{π}} + \theta } \right)} \mathord{\left/ {\vphantom {{\left( {{\text{π}} + \theta } \right)} 2}} \right. } 2}} \right]$ 时， $W$ 等于探测扇面的作用距离，即

${W_3} = R，$

(11)

当 $\ \beta \in \left[ {{{\left( {{\text{π}} + \theta } \right)} \mathord{\left/ {\vphantom {{\left( {{\text{π}} + \theta } \right)} 2}} \right. } 2},{\text{π}} - {\theta \mathord{\left/ {\vphantom {\theta 2}} \right. } 2}} \right]$ 时， $W$ 等于线段 $OB$ 沿 $\ \beta$ 方向的投影长度，因此

${W_4} = R\sin \left( {\beta - \frac{\theta }{2}} \right)。$

(12)

当 $\ \beta \in \left[ {{\text{π}} - {\theta \mathord{\left/ {\vphantom {\theta 2}} \right. } 2},{\text{π}} } \right)$ 时， $W$ 等于弦 $AB$ 构成线段沿 $\ \beta$ 方向的投影长度，因此

${W_5} = 2R\sin \frac{\theta }{2}\cos \left( {{\text{π}} - \beta } \right)。$

(13)

同理，若 $\theta > \dfrac{{\text{π}} }{2}$ ，则当 $\ \beta \in \left[ {0,{{\left( {{\text{π}} - \theta } \right)} \mathord{\left/ {\vphantom {{\left( {{\text{π}} - \theta } \right)} 2}} \right. } 2}} \right]$ 时， $W$ 等于弦 $AB$ 构成线段沿 $\ \beta$ 方向的投影长度，即

${W'_1} = {W_1}，$

(14)

当 $\ \beta \in \left[ {{{\left( {\pi - \theta } \right)} \mathord{\left/ {\vphantom {{\left( {\pi - \theta } \right)} 2}} \right. } 2},{\theta \mathord{\left/ {\vphantom {\theta 2}} \right. } 2}} \right]$ 时， $W$ 等于线段 $OB$ 沿 $\ \beta$ 方向的投影长度与扇面半径的和，因此

${W'_2} = R + R\sin \left( {\frac{\theta }{2} - \beta } \right) 。$

(15)

当 $\ \beta \in \left[ {{\theta \mathord{\left/ {\vphantom {\theta 2}} \right. } 2},{\text{π}} - {\theta \mathord{\left/ {\vphantom {\theta 2}} \right. } 2}} \right]$ 时， $W$ 等于探测扇面的作用距离，即

${W'_3} = {W_3}，$

(16)

当 $\ \beta \in \left[ {{\text{π}} - {\theta \mathord{\left/ {\vphantom {\theta 2}} \right. } 2},{{\left( {\theta + {\text{π}} } \right)} \mathord{\left/ {\vphantom {{\left( {\theta + {\text{π}} } \right)} 2}} \right. } 2}} \right]$ 时， $W$ 等于线段 $AO$ 沿 $\ \beta$ 方向的投影长度与扇面半径的和，因此

${W'_4} = R - R\sin \left( {\frac{\theta }{2} + \beta } \right)。$

(17)

当 $\ \beta \in \left[ {{{\left( {\theta + {\text{π}} } \right)} \mathord{\left/ {\vphantom {{\left( {\theta + {\text{π}} } \right)} 2}} \right. } 2},{\text{π}} } \right)$ 时， $W$ 等于弦 $AB$ 沿 $\ \beta$ 方向的投影长度，即

${W'_5} = {W_5}。$

(18)

1.2.2 仅配置舷侧声呐时搜扫宽度的确定

如图4所示，当仅配置舷侧声呐时，搜扫宽度确定方法相同。

图 4 舷侧声呐搜扫宽度确定方法示意图 Fig. 4 Daigram of side sonar search width

当 $\ \beta \in \left[ {0,{\theta \mathord{\left/ {\vphantom {\theta 2}} \right. } 2}} \right]$ 时， $W$ 显然为两扇面探测半径的和，即

${W_1} = 2R，$

(19)

当 $\ \beta \in \left[ {{\theta \mathord{\left/ {\vphantom {\theta 2}} \right. } 2},{{\text{π}} \mathord{\left/ {\vphantom {{\text{π}} 2}} \right. } 2}} \right]$ 时， $W$ 即为线段 $BD$ 沿 $\ \beta$ 方向的投影长度，因此

${W_2} = 2R\sin \left( {\frac{{\text{π}} }{2} + \frac{\theta }{2} - \beta } \right) ，$

(20)

当 $\ \beta \in \left[ {{{\text{π}} \mathord{\left/ {\vphantom {{\text{π}} 2}} \right. } 2},{\text{π}} - {\theta \mathord{\left/ {\vphantom {\theta 2}} \right. } 2}} \right]$ 时， $W$ 等于线段 $AC$ 沿 $\ \beta$ 方向的投影长度，因此

${W_3} = 2R\sin \left( {\beta + \frac{\theta }{2} - \frac{{\text{π}} }{2}} \right) ，$

(21)

当 $\ \beta \in \left[ {{\text{π}} - {\theta \mathord{\left/ {\vphantom {\theta 2}} \right. } 2},{\text{π}} } \right)$ 时，搜扫宽度显然为两扇面探测半径的和，即

${W_4} = 2R，$

(22)

综合式（6）～式（22），搜扫宽度 $W$ 的均值可表示为：

$\bar W = \int {F'\left( \beta \right)W\left( {\beta ,\theta } \right)} {\rm{d}}\beta。$

(23)

其中， $W\left( {\beta ,\theta } \right)$ 表示搜扫宽度关于 $\ \beta$ 和 $\theta$ 的分段函数。

2 仿真验证 2.1 巡逻线搜索问题的仿真验证

巡逻线搜索指的是搜索者垂直于目标可能航向所进行的线式搜索。这种搜索方式通常是在目标可能航向较为确定的情况下，为以最大概率发现目标而采用^[9]。本质上看，这种方式不属于随机搜索，因为目标航向已知从而不再满足均匀分布的条件，但前文所建立的搜索模型经适当变形后仍可用于求解该类问题。

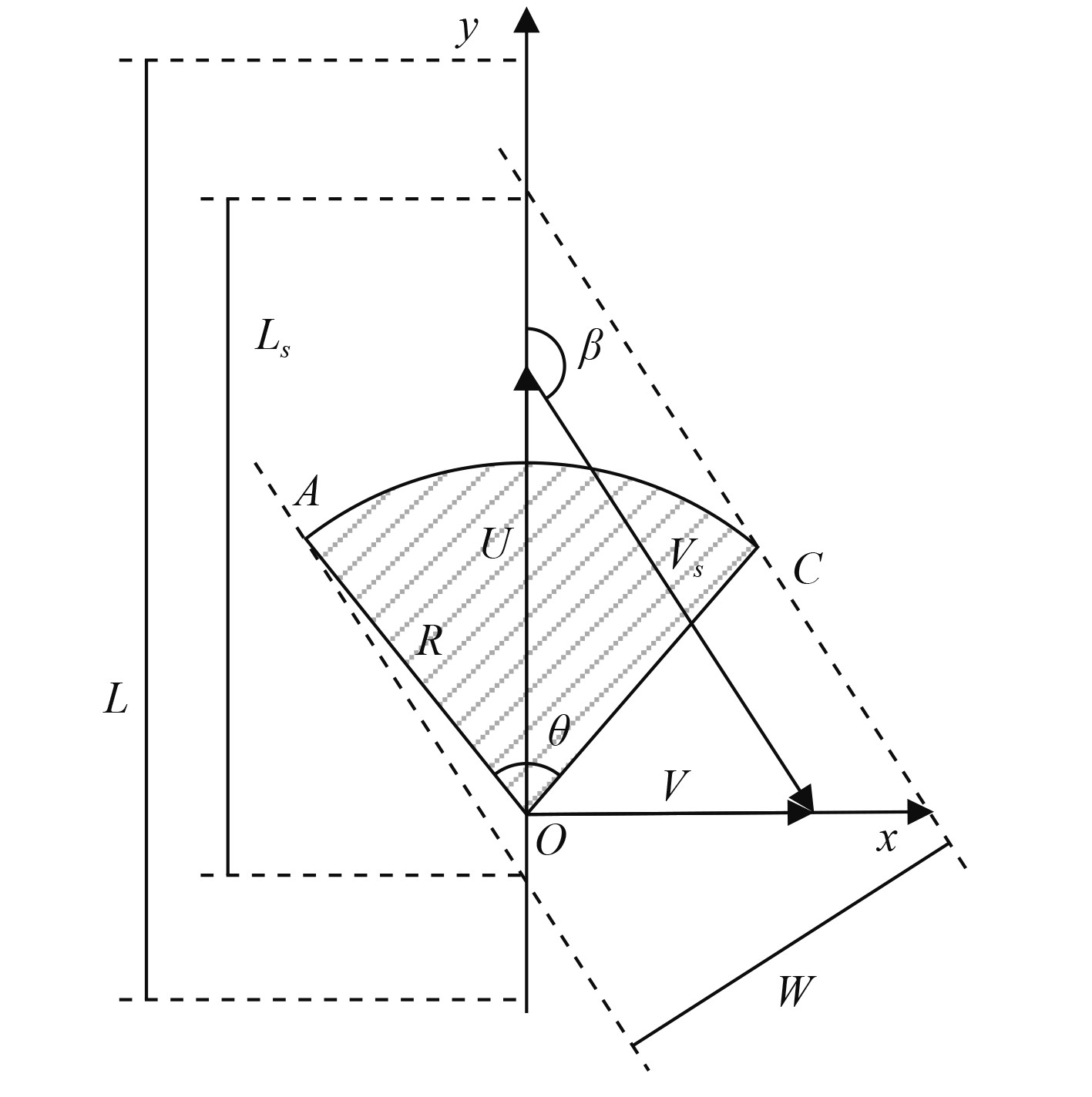
在巡逻线搜索中，显然 $V$ 和 $U$ 的方向垂直，从而显然满足 $\ \beta > {{\text{π}} \mathord{\left/ {\vphantom {{\text{π}} 2}} \right. } 2}$ 。此时，如图5所示，UUV发现目标的概率可表示为 $W$ 沿 $\ \beta$ 方向在巡逻线内投影 ${L_s}$ 的平均长度与 $L$ 的比值，即

图 5 巡逻线搜索示意图 Fig. 5 Schematic of line search

$P\left( \beta \right) = \frac{1}{{{L^2}}}\left[ {\frac{{W\left( \beta \right)L}}{{\sin \beta }} - \frac{{{W^2}\left( \beta \right)}}{{2{{\sin }^2}\beta }} - K\left( {\beta ,\theta } \right)} \right]。$

(24)

式中：当 $\ \beta \in \left( {{{3{\text{π}} }/ 4},{\text{π}} } \right)$ 时， $K\left( {\beta ,\theta } \right) = \dfrac{{\sin \left( {\beta + \dfrac{\theta }{2}} \right)\sin \left( {\beta - \dfrac{\theta }{2}} \right)}}{{{{\sin }^2}\beta }}{R^2}$ ；当 $\theta \geqslant \dfrac{{\text{π}} }{2}$ 且 $\ \beta \in \left( {\dfrac{{2{\text{π}} - \theta }}{2},\dfrac{{3{\text{π}} }}{4}} \right)$ 时， $K\left( {\beta ,\theta } \right) = \dfrac{{\sin \left( {\beta + \dfrac{\theta }{2}} \right)}}{{{{\sin }^2}\beta }}{R^2}$ ；其他情况下 $K\left( {\beta ,\theta } \right) = 0$ 。

设计仿真试验，UUV以首部声呐进行巡逻线搜索， $L = 10\;{\rm{n\; mile}}$ ， $U = 10\;{\text{kn}}$ ， $R = 2\;{\rm{n\; mile}}$ 。考虑 $\theta$ 分别取 ${{\text{π}} \mathord{\left/ {\vphantom {{\text{π}} 3}} \right. } 3}$ 和 ${{2{\text{π}} } \mathord{\left/ {\vphantom {{2{\text{π}} } 3}} \right. } 3}$ ， $V$ 分别取 $6\;{\text{kn}}$ ， $10\;{\text{kn}}$ 和 $20\;{\text{kn}}$ ，目标进入UUV探测扇面即判断为搜索到目标，则根据式（24），发现目标的理论值如表1所示。表中“全向模型”指的是基于潜艇搜索模型而计算的UUV发现概率。采用蒙特卡罗法进行仿真，仿真结果如图6及图7所示。

表 1 巡逻线搜索发现概率理论值 Tab. 1 Theoretical probability of line search

目标航速	$\theta = {{\text{π}} \mathord{\left/ {\vphantom {{\text{π}} 3}} \right. } 3}$	$\theta = 2{{\text{π}} \mathord{\left/ {\vphantom {{\text{π}} 3}} \right. } 3}$	全向模型
$V = 6\;{\text{kn}}$	0.282	0.484	0.626
$V = 10\;{\text{kn}}$	0.236	0.313	0.486
$V = 20\;{\text{kn}}$	0.199	0.199	0.392

表 1 巡逻线搜索发现概率理论值 Tab.1 Theoretical probability of line search

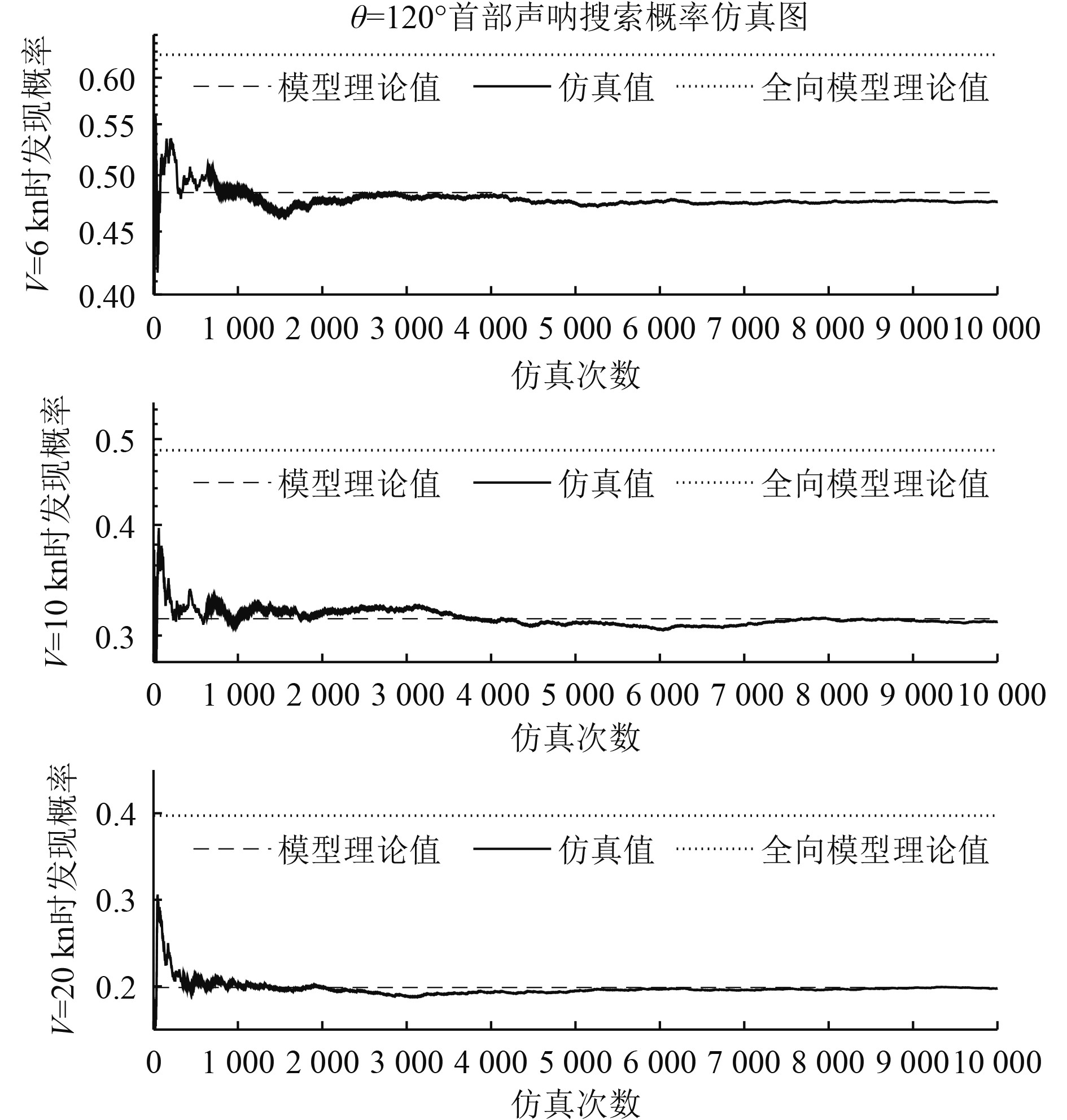
图 6 巡逻线搜索仿真结果与理论值对比图（

$\theta = {60^ \circ }$ ） Fig. 6 Comparison of detection probabilities between simulational and theoretical value（

$\theta = {60^ \circ }$ ）

图 7 巡逻线搜索仿真结果与理论值对比图（

$\theta = {120^ \circ }$ ） Fig. 7 Comparison of detection probabilities between simulational and theoretical value（

$\theta = {120^ \circ }$ ）

可以看出，随着仿真次数的增加，仿真计算给出的发现概率较快的收敛于基于式（24）给出的理论概率，且可以看出，若采用将搜扫宽度等效为传感器作用距离两倍的全向搜索模型，则发现概率的计算将有较大误差，从而验证了前文建立的模型在巡逻线搜索问题中的有效性与准确性。

2.2 随机搜索问题的仿真验证

设计仿真试验，令UUV和目标在一宽为 $10\;{\rm{n\;mile}}$ ，长为 $20\;{\rm{n\;mile}}$ 的区域内随机运动。考虑 $U = 10\;{\text{kn}}$ ， $R = 1\;{\rm{n\;mile}}$ ， $V = 15\;{\text{kn}}$ ，考虑 $\; \theta$ 分别取 ${{\text{π}} \mathord{\left/ {\vphantom {{\text{π}} 3}} \right. } 3}$ 和 ${{2{\text{π}} } \mathord{\left/ {\vphantom {{2{\text{π}} } 3}} \right. } 3}$ ，目标进入UUV探测扇面即被发现。采用蒙特卡罗方法进行仿真，仿真结果如图8及图9所示。

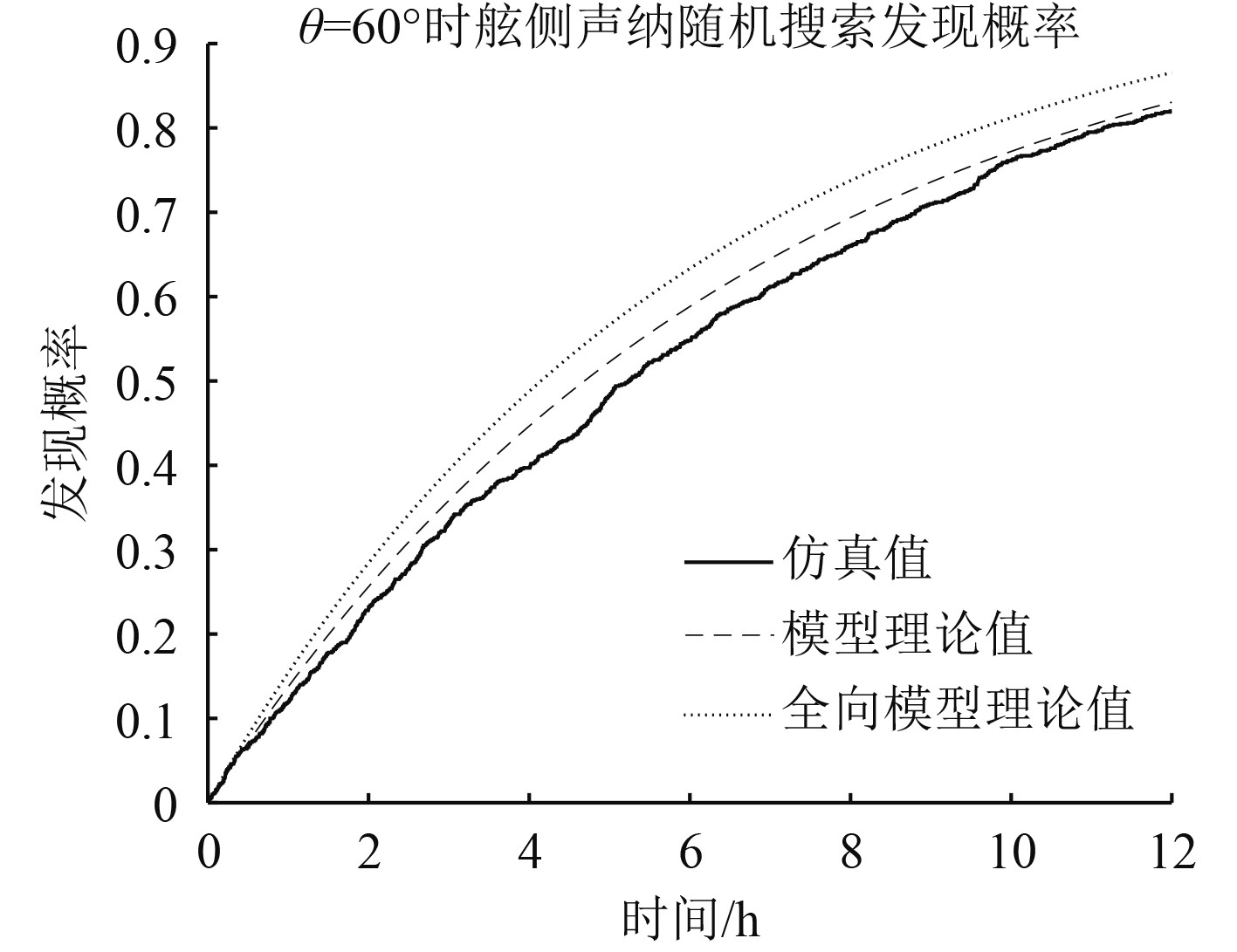
图 8 随机搜索发现概率对比图（

$\theta {\text{ = }}{60^ \circ }$ ） Fig. 8 Comparison of detection probabilities of random search（

$\theta {\text{ = }}{60^ \circ }$ ）

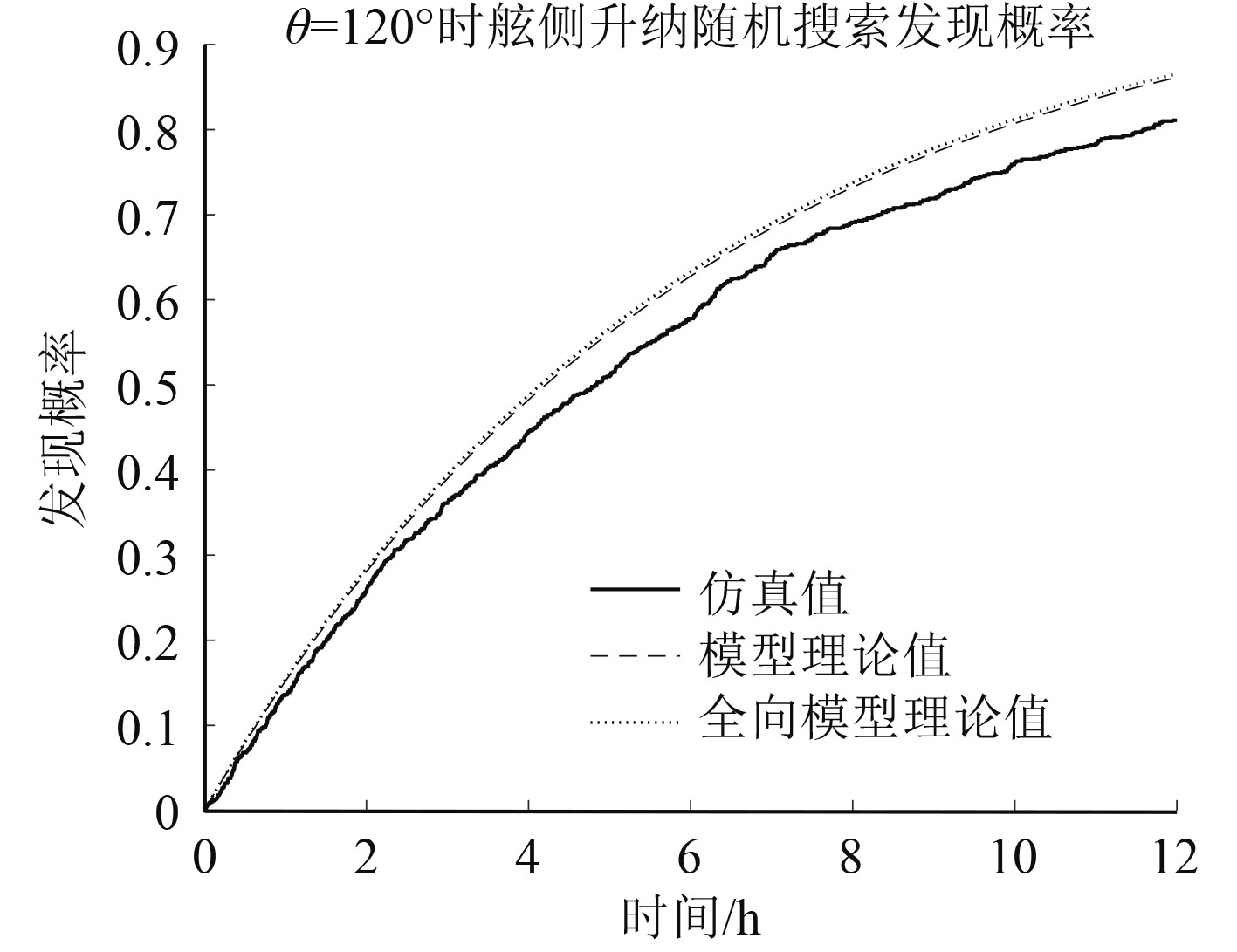
图 9 随机搜索发现概率对比图（

$\theta {\text{ = }}{120^ \circ }$ ） Fig. 9 Comparison of detection probabilities of random search（

$\theta {\text{ = }}{120^ \circ }$ ）

由图8可以看出，相较于以2倍传感器作用距离为搜扫宽度的全向模型，基于式（1）、式（5）和式（23）等给出的模型更接近于仿真试验的结果，从而验证了模型在随机搜索中的有效性和准确性。

图9表明2种模型较为接近，结合式（20）和式（21）可以看出：

$\Delta P = \left( {{e^{\frac{{\left( {2R - W} \right)Vt}}{A}}} - 1} \right){e^{\frac{{ - 2RVt}}{A}}}。$

(25)

进而表明，当 $\theta$ 取值越小（即 $W$ 取值越小）、搜索范围 $A$ 越小时，2种模型之间的差异也就越大，即采用原有的全向搜索模型确定发现概率时误差也就越大，反之两种模型则较为接近。此外，针对图8中模型理论值略高于仿真值的问题，经研究发现，在考虑探测扇面、搜索区域边界等问题约束后，在不破坏随机性的条件下，无论采取何种运动方式，都无法令UUV的探测扇面始终处于搜索区域内^[10-11]。如图10所示，当UUV在区域边界附近运动时，部分探测扇面将位于搜索范围外，从而导致有效的探测范围变小，进而降低发现概率，而式（1）所给出的模型，本质上是对 $n$ 次独立试验的重复，即

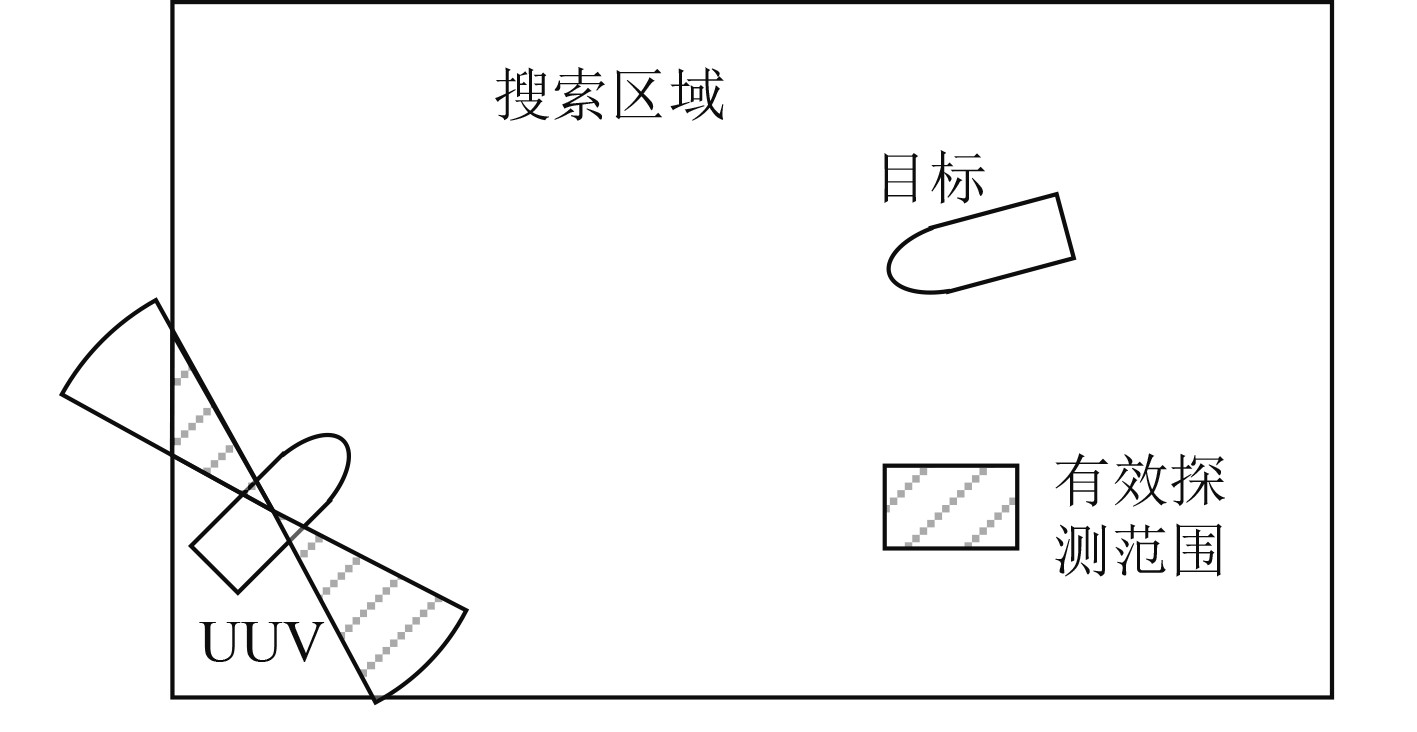
图 10 随机搜索中有效探测范围示意图 Fig. 10 Diagram of valid detection range in random search

$P\left( t \right) = 1 - {\left( {1 - \frac{{VWt}}{{nA}}} \right)^n}。$

(26)

每次独立试验时均要求探测扇面完全位于搜索区域内，而这只有当 $A$ 无限大时才能满足，即基于式（1）所确定的发现概率为随机搜索的理论上限。

3 结　语

针对当前UUV采用潜艇搜索模型从而导致搜索效率存在误差的问题，以搜索论的相关概念为基础进行研究，对相对运动速度及不同扇面角和态势下的搜扫宽度进行计算与分析，区分首部声呐和舷侧声呐2种典型配置方案，建立非全向传感器作用下水下平台的搜索模型。仿真结果与模型理论计算值吻合较好，验证了模型对水下搜索问题研究的可靠性与准确性。

参考文献

[1]	钟宏伟. 国外无人水下航行器装备与技术现状及展望[J]. 水下无人系统学报, 2017, 25(3): 215-225. ZHANG H W. Review and prospect of equipment and techniques for unmanned undersea vehicle in foreign countries[J]. Journal of Unmanned Undersea Systems, 2017, 25(3): 215-225. DOI:10.11993/j.issn.2096-3920.2017.03.001
[2]	鞠巍, 周银龙, 张浩. UUV的技术特点、作战运用及发展趋势[J]. 舰船论证参考, 2017, 1: 12-16. JU W, ZHOU Y L, ZHANG H. Technical characteristic, combat application and development tendency of UUV[J]. Ship Demonstration, 2017, 1: 12-16.
[3]	张宏瀚, 郭焱阳, 许亚杰, 等. 多UUV搜索海底声信标任务规划方法[J]. 中国舰船研究, 2020, 15(1): 13-20. ZHANG H H, GUO Y Y, XU Y J, et al. Mission planning method of multi-UUV search submarine acoustic beacon[J]. Chinese Journal of Ship Research, 2020, 15(1): 13-20. DOI:10.19693/j.issn.1673-3185.01641
[4]	徐健, 朱慧龙, 陈涛, 等. 受人观测启发的UUV前视声纳滤波方法. 仪器仪表学报, 2016, 37(5): 1094–1099. XU J, ZHU H L, CHEN T, et al. Forward looking sonar filtering method for UUV inspired by humanoid observation[J]. Chinese Journal of Scientific Instrument, 2016, 37(5): 1094–1099.
[5]	陈盼, 胡剑光, 尹志伟. UUV编队协同搜索静止目标的准最优方法[J], 火力指挥与控制, 2013, 38(4): 53–56. CHEN P, HU J G, YIN Z W. Quasi-optimal method for multiple UUVs cooperate to search static target[J]. Fire Control & Command Control, 2013, 38(4): 53–56.
[6]	周宏坤, 葛锡云, 邱中梁, 等. UUV集群协同探测与数据融合技术研究[J]. 舰船科学技术, 2017, 39(12): 70-75. ZHOU H K, GE X Y, QIU Z L, et al. Research on UUVs cooperative detection and data fusion[J]. Ship Science and Technology, 2017, 39(12): 70-75. DOI:10.3404/j.issn.1672-7649.2017.12.015
[7]	常波, 周晓光, 田怀英, 等. 舰载反潜直升机吊放声纳区域反潜策略建模[J]. 火力与指挥控制, 2017, 42(8): 68-75. CHANG B, ZHOU X G, TIAN H Y, et al. Modelling and research on area searching strategies for antisubmarine helicopter with dipping sonar[J]. Fire Control & Command Control, 2017, 42(8): 68-75. DOI:10.3969/j.issn.1002-0640.2017.08.016
[8]	郭齐胜, 曹晓东, 王文悦, 等. 战斗建模[M]. 北京: 国防工业出版社, 2002.
[9]	蔡云祥, 初磊, 陈雄民. 潜艇隐蔽突破反潜潜艇封锁区域能力评估模型研究[J]. 舰船电子工程, 2016, 36(8): 36-51. CAI Y X, CHU L, CHEN X M. Evaluation model of submarine’s capability of stealthily breaking through adverse submarine’s blocked area[J]. Ship Electronic Engineering, 2016, 36(8): 36-51. DOI:10.3969/j.issn.1672-9730.2016.08.009
[10]	张建强, 刘忠, 杨红梅. 基于搜索论的远程反舰导弹搜捕概率建模方法[J]. 国防科技大学学报, 2015, 37(4): 188–194. ZHANG J Z, LIU Z, YANG H M. The target acquisition probability modeling method of long-range anti-ship missile based on search theory[J], Journal of National University of Defense Technology, 2015, 37(4): 188–194.
[11]	邹佳运, 曲泓玥, 陈志鹏. 大规模水下滑翔机集群区域覆盖探测路径规划[J]. 水下无人系统学报, 2021, 29(1): 23-29. ZOU J Y, QU H Y, CHEN Z P. Path planning of a large-scale underwater glider swarm area coverage detection[J]. Journal of Unmanned Undersea Systems, 2021, 29(1): 23-29. DOI:10.11993/j.issn.2096-3920.2021.01.04


舰船科学技术 2022, Vol. 44 Issue (22): 63-68 DOI: 10.3404/j.issn.1672-7649.2022.22.012	PDF