0 引　言

为了保证无人船在环境监测、侦察和监视等耗时且危险的任务中的安全，采用激光雷达、毫米波雷达^[1-2]等设备进行近距离障碍物探测和跟踪是实现无人船环境感知的重要手段。传统的数据关联方法主要包括最近邻域法^[3]（NN）、概率密度数据关联^[4]（PDA）、联合概率数据关联^[5]（JPDA）、多假设追踪^[6]（MHT）等。

其中NN算法适合目标稀疏杂波较少的场景，PDA算法适用于单目标场景，JPDA是PDA算法的改进，可应用于多目标场景，但无法处理旧目标消失及新目标出现的情况，且随目标数量的增长计算量呈指数级增长^[7]，MHT算法性能优越，但需要对关联假设组合进行穷举，对系统的计算量和存储量要求较高^[8]。AzizAM等^[9]提出基于模糊C均值聚类算法（FCM）改进的NN方法，该算法将航迹作为聚类中心得到了所有量测对航迹的隶属度，根据隶属度并以最近邻的原则将量测与航迹关联，虽然取得了不错的效果，但仍然存在NN算法仅考虑最近邻测量信息的缺点。GNN^[10]（全局最近邻）算法是在NN基础上的改进，考虑了数据关联的各种可能，增强了关系的稳定性，并且已有的理论结果^[11]表明, 在不存在虚警、漏报的前提下, 平移系统误差不影响 GNN 的关联性能。相较于其他关联算法，系统误差对GNN的关联性能影响较小，是在复杂环境下较为实用的算法，但虚警、漏报会引发GNN错误关联^[11]，若阈值设置不当，轻则造成单目标的误关联，重则扰乱其他目标与航迹的配对关系。

综上所述，针对GNN算法存在的问题，对传统GNN的点迹选取方式进行改进，去掉关联可能性较小的目标，并基于 GNN算法提出了一种无人船雷达目标跟踪算法。最后，在真实的海上环境中利用装备有激光雷达与毫米波雷达的无人船进行试验，验证了算法的准确率与有效性。

1 方法思路

为了实现近岸无人船雷达目标跟踪的稳定性、准确性、实时性，需要解决的问题有：

1）由于雷达工作在无人船上，船头朝向的改变会导致目标的测量位置大幅变化，这给数据关联带来了很大的难度。

2）因海洋环境影响和传感器自身的缺陷，雷达的测量结果会出现虚警和漏检现象，导致误关联目标。

3）无人船在航行的过程中，目标会不断出现并且最终消失，目标的存在与否会直接影响数据关联的效率与正确率。

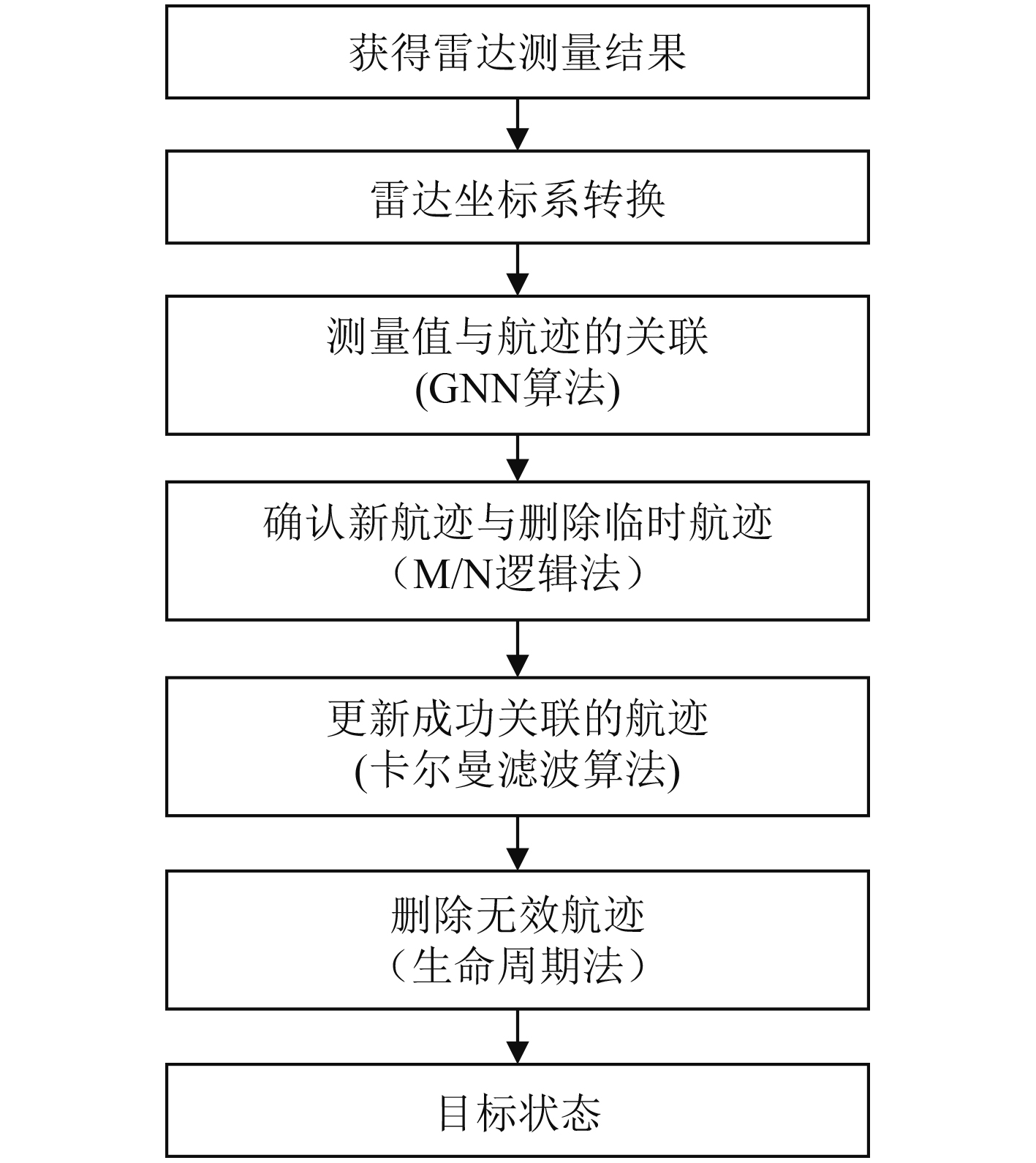
通过姿态仪的数据将雷达的测量结果转换至随船正北坐标系下，消除了首向角变化对测量结果的影响；提出一种改进的候选目标选取方式，提高GNN算法在虚警、漏检情况下的关联正确率；通过定义一种基于生命周期的有效目标维持方法，实现有效目标的持续跟踪与无效目标的删除。跟踪算法框架如图1所示。

具体算法分为以下步骤：1）雷达坐标系转换，将雷达的测量结果转换至随船正北坐标系中；2）确定航迹与测量结果的关联关系，根据改进的GNN算法进行操作；3）新航迹的确认与临时航迹的删除，满足一定条件的航迹将进行确认或删除；4）更新成功关联的航迹，根据量测值执行卡尔曼滤波；5）删除无效航迹，该步骤根据生命周期法判断已经确认的航迹是否仍然存在。最终得到目标的状态信息。

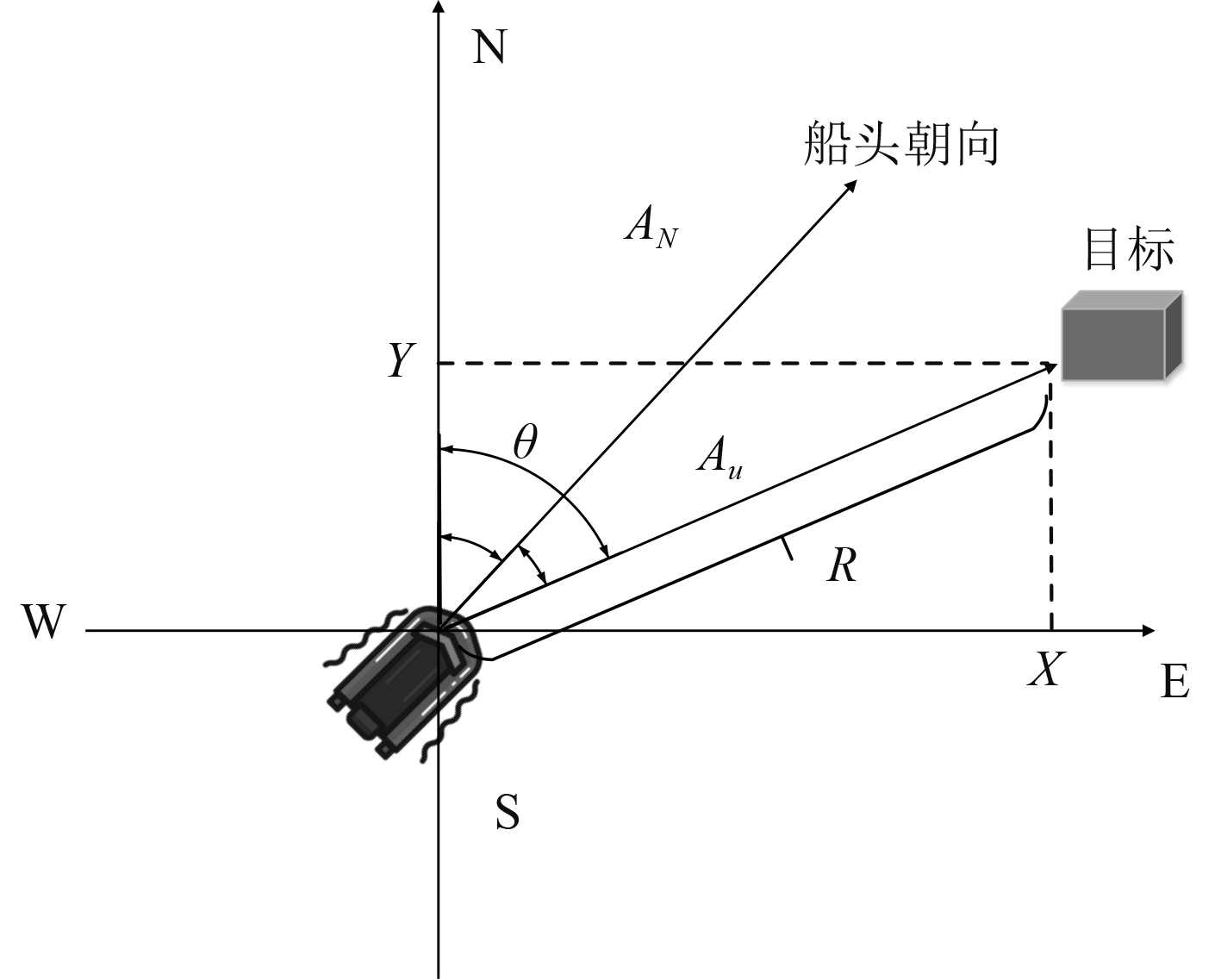
2 船载雷达坐标转换

为了消除首向角对数据关联的影响，建立随船正北坐标系如图2所示，其中 $ \theta $ 为姿态仪检测的首向角， $ A_u $ 为船载雷达检测的目标方位， $ A_N $ 为随船坐标系的修正角，R表示目标的距离。

采用姿态仪数据对雷达的数据进行修正，修正公式如下：

$ \left\{ \begin{aligned} &A_N = A_u + \theta, \\ &X = R \cdot \sin A_N , \\ &Y = R\cdot \cos A_N。\\ \end{aligned} \right. $

(1)

式中： $ X $ 和 $ Y $ 分别表示坐标转换后目标的横纵坐标。目标的位置 $ z $ 可以表示为：

$ z = {\kern 1pt} {\left[ {{\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} X&{{\kern 1pt} Y} \end{array}} \right]^{\rm{T}}}。$

(2)

3 改进的GNN目标跟踪算法

通过2次滤除目标来提高GNN的正确率，第1次通过椭圆跟踪门并辅之以特征值来初步滤除无关目标，第2次根据剩余目标在门内的分布情况再一次滤除低可能性的目标，然后利用GNN算法将剩余目标与航迹关联。最后提出一种基于生命周期的有效目标维持方法。

3.1 利用跟踪门与特征阈值滤除无关目标

利用标准卡尔曼滤波算法对障碍物的状态进行估计，采用常用的椭圆跟踪门^[12]，跟踪门G的计算公式如下式：

$ G{\text{ = 2}}{\rm{ln}}\left[ {\frac{{P_D}}{{(1 - P_D{{(2\text{π} )}^{W/2}}\beta \sqrt {\left| S \right|} )}}} \right] 。$

(3)

其中： $ P_D $ 表示探测到目标的概率； $ W $ 为测量维度； $\ \beta $ 为新回波密度；S为新息协方差。

采用椭圆跟踪门并辅之以速度阈值、目标大小来滤除无关目标，雷达测量值预处理后可以得到目标的长度和宽度。如果目标 $ i\;(i = 1,\;2,\; \cdots ,n) $ 落在 航迹 $ j\;(j = 1,\;2, \;\cdots, t) $ 的跟踪门G内（其中n为接收到的目标数量，t为系统航迹数量），速度满足速度波门 $ V_{x\max} $ 和 $ V_{y\max} $ ，并且目标长度和宽度的上下帧之比在 $ 1/\mu$ 到 $ \ \mu $ 之内则可以初步判断目标i为航迹j的待选目标，公式描述为：

$ \left\{\begin{array}{l}dij=\sqrt{（zi-H{\widehat{X}}^{\prime }k）{S}_{j}^{-1}（zi-H{\widehat{X}}^{\prime }k{）}^{{\rm{T}}}}\leqslant G，\\ \dfrac{1}{\mu } < \dfrac{zi,xwidth}{xj,width} < \mu，\\ {\scriptstyle \dfrac{1}{\mu }} < \dfrac{zi,ywidth}{yj,width} < \mu，\\ \dfrac{zi,x-{x}_{j,k-1}}{\Delta t} < V_{x\mathrm{max}}，\\ \dfrac{zi,y-{y}_{j,k-1}}{\Delta t} < V_{y\mathrm{max}}。\end{array}\right. $

(4)

其中： $d_{ij}$ 为目标i与航迹j的统计距离； $\hat X'_k$ 为状态预测值； $z_i$ 为目标i的测量矩阵； $ {S_j} $ 为航迹j的新息协方差矩阵； $x_{j,width}$ 和 $y_{j,width}$ 为航迹j上一时刻被关联目标的长和宽； $z_{i,xwidth}$ 和 $z_{i,ywidth}$ 为目标i的长和宽； $V_{x_{\max}}$ 和 $V_{y_{\max}}$ 为横纵方向的速度最大值 $z_{i,x}$ ， $z_{i,y}$ 目标i的横纵坐标； $ {x_{j,k - 1}} $ 和 $ {y_{j,k - 1}} $ 为上一时刻目标的横纵坐标。

3.2 利用关联代价滤除低可能关联的目标

由3.1节可以得到航迹j跟踪门内的所有待选目标及它们的数量 $m{\kern 1pt}_ j$ ，但其中仍然包含大量的无关目标，为此提出一种进一步滤除无关目标的滤除方法。

若目标i为航迹j的待选目标，则定义关联代价^[13] $c_{ij}$ 为 $d_{i{j}}^2 + \log \left(\left| {{S_j}} \right|\right)$ ，否则，关联代价为max，即

$ {c_{ij}} = \left\{ \begin{array}{ll} d_{i{j}}^2 + \log \left(\left| {{S_j}} \right|\right),& d \leqslant G ，\\ + \infty ,&d > G。\end{array} \right. $

(5)

采用计算模糊隶属度的方式衡量每一个目标的关联概率，定义 $ {u_{ij}} $ 为目标i对航迹j的隶属度，求取公式^[9]为：

$ {u_{ij}}{\text{ = }}\frac{{\left({\raise0.7ex\hbox{$1$} \mathord{\left/ {\vphantom {1 {{c_{ij}}}}}\right.} \lower0.7ex\hbox{${{c_{ij}}}$}}\right)}}{{\displaystyle\sum\limits_{j = 1}^t {\left({\raise0.7ex\hbox{$1$} \mathord{\left/ {\vphantom {1 {{c_{ij}}}}}\right.} \lower0.7ex\hbox{${{c_{ij}}}$}}\right)} }},i = 1,2, \cdots m_j,j = 1,2, \cdots, t。$

(6)

其中：t为航迹数量； $m{\kern 1pt} _j$ 为跟踪门内的目标数量； $ {u_{ij}} $ 为航迹隶属度。根据模糊隶属度 $ {u_{ij}} $ 与待关联目标数量 $m{\kern 1pt}_ j$ 的大小进行候选目标进行二次滤除，如果门内剩余数量 $m{\kern 1pt}_ j \leqslant Q$ 则保留门内所有候选目标，即

$ Z(j){\text{ = \{ }}{z_{ij}}{\text{,}}i{\text{ = 1,}} \cdots ,m{\kern 1pt}_j{\text{\} , }}m{\kern 1pt}_j \leqslant Q ，$

(7)

其中 $ Z(j) $ 表示属于第 $ j $ 条航迹的所有候选目标。本文根据试验海况将Q设置为3。

如果 $m{\kern 1pt}_j > Q$ ，则将隶属度 $ {u_{ij}} $ 从大到小排列，分2种情况讨论。

第1种情况：若门内最大隶属度大于 $ \varepsilon $ ，则认为此时被关联的目标比较明确，仅保留 $ Q $ 个可能性最大的目标作为候选目标，即

$ Z(j){\text{ = \{ }}{z_{ij}}{\text{,}}i{\text{ = 1,}} \cdots, Q{\text{\} , }}\max({u_{ij}}) > \varepsilon ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} m_j \geqslant Q。$

(8)

第2种情况：若门内最大隶属度小于 $ \varepsilon $ ，则认为此时目标分布较平均，从大到小累加 $ {u_{ij}} $ 直到隶属度之和大于 $ \alpha $ ，即

$ Z(j)={z}_{ij},i=1,\cdots ,s ,{\displaystyle \sum _{i=1}^{s}{u}_{ij}} > \alpha \text{；}\max({u}_{ij}) < \varepsilon。$

(9)

关于 $ \varepsilon $ 与 $ \alpha $ 的取值，考虑到既要包含尽可能多的有关目标，又要排除关联概率较低的无关目标，经过试验数据验证当 $ \alpha $ 为0.85， $ \varepsilon $ 为0.5时基本符合要求。

经过二次滤除后，最终关联代价重写为：

$ {c}_{ij}=\left\{\begin{array}{l}{c}_{ij},保留下来的目标，\\ +\infty ,其他。\end{array}\right. $

(10)

3.3 基于GNN的点迹-航迹关联

利用GNN算法求解最优关联集合^[10]，假设需要将n个测量值分配给t条航迹，最优关联问题记为：

$ \arg \min \sum\limits_{i \;=\; 1}^n {\sum\limits_{j\; = \;1}^t {c_{ij}A_{ij}} }，$

(11)

其中 $ A_{ij} $ 满足：

$ \left\{\begin{array}{l}{\displaystyle \sum _{i\;=\;1}^{n}A_{ij}}\leqslant 1,1条航迹最多分配1个测量值，\\ {\displaystyle \sum _{j\;=\;1}^{t}A_{ij}}\leqslant 1,1个目标最多分配给1条航迹。\end{array} \right.$

(12)

其中： $ A $ 为关联矩阵； $ A_{ij} $ 为0表示航迹j与目标i不关联，为1表示关联。

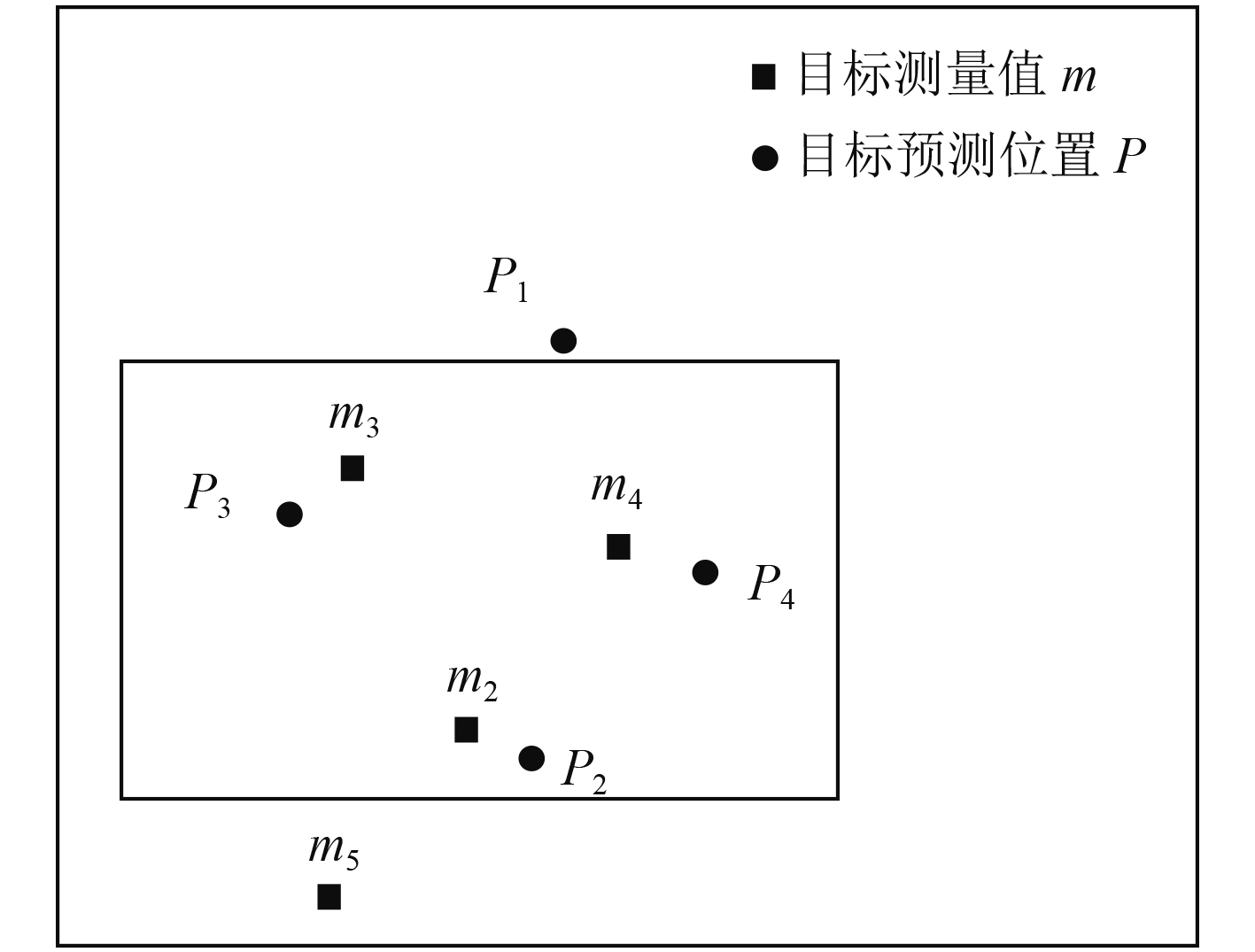
经过上述处理后，可以解决图3中的错误关联问题，假设雷达漏检了 $m_1$ ，在GNN的关联准则下，有可能会导致 $P_1$ 与 $m_3$ 关联，而 $P_3$ 则会进一步扰乱其他航迹与测量值的配对关系。

改进后的正确关联示意图，如图4所示。由于 $ P_2 $ ， $ P_3 $ ， $ P_4 $ 的关联目标比较明确，因此跟踪门内都只有3个候选目标 $ m_2 $ ， $ m_3 $ ， $ m_4 $ ，并在GNN准则下正确关联，而 $ P_1 $ 的跟踪门中则会滤除最低可能关联的目标 $ m_5 $ ，最终实现了正确关联。

最后，将已经关联到航迹目标的位置信息输入到卡尔曼滤波器中，得到最优估计值。

3.4 基于生命周期的有效目标维持方法

定义 $ L_j $ 为每条航迹的生命状态，生命状态 $ L_j $ 越大表示该航迹存在的可能性越大，反之该航迹可能由虚警产生或即将结束，生命状态 $ L_j $ 取值范围如下:

$ 0\leqslant L_j\leqslant 4,L_j为整数。$

(13)

当 $L_j > 0$ 时，认为目标存在，雷达保持跟踪。当 $L_j \leqslant 0$ 时，则认为航迹结束，停止跟踪并删除相关信息。

通过M/N逻辑法确定新航迹，只对新航迹和已有航迹进行生命状态计算，计算规则如下：

$ L_j=\left\{\begin{array}{l}3,\text{新确认航迹}，\\ \mathrm{min}(4,L_j+1),\text{航迹关联成功}，\\ L_j-1\text{，}\text{航迹关联失败}。\end{array} \right.$

(14)

在关联失败时，采用状态预测的方式继续跟踪该目标，解决跟踪过程中的漏检问题。

4 试验验证 4.1 试验准备及说明

试验船安装了相关设备，如图5所示。

此外，毫米波雷达^[2]采用矩形框表示目标，激光雷达采用盒子模型表示目标。 $ \ \mu $ 设置为3；目标的探测概率 $P_D$ 设置为0.90；新回波密度 $\ \beta $ 设置为0.01；测量维度 $ W $ 为2；航迹起始算法采用M/N逻辑法，M设置为4，N设置为3。

4.2 试验结果

从采集到的数据中选取障碍物最密集的4 min航程进行试验验证。在试验中，双雷达的检测结果中均存在以下现象：将海面波浪误识别为目标；雷达探测精度有限并且会产生虚警、漏检、目标分裂；航行时，船首角度一直变化，导致位于检测边缘的目标频繁丢失。

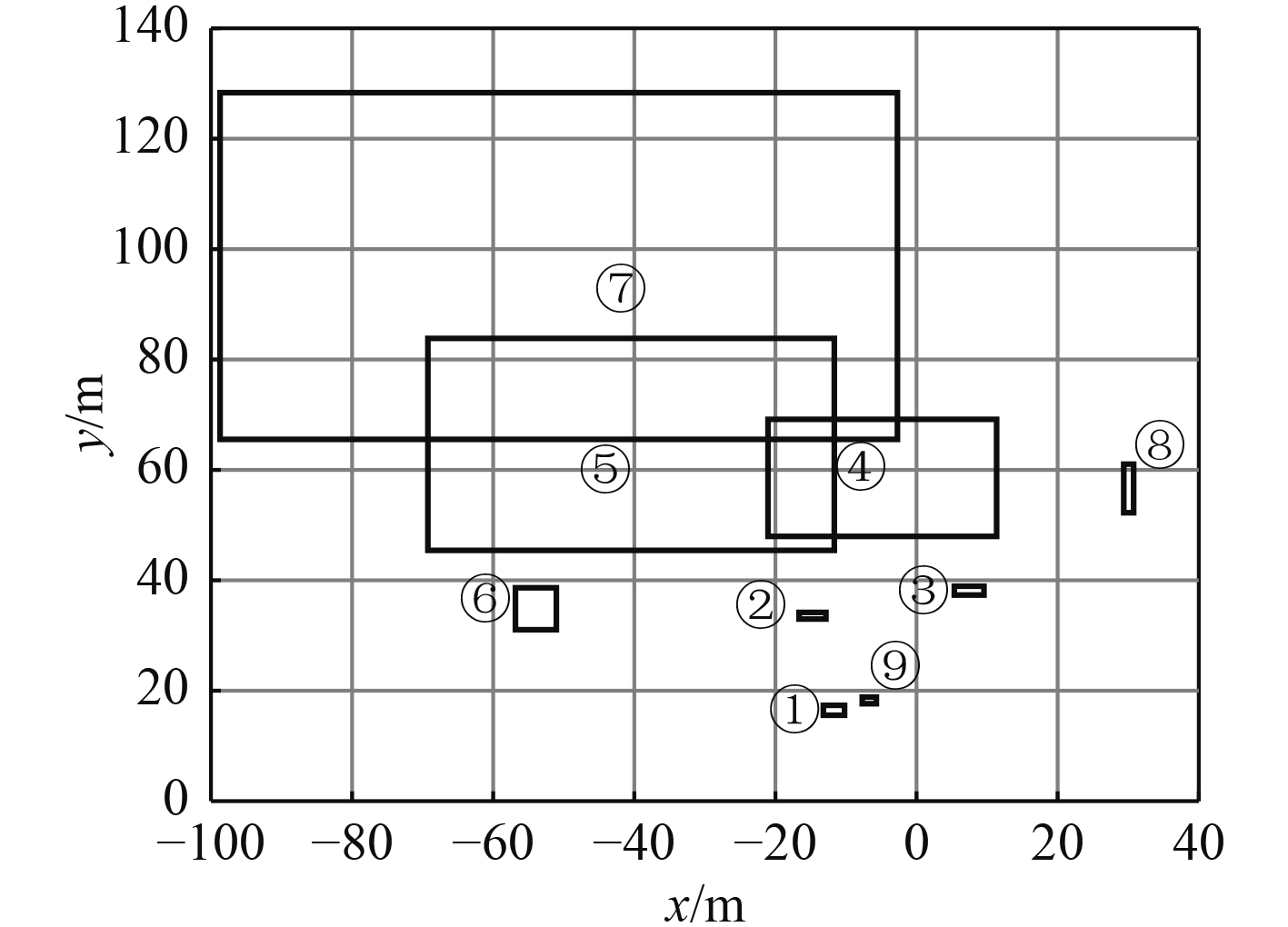
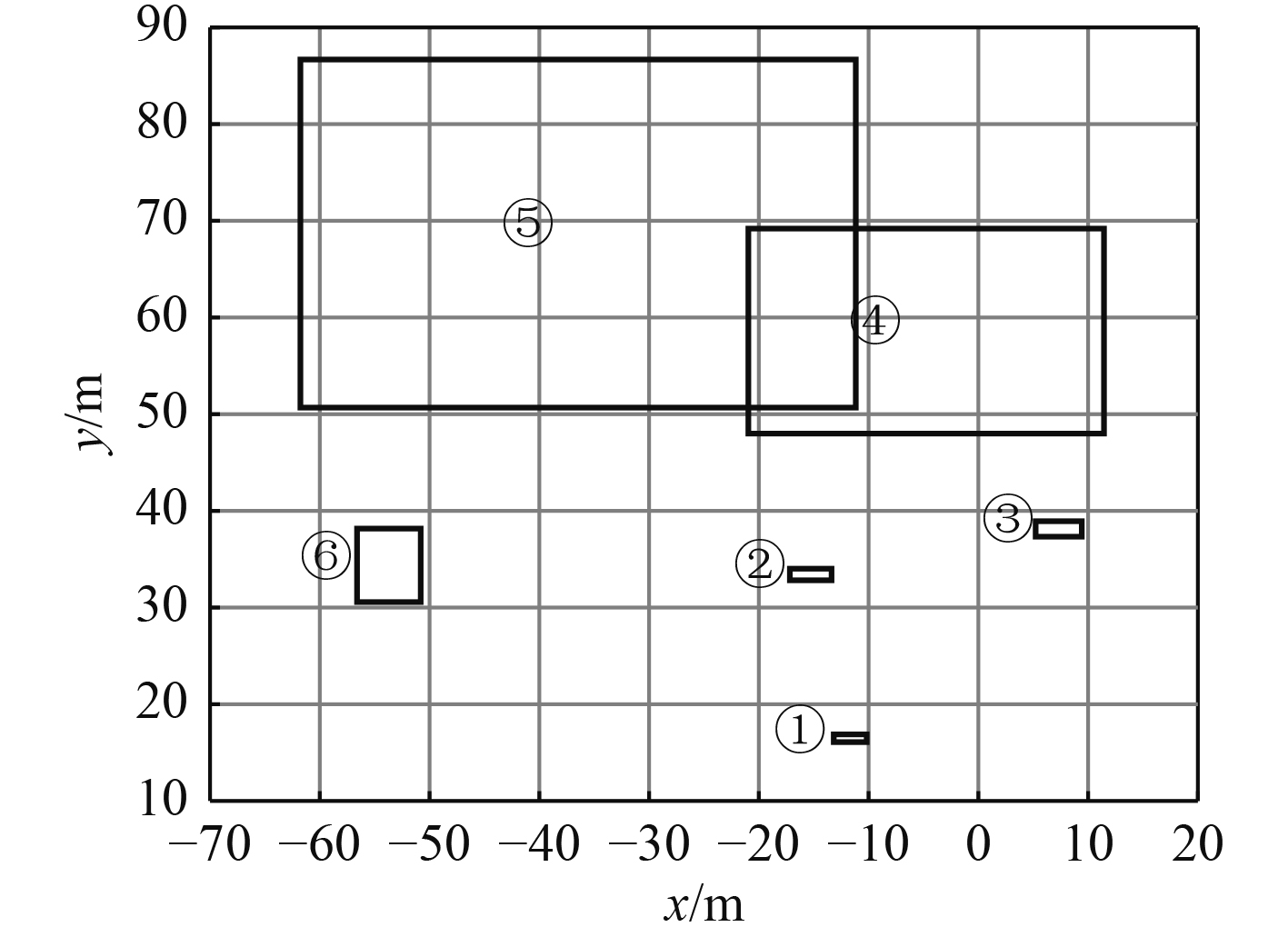
航行第80 s时，图6为毫米波雷达探测得到的全部目标，图7为经跟踪算法滤除无效目标后得到的有效目标。

可以发现，图6与图7中的①～⑥目标分别是相互对应的真实目标，⑦～⑨是虚假目标，由此看出提出的算法成功滤除了虚假目标。

本文算法与传统算法即改进之前的GNN算法试验统计数据如表1与表2所示。可以看出本文提出的雷达跟踪算法能够随着不断地迭代滤去大量虚警的干扰，更新每条航迹的生命状态，虽然有漏检的情况但仍能稳定的对毫米波雷达与激光雷达检测得到的目标进行跟踪，并且及时删除消失在探测范围内的目标，从而验证本文算法的有效性。通过与传统算法比较，可以发现传统算法由于关联正确率相对较低而将一些有效目标误滤除，导致检测到的有效目标较少并且在目标漏检时保持跟踪的能力较差，因此跟踪10 s以上的有效目标数较少。从跟踪得到的总的有效目标的数量来看，跟踪效果提高了25.87%。

在保持设置参数不变的情况下，采用传统的GNN算法进行对比，被测目标为前方50 m左右处的一个静止的渔船，本船朝向目标附近行驶。

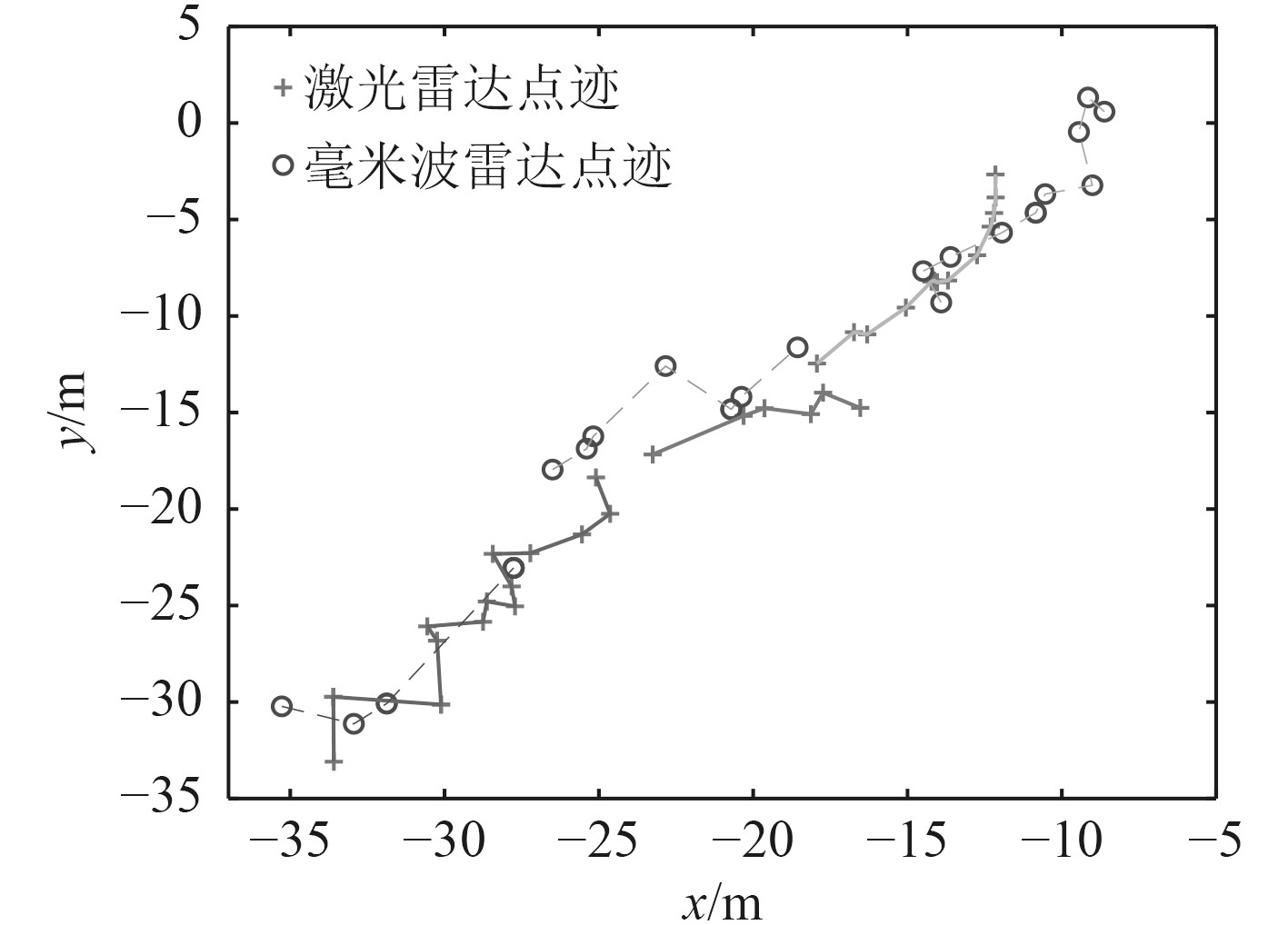
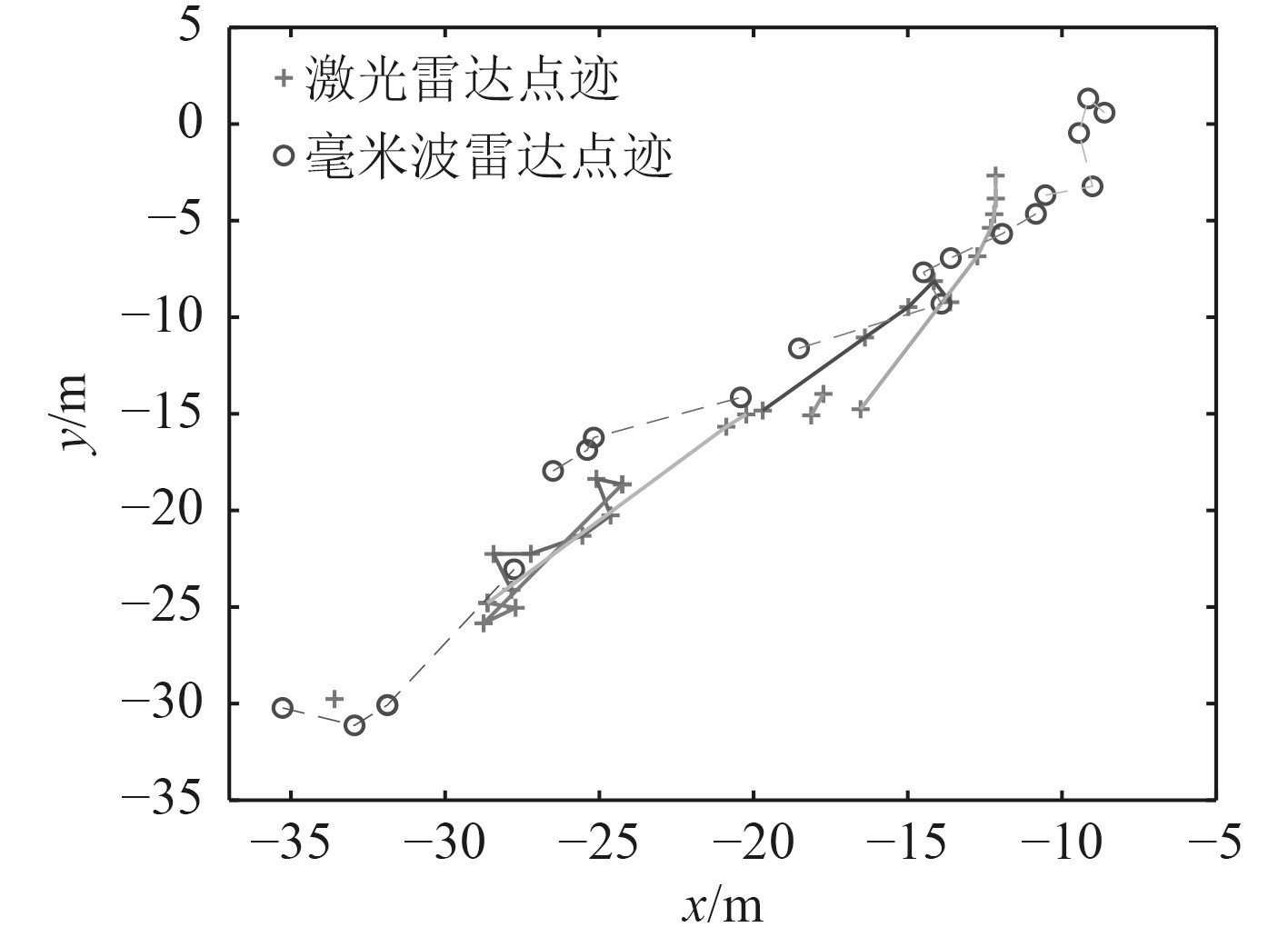
图8与图9显示了在不同算法下目标的运动轨迹。其中实线与虚线分别表示激光雷达与毫米波通过跟踪算法得到的目标的运动轨迹，临时航迹与丢失目标时目标的预测位置没有标注。目标的跟踪时间越长代表算法的跟踪正确率越高，目标的航迹数量越少代表算法应对虚警、漏检的能力越强，由于传感器有一定的测量误差并且目标具有一定的长度和宽度导致激光雷达与毫米波雷达返回的目标位置有所差异。由表3和表4可知，在整个跟踪过程中尽管2种算法对同一目标均产生多条航迹，但是通过对比可以发现，本文提出的算法通过正确的数据关联得到了更加连续、有效的航迹。

5 结　语

本文提出一种基于GNN的无人船双雷达目标跟踪算法，并通过安装有激光雷达与毫米波雷达的无人船在海上环境进行试验。针对传统GNN跟踪算法因虚警、漏检的影响易造成误关联的缺点，本文通过2次滤除无关目标，提高了数据关联的正确率，减少了特征阈值的依赖。实际检验和分析，验证了本文所提跟踪算法的有效性与优越性。

通过实验可以发现，激光雷达与毫米波雷达各有优势相互补充，在下一步的研究中可以采用分布式的航迹关联与航迹融合算法将2个雷达融合，从而为无人船避障提供更加可靠、准确、有效的目标信息。