随着世界范围内环境保护各项政策的不断出台,人类保护海洋环境的意识得到不断增强,因此全球造船以及航运界都十分重视船舶的节能减排问题。EEID的强制执行促使船舶设计利用先进的节能技术,使得船舶在设计和制造过程中达到预设的能效标准。VLCC船舶作为三大运输船舶之一,在航运过程中的能效相对较低。由于现代船舶的发展方向为大功率以及大型化,同时考虑到我国船舶的能效普遍较低,这使得我国船舶设计、生产以及运输业面临很大的挑战。本文以VLCC船舶为研究对象,对船舶在风浪中航行的速度和能效的优化方法进行研究,探索新型的船舶节能减排技术,这有利于船舶朝着低能耗方向发展。
1 风浪对VLCC船舶的影响 1.1 风浪对船舶阻力的影响船舶的水动力性能通常可以通过船模静水阻力、实船试航以及自航试验等进行验证评估,然而这些测试试验通常在没有风浪的海面上进行,但是船舶在海面上航行时,经常会遭到风、浪、流的干扰。
海面上的风会对船体产生力以及力矩,因此海面上的风载荷是船体结构负荷的重要因素之一。许多海难均是由海面上的风载荷导致的,因此从预防船舶事故、降低运营成本以及节能减排等方面来考虑,对船舶在海面上所受到的风载荷阻力进行精确求解十分重要。在对船舶进行风载荷分析时,因为船体上层建筑结构复杂,这使得基于理论分析的解算十分复杂,因此通常利用模型风洞实验对船舶的风载荷进行分析,并且分析结果可知,海面上的风速以及船舶上层建筑面积是影响船舶风载荷的主要因素。为了可以方便地研究船舶在海面上承受的风载荷,对船舶在航行过程中受到的力以及力矩进行无量纲化处理,同时引入纵向和横向风载荷系数、力矩系数,如下式:
| $ {C_X} = 2{F_X}\rho {A_T}{V^2}\text{,} $ | (1) |
| $ {C_Y} = 2{F_Y}\rho {A_L}{V^2}\text{,} $ | (2) |
| $ {C_N} = 2{N_W}{L_{OA}}{A_L}{V^2}。$ | (3) |
式中:V为海面上的风速。从某种程度上来讲,船舶的风载荷系数是船体上层结构复杂性的表现,对于VLCC船舶而言,在海面上航行过程中的风载荷系数趋近于一个常数。通过风洞实验可以得到船体的风载荷系数,在进行风洞实验的过程中,需要确保船模上层建筑的雷诺数和实船的上层建筑雷诺数相等,如式(4)所示,这样才可以实现风载系数从船模换算到实船上。
| $ {R_{es}} = \frac{{{V_s}{L_s}}}{\upsilon } = \frac{{{V_m}{L_m}}}{\upsilon } = {R_{em}}。$ | (4) |
波浪增阻是VLCC船舶在海面上航行过程中出现失速的重要原因之一,船舶波浪增阻对船舶航运的经济性以及节能减排有很大影响。船舶在海面上的波浪增阻由3部分力构成,一是由船舶自身的垂荡以及纵摇而导致的漂移力,并且船舶波浪增阻中大部分是漂移力,一般可以利用动量守恒和压力积分2种方法进行解算;二是入射波导致的绕射增阻,其计算公式如式(5)所示;三是船舶在纵摇和垂荡运动过程中受到的和阻尼力相等的阻力。
| $ {R_{AWR}} = \frac{{\rho g{\zeta _a}B{B_f}{\alpha _d}\left( {1 + {C_u}{F_n}} \right)}}{2}\text{。} $ | (5) |
船舶在风浪中航行出现失速现象,除了由于船体在风浪中受到的阻力变大之外,船舶动力系统在风浪中的工作环境出现变化也是原因之一。船舶动力系统工作环境的改变降低了船舶螺旋桨的工作效率,螺旋桨工作效率的降低又进一步降低了螺旋桨自身的推力。螺旋桨推力的降低对船舶失速的影响比风浪载荷要小得多。在小风浪情况下,螺旋桨敞水效率的降低是船舶失速的主要原因;在恶劣的风浪中,螺旋桨露出水面造成飞车现象是船舶失速最重要的原因。
作为船舶动力系统重要的设备之一,螺旋桨在不同环境下性能的变化对船舶动力系统的工作效率有很大影响,尤其是在风浪中会使敞水效率降低。螺旋桨的推力系数、转矩系数、进速系数以及效率的计算方法分别如下式:
| $ {K_T} = \frac{T}{{\rho {n^2}{D^4}}}\text{,} $ | (6) |
| $ {K_Q} = \frac{Q}{{\rho {n_2}{D^5}}}\text{,} $ | (7) |
| $ J = \frac{{{V_A}}}{{nD}}\text{,} $ | (8) |
| $ {\eta _0} = \frac{{{K_T}}}{{{K_Q}}}\frac{J}{{2{\text{π}}}}\text{。} $ | (9) |
式中:T为螺旋桨的推力;Q为螺旋桨的扭矩;VA为螺旋桨的进速。
船舶在风浪中航行遇到的增阻以及螺旋桨工作效率的降低是船舶失速最主要的2个原因,因此,船舶在海面上航行过程中对船舶的增阻以及螺旋桨工作效率的实时精确求解,是船舶安全航行的重要保障。船舶在海面上航行过程中的失速程度可以通过失速系数来描述,计算公式为:
| $ {f_w} = \frac{{{V_{wa}}}}{{{V_s}}}\text{。} $ | (10) |
在对船舶失速系数解算之前,需要对船舶在不同航行速度情况下的风载荷增阻以及波浪载荷增阻进行解算,接着以静水功率为基础对船舶在波浪载荷中的功率曲线进行解算,船舶在风浪中总阻力的计算方式为:
| $ {R_T} = R + {R_{{\rm{wind}}}} + {R_{{\rm{wave}}}}\text{。} $ | (11) |
式中:R为船舶在静水中的阻力;Rwind为船舶受到的风载荷增阻;Rwave为船舶受到的波浪载荷增阻。为了能够解算船舶在风浪中航行时的推进效率,则需要对船舶螺旋桨总的效率进行计算,计算方式为:
| $ {\eta _D} = {\eta _0} \cdot {\eta _R} \cdot {\eta _H}\text{。} $ | (12) |
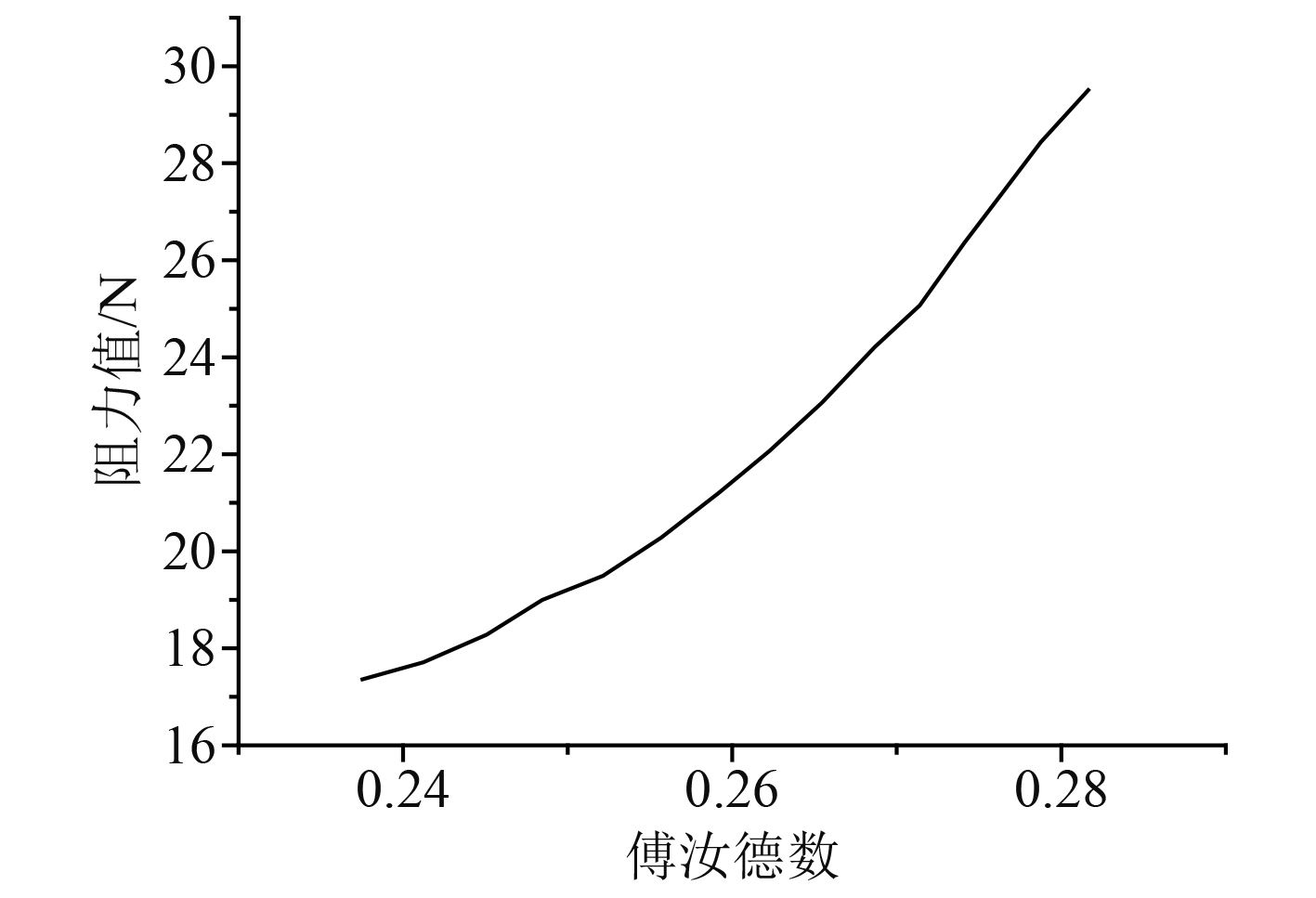
式中:η0为螺旋桨的敞水效率;ηR为螺旋桨旋转效率;ηH为船身效率。VLCC船舶阻力和傅汝德数之间的关系如图1所示。
|
图 1 VLCC船舶阻力随傅汝德数的变化曲线 Fig. 1 Curve of VLCC ship resistance changing with Froude number |
船舶在风浪中航行的时候需要克服阻力做功,其计算如式(13)所示。如果忽略海面上的风浪对船舶主机推进效率的影响,即船舶的主机推进效率和静水中的一样,则船舶主机功率可以通过式(14)来计算,单位时间内船舶主机的燃油消耗量的计算公式如式(15)所示。
| $ {P_{E - total}} = {R_{ts}} \cdot {V_s} = {P_E} + \Delta {P_E}\text{,} $ | (13) |
| $ {P_S} = \left( {{P_E} + \Delta {P_E}} \right)/{\eta _D}\text{,} $ | (14) |
| $ {F_h} = SFOC \cdot {P_S} \cdot {10^{ - 6}}\text{。} $ | (15) |
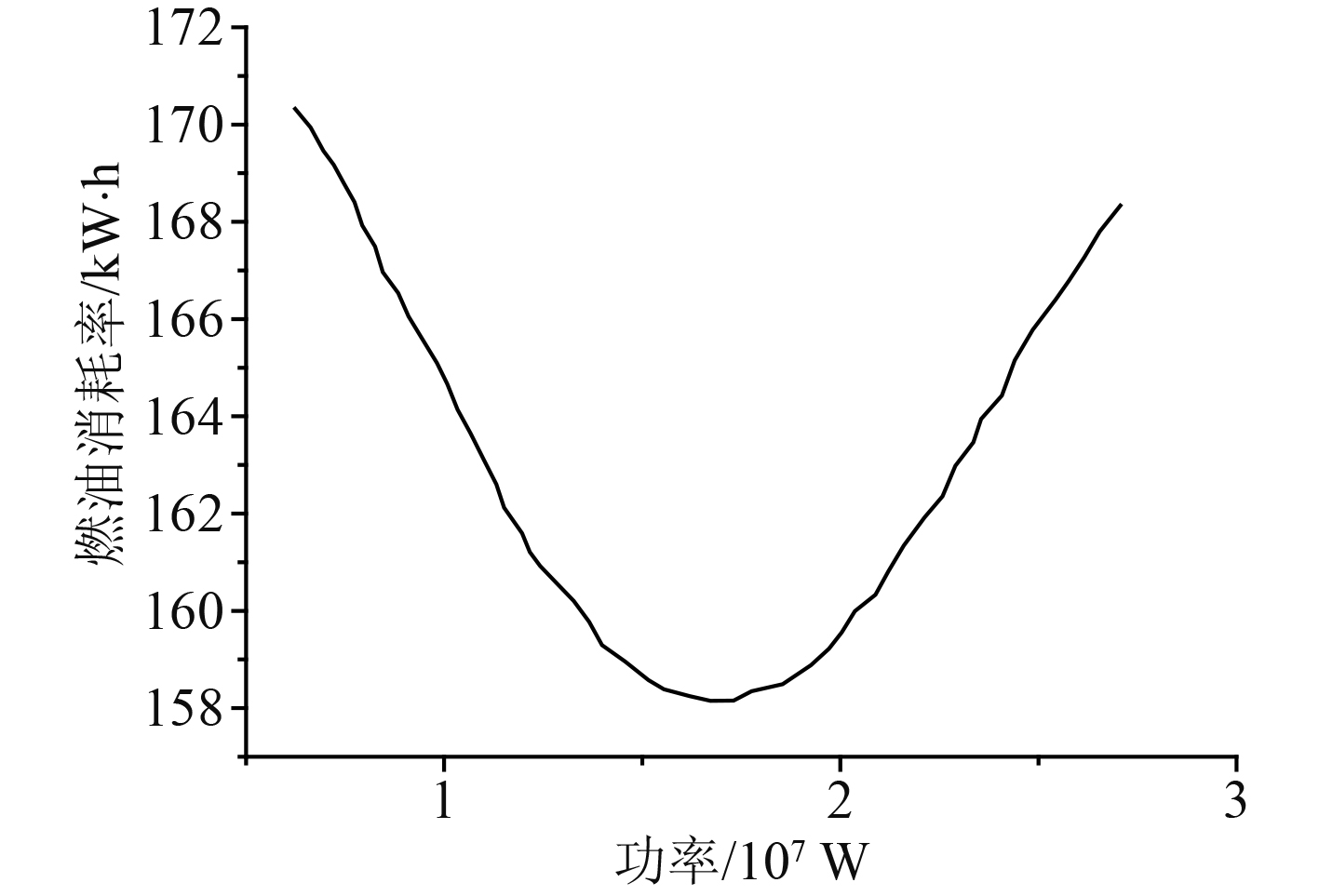
式中,SFOC为船舶主机的燃油消耗率,通过式(16)可以拟合出船舶主机功率和燃油消耗率之间的曲线关系,如图2所示。
|
图 2 燃油消耗率随主机功率变化 Fig. 2 Fuel consumption rate varies with engine power |
| $ SFOC = - 4.7{P^4} + 31.1{P^3} - 61.7{P^2} + 33.1P + 166.8\text{。} $ | (16) |
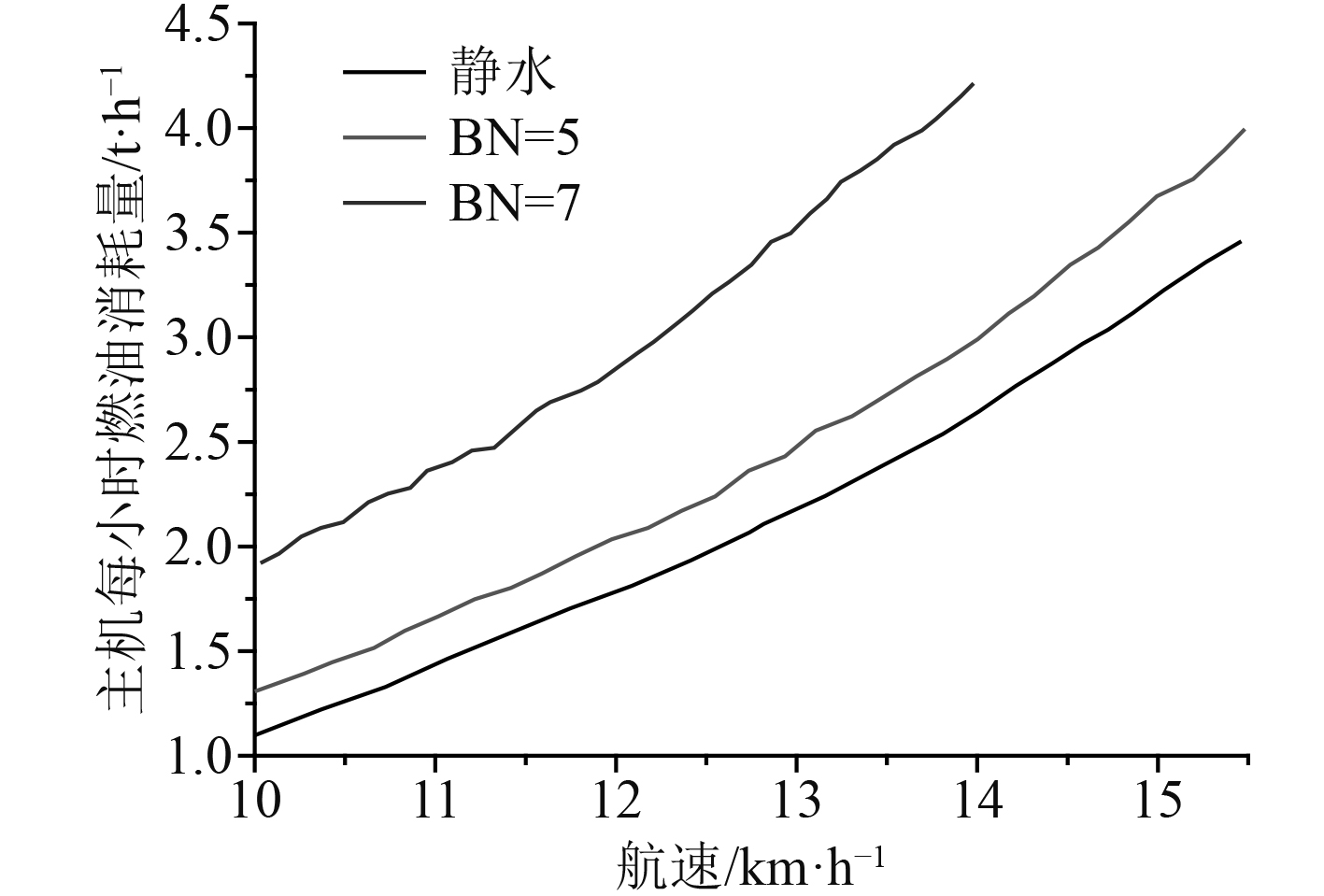
图3为在不同蒲氏风级下船舶主机在单位时间内消耗燃油量随船舶航行速度的变化情况。可以看出,在相同蒲氏风级下,船舶主机在单位时间内消耗的燃油量随着航速的增加而增加,同时航速不变的情况下,船舶主机在单位时间内消耗的燃油量随着风速的增加而增加,因此船舶在风浪中航行,适当降低航速有利于减少燃油消耗。解算出船舶主机在单位时间内的燃油消耗量之后,则可以根据船舶具体的航行时间获得船舶在航行过程中总的燃油消耗量,其计算公式如下:
|
图 3 在不同蒲氏风级下主机每小时燃油消耗量随速度变化的曲线 Fig. 3 Curve of fuel consumption per hour of main engine changing with speed under different Purkinje wind levels |
| $ Q = \sum\limits_{i = 1}^N {{F_{{h_i}}} \cdot {T_i}} \text{。} $ | (17) |
可以看出,船舶在整个航行过程中燃油消耗量和主机的功率、燃油消耗率以及航行时间相关。为了降低船舶在整个航运过程中总的燃油消耗,则必须降低对船舶主机在单位时间内燃油消耗量。从式(15)可以看出,船舶主机在单位时间内的燃油消耗率和船舶主机的功率以及航速相关。式(17)中船舶的航行时间Ti是船舶在每个航段上的航程和航行速度的比值,计算公式如式(18)所示。船舶采用高速航行,虽然可以缩短航行时间,但是会增加船舶燃油的消耗量;船舶在低速下航行的状态下,减少燃油消耗的同时会增加船舶航运总时间。因此可以采取船舶分段航速优化的方法,在确保按期到达的条件下,在船舶航行过程中不断地调整船舶航行的速度,最终使得船舶在整个航运过程中的燃油消耗量最小。
| $ {T_i} = \frac{{{S_i}}}{{{V_i}}}\text{。} $ | (18) |
船舶分段航速优化过程,是对船舶在航行过程中每一段的航行速度进行优化调整,使得船舶在航行全过程中船舶主机的耗油量最小。船舶的燃油消耗量在整个航运过程中最小,并不是要求船舶在每个航行阶段都燃油量最小,而是通过不断地迭代运算对船舶的航行速度进行实时调整,最终使得船舶主机在整个航行过程中的耗油量最小。
为了保证船舶在海面上航行过程中的安全性,船舶主机的实际转速要低于船舶主机的额定转速,同时船舶主机的实际转速需要高于船舶主机产生喘振现象时候的转速,公式为:
| $ {n_{\min }} < {n_e} < {n_{\max }}\text{。} $ | (19) |
在对船舶的分段航行速度进行优化调整的过程中,优化之后的船舶总航程需要和原航程一致,除此之外,船舶优化之后航行需要的总时间不能比船舶原始预设的航行时间大,优化之后的时间比原始预设时间大的话,会耽误船舶航行任务的执行,因此在对船舶的分段航速进行优化的过程中会使得优化之后航行所需的时间不大于船舶预设的航行时间,公式为:
| $ \left\{ \begin{aligned} &{\displaystyle\sum\limits_{i = 1}^n {{S_i} = {S_0}} },\\ &{\displaystyle\sum\limits_{i = 1}^n {\frac{{{S_i}}}{{{V_{Si}}}} \leqslant {T_0}} } 。\end{aligned} \right. $ | (20) |
式中:n为船舶在航行过程中的分段数;Si为船舶每个航段上航行的距离。通常情况下,船舶在航行过程中会采用降低船舶航行速度这一方法来降低船舶的燃油消耗量。
| $ {V_{Si}} \leqslant {V_{S\max }}\text{。} $ | (21) |
式中:VSmax为船舶的营运航行速度。根据上述分析,可以得到船舶在航行过程中最优的分段航行速度优化目标的计算方法,如式(22)所示,约束条件如式(23)所示。
| $ f = \min Q = \min \sum\limits_{i = 1}^n {\left( {{t_i} \cdot {q_i}} \right)} \text{,} $ | (22) |
| $ \left\{ {\begin{array}{*{20}{l}} {\displaystyle\sum\limits_{i = 1}^n {{S_i} = {S_0}} },\\ {\displaystyle\sum\limits_{i = 1}^n {\frac{{{S_i}}}{{{V_{Si}}}} \leqslant {T_0}} },\\ {{n_{e\min }} \leqslant {n_{ei}} \leqslant {n_{\max }}},{{V_{si}} \leqslant {V_{sma}}} 。\end{array}} \right. $ | (23) |

|
图 4 船舶分段航速优化过程 Fig. 4 Optimization process of ship sectional speed |
为了提升船舶在航行过程中的能效,并降低船舶释放的温室气体总量,全球船舶运输业提出了许多措施以及方法,其中最重要的是船舶能效设计指数,在实现船舶能效设计指标的过程中,需要考虑船舶大型化以及低速化的发展趋势,同时需要分析降低船舶主机功率获得的能效收益和船舶机动性下降带来的安全等问题。本文对VLCC船舶在波浪中航行的速度以及能效进行优化分析,这有助于船舶节能减排技术的发展。
| [1] |
张耀明, 刘和炜, 谌志新. 海带采收船线型优化及水动力特性研究[J]. 船舶工程, 2020, 42(S2): 150-154. ZHANG Yao-ming, LIU He-wei, CHEN Zhi-xin. Study on optimization of kelp harversting ship and hydrodynamic characteristics[J]. Ship Engineering, 2020, 42(S2): 150-154. DOI:10.13788/j.cnki.cbgc.2020.S2.029 |
| [2] |
熊云峰, 陈章兰, 毛筱菲. 船舶期望航速百分数的计算与分析[J]. 船舶工程, 2008, 30(5): 12-15. DOI:10.13788/j.cnki.cbgc.2008.05.005 |
| [3] |
闵德权, 江可鉴, 刘茹. 基于北极航线通航期冰情的多种船舶航速优化[J]. 重庆交通大学学报, 2022, 41(9): 53-60. MIN De-quan, JIANG Ke-jian, LIU Ru. Speed optimization of multiple ships based on ice condition of arctic route during navigation period[J]. Journal of Chongqing Jiaotong University, 2022, 41(9): 53-60. |
| [4] |
张宏森, 魏钰博, 刘万宇, 等. 一种计及海上风浪因素的船舶定航线航速优化方法研究[J]. 无线电工程, 2022, 52(5): 724-730. |
| [5] |
赵科, 张焱飞, 文逸彦. 一种融合遗传算法和二分法的船舶航速优化方法[J]. 上海船舶运输科学研究所学报, 2021, 44(4): 1-5. DOI:10.3969/j.issn.1674-5949.2021.04.001 |
| [6] |
袁裕鹏, 王康豫, 尹奇志, 等. 船舶航速优化综述[J]. 交通运输工程学报, 2020, 20(6): 18-34. DOI:10.19818/j.cnki.1671-1637.2020.06.002 |
| [7] |
孙超, 张均东, 刘超. 基于航速与实时能效综合目标的船舶主机转速优化[J]. 大连海事大学学报, 2020, 46(3): 60-67. DOI:10.16411/j.cnki.issn1006-7736.2020.03.007 |
| [8] |
李铮, 潘晓萌. 船舶航速优化算法研究[J]. 船舶科学技术, 2016, 38(12): 7-9. LI Zheng, PAN Xiao-meng. Research on optimization algorithm of ship speed[J]. Ship Science and Technology, 2016, 38(12): 7-9. |
| [9] |
张进峰, 杨涛宁, 马伟皓. 基于多目标粒子群算法的船舶航速优化[J]. 系统仿真学报, 2019, 31(4): 787-794. ZHANG Jin-feng, YANG Tao-ning, MA Wei-hao. Ship speed optimization based on multi-objective particle swarm algorithm[J]. Journal of System Simulation, 2019, 31(4): 787-794. DOI:10.16182/j.issn1004731x.joss.17-0111 |
 2022, Vol. 44
2022, Vol. 44
