2. 深海技术科学太湖实验室,江苏 无锡 214082;
3. 中船重工(上海)节能技术发展有限公司,上海 200011
2. Taihu Laboratory, Wuxi 214082, China;
3. CSIC Shanghai Marine Energy Saving Technology Development Co. Ltd., Shanghai 200011, China
目前,大型散货船的市场需求较为强劲,为了设计出经济性能优良,节能效果显著的散货船,在进行船舶设计时要兼顾船型、螺旋桨、舵以及新型节能装置等的互相协调与匹配。船舶节能措施之一就是:优化船、机、桨、舵的最佳组合匹配,提高推进效率[1]。其中,舵与螺旋桨均位于船后,距离较近,相互之间存在着流场干扰,如果能合理利用这种干扰,尽量回收尾流场的能量,则能提高螺旋桨的推进效率[2]。本文从提高船舶节能效果的角度出发,对某85 000 DWT散货船的舵进行优化设计并对优化过程中影响舵性能的各种因素比较分析,从中获得影响舵设计较为关键的某些因素,可为同类型半悬挂舵舵叶的节能优化设计提供参考。
1 85 000 DWT散货船简介本船为单螺旋桨、低速柴油机推进的远洋航行单舷侧散货船,适用于装载散货,包括煤、矿石、谷物等。船舶主要参数如表1所示。
|
|
表 1 船舶主要参数 Tab.1 Main parameters of the ship |
选用半悬挂舵系统。半悬挂舵的挂舵臂上端伸入船体,下端接近舵的压力中心,受力情况良好,强度高,可减少尾部振动,且挂舵臂相当于固定尾鳍,可改善航向稳定性,又能对螺旋桨起整流作用,从而提高推进效率[3] 。
船舵的设计以英国劳氏船级社《海船入级规范》[4]为依据,舵系统材料的选取依照《材料与焊接规范》[5]进行。
2.2 节能舵初始输入条件船体尾部为提高节能效果加装了前置预旋导轮,而为了与船体尾部的节能系统相匹配,进一步提升船舶总体节能效果,需要对舵叶剖面型值进行优化设计。出于充分节能的考虑,常规舵的设计应在强度条件允许的情况下,选用最小的厚度比[6]。但是,较小的舵叶厚度比会使舵杆、舵销等构件尺寸受到限制,且在构件尺寸相同的情况下,舵叶剖面模数较低,对强度产生不利影响[7]。因此,在设计中,需要兼顾节能和强度的要求,进行多轮分析和论证。
首先,选用与本船接近的某85 000 DWT散货船和某82 000 DWT散货船作为母型船。在参考母型舵侧投影尺寸和舵面积比的基础上,根据船尾线型以及主尺度对本船舵的侧投影尺寸和形状进行设计。选用高强度钢作为舵叶材料,这样有利于增加同等舵叶剖面型值厚度比下的舵叶剖面强度。某85 000 DWT散货船的舵型剖面为NACA0020,某82 000 DWT散货船的舵型剖面为NACA0018,根据厚度比小的舵型剖面节能效果较好的原则,选用NACA0018作为舵叶剖面型值的初始输入条件。
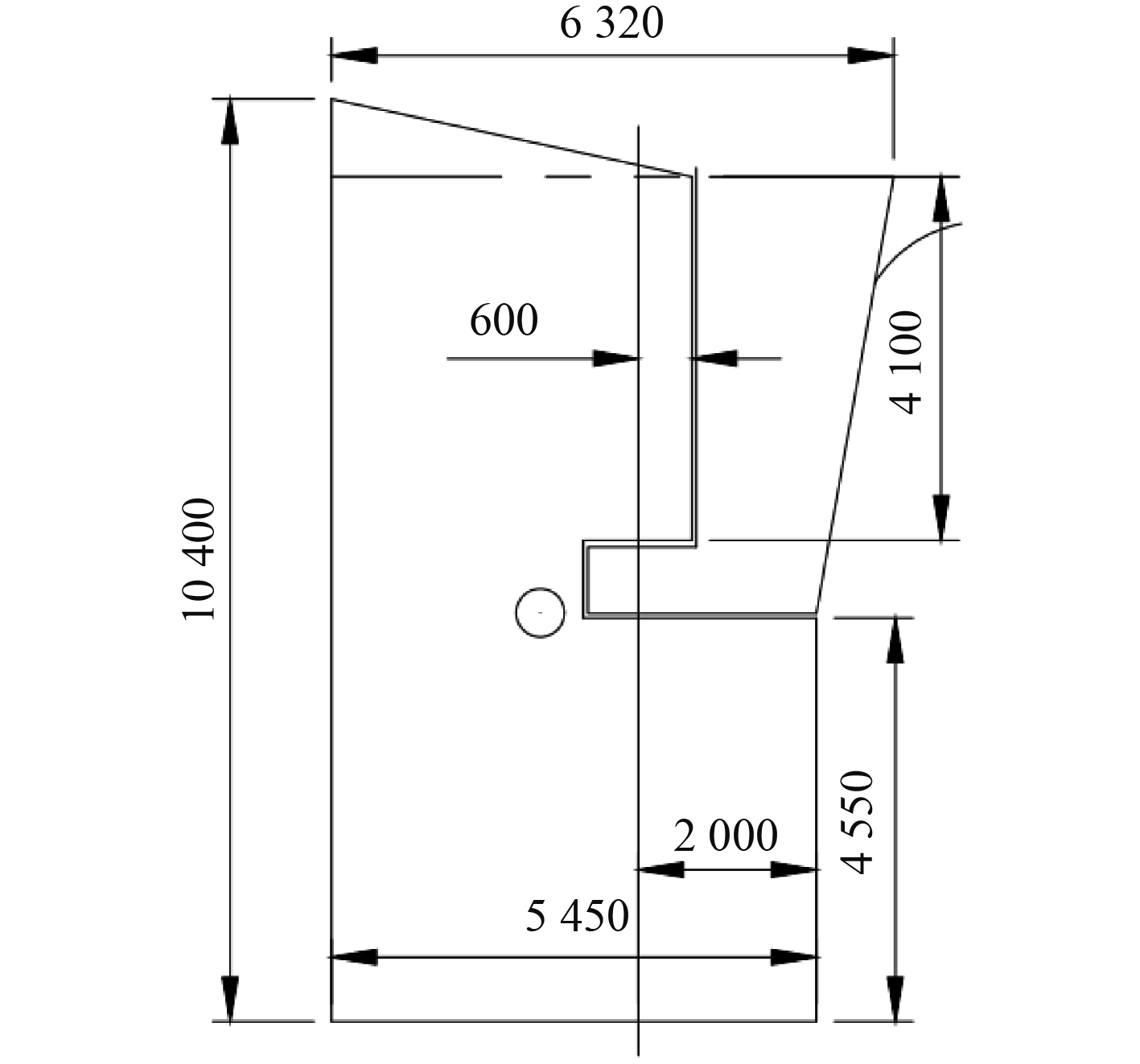
舵叶参数与母型船舵叶参数的对比如表2所示,舵叶的侧投影尺寸如图1所示。
|
|
表 2 本船舵叶参数与母型船舵叶参数对比 Tab.2 Comparison of the parameters of the rudder blade of this ship and the rudder blade of the parent ship |
|
图 1 舵叶侧投影 Fig. 1 Side projection of the rudder blade |
根据图1的舵叶侧投影对舵系尺寸和位置进行初步的计算和评估。在计算时,初步选用常用的锻钢材料(ReH=240N/mm2)对舵杆、舵销进行屈服强度的校核,后续优化过程中如果存在因为舵杆直径过大而导致舵叶型值优化受到影响的情况,可以根据需要再完善舵杆材料的选型。
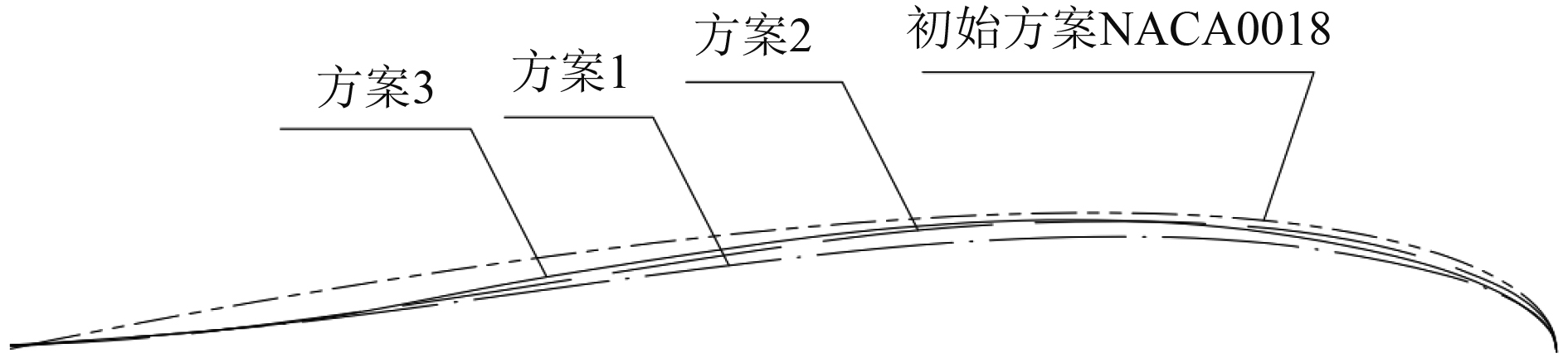
以NACA0018剖面型值为基础,进行剖面型值和舵总体设计的迭代优化,共进行了3种方案的优化与评估。3种方案的底板剖面型线如图2所示。可以看出,初始方案NACA0018的厚度比最大,方案1的厚度比最小。方案2和方案3的厚度比接近,区别在于方案2较方案3的首部更为饱满,而尾部更为瘦削。优化后的3个方案较初始舵型NACA0018,在尾部明显呈凹翼型。
|
图 2 不同方案底板舵叶剖面型线比较 Fig. 2 Comparison of profile lines of rudder blades with different schemes |
对初始NACA0018剖面进行第一轮优化设计,得到方案1,并对舵系的合理性与安全性进行了规范校核与评估。
1)校核该方案下舵叶剖面型值与舵杆、舵销的匹配是否合理
经计算,舵杆直径和舵销直径接近,但舵销直径要略大一些,二者选取相同的实际直径和锥形部分尺寸。由于舵杆处有挂舵臂,其剖面位于舵叶的偏尾部,该处舵叶剖面厚度较小,而舵销所在位置接近舵叶剖面的厚度最大处;二者相比,舵杆处较不容易满足规范的要求,因此在类似的半悬挂舵设计中,主要校核舵杆处是否满足规范要求即可。经计算该舵系舵杆处的承座直径约为舵杆锥体平均直径的1.64倍,舵销处的承座直径约为舵销锥体平均直径的1.85倍,均符合规范[4]舵杆、舵销承座铸钢件的直径也即该处的舵叶型值宽度应不小于舵杆和舵销锥形部分平均直径的1.5倍的要求。说明该剖面与舵杆和舵销的尺寸是相适应的。
2)校核该方案下舵叶剖面结构与铸钢件连接处的强度
舵叶内有2个分别与舵杆和与舵销相连的铸钢件。规范计算要求最小剖面模数为:
3)校核该方案下舵叶结构强度
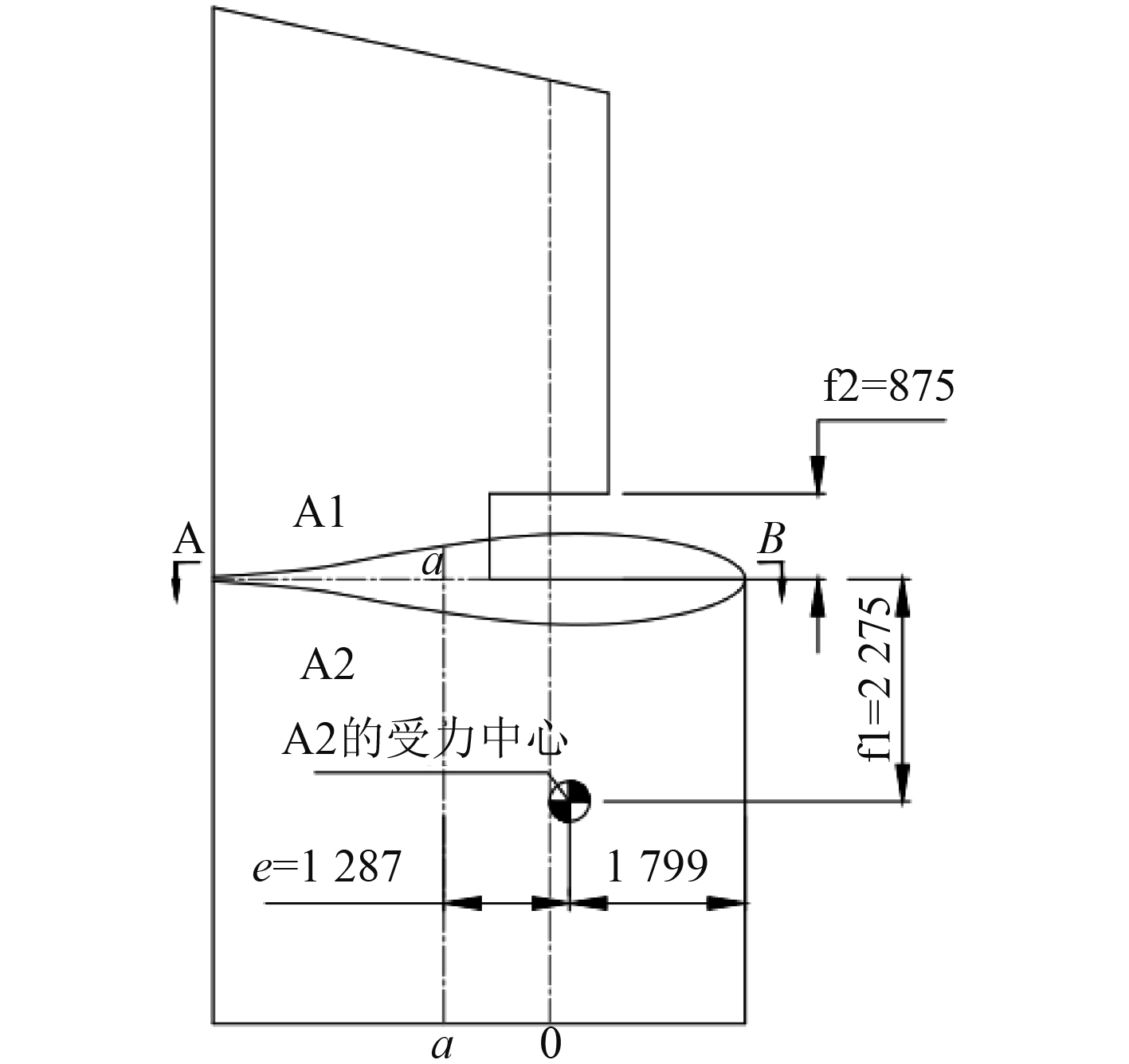
整个舵系在缺口处受到的弯矩和剪力最大,即如图3所示的A-B剖面,且舵叶缺口处的舵叶均偏尾部,剖面厚度相对较小,因此该处结构的应力最易超出规范要求的许用应力。根据规范,校核该剖面时应选用a-a附近的剖面,a-a为缺口处有效截面的中心线,位于缺口后方。
首先,校核弯曲应力,弯曲应力的计算公式如下式:
| $ {\sigma }_{b}=\frac{{M}_{R}}{{W}_{x}},$ | (1) |
| $ {\sigma }_{b}=135.36\;\text{N/}{\text{mm}}^{\text{2}} 。$ |
式中:MR为A-B剖面处的弯矩,3507200066 N·mm;Wx为校核剖面处的剖面模数,25909474 mm3。
|
图 3 舵叶强度校核最危险剖面示意 Fig. 3 Schematic diagram of the most dangerous section of rudder blade strength check |
A-B剖面处的许用弯曲应力如下式:
| $ {\sigma }_{be}=\frac{75}{k} ,$ | (2) |
| $ {\sigma }_{be}=102.2\;{\rm{N}}/{{\rm{mm}}}^{2}。$ |
式中:k为舵叶材料系数,k=0.7。
据计算结果,该处弯曲应力大于许用应力。为此,对舵叶板进行了加厚处理,但加厚后,发现对剖面模数的影响较小,依然很难满足许用应力的要求,而且板厚过大时,舵叶尾部的空间过于狭窄,不利于舵叶的焊接和隔板的布置。
其次,校核剪切应力,剪切应力的计算公式如下式:
| $ \tau =\frac{{C}_{R2}}{{A}^{\text{'}}},$ | (3) |
| $ \tau =5.45\;\text{N/}{\text{mm}}^{\text{2}}。$ |
式中:
A-B剖面处的许用剪切应力如下式:
| $ \tau =\frac{50}{k},$ | (4) |
| $ \tau =68.13\;{\rm{N}}/{{\rm{mm}}}^{2}。$ |
该剖面处的剪切应力小于许用应力,满足了规范要求。
校核扭曲应力,扭曲应力的计算公式如下式:
| $ {\tau }_{t}=\frac{{M}_{t}}{2lht},$ | (5) |
| $ {\tau }_{t}=44.78\;\text{N/}{\text{mm}}^{\text{2}}。$ |
式中:Mt为校核剖面处的舵叶扭矩,1 439 915 984 N·mm;l为校核剖面处2个垂直隔板的水平距离,690 mm;h为校核剖面处2个舵叶板的中心距离,466 mm;t为校核剖面处舵叶旁板厚度,50 mm。
A-B剖面处的许用扭曲应力如下式:
| $ {\tau }_{t}=\frac{50}{k},$ | (6) |
| $ {\tau }_{t}=68.13\;{\rm{N}}/{{\rm{mm}}}^{2}。$ |
该剖面处的扭曲应力小于许用应力,满足了规范要求。
最后,校核等效应力,等效应力的计算公式如下式:
| $ {\sigma }_{v1}=\sqrt{{{\sigma }_{b}}^{2}+3{\tau }^{2}},$ | (7) |
| $ {\sigma }_{v1}=135.69\;\text{N/}{\text{mm}}^{\text{2}}。$ |
A-B剖面处的许用等效应力如下式:
| $ {\sigma }_{v}=\frac{100}{k},$ | (8) |
| $ {\sigma }_{v}=136.26\;{\rm{N}}/{{\rm{mm}}}^{2}。$ |
综上,该剖面处的扭曲应力与剪切应力均小于许用应力,满足强度要求;等效应力也基本满足强度要求;弯曲应力则大于许用应力,不满足强度要求。
从以上舵叶强度的校核过程可以看出,最容易超出许用应力的是弯曲应力,而剪切应力及扭曲应力均未超过许用应力,因此多舵型方案选型时初期可以不用对剪切应力及扭曲应力进行强度校核。
根据对方案1的校核与评估结果可见,舵叶缺口处的弯曲应力是舵叶优化过程中最难符合规范要求的因素,因此在后续的优化方案中,主要对弯曲应力进行强度校核。
2.4 方案2在方案1的基础上增加舵叶剖面厚度比,得到方案2。
方案2有效剖面模数为:Wx=30795163 mm3;
所受弯曲应力为:
弯曲应力依然大于许用应力,不满足要求。需要进一步完善和优化。
2.5 方案3根据方案1和方案2的结果,为了满足弯曲许用应力的要求,增加了缺口后方有效剖面部分的厚度。为了不过大增加整个剖面的厚度,适当减小其余部分剖面的厚度,并进行型线光顺,得到了方案3。
方案3有效剖面的剖面模数为:Wx=34627017 mm3;
所受弯曲应力为:
弯曲应力小于许用应力,满足了规范的要求。
方案3舵剖面优化后,经CFD计算,螺旋桨收到功率降低0.33%,根据大量已有实船使用经验预计可节能0.5%左右,优化结果如表3所示。
|
|
表 3 舵叶剖面优化方案性能对比结果[8] Tab.3 Performance comparison results of rudder blade profile optimization schemes |
根据船舶模型试验,对前置预旋导轮、船型、螺旋桨、舵进行一体化优化后的船舶总体节能效果约为3.5%。
对方案3的舵叶剖面进行进一步的计算和校核,该方案舵叶剖面的厚度满足舵杆、舵销的安装要求以及舵叶与铸钢件连接处的强度要求。
舵整体的性能都较母型船有所提升。
1)增大舵叶面积,对船的回转性和航向稳定性均有益[8](见表2),本船的舵叶面积较同等载重量的某85 000 DWT散货船略大,操纵性也会略好。
2)由于减薄了舵线型和增加了材料屈服强度,舵叶实现了轻量化设计。
3)与母型船NACA0018舵叶剖面相比,由于对舵叶剖面进行了优化,可取得预计0.5%的舵叶节能效果和3.5%的船舶总体节能效果。
3 结 语通过对半悬挂舵评估的分析,可以得出如下结论:
1)下舵杆与舵销直径的规范计算值基本一致,但是由于下舵杆处舵叶剖面的厚度通常比舵销处小,该处舵叶厚度更难满足规范要求,因此在优化过程中,可以首先校核舵杆处的舵叶厚度,以减少工作量。
2)舵叶缺口处的结构为最危险剖面,需要重点校核该处的应力,该处的弯曲应力最难满足许用应力的要求。同样,可以先只校核该处结构的弯曲应力。
3)舵叶缺口处的弯曲应力不满足许用应力要求时,舵叶与舵杆、舵销连接处的应力仍然有足够的安全余量,因此,在初步的校核中,在该连接处的强度校核也可以暂时不予考虑。
4)在舵叶节能优化的过程中,尽量减薄舵杆处的舵叶厚度,同时增加缺口后附近的舵叶厚度,也就意味舵叶剖面在舵杆处和缺口后之间的过渡要平缓,到了尾端再进行较大幅度的减少,这样可最大限度提高舵叶的节能效果。
| [1] |
何苗. 一体化节能推进装置的构型设计及水动力性能预报[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [2] |
张旭婷. 船舶桨舵系统节能效果分析 [D]. 哈尔滨: 哈尔滨工程大学, 2014.
|
| [3] |
张瑞. NACA半悬挂舵舵叶流场数值模拟及舵装置辅助设计[D], 武汉: 武汉理工大学, 2009.
|
| [4] |
Lloyd’s Register. Rules and regulations for the classification of naval ships[S], 2013.
|
| [5] |
中国船级社. 材料与焊接规范[M]. 北京: 人民交通出版社, 2018.
|
| [6] |
黎峰, 胡红斌, 李邦华, 等. 高性能舵的发展及技术现状[J]. 中国舰船研究, 2020, 15(3): (61-74). |
| [7] |
黎峰, 孙高鹏, 林兆东. “绿色海豚”38000DWT散货船舵系设计[J]. 船舶设计通讯, 2016, 145(21-28).
|
| [8] |
张继静. 高速船舵优化及操纵性研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
 2022, Vol. 44
2022, Vol. 44
