2. 中国人民解放军91604部队,山东 烟台 265700
2. No. 91604 Unit of PLA, Yantai 265700, China
声学覆盖层作为吸声材料敷设于水下航行器表面以吸收敌方主动声呐发出的探测声波,同时降低自辐射噪声[1],增强其声隐身性能和提高作战效能。目前针对出现的几种空腔型覆盖层,例如圆柱或圆锥形空腔覆盖层[2-4]、组合空腔覆盖层[5]等,主要通过覆盖层的隔振作用提高对于中高频声波的吸声降噪性能,但其低频抑制及隔振能力仍很微弱,难以起到有效的吸声性能,而局域共振型薄膜材料[6-7]的出现为达到这一目的提供了新的研究方案。受质量作用定律的限制,单一结构的吸声覆盖层难以控制低频声波,开发具有良好低频吸声性能的声学覆盖层对于提高潜艇的声隐身性能具有重大意义。
在工程设计中,研究问题的最优解就是在众多可行方案中选出最合理的一种。常用的优化方法有遗传算法[8]、启发式算法[9]、模拟退火法[10]等。近年来,赵宏刚等[11]采用遗传算法对含不同柱形空腔尺寸的橡胶层在1.5~10 kHz频段上的吸声特性进行优化,获得了较好的宽频吸声效果。余依伦等[12]利用多种群遗传算法对消声涂层进行了1~14 kHz频带内的多参数优化设计研究,结果表明优化后的吸声系数得到了明显提高。陈竞超等[13]采用启发式算法中的差分进化算法对单尺寸空腔与双尺寸空腔橡胶吸声层在钢背衬条件下的吸声性能进行了优化,结果表明,20 mm厚的双尺寸空腔结构可实现1~8 kHz频段内的良好吸声性能。马先超等[14]采用差分进化与有限元相结合的方法在1~10 kHz频段内对2种内嵌双周期双尺度空腔橡胶层的吸声性能进行了优化,这些优化研究多集中在1 kHz以上的中高频段,对于1 kHz以下的低频段研究较少,而研究水下吸声结构低频吸声性能的优化问题对于水下航行器声隐身性能更具重要意义。
多物理场仿真软件COMSOL Multiphysics中优化模块中的算法有2种,一种是梯度存在的算法,如SNOPT,MMA等,其特点是在导数存在的前提下,以前一次迭代结果为基础来进行对目标函数的下一次迭代;另一种非梯度算法,如Nelder-mead,BOBYQA,COBYLA等,其特点为无需计算控制变量的导数,直接根据不同控制变量所对应的不同空间位置上对优化目标进行计算,这就使得这类算法适用于目标函数不连续或者有误差的情况。作为启发式算法中的Nelder-mead单纯形法是基于比较的直接搜索方法,其鲁棒性强,无梯度,可用于解决多维空间中寻找优化目标最优解的问题[15]。因此,采用非梯度算法中的Nelder-mead单纯形法为本文的优化算法。
本文基于空腔型覆盖层和局域共振型薄膜材料的结构特点,为拓宽覆盖层的低频吸声频带,提高其低频吸声性能,建立将局域共振结构内嵌到空腔覆盖层中的复合结构。分别以复合结构的几何参数和材料参数为优化变量,以10~1 000 Hz频段内的吸声系数最大为优化目标,以Nelder-mead单纯形法为优化方法,对优化结果进行分析比较。为分析吸声性能提高的原因,将优化前后水域中的声压级以及结构动能密度进行对比分析。
1 局域共振型空腔覆盖层的有限元模型 1.1 有限元模型的建立考虑到局域共振结构中薄膜四周需要框架固定的特点,建立局域共振型空腔覆盖层,将薄膜材料内嵌到空腔中,使空腔周围的橡胶覆盖层给局域共振结构提供支撑作用,有限元模型沿对角线截面剖开的视图如图1所示。根据复合结构模型的空间几何特征,建模时只需建立声学覆盖层的一个单元,在整个模型的4个侧面设置Floquet周期性边界条件,以此来模拟复合结构在XY平面无限延展的结构。由于Floquet周期性边界,网格划分时在竖直边界面上采用两两对称的自由三角形网格,最大尺寸为2 mm;内部薄膜质量块结构设置3层扫掠的自由三角形网格,最大尺寸为2 mm;完美匹配层区域设置6层扫掠的自由三角形网格,最大尺寸为4 mm;艇壳部分采用4层扫掠的自由三角形网格,最大尺寸为3 mm;剩余部分为自由四面体网格,网格最大尺寸为3 mm。按照海水中声速为1500 m/s计算,研究频段内声波波长最短为0.75 m,因此所划网格均小于1/6波长,满足研究要求。

|
图 1 复合结构示意图 Fig. 1 Comparison of structure diagram |
复合结构的几何初始参数和材料初始参数如表1和表2所示,其中
|
|
表 1 局域共振型空腔覆盖层的几何初始参数(mm) Tab.1 Initial geometrical parameters of cavity overburden of local resonance type (mm) |
|
|
表 2 局域共振型空腔覆盖层的材料初始参数 Tab.2 Initial material parameters of local resonant cavity cladding |
背景压力场中设置入射声压为
| $ {I_{in}} = \frac{{{p_{in}}}}{{2{\rho _0}{c_0}}} ,$ | (1) |
式中,
| $ {W_{in}} = \mathop {\oiint} \limits_{S_1} {{I_{in}}} {\rm{d}}x{\rm{d}}y ,$ | (2) |
式中,
| $ {W_{out}} = \mathop {\oiint} \limits_{S_2} {{I_{out}}} {\rm{d}}x{\rm{d}}y 。$ | (3) |
式中:
| $ {W_{refl}} = {W_{in}} - \mathop {\oiint} \limits_{S_1} {{I_t}} {\rm{d}}x{\rm{d}}y ,$ | (4) |
式中,
| $ \alpha = \frac{{{W_{in}} - {W_{refl}} - {W_{out}}}}{{{W_{in}}}}。$ | (5) |
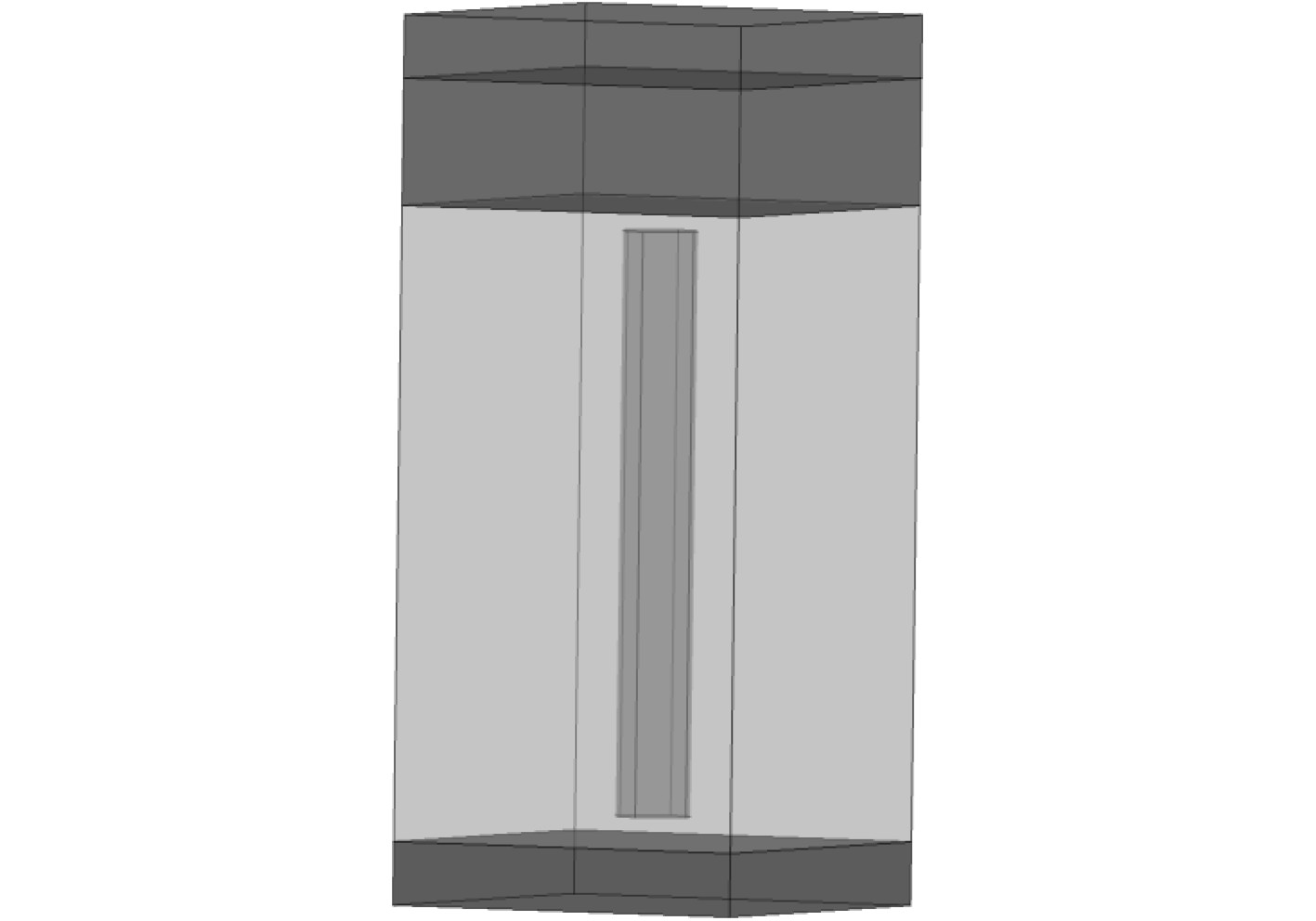
为验证基于COMSOL建立的空腔型覆盖层有限元模型的有效性,将仿真结果与文献[16]的结果进行对比分析。空腔型覆盖层的验证结构如图2所示。单胞边长为30 mm,单元分为4层,第1层为完美匹配层,厚度为10 mm;第2层为入射声场水域,厚度为20 mm;第3层为橡胶覆盖层,厚度为50 mm,其材料参数为:杨氏模量
|
图 2 空腔型覆盖层验证模型 Fig. 2 Cavity cladding validation model |
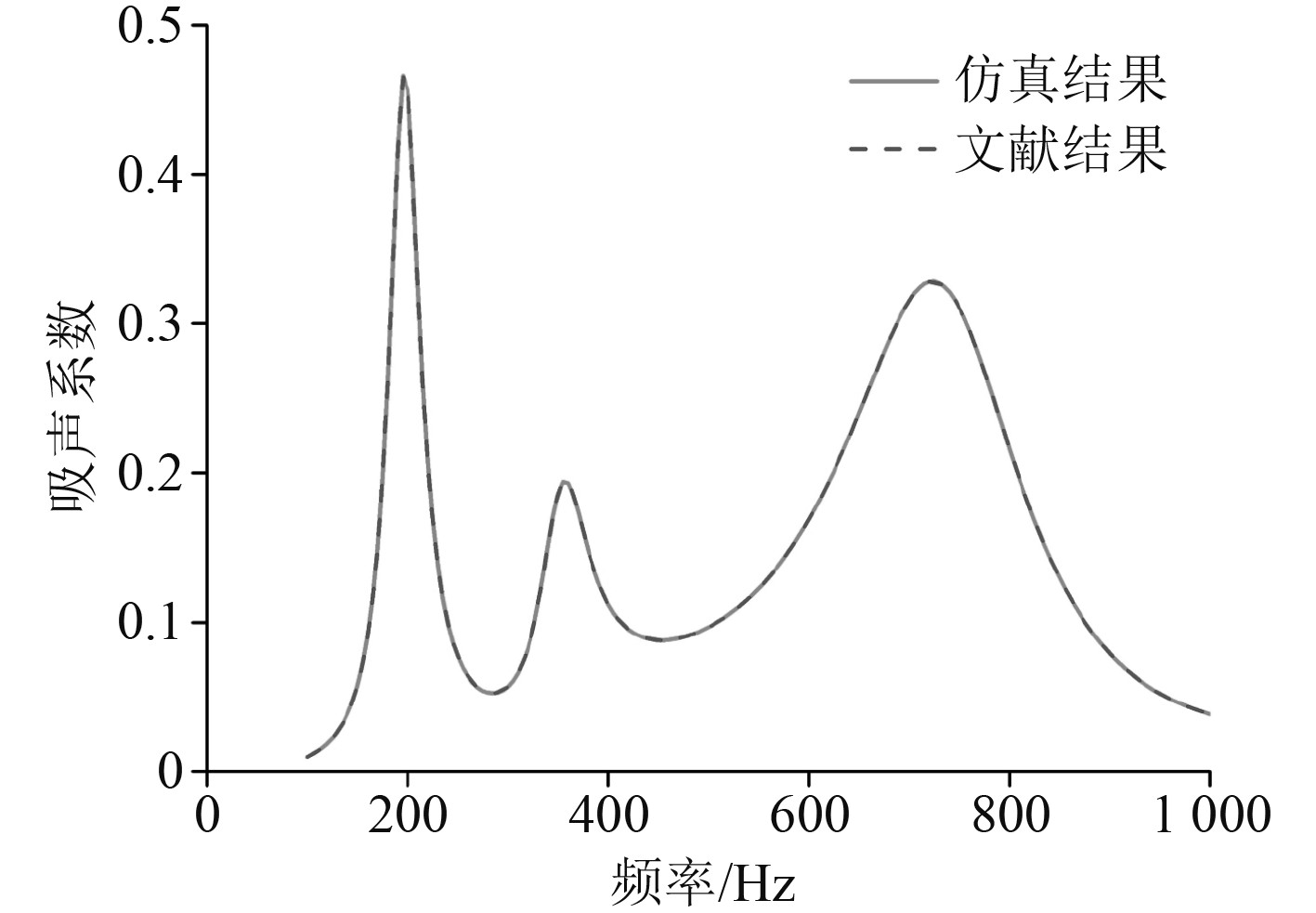
在入射声场水域中设置背景压力场来模拟入射声波。在模型的四周设置Floquet周期性边界条件,模拟结构在XY平面的无限大结构。声吸收系数仿真结果与文献[16]仿真结果对比如图3所示,二者曲线吻合良好。因此,可以采用COMSOL软件计算空腔覆盖层吸声性能的有效性。

|
图 3 有限元解与验证解对比图 Fig. 3 Comparison diagram of finite element solution and verification solution |
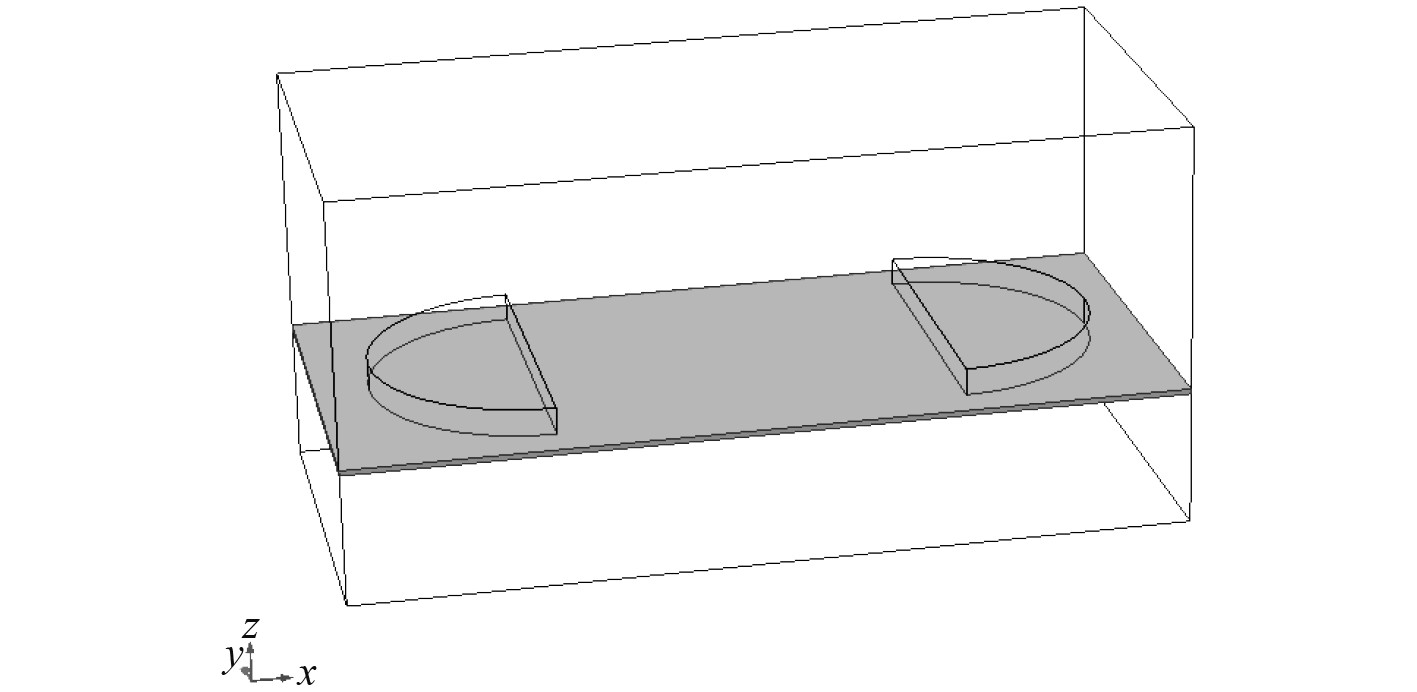
为验证基于COMSOL建立的局域共振结构有限元模型的有效性,建立文献[17]中矩形薄膜附加2个对称半圆形质量块的结构,如图4所示。材料参数与前文相同。矩形薄膜长度31 mm,宽度15 mm,厚度0.2 mm,半圆形质量块材料为钢,半径6 mm,厚度为1 mm,对称放置于y轴的两侧,薄膜与质量块材料参数与前文相同,薄膜四周为固定边界,薄膜预应力大小为
|
图 4 局域共振结构验证模型 Fig. 4 Local resonance structure validation model |
|
图 5 局域共振结构吸声系数对比图 Fig. 5 Comparison diagram of sound absorption coefficient of local resonance structure |
为验证局域共振型空腔覆盖层的低频吸声效果,采用与上述单独结构相同的仿真设置条件,将与本文复合结构模型同等大小的圆锥形空腔覆盖层结构、圆形薄膜附加一个圆形质量块局域共振结构的吸声结果和本文复合结构的吸声系数作对比,如图6所示。可以看出,复合结构相对2种单独结构,吸声峰频率向高频移动,整体吸声系数有明显提高,且吸声频带拓宽。因此,空腔型声学覆盖层与局域共振型薄膜材料的复合,不但提高了前者的吸声效果,而且对于解决后者吸声频带窄的问题具有实践指导意义。

|
图 6 吸声系数对比图 Fig. 6 Sound absorption coefficient comparison diagram |
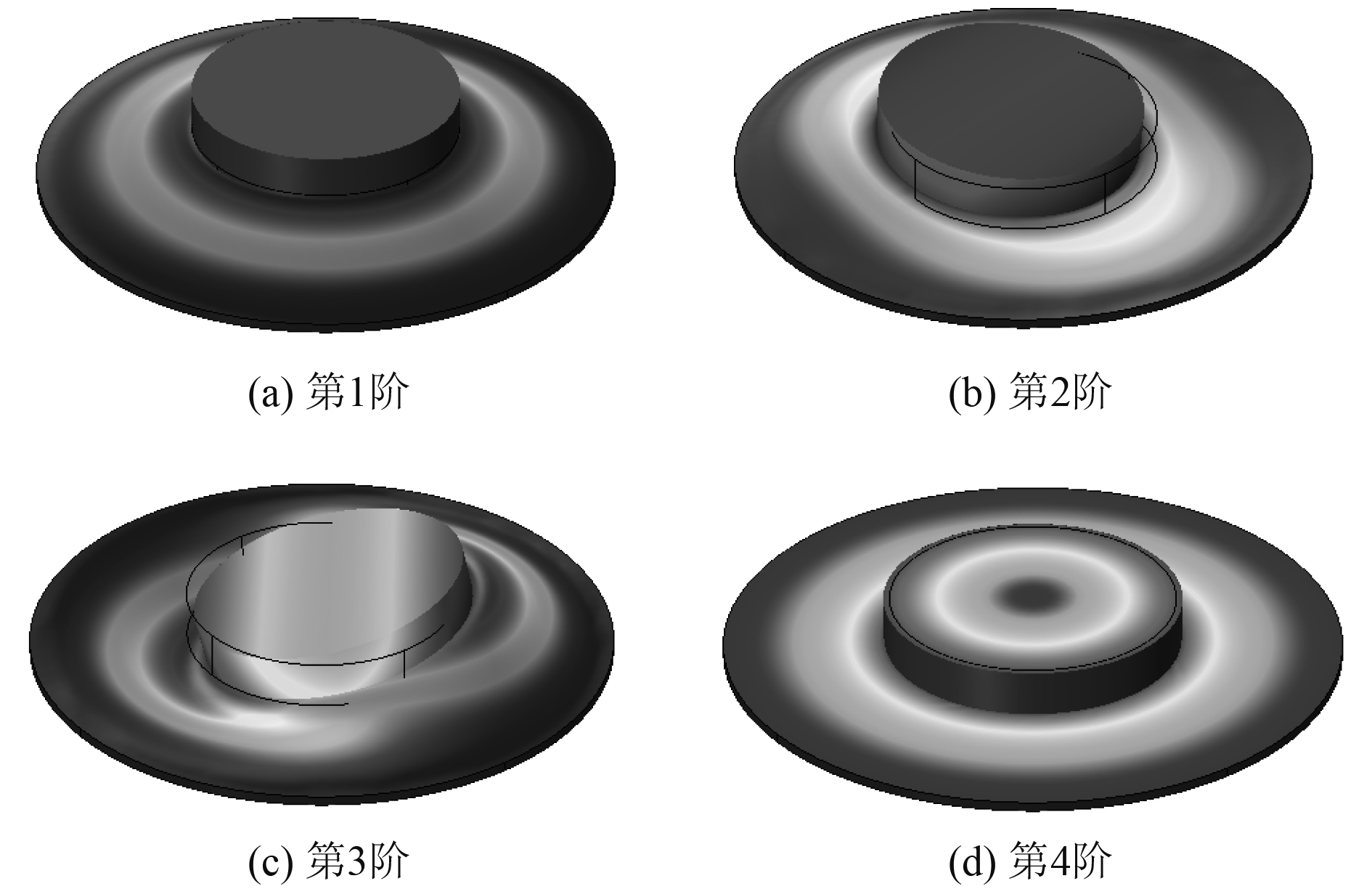
为验证复合结构的吸声机理,分别计算图6中局域共振结构与复合模型的特征频率,计算结果如表3所示,各阶特征频率对应的模态振型如图7和图8所示。
|
|
表 3 局域共振结构和复合结构的前四阶特征频率(Hz) Tab.3 The first fourth order characteristic frequencies of local resonance structures and composite structures (Hz) |
|
图 7 局域共振结构的模态振型 Fig. 7 Mode shapes of local resonance structures |

|
图 8 复合结构中局域共振结构的模态振型 Fig. 8 Mode shapes of local resonance structures in composite structures |
从图7可看出,第1阶特征频率与吸声峰频率接近,1阶模态振型中,薄膜质量块均向上振动,根据局域共振结构的反共振吸声原理,声波作为纵波,传播方向与振动方向相同,当声波向下入射时,局域共振结构向上振动且振幅达到最大时,吸声效果最佳。
图8中为复合结构前4阶特征频率中,局域共振结构的模态振型。可知,耦合之后的局域共振结构第4阶特征频率处薄膜质量块反共振振幅达到最大,但此时还未达到吸声峰峰值。
复合结构中空腔覆盖层的前4阶模态振型如图9所示。空腔覆盖层中橡胶振动位移偏小,上半部分空腔向一侧扩张,如第1,3阶模态振型所示,或者向周围扩张,如第2,4阶模态振型所示;下半部分空腔的振动位移偏大,振型为向内收缩。可见耦合之后的空腔出现变形,但振幅总体较低,所以综合局域共振结构的模态振型,可知低频吸声效果的提高主要与局域共振结构有关。

|
图 9 复合结构中空腔覆盖层的各阶模态振型 Fig. 9 Mode shapes of the cavity overburden layer of the composite structure |
为研究吸声峰的形成,给出吸声峰1340 Hz处的振动位移云图,如图10所示。橡胶覆盖层有相同的向下振动的位移,带动上半部分空腔竖直向下振动,无水平方向的挤压变形,而下半部分空腔虽然振幅较小,但空腔水平向外扩张;薄膜质量块结构振型同样是向上振动,振幅与第4阶振动模态相比,降低了3个数量级。表明此时的吸声机理为:空腔型覆盖层中的下半部分空腔周围的橡胶的横向振动带动空腔水平向外扩张,使得垂直入射的纵波转化成水平方向传播的剪切波,而剪切波具有阻尼高的特点,能够消耗更多的声能,同时结合局域共振结构反共振吸声,二者共同作用,形成吸声峰。
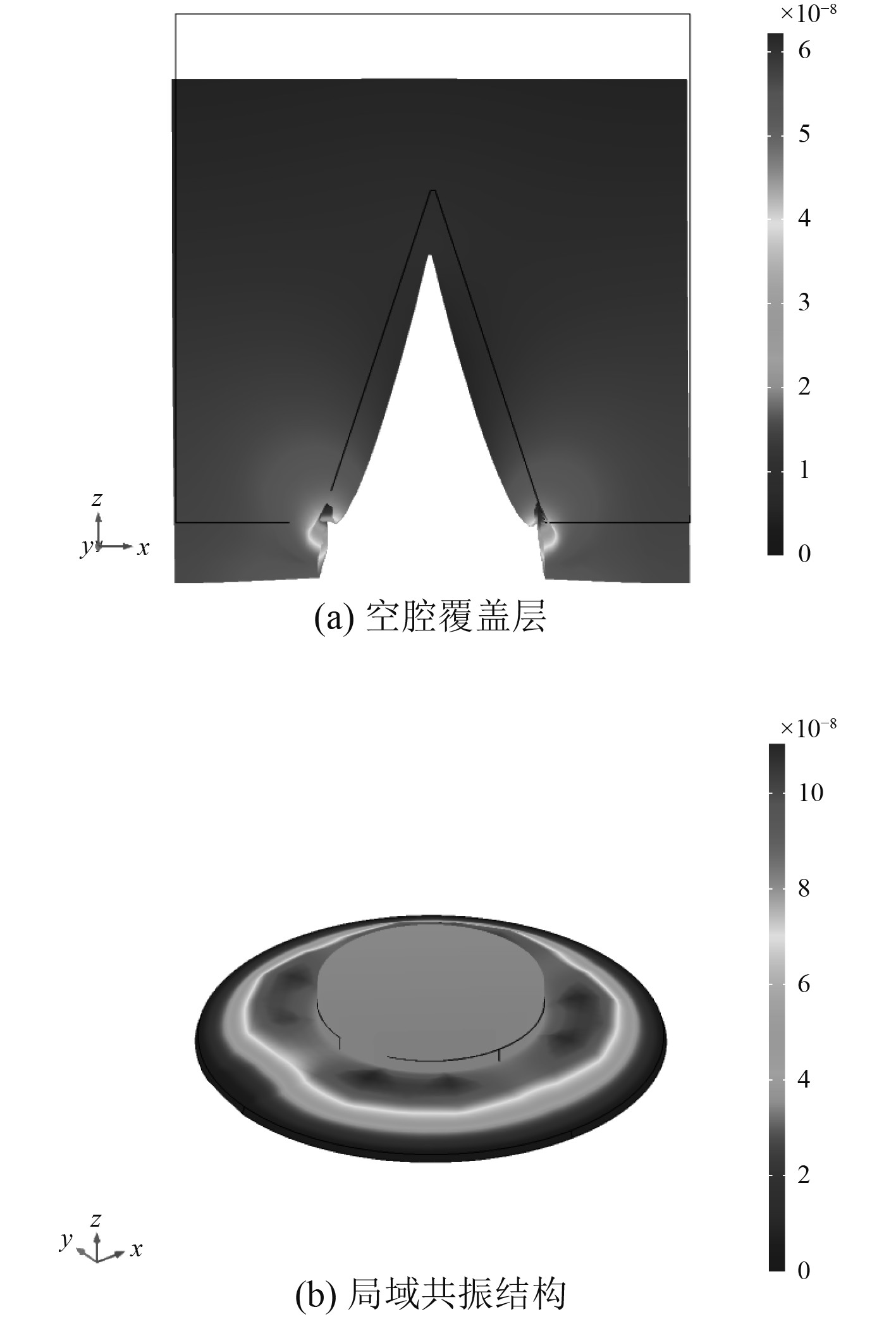
|
图 10 吸声峰处的振动位移云图 Fig. 10 Nephogram of vibration displacement at the absorption peak |
Nelder-mead单纯形法是基于比较的直接搜索方法,其鲁棒性强,无梯度,可用于解决导数不可知的非线性问题,其主要求解思路为:先找出一个基本可行解,判断是否为最优解,若不是,则按照一定的法则例如反射、扩展、压缩、收缩,找出另一改进后的更优的可行解,再进行判断,如此循环往复,直到找到某最优解为止。
分别以几何参数和材料参数为优化变量,以复合结构的吸声系数目标总和最大为优化目标,采用优化模块中的Nelder-mead单纯形法为优化方法,优化频带范围为10~1000 Hz,对优化后的吸声系数变化与优化前的进行了对比分析。
3.1 几何参数的优化根据模型结构可知通过调节穿孔率可以同时调整空腔大小和薄膜的大小,所以控制变量之一为穿孔率
| $ \left\{ \begin{gathered} \tau \in [0.1,0.5],\\ h \in [5,20],\\ H \in [10,30],\\ \end{gathered} \right. $ |
经过Nelder-mead单纯形法优化之后的几何参数为:
| $ \left\{ \begin{gathered} \tau = 0.15025,\\ h = 5.00340[\rm mm] ,\\ H = 25[\rm mm]。\\ \end{gathered} \right. $ |
优化后的几何参数与初始参数相比,空腔高度相对整个覆盖层厚度而言降低了10 mm。水下吸声材料在水压的作用下产生变形,削弱材料的吸声性能,而空腔周围橡胶材料越厚,其变形也就越小,对吸声性能的影响也就越小,因此优化后的几何结构相比初始结构的吸声性能更加稳定。优化之后的吸声系数如图11所示,整体而言,吸声系数有所提高,其中在300~800 Hz范围内有较明显改善,经计算,该频段内吸声系数提高了13%。吸声峰频率由原来的1340 Hz移动到现在的810 Hz,且600~900 Hz频带内吸声系数持续稳定在0.6附近。
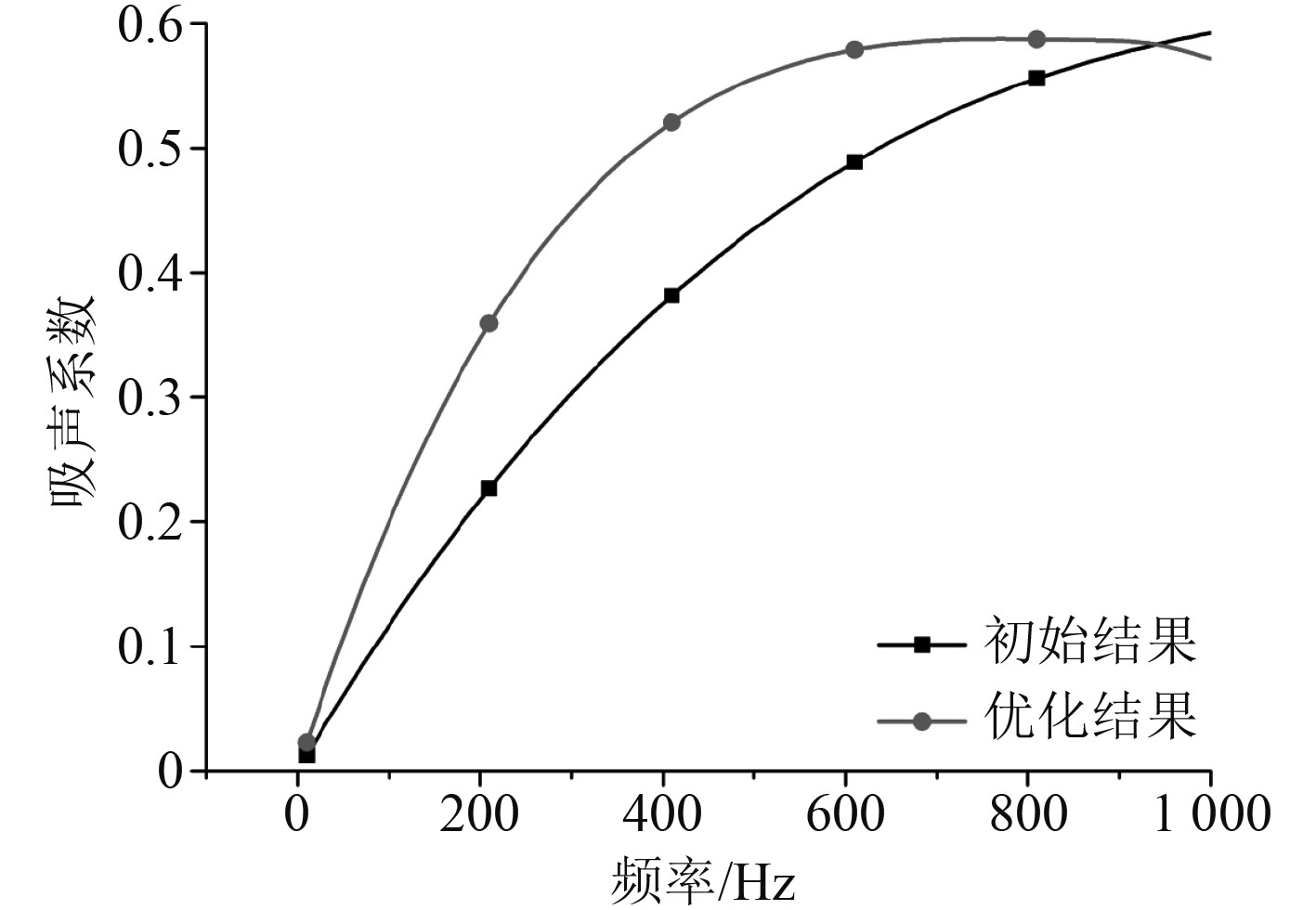
|
图 11 几何参数优化结果 Fig. 11 Optimization results of geometric parameters |
在保持结构参数为初始参数不变的前提下,以橡胶覆盖层的材料参数包括杨氏模量
| $ \left\{ \begin{gathered} E \in [1{\rm{e}}6,3{\rm{e}}8] ,\\ \upsilon \in [0.4,0.5],\\ \eta \in [0.2,0.8] ,\\ \end{gathered} \right. $ |
经过Nelder-mead单纯形法优化之后的材料参数为:
| $ \left\{ \begin{gathered} E = 1.99950 \times {10^8}\;{\rm{Pa}} ,\\ \upsilon = 0.48992,\\ \eta = 0.79983 。\\ \end{gathered} \right. $ |
优化后的参数与初始参数相比,损耗因子变化较大,杨氏模量和泊松比变化较小,一方面说明复合结构的吸声性能的大小对于橡胶覆盖层材料的损耗因子更敏感,在材料的损耗因子可变的前提下,损耗因子越大,结构的低频吸声性能就越好;另一方面,损耗因子的存在使得优化之后的参数自然而然的向着损耗因子增大的方向变化,从而很大程度的削弱其他控制参数的影响。吸声系数优化结果如图12所示,整体而言,吸声系数有较大幅度改善,平均吸声系数提高了26%。当声波频率为200 Hz时,吸声系数就能达到0.5,且随着入射声波频率的增大,吸声性能逐渐提高,在700 Hz附近,吸声性能达到峰值0.8。
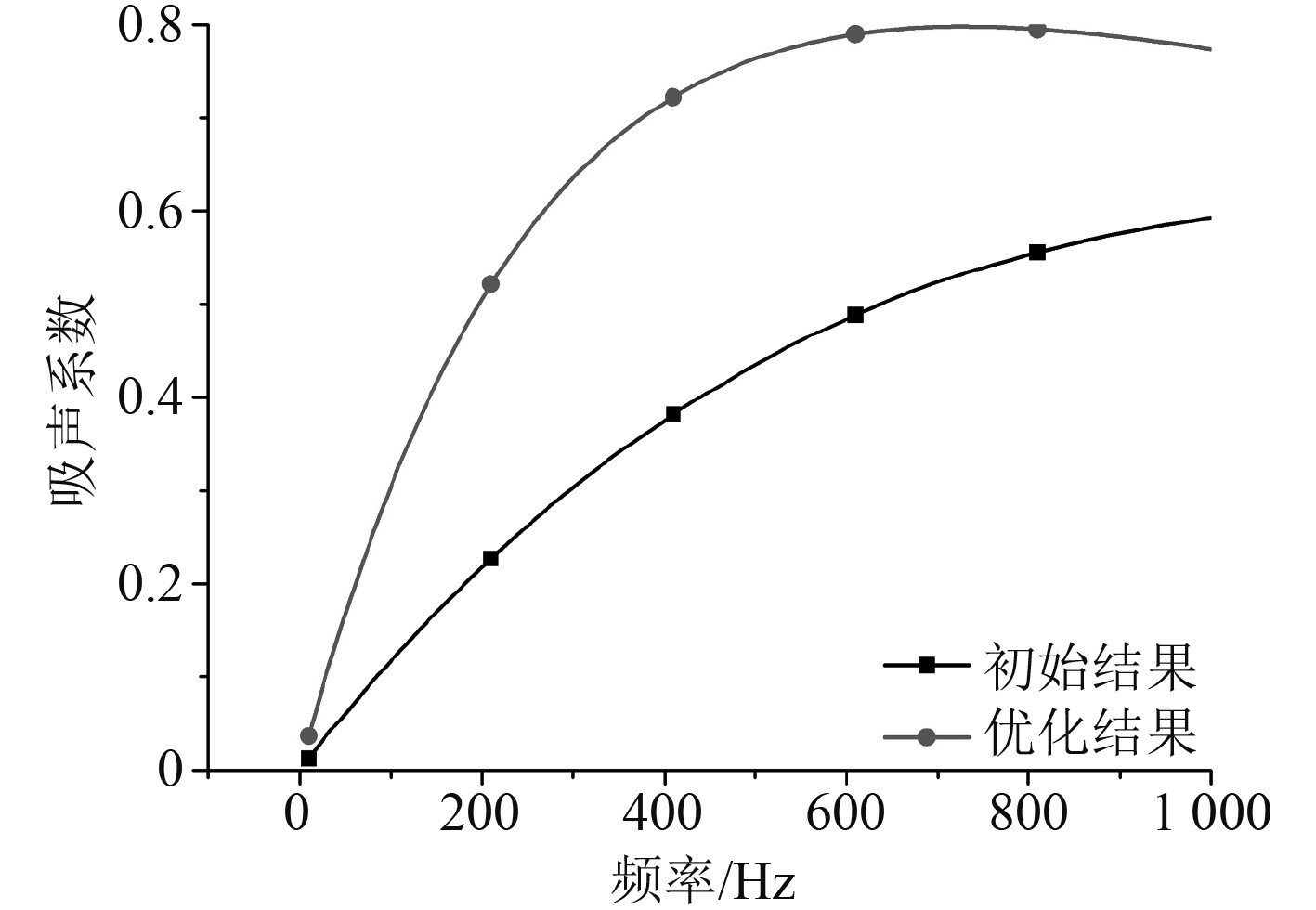
|
图 12 材料参数优化结果 Fig. 12 Optimization results of material parameters |
通过分析复合结构的动能密度来分析复合结构优化后吸声性能提高的原因。图13~图15分别为优化前1000 Hz处、几何参数优化后吸声峰810 Hz处、材料参数优化后吸声峰730 Hz处的结构动能密度分布图,由于优化前复合结构的吸声系数曲线呈递增趋势,故选取1000 Hz处的动能密度分析。可以看出,三者的结构动能密度最大值均集中在质量块处,图13与图14、图15对比发现,优化后的结构动能密度比优化前提高了一个数量级,根据动能密度越大,能量损耗越大,因此吸声性能提高。
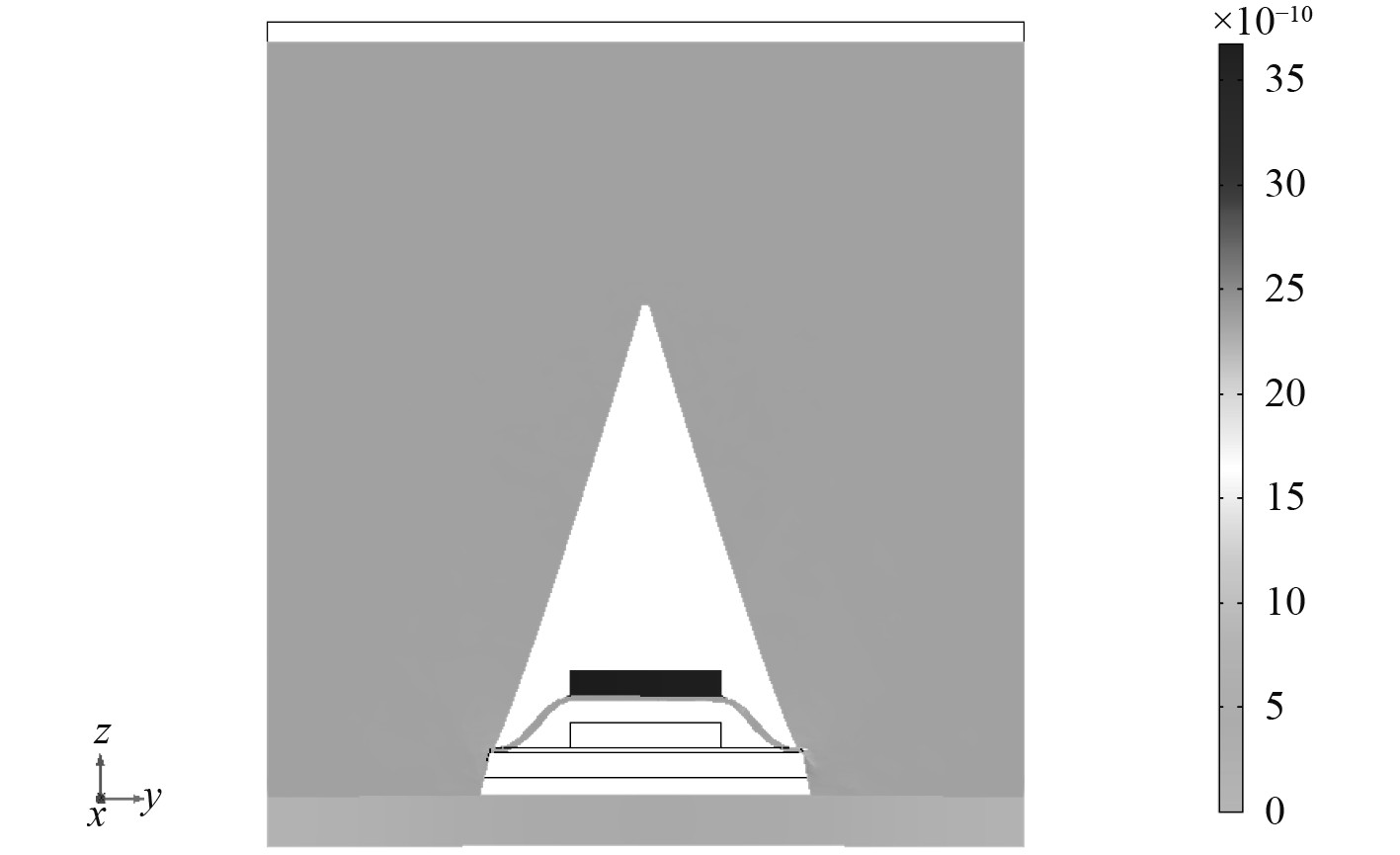
|
图 13 优化前1000 Hz处结构动能密度 Fig. 13 Structural kinetic energy density at 1000 Hz before optimization |
|
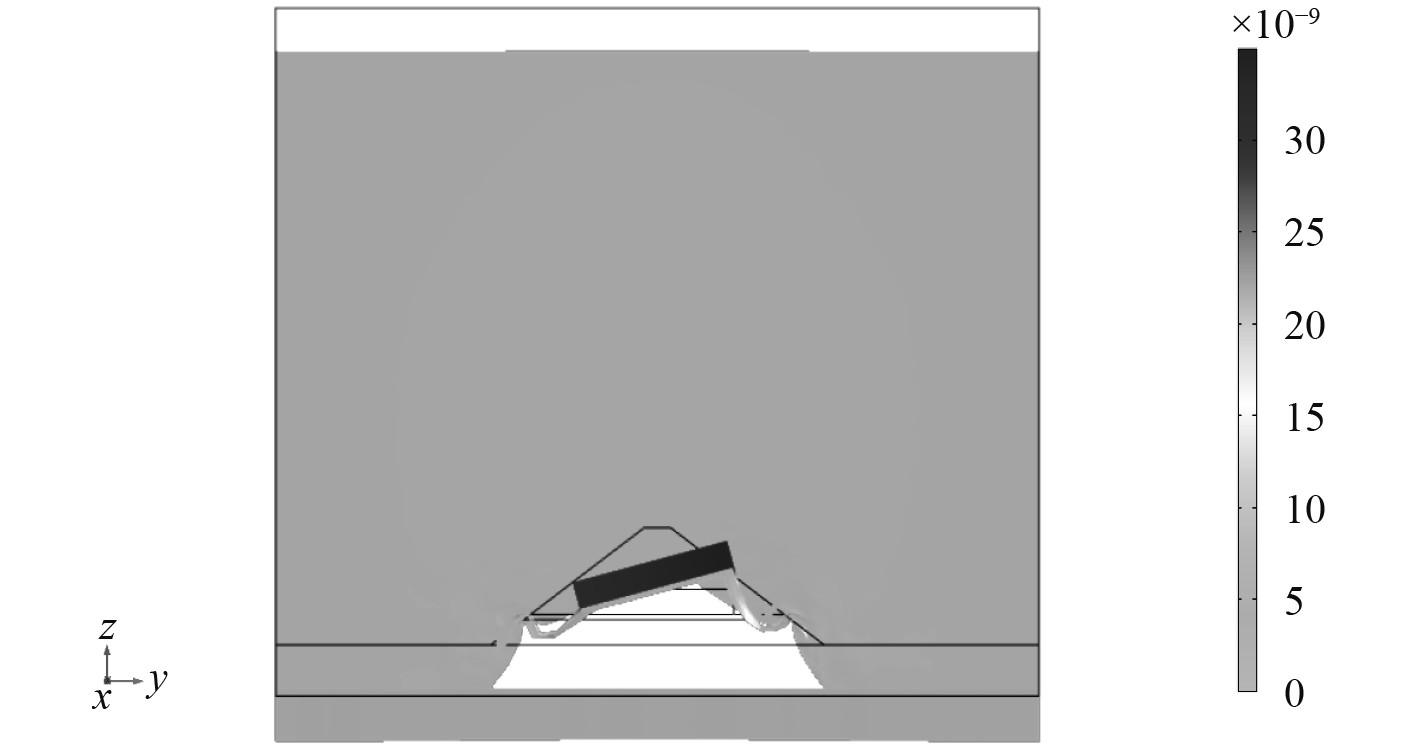
图 14 几何参数优化后810 Hz处结构动能密度 Fig. 14 Structural kinetic energy density at 810 Hz after optimization of geometric parameters |
|
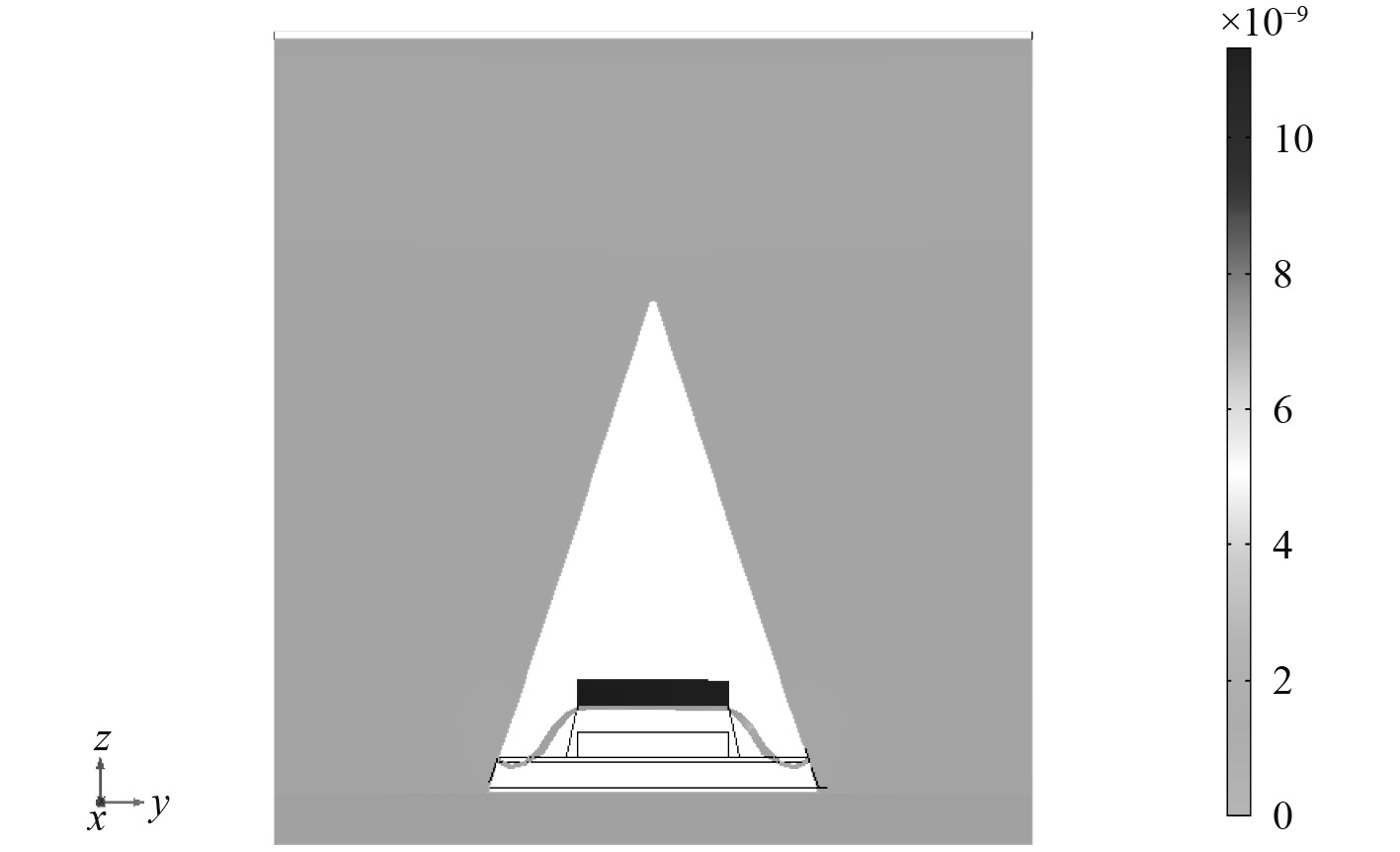
图 15 材料参数优化后730 Hz处结构动能密度 Fig. 15 Structural kinetic energy density at 730 Hz after material parameter optimization |
图14中,几何优化后的复合模型中局域共振结构的振型变化,吸声峰810 Hz处薄膜向下弯曲振动,质量块呈“翻转”状态。而图15中,对于橡胶覆盖层材料参数的改变影响了整个复合结构,进而使得内部局域共振结构的振型产生变化,在吸声峰730 Hz处,除薄膜边缘处外,其他位置均向上振动,根据局域共振结构的反共振吸声原理,当其振动方向与声波传播方向相反且振动位移最大时,吸声性能最好,因此在进行复合结构的参数优化时,一方面,提高橡胶覆盖层的损耗因子对于吸声性能的提高具有较大影响;另一方面,应注意尽量使得优化之后的局域共振结构的反共振频率向低频移动,二者结合才能最大限度的提高复合结构的吸声性能。
4 结 语本文建立局域共振结构内嵌到空腔中的水声覆盖层,通过COMSOL仿真发现复合结构相比单一的空腔型覆盖层与局域共振结构,提高了吸声性能,拓宽了吸声频带,通过分析复合结构的模态振型和振动位移云图得到其吸声机理,利用COMSOL中的优化模块,采用Nelder-mead单纯形法优化方法,对10~1000 Hz频带内的吸声系数进行了几何参数优化、材料参数优化,优化结果表明:
1)复合结构的吸声机理为:复合结构中的空腔覆盖层,其下半部分空腔向外扩张,带动其周围橡胶产生水平方向的振动,从而实现纵波向横波的转化,吸收一部分声能;局域共振结构同时向上振动,二者耦合提高覆盖层的低频吸声效果。
2)复合结构经过几何优化、材料优化后,平均吸声系数分别提高了13%和26%,通过2种优化方案对比分析,复合结构的吸声性能对橡胶覆盖层的材料参数变化更敏感,尤其是损耗因子的变化。
3)复合结构优化后吸声性能提高的原因为,优化后内部局域共振结构的反共振振型向低频移动,同时,两种方案优化后吸声峰处的结构动能密度较优化前提高了一个数量级,根据结构动能密度越大,能量损耗越大,因此吸声性能增强。
复合结构中几何参数及材料参数的变化均会改变内部局域共振结构的反共振频率,优化时应注意综合考虑结构内部能量损耗与局域共振结构的反共振频率,二者有效结合才能获得复合结构吸声系数的最优解。研究结果可为水声覆盖层的设计提供理论依据,对于工程实践具有重要意义。
| [1] |
朱蓓丽, 黄修长. 潜艇隐身关键技术—声学覆盖层的设计[M]. 上海: 上海交通大学出版社, 2012.
|
| [2] |
陶猛, 汤渭霖. Alberich型吸声覆盖层的低频吸声机理分析[J]. 振动与冲击, 2011, 30(1): 56-60. DOI:10.3969/j.issn.1000-3835.2011.01.012 |
| [3] |
刘国强, 楼京俊, 何世平, 等. 基于COMSOL多层材料吸声覆盖层的吸声特性分析[J]. 舰船科学技术, 2016, 38(4): 35-37. LIU Guoqiang, LOU Jingjun, HE Shiping, et al. Analysis of sound absorption characteristics of multilayer material based on COMSOL[J]. Ship Science and Technology, 2016, 38(4): 35-37. DOI:10.3404/j.issn.1672-7619.2016.04.007 |
| [4] |
VALENTIN L, ANATOLIY S, MAXIME L, et al. Super-absorption of acoustic waves with bubble meta-screens[J]. Physical Review B : Condensed matter and materials physics, American Physical Society, 2015, 020301(R).
|
| [5] |
柯李菊, 刘成洋, 方智. 基于COMSOL的组合空腔结构声学覆盖层的声学性能分析[J]. 中国舰船研究, 2020, DOI:10.19693/j.issn.1673-3185.01673. KE Liju, LIU Chengyang, FANG Zhi. Acoustic performance analysis of composite cavity structure acoustic overlay based on COMSOL[J]. Chinese Journal of Ship Research. 2020, DOI: 10.19693/ j.issn.1673-3185.01673. |
| [6] |
NAIFY C J, CHANG C M, MCKNIGHT G, et al. Membrane-type metamaterials: transmission loss of multi-celled arrays[J]. Journal of Applied Physics, 2011, 109: 104902. DOI:10.1063/1.3583656 |
| [7] |
MA G, YANG M, XIAO S, et al. Acoustic metasurface with hybrid resonances[J]. Nature Materials, 2014, 13(9): 873-878. DOI:10.1038/nmat3994 |
| [8] |
马勇, 贾俊芳. 遗传算法研究综述[J]. 山西大同大学学报, 2007, 23(3).
|
| [9] |
何雨. 超启发式算法综述[J]. 数字技术与应用, 2020, 38(9): 94-95. DOI:10.19695/j.cnki.cn12-1369.2020.09.36 |
| [10] |
陈培帅, 张永涛, 唐东云, 等. 模拟退火法与有限元耦合反演技术研究[J]. 现代隧道技术, 2013, 50(4): 76-83. DOI:10.3969/j.issn.1009-6582.2013.04.012 |
| [11] |
赵宏刚, 温激鸿, 杨海滨, 等. 一种含柱形空腔结构橡胶层的吸声机理及优化[J]. 物理学报, 2014, 63(13): 35−37: 134303.
|
| [12] |
余依伦, 许弘雷, 谢翔, 等. 基于多种群遗传算法的水下吸声覆盖层结构参数优化设计[J]. 科学技术与工程, 2017, 17(2).
|
| [13] |
陈竞超, 赵宏刚, 钟杰, 等. 一种单周期柱形空腔的橡胶层吸声机理及优化[C]// 第二十七届全国振动与噪声应用学术会议.
|
| [14] |
马先超, 赵宏刚. 内嵌双周期空腔橡胶层的吸声优化[J]. 声学技术, 2018, 37(6): 119-120. |
| [15] |
孟香惠, 施保昌, 胡新生. 线性规划单纯形法的动态灵敏度分析及其应用[J]. 应用数学, 2018, 31(3): 697-703. DOI:10.13642/j.cnki.42-1184/o1.2018.03.054 |
| [16] |
商超, 魏英杰, 张嘉钟, 等. 基于有限元法的Alberich型覆盖层吸声特性研究[J]. 船舶力学, 2011, 15(4): 443-448. DOI:10.3969/j.issn.1007-7294.2011.04.017 |
| [17] |
张忠刚, 朱浩宇, 罗剑, 等. 吸声型薄膜声学超材料低频宽带吸声性能研究[J]. 应用声学, 2019, 38(5): 869-875. ZHANG Zhonggang, ZHU Haoyu, LUO Jian, et al. Study on low Frequency and Wide band Sound absorption of thin film acoustic metamaterials[J]. Journal of Applied Acoustics, 2019, 38(5): 869-875. |
 2022, Vol. 44
2022, Vol. 44

