2. 江苏省安全生产科学研究院,江苏 南京 210042;
3. 南京扬子国资投资集团有限责任公司,江苏 南京 210000
2. Jiangsu Academy of Safety Science and Technology, Nanjing, 210042, China;
3. Nanjing Yangzi State-owned Investment Group Co., Ltd., Nanjing, 210000, China
起重船属于海上起重设备,在海洋石油平台安装、港建水工作业、造船工程、桥梁工程、水下打捞等工程中具有广泛用途,因此对于大型起重船而言,方形系数较大且船宽B与吃水T之比都会超出常规船舶规范B/T≤2.5,L/B>5的规定,具有其特殊性,故在作业时会受到周围环境载荷不同程度的影响。为了降低海上作业风险并提高安全性,中外众多学者展开了多方面的研究。王言英等[1]根据线形波理论和三维源汇分布方法,提出了浮体在波浪中运动的水动力系数、波浪载荷以及运动相应的计算方法。Li[2]、谢永和等[3]和刘日明等[4]提出了数值积分方法,用来计算有限水深的格林函数及其导数。杨鹏等[5]利用改进的Gauss-Laguerre积分法,提出一种可精确计算有限水深格林函数及其偏导数的方法,用于评估浮体运动和波浪载荷。Ding等[6]引入矢量后基于常系数罚函数法提出了船舶在规则波中漂浮的新方程。Chen[7]利用波浪模型SWAN研究了波浪的传播和波浪流之间的相互作用,以及对船舶航行的影响。陈剑文等[8]基于三维势流理论,以浮式栈桥为研究对象,计算在规则波入射时的水动力参数,以及在波浪作用下浮式栈桥的运动响应,但对于大型浮式起重船的相关研究较少。
本文结合势流理论和波浪的辐射/绕射理论,对3600 t起重船进行动态响应水动力系数的计算,并在危险工况下对起重船的不同航速进行研究,为大吨位起重船的航行作业提供参考依据。
1 数值计算理论对于存在浮动刚体的流场,其速度势可以分为三部分:
| $ \varPhi (x,y,z,t) = {\varPhi _\omega } + {\varPhi _d} + {\varPhi _r}。$ | (1) |
式中:
1)
| $ {\varPhi _\omega }(x,y,z,t) = - i\frac{{Ag}}{\omega }\frac{{\cosh k(z + h)}}{{\cosh kh}}{e^{ik(x\cos \beta + y\sin \beta )}}。$ | (2) |
式中,
2)
| $ \nabla {\varPhi }_{d}\cdot n=-\nabla {\varPhi }_{\omega }\cdot n 。$ | (3) |
式中,
3)
| $ {\varPhi _r} = \sum\limits_{j = 1}^6 { - i\omega {x_j}} {\varPhi _{{R_j}}}。$ | (4) |
式中,
势流是指流体中速度场,是标量函数(即速度势)梯度的流。该理论通常会设定速度势存在并满足Laplace方程和4类边界条件:自由面条件、海底条件、物体湿表面条件和辐射条件(无穷远处边界条件)。
根据Laplace方程以及边界条件可以确定出速度势,再按伯努利公式计算物体湿表面上的压力。这是目前最常用的计算浮体湿表面上波浪力的方法。
在势流理论[9]中,通常引入如下基本假设:
1)假设流体是不可压缩的理想流体,其表面张力效应可忽略不计;
2)运动是无旋的,即存在速度势
需要满足的边界条件(见图1)有
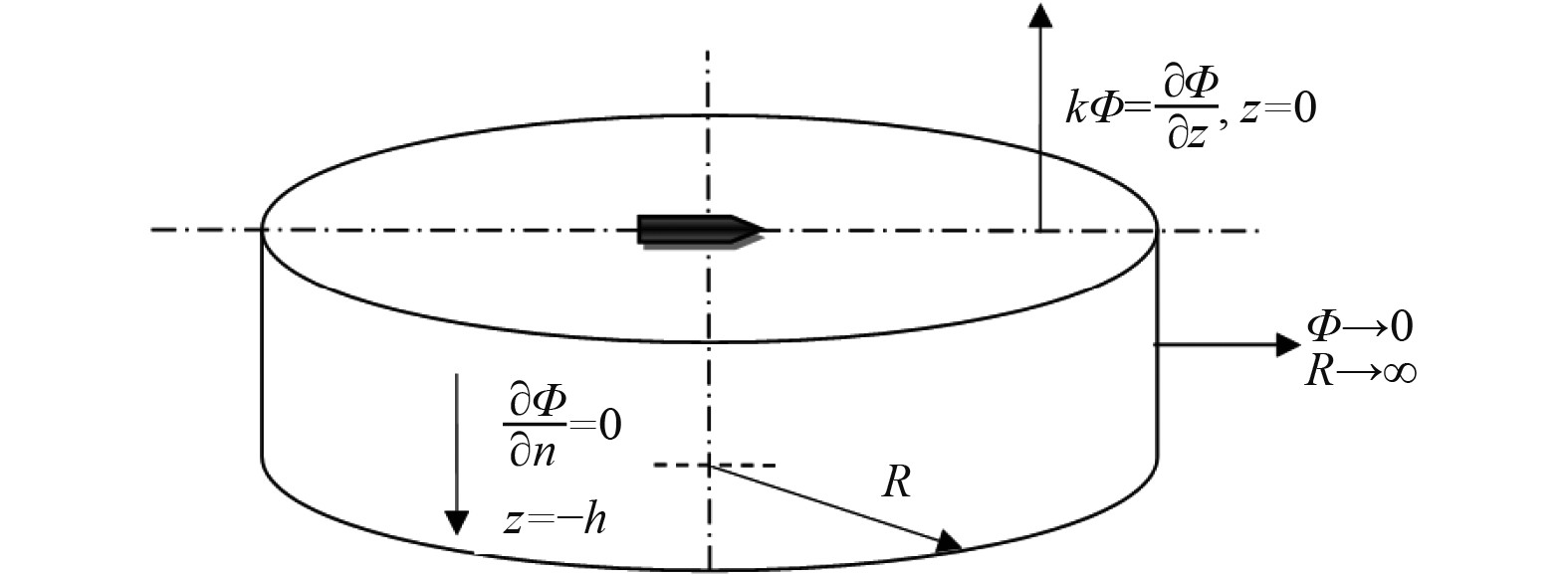
|
图 1 边界条件 Fig. 1 Boundary conditions |
Laplace方程:
| $ \frac{{{\partial ^2}\varPhi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\varPhi }}{{\partial {y^2}}} + \frac{{{\partial ^2}\varPhi }}{{\partial {z^2}}} = 0。$ | (5) |
自由表面条件:
| $ \frac{{{\partial ^2}\varPhi }}{{\partial {t^2}}} + g\frac{{\partial \varPhi }}{{\partial z}} = 0\;(z = 0)。$ | (6) |
海底边界条件:
| $ \frac{{\partial \varPhi }}{{\partial z}} = 0\;(z = - h)。$ | (7) |
物体湿表面条件:
| $ \frac{{\partial \varPhi }}{{\partial n}} = \sum\limits_{j = 1}^6 {{v_j}{f_j}(x,y,z)}。$ | (8) |
辐射条件:
| $ \mathop {\lim }\limits_{R \to \infty } \sqrt R \left(\frac{{\partial \varPhi }}{{\partial R}} - ik\varPhi \right) = 0(0航速条件)。$ | (9) |
当流场受到外界的干扰后,在其自由表面上出现波动现象,并且这种波动逐渐向外传播至远方。方程(9)为辐射条件,式中
在波浪场中浮体所受作用力由入射势、绕射势和辐射势三部分组成[10],求得式(1)中的速度势,则物体湿表面的压力分布可以利用线性化的伯努利方程得到,即
| $ p = - \rho gz - \rho \frac{{\partial \Phi }}{{\partial t}} = - \rho gz - \rho \left(\frac{{\partial {\Phi _\omega }}}{{\partial t}} + \frac{{\partial {\Phi _d}}}{{\partial t}} + \frac{{\partial {\Phi _r}}}{{\partial t}}\right)。$ | (10) |
进一步得出作用在浮体上的波浪力和波浪力矩为:
| $ {{{\boldsymbol{F}}}} = \iint\limits_S { - pn}{\rm{d}}s,$ | (11) |
| $ {{\boldsymbol{M}}} = \iint\limits_S { - p(r \times n)}{\rm{d}}s。$ | (12) |
引入
| $ {F_j}(t) = \rho \iint\limits_S {\left(gz + \frac{{\partial {\Phi _\omega }}}{{\partial t}} + \frac{{\partial {\Phi _d}}}{{\partial t}} + \frac{{\partial {\Phi _r}}}{{\partial t}}\right)}{n_j}{\rm{d}}s,j = 1, \cdots ,6 。$ | (13) |
即
| $ \begin{split}{F_j}(t) =& \iint\limits_S { - p{n_j}}{\rm{d}}s=\\ &\rho g\iint\limits_S {z{n_j}}{\rm{d}}s - \rho {Re} \left\{ {\sum\limits_{j = 1}^6 {i\omega {\zeta _j}{e^{ - i\omega t}}\iint\limits_S {{\phi _j}{n_j}{\rm{d}}s}} } \right\} -\\ &\rho {Re} \left\{ {i\omega {e^{ - i\omega t}}\iint\limits_S {({\phi _\omega } + {\phi _d})}{n_j}{\rm{d}}s} \right\}。\\[-15pt]\end{split}$ | (14) |
式中,3个积分式分别表示为浮体振荡所产生的静水力分量、辐射分量以及线性波激力。
其中第二积分式可以得出附加质量和阻尼系数,即
| $\begin{split} {f_{ij}} =& \left\{ \begin{array}{ll} - i\omega \rho \displaystyle\iint\limits_S {{n_i}{\phi _j}{\rm{d}}s}& i = 1,2,3 \\ - i\omega \rho \displaystyle\iint\limits_S {{{(r \times n)}_i}{\phi _j}{\rm{d}}s} & i = 4,5,6 \end{array} \right. = \\ &- \rho \iint\limits_S {\frac{{\partial {\phi _i}}}{{\partial n}}{\phi _j}{\rm{d}}s}。\end{split} $ | (15) |
式中:
| $ {f_{ij}} = - {\omega ^2}M_{ij}^a - i\omega {C_{ij}} 。$ | (16) |
式中:
| $ M_{ij}^a = \rho {{\rm{Re}}} \left\{ {\iint\limits_S {\frac{{\partial {\phi _i}}}{{\partial n}}}{\phi _j}{\rm{d}}s} \right\} ,$ | (17) |
| $ {C_{ij}} = \rho {\text{lm}}\left\{ {\iint\limits_S {\frac{{\partial {\phi _i}}}{{\partial n}}}{\phi _j}{\rm{d}}s} \right\}。$ | (18) |
本文采用的模型是3600 t起重船,根据表1参数建立船体的三维模型并划分网格,如图2所示。
|
|
表 1 起重船基本尺寸 Tab.1 Basic dimensions of crane ship |
|
图 2 船体模型及网格划分 Fig. 2 Hull model and meshing |
在数值计算过程当中,必须保证1个波长的长度至少要覆盖7个最大单元尺寸,若网格数量太少可能导致计算结果不收敛,而数量太多可能导致效率低,计算时间冗长。因此在划分网格过程中需要以计算最大频率设定网格尺寸。
3 入射波的设置选取的波浪入射角范围为0°~180°,(其中0°为随浪,180°为迎浪),波幅为1 m,根据划分的网格设置频率的范围为0.1~2.0 rad/s,入射角

|
图 3 波浪入射方向 Fig. 3 Wave incident direction |
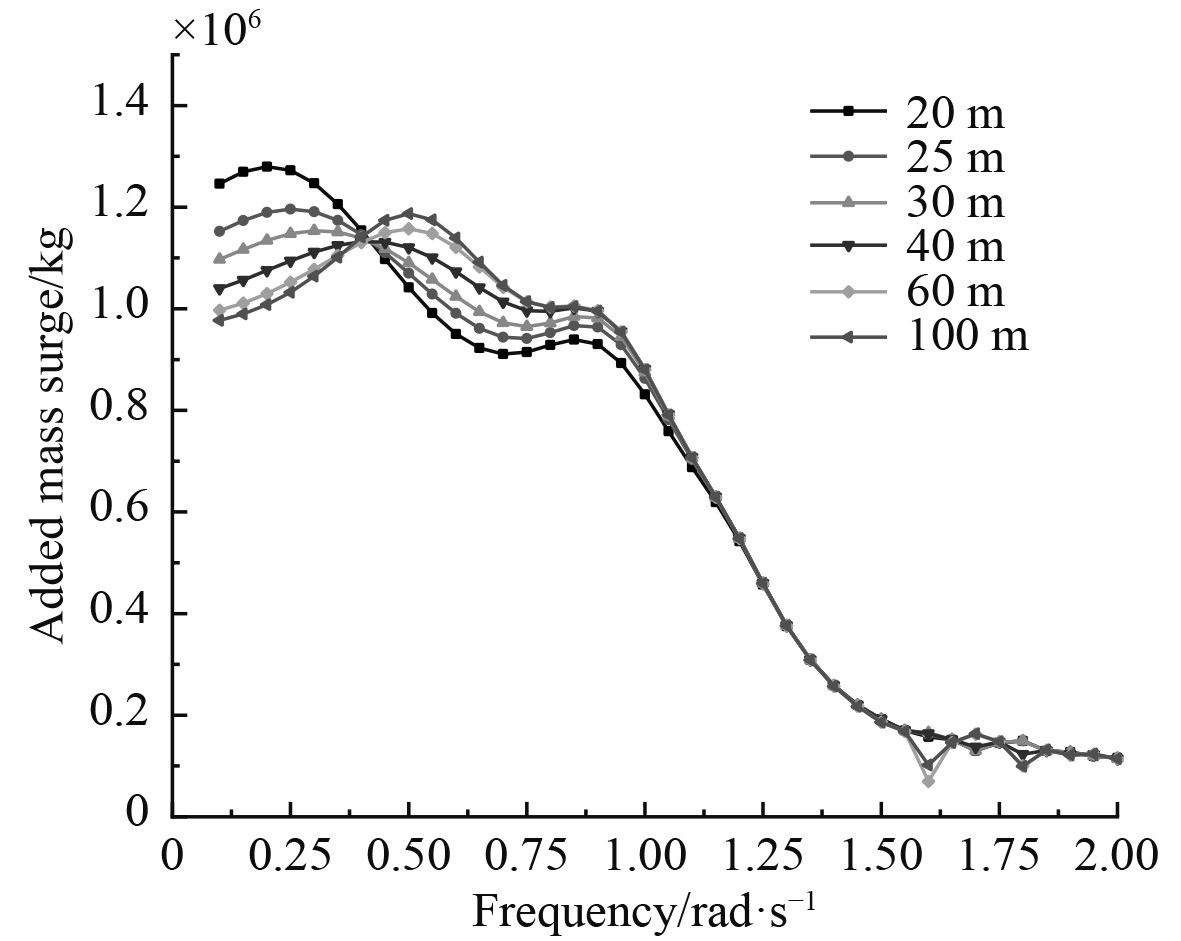
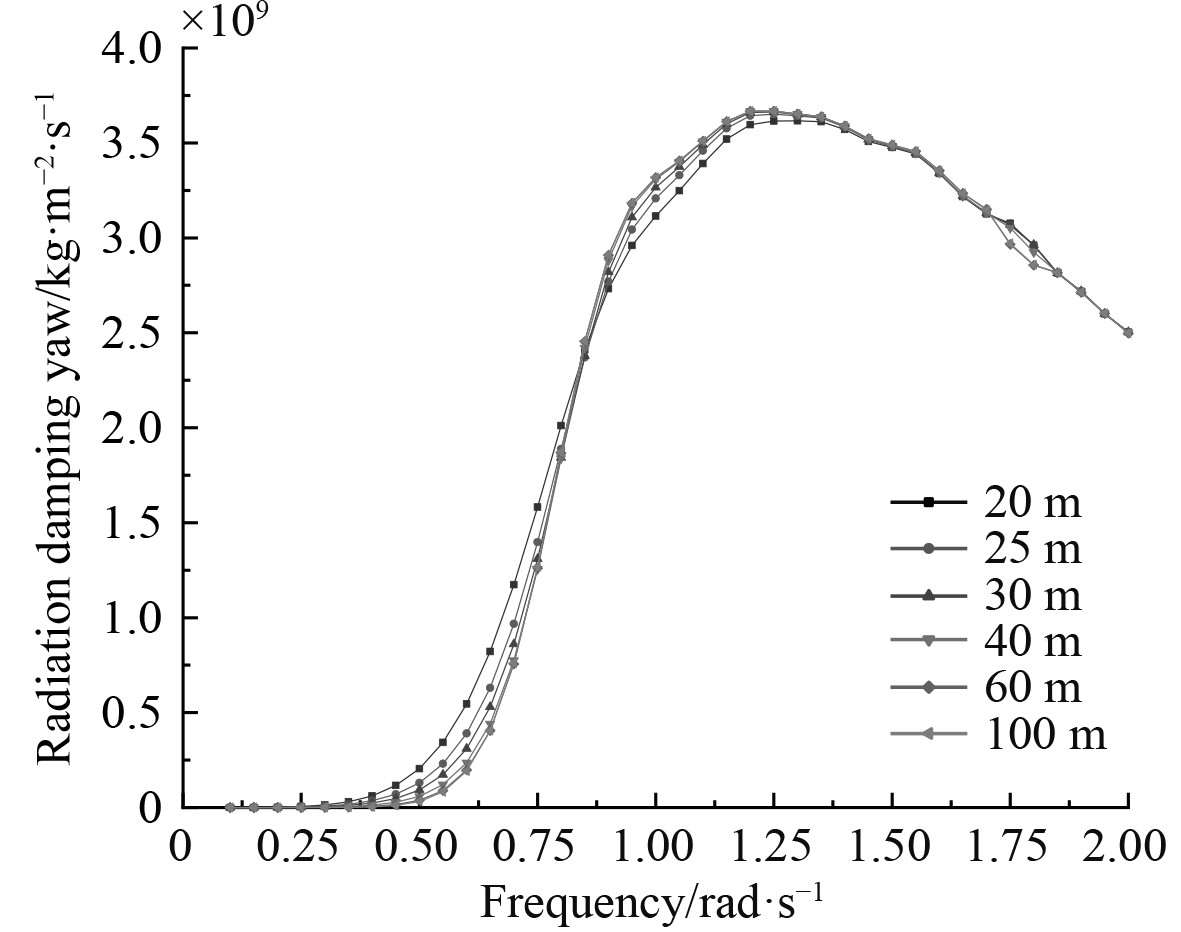
在DAT文件中分别设置6种不同的海水深度(20 m,25 m,30 m,40 m,60 m,100 m),计算结果如图4~图15所示。
|
图 4 附加质量M11随频率变化曲线 Fig. 4 Additional mass M11 varies with frequency |
|
图 15 辐射阻尼C66随频率变化的曲线 Fig. 15 Radiation damping C66 curve with frequency |
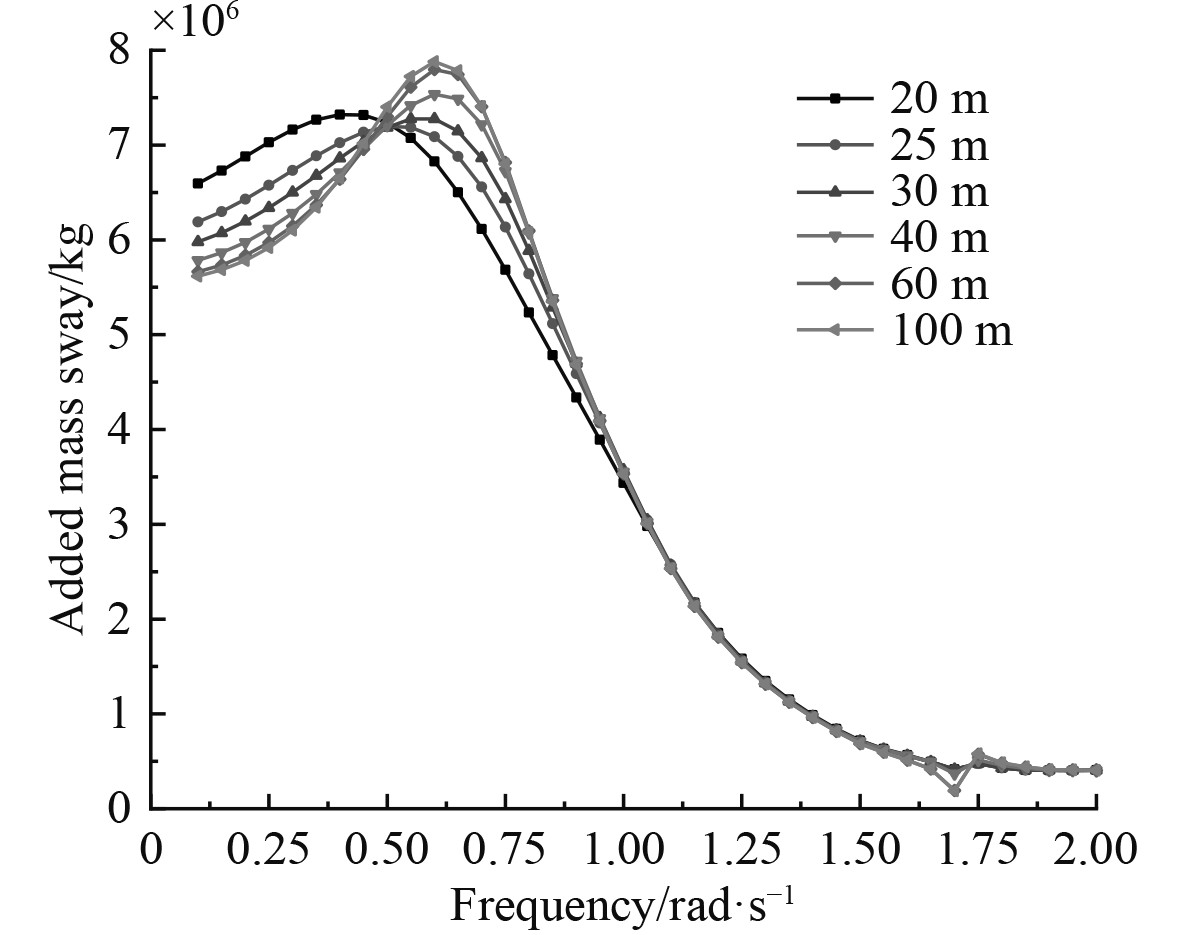
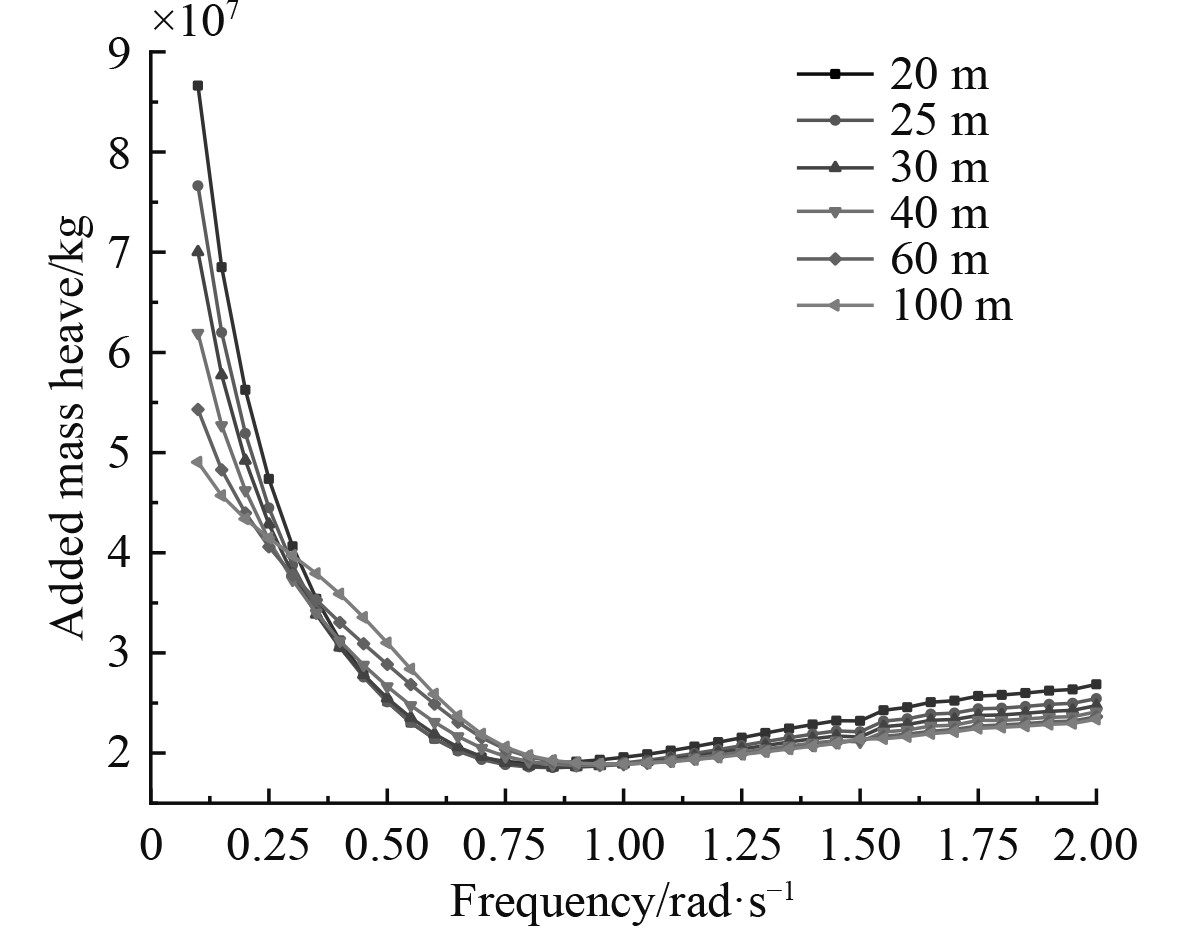
由图4~图6可知,对于线位移(纵荡、横荡和垂荡)的3个附加质量,垂荡方向的最大,纵荡方向的最小,并且随着频率的逐渐增大,垂荡方向不同于纵荡和横荡,整个阶段没有峰值,在0.1~0.75 rad/s区域内快速下降,当进入高频范围内,附加质量值几乎趋于稳定,与起重船质量的比值约为2~3。
|
图 5 附加质量M22随频率变化曲线 Fig. 5 Additional mass M22 varies with frequency |
|
图 6 附加质量M33随频率变化曲线 Fig. 6 Additional mass M33 varies with frequency |
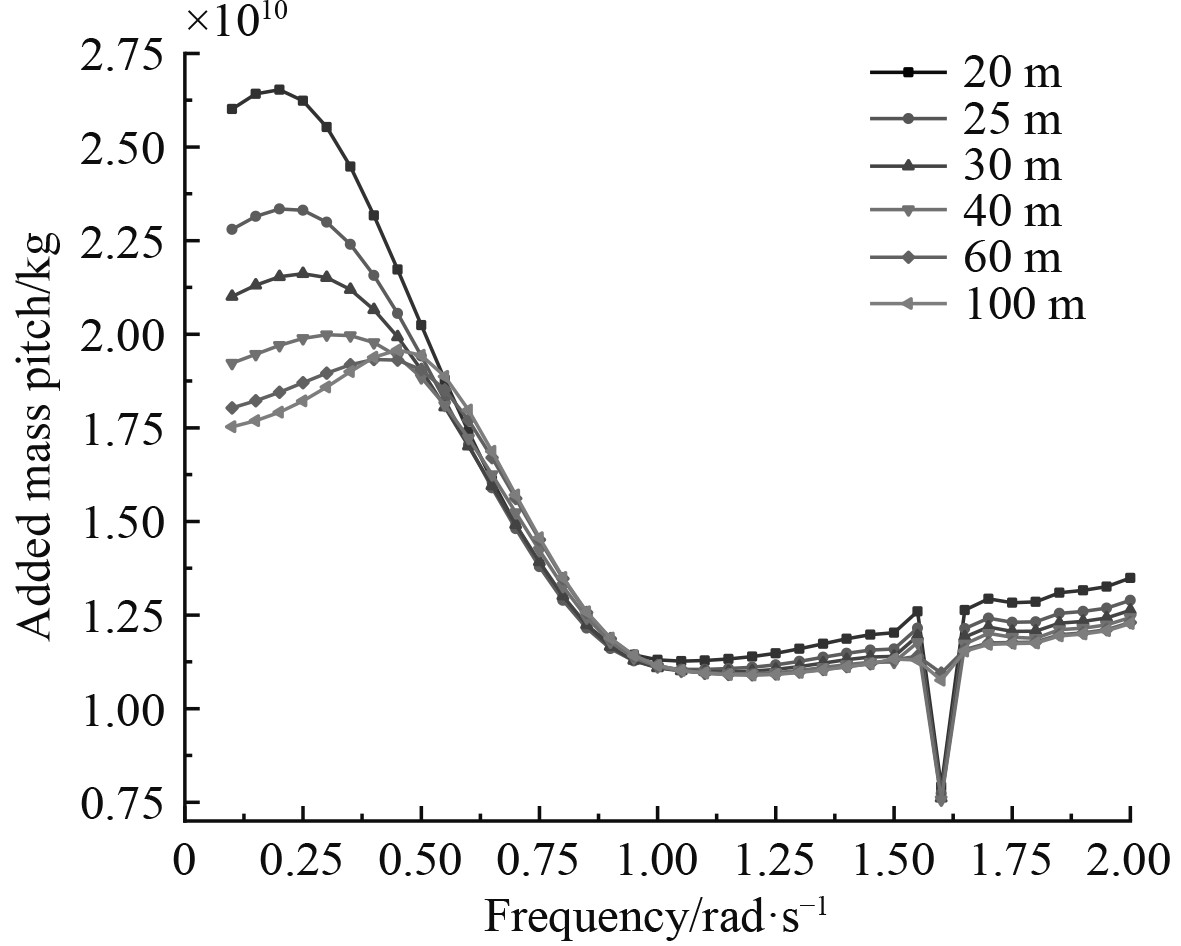
由图7~图9可知,对于角位移(横摇、纵摇和首摇)的3个附加质量,在纵摇方向最大,在横摇方向最小,并且在低频范围内都有峰值出现。

|
图 7 附加质量M44随频率变化曲线 Fig. 7 Additional mass M44 varies with frequency |
|
图 8 附加质量M55随频率变化曲线 Fig. 8 Additional mass M55 varies with frequency |

|
图 9 附加质量M66随频率变化曲线 Fig. 9 Additional mass M66 varies with frequency |
当处于低频范围时,附加质量会随海水深度的减小而增大,且随着水深差值越来越大,其附加质量的差值越来越小。但在高频范围内,附加质量值几乎不随深度变化而变化,趋于稳定。
|
图 10 辐射阻尼C11随频率变化的曲线 Fig. 10 Radiation damping C11 curve with frequency |
|
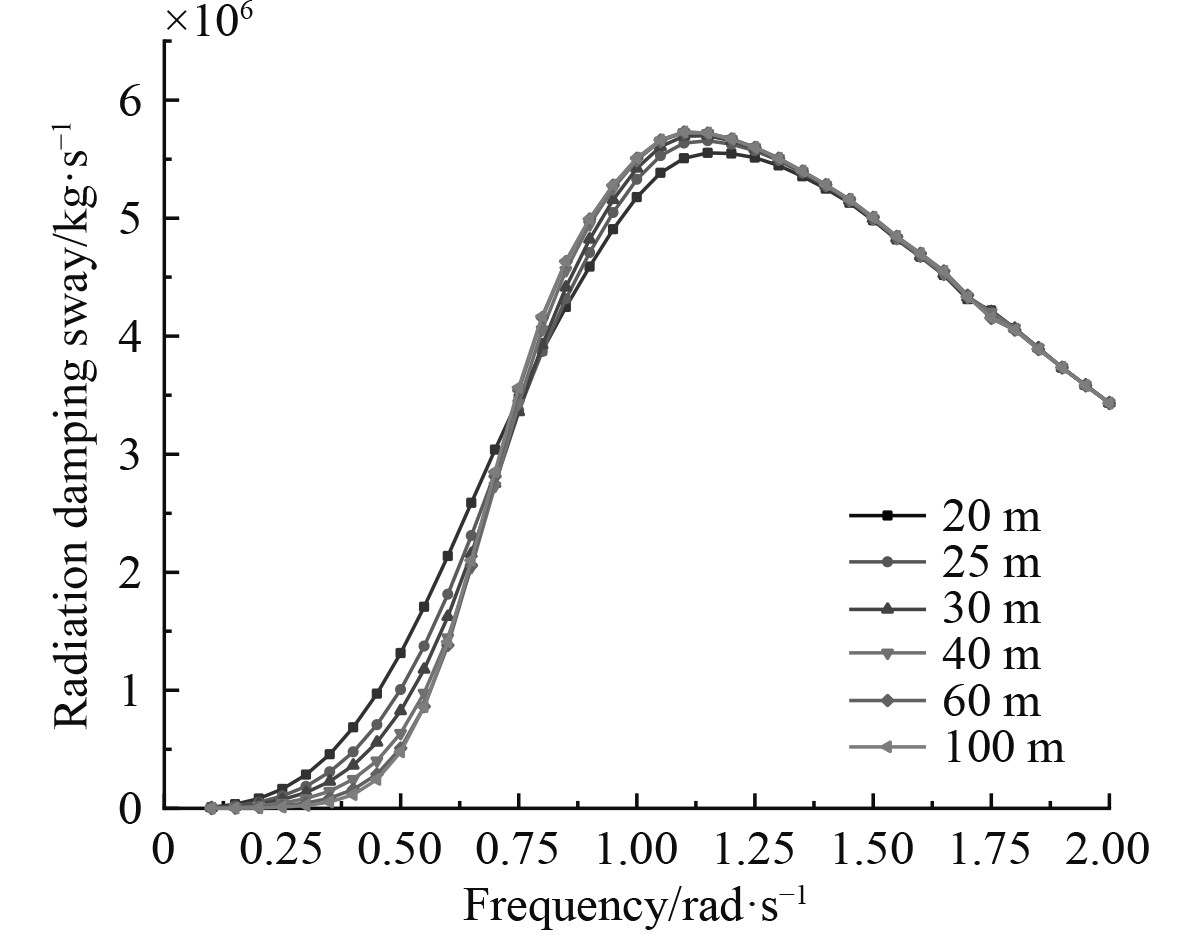
图 11 辐射阻尼C22随频率变化的曲线 Fig. 11 Radiation damping C22 curve with frequency |
|
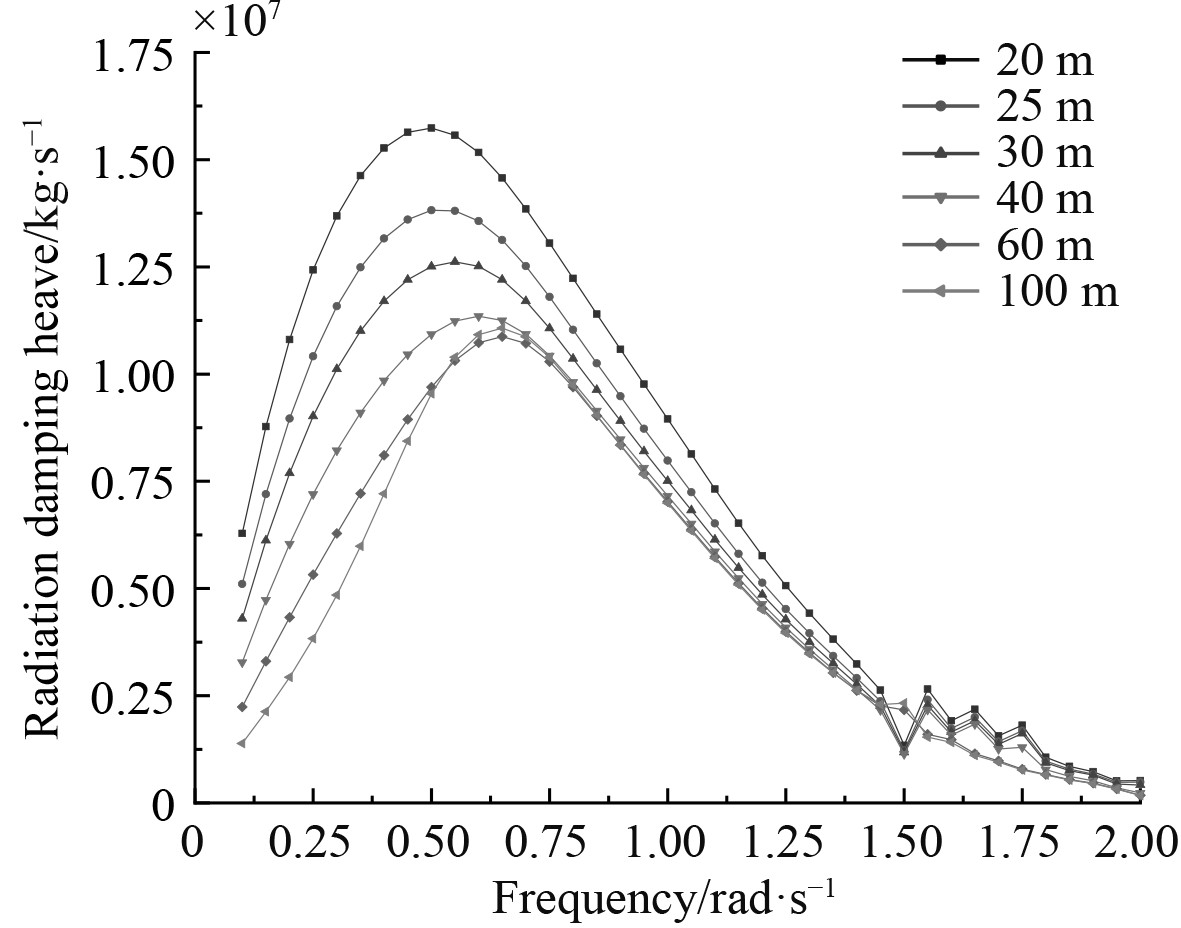
图 12 辐射阻尼C33随频率变化的曲线 Fig. 12 Radiation damping C33 curve with frequency |

|
图 13 辐射阻尼C44随频率变化的曲线 Fig. 13 Radiation damping C44 curve with frequency |
|
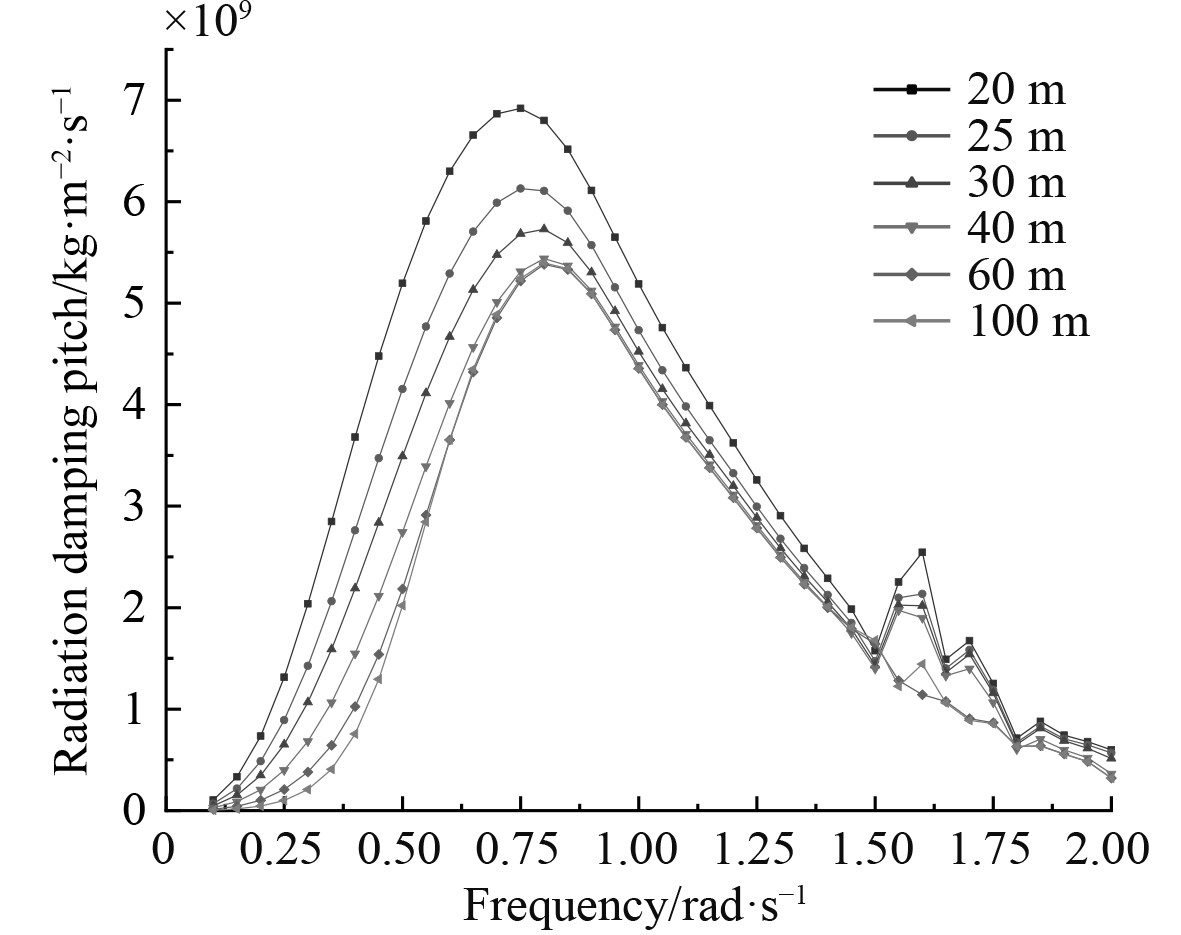
图 14 辐射阻尼C55随频率变化的曲线 Fig. 14 Radiation damping C55 curve with frequency |
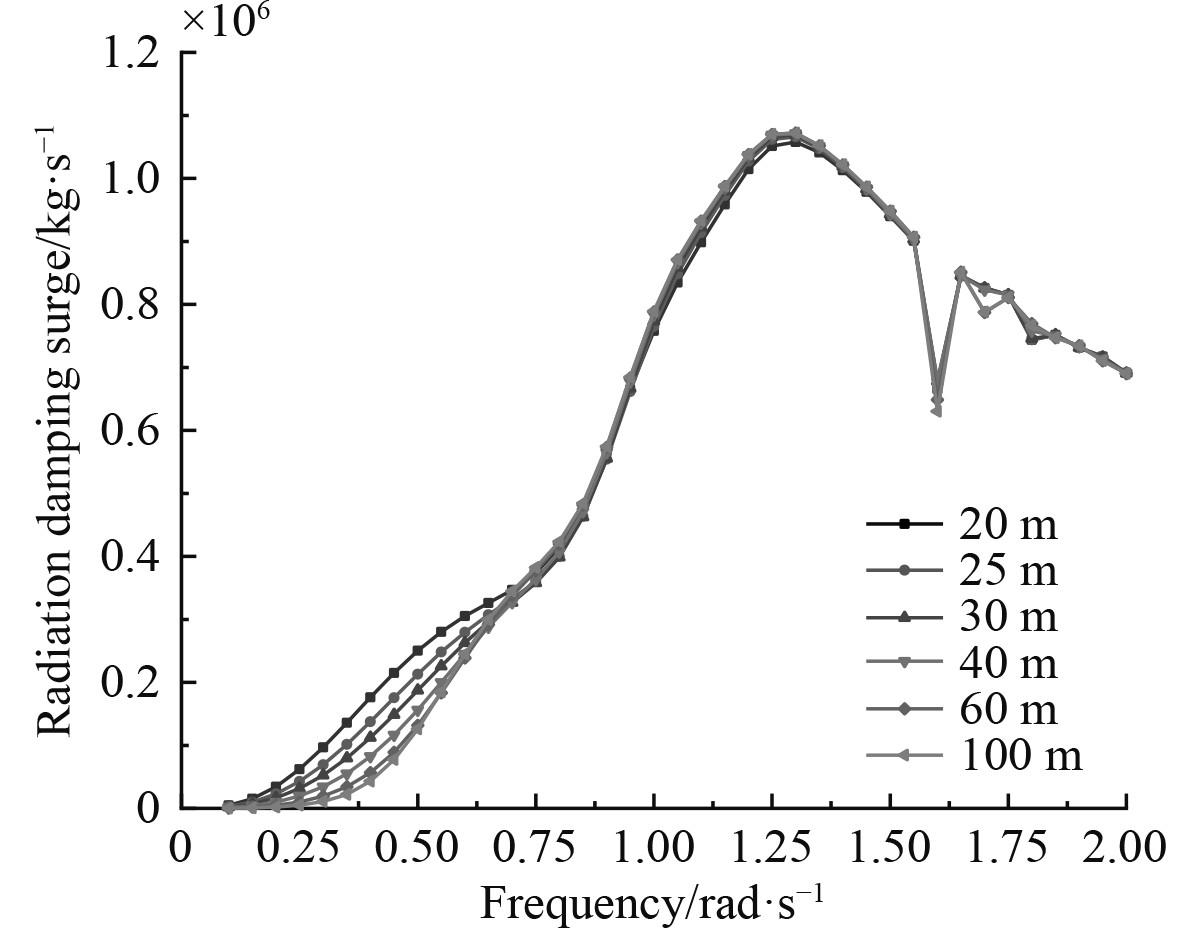
与附加质量的值类似,对于线位移(纵荡、横荡和垂荡)的3个辐射阻尼,垂荡值大于横荡值大于纵荡值;对于角位移(横摇、纵摇和首摇)的3个辐射阻尼,纵摇值大于首摇值大于横摇值,并且在整个过程中都有峰值出现。
当在低频范围内,辐射阻尼会随水深的减小而增大,并且增速较快。在频率达到0.75~1.25 rad/s范围内,6个自由度的辐射阻尼值均出现了峰值;当在高频范围内,6个自由度的辐射阻尼值下降,并且几乎不受海水深度的变化而变化。
4.2 航速对起重船的运动响应分析在规则波作用下,船体的频域运动响应方程为:
| $ [M(s) + M(a)]\ddot X + C\dot X + K(s)X = F 。$ | (19) |
式中:
在规则波中,通常会将运动响应
| $\begin{split} [M(s) + &M(a)]({X_0}{e^{ - i\omega t}})'' + C({X_0}{e^{ - i\omega t}})' + \\ &K(s)({X_0}{e^{ - i\omega t}}) = {F_0}{e^{ - i\omega t}}。\end{split}$ | (20) |
引入
| $ H = {\left\{ {K(s) - [M(s) + M(a)]{\omega ^2} - iC\omega } \right\}^{ - 1}} ,$ | (21) |
可得:
| $ {X_0} = H{F_0} 。$ | (22) |
式中:
在Aqwa-Line计算中,通常以船体的重心为基础,根据船体重心处以及船体上任意坐标到重心的位置矢量,可得出船体任一点的RAOs,即
| $ {X_p} = T \cdot {X_g}。$ | (23) |
式中:
根据文献[11]得知,横向海流载荷对起重船的冲击力较大(见图16),故将给定不同的航速(0.5 m/s,1.0 m/s,2.0 m/s),调用Aqwa-Line模块对起重船进行了运动响应分析(RAOs),计算结果如图17~图22所示。

|
图 16 船体在横向波浪中的示意图 Fig. 16 Schematic diagram of the hull in lateral waves |

|
图 17 纵荡RAO Fig. 17 Surge RAO |
|
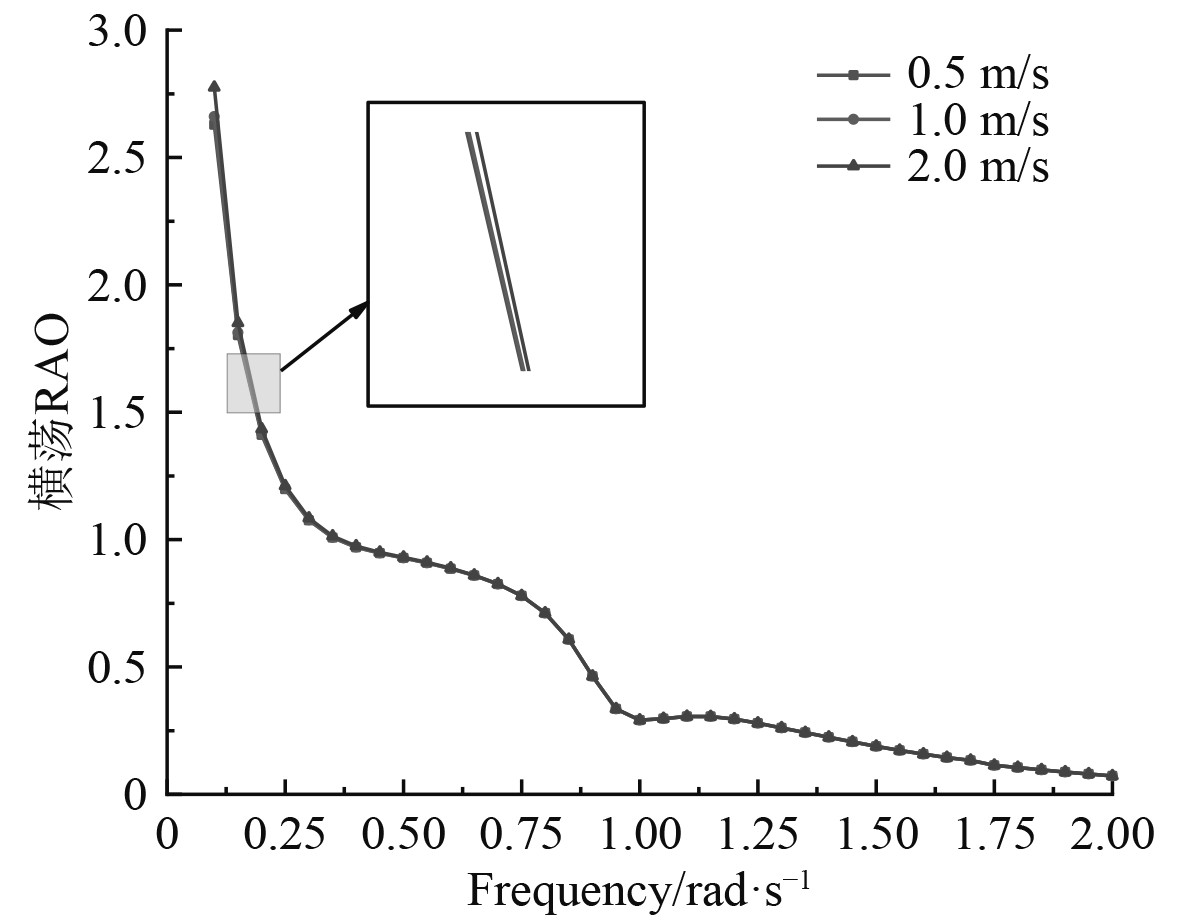
图 18 横荡RAO Fig. 18 Sway RAO |
|
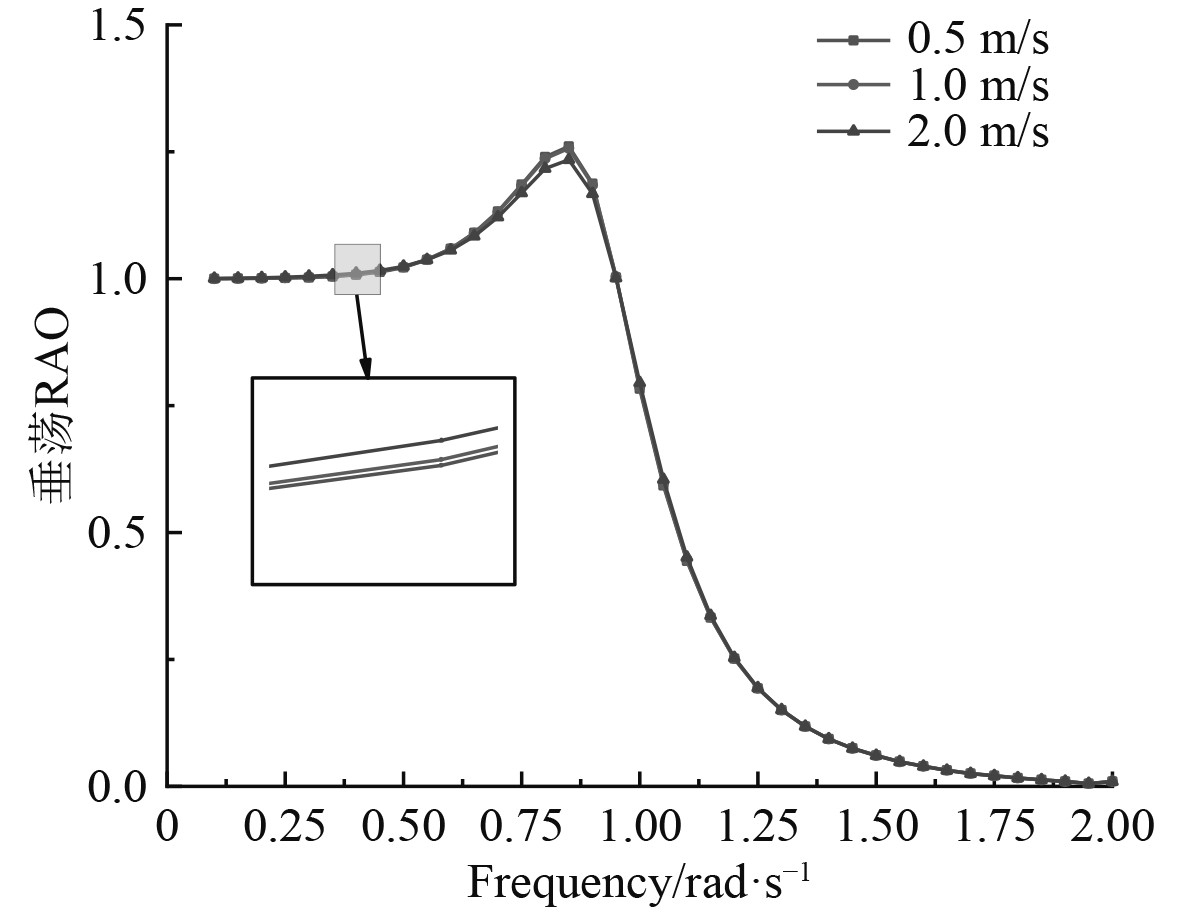
图 19 垂荡RAO Fig. 19 Heave RAO |
|
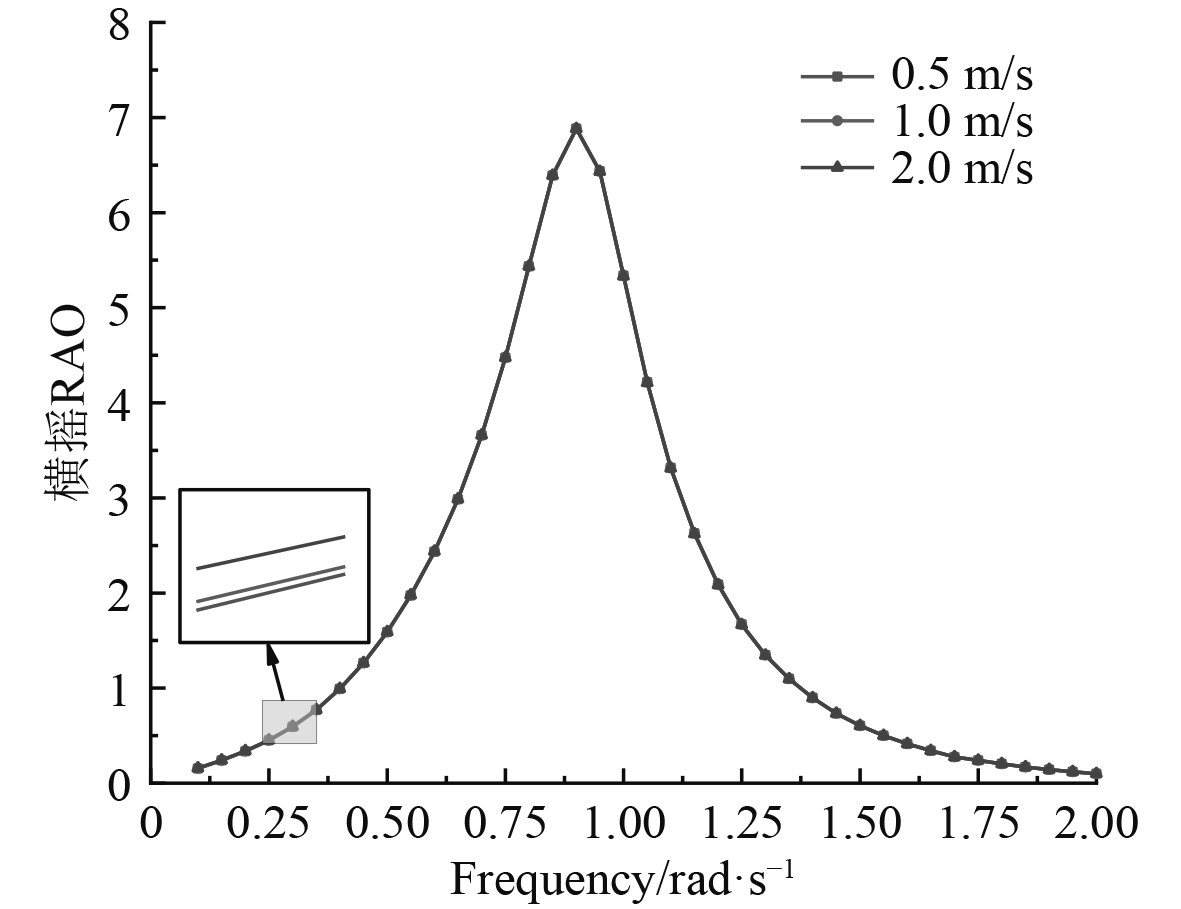
图 20 横摇RAO Fig. 20 Roll RAO |
|
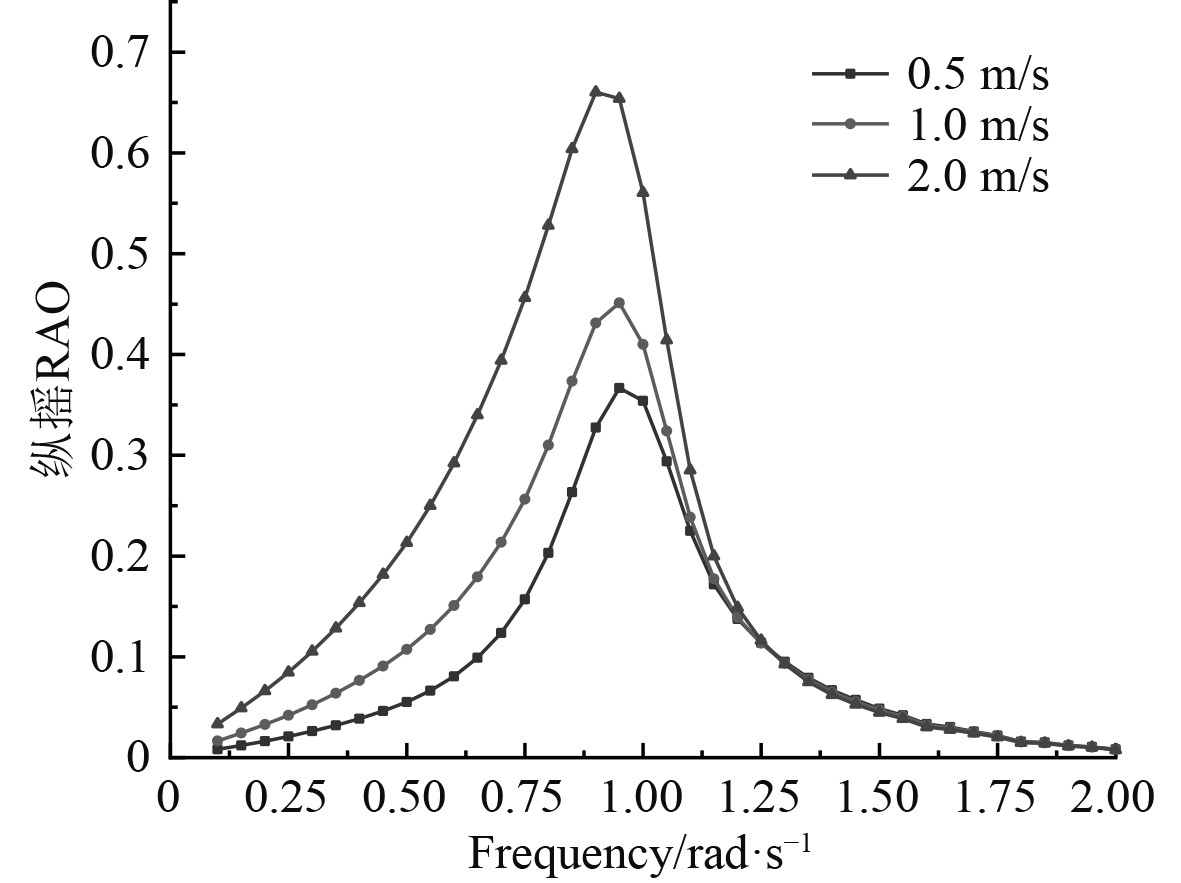
图 21 纵摇RAO Fig. 21 Pitch RAO |
|
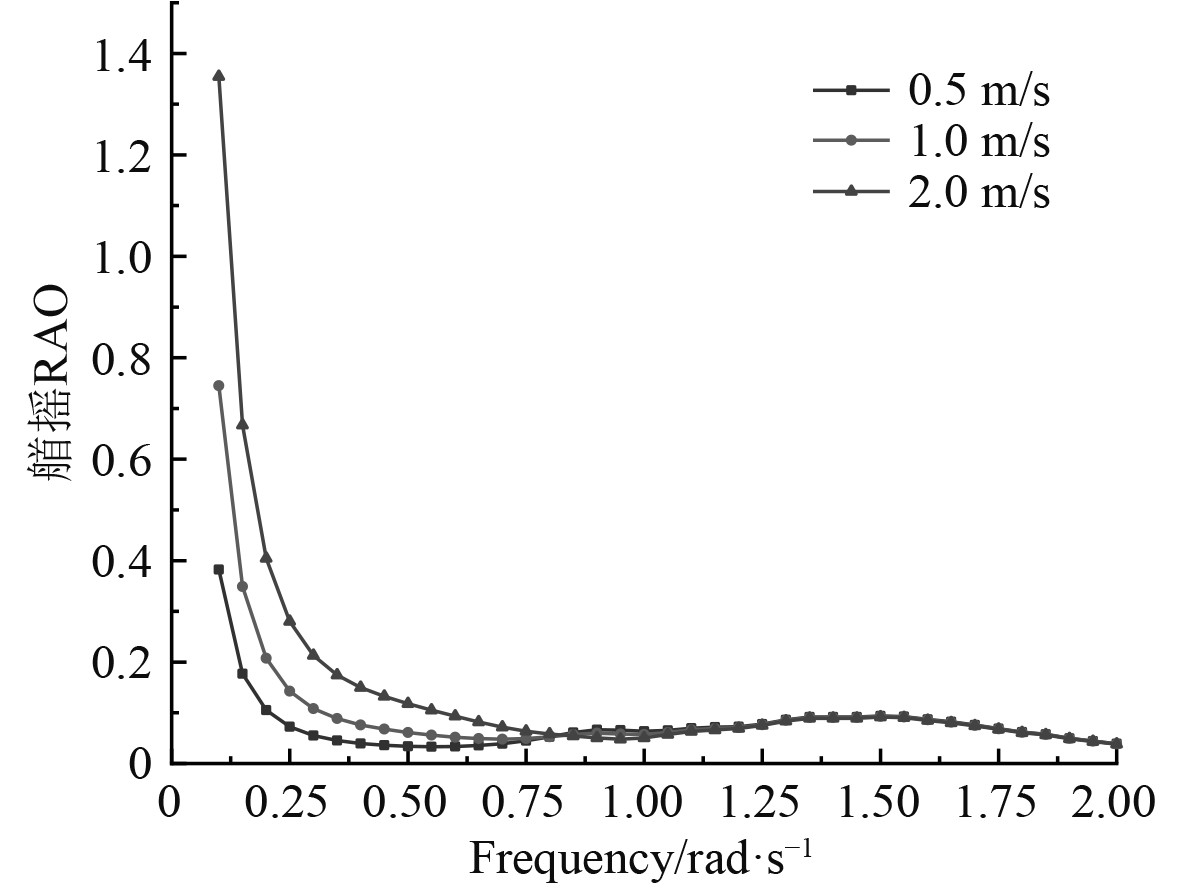
图 22 首摇RAO Fig. 22 Yaw RAO |
可以看出,横向流速对横摇影响最大,在频率介于0.75 ~1.0 rad/s之间出现了峰值,而对横荡的影响次之,并且随着频率的增大,横荡响应值逐渐减小。
相比之下,在横向海流载荷下不同航速对船体产生的影响不是很明显,横荡和首摇的运动幅值随频率的增加快速下降到最小值,而其他4个自由度的运动幅值在整个阶段都出现了峰值。当处于低频范围内,六自由度的运动幅值随着航速的增加而增大,但在高频范围内纵荡最为特殊,出现了二次峰值,随着航速增加,纵荡运动幅值反而减小。
可知,在横向海流载荷作用下,不同航速对船体本身影响较小,在频率介于0.75~1.0 rad/s之间时,横向海流载荷对起重船影响最大,在工作中尽量避免。
5 结 语本文利用Aqwa水动力分析软件研究了起重船在海流载荷作用下的运动响应问题,给出了不同海水深度下的附加质量、辐射阻尼变化曲线图,并且分析了横向海流载荷下的不同航速对起重船的影响。结果表明:
1)假设流体运动是无旋的,在规则波作用下船体上会产生流的分离,进而出现与流体粘性性质有关的阻力,故在计算过程中以8%的临界阻尼作为粘性阻尼修正量,使得计算结果较为接近真实情况。
2)除了入射波频率以及B/T以外,海水深度也是影响附加质量和辐射阻尼的重要因素,尤其在低频区域内更加显著,随着海水深度的增大起重船的附加质量和辐射阻尼反而减小。
3)起重船在横向海流载荷下工作时,对横摇的影响最大,尤其频率介于0.75 ~1.0 rad/s之间最危险。并且不同航速对起重船的动态稳定性略有影响,随着航速的增加而增大。因此在起重船航行作业时,应低速且尽量避开危险频率区间。
| [1] |
王言英, 李芳. 浮式结构物在波浪中的运动响应计算[J]. 水动力学研究与进展, 1995(6): 571-580. WANG Yan-ying, LI Fang. Calculation of motion response for floating structures in waves[J]. Journal of Hydrodynamics, 1995(6): 571-580. |
| [2] |
LI L. Numerical seakeeping predictions of shallow water effect on two ship interactions in waves[D]. Halifax, Nova Scotia: Dalhousie University, 2001.
|
| [3] |
谢永和, 李润培, 舒志. 有限水深复合格林函数的数值计算[J]. 船舶力学, 2005(1): 23-28. XIE Yong-he, LI Run-pei, SHU Zhi. Numerical calculation of finite water-depth composite Green function[J]. Journal of Ship Mechanics, 2005(1): 23-28. DOI:10.3969/j.issn.1007-7294.2005.01.004 |
| [4] |
刘日明, 任慧龙, 李辉. 有限水深格林函数及其导数的改进Gauss-Laguerre算法[J]. 船舶力学, 2008, 12(2): 188-196. LIU Ri-ming, REN Hui-long, LI Hui. An improved Gauss- Laguerr e method for finite water depth Gr een function and its derivatives[J]. Journal of Ship Mechanics, 2008, 12(2): 188-196. |
| [5] |
杨鹏, 寇冠元, 朱学康, 等. 浮体浅水波浪载荷数值计算方法研究[J]. 中国舰船研究, 2019, 14(1): 19-26. YANG Peng, KOU Guang-yuan, ZHU Xue-kang, et al. Numerical calculation method for wave loads of floating structures in shallow water[J]. Chinese Journal of Ship Research, 2019, 14(1): 19-26. DOI:10.19693/j.issn.1673-3185.01346 |
| [6] |
DING N, YU J X. Nonlinear optimization method of ship floating condition calculation in wave based on vector[J]. China Ocean Engineering, 2014, 28(4): 471-478. DOI:10.1007/s13344-014-0038-z |
| [7] |
CHEN Chen. Case study on wave-current interaction and its effects on ship navigation[J]. Journal of Hydrodynamics, 2018, 30(3): 411-419. DOI:10.1007/s42241-018-0050-5 |
| [8] |
陈剑文. 波浪载荷作用下浮式栈桥水动力及运动响应特性研究[D]. 镇江: 江苏科技大学, 2014.
|
| [9] |
戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007.
|
| [10] |
王树青, 梁丙臣. 海洋工程波浪力学[M]. 青岛: 中国海洋大学出版社, 2013.
|
| [11] |
孙为本. 大吨位起重船刚柔耦合动态性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.
|
 2022, Vol. 44
2022, Vol. 44
